Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T03:28:18.735Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke characters associated to Drinfeld modular forms

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 June 2015

Gebhard Böckle  and
Tommaso Centeleghe
Gebhard Böckle
Affiliation:
Universität Heidelberg, IWR, Im Neuenheimer Feld 368, 69120 Heidelberg, Germany email gebhard.boeckle@iwr.uni-heidelberg.de
Tommaso Centeleghe
Affiliation:
Universität Heidelberg, IWR, Im Neuenheimer Feld 368, 69120 Heidelberg, Germany email jupitert@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we explain how the results in our previous article on ‘algebraic Hecke characters and compatible systems of mod 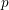$p$ Galois representations over global fields’ allow one to attach a Hecke character to every cuspidal Drinfeld modular eigenform from its associated crystal that was constructed in earlier work of the author. On the technical side, we prove along the way a number of results on endomorphism rings of ${\it\tau}$-sheaves and crystals. These are needed to exhibit the close relation between Hecke operators as endomorphisms of crystals on the one side and Frobenius automorphisms acting on étale sheaves associated to crystals on the other. We also present some partial results on the ramification of Hecke characters associated to Drinfeld modular eigenforms. An important phenomenon absent from the case of classical modular forms is that ramification can also result from places of modular curves of good but non-ordinary reduction. In an appendix, jointly with Centeleghe we prove some basic results on 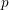$p$-adic Galois representations attached to 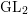$\text{GL}_{2}$-type cuspidal automorphic forms over global fields of characteristic 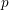$p$.

Keywords

Drinfeld modular formsGalois representationsHecke charactersramification𝜏-sheavesmodular Jacobiansp-divisible groups

MSC classification

Primary: 11F52: Modular forms associated to Drinfel'd modules 11F80: Galois representations
Secondary: 11R37: Class field theory 11R39: Langlands-Weil conjectures, nonabelian class field theory 11R58: Arithmetic theory of algebraic function fields 11F33: Congruences for modular and $p$-adic modular forms 11G09: Drinfel'd modules; higher-dimensional motives, etc.
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 11 , November 2015 , pp. 2006 - 2058
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, G. W., t-motives, Duke Math. J. 53 (1986), 457–502.CrossRefGoogle Scholar
Böckle, G., An Eichler–Shimura isomorphism over function fields between Drinfeld modular forms and cohomology classes of crystals, Preprint (2004), http://www.iwr.uni-heidelberg.de/groups/arith-geom/boeckle/EiShNew.pdf.Google Scholar
Böckle, G., Algebraic Hecke characters and compatible systems of abelian mod p Galois representations over global fields, Manuscripta Math. 140 (2013), 303–331.CrossRefGoogle Scholar
Böckle, G., Cohomological theory of crystals over function fields and applications, in Arithmetic Geometry Over Global Function Fields, Advanced Courses in Mathematics, CRM Barcelona, eds Bars, F., Longhi, I. and Trihan, F. (Birkhäuser/Springer, Basel, 2014).CrossRefGoogle Scholar
Böckle, G. and Pink, R., Cohomological theory of crystals over function fields, EMS Tracts in Mathematics, vol. 5 (European Mathematical Society, Zürich, 2009).CrossRefGoogle Scholar
Borel, A. and Jacquet, H., Automorphic forms and automorphic representations, in Automorphic forms, representations and L-functions, Part 1, Symposium in Pure Mathematics, Oregon State University, 1977, Proceedings of Symposia in Pure Mathematics, vol. 33, eds Borel, A. and Casselman, W. (American Mathematical Society, Providence, RI, 1979), 189–202.Google Scholar
Bosch, S. and Lütkebohmert, W., Degenerating abelian varieties, Topology 30 (1991), 653–698.CrossRefGoogle Scholar
Bushnell, C. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften, vol. 335 (Springer, Berlin, 2006).CrossRefGoogle Scholar
Casselman, W., On some results of Atkin and Lehner, Math. Ann. 201 (1973), 301–314.CrossRefGoogle Scholar
Chai, C.-L., Conrad, B. and Oort, F., Complex multiplication and lifting problems, Mathematical Surveys and Monographs, vol. 195 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Conrad, B., Modular forms and the Ramanujan conjecture, http://math.stanford.edu/∼conrad/papers/rambook.pdf.Google Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids 1, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530.CrossRefGoogle Scholar
Drinfeld, V. G., Elliptic modules, Math. USSR-Sb. 23 (1976), 561–592.CrossRefGoogle Scholar
Drinfeld, V. G., Moduli varieties of F-sheaves, Funct. Anal. Appl. 21 (1987), 107–122.CrossRefGoogle Scholar
Flath, D., Decomposition of representations into tensor products, in Automorphic forms, representations and L-functions, Part 1, Symposium in Pure Mathematics, Oregon State University, 1977, Proceedings of Symposia in Pure Mathematics, vol. 33, eds Borel, A. and Casselman, W. (American Mathematical Society, Providence, RI, 1979), 179–183.Google Scholar
Gardeyn, F., $t$-motives and Galois representations, PhD thesis, Universiteit Gent (2001),http://www.math.ethz.ch/∼pink/Theses/2001-Doctor-Francis-Gardeyn.pdf.Google Scholar
Gekeler, E.-U., Drinfeld-Moduln und modulare Formen über rationalen Funktionenkörpern, Bonner Mathematische Schriften, vol. 119 (University of Bonn, 1980).Google Scholar
Gekeler, E.-U., Drinfeld modular curves, Lecture Notes in Mathematics, vol. 1231 (Springer, Berlin–New York, 1986).CrossRefGoogle Scholar
Gekeler, E.-U., On the coefficients of Drinfeld modular forms, Invent. Math. 93 (1988), 667–700.CrossRefGoogle Scholar
Gekeler, E.-U. and Reversat, M., Jacobians of Drinfeld modular curves, J. Reine Angew. Math. 476 (1996), 27–93.Google Scholar
Gerritzen, L. and van der Put, M., Schottky groups and Mumford curves, Lecture Notes in Mathematics, vol. 817 (Springer, Berlin–Heidelberg–New York, 1980).CrossRefGoogle Scholar
Goss, D., Modular forms for Fr, J. Reine Angew. Math. 317 (1980), 16–39.Google Scholar
Goss, D., 𝜋-adic Eisenstein series for function fields, Compositio Math. 41 (1980), 3–38.Google Scholar
Goss, D., The algebraist’s upper half-plane, Bull. Amer. Math. Soc. (N.S.) 2 (1980), 391–415.CrossRefGoogle Scholar
Goss, D., L-series of Grössencharakters of type A 0 for function fields, in p-adic methods in number theory and algebraic geometry, Contemporary Mathematics, vol. 133 (American Mathematical Society, Providence, RI, 1992), 119–139.Google Scholar
Gross, B., Algebraic Hecke characters for function fields, in Seminar on number theory (Paris 1980–81), Progress in Mathematics, vol. 22 (Birkhäuser, Boston, MA, 1982), 87–90.Google Scholar
de Jong, A. J., Homomorphisms of Barsotti–Tate groups and crystals in positive characteristic, Invent. Math. 134 (1998), 301–333 (Erratum, Invent. Math. 138 (1999) 225).CrossRefGoogle Scholar
Katz, N., p-adic properties of modular schemes and modular varieties, in Modular functions of one variable III, Lecture Notes in Mathematics, vol. 350 (Springer, Berlin, 1973), 69–191.CrossRefGoogle Scholar
Katz, N., Slope filtrations of F-crystals, in Journées de Géométrie Algébrique de Rennes (Rennes, 1978), Vol. I), Astérisque, vol. 63 (Soc. Math. France, Paris, 1979), 113–163.Google Scholar
Katz, N. and Mazur, B., Arithmetic moduli of elliptic curves, Annals of Mathematical Studies, vol. 108 (Princeton University, Princeton, NJ, 1985).CrossRefGoogle Scholar
Khare, C., Reciprocity law for compatible systems of abelian mod p Galois representations, Canad. J. Math. 57 (2005), 1215–1223.CrossRefGoogle Scholar
Li, W.-C. W. and Meemark, Y., Hecke operators on Drinfeld cusp forms, J. Number Theory 128 (2008), 1941–1965.CrossRefGoogle Scholar
Mumford, D., Abelian varieties (Oxford University Press, Oxford, 1970).Google Scholar
Nakajima, S., p-ranks and automorphism groups of algebraic curves, Trans. Amer. Math. Soc. 303 (1987), 595–607.Google Scholar
Piatetski-Shapiro, I. I., Multiplicity one theorems, in Automorphic forms, representations and L-functions, Part 1, Symposium in Pure Mathematics, Oregon State University, 1977, Proceedings of Symposia in Pure Mathematics, vol. 33, eds Borel, A. and Casselman, W. (American Mathematical Society, Providence, RI, 1979), 209–212.Google Scholar
Pink, R., Euler–Poincaré formula in equal characteristic under ordinariness assumptions, Manuscripta Math. 102 (2000), 1–24.CrossRefGoogle Scholar
Pink, R., Compactification of Drinfeld modular varieties and Drinfeld modular forms of arbitrary rank, Manuscripta Math. 140 (2013), 333–361.CrossRefGoogle Scholar
van der Put, M. and Reversat, M., Automorphic forms and Drinfeld’s reciprocity law, in Drinfeld modules, modular schemes and applications (Alden-Biesen, 1996) (World Scientific Publishers, River Edge, NJ, 1997), 188–223.Google Scholar
Ribet, K. A., Galois representations attached to eigenforms with Nebentypus, in Modular functions of one variable V, Lecture Notes in Mathematics, vol. 601 (Springer, Berlin, 1977), 17–51.Google Scholar
Ribet, K. A., Abelian varieties over ℚ and modular forms, in Algebra and topology 1992 (Taejŏn) (Korea Advanced Institute of Science and Technology, Taejŏn, 1992), 53–79.Google Scholar
Rosen, M., Number theory in function fields, Graduate Texts in Mathematics, vol. 210 (Springer, New York, 2002).CrossRefGoogle Scholar
Scholl, A. J., Motives for modular forms, Invent. Math. 100 (1990), 419–430.CrossRefGoogle Scholar
Serre, J.-P., Abelian ℓ-adic representations and elliptic curves, McGill University Lecture Notes (W. A. Benjamin Inc., New York–Amsterdam, 1968).Google Scholar
Deligne, P., Séminaire de géométrie algébrique du Bois Marie – Cohomologie étale – $(SGA4{\textstyle \frac{1}{2}})$, Lecture Notes in Mathematics, vol. 569 (Springer, Berlin–New York, 1977).CrossRefGoogle Scholar
Serre, J.-P. and Tate, J., Good reduction of abelian varieties, Ann. of Math. (2) 88 (1968), 492–517.CrossRefGoogle Scholar
Taguchi, Y. and Wan, D., L-functions of 𝜙-sheaves and Drinfeld modules, J. Amer. Math. Soc. 9 (1996), 755–781.CrossRefGoogle Scholar
Tate, J., p-divisible groups, inProceedings of a conference on local fields (Driebergen, 1966) (Springer, Berlin, 1967).Google Scholar
Wiles, A., On p-adic representations for totally real fields, Ann. of Math. (2) 123 (1986), 407–456.CrossRefGoogle Scholar
Yang, Y., An improvement of de Jong Oort’s purity theorem, Münster J. Math. 4 (2011), 129–140.Google Scholar
Zarhin, Ju. G., Endomorphisms of Abelian varieties over fields of finite characteristic, Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 272–277, 471.Google Scholar
Zink, T., On the slope filtration, Duke Math. J. 109 (2001), 79–95.CrossRefGoogle Scholar