Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T09:28:01.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral canonical models for Spin Shimura varieties

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  07 December 2015

Keerthi Madapusi Pera
Keerthi Madapusi Pera*
Affiliation:
Department of Mathematics, 1 Oxford St, Harvard University, Cambridge, MA 02118, USA email keerthi@math.harvard.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

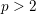We construct regular integral canonical models for Shimura varieties attached to Spin and orthogonal groups at (possibly ramified) primes $p>2$ where the level is not divisible by 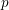$p$. We exhibit these models as schemes of ‘relative PEL type’ over integral canonical models of larger Spin Shimura varieties with good reduction at 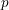$p$. Work of Vasiu–Zink then shows that the classical Kuga–Satake construction extends over the integral models and that the integral models we construct are canonical in a very precise sense. Our results have applications to the Tate conjecture for K3 surfaces, as well as to Kudla’s program of relating intersection numbers of special cycles on orthogonal Shimura varieties to Fourier coefficients of modular forms.

Keywords

Shimura varietiesintegral canonical modelsSpin groups

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 4 , April 2016 , pp. 769 - 824
Copyright
© The Author 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baily, W. L. Jr. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains, Ann. of Math. (2) 84 (1966), 442–528; MR 0216035 (35 #6870).Google Scholar
Bass, H., Clifford algebras and spinor norms over a commutative ring, Amer. J. Math. 96 (1974), 156–206; MR 0360645 (50 #13092).CrossRefGoogle Scholar
Berthelot, P. and Messing, W., Théorie de Dieudonné cristalline. III. Théorèmes d’équivalence et de pleine fidélité, in The Grothendieck Festschrift, vol. I, Progress in Mathematics, vol. 86 (Birkhäuser, Boston, MA, 1990), 173–247; (in French); MR 1086886 (92h:14012).Google Scholar
Blasius, D., A p-adic property of Hodge classes on abelian varieties, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55 (American Mathematical Society, Providence, RI, 1994), 293–308; MR 1265557 (95j:14022).Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre (Springer, Berlin, 2007), ch. 5 (in French); reprint of the 1959 original; MR 2325344 (2008f:15001).Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376 (in French); MR 756316 (86c:20042).Google Scholar
Chai, C.-L. and Norman, P., Bad reduction of the Siegel moduli scheme of genus two with Γ0(p)-level structure, Amer. J. Math. 112 (1990), 1003–1071, doi:10.2307/2374734;MR 1081813 (91i:14033).Google Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques, in Automorphic Forms, Representations and L-functions (Proc. Symp. Pure Math., Oregon State Univ., Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 247–289 (in French); MR 546620 (81i:10032).Google Scholar
Deligne, P., Relèvement des surfaces K3 en caractéristique nulle, in Algebraic surfaces (Orsay, 1976), Lecture Notes in Mathematics, vol. 868 (Springer, Berlin, 1981), 58–79 (in French); prepared for publication by Luc Illusie; MR 638598 (83j:14034).Google Scholar
Deligne, P., Milne, J. S., Ogus, A. and Shih, K.-Y., Hodge Cycles, Motives, and Shimura Varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1982); MR 654325 (84m:14046).Google Scholar
Deligne, P. and Pappas, G., Singularités des espaces de modules de Hilbert, en les caractéristiques divisant le discriminant, Compositio Math. 90 (1994), 59–79 (in French); MR 1266495 (95a:11041).Google Scholar
Faltings, G., Integral crystalline cohomology over very ramified valuation rings, J. Amer. Math. Soc. 12 (1999), 117–144, doi:10.1090/S0894-0347-99-00273-8; MR 1618483 (99e:14022).Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 22 (Springer, Berlin, 1990), with an appendix by David Mumford; MR 1083353 (92d:14036).Google Scholar
Görtz, U., On the flatness of local models for the symplectic group, Adv. Math. 176 (2003), 89–115, doi:10.1016/S0001-8708(02)00062-2; MR 1978342 (2004d:14023).Google Scholar
Harris, M., Arithmetic vector bundles and automorphic forms on Shimura varieties. I, Invent. Math. 82 (1985), 151–189, doi:10.1007/BF01394784; MR 808114 (88e:11046).Google Scholar
Harris, M., Arithmetic of the oscillator representation,www.math.jussieu.fr/∼harris/Arithmetictheta.pdf.Google Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, in Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, 1972), Lecture Notes in Mathematics, vol. 350 (Springer, Berlin, 1973), 69–190; MR 0447119 (56 #5434).Google Scholar
Katz, N. M., Slope filtration of F-crystals, in Journées de géométrie algébrique de Rennes, (Rennes, 1978), Astérisque, vol. 63 (Société Mathématiques de France, Paris, 1979), 113–163; MR 563463 (81i:14014).Google Scholar
Katz, N., Serre–Tate local moduli, in Algebraic surfaces (Orsay, 1976), Lecture Notes in Mathematics, vol. 868 (Springer, Berlin, 1981), 138–202; MR 638600 (83k:14039b).Google Scholar
Kisin, M., Integral models for Shimura varieties of abelian type, J. Amer. Math. Soc. 23 (2010), 967–1012, doi:10.1090/S0894-0347-10-00667-3; MR 2669706 (2011j:11109).CrossRefGoogle Scholar
Kudla, S. S., Algebraic cycles on Shimura varieties of orthogonal type, Duke Math. J. 86 (1997), 39–78, doi:10.1215/S0012-7094-97-08602-6; MR 1427845 (98e:11058).Google Scholar
Kudla, S. S. and Rapoport, M., Arithmetic Hirzebruch–Zagier cycles, J. reine angew. Math. 515 (1999), 155–244, doi:10.1515/crll.1999.076; MR 1717613 (2002e:11076a).Google Scholar
Kudla, S. S., Rapoport, M. and Yang, T., Modular Forms and Special Cycles on Shimura Curves, Annals of Mathematics Studies, vol. 161 (Princeton University Press, Princeton, NJ, 2006); MR 2220359 (2007i:11084).Google Scholar
Laffaille, G., Groupes p-divisibles et modules filtrés: le cas peu ramifié, Bull. Soc. Math. France 108 (1980), 187–206 (in French, with English summary); MR 606088 (82i:14028).Google Scholar
Lan, K.-W., Arithmetic compactifications of PEL-type Shimura varieties, PhD thesis, Harvard University, ProQuest LLC, Ann Arbor, MI (2008); MR 2711676.Google Scholar
Madapusi Pera, K., The Tate conjecture for K3 surfaces in odd characteristic, Invent. Math. 201 (2014), 625–668, doi:10.1007/s00222-014-0557-5.Google Scholar
Madapusi Pera, K., Toroidal compactifications of integral models of Shimura varieties of Hodge type, Preprint (2015), pp. 98, available at:http://www.math.uchicago.edu/∼keerthi/papers/toroidal.pdf.Google Scholar
Madapusi Sampath, K. S., Toroidal compactifications of integral models of Shimura varieties of Hodge type, PhD thesis, The University of Chicago, ProQuest LLC, Ann Arbor, MI (2011);MR 2898617.Google Scholar
Manin, Ju. I., On the classification of formal Abelian groups, Dokl. Akad. Nauk SSSR 144 (1962), 490–492 (in Russian); MR 0162802 (29 #106).Google Scholar
Maulik, D., Supersingular K3 surfaces for large primes, Duke Math. J. 163 (2014), 2357–2425, doi:10.1215/00127094-2804783, with an appendix by Andrew Snowden; MR 3265555.CrossRefGoogle Scholar
Messing, W., The Crystals Associated to Barsotti–Tate Groups: with Applications to Abelian Schemes, Lecture Notes in Mathematics, vol. 264 (Springer, Berlin, 1972); MR 0347836 (50 #337).CrossRefGoogle Scholar
Moonen, B., Models of Shimura varieties in mixed characteristics, in Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996), London Mathematical Society Lecture Note Series, vol. 254 (Cambridge University Press, Cambridge, 1998), 267–350, doi:10.1017/CBO9780511662010.008; MR 1696489 (2000e:11077).Google Scholar
Ogus, A., Supersingular K3 crystals, in Journées de géométrie algébrique de Rennes (Rennes, 1978), Astérisque, vol. 64 (Société Mathématique de France, Paris, 1979), 3–86; MR 563467 (81e:14024).Google Scholar
Pappas, G., On the arithmetic moduli schemes of PEL Shimura varieties, J. Algebraic Geom. 9 (2000), 577–605; MR 1752014 (2001g:14042).Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Pure and Applied Mathematics, vol. 139 (Academic Press, Boston, MA, 1994), translated from the 1991 Russian original by Rachel Rowen; MR 1278263 (95b:11039).Google Scholar
Rapoport, M. and Zink, Th., Period Spaces for p-divisible Groups, Annals of Mathematics Studies, vol. 141 (Princeton University Press, Princeton, NJ, 1996); MR 1393439 (97f:14023).Google Scholar
Vasiu, A., Integral canonical models of Shimura varieties of preabelian type, Asian J. Math. 3 (1999), 401–518; MR 1796512 (2002b:11087).CrossRefGoogle Scholar
Vasiu, A., Integral models in unramified mixed characteristic (0,2) of hermitian orthogonal Shimura varieties of PEL type, Part II, Math. Nachr. 287 (2014), 1756–1773.CrossRefGoogle Scholar
Vasiu, A. and Zink, T., Purity results for p-divisible groups and abelian schemes over regular bases of mixed characteristic, Doc. Math. 15 (2010), 571–599; MR 2679067.CrossRefGoogle Scholar