Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T09:32:50.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Locality in the Fukaya category of a hyperkähler manifold

Part of: Global differential geometry Symplectic geometry, contact geometry

Published online by Cambridge University Press:  06 September 2019

Jake P. Solomon  and
Misha Verbitsky
Jake P. Solomon
Affiliation:
Institute of Mathematics, Hebrew University, Givat Ram, Jerusalem, Israel email jake@math.huji.ac.il
Misha Verbitsky
Affiliation:
Laboratory of Algebraic Geometry, National Research University HSE, Department of Mathematics, 7 Vavilova Str. Moscow, Russia email verbit@mccme.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 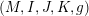$(M,I,J,K,g)$ be a hyperkähler manifold. Then the complex manifold 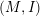$(M,I)$ is holomorphic symplectic. We prove that for all real 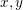$x,y$, with 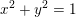$x^{2}+y^{2}=1$ except countably many, any finite-energy 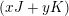$(xJ+yK)$-holomorphic curve with boundary in a collection of 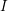$I$-holomorphic Lagrangians must be constant. By an argument based on the Łojasiewicz inequality, this result holds no matter how the Lagrangians intersect each other. It follows that one can choose perturbations such that the holomorphic polygons of the associated Fukaya category lie in an arbitrarily small neighborhood of the Lagrangians. That is, the Fukaya category is local. We show that holomorphic Lagrangians are tautologically unobstructed. Moreover, the Fukaya 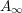$A_{\infty }$ algebra of a holomorphic Lagrangian is formal. Our result also explains why the special Lagrangian condition holds without instanton corrections for holomorphic Lagrangians.

Keywords

Floer cohomologyFukaya categoryholomorphic LagrangianhyperkählerlocalŁojasiewicz inequalitypseudoholomorphic mapreal analyticspecial Lagrangian

MSC classification

Primary: 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Secondary: 53C38: Calibrations and calibrated geometries 53D12: Lagrangian submanifolds; Maslov index 32B20: Semi-analytic sets and subanalytic sets
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 10 , October 2019 , pp. 1924 - 1958
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Instituto Nacional de Matemática Pura e Aplicada (IMPA), Estrada Dona Castorina, 110, Jardim Botânico, CEP 22460-320, Rio de Janeiro, RJ, Brasil

J.S. was partially supported by ERC starting grant 337560 and ISF Grant 1747/13. M.V. was partially supported by the Russian Academic Excellence Project ‘5-100’ and CNPq - Process 313608/2017-2.

References

Abouzaid, M. and Smith, I., The symplectic arc algebra is formal , Duke Math. J. 165 (2016), 985–1060.Google Scholar
Behrend, K. and Fantechi, B., Gerstenhaber and Batalin-Vilkovisky structures on Lagrangian intersections , in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. I, Progress in Mathematics, vol. 269 (Birkhäuser Boston, Boston, MA, 2009), 1–47.Google Scholar
Besse, A., Einstein manifolds (Springer, New York, NY, 1987).Google Scholar
Bierstone, E., Differentiable functions , Bol. Soc. Bras. Mat. 11 (1980), 139–189.Google Scholar
Bierstone, E. and Milman, P. D., Semianalytic and subanalytic sets , Publ. Math. Inst. Hautes Études Sci. 67 (1998), 5–42.Google Scholar
Brav, C., Bussi, V., Dupont, D., Joyce, D. and Szendroi, B., Symmetries and stabilization for sheaves of vanishing cycles , J. Singul. 11 (2015), 85–151.Google Scholar
Bridgeland, T., Stability conditions on triangulated categories , Ann. of Math. (2) 166 (2007), 317–345.Google Scholar
Bryant, R. L., Minimal Lagrangian submanifolds of Kähler–Einstein manifolds , in Differential geometry and differential equations, Shanghai, 1985, Lecture Notes in Mathematics, vol. 1255 (Springer, Berlin, 1987), 1–12.Google Scholar
Bussi, V., Categorification of Lagrangian intersections on complex symplectic manifolds using perverse sheaves of vanishing cycles, Preprint (2014), arXiv:1404.1329.Google Scholar
Colding, T. H. and Minicozzi, W. P. II, Uniqueness of blowups and Łojasiewicz inequalities , Ann. of Math. (2) 182 (2015), 221–285.Google Scholar
D’Agnolo, A. and Schapira, P., Quantization of complex Lagrangian submanifolds , Adv. Math. 213 (2007), 358–379.Google Scholar
Deligne, P., Griffiths, P., Morgan, J. and Sullivan, D., Real homotopy theory of Kähler manifolds , Invent. Math. 29 (1975), 245–274.Google Scholar
Douglas, M. R., Dirichlet branes, homological mirror symmetry, and stability , in Proceedings of the International Congress of Mathematicians, Vol. 3 (2002, Beijing), (Higher Education Press, Beijing, 2002), 395–408.Google Scholar
Floer, A., Morse theory for Lagrangian intersections , J. Differential Geom. 28 (1988), 513–547.Google Scholar
Fukaya, K., Cyclic symmetry and adic convergence in Lagrangian Floer theory , Kyoto J. Math. 50 (2010), 521–590.Google Scholar
Fukaya, K., Oh, Y.-G., Ohta, H. and Ono, K., Lagrangian intersection Floer theory: anomaly and obstruction, AMS/IP Studies in Advanced Mathematics, vol. 46, parts 1, 2 (American Mathematical Society/International Press, Providence, RI/Somerville, MA, 2009).Google Scholar
Fukaya, K., Oh, Y.-G., Ohta, H. and Ono, K., Anti-symplectic involution and Floer cohomology , Geom. Topol. 21 (2017), 1–106.Google Scholar
Gromov, M., Pseudoholomorphic curves in symplectic manifolds , Invent. Math. 82 (1985), 307–347.Google Scholar
Hardt, R. M., Some analytic bounds for subanalytic sets , in Differential geometric control theory, Houghton, MI, 1982, Progress in Mathematics, vol. 27 (Birkhäuser, Boston, MA, 1983), 259–267.Google Scholar
Harvey, R. and Lawson, B., Calibrated geometries , Acta Math. 148 (1982), 47–157.Google Scholar
Hirsch, M. W., Differential topology, Graduate Texts in Mathematics, vol. 33, corrected reprint of the 1976 original (Springer, New York, NY, 1997).Google Scholar
Hitchin, N. J., The self-duality equations on a Riemann surface , Proc. Lond. Math. Soc. (3) 55 (1987), 59–126.Google Scholar
Hofer, H., Wysocki, K. and Zehnder, E., Integration theory on the zero sets of polyfold Fredholm sections , Math. Ann. 346 (2010), 139–198.Google Scholar
Kapustin, A., Topological strings on noncommutative manifolds , Int. J. Geom. Methods Mod. Phys. 1 (2004), 49–81.Google Scholar
Kapustin, A., A-branes and noncommutative geometry, Preprint (2005),arXiv:hep-th/0502212.Google Scholar
Kapustin, A. and Witten, E., Electric-magnetic duality and the geometric Langlands program , Commun. Number Theory Phys. 1 (2007), 1–236.Google Scholar
Kashiwara, M. and Schapira, P., Constructibility and duality for simple holonomic modules on complex symplectic manifolds , Amer. J. Math. 130 (2008), 207–237.Google Scholar
Kashiwara, M. and Schapira, P., Deformation quantization modules , Astérisque 345 (2012).Google Scholar
Kurdyka, K., Mostowski, T. and Parusiński, A., Proof of the gradient conjecture of R. Thom , Ann. of Math. (2) 152 (2000), 763–792.Google Scholar
Łojasiewicz, S., Triangulation of semi-analytic sets , Ann. Sc. Norm. Super. Pisa Cl. Sci. (3) 18 (1964), 449–474.Google Scholar
Łojasiewicz, S., Ensembles semi-analytiques, Institut des hautes Études scientifiques, Preprint (1965).Google Scholar
Łojasiewicz, S., Sur les trajectoires du gradient d’une fonction analytique , Semin. Geom., Univ. Studi Bologna 1982–1983 (1984), 115–117.Google Scholar
McDuff, D. and Salamon, D., J-holomorphic curves and symplectic topology, American Mathematical Society Colloquium Publications, vol. 52, second edition (American Mathematical Society, Providence, RI, 2012).Google Scholar
McLean, R. C., Deformations of calibrated submanifolds , Comm. Anal. Geom. 6 (1998), 705–747.Google Scholar
Morgan, J. W., Mrowka, T. and Ruberman, D., The L 2 -moduli space and a vanishing theorem for Donaldson polynomial invariants, Monographs in Geometry and Topology, vol. 2 (International Press, Cambridge, MA, 1994).Google Scholar
Nakajima, H., Instantons on ALE spaces, quiver varieties, and Kac-Moody algebras , Duke Math. J. 76 (1994), 365–416.Google Scholar
Seidel, P., Fukaya categories and Picard-Lefschetz theory, Zurich Lectures in Advanced Mathematics (European Mathematical Society (EMS), Zürich, 2008).Google Scholar
Seidel, P. and Smith, I., A link invariant from the symplectic geometry of nilpotent slices , Duke Math. J. 134 (2006), 453–514.Google Scholar
Simon, L., Asymptotics for a class of nonlinear evolution equations, with applications to geometric problems , Ann. of Math. (2) 118 (1983), 525–571.Google Scholar
Solomon, J. P. and Tian, G., Entropy of Lagrangian submanifolds, to appear.Google Scholar
Solomon, J. P. and Tukachinsky, S. B., Differential forms, Fukaya $A_{\infty }$ algebras, and Gromov–Witten axioms, Preprint (2016), arXiv:1608.01304.Google Scholar
Spanier, E. H., Algebraic topology, corrected reprint of 1966 original (Springer, New York, NY, 1995).Google Scholar
Taubes, C. H., L 2 moduli spaces on 4-manifolds with cylindrical ends, Monographs in Geometry and Topology, vol. 1 (International Press, Cambridge, MA, 1993).Google Scholar
Thomas, R. P. and Yau, S.-T., Special Lagrangians, stable bundles and mean curvature flow , Comm. Anal. Geom. 10 (2002), 1075–1113.Google Scholar
Verbitsky, M., Tri-analytic subvarieties of hyperkaehler manifolds , Geom. Funct. Anal. 5 (1995), 92–104.Google Scholar
Verbitsky, M., Subvarieties in non-compact hyperkaehler manifolds , Math. Res. Lett. 11 (2004), 413–418.Google Scholar
Woodward, C. T., Gauged Floer theory of toric moment fibers , Geom. Funct. Anal. 21 (2011), 680–749.Google Scholar
Yau, S. T., On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation. I , Comm. Pure Appl. Math. 31 (1978), 339–411.Google Scholar