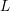Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-07T09:58:27.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Low-lying zeros of quadratic Dirichlet $L$-functions: lower order terms for extended support

Part of: Zeta and $L$-functions: analytic theory Exponential sums and character sums

Published online by Cambridge University Press:  26 April 2017

Daniel Fiorilli ,
James Parks  and
Anders Södergren
Daniel Fiorilli
Affiliation:
Département de mathématiques et de statistique, Université d’Ottawa, 585 King Edward, Ottawa, ON K1N 6N5, Canada email daniel.fiorilli@uottawa.ca
James Parks
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, 4401 University Drive, Lethbridge, AB T1K 3M4, Canada email jparks@kth.se Current address: Department of Mathematics, KTH Royal Institute of Technology, Lindstedtsvägen, SE-100 44 Stockholm, Sweden
Anders Södergren
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark email andesod@chalmers.se Current address: Department of Mathematical Sciences, Chalmers University of Technology and the University of Gothenburg, SE-412 96 Gothenburg, Sweden
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the 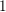$1$-level density of low-lying zeros of Dirichlet 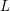$L$-functions attached to real primitive characters of conductor at most $X$. Under the generalized Riemann hypothesis, we give an asymptotic expansion of this quantity in descending powers of 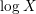$\log X$, which is valid when the support of the Fourier transform of the corresponding even test function $\unicode[STIX]{x1D719}$ is contained in 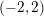$(-2,2)$. We uncover a phase transition when the supremum $\unicode[STIX]{x1D70E}$ of the support of 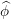$\widehat{\unicode[STIX]{x1D719}}$ reaches 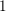$1$, both in the main term and in the lower order terms. A new lower order term appearing at 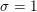$\unicode[STIX]{x1D70E}=1$ involves the quantity 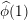$\widehat{\unicode[STIX]{x1D719}}(1)$, and is analogous to a lower order term which was isolated by Rudnick in the function field case.

Keywords

zeros of L-functionsKatz–Sarnak heuristicsquadratic Dirichlet L-functions1-level density

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11M50: Relations with random matrices
Secondary: 11L40: Estimates on character sums
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 6 , June 2017 , pp. 1196 - 1216
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bucur, A., Costa, E., David, C., Guerreiro, J. and Lowry-Duda, D., Traces, high powers and one level density for families of curves over finite fields, Preprint (2016), arXiv:1610.00164.Google Scholar
Chinis, I. J., Traces of high powers of the Frobenius class in the moduli space of hyperelliptic curves , Res. Number Theory 2 (2016), Art. ID 13, 18 pp.Google Scholar
Conrey, J. B., Farmer, D. W. and Zirnbauer, M. R., Autocorrelation of ratios of L-functions , Commun. Number Theory Phys. 2 (2008), 593–636.Google Scholar
Conrey, J. B. and Snaith, N. C., Applications of the L-functions ratios conjectures , Proc. Lond. Math. Soc. (3) 94 (2007), 594–646.Google Scholar
Entin, A., Roditty-Gershon, E. and Rudnick, Z., Low-lying zeros of quadratic DirichletL-functions, hyper-elliptic curves and random matrix theory , Geom. Funct. Anal. 23 (2013), 1230–1261.Google Scholar
Fiorilli, D. and Miller, S. J., Surpassing the ratios conjecture in the 1-level density of Dirichlet L-functions , Algebra Number Theory 9 (2015), 13–52.Google Scholar
Fiorilli, D., Parks, J. and Södergren, A., Low-lying zeros of elliptic curve L-functions: beyond the ratios conjecture , Math. Proc. Cambridge Philos. Soc. 160 (2016), 315–351.Google Scholar
Gao, P., $n$ -level density of the low-lying zeros of quadratic Dirichlet $L$ -functions, PhD thesis, University of Michigan (2005).Google Scholar
Gao, P., n-level density of the low-lying zeros of quadratic Dirichlet L-functions , Int. Math. Res. Not. IMRN 2014 (2014), 1699–1728.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H., Luo, W. and Sarnak, P., Low lying zeros of families of L-functions , Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.Google Scholar
Katz, N. M. and Sarnak, P., Zeros of zeta functions, their spacings and their spectral nature, Preprint (1997).Google Scholar
Katz, N. M. and Sarnak, P., Zeroes of zeta functions and symmetry , Bull. Amer. Math. Soc. (N.S.) 36 (1999), 1–26.Google Scholar
Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, American Mathematical Society Colloquium Publications, vol. 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Levinson, J. and Miller, S. J., The n-level densities of low-lying zeros of quadratic Dirichlet L-functions , Acta Arith. 161 (2013), 145–182.Google Scholar
Miller, S. J., A symplectic test of the L-functions ratios conjecture , Int. Math. Res. Not. IMRN (2008), doi:10.1093/imrn/rnm146.Google Scholar
Montgomery, H. L., The pair correlation of zeros of the zeta function , in Analytic number theory, Proc. sympos. in pure mathematics, vol. XXIV, St. Louis University, St. Louis, MO, 1972 (American Mathematical Society, Providence, RI, 1973), 181–193.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory. I. Classical theory, Cambridge Studies in Advanced Mathematics, vol. 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Özlük, A. E. and Snyder, C., Small zeros of quadratic L-functions , Bull. Aust. Math. Soc. 47 (1993), 307–319.CrossRefGoogle Scholar
Özlük, A. E. and Snyder, C., On the distribution of the nontrivial zeros of quadratic L-functions close to the real axis , Acta Arith. 91 (1999), 209–228.Google Scholar
Rubinstein, M., Low-lying zeros of L-functions and random matrix theory , Duke Math. J. 109 (2001), 147–181.Google Scholar
Rudnick, Z., Traces of high powers of the Frobenius class in the hyperelliptic ensemble , Acta Arith. 143 (2010), 81–99.CrossRefGoogle Scholar
Sarnak, P., Shin, S. W. and Templier, N., Families of L-functions and their symmetry , in Families of Automorphic Forms and the Trace Formula, Proceedings of Simons Symposia (Springer, 2016), 531–578.Google Scholar
Shankar, A., Södergren, A. and Templier, N., Sato–Tate equidistribution of certain families of Artin $L$ -functions, Preprint (2015), arXiv:1507.07031.Google Scholar
Soundararajan, K., Nonvanishing of quadratic Dirichlet L-functions at s = 1/2 , Ann. of Math. (2) 152 (2000), 447–488.Google Scholar
Young, M. P., Low-lying zeros of families of elliptic curves , J. Amer. Math. Soc. 19 (2006), 205–250.Google Scholar