Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Greenstein, Jacob
and
Hernandez, David
2021.
Interactions of Quantum Affine Algebras with Cluster Algebras, Current Algebras and Categorification.
Vol. 337,
Issue. ,
p.
69.
Kashiwara, Masaki
Kim, Myungho
Oh, Se-jin
and
Park, Euiyong
2021.
PBW theoretic approach to the module category of quantum affine algebras.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 97,
Issue. 6,
Kashiwara, Masaki
Kim, Myungho
Oh, Se-jin
and
Park, Euiyong
2021.
Categories over quantum affine algebras and monoidal categorification.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 97,
Issue. 7,
Fujita, Ryo
and
Oh, Se-jin
2021.
Q-data and Representation Theory of Untwisted Quantum Affine Algebras.
Communications in Mathematical Physics,
Vol. 384,
Issue. 2,
p.
1351.
Kashiwara, Masaki
Kim, Myungho
Oh, Se-jin
and
Park, Euiyong
2022.
Simply laced root systems arising from quantum affine algebras.
Compositio Mathematica,
Vol. 158,
Issue. 1,
p.
168.
Fujita, Ryo
Hernandez, David
Oh, Se-jin
and
Oya, Hironori
2022.
Isomorphisms among quantum Grothendieck rings and propagation of positivity.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 785,
p.
117.
Kashiwara, Masaki
and
Park, Euiyong
2022.
Categorical crystals for quantum affine algebras.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 792,
p.
223.
Kwon, Jae-Hoon
and
Lee, Sin-Myung
2022.
Super Duality for Quantum Affine Algebras of Type A
.
International Mathematics Research Notices,
Vol. 2022,
Issue. 23,
p.
18446.
Frenkel, Edward
Hernandez, David
and
Reshetikhin, Nicolai
2022.
Folded quantum integrable models and deformed W-algebras.
Letters in Mathematical Physics,
Vol. 112,
Issue. 4,
Park, Euiyong
2023.
Braid group action on extended crystals.
Advances in Mathematics,
Vol. 429,
Issue. ,
p.
109193.
Kwon, Jae-Hoon
and
Lee, Sin-Myung
2023.
Affinization of q-oscillator representations of $$U_q(\mathfrak {gl}_n)$$.
Letters in Mathematical Physics,
Vol. 113,
Issue. 3,
Kashiwara, Masaki
Kim, Myungho
Oh, Se‐jin
and
Park, Euiyong
2023.
Localizations for quiver Hecke algebras II.
Proceedings of the London Mathematical Society,
Vol. 127,
Issue. 4,
p.
1134.
Kashiwara, Masaki
and
Oh, Se-jin
2023.
The (q, t)-Cartan matrix specialized at $$q=1$$ and its applications.
Mathematische Zeitschrift,
Vol. 303,
Issue. 2,
Jang, Il-Seung
Lee, Kyu-Hwan
and
Oh, Se-jin
2024.
Quantization of Virtual Grothendieck Rings and Their Structure Including Quantum Cluster Algebras.
Communications in Mathematical Physics,
Vol. 405,
Issue. 7,
Kwon, Jae-Hoon
Lee, Sin-Myung
and
Okado, Masato
2024.
Oscillator Representations of Quantum Affine Orthosymplectic Superalgebras.
Communications in Mathematical Physics,
Vol. 405,
Issue. 4,
Kashiwara, Masaki
and
Oh, Se-jin
2024.
t-quantized Cartan matrix and R-matrices for cuspidal modules over quiver Hecke algebras.
Advances in Mathematics,
Vol. 441,
Issue. ,
p.
109551.
Kashiwara, Masaki
Kim, Myungho
Oh, Se-jin
and
Park, Euiyong
2024.
Affinizations, R-matrices and reflection functors.
Advances in Mathematics,
Vol. 443,
Issue. ,
p.
109598.
Geiss, Christof
Hernandez, David
and
Leclerc, Bernard
2024.
Representations of shifted quantum affine algebras and cluster algebras I: The simply laced case.
Proceedings of the London Mathematical Society,
Vol. 129,
Issue. 3,
Kashiwara, Masaki
Kim, Myungho
Oh, Se-jin
and
Park, Euiyong
2024.
Monoidal categorification and quantum affine algebras II.
Inventiones mathematicae,
Vol. 236,
Issue. 2,
p.
837.
Early, Nick
and
Li, Jian-Rong
2024.
Tropical geometry, quantum affine algebras, and scattering amplitudes.
Journal of Physics A: Mathematical and Theoretical,
Vol. 57,
Issue. 49,
p.
495201.
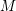 $M$ and
$M$ and 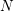 $N$ over quantum affine algebras
$N$ over quantum affine algebras 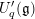 $U_{q}^{\prime }(\mathfrak{g})$ by analyzing their associated
$U_{q}^{\prime }(\mathfrak{g})$ by analyzing their associated 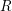 $R$-matrices. Using these new invariants, we provide a criterion for a monoidal category of finite-dimensional integrable
$R$-matrices. Using these new invariants, we provide a criterion for a monoidal category of finite-dimensional integrable 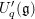 $U_{q}^{\prime }(\mathfrak{g})$-modules to become a monoidal categorification of a cluster algebra.
$U_{q}^{\prime }(\mathfrak{g})$-modules to become a monoidal categorification of a cluster algebra.
