Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T09:11:55.905Z Has data issue: false hasContentIssue false
  • English
  • Français

A new proof of Halász’s theorem, and its consequences

Part of: Zeta and $L$-functions: analytic theory Multiplicative number theory

Published online by Cambridge University Press:  23 November 2018

Andrew Granville ,
Adam J. Harper  and
K. Soundararajan
Andrew Granville
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, CP 6128 succ. Centre-Ville, Montréal, QC H3C 3J7, Canada email andrew@dms.umontreal.ca Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
Adam J. Harper
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK email a.harper@warwick.ac.uk
K. Soundararajan
Affiliation:
Department of Mathematics, Stanford University, Stanford CA 94305, USA email ksound@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Halász’s theorem gives an upper bound for the mean value of a multiplicative function 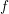$f$. The bound is sharp for general such 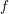$f$, and, in particular, it implies that a multiplicative function with 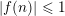$|f(n)|\leqslant 1$ has either mean value 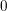$0$, or is ‘close to’ 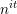$n^{it}$ for some fixed 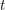$t$. The proofs in the current literature have certain features that are difficult to motivate and which are not particularly flexible. In this article we supply a different, more flexible, proof, which indicates how one might obtain asymptotics, and can be modified to treat short intervals and arithmetic progressions. We use these results to obtain new, arguably simpler, proofs that there are always primes in short intervals (Hoheisel’s theorem), and that there are always primes near to the start of an arithmetic progression (Linnik’s theorem).

Keywords

multiplicative functionsHalász’s theoremHoheisel’s theoremLinnik’s theoremSiegel zeroes

MSC classification

Primary: 11N56: Rate of growth of arithmetic functions 11M20: Real zeros of $L(s, chi)$; results on $L(1, chi)$
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 1 , January 2019 , pp. 126 - 163
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

A.G. has received funding in aid of this research from the European Research Council grant agreement no 670239, and from NSERC Canada under the CRC program. A.H. was supported, for parts of the research, by a postdoctoral fellowship from the Centre de recherches mathématiques in Montréal, and by a research fellowship at Jesus College, Cambridge. K.S. was partially supported by NSF grant DMS 1500237, and a Simons Investigator grant from the Simons Foundation. In addition, part of this work was carried out at MSRI, Berkeley during the Spring semester of 2017, supported in part by NSF grant DMS 1440140.

References

Davenport, H., Multiplicative number theory, Graduate Texts in Mathematics, vol. 74 (Springer, 2000).Google Scholar
Elliott, P. D. T. A., Extrapolating the mean-values of multiplicative functions , Nederl. Akad. Wetensch. Indag. Math. 51 (1989), 409–420.Google Scholar
Elliott, P. D. T. A., Multiplicative functions on arithmetic progressions. VII. Large moduli , J. Lond. Math. Soc. (2) 66 (2002), 14–28.Google Scholar
Elliott, P. D. T. A., The least prime primitive root and Linnik’s theorem , inNumber theory for the millennium, I (Urbana, IL, 2000), 393–418. (A. K. Peters, Natick, MA, 2002).Google Scholar
Friedlander, J. B. and Iwaniec, H., Opera de Cribro, Colloquium Publications, vol. 57 (American Mathematical Society, Providence, MA, 2010).Google Scholar
Granville, A., Harper, A. J. and Soundararajan, K., Mean values of multiplicative functions over function fields , Res. Number Theory 1 (2015), 25; doi:10.1007/s40993-015-0023-5.Google Scholar
Granville, A., Harper, A. J. and Soundararajan, K., A more intuitive proof of a sharp version of Halász’s theorem , Proc. Amer. Math. Soc. 146 (2018), 4099–4104.Google Scholar
Granville, A. and Soundararajan, K., Decay of mean values of multiplicative functions , Canad. J. Math. 55 (2003), 1191–1230.Google Scholar
Halász, G., Über die Mittelwerte multiplikativer zahlentheoretischer Funktionen , Acta Math. Acad. Sci. Hungar. 19 (1968), 365–403.Google Scholar
Halász, G., On the distribution of additive and the mean values of multiplicative arithmetic functions , Studia Sci. Math. Hungar. 6 (1971), 211–233.Google Scholar
Koukoulopoulos, D., Pretentious multiplicative functions and the prime number theorem for arithmetic progressions , Compos. Math. 149 (2013), 1129–1149.Google Scholar
Montgomery, H. L., A note on the mean values of multiplicative functions, Inst. Mittag-Leffler, (Report #17).Google Scholar
Montgomery, H. L. and Vaughan, R. C., Mean values of multiplicative functions , Period. Math. Hungar. 43 (2001), 199–214.Google Scholar
Shiu, P., A Brun-Titchmarsh theorem for multiplicative functions , J. Reine Angew. Math. 313 (1980), 161–170.Google Scholar
Soundararajan, K., Weak subconvexity for central values of L-functions , Ann. of Math. (2) 172 (2010), 1469–1498.Google Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory (Cambridge University Press, Cambridge, 1995).Google Scholar