Article contents
A note on the number of irrational odd zeta values
Published online by Cambridge University Press: 09 October 2020
Abstract
We prove that, for any small 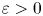 $\varepsilon > 0$, the number of irrationals among the following odd zeta values:
$\varepsilon > 0$, the number of irrationals among the following odd zeta values: 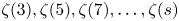 $\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)$ is at least
$\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)$ is at least 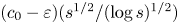 $( c_0 - \varepsilon )({s^{1/2}}/{(\log s)^{1/2}})$, provided
$( c_0 - \varepsilon )({s^{1/2}}/{(\log s)^{1/2}})$, provided 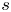 $s$ is a sufficiently large odd integer with respect to
$s$ is a sufficiently large odd integer with respect to 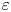 $\varepsilon$. The constant
$\varepsilon$. The constant 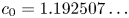 $c_0 = 1.192507\ldots$ can be expressed in closed form. Our work improves the lower bound
$c_0 = 1.192507\ldots$ can be expressed in closed form. Our work improves the lower bound 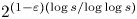 $2^{(1-\varepsilon )({\log s}/{\log \log s})}$ of the previous work of Fischler, Sprang and Zudilin. We follow the same strategy of Fischler, Sprang and Zudilin. The main new ingredient is an asymptotically optimal design for the zeros of the auxiliary rational functions, which relates to the inverse totient problem.
$2^{(1-\varepsilon )({\log s}/{\log \log s})}$ of the previous work of Fischler, Sprang and Zudilin. We follow the same strategy of Fischler, Sprang and Zudilin. The main new ingredient is an asymptotically optimal design for the zeros of the auxiliary rational functions, which relates to the inverse totient problem.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s) 2020
References
- 6
- Cited by

