Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T16:07:39.735Z Has data issue: false hasContentIssue false
  • English
  • Français

On higher direct images of convergent isocrystals

Part of: (Co)homology theory

Published online by Cambridge University Press:  25 September 2019

Daxin Xu
Daxin Xu*
Affiliation:
Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, USA email daxinxu@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 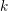$k$ be a perfect field of characteristic 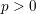$p>0$ and let 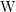$\operatorname{W}$ be the ring of Witt vectors of 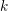$k$. In this article, we give a new proof of the Frobenius descent for convergent isocrystals on a variety over 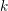$k$ relative to 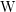$\operatorname{W}$. This proof allows us to deduce an analogue of the de Rham complexes comparison theorem of Berthelot [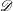$\mathscr{D}$-modules arithmétiques. II. Descente par Frobenius, Mém. Soc. Math. Fr. (N.S.) 81 (2000)] without assuming a lifting of the Frobenius morphism. As an application, we prove a version of Berthelot’s conjecture on the preservation of convergent isocrystals under the higher direct image by a smooth proper morphism of 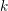$k$-varieties.

Keywords

convergent isocrystalsp-adic cohomologycrystalline cohomology

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology
Secondary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 11 , November 2019 , pp. 2180 - 2213
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbes, A., Éléments de géométrie rigide: Vol. I. Construction et étude géométrique des espaces rigides (Birkhäuser/Springer, Basel, 2010).Google Scholar
Abbes, A., Gros, M. and Tsuji, T., The p-adic Simpson correspondence , Ann. of Math. Stud. 193 (2016).Google Scholar
Berthelot, P., Cohomologie cristalline des schémas de caractéristique p > 0, Lecture Notes in Mathematics, vol. 407 (Springer, 1974).+0,+Lecture+Notes+in+Mathematics,+vol.+407+(Springer,+1974).>Google Scholar
Berthelot, P., Géométrie rigide et cohomologie des variétés algébriques de caractéristique p , in Introductions aux cohomologies p-adiques, Mémoires de la Société Mathématique de France, vol. 23, eds Barsky, D. and Robba, P. (Société Mathématique de France, 1986), 7–32.Google Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres, première partie, Preprint (1996), https://perso.univ-rennes1.fr/pierre.berthelot/publis/Cohomologie_Rigide_I.pdf.Google Scholar
Berthelot, P., 𝒟-modules arithmétiques. I. Opérateurs différentiels de niveau fini , Ann. Sci. Éc. Norm. Supér. (4) 29 (1996), 185–272.Google Scholar
Berthelot, P., 𝒟-modules arithmétiques. II. Descente par Frobenius , Mém. Soc. Math. Fr. (N.S.) 81 (2000).Google Scholar
Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné cristalline II, Lecture Notes in Mathematics, vol. 930 (Springer, 1982).Google Scholar
Berthelot, P. and Ogus, A., Notes on crystalline cohomology (MN-21) (Princeton University Press, Princeton, NJ, 2015).Google Scholar
Bosch, S. and Görtz, U., Coherent modules and their descent on relative rigid spaces , J. Reine Angew. Math. 495 (1998), 119–134.Google Scholar
Caro, D., Sur la préservation de la surconvergence par l’image directe d’un morphisme propre et lisse , Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 131–169.Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations , Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.Google Scholar
Di Proietto, V., Tonini, F. and Zhang, L., A crystalline version of Berthelot’s conjecture and Künneth formula for isocrystals, Preprint (2018), arXiv:1812.05153.Google Scholar
Grothendieck, A. and Dieudonné, J. A., Éléments de géométrie algébrique I, second edition (Springer, Berlin, 1971).Google Scholar
Grothendieck, A. and Dieudonné, J. A., Éléments de géométrie algébrique II. Étude globale élémentaire de quelques classes de morphismes , Publ. Math. Inst. Hautes Études Sci. 8 (1961).Google Scholar
Étesse, J.-Y., Images directes I: espaces rigides analytiques et images directes , J. Théor. Nombres Bordeaux 24 (2012), 101–151.Google Scholar
Illusie, L., Frobenius et dégénérescence de Hodge , in Introduction à la théorie de Hodge, Panoramas et Synthèses, vol. 3 (Société Mathématique de France, Paris, 1996), 113–168.Google Scholar
Katz, N., Nilpotent connections and the monodromy theorem: applications of a result of Turrittin , Publ. Math. Inst. Hautes Études Sci. 39 (1970), 175–232.Google Scholar
Kedlaya, K., Good formal structures for flat meromorphic connections, I: surfaces , Duke Math. J. 154 (2010), 343–418.Google Scholar
Lazda, C., Incarnations of Berthelot’s conjecture , J. Number Theory 166 (2016), 137–157.Google Scholar
Morrow, M., A note on higher direct images in crystalline cohomology, appendix to A variational Tate conjecture in crystalline cohomology, J. Eur. Math. Soc. (JEMS) 21 (2019), 3467–3511.Google Scholar
Ogus, A., F-isocrystals and de Rham cohomology. II. Convergent isocrystals , Duke Math. J. 51 (1984), 765–850.Google Scholar
Ogus, A., The convergent topos in characteristic p , in The Grothendieck Festschrift, Vol. III, Progress in Mathematics, vol. 88 (Birkhäuser, Boston, MA, 1990), 133–162; republished in 2007 (Modern Birkhäuser Classics).Google Scholar
Ogus, A. and Vologodsky, V., Nonabelian Hodge theory in characteristic p , Publ. Math. Inst. Hautes Études Sci. 106 (2007), 1–138.Google Scholar
Oyama, H., PD Higgs crystals and Higgs cohomology in characteristic p , J. Algebraic Geom. 26 (2017), 735–802.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Séminaire de Géométrie Algébrique du Bois Marie – 1963–64 – Théorie des topos et cohomologie étale des schémas (SGA 4), Tome 1, Lecture Notes in Mathematics, vol. 269 (Springer, 1972); Tome 2, Lecture Notes in Mathematics, vol. 270 (1972); Tome 3, Lecture Notes in Mathematics, vol. 305 (1973).Google Scholar
Berthelot, P., Grothendieck, A. and Illusie, L., Séminaire de Géométrie Algébrique du Bois Marie – 1966–67 – Théorie des intersections et théorème de Riemann-Roch (SGA 6), Lecture Notes in Mathematics, vol. 225 (Springer, 1971).Google Scholar
Shiho, A., Crystalline fundamental groups. II. Log convergent cohomology and rigid cohomology , J. Math. Sci. Univ. Tokyo 9 (2002), 1–163.Google Scholar
Shiho, A., Relative log convergent cohomology and relative rigid cohomology I, Preprint (2007),arXiv:0707.1742.Google Scholar
Shiho, A., Relative log convergent cohomology and relative rigid cohomology II, Preprint (2007),arXiv:0707.1743.Google Scholar
The Stacks Project Authors, Stacks project, http://stacks.math.columbia.edu (2019).Google Scholar
Tsuzuki, N., On base change theorem and coherence in rigid cohomology , Doc. Math. Extra Vol. (2003), 891–918.Google Scholar
Xu, D., Lifting the Cartier transform of Ogus–Vologodsky modulo p n , Mém. Soc. Math. Fr. (N.S.) 163 (2019).Google Scholar