Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T08:21:19.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms

Part of: Multiplicative number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  18 October 2018

Yuri F. Bilu ,
Jean-Marc Deshouillers ,
Sanoli Gun  and
Florian Luca
Yuri F. Bilu
Affiliation:
Université de Bordeaux and CNRS, Institut de Mathématiques de Bordeaux UMR 5251, 33405 Talence, France email yuri@math.u-bordeaux.fr
Jean-Marc Deshouillers
Affiliation:
Université de Bordeaux, CNRS and Bordeaux INP, Institut de Mathématiques de Bordeaux UMR 5251, F-33405 Talence, France email jean-marc.deshouillers@math.u-bordeaux.fr
Sanoli Gun
Affiliation:
Institute of Mathematical Sciences, HBNI, C.I.T. Campus, Taramani, Chennai 600 113, India email sanoli@imsc.res.in
Florian Luca
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag X3, Wits 2050, South Africa Department of Mathematics, Faculty of Sciences, University of Ostrava, 30. dubna 22, 701 03 Ostrava 1, Czech Republic email florian.luca@wits.ac.za
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 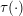$\unicode[STIX]{x1D70F}(\cdot )$ be the classical Ramanujan $\unicode[STIX]{x1D70F}$-function and let 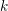$k$ be a positive integer such that 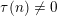$\unicode[STIX]{x1D70F}(n)\neq 0$ for 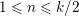$1\leqslant n\leqslant k/2$. (This is known to be true for 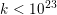$k<10^{23}$, and, conjecturally, for all 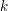$k$.) Further, let $\unicode[STIX]{x1D70E}$ be a permutation of the set 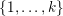$\{1,\ldots ,k\}$. We show that there exist infinitely many positive integers 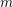$m$ such that 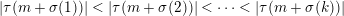$|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(1))|<|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(2))|<\cdots <|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(k))|$. We also obtain a similar result for Hecke eigenvalues of primitive forms of square-free level.

Keywords

Fourier coefficients of modular formssieveSato–Tate

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms
Secondary: 11F11: Holomorphic modular forms of integral weight 11N36: Applications of sieve methods
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 11 , November 2018 , pp. 2441 - 2461
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi-Yau varieties and potential automorphy II , Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some ℓ-adic lifts of automorphic mod ℓ Galois representations. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181.Google Scholar
Deligne, P., La conjecture de Weil , Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.Google Scholar
Derickx, M., van Hoeij, M. and Zeng, J., Computing Galois representations and equations for modular curves $X_{H}(\ell )$ , Preprint (2013), arXiv:1312.6819.Google Scholar
Diamond, F. and Shurman, J., A first course in modular forms, Graduate Texts in Mathematics, vol. 228 (Springer, Berlin, 2005).Google Scholar
Friedlander, J. and Iwaniec, H., Opera de Cribro, Colloquium Publications, vol. 57 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Ghosh, A. and Sarnak, P., Real zeros of holomorphic Hecke cusp forms , J. Eur. Math. Soc. (JEMS) 14 (2012), 465–487.Google Scholar
Gun, S., Kohnen, W. and Rath, P., Simultaneous sign change of Fourier-coefficients of two cusp forms , Arch. Math. (Basel) 105 (2015), 413–424.Google Scholar
Halberstam, H. and Richert, H.-E., Sieve methods, LMS Monographs, vol. 4 (Academic Press, London, 1974).Google Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, fourth edition (Clarendon Press, Oxford, 1960).Google Scholar
Harris, M., Shepherd-Barron, N. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy , Ann. of Math. (2) 171 (2010), 779–813.Google Scholar
Hida, H. and Maeda, Y., Non-abelian base change for totally real fields , in Olga Taussky-Todd: In memoriam, Special issue of the Pacific Journal of Mathematics (1997), 189–217.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Kohnen, W. and Sengupta, J., Signs of Fourier coefficients of two cusp forms of different weights , Proc. Amer. Math. Soc. 137 (2009), 3563–3567.Google Scholar
Kowalski, E., Robert, O. and Wu, J., Small gaps in coefficients of L-functions and B-free numbers in short intervals , Rev. Mat. Iberoam. 23 (2007), 281–326.Google Scholar
Matomäki, K., On signs of Fourier coefficients of cusp forms , Math. Proc. Cambridge Philos. Soc. 152 (2012), 207–222.Google Scholar
Matomäki, K. and Radziwiłł, M., Sign changes of Hecke eigenvalues , Geom. Funct. Anal. 25 (2015), 1937–1955.Google Scholar
Mordell, L. J., On Mr. Ramanujan’s empirical expansions of modular functions , Proc. Cambridge Philos. Soc. 19 (1917), 117–124.Google Scholar
Ram Murty, M. and Kumar Murty, V., Odd values of Fourier coefficients of certain modular forms , Int. J. Number Theory 3 (2007), 455–470.Google Scholar
Ono, K., The web of modularity: arithmetic of the coefficients of modular forms and q-series, CBMS Regional Conference Series in Mathematics, vol. 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Rankin, R. A., Contributions to the theory of Ramanujan’s function 𝜏(n) and similar arithmetical functions. I. The zeros of the function ∑ n=1 ∞ 𝜏(n)/n s on the line ℜs = 13/2. II. The order of the Fourier coefficients of integral modular forms , Proc. Cambridge Philos. Soc. 35 (1939), 351–372.Google Scholar
Rankin, R. A., An 𝛺-result for the coefficients of cusp forms , Math. Ann. 203 (1970), 239–250.Google Scholar
Ribet, K. A., Galois representations attached to eigenforms with Nebentypus , in Modular Functions of One Variable V, Lecture Notes in Mathematics, vol. 601 (Springer, Berlin, 1977), 17–51.Google Scholar
Ribet, K. A., Twists of modular forms and endomorphisms of abelian varieties , Math. Ann. 253 (1980), 43–62.Google Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev , Publ. Math. Inst. Hautes Études Sci. 54 (1981), 123–201.Google Scholar
Tenenbaum, G. and Wu, J., Théorie analytique et probabiliste des nombres, 307 exercices corrigés (Belin, 2014).Google Scholar
Zeng, J. and Yin, L., On the computation of coefficients of modular forms: the reduction modulo p approach , Math. Comp. 84 (2015), 1469–1488.Google Scholar