Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T09:05:37.779Z Has data issue: false hasContentIssue false
  • English
  • Français

A spectral incarnation of affine character sheaves

Part of: Representation theory of groups Families, fibrations

Published online by Cambridge University Press:  30 June 2017

David Ben-Zvi ,
David Nadler  and
Anatoly Preygel
David Ben-Zvi
Affiliation:
Department of Mathematics, University of Texas, Austin, TX 78712-0257, USA email benzvi@math.utexas.edu
David Nadler
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA email nadler@math.berkeley.edu
Anatoly Preygel
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA email preygel@math.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a Langlands dual realization of the putative category of affine character sheaves. Namely, we calculate the categorical center and trace (also known as the Drinfeld center and trace, or categorical Hochschild cohomology and homology) of the affine Hecke category starting from its spectral presentation. The resulting categories comprise coherent sheaves on the commuting stack of local systems on the two-torus satisfying prescribed support conditions, in particular singular support conditions, which appear in recent advances in the geometric Langlands program. The key technical tools in our arguments are a new descent theory for coherent sheaves or 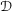${\mathcal{D}}$-modules with prescribed singular support and the theory of integral transforms for coherent sheaves developed in the companion paper by Ben-Zvi et al. [Integral transforms for coherent sheaves, J. Eur. Math. Soc. (JEMS), to appear].

Keywords

geometric Langlands programaffine Hecke algebracharacter sheaves

MSC classification

Primary: 20C08: Hecke algebras and their representations 14D24: Geometric Langlands program
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 9 , September 2017 , pp. 1908 - 1944
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arinkin, D. and Gaitsgory, D., Singular support of coherent sheaves, and the geometric langlands conjecture , Selecta Math. (N.S.) 21 (2015), 1–199.Google Scholar
Beilinson, A. and Drinfeld, V., Quantization of Hitchin Hamiltonians and Hecke eigensheaves, Preprint, http://www.math.uchicago.edu/∼mitya/langlands/hitchin/BD-hitchin.pdf.Google Scholar
Benson, D., Iyengar, S. B. and Krause, H., Local cohomology and support for triangulated categories , Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 573–619.Google Scholar
Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry , J. Amer. Math. Soc. 23 (2010), 909–966.Google Scholar
Ben-Zvi, D., Helm, D. and Nadler, D., Deligne–Langlands in families and coherent Springer theory, 2014, in preparation.Google Scholar
Ben-Zvi, D. and Nadler, D., The character theory of a complex group, Preprint (2009),arXiv:math/0904.1247.Google Scholar
Ben-Zvi, D. and Nadler, D., Loop spaces and connections , J. Topology 5 (2012), 377–430.Google Scholar
Ben-Zvi, D. and Nadler, D., Loop spaces and representations , Duke Math J. 162 (2013), 1587–1619.Google Scholar
Ben-Zvi, D. and Nadler, D., Elliptic springer theory, Preprint (2013), arXiv:math/1302.7053.Google Scholar
Ben-Zvi, D., Nadler, D. and Preygel, A., Integral transforms for coherent sheaves, J. Eur. Math. Soc. (JEMS), to appear.Google Scholar
Bezrukavnikov, R., Noncommutative counterparts of the Springer resolution , in Proceedings of the International Congress of Mathematicians, Vol. II (European Mathematical Society, 2006), 1119–1144.Google Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra , Publ. Math. Inst. Hautes Études Sci. 123 (2016), 1–67.Google Scholar
Bezrukavnikov, R., Finkelberg, M. and Ostrik, V., Character D-modules via Drinfeld center of Harish-Chandra bimodules , Invent. Math. 188 (2012), 589–620.Google Scholar
Bezrukavnikov, R., Kazhdan, D. and Varshavsky, Y., A categorical approach to the stable center conjecture , Astérisque 369 (2015), 27–97.Google Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, MA, 1997).Google Scholar
Drinfeld, V. and Gaitsgory, D., On some finiteness questions for algebraic stacks , Geom. Funct. Anal. 23 (2013), 149–294.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry, Preprint,http://www.math.harvard.edu/∼gaitsgde/GL/.Google Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras , Invent. Math. 87 (1987), 153–215.Google Scholar
Lurie, J., Higher algebra, Preprint, http://math.harvard.edu/∼lurie/papers/HigherAlgebra.pdf.Google Scholar
Lusztig, G., Unipotent almost characters of simple $p$ -adic groups, Preprint (2012), arXiv:1212.6540.Google Scholar
Lusztig, G., Unipotent almost characters of simple p-adic groups II , Transform. Groups 19 (2014), 527–547.Google Scholar
Preygel, A., Thom–Sebastiani and duality for matrix factorizations, Preprint (2011), arXiv:1101.5834.Google Scholar
Schiffmann, O. and Vasserot, E., The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials , Compositio Math. 147 (2011), 188–234.Google Scholar
Schiffmann, O. and Vasserot, E., Hall algebras of curves, commuting varieties and Langlands duality , Math. Ann. 353 (2012), 1399–1451.Google Scholar