No CrossRef data available.
Article contents
Absolute Hodge and ℓ-adic monodromy
Published online by Cambridge University Press: 13 May 2022
Abstract
Let 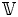 $\mathbb {V}$ be a motivic variation of Hodge structure on a
$\mathbb {V}$ be a motivic variation of Hodge structure on a 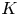 $K$-variety
$K$-variety 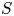 $S$, let
$S$, let 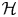 $\mathcal {H}$ be the associated
$\mathcal {H}$ be the associated 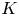 $K$-algebraic Hodge bundle, and let
$K$-algebraic Hodge bundle, and let 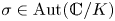 $\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ be an automorphism. The absolute Hodge conjecture predicts that given a Hodge vector
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ be an automorphism. The absolute Hodge conjecture predicts that given a Hodge vector 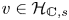 $v \in \mathcal {H}_{\mathbb {C}, s}$ above
$v \in \mathcal {H}_{\mathbb {C}, s}$ above 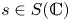 $s \in S(\mathbb {C})$ which lies inside
$s \in S(\mathbb {C})$ which lies inside 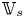 $\mathbb {V}_{s}$, the conjugate vector
$\mathbb {V}_{s}$, the conjugate vector 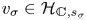 $v_{\sigma } \in \mathcal {H}_{\mathbb {C}, s_{\sigma }}$ is Hodge and lies inside
$v_{\sigma } \in \mathcal {H}_{\mathbb {C}, s_{\sigma }}$ is Hodge and lies inside 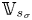 $\mathbb {V}_{s_{\sigma }}$. We study this problem in the situation where we have an algebraic subvariety
$\mathbb {V}_{s_{\sigma }}$. We study this problem in the situation where we have an algebraic subvariety 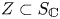 $Z \subset S_{\mathbb {C}}$ containing
$Z \subset S_{\mathbb {C}}$ containing 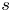 $s$ whose algebraic monodromy group
$s$ whose algebraic monodromy group 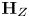 $\textbf {H}_{Z}$ fixes
$\textbf {H}_{Z}$ fixes  $v$. Using relationships between
$v$. Using relationships between 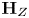 $\textbf {H}_{Z}$ and
$\textbf {H}_{Z}$ and 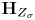 $\textbf {H}_{Z_{\sigma }}$ coming from the theories of complex and
$\textbf {H}_{Z_{\sigma }}$ coming from the theories of complex and 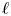 $\ell$-adic local systems, we establish a criterion that implies the absolute Hodge conjecture for
$\ell$-adic local systems, we establish a criterion that implies the absolute Hodge conjecture for 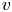 $v$ subject to a group-theoretic condition on
$v$ subject to a group-theoretic condition on 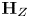 $\textbf {H}_{Z}$. We then use our criterion to establish new cases of the absolute Hodge conjecture.
$\textbf {H}_{Z}$. We then use our criterion to establish new cases of the absolute Hodge conjecture.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence


