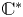1. Introduction
Since their introduction in Hitchin's seminal paper [Reference HitchinHit87], Higgs bundles over a compact Riemann surface have been of tremendous interest in geometry, topology and theoretical physics. Within the moduli space of Higgs bundles there is a special subvariety determined by the fixed points of a natural ![]() $\mathbb {C}^*$-action. These fixed points are called Hodge bundles and correspond to holonomies of complex variations of Hodge structure. They are part of the global nilpotent cone, and coincide with critical points of a natural energy function on the moduli space. The importance of the
$\mathbb {C}^*$-action. These fixed points are called Hodge bundles and correspond to holonomies of complex variations of Hodge structure. They are part of the global nilpotent cone, and coincide with critical points of a natural energy function on the moduli space. The importance of the ![]() $\mathbb {C}^*$-fixed points also stems from the fact that, roughly speaking, the subvariety of Hodge bundles determines the topology of the moduli space of Higgs bundles (see [Reference HitchinHit87, Reference García-Prada, Heinloth and SchmittGHS14, Reference García-Prada and HeinlothGH13, Reference GothenGot94]). In this paper we investigate some basic properties of Hodge bundles and their moduli.
$\mathbb {C}^*$-fixed points also stems from the fact that, roughly speaking, the subvariety of Hodge bundles determines the topology of the moduli space of Higgs bundles (see [Reference HitchinHit87, Reference García-Prada, Heinloth and SchmittGHS14, Reference García-Prada and HeinlothGH13, Reference GothenGot94]). In this paper we investigate some basic properties of Hodge bundles and their moduli.
To describe our results, let ![]() $\mathrm {G}$ be a complex semisimple Lie group with Lie algebra
$\mathrm {G}$ be a complex semisimple Lie group with Lie algebra ![]() $\mathfrak {g}$, and let
$\mathfrak {g}$, and let ![]() $X$ be a compact Riemann surface with genus
$X$ be a compact Riemann surface with genus ![]() $g\geqslant 2$ and canonical bundle
$g\geqslant 2$ and canonical bundle ![]() $K.$ A
$K.$ A ![]() $\mathrm {G}$-Higgs bundle on
$\mathrm {G}$-Higgs bundle on ![]() $X$ is a pair
$X$ is a pair ![]() $(E,\varphi )$, where
$(E,\varphi )$, where ![]() $E$ is a holomorphic principal
$E$ is a holomorphic principal ![]() $\mathrm {G}$-bundle on
$\mathrm {G}$-bundle on ![]() $X$ and
$X$ and ![]() $\varphi \in H^0(E(\mathfrak {g})\otimes K)$ is a holomorphic section of the Lie algebra bundle twisted by
$\varphi \in H^0(E(\mathfrak {g})\otimes K)$ is a holomorphic section of the Lie algebra bundle twisted by ![]() $K.$ The moduli space of polystable
$K.$ The moduli space of polystable ![]() $\mathrm {G}$-Higgs bundles will be denoted by
$\mathrm {G}$-Higgs bundles will be denoted by ![]() ${\mathcal {M}}(\mathrm {G})$. By the nonabelian Hodge correspondence, the moduli space
${\mathcal {M}}(\mathrm {G})$. By the nonabelian Hodge correspondence, the moduli space ![]() ${\mathcal {M}}(\mathrm {G})$ is homeomorphic to the character variety
${\mathcal {M}}(\mathrm {G})$ is homeomorphic to the character variety ![]() ${\mathcal {R}}(\mathrm {G})$ of conjugacy classes of reductive representations
${\mathcal {R}}(\mathrm {G})$ of conjugacy classes of reductive representations ![]() $\rho :\pi _1(X)\to \mathrm {G}.$
$\rho :\pi _1(X)\to \mathrm {G}.$
The ![]() $\mathbb {C}^*$-action on the Higgs bundle moduli space is defined by
$\mathbb {C}^*$-action on the Higgs bundle moduli space is defined by ![]() $\lambda \cdot (E,\varphi )=(E,\lambda \varphi )$. To describe the
$\lambda \cdot (E,\varphi )=(E,\lambda \varphi )$. To describe the ![]() $\mathbb {C}^*$-fixed points, fix a
$\mathbb {C}^*$-fixed points, fix a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$. Let
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$. Let ![]() $\zeta \in \mathfrak {g}_0$ be the grading element, that is,
$\zeta \in \mathfrak {g}_0$ be the grading element, that is, ![]() $[\zeta,x]=jx$ for all
$[\zeta,x]=jx$ for all ![]() $x\in \mathfrak {g}_j$, and let
$x\in \mathfrak {g}_j$, and let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta.$ A Higgs bundle
$\zeta.$ A Higgs bundle ![]() $(E,\varphi )$ is said to be a Hodge bundle of type
$(E,\varphi )$ is said to be a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$ if
$(\mathrm {G}_0,\mathfrak {g}_k)$ if ![]() $E$ reduces to a holomorphic
$E$ reduces to a holomorphic ![]() $\mathrm {G}_0$-bundle
$\mathrm {G}_0$-bundle ![]() $E_{\mathrm {G}_0},$ and
$E_{\mathrm {G}_0},$ and ![]() $\varphi \in H^0(E_{\mathrm {G}_0}(\mathfrak {g}_k)\otimes K).$ A polystable Higgs bundle is a fixed point if and only if it is a Hodge bundle [Reference SimpsonSim92]. In fact it suffices to consider Hodge bundles of type
$\varphi \in H^0(E_{\mathrm {G}_0}(\mathfrak {g}_k)\otimes K).$ A polystable Higgs bundle is a fixed point if and only if it is a Hodge bundle [Reference SimpsonSim92]. In fact it suffices to consider Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ (see § 4.2 for more details).
$(\mathrm {G}_0,\mathfrak {g}_1)$ (see § 4.2 for more details).
The representations ![]() $\rho :\pi _1(X)\to \mathrm {G}$ associated to Hodge bundles factor through a real form
$\rho :\pi _1(X)\to \mathrm {G}$ associated to Hodge bundles factor through a real form ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}\to \mathrm {G}$ of Hodge type, that is, a real form such that the rank of its maximal compact subgroup is equal to the rank of
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}\to \mathrm {G}$ of Hodge type, that is, a real form such that the rank of its maximal compact subgroup is equal to the rank of ![]() $\mathrm {G}_0$. If
$\mathrm {G}_0$. If ![]() $\mathrm {H}_0^\mathbb {R}<\mathrm {G}_0$ is a maximal compact subgroup, then the homogeneous space
$\mathrm {H}_0^\mathbb {R}<\mathrm {G}_0$ is a maximal compact subgroup, then the homogeneous space ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ has a natural complex structure and is called a period domain. The holomorphic tangent bundle of
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ has a natural complex structure and is called a period domain. The holomorphic tangent bundle of ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ decomposes as
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ decomposes as ![]() $\bigoplus _{j\geqslant 0}\mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {g}_j$. In [Reference SimpsonSim92], Simpson showed that the representations
$\bigoplus _{j\geqslant 0}\mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {g}_j$. In [Reference SimpsonSim92], Simpson showed that the representations ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}<\mathrm {G}$ arising from Hodge bundles of type
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}<\mathrm {G}$ arising from Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ define
$(\mathrm {G}_0,\mathfrak {g}_1)$ define ![]() $\rho$-equivariant holomorphic maps
$\rho$-equivariant holomorphic maps
such that ![]() $\partial f_\rho$ is valued in the first graded piece
$\partial f_\rho$ is valued in the first graded piece ![]() $\mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {g}_1$ of the holomorphic tangent bundle. Such pairs
$\mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {g}_1$ of the holomorphic tangent bundle. Such pairs ![]() $(\rho,f_\rho )$ are called variations of Hodge structure.
$(\rho,f_\rho )$ are called variations of Hodge structure.
When the grading in the above discussion is ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1,$ the real form
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1,$ the real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a group of Hermitian type and the period domain
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a group of Hermitian type and the period domain ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is the Riemannian symmetric space of
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is the Riemannian symmetric space of ![]() $\mathrm {G}^\mathbb {R}.$ In this case, the symmetric space is Kähler and Hodge bundles define representations
$\mathrm {G}^\mathbb {R}.$ In this case, the symmetric space is Kähler and Hodge bundles define representations ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ and
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ and ![]() $\rho$-equivariant holomorphic maps to the symmetric space of
$\rho$-equivariant holomorphic maps to the symmetric space of ![]() $\mathrm {G}^\mathbb {R}.$ Pulling back the Kähler form and integrating it over
$\mathrm {G}^\mathbb {R}.$ Pulling back the Kähler form and integrating it over ![]() $X$ defines an invariant which is usually called the Toledo invariant
$X$ defines an invariant which is usually called the Toledo invariant ![]() $\tau (\rho )$. The Toledo invariant is defined for all representations into Hermitian Lie groups and satisfies the Milnor–Wood inequality
$\tau (\rho )$. The Toledo invariant is defined for all representations into Hermitian Lie groups and satisfies the Milnor–Wood inequality
This inequality was first proven by Milnor [Reference MilnorMil58] for ![]() $\mathrm {PSL}_2\mathbb {R}$, and more generally in [Reference Domic and ToledoDT87, Reference Burger, Iozzi and WienhardBIW03]. Using Higgs bundles, one can also define the Toledo invariant and obtain the Milnor–Wood inequality [Reference HitchinHit87, Reference Bradlow, García-Prada and GothenBGG03, Reference Biquard, García-Prada and RubioBGR17].
$\mathrm {PSL}_2\mathbb {R}$, and more generally in [Reference Domic and ToledoDT87, Reference Burger, Iozzi and WienhardBIW03]. Using Higgs bundles, one can also define the Toledo invariant and obtain the Milnor–Wood inequality [Reference HitchinHit87, Reference Bradlow, García-Prada and GothenBGG03, Reference Biquard, García-Prada and RubioBGR17].
The set of representations which maximize the invariant are called maximal representations and have many interesting geometric features. For example, maximal representations define connected components of the character variety which consist entirely of discrete and faithful representations [Reference Burger, Iozzi and WienhardBIW10]. For ![]() $\mathrm {PSL}_2\mathbb {R}$, maximal representations correspond to Fuchsian representations and the representation uniformizing the Riemann surface
$\mathrm {PSL}_2\mathbb {R}$, maximal representations correspond to Fuchsian representations and the representation uniformizing the Riemann surface ![]() $X$ defines the unique maximal Hodge bundle. There are two classes of Hermitian groups, those of tube type and those of nontube type. Generalizing the complex hyperbolic geometry results of [Reference ToledoTol89], maximal representations into nontube-type groups always factor through a maximal subtube up to a compact factor [Reference Bradlow, García-Prada and GothenBGG03, Reference Burger, Iozzi and WienhardBIW03, Reference Biquard, García-Prada and RubioBGR17]. For example
$X$ defines the unique maximal Hodge bundle. There are two classes of Hermitian groups, those of tube type and those of nontube type. Generalizing the complex hyperbolic geometry results of [Reference ToledoTol89], maximal representations into nontube-type groups always factor through a maximal subtube up to a compact factor [Reference Bradlow, García-Prada and GothenBGG03, Reference Burger, Iozzi and WienhardBIW03, Reference Biquard, García-Prada and RubioBGR17]. For example ![]() $\mathrm {SU}(p,p)$ is the maximal subtube of
$\mathrm {SU}(p,p)$ is the maximal subtube of ![]() $\mathrm {SU}(p,q)$ when
$\mathrm {SU}(p,q)$ when ![]() $q\geqslant p$.
$q\geqslant p$.
Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ form their own moduli space
$(\mathrm {G}_0,\mathfrak {g}_1)$ form their own moduli space ![]() ${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1)$. Consider a
${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1)$. Consider a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element ![]() $\zeta$. Define a character of the Lie algebra
$\zeta$. Define a character of the Lie algebra ![]() $\mathfrak {g}_0$,
$\mathfrak {g}_0$,
where ![]() $B$ is the Killing form of
$B$ is the Killing form of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\gamma$ is the longest root such that the root space
$\gamma$ is the longest root such that the root space ![]() $\mathfrak {g}_\gamma \subset \mathfrak {g}_1.$ As explained in § 3.3, the normalization constant
$\mathfrak {g}_\gamma \subset \mathfrak {g}_1.$ As explained in § 3.3, the normalization constant ![]() $B(\gamma,\gamma )$ normalizes the minimum of the holomorphic sectional curvature of the period domain to be
$B(\gamma,\gamma )$ normalizes the minimum of the holomorphic sectional curvature of the period domain to be ![]() $-1$. Recall that a Hodge bundle of type
$-1$. Recall that a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a pair
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a pair ![]() $(E,\varphi )$, where
$(E,\varphi )$, where ![]() $E$ is a holomorphic
$E$ is a holomorphic ![]() $\mathrm {G}_0$-bundle and
$\mathrm {G}_0$-bundle and ![]() $\varphi \in H^0(E(\mathfrak {g}_1)\otimes K).$ For some positive integer
$\varphi \in H^0(E(\mathfrak {g}_1)\otimes K).$ For some positive integer ![]() $q,$ the multiple
$q,$ the multiple ![]() $q\cdot \chi _T$ exponentiates to a character
$q\cdot \chi _T$ exponentiates to a character ![]() $\chi :\mathrm {G}_0\to \mathbb {C}^*$ of the Lie group
$\chi :\mathrm {G}_0\to \mathbb {C}^*$ of the Lie group ![]() $\mathrm {G}_0$ and defines a line bundle
$\mathrm {G}_0$ and defines a line bundle ![]() $E(\chi ).$ We define the Toledo invariant of a Hodge bundle
$E(\chi ).$ We define the Toledo invariant of a Hodge bundle ![]() $(E,\varphi )$ by
$(E,\varphi )$ by
For gradings ![]() $\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the Lie algebra character
$\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the Lie algebra character ![]() $\chi _T$ and the invariant
$\chi _T$ and the invariant ![]() $\tau$ agree with the definitions of the Toledo character and invariant for Hermitian groups in [Reference Biquard, García-Prada and RubioBGR17].
$\tau$ agree with the definitions of the Toledo character and invariant for Hermitian groups in [Reference Biquard, García-Prada and RubioBGR17].
To generalize the notion of rank, we use the fact that the space ![]() $\mathfrak {g}_1$ is a prehomogeneous vector space (PHVS) for the action of
$\mathfrak {g}_1$ is a prehomogeneous vector space (PHVS) for the action of ![]() $\mathrm {G}_0.$ That is,
$\mathrm {G}_0.$ That is, ![]() $\mathfrak {g}_1$ has a unique open dense
$\mathfrak {g}_1$ has a unique open dense ![]() $\mathrm {G}_0$-orbit
$\mathrm {G}_0$-orbit ![]() $\Omega \subset \mathfrak {g}_1.$ The theory of PHVSs was introduced by Sato (see [Reference Sato and KimuraSK77, Reference KimuraKim03, Reference MortajineMor91, Reference ManivelMan13]) and provides an ideal set of tools to study our problem. Let
$\Omega \subset \mathfrak {g}_1.$ The theory of PHVSs was introduced by Sato (see [Reference Sato and KimuraSK77, Reference KimuraKim03, Reference MortajineMor91, Reference ManivelMan13]) and provides an ideal set of tools to study our problem. Let ![]() $e\in \Omega \subset \mathfrak {g}_1$ be any point in the open orbit and complete it to an
$e\in \Omega \subset \mathfrak {g}_1$ be any point in the open orbit and complete it to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ with
$\{f,h,e\}$ with ![]() $h\in \mathfrak {g}_0.$ We define the rank of
$h\in \mathfrak {g}_0.$ We define the rank of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ by
$(\mathrm {G}_0,\mathfrak {g}_1)$ by
In § 3 we show that this is independent of the choices made. Again, for Hermitian groups this definition recovers the rank of the symmetric space.
Let us state our first main result.
Theorem A (Corollary 5.5)
A polystable Hodge bundle ![]() $(E,\varphi )$ of type
$(E,\varphi )$ of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ satisfies the inequality
$(\mathrm {G}_0,\mathfrak {g}_1)$ satisfies the inequality
Remark 1.1 In terms of variations of Hodge structure, the Toledo invariant is the degree of the pullback of a natural line bundle on the period domain ![]() $\mathrm {G}^\mathbb {R}/(\mathrm {G}_0\cap \mathrm {H}^\mathbb {R})$. Inequality (1.1) is simply saying that this is bounded by the Euler characteristic times a number (the rank) which is determined by the Lie theory of the period domain. In Proposition 3.12, we prove that the rank is the negative inverse of the maximal value of the holomorphic sectional curvature (in the
$\mathrm {G}^\mathbb {R}/(\mathrm {G}_0\cap \mathrm {H}^\mathbb {R})$. Inequality (1.1) is simply saying that this is bounded by the Euler characteristic times a number (the rank) which is determined by the Lie theory of the period domain. In Proposition 3.12, we prove that the rank is the negative inverse of the maximal value of the holomorphic sectional curvature (in the ![]() $+1$ space) of the period domain, which coincides with the usual rank in the case of Hermitian symmetric spaces.
$+1$ space) of the period domain, which coincides with the usual rank in the case of Hermitian symmetric spaces.
Remark 1.2 We refer to inequality (1.1) as the Arakelov–Milnor inequality as it generalizes the Milnor–Wood inequality when the Higgs bundle defines a variation of Hodge structure in a Hermitian symmetric space, and is analogous to the Arakelov inequalities for variations of Hodge structure. These are generalizations of the classical Arakelov inequality for the degree of the relative canonical bundle of a family of curves over another curve (see, for example, [Reference PetersPet90, Reference Jost and ZuoJZ02, Reference ViehwegVie09, Reference Viehweg and ZuoVZ03, Reference Möller, Viehweg and ZuoMVZ12]). As in the Milnor–Wood case, maximality of the bound in the Arakelov inequalities is accompanied by some rigidity phenomena. As already mentioned, in the Hermitian case for the grading ![]() $\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the character
$\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the character ![]() $\chi _T$ and the invariant
$\chi _T$ and the invariant ![]() $\tau$ agree with the definition of the Toledo character and the Toledo invariant for Hermitian groups in [Reference Biquard, García-Prada and RubioBGR17], and the rank of
$\tau$ agree with the definition of the Toledo character and the Toledo invariant for Hermitian groups in [Reference Biquard, García-Prada and RubioBGR17], and the rank of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ coincides, as mentioned above, with the rank of the symmetric space.
$(\mathrm {G}_0,\mathfrak {g}_1)$ coincides, as mentioned above, with the rank of the symmetric space.
We refer to Hodge bundles with ![]() $|\tau (E,\varphi )|=\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2)$ as maximal Hodge bundles of type
$|\tau (E,\varphi )|=\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2)$ as maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$. As in the Hermitian case of [Reference Biquard, García-Prada and RubioBGR17], the Arakelov–Milnor inequality follows from a more general and more precise inequality established in Theorem 5.3. Indeed, the stability of a Hodge bundle of type
$(\mathrm {G}_0,\mathfrak {g}_1)$. As in the Hermitian case of [Reference Biquard, García-Prada and RubioBGR17], the Arakelov–Milnor inequality follows from a more general and more precise inequality established in Theorem 5.3. Indeed, the stability of a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ depends on a parameter
$(\mathrm {G}_0,\mathfrak {g}_1)$ depends on a parameter ![]() $\alpha =\lambda \zeta$ with
$\alpha =\lambda \zeta$ with ![]() $\lambda \in \mathbb {R}$. In Theorem 5.3 we give an inequality for an
$\lambda \in \mathbb {R}$. In Theorem 5.3 we give an inequality for an ![]() $\alpha$-semistable Hodge bundle
$\alpha$-semistable Hodge bundle ![]() $(E,\varphi )$. Moreover, we give a refined inequality which depends on the orbit in
$(E,\varphi )$. Moreover, we give a refined inequality which depends on the orbit in ![]() $\mathfrak {g}_1$ which contains the generic value of
$\mathfrak {g}_1$ which contains the generic value of ![]() $\varphi$. While we are mostly interested in the case
$\varphi$. While we are mostly interested in the case ![]() $\alpha =0$, since this relates to the stability of the Higgs bundle obtained from
$\alpha =0$, since this relates to the stability of the Higgs bundle obtained from ![]() $(E,\varphi )$ by extension of structure group, considering the arbitrary value of the
$(E,\varphi )$ by extension of structure group, considering the arbitrary value of the ![]() $\alpha$ case has proven to be a powerful tool to study the moduli space for
$\alpha$ case has proven to be a powerful tool to study the moduli space for ![]() $\alpha =0$ (see [Reference Bradlow, García-Prada and GothenBGG03, Reference García-Prada, Heinloth and SchmittGHS14]). We believe that the same principle will apply in this general situation.
$\alpha =0$ (see [Reference Bradlow, García-Prada and GothenBGG03, Reference García-Prada, Heinloth and SchmittGHS14]). We believe that the same principle will apply in this general situation.
Example 1.3 The inequality is usually easy to write down in concrete cases. For example, for ![]() $\mathrm {G}=\mathrm {SO}_{2p+q}\mathbb {C}$ and
$\mathrm {G}=\mathrm {SO}_{2p+q}\mathbb {C}$ and ![]() $\mathrm {G}_0=\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$, one finds that
$\mathrm {G}_0=\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$, one finds that ![]() $\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=2\min (p,q)$ if
$\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=2\min (p,q)$ if ![]() $q>1$ and
$q>1$ and ![]() $1$ if
$1$ if ![]() $q=1$. Let us take
$q=1$. Let us take ![]() $q>1$. A bundle
$q>1$. A bundle ![]() $(E,\varphi )$ of type
$(E,\varphi )$ of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ can be written as
$(\mathrm {G}_0,\mathfrak {g}_1)$ can be written as ![]() $E=V\oplus W\oplus V^*$, where
$E=V\oplus W\oplus V^*$, where ![]() $V$ is a
$V$ is a ![]() $\mathrm {GL}_p\mathbb {C}$-bundle and
$\mathrm {GL}_p\mathbb {C}$-bundle and ![]() $W$ is a
$W$ is a ![]() $\mathrm {SO}_q\mathbb {C}$-bundle, and the Higgs field has the form
$\mathrm {SO}_q\mathbb {C}$-bundle, and the Higgs field has the form
 \[ \varphi =\left(\begin{pmatrix} 0 & \theta & 0 \\ 0 & 0 & - \theta^\mathrm{T} \\ 0 & 0 & 0 \end{pmatrix}\right) \]
\[ \varphi =\left(\begin{pmatrix} 0 & \theta & 0 \\ 0 & 0 & - \theta^\mathrm{T} \\ 0 & 0 & 0 \end{pmatrix}\right) \]
where ![]() $\theta :W\rightarrow V\otimes K$. One obtains
$\theta :W\rightarrow V\otimes K$. One obtains ![]() $\tau (E,\varphi )=2 \deg V$, and it follows that inequality (1.1) takes the form (actually
$\tau (E,\varphi )=2 \deg V$, and it follows that inequality (1.1) takes the form (actually ![]() $\deg V\leqslant 0$)
$\deg V\leqslant 0$)
As mentioned above, we actually prove a more precise inequality, which depends on the orbit which contains the generic value of ![]() $\varphi$. In our case, if the image of
$\varphi$. In our case, if the image of ![]() $\theta ^\mathrm {T}$ in
$\theta ^\mathrm {T}$ in ![]() $W$ is the sum of a nondegenerate subspace of dimension
$W$ is the sum of a nondegenerate subspace of dimension ![]() $r_1$ and of a totally isotropic subspace of dimension
$r_1$ and of a totally isotropic subspace of dimension ![]() $r_2$, then the inequality can be refined as
$r_2$, then the inequality can be refined as
These values are calculated in Example 3.7.
Fundamental in the proof of the Arakelov–Milnor inequality (1.1) is the construction of a maximal Jacobson–Morozov (JM) regular prehomogeneous vector subspace (PHVSS) of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ and the existence of a polynomial relative invariant for this subspace. This is the analogue of a maximal subtube in the Hermitian case. To explain this, let
$(\mathrm {G}_0,\mathfrak {g}_1)$ and the existence of a polynomial relative invariant for this subspace. This is the analogue of a maximal subtube in the Hermitian case. To explain this, let ![]() $\{f,h,e\}\subset \mathfrak {g}$ be an
$\{f,h,e\}\subset \mathfrak {g}$ be an ![]() $\mathfrak {sl}_2$-triple such that
$\mathfrak {sl}_2$-triple such that ![]() $[h,e]=2e$ and
$[h,e]=2e$ and ![]() $[e,f]=h$. The weights of
$[e,f]=h$. The weights of ![]() ${\operatorname {ad}}_h$ are integral. When the weights of
${\operatorname {ad}}_h$ are integral. When the weights of ![]() ${\operatorname {ad}}_h$ are all even,
${\operatorname {ad}}_h$ are all even, ![]() $\{f,h,e\}$ is called an even
$\{f,h,e\}$ is called an even ![]() $\mathfrak {sl}_2$-triple and defines a
$\mathfrak {sl}_2$-triple and defines a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element ![]() $ {h}/{2}$ and
$ {h}/{2}$ and ![]() $e\in \mathfrak {g}_1.$ In fact
$e\in \mathfrak {g}_1.$ In fact ![]() $e\in \Omega \subset \mathfrak {g}_1$ is in the open
$e\in \Omega \subset \mathfrak {g}_1$ is in the open ![]() $\mathrm {G}_0$-orbit (see § 2.2). A PHVS
$\mathrm {G}_0$-orbit (see § 2.2). A PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is called regular if the
$(\mathrm {G}_0,\mathfrak {g}_1)$ is called regular if the ![]() $\mathrm {G}_0$-stabilizer of a point in the open orbit
$\mathrm {G}_0$-stabilizer of a point in the open orbit ![]() $\Omega$ is reductive. For gradings arising from even
$\Omega$ is reductive. For gradings arising from even ![]() $\mathfrak {sl}_2$-triples
$\mathfrak {sl}_2$-triples ![]() $\{f,h,e\}$,
$\{f,h,e\}$, ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is regular since the
$(\mathrm {G}_0,\mathfrak {g}_1)$ is regular since the ![]() $\mathrm {G}_0$-centralizer of
$\mathrm {G}_0$-centralizer of ![]() $e\in \Omega$ coincides with the
$e\in \Omega$ coincides with the ![]() $\mathrm {G}$-centralizer of the
$\mathrm {G}$-centralizer of the ![]() $\mathfrak {sl}_2\mathbb {C}$-subalgebra. In this case, we refer to
$\mathfrak {sl}_2\mathbb {C}$-subalgebra. In this case, we refer to ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ as a JM-regular PHVS.
$(\mathrm {G}_0,\mathfrak {g}_1)$ as a JM-regular PHVS.
Fix a basis ![]() $\{f,h,e\}$ of
$\{f,h,e\}$ of ![]() $\mathfrak {sl}_2\mathbb {C}$ and let
$\mathfrak {sl}_2\mathbb {C}$ and let ![]() $\mathrm {T}<\mathrm {PSL}_2\mathbb {C}$ be the connected subgroup with Lie algebra
$\mathrm {T}<\mathrm {PSL}_2\mathbb {C}$ be the connected subgroup with Lie algebra ![]() $\langle h\rangle.$ The Hodge bundle associated to the representation uniformizing the Riemann surface
$\langle h\rangle.$ The Hodge bundle associated to the representation uniformizing the Riemann surface ![]() $X$ is given by
$X$ is given by ![]() $(E_\mathrm {T},e)$, where
$(E_\mathrm {T},e)$, where ![]() $E_\mathrm {T}$ is the holomorphic frame bundle of
$E_\mathrm {T}$ is the holomorphic frame bundle of ![]() $K^{-1}$ and
$K^{-1}$ and ![]() $e\in H^0(E_\mathrm {T}(\langle e\rangle )\otimes K).$ For
$e\in H^0(E_\mathrm {T}(\langle e\rangle )\otimes K).$ For ![]() $\mathrm {SL}_2\mathbb {C},$ we take
$\mathrm {SL}_2\mathbb {C},$ we take ![]() $E_\mathrm {T}$ to be the frame bundle of a square root of
$E_\mathrm {T}$ to be the frame bundle of a square root of ![]() $K^{-1}.$ Suppose
$K^{-1}.$ Suppose ![]() $\{f,h,e\}\subset \mathfrak {g}$ is an even
$\{f,h,e\}\subset \mathfrak {g}$ is an even ![]() $\mathfrak {sl}_2$-triple and consider the associated JM-regular PHVS
$\mathfrak {sl}_2$-triple and consider the associated JM-regular PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1).$ From our setup, it follows that extending structure group
$(\mathrm {G}_0,\mathfrak {g}_1).$ From our setup, it follows that extending structure group ![]() $(E_\mathrm {T}(\mathrm {G}_0),e)$ defines a maximal Hodge bundle,
$(E_\mathrm {T}(\mathrm {G}_0),e)$ defines a maximal Hodge bundle,
Let ![]() $\mathrm {C}<\mathrm {G}_0$ be the
$\mathrm {C}<\mathrm {G}_0$ be the ![]() $\mathrm {G}$-centralizer of the
$\mathrm {G}$-centralizer of the ![]() $\mathfrak {sl}_2\mathbb {C}$-subalgebra. Since
$\mathfrak {sl}_2\mathbb {C}$-subalgebra. Since ![]() $\mathrm {T}$ and
$\mathrm {T}$ and ![]() $\mathrm {C}$ are commuting subgroups of
$\mathrm {C}$ are commuting subgroups of ![]() $\mathrm {G}_0$, we can form a
$\mathrm {G}_0$, we can form a ![]() $\mathrm {G}_0$-bundle
$\mathrm {G}_0$-bundle ![]() $E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ out of
$E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ out of ![]() $E_\mathrm {T}$ and a holomorphic
$E_\mathrm {T}$ and a holomorphic ![]() $\mathrm {C}$-bundle
$\mathrm {C}$-bundle ![]() $E_\mathrm {C}$. Since
$E_\mathrm {C}$. Since ![]() $\mathrm {C}$ acts trivially on
$\mathrm {C}$ acts trivially on ![]() $\langle e\rangle,$ we have
$\langle e\rangle,$ we have ![]() $e\in H^0(E_\mathrm {C}\otimes _{\mathrm {G}_0} E_\mathrm {T}(\langle e\rangle )\otimes K)$. Moreover, this process does not change the Toledo invariant and defines a map
$e\in H^0(E_\mathrm {C}\otimes _{\mathrm {G}_0} E_\mathrm {T}(\langle e\rangle )\otimes K)$. Moreover, this process does not change the Toledo invariant and defines a map

from the moduli space of degree zero polystable ![]() $\mathrm {C}$-bundles to the moduli space of maximal Hodge bundles of type
$\mathrm {C}$-bundles to the moduli space of maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1).$
$(\mathrm {G}_0,\mathfrak {g}_1).$
Theorem B (Theorem 6.2)
If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular prehomogeneous vector space, then the map
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular prehomogeneous vector space, then the map ![]() $\Psi _e$ defines an isomorphism between the moduli space of degree zero polystable
$\Psi _e$ defines an isomorphism between the moduli space of degree zero polystable ![]() $\mathrm {C}$-bundles and the moduli space of maximal Hodge bundles of type
$\mathrm {C}$-bundles and the moduli space of maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$.
$(\mathrm {G}_0,\mathfrak {g}_1)$.
Remark 1.4 We note that the map ![]() $\Psi _e$ is a moduli space version of a restriction of the so-called global Slodowy slice map of [Reference Collier and SandersCS21]. In [Reference Bradlow, Collier, García-Prada, Gothen and OliveiraBCGGO21], an extension of the map
$\Psi _e$ is a moduli space version of a restriction of the so-called global Slodowy slice map of [Reference Collier and SandersCS21]. In [Reference Bradlow, Collier, García-Prada, Gothen and OliveiraBCGGO21], an extension of the map ![]() $\Psi _e$ to the entire Slodowy slice gives rise to the Cayley correspondence used to describe certain components of the moduli space of
$\Psi _e$ to the entire Slodowy slice gives rise to the Cayley correspondence used to describe certain components of the moduli space of ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles related to higher Teichmüller theory, generalizing the Cayley correspondence for the Hermitian group case given in [Reference Biquard, García-Prada and RubioBGR17]. It would be interesting to extend these results to the full Slodowy slice for every even
$\mathrm {G}^\mathbb {R}$-Higgs bundles related to higher Teichmüller theory, generalizing the Cayley correspondence for the Hermitian group case given in [Reference Biquard, García-Prada and RubioBGR17]. It would be interesting to extend these results to the full Slodowy slice for every even ![]() $\mathfrak {sl}_2$-triple.
$\mathfrak {sl}_2$-triple.
When ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular, the representations
$(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular, the representations ![]() $\rho :\pi _1(X)\to \mathrm {G}$ associated to maximal Hodge bundles of type
$\rho :\pi _1(X)\to \mathrm {G}$ associated to maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ are described by the following theorem.
$(\mathrm {G}_0,\mathfrak {g}_1)$ are described by the following theorem.
Theorem C (Theorem 6.5)
Fix a Riemann surface ![]() $X$ of genus
$X$ of genus ![]() $g\geqslant 2$ and suppose
$g\geqslant 2$ and suppose ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS associated to an even
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS associated to an even ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$. Let
$\{f,h,e\}$. Let ![]() $\mathrm {S}<\mathrm {G}$ be the associated connected subgroup and let
$\mathrm {S}<\mathrm {G}$ be the associated connected subgroup and let ![]() $\mathrm {C}$ be the
$\mathrm {C}$ be the ![]() $\mathrm {G}$-centralizer of
$\mathrm {G}$-centralizer of ![]() $\{f,h,e\}$. The Higgs bundle associated to a reductive representation
$\{f,h,e\}$. The Higgs bundle associated to a reductive representation ![]() $\rho :\pi _1(X)\to \mathrm {G}$ is a maximal Hodge bundle of type
$\rho :\pi _1(X)\to \mathrm {G}$ is a maximal Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if ![]() $\rho$ is a product
$\rho$ is a product ![]() $\rho =\rho _u*\rho _\mathrm {C}$, where
$\rho =\rho _u*\rho _\mathrm {C}$, where
−
 $\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is the uniformizing
$\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is the uniformizing  $\mathrm {PSL}_2\mathbb {R}$-representation of
$\mathrm {PSL}_2\mathbb {R}$-representation of  $X$ if
$X$ if  $\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and a lift of the uniformizing representation to
$\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and a lift of the uniformizing representation to  $\mathrm {SL}_2\mathbb {R}$ if
$\mathrm {SL}_2\mathbb {R}$ if  $\mathrm {S}\cong \mathrm {SL}_2\mathbb {C},$ and
$\mathrm {S}\cong \mathrm {SL}_2\mathbb {C},$ and−
 $\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is any representation into the compact real form of
$\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is any representation into the compact real form of  $\mathrm {C}.$
$\mathrm {C}.$
The representations ![]() $\rho =\rho _u*\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G}$ all factor through a real form of Hodge type
$\rho =\rho _u*\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G}$ all factor through a real form of Hodge type ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ which is canonically associated to the grading
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ which is canonically associated to the grading ![]() $\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ (see Proposition 3.8). Moreover, the
$\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ (see Proposition 3.8). Moreover, the ![]() $\mathrm {G}^\mathbb {R}$-centralizer of any such representation is compact, and hence these representations do not factor through any proper parabolic subgroups
$\mathrm {G}^\mathbb {R}$-centralizer of any such representation is compact, and hence these representations do not factor through any proper parabolic subgroups ![]() $\mathrm {P}^\mathbb {R}<\mathrm {G}^\mathbb {R}.$
$\mathrm {P}^\mathbb {R}<\mathrm {G}^\mathbb {R}.$
From the above results, it follows that the equivariant holomorphic map ![]() $f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ associated to such a maximal variation of Hodge structure
$f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ associated to such a maximal variation of Hodge structure ![]() $(\rho,f_\rho )$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. In this paper we discuss how the choice of the Toledo character is related to a metric of minimal holomorphic sectional curvature
$(\rho,f_\rho )$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. In this paper we discuss how the choice of the Toledo character is related to a metric of minimal holomorphic sectional curvature ![]() $-1$ on
$-1$ on ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$, providing an alternative proof of Theorem A. Our bounds for the sectional curvature give the bounds found in [Reference LiLi22] in the case of
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$, providing an alternative proof of Theorem A. Our bounds for the sectional curvature give the bounds found in [Reference LiLi22] in the case of ![]() $\mathrm {SL}_n\mathbb {C}$.
$\mathrm {SL}_n\mathbb {C}$.
Now consider a general grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element ![]() $\zeta$, not necessarily coming from an
$\zeta$, not necessarily coming from an ![]() $\mathfrak {sl}_2$-triple. Pick a point
$\mathfrak {sl}_2$-triple. Pick a point ![]() $e\in \Omega \subset \mathfrak {g}_1$ in the open
$e\in \Omega \subset \mathfrak {g}_1$ in the open ![]() $\mathrm {G}_0$-orbit, and complete
$\mathrm {G}_0$-orbit, and complete ![]() $e$ to an
$e$ to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ with
$\{f,h,e\}$ with ![]() $h\in \mathfrak {g}_0.$ If
$h\in \mathfrak {g}_0.$ If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not a JM-regular PHVS, then
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not a JM-regular PHVS, then ![]() $s=\zeta - {h}/{2}$ is nonzero and we define
$s=\zeta - {h}/{2}$ is nonzero and we define ![]() $\hat {\mathrm {G}}_0<\mathrm {G}_0$ to be the
$\hat {\mathrm {G}}_0<\mathrm {G}_0$ to be the ![]() $\mathrm {G}_0$ centralizer of
$\mathrm {G}_0$ centralizer of ![]() $s$ and
$s$ and ![]() $\hat {\mathfrak {g}}_1=\{x\in \mathfrak {g}_1\,|\,[s,x]\}=0.$ With this setup,
$\hat {\mathfrak {g}}_1=\{x\in \mathfrak {g}_1\,|\,[s,x]\}=0.$ With this setup, ![]() $\hat {\mathrm {G}}_0$ is reductive and
$\hat {\mathrm {G}}_0$ is reductive and ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ defines a PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ defines a PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ which contains
$(\mathrm {G}_0,\mathfrak {g}_1)$ which contains ![]() $e\in \hat \Omega \subset \hat {\mathfrak {g}}_1$ in the open orbit (see § 2.4). Moreover, the
$e\in \hat \Omega \subset \hat {\mathfrak {g}}_1$ in the open orbit (see § 2.4). Moreover, the ![]() $\mathrm {G}_0$-centralizer
$\mathrm {G}_0$-centralizer ![]() $\hat {\mathrm {C}}$ of the
$\hat {\mathrm {C}}$ of the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ satisfies
$\{f,h,e\}$ satisfies ![]() $\hat {\mathrm {C}}<\hat {\mathrm {G}}_0.$ We call
$\hat {\mathrm {C}}<\hat {\mathrm {G}}_0.$ We call ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ a maximal JM-regular PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ a maximal JM-regular PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1).$
$(\mathrm {G}_0,\mathfrak {g}_1).$
In § 6.3, we show that all maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ reduce to a maximal Hodge bundles of type
$(\mathrm {G}_0,\mathfrak {g}_1)$ reduce to a maximal Hodge bundles of type ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ (see Proposition 6.15). We then show that the moduli space
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ (see Proposition 6.15). We then show that the moduli space ![]() ${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ of maximal Hodge bundles of type
${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ of maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is isomorphic to the moduli space of polystable
$(\mathrm {G}_0,\mathfrak {g}_1)$ is isomorphic to the moduli space of polystable ![]() $\hat {\mathrm {C}}$-bundles and deduce rigidity results for maximal variations of Hodge structure (see Theorems 6.16 and 6.17). This recovers rigidity results for maximal variations of Hodge structure in the Hermitian case.
$\hat {\mathrm {C}}$-bundles and deduce rigidity results for maximal variations of Hodge structure (see Theorems 6.16 and 6.17). This recovers rigidity results for maximal variations of Hodge structure in the Hermitian case.
2. Prehomogeneous vector spaces,  $\mathbb {Z}$-gradings and the Toledo character
$\mathbb {Z}$-gradings and the Toledo character
For this section, let ![]() $\mathrm {G}$ be a complex reductive Lie group with Lie algebra
$\mathrm {G}$ be a complex reductive Lie group with Lie algebra ![]() $\mathfrak {g}.$ Throughout the paper, the word character will be used to refer to a Lie group morphism
$\mathfrak {g}.$ Throughout the paper, the word character will be used to refer to a Lie group morphism ![]() $\chi :\mathrm {G}\to \mathbb {C}^*$ and also a Lie algebra morphism
$\chi :\mathrm {G}\to \mathbb {C}^*$ and also a Lie algebra morphism ![]() $\chi :\mathfrak {g}\to \mathbb {C}$, what type of object is being considered should be clear from the context.
$\chi :\mathfrak {g}\to \mathbb {C}$, what type of object is being considered should be clear from the context.
2.1 Prehomogeneous vector spaces
We gather together some basic facts about PHVSs. The main references are [Reference KimuraKim03, Reference KnappKna02, Reference MortajineMor91, Reference Sato and KimuraSK77].
A prehomogeneous vector space for ![]() $\mathrm {G}$ is a finite-dimensional complex vector space
$\mathrm {G}$ is a finite-dimensional complex vector space ![]() $V$ together with a holomorphic representation
$V$ together with a holomorphic representation ![]() $\rho :\mathrm {G}\to \mathrm {GL}(V)$ such that
$\rho :\mathrm {G}\to \mathrm {GL}(V)$ such that ![]() $V$ has an open
$V$ has an open ![]() $\mathrm {G}$-orbit. Such an open orbit is necessarily unique and dense. If
$\mathrm {G}$-orbit. Such an open orbit is necessarily unique and dense. If ![]() $V$ is a PHVS, let
$V$ is a PHVS, let ![]() $\Omega$ denote the open orbit in
$\Omega$ denote the open orbit in ![]() $V$ and
$V$ and ![]() $S=V\setminus \Omega$ be the singular set. For
$S=V\setminus \Omega$ be the singular set. For ![]() $x\in V$, denote the
$x\in V$, denote the ![]() $\mathrm {G}$-stabilizer of
$\mathrm {G}$-stabilizer of ![]() $x$ by
$x$ by ![]() $\mathrm {G}^x.$ A PHVS vector space
$\mathrm {G}^x.$ A PHVS vector space ![]() $V$ is called regular if
$V$ is called regular if ![]() $\mathrm {G}^x$ is reductive for
$\mathrm {G}^x$ is reductive for ![]() $x\in \Omega$, otherwise it is called nonregular.
$x\in \Omega$, otherwise it is called nonregular.
We say that ![]() $(\mathrm {H},W)$ is a PHVSS of
$(\mathrm {H},W)$ is a PHVSS of ![]() $(\mathrm {G},V)$ if
$(\mathrm {G},V)$ if ![]() $(\mathrm {H},W)$ is a PHVS,
$(\mathrm {H},W)$ is a PHVS, ![]() $\mathrm {H}\subset \mathrm {G}$ is a subgroup,
$\mathrm {H}\subset \mathrm {G}$ is a subgroup, ![]() $W\subset V$ is a vector subspace, and the action of
$W\subset V$ is a vector subspace, and the action of ![]() $\mathrm {H}$ is the restriction of the action of
$\mathrm {H}$ is the restriction of the action of ![]() $\mathrm {G}$.
$\mathrm {G}$.
Example 2.1
(1) The vector space
 $\mathbb {C}^n$ is a PHVS for the standard representation of
$\mathbb {C}^n$ is a PHVS for the standard representation of  $\mathrm {GL}_n\mathbb {C}$. For this example,
$\mathrm {GL}_n\mathbb {C}$. For this example,  $\Omega =\mathbb {C}^n\setminus \{0\}$, and it is regular only when
$\Omega =\mathbb {C}^n\setminus \{0\}$, and it is regular only when  $n=1.$
$n=1.$(2) The vector space
 $M_{p,q}$ of
$M_{p,q}$ of  $p\times q$ matrices is a PHVS for the action of
$p\times q$ matrices is a PHVS for the action of  $\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C})$ given by
$\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C})$ given by  $(A,B)\cdot M= AMB^{-1}.$ Here,
$(A,B)\cdot M= AMB^{-1}.$ Here,  $\Omega =\{M\in M_{p,q}\,|\, \operatorname {rk}(M)=\min (p,q)\}.$ This example is regular only when
$\Omega =\{M\in M_{p,q}\,|\, \operatorname {rk}(M)=\min (p,q)\}.$ This example is regular only when  $p=q$.
$p=q$.(3) The vector space
 $M_{p,q}$ is also a PHVS for the action of
$M_{p,q}$ is also a PHVS for the action of  $\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ given by
$\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ given by  $(A,B)\cdot M=AMB^{-1}.$ Here
$(A,B)\cdot M=AMB^{-1}.$ Here  $\Omega =\{ M\in M_{p,q}\,|\,\operatorname {rk}(M\cdot M^\mathrm {T})=\min (p,q)\}$. Also, the vector space
$\Omega =\{ M\in M_{p,q}\,|\,\operatorname {rk}(M\cdot M^\mathrm {T})=\min (p,q)\}$. Also, the vector space  $M_{p,q}\oplus M_{q,r}$ is a PHVS for the action of
$M_{p,q}\oplus M_{q,r}$ is a PHVS for the action of  $\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C})$ given by
$\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C})$ given by  $(A,B,C)\cdot (M,N)=(AMB^{-1},BNC^{-1}).$ Here
$(A,B,C)\cdot (M,N)=(AMB^{-1},BNC^{-1}).$ Here  $\Omega =\{(M,N)\in M_{p,q}\oplus M_{q,r}\,|\,\operatorname {rk}(MN)=\min (p,q,r)\}$.
$\Omega =\{(M,N)\in M_{p,q}\oplus M_{q,r}\,|\,\operatorname {rk}(MN)=\min (p,q,r)\}$.The first example is regular when
 $p\leqslant q$ and the second example is regular when
$p\leqslant q$ and the second example is regular when  $p=r$ and
$p=r$ and  $p\leqslant q$. Note that the inclusions
make
$p\leqslant q$. Note that the inclusions
make
 $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ a PHVSS of
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ a PHVSS of  $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p}).$
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p}).$
Let ![]() $V$ be a PHVS for
$V$ be a PHVS for ![]() $\mathrm {G}$ with representation
$\mathrm {G}$ with representation ![]() $\rho.$ A nonconstant rational function
$\rho.$ A nonconstant rational function ![]() $F:V\to \mathbb {C}$ is called a relative invariant if there exists a Lie group character
$F:V\to \mathbb {C}$ is called a relative invariant if there exists a Lie group character ![]() $\chi :\mathrm {G}\to \mathbb {C}^*$ such that
$\chi :\mathrm {G}\to \mathbb {C}^*$ such that
Here are some fundamental facts appearing in [Reference Sato and KimuraSK77, §4].
Proposition 2.2 Let ![]() $V$ be a PHVS for
$V$ be a PHVS for ![]() $\mathrm {G}$ with representation
$\mathrm {G}$ with representation ![]() $\rho$.
$\rho$.
(i) Up to a constant, a relative invariant is uniquely determined by its corresponding character. In particular, any relative invariant is a homogeneous function.
(ii)
 $V$ is regular if and only if the singular set
$V$ is regular if and only if the singular set  $S$ is a hypersurface.
$S$ is a hypersurface.(iii) Let
 $\chi :\mathrm {G}\to \mathbb {C}^*$ be a character. Then there is a relative invariant for
$\chi :\mathrm {G}\to \mathbb {C}^*$ be a character. Then there is a relative invariant for  $\chi$ if and only if
$\chi$ if and only if  $\chi$ is trivial on the stabilizers of points in
$\chi$ is trivial on the stabilizers of points in  $\Omega,$ that is,
$\Omega,$ that is,  $\chi |_{\mathrm {G}^x}=1$ for all
$\chi |_{\mathrm {G}^x}=1$ for all  $x\in \Omega.$
$x\in \Omega.$
Example 2.3 The regular PHVS ![]() $M_{p,p}$ from Example 2.1(2) has a relative invariant
$M_{p,p}$ from Example 2.1(2) has a relative invariant ![]() $F:M_{p,p}\to \mathbb {C}$ given by
$F:M_{p,p}\to \mathbb {C}$ given by ![]() $F(M)=\det (M).$ The associated character
$F(M)=\det (M).$ The associated character ![]() $\chi :\mathrm {G}\to \mathbb {C}^*$ is given by
$\chi :\mathrm {G}\to \mathbb {C}^*$ is given by ![]() $\chi (A,B)=\det (A)\det (B)^{-1}$ since
$\chi (A,B)=\det (A)\det (B)^{-1}$ since
The regular PHVS ![]() $M_{p,q}\oplus M_{q,p}$ with
$M_{p,q}\oplus M_{q,p}$ with ![]() $p\leqslant q$ from Example 2.1(3) has a relative-invariant given by
$p\leqslant q$ from Example 2.1(3) has a relative-invariant given by ![]() $F(M,N)=\det (MN)$. The associated character is
$F(M,N)=\det (MN)$. The associated character is ![]() $\chi (A,B,C)=\det (A)\det (C^{-1})$ since
$\chi (A,B,C)=\det (A)\det (C^{-1})$ since
This relative invariant also defines a relative invariant for the ![]() $\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ PHVSS given by
$\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ PHVSS given by ![]() $(M,N)=(M,-M^\mathrm {T})$. For
$(M,N)=(M,-M^\mathrm {T})$. For ![]() $(A,B)\in \mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$, the associated character is
$(A,B)\in \mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$, the associated character is ![]() $\chi (A,B)=\det (AA^\mathrm {T})=\det (A)^2.$
$\chi (A,B)=\det (AA^\mathrm {T})=\det (A)^2.$
2.2 Prehomogeneous vector spaces associated to  $\mathbb {Z}$-gradings
$\mathbb {Z}$-gradings
A ![]() $\mathbb {Z}$-grading of a semisimple Lie algebra
$\mathbb {Z}$-grading of a semisimple Lie algebra ![]() $\mathfrak {g}$ is a decomposition
$\mathfrak {g}$ is a decomposition
The subalgebra ![]() $\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j$ is a parabolic subalgebra with Levi subalgebra
$\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j$ is a parabolic subalgebra with Levi subalgebra ![]() $\mathfrak {g}_0\subset \mathfrak {p}.$ There is an element
$\mathfrak {g}_0\subset \mathfrak {p}.$ There is an element ![]() $\zeta \in \mathfrak {g}_0$ such that
$\zeta \in \mathfrak {g}_0$ such that ![]() $\mathfrak {g}_j=\{X\in \mathfrak {g}\,|\,[\zeta,x]=jx\}$; the element
$\mathfrak {g}_j=\{X\in \mathfrak {g}\,|\,[\zeta,x]=jx\}$; the element ![]() $\zeta$ is called the grading element of the
$\zeta$ is called the grading element of the ![]() $\mathbb {Z}$-grading.
$\mathbb {Z}$-grading.
Given a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, let
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta$;
$\zeta$; ![]() $\mathrm {G}_0$ acts on each factor
$\mathrm {G}_0$ acts on each factor ![]() $\mathfrak {g}_j$. The relation between
$\mathfrak {g}_j$. The relation between ![]() $\mathbb {Z}$-gradings and PHVSs is given by the following theorem of Vinberg (see [Reference KnappKna02, Theorem 10.19]).
$\mathbb {Z}$-gradings and PHVSs is given by the following theorem of Vinberg (see [Reference KnappKna02, Theorem 10.19]).
Proposition 2.4 For each ![]() $j\neq 0,$
$j\neq 0,$ ![]() $\mathfrak {g}_j$ is a PHVS for
$\mathfrak {g}_j$ is a PHVS for ![]() $\mathrm {G}_0.$
$\mathrm {G}_0.$
Prehomogeneous vector spaces arising from ![]() $\mathbb {Z}$-gradings of
$\mathbb {Z}$-gradings of ![]() $\mathfrak {g}$ are said to be of parabolic type. From now on, we will consider only PHVSs of parabolic type.
$\mathfrak {g}$ are said to be of parabolic type. From now on, we will consider only PHVSs of parabolic type.
Example 2.5 All of the PHVSs from Example 2.1 are of parabolic type. Below the parabolic refers to the subgroup with Lie algebra ![]() $\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j.$
$\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j.$
− For
 $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}),M_{p,q})$,
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}),M_{p,q})$,  $\mathrm {G}=\mathrm {SL}_{p+q}\mathbb {C}$ and the parabolic is the stabilizer a
$\mathrm {G}=\mathrm {SL}_{p+q}\mathbb {C}$ and the parabolic is the stabilizer a  $p$-plane in
$p$-plane in  $\mathbb {C}^{p+q}.$
$\mathbb {C}^{p+q}.$− For
 $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$,
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$,  $\mathrm {G}=\mathrm {SO}_{2p+q}\mathbb {C}$ and the parabolic is the stabilizer of an isotropic
$\mathrm {G}=\mathrm {SO}_{2p+q}\mathbb {C}$ and the parabolic is the stabilizer of an isotropic  $p$-plane in
$p$-plane in  $\mathbb {C}^{2p+q}$.
$\mathbb {C}^{2p+q}$.− For
 $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$,
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$,  $\mathrm {G}=\mathrm {SL}_{p+q+r}\mathbb {C}$ and the parabolic is the stabilizer of a flag
$\mathrm {G}=\mathrm {SL}_{p+q+r}\mathbb {C}$ and the parabolic is the stabilizer of a flag  $\mathbb {C}^p\subset \mathbb {C}^{p+q}\subset \mathbb {C}^{p+q+r}.$
$\mathbb {C}^p\subset \mathbb {C}^{p+q}\subset \mathbb {C}^{p+q+r}.$
Consider a nonzero nilpotent element ![]() $e\in \mathfrak {g}.$ By the Jacobson–Morozov theorem,
$e\in \mathfrak {g}.$ By the Jacobson–Morozov theorem, ![]() $e$ can be completed to an
$e$ can be completed to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}\subset \mathfrak {g}$, that is, a triple satisfying the bracket relations of
$\{f,h,e\}\subset \mathfrak {g}$, that is, a triple satisfying the bracket relations of ![]() $\mathfrak {sl}_2\mathbb {C}$:
$\mathfrak {sl}_2\mathbb {C}$:
Moreover, given ![]() $\{h,e\}$ so that
$\{h,e\}$ so that ![]() $[h,e]=2e$ and
$[h,e]=2e$ and ![]() $h\in {\operatorname {ad}}_e(\mathfrak {g})$, there is a unique
$h\in {\operatorname {ad}}_e(\mathfrak {g})$, there is a unique ![]() $f\in \mathfrak {g}$ such that
$f\in \mathfrak {g}$ such that ![]() $\{f,h,e\}$ is an
$\{f,h,e\}$ is an ![]() $\mathfrak {sl}_2$-triple.
$\mathfrak {sl}_2$-triple.
Given an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$, the semisimple element
$\{f,h,e\}$, the semisimple element ![]() $h$ acts on
$h$ acts on ![]() $\mathfrak {g}$ with integral weights and thus defines a
$\mathfrak {g}$ with integral weights and thus defines a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, where
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, where ![]() $\mathfrak {g}_j=\{x\in \mathfrak {g}\,|\, {\operatorname {ad}}_h(x)=jx\}.$ Note that
$\mathfrak {g}_j=\{x\in \mathfrak {g}\,|\, {\operatorname {ad}}_h(x)=jx\}.$ Note that ![]() $e\in \mathfrak {g}_2.$ We have the following result of Kostant and Malcev (see [Reference KnappKna02, Theorem 10.10]).
$e\in \mathfrak {g}_2.$ We have the following result of Kostant and Malcev (see [Reference KnappKna02, Theorem 10.10]).
Proposition 2.6 Let ![]() $\{f,h,e\}\subset \mathfrak {g}$ be an
$\{f,h,e\}\subset \mathfrak {g}$ be an ![]() $\mathfrak {sl}_2$-triple with associated
$\mathfrak {sl}_2$-triple with associated ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, and let
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, and let ![]() $\mathrm {G}_0<\mathrm {G}$ be the associated analytic subgroup with Lie algebra
$\mathrm {G}_0<\mathrm {G}$ be the associated analytic subgroup with Lie algebra ![]() $\mathfrak {g}_0.$ Then
$\mathfrak {g}_0.$ Then ![]() $e$ is in the open orbit
$e$ is in the open orbit ![]() $\Omega$ of the PHVS
$\Omega$ of the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_2)$.
$(\mathrm {G}_0,\mathfrak {g}_2)$.
Corollary 2.7 The PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_2)$ arising from an
$(\mathrm {G}_0,\mathfrak {g}_2)$ arising from an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ is regular.
$\{f,h,e\}$ is regular.
Proof. Since ![]() $e\in \Omega \subset \mathfrak {g}_2$, we need to show that the stabilizer
$e\in \Omega \subset \mathfrak {g}_2$, we need to show that the stabilizer ![]() $\mathrm {G}_0^e$ is reductive. The group
$\mathrm {G}_0^e$ is reductive. The group ![]() $\mathrm {G}_0$ centralizes
$\mathrm {G}_0$ centralizes ![]() $h,$ so the stabilizer
$h,$ so the stabilizer ![]() $\mathrm {G}_0^e$ of
$\mathrm {G}_0^e$ of ![]() $e$ stabilizes both
$e$ stabilizes both ![]() $h$ and
$h$ and ![]() $e$. By the uniqueness part of the Jacobson–Morozov theorem,
$e$. By the uniqueness part of the Jacobson–Morozov theorem, ![]() $\mathrm {G}_0^e$ stabilizes the
$\mathrm {G}_0^e$ stabilizes the ![]() $\mathfrak {sl}_2$-triple. As the centralizer of an
$\mathfrak {sl}_2$-triple. As the centralizer of an ![]() $\mathfrak {sl}_2$-subalgebra is reductive (see [Reference Collingwood and McGovernCM93, Lemma 3.7.3]), we conclude that
$\mathfrak {sl}_2$-subalgebra is reductive (see [Reference Collingwood and McGovernCM93, Lemma 3.7.3]), we conclude that ![]() $\mathrm {G}_0^e$ is reductive.
$\mathrm {G}_0^e$ is reductive.
Let ![]() $B:\mathfrak {g}\times \mathfrak {g}\to \mathbb {C}$ denote the Killing form of
$B:\mathfrak {g}\times \mathfrak {g}\to \mathbb {C}$ denote the Killing form of ![]() $\mathfrak {g}.$ Given an
$\mathfrak {g}.$ Given an ![]() $\mathfrak {sl}_2$-triple,
$\mathfrak {sl}_2$-triple, ![]() $\{f,h,e\}\subset \mathfrak {g}$ with associated
$\{f,h,e\}\subset \mathfrak {g}$ with associated ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, define the Lie algebra character
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, define the Lie algebra character ![]() $\chi _{h}:\mathfrak {g}_0\to \mathbb {C}$ by
$\chi _{h}:\mathfrak {g}_0\to \mathbb {C}$ by
Proposition 2.8 There is a positive integer ![]() $q$ such that
$q$ such that ![]() $q\cdot \chi _{h}$ exponentiates to a character
$q\cdot \chi _{h}$ exponentiates to a character
which has a relative invariant of degree ![]() $q\cdot B( {h}/{2}, {h}/{2})$.
$q\cdot B( {h}/{2}, {h}/{2})$.
Remark 2.9 In fact, we will prove that the associated relative invariant is a polynomial in Proposition 3.16.
Proof. Let ![]() $\mathfrak {g}_0^e\subset \mathfrak {g}_0$ be the Lie algebra of the
$\mathfrak {g}_0^e\subset \mathfrak {g}_0$ be the Lie algebra of the ![]() $\mathrm {G}_0$-stabilizer of
$\mathrm {G}_0$-stabilizer of ![]() $e\in \mathfrak {g}_2.$ For
$e\in \mathfrak {g}_2.$ For ![]() $x\in \mathfrak {g}^e_0$, we have
$x\in \mathfrak {g}^e_0$, we have
Thus, ![]() $\chi _h(\mathfrak {g}_0^e)=0$, and there is a positive integer
$\chi _h(\mathfrak {g}_0^e)=0$, and there is a positive integer ![]() $q$ so that
$q$ so that ![]() $q\cdot \chi _h$ exponentiates to a character which is trivial on the identity component of
$q\cdot \chi _h$ exponentiates to a character which is trivial on the identity component of ![]() $\mathrm {G}_0^e.$ Since
$\mathrm {G}_0^e.$ Since ![]() $\mathrm {G}_0^e$ has a finite number of components, we can choose
$\mathrm {G}_0^e$ has a finite number of components, we can choose ![]() $q$ so that
$q$ so that ![]() $q\cdot \chi _h$ exponentiates to a character
$q\cdot \chi _h$ exponentiates to a character ![]() $\chi _{h,q}:\mathrm {G}_0\to \mathbb {C}^*$ whose restriction to
$\chi _{h,q}:\mathrm {G}_0\to \mathbb {C}^*$ whose restriction to ![]() $\mathrm {G}_0^e$ is trivial. Hence, by part (iii) of Proposition 2.2, the character
$\mathrm {G}_0^e$ is trivial. Hence, by part (iii) of Proposition 2.2, the character ![]() $\chi _{h,q}$ has a relative invariant
$\chi _{h,q}$ has a relative invariant ![]() $F:\mathfrak {g}_2\to \mathbb {C}$ such that
$F:\mathfrak {g}_2\to \mathbb {C}$ such that ![]() $F(e)\neq 0$. For the degree, we have
$F(e)\neq 0$. For the degree, we have ![]() $\operatorname {Ad}_{\exp (t h)}(e)=\exp (2t) e$. Thus,
$\operatorname {Ad}_{\exp (t h)}(e)=\exp (2t) e$. Thus,
By Proposition 2.2 ![]() $F$ is homogeneous, and so has degree
$F$ is homogeneous, and so has degree ![]() $q\cdot B( {h}/{2}, {h}/{2}).$
$q\cdot B( {h}/{2}, {h}/{2}).$
Remark 2.10 Not every regular PHVS of the form ![]() $(\mathrm {G}_0,\mathfrak {g}_2)$ arises from an
$(\mathrm {G}_0,\mathfrak {g}_2)$ arises from an ![]() $\mathfrak {sl}_2$-triple. For examples in
$\mathfrak {sl}_2$-triple. For examples in ![]() $\mathrm {E}_6$,
$\mathrm {E}_6$, ![]() $\mathrm {E}_7$ and
$\mathrm {E}_7$ and ![]() $\mathrm {E}_8$ see [Reference RubenthalerRub11, Remark 4.18]. In fact, the
$\mathrm {E}_8$ see [Reference RubenthalerRub11, Remark 4.18]. In fact, the ![]() $\mathrm {B}_3$ example in [Reference RubenthalerRub11, Table 1] gives a very simple example of a regular PHVS which does not arise from an
$\mathrm {B}_3$ example in [Reference RubenthalerRub11, Table 1] gives a very simple example of a regular PHVS which does not arise from an ![]() $\mathfrak {sl}_2$-triple. For such regular PHVSs the grading element
$\mathfrak {sl}_2$-triple. For such regular PHVSs the grading element ![]() $\zeta$ does not have a relative invariant.
$\zeta$ does not have a relative invariant.
2.3 Canonical  $\mathbb {Z}$-gradings associated to parabolics
$\mathbb {Z}$-gradings associated to parabolics
In this section we fix some normalizations for the ![]() $\mathbb {Z}$-gradings we will consider.
$\mathbb {Z}$-gradings we will consider.
Up to conjugation, all ![]() $\mathbb {Z}$-gradings of
$\mathbb {Z}$-gradings of ![]() $\mathfrak {g}$ arise from labeling the nodes of the Dynkin diagram of
$\mathfrak {g}$ arise from labeling the nodes of the Dynkin diagram of ![]() $\mathfrak {g}$ with nonnegative integers [Reference VinbergVin94, Chapter 3.5]. This works as follows. Let
$\mathfrak {g}$ with nonnegative integers [Reference VinbergVin94, Chapter 3.5]. This works as follows. Let ![]() $\mathfrak {t}\subset \mathfrak {g}$ be a Cartan subalgebra and
$\mathfrak {t}\subset \mathfrak {g}$ be a Cartan subalgebra and ![]() $\Delta =\Delta (\mathfrak {g},\mathfrak {t})$ be the corresponding set of roots. Pick a set of simple roots
$\Delta =\Delta (\mathfrak {g},\mathfrak {t})$ be the corresponding set of roots. Pick a set of simple roots ![]() $\Pi \subset \Delta$ and let
$\Pi \subset \Delta$ and let ![]() $\Delta ^+\subset \Delta$ be the set of positive roots. Every root
$\Delta ^+\subset \Delta$ be the set of positive roots. Every root ![]() $\alpha \in \Delta ^+$ can be written as
$\alpha \in \Delta ^+$ can be written as ![]() $\alpha =\sum _{\alpha _i\in \Pi }n_i\alpha _i$, where all
$\alpha =\sum _{\alpha _i\in \Pi }n_i\alpha _i$, where all ![]() $n_i$ are nonnegative integers. For each
$n_i$ are nonnegative integers. For each ![]() $\alpha _i\in \Pi$, choose nonnegative integers
$\alpha _i\in \Pi$, choose nonnegative integers ![]() $p_i$, that is, label the nodes of the Dynkin diagram of
$p_i$, that is, label the nodes of the Dynkin diagram of ![]() $\Pi$ with nonnegative integers
$\Pi$ with nonnegative integers ![]() $p_i$. This choice defines a
$p_i$. This choice defines a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, where
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, where ![]() $\mathfrak {g}_j$ is the direct sum of all root spaces
$\mathfrak {g}_j$ is the direct sum of all root spaces ![]() $\mathfrak {g}_\alpha$ such that
$\mathfrak {g}_\alpha$ such that ![]() $\alpha =\sum _{\alpha _i\in \Pi }n_i\alpha _i$ and
$\alpha =\sum _{\alpha _i\in \Pi }n_i\alpha _i$ and ![]() $j=\sum _{i}n_ip_i.$
$j=\sum _{i}n_ip_i.$
In the above construction, the associated parabolic ![]() $\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j$ and the Levi subalgebra
$\mathfrak {p}=\bigoplus _{j\geqslant 0}\mathfrak {g}_j$ and the Levi subalgebra ![]() $\mathfrak {g}_0$ depend only on the labels
$\mathfrak {g}_0$ depend only on the labels ![]() $p_i\text { mod}~2$. Namely, up to conjugation, parabolic subalgebras
$p_i\text { mod}~2$. Namely, up to conjugation, parabolic subalgebras ![]() $\mathfrak {p}$ are determined by subsets
$\mathfrak {p}$ are determined by subsets ![]() $\Theta \subset \Pi$, where
$\Theta \subset \Pi$, where
We define the canonical ![]() $\mathbb {Z}$-grading of
$\mathbb {Z}$-grading of ![]() $\mathfrak {p}_\Theta$ by labeling the
$\mathfrak {p}_\Theta$ by labeling the ![]() $\alpha _i$-node of the Dynkin diagram
$\alpha _i$-node of the Dynkin diagram ![]() $0$ if
$0$ if ![]() $\alpha _i\in \Theta$ and
$\alpha _i\in \Theta$ and ![]() $1$ if
$1$ if ![]() $\alpha _i\in \Pi \setminus \Theta.$ That is,
$\alpha _i\in \Pi \setminus \Theta.$ That is, ![]() $\mathfrak {g}_j$ is given by
$\mathfrak {g}_j$ is given by
Remark 2.11 We will often consider PHVSs of parabolic type and of the form ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ where
$(\mathrm {G}_0,\mathfrak {g}_1)$ where ![]() $\mathfrak {g}_1$ is the weight-1 piece of the canonical grading of a parabolic subalgebra of
$\mathfrak {g}_1$ is the weight-1 piece of the canonical grading of a parabolic subalgebra of ![]() $\mathfrak {g}.$ This is not a major restriction since, given a general PHVS
$\mathfrak {g}.$ This is not a major restriction since, given a general PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$ of parabolic type, the subalgebra consisting of graded pieces
$(\mathrm {G}_0,\mathfrak {g}_k)$ of parabolic type, the subalgebra consisting of graded pieces ![]() $\mathfrak {g}_j$ with
$\mathfrak {g}_j$ with ![]() $j=0\text { mod}~k$ is reductive and
$j=0\text { mod}~k$ is reductive and ![]() $\mathfrak {g}_k$ is the weight 1 piece of the canonical grading of a parabolic in this subalgebra.
$\mathfrak {g}_k$ is the weight 1 piece of the canonical grading of a parabolic in this subalgebra.
An ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}\subset \mathfrak {g}$ is called even if
$\{f,h,e\}\subset \mathfrak {g}$ is called even if ![]() ${\operatorname {ad}}_h$ has only even eigenvalues. Parabolic subalgebras arising from even
${\operatorname {ad}}_h$ has only even eigenvalues. Parabolic subalgebras arising from even ![]() $\mathfrak {sl}_2$-triples are called even Jacobson–Morozov parabolics. For such parabolics, the canonical grading is given by
$\mathfrak {sl}_2$-triples are called even Jacobson–Morozov parabolics. For such parabolics, the canonical grading is given by ![]() ${\operatorname {ad}}_{ {h}/{2}}$; the PHVS
${\operatorname {ad}}_{ {h}/{2}}$; the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is regular by Corollary 2.7 and, by Proposition 2.8, there is a relative invariant associated to the character
$(\mathrm {G}_0,\mathfrak {g}_1)$ is regular by Corollary 2.7 and, by Proposition 2.8, there is a relative invariant associated to the character ![]() $\chi _h$ from (2.1). As a result we will call a PHVS
$\chi _h$ from (2.1). As a result we will call a PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ which arises from an even
$(\mathrm {G}_0,\mathfrak {g}_1)$ which arises from an even ![]() $\mathfrak {sl}_2$-triple a JM-regular PHVS.
$\mathfrak {sl}_2$-triple a JM-regular PHVS.
Example 2.12 When ![]() $\Theta =\emptyset,$
$\Theta =\emptyset,$ ![]() $\mathrm {G}_0$ is Cartan subgroup and
$\mathrm {G}_0$ is Cartan subgroup and ![]() $\mathfrak {g}_1$ is the direct sum of simple root spaces. Such a PHVS
$\mathfrak {g}_1$ is the direct sum of simple root spaces. Such a PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is always JM-regular and arises from a principal
$(\mathrm {G}_0,\mathfrak {g}_1)$ is always JM-regular and arises from a principal ![]() $\mathfrak {sl}_2$-triple. Here
$\mathfrak {sl}_2$-triple. Here ![]() $\Omega \subset \mathfrak {g}$ consists of vectors with nonzero projection onto each simple root space and the stabilizer of such a point is the center of
$\Omega \subset \mathfrak {g}$ consists of vectors with nonzero projection onto each simple root space and the stabilizer of such a point is the center of ![]() $\mathrm {G}.$
$\mathrm {G}.$
Example 2.13 Let ![]() $\eta =\sum _{\alpha _i\in \Pi }n_i\alpha _i$ be the longest root of
$\eta =\sum _{\alpha _i\in \Pi }n_i\alpha _i$ be the longest root of ![]() $\Delta ^+.$ For
$\Delta ^+.$ For ![]() $\mathfrak {g}$ not of type
$\mathfrak {g}$ not of type ![]() $\mathrm {E}_8,\mathrm {F}_4,\mathrm {G}_2,$ there is at least one simple root
$\mathrm {E}_8,\mathrm {F}_4,\mathrm {G}_2,$ there is at least one simple root ![]() $\alpha _i$ with
$\alpha _i$ with ![]() $n_i=1$. For such a root set
$n_i=1$. For such a root set ![]() $\Theta =\Pi \setminus \{\alpha _i\}.$ In this case, the canonical
$\Theta =\Pi \setminus \{\alpha _i\}.$ In this case, the canonical ![]() $\mathbb {Z}$-grading of the parabolic
$\mathbb {Z}$-grading of the parabolic ![]() $\mathfrak {p}_\Theta$ is given by
$\mathfrak {p}_\Theta$ is given by
For these examples, ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if it is JM-regular. The associated flag variety
$(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if it is JM-regular. The associated flag variety ![]() $\mathrm {G}/\mathrm {P}_\Theta$ is the compact dual of a Hermitian symmetric space and
$\mathrm {G}/\mathrm {P}_\Theta$ is the compact dual of a Hermitian symmetric space and ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if the associated Hermitian symmetric space is of tube type. An example of this is given in Example 2.1, in which case the symmetric space of
$(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if the associated Hermitian symmetric space is of tube type. An example of this is given in Example 2.1, in which case the symmetric space of ![]() $\mathrm {SU}(p,q)$ is the relevant Hermitian symmetric space; it is of tube type only when
$\mathrm {SU}(p,q)$ is the relevant Hermitian symmetric space; it is of tube type only when ![]() $q=p$.
$q=p$.
Remark 2.14 In Example 2.13, the space ![]() $\mathfrak {g}_1$ is an irreducible
$\mathfrak {g}_1$ is an irreducible ![]() $\mathrm {G}_0$-representation. In general, if
$\mathrm {G}_0$-representation. In general, if ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a PHVS such that
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a PHVS such that ![]() $\mathrm {G}_0$ acts irreducibly on
$\mathrm {G}_0$ acts irreducibly on ![]() $\mathfrak {g}_1,$ then
$\mathfrak {g}_1,$ then ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if it is JM-regular. For example, this implies that the PHVS
$(\mathrm {G}_0,\mathfrak {g}_1)$ is regular if and only if it is JM-regular. For example, this implies that the PHVS ![]() $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}, M_{p,q})$ from Examples 2.1 and 2.5 is JM-regular whenever
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}, M_{p,q})$ from Examples 2.1 and 2.5 is JM-regular whenever ![]() $p\leqslant q.$ The regular PHVS
$p\leqslant q.$ The regular PHVS ![]() $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p})$ from Examples 2.1 and 2.5 does not come from a maximal parabolic of
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p})$ from Examples 2.1 and 2.5 does not come from a maximal parabolic of ![]() $\mathrm {SL}_{2p+q}\mathbb {C}$ but it is still a JM-regular PHVS when
$\mathrm {SL}_{2p+q}\mathbb {C}$ but it is still a JM-regular PHVS when ![]() $p\leqslant q$.
$p\leqslant q$.
Example 2.15 The simplest example of a PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ which is regular but not JM-regular occurs in
$(\mathrm {G}_0,\mathfrak {g}_1)$ which is regular but not JM-regular occurs in ![]() $\mathrm {SO}_7\mathbb {C}$ with
$\mathrm {SO}_7\mathbb {C}$ with ![]() $\Theta =\{\alpha _2\}$, that is, with labeled Dynkin diagram
$\Theta =\{\alpha _2\}$, that is, with labeled Dynkin diagram
Here ![]() $(\mathrm {G}_0,\mathfrak {g}_1)\cong (\mathrm {GL}_1\mathbb {C}\times \mathrm {GL}_2\mathbb {C}, \mathbb {C}^2\oplus \mathbb {C}^2)$ for the action
$(\mathrm {G}_0,\mathfrak {g}_1)\cong (\mathrm {GL}_1\mathbb {C}\times \mathrm {GL}_2\mathbb {C}, \mathbb {C}^2\oplus \mathbb {C}^2)$ for the action ![]() $(\lambda,A)\cdot (v,w)=(\lambda v A^{-1},Aw^\mathrm {T}).$ A point in the open orbit is given by
$(\lambda,A)\cdot (v,w)=(\lambda v A^{-1},Aw^\mathrm {T}).$ A point in the open orbit is given by ![]() $v=(1,0)$ and
$v=(1,0)$ and ![]() $w=(1,0).$ For this point, the
$w=(1,0).$ For this point, the ![]() $\mathrm {G}_0$-stabilizer is given by
$\mathrm {G}_0$-stabilizer is given by ![]() $\lambda =1$ and
$\lambda =1$ and ![]() for
for ![]() $\xi \in \mathbb {C}^*.$ Geometrically, this parabolic stabilizes an isotropic flag of the form
$\xi \in \mathbb {C}^*.$ Geometrically, this parabolic stabilizes an isotropic flag of the form ![]() $\mathbb {C}\subset \mathbb {C}^3\subset \mathbb {C}^7$.
$\mathbb {C}\subset \mathbb {C}^3\subset \mathbb {C}^7$.
2.4 Jacobson–Morozov regular prehomogeneous vector subspaces
Fix a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}} \mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}} \mathfrak {g}_j$ with grading element ![]() $\zeta$ and consider a PHVS
$\zeta$ and consider a PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$. Following the proof [Reference Collingwood and McGovernCM93, Theorem 3.3.1] of the Jacobson–Morozov theorem, one can show that any nonzero element
$(\mathrm {G}_0,\mathfrak {g}_1)$. Following the proof [Reference Collingwood and McGovernCM93, Theorem 3.3.1] of the Jacobson–Morozov theorem, one can show that any nonzero element ![]() $e\in \mathfrak {g}_1$ can be completed to an
$e\in \mathfrak {g}_1$ can be completed to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ with
$\{f,h,e\}$ with ![]() $f\in \mathfrak {g}_{-1}$ and
$f\in \mathfrak {g}_{-1}$ and ![]() $h\in \mathfrak {g}_0.$
$h\in \mathfrak {g}_0.$
The semisimple element ![]() $h$ defines a new grading
$h$ defines a new grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}} \tilde {\mathfrak {g}}_j$ where
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}} \tilde {\mathfrak {g}}_j$ where
Define ![]() $\hat {\mathfrak {g}}_j=\mathfrak {g}_j\cap \tilde {\mathfrak {g}}_{2j}$ and the subalgebra
$\hat {\mathfrak {g}}_j=\mathfrak {g}_j\cap \tilde {\mathfrak {g}}_{2j}$ and the subalgebra ![]() $\hat {\mathfrak {g}}\subset \mathfrak {g}$ given by
$\hat {\mathfrak {g}}\subset \mathfrak {g}$ given by
Note that ![]() $h$ and
$h$ and ![]() $\zeta$ are both in
$\zeta$ are both in ![]() $\hat {\mathfrak {g}}_0$ and
$\hat {\mathfrak {g}}_0$ and ![]() $e\in \hat {\mathfrak {g}}_1.$ The difference
$e\in \hat {\mathfrak {g}}_1.$ The difference ![]() $s=\zeta - {h}/{2}$ is semisimple or zero since
$s=\zeta - {h}/{2}$ is semisimple or zero since ![]() $\zeta$ and
$\zeta$ and ![]() $ {h}/{2}$ are semisimple and
$ {h}/{2}$ are semisimple and ![]() $[\zeta, {h}/{2}]=0$. Thus,
$[\zeta, {h}/{2}]=0$. Thus, ![]() $\hat {\mathfrak {g}}$ is reductive since
$\hat {\mathfrak {g}}$ is reductive since ![]() $\hat {\mathfrak {g}}=\mathfrak {g}^{s}$ is the centralizer of
$\hat {\mathfrak {g}}=\mathfrak {g}^{s}$ is the centralizer of ![]() $s.$ The following proposition is immediate.
$s.$ The following proposition is immediate.
Proposition 2.16 Let ![]() $\hat {\mathrm {G}}_0<\mathrm {G}$ be the
$\hat {\mathrm {G}}_0<\mathrm {G}$ be the ![]() $\mathrm {G}_0$-centralizer of
$\mathrm {G}_0$-centralizer of ![]() $h$. Then
$h$. Then ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ is a PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ is a PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ which is JM-regular and
$(\mathrm {G}_0,\mathfrak {g}_1)$ which is JM-regular and ![]() $e$ is in the open
$e$ is in the open ![]() $\hat {\mathrm {G}}_0$-orbit
$\hat {\mathrm {G}}_0$-orbit ![]() $\hat \Omega \subset \hat {\mathfrak {g}}_1$.
$\hat \Omega \subset \hat {\mathfrak {g}}_1$.
Definition 2.17 If ![]() $e\in \Omega$ is in the open
$e\in \Omega$ is in the open ![]() $\mathrm {G}_0$-orbit, then
$\mathrm {G}_0$-orbit, then ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ will be called a maximal JM-regular PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ will be called a maximal JM-regular PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1).$ For any
$(\mathrm {G}_0,\mathfrak {g}_1).$ For any ![]() $e\in \mathfrak {g}_1\setminus \{0\}$, we will call
$e\in \mathfrak {g}_1\setminus \{0\}$, we will call ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ a maximal JM-regular PHVSS for
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ a maximal JM-regular PHVSS for ![]() $e$.
$e$.
Remark 2.18 If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular, then for any
$(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular, then for any ![]() $e\in \Omega$ an associated
$e\in \Omega$ an associated ![]() $\mathfrak {sl}_2$-triple has the form
$\mathfrak {sl}_2$-triple has the form ![]() $\{f,2\zeta,e\}$. In this case,
$\{f,2\zeta,e\}$. In this case, ![]() $(\mathrm {G}_0,\mathfrak {g}_1)=(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1).$
$(\mathrm {G}_0,\mathfrak {g}_1)=(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1).$
Example 2.19 Consider the PHVS ![]() $(\mathrm {S}(\mathrm {GL}_{p}\mathbb {C}\times \mathrm {GL}_q\mathbb {C}), M_{p,q})$ from Example 2.1(2). If
$(\mathrm {S}(\mathrm {GL}_{p}\mathbb {C}\times \mathrm {GL}_q\mathbb {C}), M_{p,q})$ from Example 2.1(2). If ![]() $p\neq q$, then the PHVS is not JM-regular. For
$p\neq q$, then the PHVS is not JM-regular. For ![]() $p>q,$ a maximal JM-regular PHVSS is isomorphic to
$p>q,$ a maximal JM-regular PHVSS is isomorphic to ![]() $(\mathrm {S}(\mathrm {GL}_{q}\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}),M_{q,q})$, for the action
$(\mathrm {S}(\mathrm {GL}_{q}\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}),M_{q,q})$, for the action ![]() $(A,B,C)\cdot M=AMB^{-1}.$ In general, the maximal JM-regular PHVSS of the PHVSs
$(A,B,C)\cdot M=AMB^{-1}.$ In general, the maximal JM-regular PHVSS of the PHVSs ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.13 is related to the maximal subtube of the associated Hermitian symmetric space.
$(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.13 is related to the maximal subtube of the associated Hermitian symmetric space.
For the PHVS ![]() $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ from the first example of Example 2.1(3) with
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ from the first example of Example 2.1(3) with ![]() $p>q,$ the PHVS is not JM-regular and a maximal JM-regular PHVSS is isomorphic to
$p>q,$ the PHVS is not JM-regular and a maximal JM-regular PHVSS is isomorphic to ![]() $(\mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}\times \mathrm {SO}_q\mathbb {C}, M_{q,q})$, where the action is given by
$(\mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}\times \mathrm {SO}_q\mathbb {C}, M_{q,q})$, where the action is given by ![]() $(A,B,C)\cdot M=AMC^{-1}$. The maximal JM-regular PHVSS of
$(A,B,C)\cdot M=AMC^{-1}$. The maximal JM-regular PHVSS of ![]() $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$ can be described similarly. For the regular (non-JM-regular) PHVS
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$ can be described similarly. For the regular (non-JM-regular) PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)=(\mathrm {GL}_1\mathbb {C}\times \mathrm {GL}_2\mathbb {C},\mathbb {C}^2\oplus \mathbb {C}^2)$ from Example 2.15, the maximal JM-regular PHVSS
$(\mathrm {G}_0,\mathfrak {g}_1)=(\mathrm {GL}_1\mathbb {C}\times \mathrm {GL}_2\mathbb {C},\mathbb {C}^2\oplus \mathbb {C}^2)$ from Example 2.15, the maximal JM-regular PHVSS ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ containing
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ containing ![]() $(v,w)=((1,0),(1,0))$ is
$(v,w)=((1,0),(1,0))$ is
The construction of a maximal JM-regular PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ containing
$(\mathrm {G}_0,\mathfrak {g}_1)$ containing ![]() $e\in \mathfrak {g}_1$ depends on
$e\in \mathfrak {g}_1$ depends on ![]() $e$ and a choice of
$e$ and a choice of ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$. However, if
$\{f,h,e\}$. However, if ![]() $e,e'\in \mathfrak {g}_1$ are in the same
$e,e'\in \mathfrak {g}_1$ are in the same ![]() $\mathrm {G}_0$-orbit then any two maximal JM-regular PHVSSs containing
$\mathrm {G}_0$-orbit then any two maximal JM-regular PHVSSs containing ![]() $e$ and
$e$ and ![]() $e'$ are
$e'$ are ![]() $\mathrm {G}_0$-conjugate.
$\mathrm {G}_0$-conjugate.
Proposition 2.20 Let ![]() $e,e'\in \mathfrak {g}_1$ so that
$e,e'\in \mathfrak {g}_1$ so that ![]() $e'\in \mathrm {G}_0\cdot e$, and let
$e'\in \mathrm {G}_0\cdot e$, and let ![]() $\{f,h,e\}, \{f',h',e'\}$ be two
$\{f,h,e\}, \{f',h',e'\}$ be two ![]() $\mathfrak {sl}_2$-triples with
$\mathfrak {sl}_2$-triples with ![]() $h,h'\in \mathfrak {g}_0$. Then there is
$h,h'\in \mathfrak {g}_0$. Then there is ![]() $g\in \mathrm {G}_0$ so that
$g\in \mathrm {G}_0$ so that
In particular, the associated maximal JM-regular PHVSSs ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ and
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ and ![]() $(\hat {\mathrm {G}}_0',\hat {\mathfrak {g}}_1')$ containing
$(\hat {\mathrm {G}}_0',\hat {\mathfrak {g}}_1')$ containing ![]() $e$ and
$e$ and ![]() $e'$ respectively are
$e'$ respectively are ![]() $\mathrm {G}_0$-conjugate.
$\mathrm {G}_0$-conjugate.
Proof. We may assume ![]() $e=e'.$ Let
$e=e'.$ Let ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\tilde {\mathfrak {g}}_j$ be the
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\tilde {\mathfrak {g}}_j$ be the ![]() $\mathbb {Z}$-grading associated to the
$\mathbb {Z}$-grading associated to the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ and
$\{f,h,e\}$ and ![]() $\mathfrak {g}^e$ be the centralizer of
$\mathfrak {g}^e$ be the centralizer of ![]() $e$ and
$e$ and ![]() $\mathfrak {u}^e\!=\![e,\mathfrak {g}]\cap \mathfrak {g}^e\!=\!\mathfrak {g}^e\cap \bigoplus _{j>0}\tilde {\mathfrak {g}}_j.$ We have
$\mathfrak {u}^e\!=\![e,\mathfrak {g}]\cap \mathfrak {g}^e\!=\!\mathfrak {g}^e\cap \bigoplus _{j>0}\tilde {\mathfrak {g}}_j.$ We have ![]() $h'-h\in \mathfrak {u}^e$ since
$h'-h\in \mathfrak {u}^e$ since ![]() $[h-h',e]=0$ and
$[h-h',e]=0$ and ![]() $[e,f-f']=h'-h$. Since
$[e,f-f']=h'-h$. Since ![]() $h,h'\in \mathfrak {g}_0$, following the proof [Reference Collingwood and McGovernCM93, Theorem 3.4.7], we can inductively construct
$h,h'\in \mathfrak {g}_0$, following the proof [Reference Collingwood and McGovernCM93, Theorem 3.4.7], we can inductively construct ![]() $Z\in \mathfrak {g}_0\cap \mathfrak {u}^e$ so that
$Z\in \mathfrak {g}_0\cap \mathfrak {u}^e$ so that ![]() $\operatorname {Ad}_{\exp (Z)}(h)=\!h\!+(h'-h)\!=h'.$ Note that
$\operatorname {Ad}_{\exp (Z)}(h)=\!h\!+(h'-h)\!=h'.$ Note that ![]() $\operatorname {Ad}_{\exp (Z)}e=e$, and, by the uniqueness part of the Jacobson–Morozov theorem, we have
$\operatorname {Ad}_{\exp (Z)}e=e$, and, by the uniqueness part of the Jacobson–Morozov theorem, we have ![]() $\operatorname {Ad}_{\exp (Z)}f=f'.$
$\operatorname {Ad}_{\exp (Z)}f=f'.$
Finally, we note that every ![]() $e\in \mathfrak {g}_1$ defines a parabolic subgroup of
$e\in \mathfrak {g}_1$ defines a parabolic subgroup of ![]() $\mathrm {P}_{0,e}<\mathrm {G}_0.$ For
$\mathrm {P}_{0,e}<\mathrm {G}_0.$ For ![]() $e\in \mathfrak {g}_1\setminus \{0\}$, let
$e\in \mathfrak {g}_1\setminus \{0\}$, let ![]() $\{f,h,e\}$ be an associated
$\{f,h,e\}$ be an associated ![]() $\mathfrak {sl}_2$-triple with
$\mathfrak {sl}_2$-triple with ![]() $h\in \mathfrak {g}_0.$ If
$h\in \mathfrak {g}_0.$ If ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\tilde {\mathfrak {g}}_j$ is the
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\tilde {\mathfrak {g}}_j$ is the ![]() $\mathbb {Z}$-grading with grading element
$\mathbb {Z}$-grading with grading element ![]() $h,$ then
$h,$ then ![]() $\tilde {\mathfrak {p}}=\bigoplus _{j\geqslant 0}\tilde {\mathfrak {g}}_j$ is a parabolic subalgebra of
$\tilde {\mathfrak {p}}=\bigoplus _{j\geqslant 0}\tilde {\mathfrak {g}}_j$ is a parabolic subalgebra of ![]() $\mathfrak {g}.$ Moreover,
$\mathfrak {g}.$ Moreover, ![]() $\tilde {\mathfrak {p}}$ depends only on
$\tilde {\mathfrak {p}}$ depends only on ![]() $e\in \mathfrak {g}_1\setminus \{0\}$ and not on the
$e\in \mathfrak {g}_1\setminus \{0\}$ and not on the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ (see, for example, [Reference Collingwood and McGovernCM93, Remark 3.8.5]). Note that the parabolic
$\{f,h,e\}$ (see, for example, [Reference Collingwood and McGovernCM93, Remark 3.8.5]). Note that the parabolic ![]() $\tilde {\mathfrak {p}}$ can also be defined by
$\tilde {\mathfrak {p}}$ can also be defined by
The parabolic subalgebra ![]() $\mathfrak {p}_0(e)\subset \mathfrak {g}_0$ is defined by
$\mathfrak {p}_0(e)\subset \mathfrak {g}_0$ is defined by
We will denote the associated parabolic subgroup by ![]() $\mathrm {P}_{0,e}<\mathrm {G}_0.$ Note that
$\mathrm {P}_{0,e}<\mathrm {G}_0.$ Note that ![]() $\hat {\mathfrak {g}}_0\subset \mathfrak {p}_{0,e}$ and
$\hat {\mathfrak {g}}_0\subset \mathfrak {p}_{0,e}$ and ![]() $\hat {\mathrm {G}}_0<\mathrm {P}_{0,e}$ define a Levi subalgebra and subgroup, respectively.
$\hat {\mathrm {G}}_0<\mathrm {P}_{0,e}$ define a Levi subalgebra and subgroup, respectively.
Proposition 2.21 Let ![]() $e\in \mathfrak {g}_1\setminus \{0\}$ and
$e\in \mathfrak {g}_1\setminus \{0\}$ and ![]() $\{f,h,e\}$ be an
$\{f,h,e\}$ be an ![]() $\mathfrak {sl}_2$-triple with
$\mathfrak {sl}_2$-triple with ![]() $h\in \mathfrak {g}_0.$ If
$h\in \mathfrak {g}_0.$ If ![]() $s=\zeta - {h}/{2}$, then
$s=\zeta - {h}/{2}$, then
Proof. The proposition follows immediately from the description of ![]() $\tilde {\mathfrak {p}}$ in (2.4) and the fact that
$\tilde {\mathfrak {p}}$ in (2.4) and the fact that ![]() $\operatorname {Ad}_{\exp (t\zeta )}x=x$ for all
$\operatorname {Ad}_{\exp (t\zeta )}x=x$ for all ![]() $x\in \mathfrak {g}_0.$
$x\in \mathfrak {g}_0.$
3. The Toledo character and period domains
In this section we generalize notions from [Reference Biquard, García-Prada and RubioBGR17], which concerned ![]() $\mathbb {Z}$-gradings
$\mathbb {Z}$-gradings ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, to arbitrary
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, to arbitrary ![]() $\mathbb {Z}$-gradings.
$\mathbb {Z}$-gradings.
3.1 The Toledo character and rank
Let ![]() $\mathrm {G}$ be a complex semisimple Lie group with Lie algebra
$\mathrm {G}$ be a complex semisimple Lie group with Lie algebra ![]() $\mathfrak {g}$ and Killing form
$\mathfrak {g}$ and Killing form ![]() $B.$ Fix a
$B.$ Fix a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element ![]() $\zeta.$ Recall that
$\zeta.$ Recall that ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a PHVS, and let
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a PHVS, and let ![]() $\Omega \subset \mathfrak {g}_1$ be the open
$\Omega \subset \mathfrak {g}_1$ be the open ![]() $\mathrm {G}_0$-orbit. Since
$\mathrm {G}_0$-orbit. Since ![]() $\mathfrak {g}_0$ is the centralizer of
$\mathfrak {g}_0$ is the centralizer of ![]() $\zeta,$
$\zeta,$ ![]() $B(\zeta,-):\mathfrak {g}_0\to \mathbb {C}$ defines a character.
$B(\zeta,-):\mathfrak {g}_0\to \mathbb {C}$ defines a character.
Definition 3.1 The Toledo character ![]() $\chi _T:\mathfrak {g}_0\to \mathbb {C}$ is defined by
$\chi _T:\mathfrak {g}_0\to \mathbb {C}$ is defined by
where ![]() $\gamma$ is the longest root such that
$\gamma$ is the longest root such that ![]() $\mathfrak {g}_\gamma \subset \mathfrak {g}_1.$
$\mathfrak {g}_\gamma \subset \mathfrak {g}_1.$
Remark 3.2 The normalization factor ![]() $B(\gamma,\gamma )$ guarantees that the Toledo character is independent of the choice of invariant bilinear form
$B(\gamma,\gamma )$ guarantees that the Toledo character is independent of the choice of invariant bilinear form ![]() $B.$
$B.$
Let ![]() $e,e'\in \mathfrak {g}_1\setminus \{0\}$ such that
$e,e'\in \mathfrak {g}_1\setminus \{0\}$ such that ![]() $e'\in \mathrm {G}_0\cdot e$ and let
$e'\in \mathrm {G}_0\cdot e$ and let ![]() $\{f,h,e\}$,
$\{f,h,e\}$, ![]() $\{f',h',e'\}$ be two
$\{f',h',e'\}$ be two ![]() $\mathfrak {sl}_2$-triples with
$\mathfrak {sl}_2$-triples with ![]() $h,h'\in \mathfrak {g}_0.$ By Proposition 2.20, there is
$h,h'\in \mathfrak {g}_0.$ By Proposition 2.20, there is ![]() $g\in \mathrm {G}_0$ such that
$g\in \mathrm {G}_0$ such that ![]() $\{\operatorname {Ad}_g f,\operatorname {Ad}_g h,\operatorname {Ad}_g e\}=\{f',h',e'\}$. Since
$\{\operatorname {Ad}_g f,\operatorname {Ad}_g h,\operatorname {Ad}_g e\}=\{f',h',e'\}$. Since ![]() $\operatorname {Ad}_g\zeta =\zeta,$ we have
$\operatorname {Ad}_g\zeta =\zeta,$ we have
As a result, we make the following definition.
Definition 3.3 Let ![]() $e\in \mathfrak {g}_1$ and
$e\in \mathfrak {g}_1$ and ![]() $\{f,h,e\}$ be an
$\{f,h,e\}$ be an ![]() $\mathfrak {sl}_2$-triple with
$\mathfrak {sl}_2$-triple with ![]() $h\in \mathfrak {g}_0.$ Define the Toledo rank of
$h\in \mathfrak {g}_0.$ Define the Toledo rank of ![]() $e$ by
$e$ by
Define the Toledo rank of the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ by
$(\mathrm {G}_0,\mathfrak {g}_1)$ by
Remark 3.4 Note that if ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS, then
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS, then ![]() $\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=B(\zeta,\zeta )B(\gamma,\gamma ).$
$\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=B(\zeta,\zeta )B(\gamma,\gamma ).$
Example 3.5 For the PHVSs ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.13, the Toledo rank of
$(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.13, the Toledo rank of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ agrees with the rank of the associated Hermitian symmetric space.
$(\mathrm {G}_0,\mathfrak {g}_1)$ agrees with the rank of the associated Hermitian symmetric space.
Proposition 3.6 Let ![]() $e\in \mathfrak {g}_1$ and
$e\in \mathfrak {g}_1$ and ![]() $\{f,h,e\}$ be an associated
$\{f,h,e\}$ be an associated ![]() $\mathfrak {sl}_2$-triples with
$\mathfrak {sl}_2$-triples with ![]() $h\in \mathfrak {g}_0.$ Then
$h\in \mathfrak {g}_0.$ Then
Proof. Write ![]() $\zeta = {h}/{2}+s$. Note that
$\zeta = {h}/{2}+s$. Note that ![]() $s\in \mathfrak {g}^e$ and
$s\in \mathfrak {g}^e$ and ![]() $ {h}/{2}\in {\operatorname {ad}}_e(\mathfrak {g}).$ Thus,
$ {h}/{2}\in {\operatorname {ad}}_e(\mathfrak {g}).$ Thus, ![]() $B( {h}/{2},s)=0$ and
$B( {h}/{2},s)=0$ and
Example 3.7 We illustrate these notions in the case of Example 1.3, with ![]() $G=\mathrm {SO}_{2p+q}\mathbb {C}$ and
$G=\mathrm {SO}_{2p+q}\mathbb {C}$ and ![]() $G_0=\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$. Taking an isotropic basis of
$G_0=\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$. Taking an isotropic basis of ![]() $\mathbb {C}^{2p+q}=\mathbb {C}^p\oplus \mathbb {C}^q\oplus \mathbb {C}^p$, such that
$\mathbb {C}^{2p+q}=\mathbb {C}^p\oplus \mathbb {C}^q\oplus \mathbb {C}^p$, such that ![]() $\langle e_i,e_{2p+q+1-i}\rangle =1$, we have the grading element
$\langle e_i,e_{2p+q+1-i}\rangle =1$, we have the grading element
 \[ \zeta = \begin{pmatrix} \operatorname{Id}_p & & \\ & 0 & \\ & & - \operatorname{Id}_p \end{pmatrix}. \]
\[ \zeta = \begin{pmatrix} \operatorname{Id}_p & & \\ & 0 & \\ & & - \operatorname{Id}_p \end{pmatrix}. \]
Then ![]() $\mathfrak {g}_1=\operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$, where
$\mathfrak {g}_1=\operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$, where ![]() $u\in \operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$ represents the matrix
$u\in \operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$ represents the matrix
 \[ e =\left(\begin{array}{c|c|c} \phantom{u} & - u^\mathrm{T} & \\ \hline & & u \\ \hline & & \end{array}\right),\quad \text{in which } u^\mathrm{T}_{ij}=u_{p+1-j,q+1-i}. \]
\[ e =\left(\begin{array}{c|c|c} \phantom{u} & - u^\mathrm{T} & \\ \hline & & u \\ \hline & & \end{array}\right),\quad \text{in which } u^\mathrm{T}_{ij}=u_{p+1-j,q+1-i}. \]
The orbits are classified by two integers ![]() $(r_1,r_2)$, such that the image of
$(r_1,r_2)$, such that the image of ![]() $u\in \operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$ is the sum of a nondegenerate subspace of dimension
$u\in \operatorname {Hom}(\mathbb {C}^p,\mathbb {C}^q)$ is the sum of a nondegenerate subspace of dimension ![]() $r_1$ and a totally isotropic subspace of dimension
$r_1$ and a totally isotropic subspace of dimension ![]() $r_2$. Let
$r_2$. Let ![]() $J_r$ be the rank
$J_r$ be the rank ![]() $r$ matrix
$r$ matrix
Then one can take
 \[ u = \begin{pmatrix} \operatorname{Id}_{r_2} & & \\ & \operatorname{Id}_{r_1} & \\ & 0 & \\ & J_{r_1} & \\ & & 0 \end{pmatrix},\quad h = \left(\begin{array}{ccc|ccc|ccc} 0 & & & & & & & & \\ & 2\operatorname{Id}_{r_1} & & & & & & & \\ & & \operatorname{Id}_{r_2} & & & & & & \\ \hline & & & \operatorname{Id}_{r_2} & & & & & \\ & & & & 0 & & & & \\ & & & & & -\operatorname{Id}_{r_2} & & & \\ \hline & & & & & & -\operatorname{Id}_{r_2} & & \\ & & & & & & & -2 \operatorname{Id}_{r_1} & \\ & & & & & & & & 0 \end{array}\right). \]
\[ u = \begin{pmatrix} \operatorname{Id}_{r_2} & & \\ & \operatorname{Id}_{r_1} & \\ & 0 & \\ & J_{r_1} & \\ & & 0 \end{pmatrix},\quad h = \left(\begin{array}{ccc|ccc|ccc} 0 & & & & & & & & \\ & 2\operatorname{Id}_{r_1} & & & & & & & \\ & & \operatorname{Id}_{r_2} & & & & & & \\ \hline & & & \operatorname{Id}_{r_2} & & & & & \\ & & & & 0 & & & & \\ & & & & & -\operatorname{Id}_{r_2} & & & \\ \hline & & & & & & -\operatorname{Id}_{r_2} & & \\ & & & & & & & -2 \operatorname{Id}_{r_1} & \\ & & & & & & & & 0 \end{array}\right). \]
(The formula for ![]() $u$ is valid if
$u$ is valid if ![]() $r_2+r_1\leqslant q/2$; the reader will modify
$r_2+r_1\leqslant q/2$; the reader will modify ![]() $u$ accordingly if
$u$ accordingly if ![]() $r_2+r_1> {q}/{2}$. The formula for
$r_2+r_1> {q}/{2}$. The formula for ![]() $h$ remains the same.) Take the standard invariant form
$h$ remains the same.) Take the standard invariant form ![]() $B(X,Y)=\operatorname {tr}(XY)$. If
$B(X,Y)=\operatorname {tr}(XY)$. If ![]() $q>1$ we have
$q>1$ we have ![]() $B(\gamma,\gamma )=1$ and therefore
$B(\gamma,\gamma )=1$ and therefore ![]() $\operatorname {rk}_Te=\frac 14 B(h,h)=2r_1+r_2$. On the other hand
$\operatorname {rk}_Te=\frac 14 B(h,h)=2r_1+r_2$. On the other hand ![]() $\chi _T(x)=B(\zeta,x)$, so that we will have
$\chi _T(x)=B(\zeta,x)$, so that we will have ![]() $\tau (E,\varphi )=2\deg V$ if the Higgs bundle
$\tau (E,\varphi )=2\deg V$ if the Higgs bundle ![]() $(E,\varphi )$ is given as
$(E,\varphi )$ is given as ![]() $V\oplus W\oplus V^*$ with
$V\oplus W\oplus V^*$ with ![]() $V$ a
$V$ a ![]() $\mathrm {GL}_p\mathbb {C}$-bundle and
$\mathrm {GL}_p\mathbb {C}$-bundle and ![]() $W$ a
$W$ a ![]() $\mathrm {SO}_q\mathbb {C}$-bundle. This justifies inequality (1.2) as a consequence of Corollary 5.5.
$\mathrm {SO}_q\mathbb {C}$-bundle. This justifies inequality (1.2) as a consequence of Corollary 5.5.
3.2 Real forms and period domains
Let ![]() $\mathfrak {g}$ be a complex semisimple Lie algebra and consider a conjugate linear involution
$\mathfrak {g}$ be a complex semisimple Lie algebra and consider a conjugate linear involution ![]() $\sigma :\mathfrak {g}\to \mathfrak {g}.$ The fixed point set
$\sigma :\mathfrak {g}\to \mathfrak {g}.$ The fixed point set ![]() $\mathfrak {g}^\sigma \subset \mathfrak {g}$ is a real subalgebra such that
$\mathfrak {g}^\sigma \subset \mathfrak {g}$ is a real subalgebra such that ![]() $\mathfrak {g}^\sigma \otimes \mathbb {C}=\mathfrak {g}.$ Such a subalgebra is called a real form of
$\mathfrak {g}^\sigma \otimes \mathbb {C}=\mathfrak {g}.$ Such a subalgebra is called a real form of ![]() $\mathfrak {g}.$ On the level of groups, a real form
$\mathfrak {g}.$ On the level of groups, a real form ![]() $\mathrm {G}^\sigma <\mathrm {G}$ is the fixed point set of an anti-holomorphic involution
$\mathrm {G}^\sigma <\mathrm {G}$ is the fixed point set of an anti-holomorphic involution ![]() $\sigma :\mathrm {G}\to \mathrm {G}.$ A real form is called compact if
$\sigma :\mathrm {G}\to \mathrm {G}.$ A real form is called compact if ![]() $\mathrm {G}^\sigma$ is compact or
$\mathrm {G}^\sigma$ is compact or ![]() $\mathfrak {g}^\sigma$ is the Lie algebra of a maximal compact subgroup. Compact real forms exist and are unique up to conjugation.
$\mathfrak {g}^\sigma$ is the Lie algebra of a maximal compact subgroup. Compact real forms exist and are unique up to conjugation.
Real forms of ![]() $\mathfrak {g}$ can be equivalently defined in terms of complex linear involutions
$\mathfrak {g}$ can be equivalently defined in terms of complex linear involutions ![]() $\theta :\mathfrak {g}\to \mathfrak {g}.$ Namely, Cartan proved that, given a real form
$\theta :\mathfrak {g}\to \mathfrak {g}.$ Namely, Cartan proved that, given a real form ![]() $\sigma$, there is a compact real form
$\sigma$, there is a compact real form ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ such that
$\tau :\mathfrak {g}\to \mathfrak {g}$ such that ![]() $\sigma \circ \tau =\tau \circ \sigma$, and that given a complex linear involution
$\sigma \circ \tau =\tau \circ \sigma$, and that given a complex linear involution ![]() $\theta$, there is a compact real form
$\theta$, there is a compact real form ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ such that
$\tau :\mathfrak {g}\to \mathfrak {g}$ such that ![]() $\theta \circ \tau =\tau \circ \theta.$ The correspondence is then given by setting
$\theta \circ \tau =\tau \circ \theta.$ The correspondence is then given by setting ![]() $\theta =\sigma \circ \tau$. A real subalgebra
$\theta =\sigma \circ \tau$. A real subalgebra ![]() $\sigma :\mathfrak {g}\to \mathfrak {g}$ is said to be of Hodge type if
$\sigma :\mathfrak {g}\to \mathfrak {g}$ is said to be of Hodge type if ![]() $\sigma$ is an inner automorphism of
$\sigma$ is an inner automorphism of ![]() $\mathfrak {g}$. If
$\mathfrak {g}$. If ![]() $\tau$ is a compact real form such that
$\tau$ is a compact real form such that ![]() $\theta =\tau \circ \sigma =\sigma \circ \tau,$ then
$\theta =\tau \circ \sigma =\sigma \circ \tau,$ then ![]() $\sigma$ is of Hodge type if and only if there is a Cartan subalgebra
$\sigma$ is of Hodge type if and only if there is a Cartan subalgebra ![]() $\mathfrak {t}\subset \mathfrak {g}$ such that
$\mathfrak {t}\subset \mathfrak {g}$ such that ![]() $\theta |_{\mathfrak {t}}=\operatorname {Id}.$
$\theta |_{\mathfrak {t}}=\operatorname {Id}.$
Given a complex linear involution ![]() $\theta :\mathfrak {g}\to \mathfrak {g}$, we will write
$\theta :\mathfrak {g}\to \mathfrak {g}$, we will write ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ for
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ for ![]() $\pm 1$-eigenspaces of
$\pm 1$-eigenspaces of ![]() $\theta$, namely
$\theta$, namely ![]() $\theta |_\mathfrak {h}=\operatorname {Id}$ and
$\theta |_\mathfrak {h}=\operatorname {Id}$ and ![]() $\theta _\mathfrak {m}=-\operatorname {Id}$. We will call the decomposition
$\theta _\mathfrak {m}=-\operatorname {Id}$. We will call the decomposition ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ the complexified Cartan decomposition of a real form
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ the complexified Cartan decomposition of a real form ![]() $\mathfrak {g}^\mathbb {R}\subset \mathfrak {g}$. There is a real form of Hodge type associated to every
$\mathfrak {g}^\mathbb {R}\subset \mathfrak {g}$. There is a real form of Hodge type associated to every ![]() $\mathbb {Z}$-grading of
$\mathbb {Z}$-grading of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Proposition 3.8 Let ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a ![]() $\mathbb {Z}$-grading, and define
$\mathbb {Z}$-grading, and define ![]() $\theta :\mathfrak {g}\to \mathfrak {g}$ by
$\theta :\mathfrak {g}\to \mathfrak {g}$ by
Then ![]() $\theta$ is a Lie algebra involution which defines a real form of Hodge type.
$\theta$ is a Lie algebra involution which defines a real form of Hodge type.
Proof. It is clear that ![]() $\theta$ is a Lie algebra involution. Moreover, from the constructions in § 2.3,
$\theta$ is a Lie algebra involution. Moreover, from the constructions in § 2.3, ![]() $\mathfrak {g}_0$ contains a Cartan subalgebra of
$\mathfrak {g}_0$ contains a Cartan subalgebra of ![]() $\mathfrak {g}.$ Hence, the real form associated to the involution
$\mathfrak {g}.$ Hence, the real form associated to the involution ![]() $\theta$ is of Hodge type.
$\theta$ is of Hodge type.
Example 3.9 For gradings of the form ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the canonical real forms are exactly the set of real forms of Hermitian type. For example, the real form of
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the canonical real forms are exactly the set of real forms of Hermitian type. For example, the real form of ![]() $\mathrm {SL}_{p+q}\mathbb {C}$ associated to the PHVS
$\mathrm {SL}_{p+q}\mathbb {C}$ associated to the PHVS ![]() $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}, M_{p,q})$ from Examples 2.1 and 2.5 is
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}, M_{p,q})$ from Examples 2.1 and 2.5 is ![]() $\mathrm {SU}(p,q).$
$\mathrm {SU}(p,q).$
The real form of ![]() $\mathrm {SO}_{2p+q}\mathbb {C}$ associated to the PHVS
$\mathrm {SO}_{2p+q}\mathbb {C}$ associated to the PHVS ![]() $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ from Examples 2.1 and 2.5 is
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ from Examples 2.1 and 2.5 is ![]() $\mathrm {SO}(2p,q).$ Similarly, the real form of
$\mathrm {SO}(2p,q).$ Similarly, the real form of ![]() $\mathrm {SL}_{p+q+r}\mathbb {C}$ associated to the PHVS
$\mathrm {SL}_{p+q+r}\mathbb {C}$ associated to the PHVS ![]() $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$ is
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_r\mathbb {C}),M_{p,q}\oplus M_{q,r})$ is ![]() $\mathrm {SU}(p+r,q).$ For the regular (non JM-regular) PHVS from Example 2.15, the associated real form of
$\mathrm {SU}(p+r,q).$ For the regular (non JM-regular) PHVS from Example 2.15, the associated real form of ![]() $\mathrm {SO}_7\mathbb {C}$ is
$\mathrm {SO}_7\mathbb {C}$ is ![]() $\mathrm {SO}(3,4).$ For the JM-regular PHVS associated to a principal
$\mathrm {SO}(3,4).$ For the JM-regular PHVS associated to a principal ![]() $\mathfrak {sl}_2$-triple (Example 2.12), the associated real form is the split real form if the split real form is of Hodge type, otherwise it is the quasisplit real form which is nonsplit. For example, for
$\mathfrak {sl}_2$-triple (Example 2.12), the associated real form is the split real form if the split real form is of Hodge type, otherwise it is the quasisplit real form which is nonsplit. For example, for ![]() $\mathrm {G}=\mathrm {SL}_{2p}\mathbb {C},$ the split real form is
$\mathrm {G}=\mathrm {SL}_{2p}\mathbb {C},$ the split real form is ![]() $\mathrm {SL}_{2p}\mathbb {R}$ but the canonical real form associated to the grading is
$\mathrm {SL}_{2p}\mathbb {R}$ but the canonical real form associated to the grading is ![]() $\mathrm {SU}(p,p).$
$\mathrm {SU}(p,p).$
Remark 3.10 Given a compact real form ![]() $\tau,$
$\tau,$ ![]() $B(-\tau (x),y)$ defines a nondegenerate positive definite Hermitian inner product on
$B(-\tau (x),y)$ defines a nondegenerate positive definite Hermitian inner product on ![]() $\mathfrak {g}.$ Thus,
$\mathfrak {g}.$ Thus, ![]() $\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ for any
$\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ for any ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _j\mathfrak {g}_j$.
$\mathfrak {g}=\bigoplus _j\mathfrak {g}_j$.
Let ![]() $\theta$ be the involution from Proposition 3.8 and
$\theta$ be the involution from Proposition 3.8 and ![]() $\tau$ be a compact real form such that
$\tau$ be a compact real form such that ![]() $\sigma =\theta \circ \tau :\mathfrak {g}\to \mathfrak {g}$ is the associated real form of Hodge type. Let
$\sigma =\theta \circ \tau :\mathfrak {g}\to \mathfrak {g}$ is the associated real form of Hodge type. Let ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ be the associated real form of
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ be the associated real form of ![]() $\mathrm {G}$ and let
$\mathrm {G}$ and let ![]() $\mathrm {H}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be the associated maximal compact subgroup. Note that the real form
$\mathrm {H}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be the associated maximal compact subgroup. Note that the real form ![]() $\sigma$ restricts to a compact real form on
$\sigma$ restricts to a compact real form on ![]() $\mathfrak {g}_0$. Set
$\mathfrak {g}_0$. Set ![]() $\mathrm {H}_0^\mathbb {R}=\mathrm {G}_0\cap \mathrm {G}^\mathbb {R}.$
$\mathrm {H}_0^\mathbb {R}=\mathrm {G}_0\cap \mathrm {G}^\mathbb {R}.$
Consider the homogeneous space
Note that there is a fibration ![]() $D\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ over the Riemannian symmetric space of
$D\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ over the Riemannian symmetric space of ![]() $\mathrm {G}^\mathbb {R}.$ In fact, the homogeneous space
$\mathrm {G}^\mathbb {R}.$ In fact, the homogeneous space ![]() $D$ has a natural homogeneous complex structure. Indeed, the tangent bundle of
$D$ has a natural homogeneous complex structure. Indeed, the tangent bundle of ![]() $D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is isomorphic to the associated bundle
$D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is isomorphic to the associated bundle
Let ![]() $\mathfrak {g}^\mathbb {R}=\mathfrak {h}_0^\mathbb {R}\oplus \mathfrak {q}^\mathbb {R}$ be an orthogonal decomposition and
$\mathfrak {g}^\mathbb {R}=\mathfrak {h}_0^\mathbb {R}\oplus \mathfrak {q}^\mathbb {R}$ be an orthogonal decomposition and ![]() $\mathfrak {q}=\mathfrak {q}^\mathbb {R}\otimes \mathbb {C}$. Then the complexified tangent bundle is
$\mathfrak {q}=\mathfrak {q}^\mathbb {R}\otimes \mathbb {C}$. Then the complexified tangent bundle is ![]() $T_\mathbb {C} D\cong \mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {q},$ and a complex structure on
$T_\mathbb {C} D\cong \mathrm {G}^\mathbb {R}\times _{\mathrm {H}_0^\mathbb {R}}\mathfrak {q},$ and a complex structure on ![]() $D$ is equivalent to an
$D$ is equivalent to an ![]() $\mathrm {H}_0^\mathbb {R}$-invariant decomposition
$\mathrm {H}_0^\mathbb {R}$-invariant decomposition ![]() $\mathfrak {q}=\mathfrak {q}_-\oplus \mathfrak {q}_+$ such that
$\mathfrak {q}=\mathfrak {q}_-\oplus \mathfrak {q}_+$ such that ![]() $\sigma (\mathfrak {q}_+)=\mathfrak {q}_-$ and
$\sigma (\mathfrak {q}_+)=\mathfrak {q}_-$ and ![]() $[\mathfrak {q}_\pm,\mathfrak {q}_\pm ]\subset \mathfrak {q}_\pm$. The decomposition
$[\mathfrak {q}_\pm,\mathfrak {q}_\pm ]\subset \mathfrak {q}_\pm$. The decomposition ![]() $\mathfrak {q}=\mathfrak {q}_-\oplus \mathfrak {q}_+$ is given by setting
$\mathfrak {q}=\mathfrak {q}_-\oplus \mathfrak {q}_+$ is given by setting
The complex manifold ![]() $D$ is called a period domain for
$D$ is called a period domain for ![]() $\mathrm {G}^\mathbb {R}$. Note that the holomorphic tangent bundle of a period domain decomposes as
$\mathrm {G}^\mathbb {R}$. Note that the holomorphic tangent bundle of a period domain decomposes as
Example 3.11 For the PHVSs from Example 2.13, ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a Hermitian real form and
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a Hermitian real form and ![]() $\mathrm {H}_0^\mathbb {R}<\mathrm {G}^\mathbb {R}$ is a maximal compact subgroup. Hence, the period domain
$\mathrm {H}_0^\mathbb {R}<\mathrm {G}^\mathbb {R}$ is a maximal compact subgroup. Hence, the period domain ![]() $D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is the Riemannian symmetric space for
$D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is the Riemannian symmetric space for ![]() $\mathrm {G}^\mathbb {R}.$ For the PHVS
$\mathrm {G}^\mathbb {R}.$ For the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.12,
$(\mathrm {G}_0,\mathfrak {g}_1)$ from Example 2.12, ![]() $\mathrm {G}_0<\mathrm {G}$ is a Cartan subgroup,
$\mathrm {G}_0<\mathrm {G}$ is a Cartan subgroup, ![]() $\mathrm {G}^\mathbb {R}$ is the quasisplit real form of Hodge type and the period domain is
$\mathrm {G}^\mathbb {R}$ is the quasisplit real form of Hodge type and the period domain is ![]() $D=\mathrm {G}^\mathbb {R}/\mathrm {U}(1)^{\operatorname {rk}(\mathfrak {g})}$. For the PHVS
$D=\mathrm {G}^\mathbb {R}/\mathrm {U}(1)^{\operatorname {rk}(\mathfrak {g})}$. For the PHVS ![]() $(\mathrm {GL}_{p}\mathbb {C}\times \mathrm {SO}(p,\mathbb {C}), M_{p,q})$ from Examples 2.1 and 3.9,
$(\mathrm {GL}_{p}\mathbb {C}\times \mathrm {SO}(p,\mathbb {C}), M_{p,q})$ from Examples 2.1 and 3.9, ![]() $\mathrm {G}^\mathbb {R}=\mathrm {SO}(2p,q)$ and the period domain is
$\mathrm {G}^\mathbb {R}=\mathrm {SO}(2p,q)$ and the period domain is ![]() $D=\mathrm {SO}(2p,q)/(\mathrm {U}_{p}\times \mathrm {SO}_q).$
$D=\mathrm {SO}(2p,q)/(\mathrm {U}_{p}\times \mathrm {SO}_q).$
3.3 The Toledo character and holomorphic sectional curvature
Here we discuss how the choice of the Toledo character is related to a metric of minimal holomorphic sectional curvature ![]() $-1$ on
$-1$ on ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$.
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$.
As is well known, one can define an invariant Hermitian metric on ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ by using the Hermitian scalar product
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ by using the Hermitian scalar product
where ![]() $x^*=-\tau (x)$ and
$x^*=-\tau (x)$ and ![]() $\tau$ is the compact conjugation fixed on
$\tau$ is the compact conjugation fixed on ![]() $\mathfrak {g}$. This does not give a Kähler metric (the corresponding 2-form is not closed) but one can still define the holomorphic sectional curvature
$\mathfrak {g}$. This does not give a Kähler metric (the corresponding 2-form is not closed) but one can still define the holomorphic sectional curvature ![]() $K$ of its Chern connection. We have the well-known formula (see, for example, [Reference Carlson, Müller-Stach and PetersCMSP17])
$K$ of its Chern connection. We have the well-known formula (see, for example, [Reference Carlson, Müller-Stach and PetersCMSP17])
We are interested in the function ![]() $K$ on
$K$ on ![]() $\mathfrak {g}_1$. It is known (and re-proved quickly below) that critical points of
$\mathfrak {g}_1$. It is known (and re-proved quickly below) that critical points of ![]() $K$ are obtained on elements
$K$ are obtained on elements ![]() $e$ such that
$e$ such that ![]() $\{e^*,h=[e,e^*],e\}$ is an
$\{e^*,h=[e,e^*],e\}$ is an ![]() $\mathfrak {sl}_2$-triple. For such
$\mathfrak {sl}_2$-triple. For such ![]() $e$, we have
$e$, we have ![]() $|[e,e^*]|^2=\langle [[e,e^*],e],e \rangle =2|e|^2$, and
$|[e,e^*]|^2=\langle [[e,e^*],e],e \rangle =2|e|^2$, and ![]() $|e|^2=\langle [\zeta,e],e \rangle =\langle \zeta,[e,e^*]\rangle$, therefore
$|e|^2=\langle [\zeta,e],e \rangle =\langle \zeta,[e,e^*]\rangle$, therefore
which is, up to a constant, the inverse of the Toledo rank defined earlier. Then we will prove the following proposition.
Proposition 3.12 The maximum of ![]() $K$ on
$K$ on ![]() $\mathfrak {g}_1$ is attained on the open orbit, and is equal to
$\mathfrak {g}_1$ is attained on the open orbit, and is equal to ![]() $- 2/{B(\zeta,h_{\rm reg})}$, where
$- 2/{B(\zeta,h_{\rm reg})}$, where ![]() $e$ is in the open orbit and
$e$ is in the open orbit and ![]() $\{e^*,h_{\rm reg}=[e,e^*],e\}$ is an
$\{e^*,h_{\rm reg}=[e,e^*],e\}$ is an ![]() $\mathfrak {sl}_2$-triple.
$\mathfrak {sl}_2$-triple.
The minimum of ![]() $K$ on
$K$ on ![]() $\mathfrak {g}_1$ is attained on a minimal orbit, and is equal to
$\mathfrak {g}_1$ is attained on a minimal orbit, and is equal to ![]() $-B(\gamma,\gamma )$ for a long root
$-B(\gamma,\gamma )$ for a long root ![]() $\gamma \in \Delta _1$ (the minimum is attained on
$\gamma \in \Delta _1$ (the minimum is attained on ![]() $e_\gamma$, which belongs to a minimal orbit).
$e_\gamma$, which belongs to a minimal orbit).
Therefore, after multiplying the Hermitian metric by ![]() $B(\gamma,\gamma )$, we obtain a normalized metric with normalized holomorphic sectional curvature
$B(\gamma,\gamma )$, we obtain a normalized metric with normalized holomorphic sectional curvature
At a general critical point ![]() $e\in \mathfrak {g}_1$ of the curvature (therefore
$e\in \mathfrak {g}_1$ of the curvature (therefore ![]() $\{e^*,[e,e^*],e\}$ is an
$\{e^*,[e,e^*],e\}$ is an ![]() $\mathfrak {sl}_2$-triple), we have the normalized value
$\mathfrak {sl}_2$-triple), we have the normalized value ![]() $K_{\rm norm}(e) = - 1/{\operatorname {rk}_T(e)}$.
$K_{\rm norm}(e) = - 1/{\operatorname {rk}_T(e)}$.
From the Toledo character we obtain a ![]() $\mathrm {G}^\mathbb {R}$-invariant 2-form on
$\mathrm {G}^\mathbb {R}$-invariant 2-form on ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ by
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ by
where ![]() $[x,y]_0$ is the projection of the bracket onto
$[x,y]_0$ is the projection of the bracket onto ![]() $\mathfrak {g}_0.$ This actually defines a pseudo-Hermitian metric, which coincides with the previous normalized metric in the horizontal directions (i.e., in
$\mathfrak {g}_0.$ This actually defines a pseudo-Hermitian metric, which coincides with the previous normalized metric in the horizontal directions (i.e., in ![]() $\mathfrak {g}_1$). This explains the choice of the normalization for the Toledo character.
$\mathfrak {g}_1$). This explains the choice of the normalization for the Toledo character.
Proof of Proposition 3.12 For completeness, we begin by proving that the critical points come from ![]() $\mathfrak {sl}_2$-triples
$\mathfrak {sl}_2$-triples ![]() $\{e^*,[e,e^*],e\}$. Since
$\{e^*,[e,e^*],e\}$. Since ![]() $K(e)$ is invariant by homothety, we can restrict to variations
$K(e)$ is invariant by homothety, we can restrict to variations ![]() $\dot e\perp e$. Then
$\dot e\perp e$. Then
It follows that for a critical point, ![]() $[[e,e^*],e]=\lambda e$, and up to renormalizing
$[[e,e^*],e]=\lambda e$, and up to renormalizing ![]() $e$ one can suppose
$e$ one can suppose ![]() $\lambda =2$.
$\lambda =2$.
We will now establish a second variation formula. Start from an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $(h=[e,e^*],e,e^*)$ and take a vector
$(h=[e,e^*],e,e^*)$ and take a vector ![]() $x\perp e$ such that
$x\perp e$ such that ![]() $|x|=|e|$. Consider
$|x|=|e|$. Consider
Then ![]() $e(t)$ has constant norm, and, up to order 2,
$e(t)$ has constant norm, and, up to order 2,
Therefore, again up to order 2,
 \begin{align*} - |e|^4 K(e(t)) &= |[e(t),e(t)^*]|^2 \\ &= |[e,e^*]|^2 + t^2 ( |[x,e^*]+[e,x^*]|^2 + 2 \Re \langle [e,e^*],[x,x^*]-[e,e^*] \rangle). \end{align*}
\begin{align*} - |e|^4 K(e(t)) &= |[e(t),e(t)^*]|^2 \\ &= |[e,e^*]|^2 + t^2 ( |[x,e^*]+[e,x^*]|^2 + 2 \Re \langle [e,e^*],[x,x^*]-[e,e^*] \rangle). \end{align*}
We have already noticed above that ![]() $|[e,e^*]|^2=2|e|^2=2|x|^2$, and therefore
$|[e,e^*]|^2=2|e|^2=2|x|^2$, and therefore
 \begin{align}
\frac{d^2}{dt^2}\bigg|_{t=0}|e|^4 K(e(t)) &= 2( 4 |x|^2 - 2
\langle [h,x],x \rangle - |[x,e^*]+[e,x^*]|^2) \nonumber\\
&= 4 \langle (2- {\operatorname{ad}}_{h})x,x \rangle - 2
|[x,e^*]+[e,x^*]|^2.
\end{align}
\begin{align}
\frac{d^2}{dt^2}\bigg|_{t=0}|e|^4 K(e(t)) &= 2( 4 |x|^2 - 2
\langle [h,x],x \rangle - |[x,e^*]+[e,x^*]|^2) \nonumber\\
&= 4 \langle (2- {\operatorname{ad}}_{h})x,x \rangle - 2
|[x,e^*]+[e,x^*]|^2.
\end{align} We first deduce that the maximum is attained on the open orbit. Observe that ![]() $e$ is in the open orbit if and only if
$e$ is in the open orbit if and only if ![]() $\mathfrak {g}_1 \cap \ker {\operatorname {ad}}_{e^*}=0$. Therefore, if
$\mathfrak {g}_1 \cap \ker {\operatorname {ad}}_{e^*}=0$. Therefore, if ![]() $e$ is not in the open orbit, we can take
$e$ is not in the open orbit, we can take ![]() $x\in \ker {\rm ad}_{e^*}$. Since
$x\in \ker {\rm ad}_{e^*}$. Since ![]() ${\operatorname {ad}}_h \leqslant 0$ on
${\operatorname {ad}}_h \leqslant 0$ on ![]() $\ker {\operatorname {ad}}_{e^*}$, it follows from (3.3) that in the direction of
$\ker {\operatorname {ad}}_{e^*}$, it follows from (3.3) that in the direction of ![]() $x$ we have
$x$ we have
and therefore the maximum cannot be attained at ![]() $e$. This proves the claim that the maximum is obtained on the open orbit.
$e$. This proves the claim that the maximum is obtained on the open orbit.
To find the minimum, we use the following fact [Reference ManivelMan13, Corollary 7, p. 100]. Denote ![]() $\mathfrak {u}$ the subspace of
$\mathfrak {u}$ the subspace of ![]() $\mathfrak {g}_1$ given as the sum of the eigenspaces of
$\mathfrak {g}_1$ given as the sum of the eigenspaces of ![]() ${\operatorname {ad}}_h$ for the eigenvalues at least
${\operatorname {ad}}_h$ for the eigenvalues at least ![]() $2$. Then all orbits in the closure of the orbit of
$2$. Then all orbits in the closure of the orbit of ![]() $e$ meet
$e$ meet ![]() $\mathfrak {u}$. Therefore, suppose that the orbit of
$\mathfrak {u}$. Therefore, suppose that the orbit of ![]() $e$ is not minimal. It follows that we can take
$e$ is not minimal. It follows that we can take ![]() $x\in \mathfrak {u}$, and (3.3) gives us, in the direction of
$x\in \mathfrak {u}$, and (3.3) gives us, in the direction of ![]() $x$,
$x$,
Such ![]() $x$ cannot be in the kernel of
$x$ cannot be in the kernel of ![]() ${\operatorname {ad}}_{e^*}$ (
${\operatorname {ad}}_{e^*}$ (![]() ${\operatorname {ad}}_h\leqslant 0$ on this kernel). Therefore, the right-hand side is nonzero, so that the minimum cannot be attained at
${\operatorname {ad}}_h\leqslant 0$ on this kernel). Therefore, the right-hand side is nonzero, so that the minimum cannot be attained at ![]() $e$. Therefore, the minimum can be attained only at a minimal orbit.
$e$. Therefore, the minimum can be attained only at a minimal orbit.
There can be several minimal orbits if the prehomogeneous space is not irreducible. They are the orbits of elements ![]() $e_\gamma$ for
$e_\gamma$ for ![]() $\gamma \in \Delta$ the longest root. As we have seen,
$\gamma \in \Delta$ the longest root. As we have seen, ![]() $K(e_\gamma )=- 2/{|e_\gamma |^2}=- 4/{|h_\gamma |^2}=- B(\gamma,\gamma )$. The result follows.
$K(e_\gamma )=- 2/{|e_\gamma |^2}=- 4/{|h_\gamma |^2}=- B(\gamma,\gamma )$. The result follows.
Remark 3.13 If we fix an orbit ![]() ${\mathcal {O}}$, then
${\mathcal {O}}$, then ![]() $K_{\rm norm}$ must have a maximum on
$K_{\rm norm}$ must have a maximum on ![]() $\overline {{\mathcal {O}}}$. It follows from the proof of the proposition, and in particular from the description of the orbits in the closure of
$\overline {{\mathcal {O}}}$. It follows from the proof of the proposition, and in particular from the description of the orbits in the closure of ![]() ${\mathcal {O}}$, that the maximum on
${\mathcal {O}}$, that the maximum on ![]() $\overline {{\mathcal {O}}}$ is achieved at some element
$\overline {{\mathcal {O}}}$ is achieved at some element ![]() $e\in {\mathcal {O}}$ such that
$e\in {\mathcal {O}}$ such that ![]() $(e^*,[e,e^*],e)$ is an
$(e^*,[e,e^*],e)$ is an ![]() $\mathfrak {sl}_2$-triple; it is therefore equal to
$\mathfrak {sl}_2$-triple; it is therefore equal to ![]() $K_{\rm norm}(e)=- 1/{\operatorname {rk}_T(e)}$. In particular, we obtain that for any
$K_{\rm norm}(e)=- 1/{\operatorname {rk}_T(e)}$. In particular, we obtain that for any ![]() $x\in \overline {{\mathcal {O}}}$,
$x\in \overline {{\mathcal {O}}}$,
Example 3.14 The case ![]() $\mathrm {G}=\mathrm {SL}_n\mathbb {C}$ is particularly simple to calculate. A first observation is that any nilpotent element
$\mathrm {G}=\mathrm {SL}_n\mathbb {C}$ is particularly simple to calculate. A first observation is that any nilpotent element ![]() $e\in \mathfrak {sl}_n\mathbb {C}$ belongs to the open orbit of the nilpotent subalgebra of a parabolic algebra of
$e\in \mathfrak {sl}_n\mathbb {C}$ belongs to the open orbit of the nilpotent subalgebra of a parabolic algebra of ![]() $\mathfrak {sl}_n\mathbb {C}$. It follows that
$\mathfrak {sl}_n\mathbb {C}$. It follows that ![]() $e$ can be considered as a point in the open orbit of a
$e$ can be considered as a point in the open orbit of a ![]() $\mathfrak {g}_1$ for some grading of
$\mathfrak {g}_1$ for some grading of ![]() $\mathfrak {sl}_n\mathbb {C}$. This observation is not essential for our calculation but relates every nilpotent
$\mathfrak {sl}_n\mathbb {C}$. This observation is not essential for our calculation but relates every nilpotent ![]() $e$ to variations of Hodge structures.
$e$ to variations of Hodge structures.
We now calculate the corresponding bounds for the holomorphic sectional curvature,
where, by (3.2), we have ![]() $\operatorname {rk}_Te=\frac 14 B(h,h)B(\gamma,\gamma )=\frac 12 B(h,h)$ since
$\operatorname {rk}_Te=\frac 14 B(h,h)B(\gamma,\gamma )=\frac 12 B(h,h)$ since ![]() $B(\gamma,\gamma )=2$ in
$B(\gamma,\gamma )=2$ in ![]() $\mathfrak {sl}_n$ for the standard invariant form
$\mathfrak {sl}_n$ for the standard invariant form ![]() $\operatorname {tr}(XY)$. If we have a Jordan block of size
$\operatorname {tr}(XY)$. If we have a Jordan block of size ![]() $k$, the eigenvalues of
$k$, the eigenvalues of ![]() $h$ are
$h$ are ![]() $k-1$,
$k-1$, ![]() $k-3$,…,
$k-3$,…, ![]() $-(k-1)$, therefore
$-(k-1)$, therefore ![]() $B(h,h)=(k-1)^2+(k-3)^2+\cdots +(-(k-1))^2=\frac 13 k(k^2-1)$. Finally, if
$B(h,h)=(k-1)^2+(k-3)^2+\cdots +(-(k-1))^2=\frac 13 k(k^2-1)$. Finally, if ![]() $e$ has Jordan blocks of size
$e$ has Jordan blocks of size ![]() $k_1, k_2,\ldots,k_j$ we obtain
$k_1, k_2,\ldots,k_j$ we obtain
 \[ \operatorname{rk}_Te = \frac16 \sum_1^j k_i(k_i^2-1). \]
\[ \operatorname{rk}_Te = \frac16 \sum_1^j k_i(k_i^2-1). \]
This gives immediately some curvature bounds in [Reference LiLi22].
Proposition 3.15 Let ![]() $e\in \mathfrak {g}_1$ and let
$e\in \mathfrak {g}_1$ and let ![]() $\Omega \subset \mathfrak {g}_1$ be the open
$\Omega \subset \mathfrak {g}_1$ be the open ![]() $\mathrm {G}_0$-orbit of the PHVS
$\mathrm {G}_0$-orbit of the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$. Then
$(\mathrm {G}_0,\mathfrak {g}_1)$. Then
with equality if and only if ![]() $e\in \Omega$.
$e\in \Omega$.
Proof. We give an indirect proof applying Proposition 3.12 and Remark 3.13. The Toledo rank is related to the normalized holomorphic sectional curvature ![]() $K_{\rm norm}$ of the corresponding period domain by
$K_{\rm norm}$ of the corresponding period domain by ![]() $K_{\rm norm}(e)=- 1/{\operatorname {rk}_T(e)}$ if
$K_{\rm norm}(e)=- 1/{\operatorname {rk}_T(e)}$ if ![]() $(f,h,e)$ is a real
$(f,h,e)$ is a real ![]() $\mathfrak {sl}_2$-triple (in a given orbit one can always find an
$\mathfrak {sl}_2$-triple (in a given orbit one can always find an ![]() $e$ which is part of such a triple; see Remark 3.13). Then it is proved that
$e$ which is part of such a triple; see Remark 3.13). Then it is proved that ![]() $K_{\rm norm}(e)\leqslant K_{\rm norm}(e')$ if the orbit of
$K_{\rm norm}(e)\leqslant K_{\rm norm}(e')$ if the orbit of ![]() $e$ is included in the closure of the orbit of
$e$ is included in the closure of the orbit of ![]() $e'$. Moreover, the maximum of
$e'$. Moreover, the maximum of ![]() $K_{\rm norm}$ is attained only on the open orbit. The proposition follows.
$K_{\rm norm}$ is attained only on the open orbit. The proposition follows.
We end this section with a proposition which will be used often in subsequent sections.
Proposition 3.16 If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS, then there is positive integer multiple
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS, then there is positive integer multiple ![]() $q\cdot \chi _T$ of the Toledo character which exponentiates to a character
$q\cdot \chi _T$ of the Toledo character which exponentiates to a character ![]() $\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a polynomial relative invariant of degree
$\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a polynomial relative invariant of degree ![]() $q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$
$q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$
Proof. By Proposition 2.8, there is a positive integer multiple ![]() $q\cdot \chi _T$ of the Toledo character which exponentiates to a character
$q\cdot \chi _T$ of the Toledo character which exponentiates to a character ![]() $\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a relative invariant
$\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a relative invariant ![]() $F$ of degree
$F$ of degree ![]() $q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$ We prove that
$q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$ We prove that ![]() $F$ is a polynomial by proving that it attains a finite value on any element
$F$ is a polynomial by proving that it attains a finite value on any element ![]() $e'\in \mathfrak {g}_1$.
$e'\in \mathfrak {g}_1$.
First note that if ![]() $e'=0,$ then (2.2) implies
$e'=0,$ then (2.2) implies ![]() $F(0)=0.$ For
$F(0)=0.$ For ![]() $e'\neq 0,$ complete
$e'\neq 0,$ complete ![]() $e'$ into an
$e'$ into an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f',h',e'\}$ with
$\{f',h',e'\}$ with ![]() $f'\in \mathfrak {g}_{-1}$ and
$f'\in \mathfrak {g}_{-1}$ and ![]() $h'\in \mathfrak {g}_0$. Then
$h'\in \mathfrak {g}_0$. Then ![]() $e'+\ker ({\operatorname {ad}}_{f'})$ cuts all other
$e'+\ker ({\operatorname {ad}}_{f'})$ cuts all other ![]() $\mathrm {G}$-orbits, but this is not true in general for
$\mathrm {G}$-orbits, but this is not true in general for ![]() $\mathrm {G}_0$-orbits. Nevertheless, it remains true that
$\mathrm {G}_0$-orbits. Nevertheless, it remains true that ![]() $e'+\ker ({\operatorname {ad}}_{f'})$ cuts the open orbit, because
$e'+\ker ({\operatorname {ad}}_{f'})$ cuts the open orbit, because ![]() $\mathfrak {g}_0\cdot e'+(\ker ({\operatorname {ad}}_{f'})\cap \mathfrak {g}_1)=\mathfrak {g}_1$, which implies that
$\mathfrak {g}_0\cdot e'+(\ker ({\operatorname {ad}}_{f'})\cap \mathfrak {g}_1)=\mathfrak {g}_1$, which implies that ![]() $\mathrm {G}_0\cdot (e'+\ker ({\operatorname {ad}}_{f'}))$ contains an open neighborhood of
$\mathrm {G}_0\cdot (e'+\ker ({\operatorname {ad}}_{f'}))$ contains an open neighborhood of ![]() $e'$. So up to conjugating by some element of
$e'$. So up to conjugating by some element of ![]() $\mathrm {G}_0$ we can suppose that
$\mathrm {G}_0$ we can suppose that ![]() $e=e'+X$ with
$e=e'+X$ with ![]() $[f',X]=0$. Since
$[f',X]=0$. Since ![]() $X$ belongs to the nonpositive eigenspaces of
$X$ belongs to the nonpositive eigenspaces of ![]() ${\operatorname {ad}}_{h'}$, it follows that
${\operatorname {ad}}_{h'}$, it follows that ![]() $e'=\lim _{t\rightarrow +\infty }e^{t(h'-h)}\cdot e$. Therefore,
$e'=\lim _{t\rightarrow +\infty }e^{t(h'-h)}\cdot e$. Therefore,
This is finite if ![]() $\chi _h(h'-h)\leqslant 0$, that is, if
$\chi _h(h'-h)\leqslant 0$, that is, if ![]() $B(h,h')\leqslant B(h,h)$. Since
$B(h,h')\leqslant B(h,h)$. Since ![]() $h'=[e',f']$ and
$h'=[e',f']$ and ![]() $[h,e']=2e',$ we have
$[h,e']=2e',$ we have ![]() $B(h,h')=2B(e',f')$ and
$B(h,h')=2B(e',f')$ and ![]() $B(h,h)=2B(e,f)$, so the inequality to prove is
$B(h,h)=2B(e,f)$, so the inequality to prove is
As before, we may use the Hermitian scalar product from the associate real form and assume that ![]() $(e')^*=f'$. We claim that we can also assume
$(e')^*=f'$. We claim that we can also assume ![]() $e^*=f$ while keeping the condition
$e^*=f$ while keeping the condition ![]() $e\in e'+\ker ({\operatorname {ad}}_{f'})$. Indeed, since
$e\in e'+\ker ({\operatorname {ad}}_{f'})$. Indeed, since ![]() $[f',X]=0$ we have
$[f',X]=0$ we have ![]() $[e,e^*]=[e',f']\!+\![X,X^*]$ so we want
$[e,e^*]=[e',f']\!+\![X,X^*]$ so we want ![]() $[X,X^*]\!=\!h-h'$; but
$[X,X^*]\!=\!h-h'$; but ![]() $h-h'$ centralizes the triple
$h-h'$ centralizes the triple ![]() $\{e',f',h'\}$ and preserves the slice
$\{e',f',h'\}$ and preserves the slice ![]() $e'+\ker ({\operatorname {ad}}_{f'}).$ Thus, it is sufficient to conjugate
$e'+\ker ({\operatorname {ad}}_{f'}).$ Thus, it is sufficient to conjugate ![]() $e$ by an element of the centralizer of
$e$ by an element of the centralizer of ![]() $\{e',f',h'\}$ in
$\{e',f',h'\}$ in ![]() $G_0$ to obtain
$G_0$ to obtain ![]() $[e,e^*]=h$.
$[e,e^*]=h$.
Then ![]() $\langle e',X \rangle =\frac 12 \langle [h',e'],X \rangle =\frac 12 \langle h',[X,f'] \rangle =0$. It follows that
$\langle e',X \rangle =\frac 12 \langle [h',e'],X \rangle =\frac 12 \langle h',[X,f'] \rangle =0$. It follows that ![]() $B(e',f')=|e'|^2$ and
$B(e',f')=|e'|^2$ and ![]() $B(e,f)=|e|^2=|e'|^2+|X|^2\geqslant B(e',f')$. The proposition follows.
$B(e,f)=|e|^2=|e'|^2+|X|^2\geqslant B(e',f')$. The proposition follows.
4. Higgs bundles and variations of Hodge structure
For this section let ![]() $X$ be a compact Riemann surface of genus
$X$ be a compact Riemann surface of genus ![]() $g\geqslant 2$ and let
$g\geqslant 2$ and let ![]() $K$ be its canonical bundle.
$K$ be its canonical bundle.
4.1 Higgs bundles and Hodge bundles
Let ![]() $\mathrm {G}$ be a complex reductive Lie group with Lie algebra
$\mathrm {G}$ be a complex reductive Lie group with Lie algebra ![]() $\mathfrak {g}$ and nondegenerate
$\mathfrak {g}$ and nondegenerate ![]() $\mathrm {G}$-invariant bilinear
$\mathrm {G}$-invariant bilinear ![]() $\langle \cdot,\cdot \rangle$. Let
$\langle \cdot,\cdot \rangle$. Let ![]() $\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. If
$\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. If ![]() $E\to X$ is a
$E\to X$ is a ![]() $\mathrm {G}$-bundle, we will denote the
$\mathrm {G}$-bundle, we will denote the ![]() $V$-bundle
$V$-bundle ![]() $E\times _\mathrm {G} V$ associated to
$E\times _\mathrm {G} V$ associated to ![]() $E$ via the representation
$E$ via the representation ![]() $\rho$ by
$\rho$ by ![]() $E(V).$
$E(V).$
Definition 4.1 A ![]() $(\mathrm {G},V)$-Higgs pair is a pair
$(\mathrm {G},V)$-Higgs pair is a pair ![]() $(E,\varphi )$ where
$(E,\varphi )$ where ![]() $E$ is a holomorphic principal
$E$ is a holomorphic principal ![]() $\mathrm {G}$-bundle on
$\mathrm {G}$-bundle on ![]() $X$ and
$X$ and ![]() $\varphi$ is a holomorphic section of
$\varphi$ is a holomorphic section of ![]() $E(V)\otimes K.$
$E(V)\otimes K.$
When ![]() $V=\mathfrak {g}$ and the representation
$V=\mathfrak {g}$ and the representation ![]() $\rho$ is the adjoint representation, a
$\rho$ is the adjoint representation, a ![]() $(\mathrm {G},\mathfrak {g})$-Higgs pair is called a
$(\mathrm {G},\mathfrak {g})$-Higgs pair is called a ![]() $\mathrm {G}$-Higgs bundle. Suppose
$\mathrm {G}$-Higgs bundle. Suppose ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a real form with complexified maximal compact
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a real form with complexified maximal compact ![]() $\mathrm {H}<\mathrm {G}$ and complexified Cartan decomposition
$\mathrm {H}<\mathrm {G}$ and complexified Cartan decomposition ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$. When
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$. When ![]() $\rho :\mathrm {H}\to \mathrm {GL}(\mathfrak {m})$ is the restriction of the adjoint representation of
$\rho :\mathrm {H}\to \mathrm {GL}(\mathfrak {m})$ is the restriction of the adjoint representation of ![]() $\mathrm {G}$, then an
$\mathrm {G}$, then an ![]() $(\mathrm {H},\mathfrak {m})$-Higgs pair is called a
$(\mathrm {H},\mathfrak {m})$-Higgs pair is called a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle.
$\mathrm {G}^\mathbb {R}$-Higgs bundle.
Remark 4.2 When ![]() $\mathrm {G}^\mathbb {R}$ is compact, a
$\mathrm {G}^\mathbb {R}$ is compact, a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle is just a holomorphic
$\mathrm {G}^\mathbb {R}$-Higgs bundle is just a holomorphic ![]() $\mathrm {G}$-bundle. When
$\mathrm {G}$-bundle. When ![]() $\mathrm {G}^\mathbb {R}=\mathrm {G}$ (viewed as a real form of
$\mathrm {G}^\mathbb {R}=\mathrm {G}$ (viewed as a real form of ![]() $\mathrm {G}\times \mathrm {G}$), a
$\mathrm {G}\times \mathrm {G}$), a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle is a
$\mathrm {G}^\mathbb {R}$-Higgs bundle is a ![]() $\mathrm {G}$-Higgs bundle.
$\mathrm {G}$-Higgs bundle.
If ![]() $E$ is a principal
$E$ is a principal ![]() $\mathrm {G}$-bundle and
$\mathrm {G}$-bundle and ![]() $\hat {\mathrm {G}}<\mathrm {G}$ is a subgroup, then a structure group reduction of
$\hat {\mathrm {G}}<\mathrm {G}$ is a subgroup, then a structure group reduction of ![]() $E$ to
$E$ to ![]() $\hat {\mathrm {G}}$ is a section
$\hat {\mathrm {G}}$ is a section ![]() $\sigma$ of the bundle
$\sigma$ of the bundle ![]() $E(\mathrm {G}/\hat {\mathrm {G}}).$ Associated to such a reduction is a principal
$E(\mathrm {G}/\hat {\mathrm {G}}).$ Associated to such a reduction is a principal ![]() $\hat {\mathrm {G}}$-subbundle
$\hat {\mathrm {G}}$-subbundle ![]() $E_\sigma \subset E$ such that
$E_\sigma \subset E$ such that ![]() $E_\sigma (\mathrm {G})$ is canonically isomorphic to
$E_\sigma (\mathrm {G})$ is canonically isomorphic to ![]() $E.$
$E.$
Definition 4.3 Let ![]() $\mathrm {G}$ be a complex reductive Lie group and
$\mathrm {G}$ be a complex reductive Lie group and ![]() $\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. Let
$\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. Let ![]() $\hat {\mathrm {G}}<\mathrm {G}$ and
$\hat {\mathrm {G}}<\mathrm {G}$ and ![]() $\hat V\subset V$ be a
$\hat V\subset V$ be a ![]() $\rho (\hat {\mathrm {G}})$-invariant subspace. We say that a
$\rho (\hat {\mathrm {G}})$-invariant subspace. We say that a ![]() $(\mathrm {G},V)$-Higgs pair
$(\mathrm {G},V)$-Higgs pair ![]() $(E,\varphi )$ reduces to a
$(E,\varphi )$ reduces to a ![]() $(\hat {\mathrm {G}},\hat V)$-Higgs pair, if there is a holomorphic reduction
$(\hat {\mathrm {G}},\hat V)$-Higgs pair, if there is a holomorphic reduction ![]() $E_{\hat {\mathrm {G}}}$ of
$E_{\hat {\mathrm {G}}}$ of ![]() $E$ to
$E$ to ![]() $\hat {\mathrm {G}}$ such that
$\hat {\mathrm {G}}$ such that ![]() $\varphi \in H^0(E_{\hat {\mathrm {G}}}(\hat V)\otimes K)\subset H^0(E_{\hat {\mathrm {G}}}(V)\otimes K).$
$\varphi \in H^0(E_{\hat {\mathrm {G}}}(\hat V)\otimes K)\subset H^0(E_{\hat {\mathrm {G}}}(V)\otimes K).$
For example, if ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a real form,
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a real form, ![]() $\mathrm {H}<\mathrm {G}$ is the complexification of a maximal compact of
$\mathrm {H}<\mathrm {G}$ is the complexification of a maximal compact of ![]() $\mathrm {G}^\mathbb {R}$ and
$\mathrm {G}^\mathbb {R}$ and ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ is complexified Cartan decomposition, then a
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ is complexified Cartan decomposition, then a ![]() $\mathrm {G}$-Higgs bundle
$\mathrm {G}$-Higgs bundle ![]() $(E,\varphi )$ reduces to a
$(E,\varphi )$ reduces to a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle if there is a holomorphic reduction
$\mathrm {G}^\mathbb {R}$-Higgs bundle if there is a holomorphic reduction ![]() $E_{\mathrm {H}}$ of
$E_{\mathrm {H}}$ of ![]() $E$ to
$E$ to ![]() $\mathrm {H}$ such that
$\mathrm {H}$ such that ![]() $\varphi \in H^0(E_{\mathrm {H}}(\mathfrak {m})\otimes K).$
$\varphi \in H^0(E_{\mathrm {H}}(\mathfrak {m})\otimes K).$
Example 4.4 Let ![]() $\{f,h,e\}$ be a basis for
$\{f,h,e\}$ be a basis for ![]() $\mathfrak {sl}_2\mathbb {C}$, and let
$\mathfrak {sl}_2\mathbb {C}$, and let ![]() $\mathrm {T}<\mathrm {P}\mathrm {SL}_2\mathbb {C}$ be the subgroup with Lie algebra
$\mathrm {T}<\mathrm {P}\mathrm {SL}_2\mathbb {C}$ be the subgroup with Lie algebra ![]() $\langle h\rangle.$ Note that
$\langle h\rangle.$ Note that ![]() $\mathrm {T}\cong \mathbb {C}^*$ and the adjoint action of
$\mathrm {T}\cong \mathbb {C}^*$ and the adjoint action of ![]() $\mathrm {T}$ on
$\mathrm {T}$ on ![]() $\langle e\rangle$ is given by
$\langle e\rangle$ is given by ![]() $\lambda \cdot e=\lambda e.$ So, if
$\lambda \cdot e=\lambda e.$ So, if ![]() $E_\mathrm {T}$ is the frame bundle of
$E_\mathrm {T}$ is the frame bundle of ![]() $K^{-1},$ then the associated bundle
$K^{-1},$ then the associated bundle ![]() $E_\mathrm {T}(\langle e\rangle )\otimes K\cong {\mathcal {O}}_X$. Hence, we have a
$E_\mathrm {T}(\langle e\rangle )\otimes K\cong {\mathcal {O}}_X$. Hence, we have a ![]() $\mathrm {P}\mathrm {SL}_2\mathbb {C}$-Higgs bundle
$\mathrm {P}\mathrm {SL}_2\mathbb {C}$-Higgs bundle
Since ![]() $\deg (K)$ is even, this example can be lifted to
$\deg (K)$ is even, this example can be lifted to ![]() $\mathrm {SL}_2\mathbb {C}.$ The lifted action of the subgroup
$\mathrm {SL}_2\mathbb {C}.$ The lifted action of the subgroup ![]() $\mathbb {C}^*\cong \hat {\mathrm {T}}<\mathrm {SL}_2\mathbb {C}$ with Lie algebra
$\mathbb {C}^*\cong \hat {\mathrm {T}}<\mathrm {SL}_2\mathbb {C}$ with Lie algebra ![]() $\langle h\rangle$ is given by
$\langle h\rangle$ is given by ![]() $\lambda \cdot e=\lambda ^2e.$ As a result, if
$\lambda \cdot e=\lambda ^2e.$ As a result, if ![]() $E_{\hat {\mathrm {T}}}$ is the frame bundle of a square root
$E_{\hat {\mathrm {T}}}$ is the frame bundle of a square root ![]() $K^{- {1}/{2}}$ of
$K^{- {1}/{2}}$ of ![]() $K^{-1}$, then
$K^{-1}$, then ![]() $(E_{\hat {\mathrm {T}}}(\mathrm {SL}_2\mathbb {C}),e)$ defines an
$(E_{\hat {\mathrm {T}}}(\mathrm {SL}_2\mathbb {C}),e)$ defines an ![]() $\mathrm {SL}_2\mathbb {C}$-Higgs bundle. These Higgs bundles will be the fundamental building blocks for the results of § 6.
$\mathrm {SL}_2\mathbb {C}$-Higgs bundle. These Higgs bundles will be the fundamental building blocks for the results of § 6.
Now suppose ![]() $\mathrm {G}$ is a complex reductive Lie group and
$\mathrm {G}$ is a complex reductive Lie group and ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ is a
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ is a ![]() $\mathbb {Z}$-grading of its Lie algebra with grading element
$\mathbb {Z}$-grading of its Lie algebra with grading element ![]() $\zeta \in \mathfrak {g}_0.$ Let
$\zeta \in \mathfrak {g}_0.$ Let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta.$ Note that
$\zeta.$ Note that ![]() $\exp (\lambda \zeta )$ is in the center of
$\exp (\lambda \zeta )$ is in the center of ![]() $\mathrm {G}_0$ and
$\mathrm {G}_0$ and ![]() $\operatorname {Ad}(\exp (\lambda \zeta ))$ acts on each
$\operatorname {Ad}(\exp (\lambda \zeta ))$ acts on each ![]() $\mathfrak {g}_j$ by
$\mathfrak {g}_j$ by ![]() $\lambda ^j\cdot \operatorname {Id}$. Let
$\lambda ^j\cdot \operatorname {Id}$. Let ![]() $(E_{\mathrm {G}_0},\varphi )$ be a
$(E_{\mathrm {G}_0},\varphi )$ be a ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair. Note that the central element
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair. Note that the central element ![]() $\exp ( ({\lambda }/{k})\zeta )\in \mathrm {G}_0$ defines a holomorphic automorphism of
$\exp ( ({\lambda }/{k})\zeta )\in \mathrm {G}_0$ defines a holomorphic automorphism of ![]() $E_{\mathrm {G}_0}$ and acts on
$E_{\mathrm {G}_0}$ and acts on ![]() $\varphi$ by multiplication by
$\varphi$ by multiplication by ![]() $\lambda$. As a result we have an isomorphism of
$\lambda$. As a result we have an isomorphism of ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs
Extending the structure group defines a ![]() $\mathrm {G}$-Higgs bundle
$\mathrm {G}$-Higgs bundle ![]() $(E_\mathrm {G},\varphi )$,
$(E_\mathrm {G},\varphi )$,
since ![]() $E_{\mathrm {G}_0}(\mathfrak {g}_k)\subset E_{\mathrm {G}_0}[\mathfrak {g}]\cong E_{\mathrm {G}}(\mathfrak {g})$. Moreover,
$E_{\mathrm {G}_0}(\mathfrak {g}_k)\subset E_{\mathrm {G}_0}[\mathfrak {g}]\cong E_{\mathrm {G}}(\mathfrak {g})$. Moreover, ![]() $(E_\mathrm {G},\varphi )\cong (E_{\mathrm {G}},\lambda \varphi )$ for all
$(E_\mathrm {G},\varphi )\cong (E_{\mathrm {G}},\lambda \varphi )$ for all ![]() $\lambda \in \mathbb {C}^*.$
$\lambda \in \mathbb {C}^*.$
Definition 4.5 A ![]() $\mathrm {G}$-Higgs bundle
$\mathrm {G}$-Higgs bundle ![]() $(E,\varphi )$ is called a Hodge bundle of type
$(E,\varphi )$ is called a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$ if it reduces to a
$(\mathrm {G}_0,\mathfrak {g}_k)$ if it reduces to a ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair.
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair.
Example 4.6 The Higgs bundles from Example 4.4 are Hodge bundles for the grading ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1=\langle f\rangle \oplus \langle h\rangle \oplus \langle e\rangle.$ In these cases,
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1=\langle f\rangle \oplus \langle h\rangle \oplus \langle e\rangle.$ In these cases, ![]() $\mathrm {G}_0$ is a Cartan subgroup of
$\mathrm {G}_0$ is a Cartan subgroup of ![]() $\mathrm {G}.$
$\mathrm {G}.$
Given a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, we can define a subalgebra
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, we can define a subalgebra ![]() $\tilde {\mathfrak {g}}$ consisting of summands
$\tilde {\mathfrak {g}}$ consisting of summands ![]() $\mathfrak {g}_j$ with
$\mathfrak {g}_j$ with ![]() $j=0\text { mod}~k$. Note that
$j=0\text { mod}~k$. Note that ![]() $\tilde {\mathfrak {g}}$ has an associated
$\tilde {\mathfrak {g}}$ has an associated ![]() $\mathbb {Z}$-grading with
$\mathbb {Z}$-grading with ![]() $\mathfrak {g}_k=\tilde {\mathfrak {g}}_1.$ Let
$\mathfrak {g}_k=\tilde {\mathfrak {g}}_1.$ Let ![]() $\tilde {\mathrm {G}}<\mathrm {G}$ be the associated reductive subgroup. The following proposition is immediate.
$\tilde {\mathrm {G}}<\mathrm {G}$ be the associated reductive subgroup. The following proposition is immediate.
Proposition 4.7 Let ![]() $(E,\varphi )$ be a
$(E,\varphi )$ be a ![]() $\mathrm {G}$-Higgs bundle which is a Hodge bundle of type
$\mathrm {G}$-Higgs bundle which is a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$. Then
$(\mathrm {G}_0,\mathfrak {g}_k)$. Then ![]() $(E,\varphi )$ reduces to a
$(E,\varphi )$ reduces to a ![]() $\tilde {\mathrm {G}}$-Higgs bundle and, as a
$\tilde {\mathrm {G}}$-Higgs bundle and, as a ![]() $\tilde {\mathrm {G}}$-Higgs bundle, it is a Hodge bundle of type
$\tilde {\mathrm {G}}$-Higgs bundle, it is a Hodge bundle of type ![]() $(\mathrm {G}_0,\tilde {\mathfrak {g}}_1).$
$(\mathrm {G}_0,\tilde {\mathfrak {g}}_1).$
As a result, we will usually consider Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$. Recall from Proposition 3.8 that there is a canonical real form
$(\mathrm {G}_0,\mathfrak {g}_1)$. Recall from Proposition 3.8 that there is a canonical real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ of Hodge type associated to a
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ of Hodge type associated to a ![]() $\mathbb {Z}$-grading. The complexified Cartan decomposition
$\mathbb {Z}$-grading. The complexified Cartan decomposition ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ satisfies
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ satisfies ![]() $\mathfrak {g}_{2j}\subset \mathfrak {h}$ and
$\mathfrak {g}_{2j}\subset \mathfrak {h}$ and ![]() $\mathfrak {g}_{2j+1}\subset \mathfrak {m},$ in particular
$\mathfrak {g}_{2j+1}\subset \mathfrak {m},$ in particular ![]() $\mathrm {G}_0<\mathrm {H}.$ As a result, a
$\mathrm {G}_0<\mathrm {H}.$ As a result, a ![]() $\mathrm {G}$-Higgs bundle which is a Hodge bundle of type
$\mathrm {G}$-Higgs bundle which is a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ reduces to a
$(\mathrm {G}_0,\mathfrak {g}_1)$ reduces to a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle. Combining this observation with Proposition 4.7 gives the following result which was first observed by Simpson [Reference SimpsonSim92, § 4].
$\mathrm {G}^\mathbb {R}$-Higgs bundle. Combining this observation with Proposition 4.7 gives the following result which was first observed by Simpson [Reference SimpsonSim92, § 4].
Proposition 4.8 Let ![]() $(E,\varphi )$ be a
$(E,\varphi )$ be a ![]() $\mathrm {G}$-Higgs bundle which is a Hodge bundle of type
$\mathrm {G}$-Higgs bundle which is a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$. Then
$(\mathrm {G}_0,\mathfrak {g}_k)$. Then ![]() $(E,\varphi )$-reduces to a
$(E,\varphi )$-reduces to a ![]() $\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle, where
$\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle, where ![]() $\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}$ is a real group of Hodge type. In fact,
$\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}$ is a real group of Hodge type. In fact, ![]() $\tilde {\mathrm {G}}^\mathbb {R}$ is the real form of the subgroup
$\tilde {\mathrm {G}}^\mathbb {R}$ is the real form of the subgroup ![]() $\tilde {\mathrm {G}}<\mathrm {G}$ from Proposition 4.7 associated to the grading of
$\tilde {\mathrm {G}}<\mathrm {G}$ from Proposition 4.7 associated to the grading of ![]() $\tilde {\mathfrak {g}}.$
$\tilde {\mathfrak {g}}.$
Example 4.9 The Hodge bundles in Example 4.4 thus reduce to the real forms ![]() $\mathrm {PSL}_2\mathbb {R}<\mathrm {PSL}_2\mathbb {C}$ and
$\mathrm {PSL}_2\mathbb {R}<\mathrm {PSL}_2\mathbb {C}$ and ![]() $\mathrm {SL}_2\mathbb {R}<\mathrm {SL}_2\mathbb {C}.$
$\mathrm {SL}_2\mathbb {R}<\mathrm {SL}_2\mathbb {C}.$
The above results also apply to ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles. Namely, fix a real form
$\mathrm {G}^\mathbb {R}$-Higgs bundles. Namely, fix a real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ with a maximal compact subgroup
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ with a maximal compact subgroup ![]() $\mathrm {H}^\mathbb {R}<\mathrm {G}^\mathbb {R}$. Let
$\mathrm {H}^\mathbb {R}<\mathrm {G}^\mathbb {R}$. Let ![]() $\mathrm {H}<\mathrm {G}$ be the complexification of
$\mathrm {H}<\mathrm {G}$ be the complexification of ![]() $\mathrm {H}^\mathbb {R}$ and
$\mathrm {H}^\mathbb {R}$ and ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ be a complexified Cartan decomposition. Consider a
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ be a complexified Cartan decomposition. Consider a ![]() $\mathbb {Z}$-grading of
$\mathbb {Z}$-grading of ![]() $\mathfrak {g}$ given by
$\mathfrak {g}$ given by ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {h}_j\oplus \mathfrak {m}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {h}_j\oplus \mathfrak {m}_j$ with grading element ![]() $\zeta \in \mathfrak {h}_0.$ Let
$\zeta \in \mathfrak {h}_0.$ Let ![]() $\mathrm {H}_0<\mathrm {H}$ be the centralizer of
$\mathrm {H}_0<\mathrm {H}$ be the centralizer of ![]() $\zeta.$ Given an
$\zeta.$ Given an ![]() $(\mathrm {H}_0,\mathfrak {m}_k)$-Higgs pair
$(\mathrm {H}_0,\mathfrak {m}_k)$-Higgs pair ![]() $(E_{\mathrm {H}_0},\varphi )$, extending the structure group to
$(E_{\mathrm {H}_0},\varphi )$, extending the structure group to ![]() $\mathrm {H}$ defines a
$\mathrm {H}$ defines a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E_{\mathrm {H}_0}(\mathrm {H}),\varphi )$ such that
$(E_{\mathrm {H}_0}(\mathrm {H}),\varphi )$ such that ![]() $(E_{\mathrm {H}_0}(\mathrm {H}),\varphi )\cong (E_{\mathrm {H}_0}(\mathrm {H}),\lambda \varphi )$ for all
$(E_{\mathrm {H}_0}(\mathrm {H}),\varphi )\cong (E_{\mathrm {H}_0}(\mathrm {H}),\lambda \varphi )$ for all ![]() $\lambda \in \mathbb {C}^*$.
$\lambda \in \mathbb {C}^*$.
A ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E,\varphi )$ is called a Hodge bundle of type
$(E,\varphi )$ is called a Hodge bundle of type ![]() $(\mathrm {H}_0,\mathfrak {m}_k)$ if it reduces to a
$(\mathrm {H}_0,\mathfrak {m}_k)$ if it reduces to a ![]() $(\mathrm {H}_0,\mathfrak {m}_k)$-Higgs pair. Consider the subalgebra
$(\mathrm {H}_0,\mathfrak {m}_k)$-Higgs pair. Consider the subalgebra ![]() $\tilde {\mathfrak {g}}=\tilde {\mathfrak {h}}\oplus \tilde {\mathfrak {m}}$ given by
$\tilde {\mathfrak {g}}=\tilde {\mathfrak {h}}\oplus \tilde {\mathfrak {m}}$ given by
Let ![]() $\tilde {\mathfrak {g}}^\mathbb {R}\subset \tilde {\mathfrak {g}}$ be the associated real form of Hodge type with complexified Cartan decomposition
$\tilde {\mathfrak {g}}^\mathbb {R}\subset \tilde {\mathfrak {g}}$ be the associated real form of Hodge type with complexified Cartan decomposition ![]() $\tilde {\mathfrak {g}}=\tilde {\mathfrak {h}}\oplus \tilde {\mathfrak {m}}.$ As in the complex case, we have the following result.
$\tilde {\mathfrak {g}}=\tilde {\mathfrak {h}}\oplus \tilde {\mathfrak {m}}.$ As in the complex case, we have the following result.
Proposition 4.10 Let ![]() $(E,\varphi )$ be a
$(E,\varphi )$ be a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle which is a Hodge bundle of type
$\mathrm {G}^\mathbb {R}$-Higgs bundle which is a Hodge bundle of type ![]() $(\mathrm {H}_0,\mathfrak {m}_k).$ Then there is a reductive subgroup
$(\mathrm {H}_0,\mathfrak {m}_k).$ Then there is a reductive subgroup ![]() $\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ of Hodge type such that
$\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ of Hodge type such that ![]() $(E,\varphi )$ reduces to a
$(E,\varphi )$ reduces to a ![]() $\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle. Moreover, the resulting
$\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle. Moreover, the resulting ![]() $\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle is a
$\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle is a ![]() $(\mathrm {H}_0,\tilde {\mathfrak {m}}_1)=(\tilde {\mathrm {G}}_0,\tilde {\mathfrak {g}}_1)$-Hodge bundle.
$(\mathrm {H}_0,\tilde {\mathfrak {m}}_1)=(\tilde {\mathrm {G}}_0,\tilde {\mathfrak {g}}_1)$-Hodge bundle.
As a result, we will mostly consider Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$.
$(\mathrm {G}_0,\mathfrak {g}_1)$.
4.2 Moduli spaces and fixed points
To form a moduli space of Higgs pairs, we need to define suitable notions of stability. We describe this below and refer to [Reference García-Prada, Gothen and Mundet i RieraGGM09, Reference Bradlow, García-Prada and Mundet i RieraBGM03] for more details. Let ![]() $\mathrm {G}$ be a complex reductive Lie group and
$\mathrm {G}$ be a complex reductive Lie group and ![]() $\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. Fix a maximal compact subgroup
$\rho :\mathrm {G}\to \mathrm {GL}(V)$ be a holomorphic representation. Fix a maximal compact subgroup ![]() $\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let
$\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let ![]() $\mathfrak {k}^\mathbb {R}$ be its Lie algebra. An element
$\mathfrak {k}^\mathbb {R}$ be its Lie algebra. An element ![]() $s\in i\mathfrak {k}^\mathbb {R}$ defines subspaces of
$s\in i\mathfrak {k}^\mathbb {R}$ defines subspaces of ![]() $V$ via the representation
$V$ via the representation ![]() $\rho$:
$\rho$:
When ![]() $\rho :\mathrm {G}\to \mathrm {GL}(\mathfrak {g})$ is the adjoint representation,
$\rho :\mathrm {G}\to \mathrm {GL}(\mathfrak {g})$ is the adjoint representation, ![]() $\mathfrak {g}_s=\mathfrak {p}_s\subset \mathfrak {g}$ is a parabolic subalgebra with Levi subalgebra
$\mathfrak {g}_s=\mathfrak {p}_s\subset \mathfrak {g}$ is a parabolic subalgebra with Levi subalgebra ![]() $\mathfrak {g}_s^0=\mathfrak {l}_s\subset \mathfrak {p}_s.$ The associated subgroups
$\mathfrak {g}_s^0=\mathfrak {l}_s\subset \mathfrak {p}_s.$ The associated subgroups ![]() $\mathrm {L}_s<\mathrm {P}_s$ are given by
$\mathrm {L}_s<\mathrm {P}_s$ are given by
Moreover, ![]() $s$ defines a character
$s$ defines a character ![]() $\chi _s:\mathfrak {p}_s\to \mathbb {C}$ by
$\chi _s:\mathfrak {p}_s\to \mathbb {C}$ by
Let ![]() $E$ be a
$E$ be a ![]() $\mathrm {G}$-bundle,
$\mathrm {G}$-bundle, ![]() $s\in i\mathfrak {k}^\mathbb {R}$ and
$s\in i\mathfrak {k}^\mathbb {R}$ and ![]() $\mathrm {P}_s<\mathrm {G}$ be the associated parabolic subgroup. A reduction of structure group of
$\mathrm {P}_s<\mathrm {G}$ be the associated parabolic subgroup. A reduction of structure group of ![]() $E$ to
$E$ to ![]() $\mathrm {P}_s$ is a
$\mathrm {P}_s$ is a ![]() $\mathrm {P}_s$-subbundle
$\mathrm {P}_s$-subbundle ![]() $E_{\mathrm {P}_s}\subset E$; this is equivalent to a section
$E_{\mathrm {P}_s}\subset E$; this is equivalent to a section ![]() $\sigma \in \Gamma (E(\mathrm {G}/\mathrm {P}_s))$ of the associated bundle. We will denote the associated
$\sigma \in \Gamma (E(\mathrm {G}/\mathrm {P}_s))$ of the associated bundle. We will denote the associated ![]() $\mathrm {P}_s$-subbundle by
$\mathrm {P}_s$-subbundle by ![]() $E_\sigma.$ The degree of such a reduction will be defined using Chern–Weil theory. Since
$E_\sigma.$ The degree of such a reduction will be defined using Chern–Weil theory. Since ![]() $\mathrm {P}_s$ is homotopy equivalent to the maximal compact
$\mathrm {P}_s$ is homotopy equivalent to the maximal compact ![]() $\mathrm {K}_s^\mathbb {R}=\mathrm {K}^\mathbb {R}\cap \mathrm {L}_s$ of
$\mathrm {K}_s^\mathbb {R}=\mathrm {K}^\mathbb {R}\cap \mathrm {L}_s$ of ![]() $\mathrm {L}_s$, given a reduction of structure
$\mathrm {L}_s$, given a reduction of structure ![]() $\sigma$ of
$\sigma$ of ![]() $E$ to
$E$ to ![]() $\mathrm {P}_s$, there is a further reduction of
$\mathrm {P}_s$, there is a further reduction of ![]() $E$ to
$E$ to ![]() $\mathrm {K}_s^\mathbb {R}$ which is unique up to homotopy. Let
$\mathrm {K}_s^\mathbb {R}$ which is unique up to homotopy. Let ![]() $E_{\sigma '}\subset E$ be the resulting
$E_{\sigma '}\subset E$ be the resulting ![]() $\mathrm {K}^\mathbb {R}_s$ principal bundle. The curvature
$\mathrm {K}^\mathbb {R}_s$ principal bundle. The curvature ![]() $F_A$ of a connection
$F_A$ of a connection ![]() $A$ on
$A$ on ![]() $E_{\sigma '}$ satisfies
$E_{\sigma '}$ satisfies ![]() $F_A\in \Omega ^2(X,E_{\sigma '}(\mathfrak {k}_s^\mathbb {R})).$ Thus, evaluating the character
$F_A\in \Omega ^2(X,E_{\sigma '}(\mathfrak {k}_s^\mathbb {R})).$ Thus, evaluating the character ![]() $\chi _s$ on the curvature, we have
$\chi _s$ on the curvature, we have ![]() $\chi _s(F_A)\in \Omega (X,i\mathbb {R}),$ and we define the degree of
$\chi _s(F_A)\in \Omega (X,i\mathbb {R}),$ and we define the degree of ![]() $\sigma$ as
$\sigma$ as
If a multiple of ![]() $q\cdot \chi _s$ exponentiates to a character
$q\cdot \chi _s$ exponentiates to a character ![]() $\tilde \chi _s:\mathrm {P}_s\to \mathbb {C}^*$ and
$\tilde \chi _s:\mathrm {P}_s\to \mathbb {C}^*$ and ![]() $\sigma \in \Gamma (E(\mathrm {G}/\mathrm {P}_s))$ is a reduction, then
$\sigma \in \Gamma (E(\mathrm {G}/\mathrm {P}_s))$ is a reduction, then ![]() $E_{\sigma }\times _{\chi _s}\mathbb {C}^*=E_{\sigma }(\tilde \chi _s)$ is a line bundle and
$E_{\sigma }\times _{\chi _s}\mathbb {C}^*=E_{\sigma }(\tilde \chi _s)$ is a line bundle and ![]() $\deg E(\sigma,s)= ({1}/{q})\deg E_\sigma (\tilde \chi _s).$ When
$\deg E(\sigma,s)= ({1}/{q})\deg E_\sigma (\tilde \chi _s).$ When ![]() $s$ is in the center
$s$ is in the center ![]() $\mathfrak {z}$ of
$\mathfrak {z}$ of ![]() $\mathfrak {g}$ then
$\mathfrak {g}$ then ![]() $\mathrm {P}_s=\mathrm {G}$. In this case, the degree given in (4.2) is simply the degree of
$\mathrm {P}_s=\mathrm {G}$. In this case, the degree given in (4.2) is simply the degree of ![]() $E$ with respect to
$E$ with respect to ![]() $\chi _s,$ and will be denoted by
$\chi _s,$ and will be denoted by ![]() $\deg _\chi (E)$. Again, if a multiple
$\deg _\chi (E)$. Again, if a multiple ![]() $q\cdot \chi _s$ exponentiates to a character
$q\cdot \chi _s$ exponentiates to a character ![]() $\tilde \chi :\mathrm {G}\to \mathbb {C}^*$ we have
$\tilde \chi :\mathrm {G}\to \mathbb {C}^*$ we have
Let ![]() $d\rho :\mathfrak {g}\to \mathfrak {gl}(V)$ be the differential of
$d\rho :\mathfrak {g}\to \mathfrak {gl}(V)$ be the differential of ![]() $\rho$ and let
$\rho$ and let ![]() $\mathfrak {z}^\mathbb {R}$ be the center of
$\mathfrak {z}^\mathbb {R}$ be the center of ![]() $\mathfrak {k}^\mathbb {R}$ and
$\mathfrak {k}^\mathbb {R}$ and ![]() $\mathfrak {k}^\mathbb {R}=\mathfrak {k}_{ss}^\mathbb {R}=\mathfrak {z}^\perp$. Define
$\mathfrak {k}^\mathbb {R}=\mathfrak {k}_{ss}^\mathbb {R}=\mathfrak {z}^\perp$. Define
We are now ready to define ![]() $\alpha$-stability notions for
$\alpha$-stability notions for ![]() $\alpha \in i\mathfrak {z}^\mathbb {R}.$
$\alpha \in i\mathfrak {z}^\mathbb {R}.$
Definition 4.11 Let ![]() $\alpha \in i\mathfrak {z}^\mathbb {R}$. A
$\alpha \in i\mathfrak {z}^\mathbb {R}$. A ![]() $(\mathrm {G},V)$-Higgs pair
$(\mathrm {G},V)$-Higgs pair ![]() $(E,\varphi )$ is:
$(E,\varphi )$ is:
−
 $\alpha$-semistable if for any
$\alpha$-semistable if for any  $s\in i\mathfrak {k}^\mathbb {R}$ and any holomorphic reduction
$s\in i\mathfrak {k}^\mathbb {R}$ and any holomorphic reduction  $\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s))$ such that
$\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s))$ such that  $\varphi \in H^0(E_\sigma (V_s)\otimes K)$, we have
$\varphi \in H^0(E_\sigma (V_s)\otimes K)$, we have  $\deg E(\sigma,s)\geqslant \langle \alpha,s\rangle$;
$\deg E(\sigma,s)\geqslant \langle \alpha,s\rangle$;−
 $\alpha$-stable if it is
$\alpha$-stable if it is  $\alpha$-semistable and for any
$\alpha$-semistable and for any  $s\in i\mathfrak {k}^\mathbb {R}_\rho$ and any holomorphic reduction
$s\in i\mathfrak {k}^\mathbb {R}_\rho$ and any holomorphic reduction  $\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s)$ such that
$\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s)$ such that  $\varphi \in H^0(E_\sigma (V_s)\otimes K)$, we have
$\varphi \in H^0(E_\sigma (V_s)\otimes K)$, we have  $\deg E(\sigma,s)> \langle \alpha,s\rangle$;
$\deg E(\sigma,s)> \langle \alpha,s\rangle$;−
 $\alpha$-polystable if it is
$\alpha$-polystable if it is  $\alpha$-semistable and whenever
$\alpha$-semistable and whenever  $s\in i\mathfrak {k}^\mathbb {R}$ and
$s\in i\mathfrak {k}^\mathbb {R}$ and  $\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s))$ satisfy
$\sigma \in H^0(E(\mathrm {G}/\mathrm {P}_s))$ satisfy  $\varphi \in H^0(E_\sigma (V_s)\otimes K)$ and
$\varphi \in H^0(E_\sigma (V_s)\otimes K)$ and  $\deg E(\sigma,s)=\langle \alpha,s\rangle$, there is a further holomorphic reduction
$\deg E(\sigma,s)=\langle \alpha,s\rangle$, there is a further holomorphic reduction  $\sigma '\in H^0(E_\sigma (\mathrm {P}_s/\mathrm {L}_s))$ such that
$\sigma '\in H^0(E_\sigma (\mathrm {P}_s/\mathrm {L}_s))$ such that  $\varphi \in H^0(E_{\sigma '}(V_s^0)\otimes K)$.
$\varphi \in H^0(E_{\sigma '}(V_s^0)\otimes K)$.
The moduli space of ![]() $\alpha$-polystable
$\alpha$-polystable ![]() $(\mathrm {G},V)$-Higgs pairs over
$(\mathrm {G},V)$-Higgs pairs over ![]() $X$ is defined as the set of isomorphism classes of
$X$ is defined as the set of isomorphism classes of ![]() $\alpha$-polystable
$\alpha$-polystable ![]() $(\mathrm {G},V)$-Higgs pairs and will be denoted by
$(\mathrm {G},V)$-Higgs pairs and will be denoted by ![]() ${\mathcal {M}}^\alpha (\mathrm {G},V).$ A GIT construction of these spaces is given by Schmitt in [Reference SchmittSch08] and by Simpson for the moduli space of
${\mathcal {M}}^\alpha (\mathrm {G},V).$ A GIT construction of these spaces is given by Schmitt in [Reference SchmittSch08] and by Simpson for the moduli space of ![]() $0$-polystable
$0$-polystable ![]() $\mathrm {G}$-Higgs bundles [Reference SimpsonSim94].
$\mathrm {G}$-Higgs bundles [Reference SimpsonSim94].
Remark 4.12 When ![]() $\alpha =0$, we refer to
$\alpha =0$, we refer to ![]() $0$-stability simply as stability (similarly for semistability and polystability), and denote the moduli space by
$0$-stability simply as stability (similarly for semistability and polystability), and denote the moduli space by ![]() ${\mathcal {M}}(\mathrm {G},V).$ The moduli space of polystable
${\mathcal {M}}(\mathrm {G},V).$ The moduli space of polystable ![]() $\mathrm {G}$-Higgs bundles will be denoted by
$\mathrm {G}$-Higgs bundles will be denoted by ![]() ${\mathcal {M}}(\mathrm {G})$, and, for a real form
${\mathcal {M}}(\mathrm {G})$, and, for a real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G},$ the moduli space of polystable
$\mathrm {G}^\mathbb {R}<\mathrm {G},$ the moduli space of polystable ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles will be denoted by
$\mathrm {G}^\mathbb {R}$-Higgs bundles will be denoted by ![]() ${\mathcal {M}}(\mathrm {G}^\mathbb {R}).$
${\mathcal {M}}(\mathrm {G}^\mathbb {R}).$
There is a natural ![]() $\mathbb {C}^*$-action on the moduli spaces of
$\mathbb {C}^*$-action on the moduli spaces of ![]() $\alpha$-polystable Higgs pairs given by
$\alpha$-polystable Higgs pairs given by ![]() $\lambda \cdot (E,\varphi )=(E,\lambda \varphi ).$ If
$\lambda \cdot (E,\varphi )=(E,\lambda \varphi ).$ If ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ is a
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ is a ![]() $\mathbb {Z}$-grading, then the
$\mathbb {Z}$-grading, then the ![]() $\mathbb {C}^*$-action is trivial on the moduli space of
$\mathbb {C}^*$-action is trivial on the moduli space of ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs by (4.1). As a result, polystable Higgs bundles which are Hodge bundles define fixed points of the
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs by (4.1). As a result, polystable Higgs bundles which are Hodge bundles define fixed points of the ![]() $\mathbb {C}^*$-action on the moduli space of Higgs bundles. Simpson proved the converse [Reference SimpsonSim88, Reference SimpsonSim92]. Namely, all
$\mathbb {C}^*$-action on the moduli space of Higgs bundles. Simpson proved the converse [Reference SimpsonSim88, Reference SimpsonSim92]. Namely, all ![]() $\mathbb {C}^*$-fixed points in the moduli space of Higgs bundles are Hodge bundles. In fact, if a Higgs bundle is a Hodge bundle, then polystability of the Higgs bundle is equivalent to polystability of the associated pair. To explain why this is true, we need to use the correspondence between stability and solutions to gauge-theoretic equations.
$\mathbb {C}^*$-fixed points in the moduli space of Higgs bundles are Hodge bundles. In fact, if a Higgs bundle is a Hodge bundle, then polystability of the Higgs bundle is equivalent to polystability of the associated pair. To explain why this is true, we need to use the correspondence between stability and solutions to gauge-theoretic equations.
We first describe this for ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles. Fix a maximal compact subgroup
$\mathrm {G}^\mathbb {R}$-Higgs bundles. Fix a maximal compact subgroup ![]() $\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let
$\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ be the resulting conjugate linear involution. Now fix a real form
$\tau :\mathfrak {g}\to \mathfrak {g}$ be the resulting conjugate linear involution. Now fix a real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ such that
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ such that ![]() $\mathrm {K}^\mathbb {R}\cap \mathrm {G}^\mathbb {R}=\mathrm {H}^\mathbb {R}$ is a maximal compact subgroup of
$\mathrm {K}^\mathbb {R}\cap \mathrm {G}^\mathbb {R}=\mathrm {H}^\mathbb {R}$ is a maximal compact subgroup of ![]() $\mathrm {G}^\mathbb {R}$ and let
$\mathrm {G}^\mathbb {R}$ and let ![]() $\mathrm {H}<\mathrm {G}$ be the complexification of
$\mathrm {H}<\mathrm {G}$ be the complexification of ![]() $\mathrm {H}^\mathbb {R}.$ Let
$\mathrm {H}^\mathbb {R}.$ Let ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ be the complexified Cartan decomposition of the real form. Consider a
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}$ be the complexified Cartan decomposition of the real form. Consider a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E,\varphi )$. A metric on
$(E,\varphi )$. A metric on ![]() $E$ is by definition a structure group reduction
$E$ is by definition a structure group reduction ![]() $h\in \Gamma (E(\mathrm {H}/\mathrm {H}^\mathbb {R}))$ of
$h\in \Gamma (E(\mathrm {H}/\mathrm {H}^\mathbb {R}))$ of ![]() $E$ to
$E$ to ![]() $\mathrm {H}^\mathbb {R}.$ Associated to a metric
$\mathrm {H}^\mathbb {R}.$ Associated to a metric ![]() $h$, there is a unique connection
$h$, there is a unique connection ![]() $A_h$ (the Chern connection) which is compatible with the reduction and the holomorphic structure. Let
$A_h$ (the Chern connection) which is compatible with the reduction and the holomorphic structure. Let ![]() $E_h$ be the
$E_h$ be the ![]() $\mathrm {H}^\mathbb {R}$-subbundle associated to a metric h. Then
$\mathrm {H}^\mathbb {R}$-subbundle associated to a metric h. Then ![]() $E(\mathfrak {m})$ is canonically identified with
$E(\mathfrak {m})$ is canonically identified with ![]() $E_h(\mathfrak {m})$. The compact real form
$E_h(\mathfrak {m})$. The compact real form ![]() $\tau$ defines an anti-holomorphic involution of
$\tau$ defines an anti-holomorphic involution of ![]() $E_h(\mathfrak {m})$. Combining this with conjugation of 1-forms defines an involution
$E_h(\mathfrak {m})$. Combining this with conjugation of 1-forms defines an involution
The Higgs field ![]() $\varphi \in H^0(E(\mathfrak {m})\otimes K)$ defines a
$\varphi \in H^0(E(\mathfrak {m})\otimes K)$ defines a ![]() $(1,0)$-form valued in
$(1,0)$-form valued in ![]() $E(\mathfrak {m})$. Thus
$E(\mathfrak {m})$. Thus ![]() $[\varphi,-\tau (\varphi )]$ defines a 2-form valued in
$[\varphi,-\tau (\varphi )]$ defines a 2-form valued in ![]() $E_h[\mathfrak {h}^\mathbb {R}]$, and we can make sense of the equation
$E_h[\mathfrak {h}^\mathbb {R}]$, and we can make sense of the equation
where ![]() $F_h$ is the curvature of the Chern connection. These are the Hitchin equations. The following theorem relates solutions of the Hitchin equations with stability; it was proven by Hitchin [Reference HitchinHit87] for
$F_h$ is the curvature of the Chern connection. These are the Hitchin equations. The following theorem relates solutions of the Hitchin equations with stability; it was proven by Hitchin [Reference HitchinHit87] for ![]() $\mathrm {SL}_2\mathbb {C}$ and by Simpson [Reference SimpsonSim88] for complex reductive Lie groups (see [Reference García-Prada, Gothen and Mundet i RieraGGM09] for the general statement).
$\mathrm {SL}_2\mathbb {C}$ and by Simpson [Reference SimpsonSim88] for complex reductive Lie groups (see [Reference García-Prada, Gothen and Mundet i RieraGGM09] for the general statement).
Theorem 4.13 A ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E,\varphi )$ is polystable if and only if there exists a metric
$(E,\varphi )$ is polystable if and only if there exists a metric ![]() $h$ on
$h$ on ![]() $E$ which solves the Hitchin equations (4.4).
$E$ which solves the Hitchin equations (4.4).
Remark 4.14 When the group ![]() $\mathrm {G}^\mathbb {R}$ is compact, then the Hitchin equations are just
$\mathrm {G}^\mathbb {R}$ is compact, then the Hitchin equations are just ![]() $F_h=0.$ That is, there is a flat metric on the bundle, and the classical results of Narasimhan and Seshadri [Reference Narasimhan and SeshadriNS65] and of Ramanathan [Reference RamanathanRam75].
$F_h=0.$ That is, there is a flat metric on the bundle, and the classical results of Narasimhan and Seshadri [Reference Narasimhan and SeshadriNS65] and of Ramanathan [Reference RamanathanRam75].
For general ![]() $(\mathrm {G},V)$-Higgs pairs, we fix a maximal compact
$(\mathrm {G},V)$-Higgs pairs, we fix a maximal compact ![]() $\mathrm {K}^\mathbb {R}<\mathrm {G}$ and a
$\mathrm {K}^\mathbb {R}<\mathrm {G}$ and a ![]() $\mathrm {K}^\mathbb {R}$ invariant Hermitian inner product on V. Now the action of
$\mathrm {K}^\mathbb {R}$ invariant Hermitian inner product on V. Now the action of ![]() $\mathrm {K}^\mathbb {R}$ on
$\mathrm {K}^\mathbb {R}$ on ![]() $V$ is Hamiltonian and has an associated moment map
$V$ is Hamiltonian and has an associated moment map ![]() $\mu :V\to (\mathfrak {k}^\mathbb {R})^*\to \mathfrak {k}^\mathbb {R}$, where we use the inner product on
$\mu :V\to (\mathfrak {k}^\mathbb {R})^*\to \mathfrak {k}^\mathbb {R}$, where we use the inner product on ![]() $\mathfrak {k}^\mathbb {R}$ to identify
$\mathfrak {k}^\mathbb {R}$ to identify ![]() $(\mathfrak {k}^\mathbb {R})^*$ with
$(\mathfrak {k}^\mathbb {R})^*$ with ![]() $\mathfrak {k}^\mathbb {R}$. If
$\mathfrak {k}^\mathbb {R}$. If ![]() $\varphi \in \Omega ^{1,0}(E(V)),$ then one can define a bundle version of the moment map so that
$\varphi \in \Omega ^{1,0}(E(V)),$ then one can define a bundle version of the moment map so that ![]() $\mu (\varphi )\in \Omega ^{1,1}(E(\mathfrak {k}^\mathbb {R}))$, and polystability of
$\mu (\varphi )\in \Omega ^{1,1}(E(\mathfrak {k}^\mathbb {R}))$, and polystability of ![]() $(\mathrm {G},V)$-Higgs pairs is equivalent the existence of a metric
$(\mathrm {G},V)$-Higgs pairs is equivalent the existence of a metric ![]() $h$ solving the equation
$h$ solving the equation ![]() $F_h+\mu (\varphi )=0$ (see [Reference García-Prada, Gothen and Mundet i RieraGGM09] for more details). For
$F_h+\mu (\varphi )=0$ (see [Reference García-Prada, Gothen and Mundet i RieraGGM09] for more details). For ![]() $\mathrm {G}$-Higgs bundles, we fix a compact real form
$\mathrm {G}$-Higgs bundles, we fix a compact real form ![]() $\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let
$\mathrm {K}^\mathbb {R}<\mathrm {G}$ and let ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ be the associated involution. The Hermitian inner product on
$\tau :\mathfrak {g}\to \mathfrak {g}$ be the associated involution. The Hermitian inner product on ![]() $\mathfrak {g}$ is given by
$\mathfrak {g}$ is given by ![]() $B(\cdot,-\tau (\cdot ))$ and the moment map
$B(\cdot,-\tau (\cdot ))$ and the moment map ![]() $\mu _\mathrm {G}:\mathfrak {g}\to \mathfrak {k}^\mathbb {R}$ is given by
$\mu _\mathrm {G}:\mathfrak {g}\to \mathfrak {k}^\mathbb {R}$ is given by ![]() $\mu _\mathrm {G}(x)=[x,-\tau (x)]$.
$\mu _\mathrm {G}(x)=[x,-\tau (x)]$.
For ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs, we choose a compact real form
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pairs, we choose a compact real form ![]() $\mathrm {K}^\mathbb {R}<\mathrm {G}$ such that
$\mathrm {K}^\mathbb {R}<\mathrm {G}$ such that ![]() $\tau |_{\mathfrak {g}_0}=\operatorname {Id}.$ Recall from Remark 3.10 that
$\tau |_{\mathfrak {g}_0}=\operatorname {Id}.$ Recall from Remark 3.10 that ![]() $\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ for all
$\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ for all ![]() $j.$ As a result,
$j.$ As a result, ![]() $\mathrm {K}_0^\mathbb {R}=\mathrm {G}_0\cap \mathrm {K}^\mathbb {R}$ is a compact form of
$\mathrm {K}_0^\mathbb {R}=\mathrm {G}_0\cap \mathrm {K}^\mathbb {R}$ is a compact form of ![]() $\mathrm {G}_0$ and
$\mathrm {G}_0$ and ![]() $B(x,-\tau (y))$ defines a
$B(x,-\tau (y))$ defines a ![]() $\mathrm {K}_0^\mathbb {R}$-invariant Hermitian form on
$\mathrm {K}_0^\mathbb {R}$-invariant Hermitian form on ![]() $\mathfrak {g}_k.$ The moment map
$\mathfrak {g}_k.$ The moment map ![]() $\mu _{\mathrm {G}_0}:\mathfrak {g}_k\to \mathfrak {k}_0^\mathbb {R}$ is then given by restricting the moment map
$\mu _{\mathrm {G}_0}:\mathfrak {g}_k\to \mathfrak {k}_0^\mathbb {R}$ is then given by restricting the moment map ![]() $\mu _\mathrm {G}:\mathfrak {g}\to \mathfrak {k}^\mathbb {R}$ and orthogonally projecting onto
$\mu _\mathrm {G}:\mathfrak {g}\to \mathfrak {k}^\mathbb {R}$ and orthogonally projecting onto ![]() $\mathfrak {k}_0^\mathbb {R}$. That is,
$\mathfrak {k}_0^\mathbb {R}$. That is, ![]() $\mu _{\mathrm {G}_0}(x)$ is the orthogonal projection of
$\mu _{\mathrm {G}_0}(x)$ is the orthogonal projection of ![]() $[x,-\tau (x)]$ onto
$[x,-\tau (x)]$ onto ![]() $\mathfrak {k}_0^\mathbb {R}.$ But for
$\mathfrak {k}_0^\mathbb {R}.$ But for ![]() $x\in \mathfrak {g}_k,$ orthogonal projection is unnecessary since
$x\in \mathfrak {g}_k,$ orthogonal projection is unnecessary since ![]() $[x,-\tau (x)]\in \mathfrak {k}_0^\mathbb {R}$. Thus, a
$[x,-\tau (x)]\in \mathfrak {k}_0^\mathbb {R}$. Thus, a ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair ![]() $(E,\varphi )$ is polystable if and only if there is a metric
$(E,\varphi )$ is polystable if and only if there is a metric ![]() $h\in \Gamma (E/\mathrm {K}_0^\mathbb {R})$ such that
$h\in \Gamma (E/\mathrm {K}_0^\mathbb {R})$ such that ![]() $F_h+[\varphi,-\tau (\varphi )]=0.$ Such a metric solves the Hitchin equations (4.4) for the associated
$F_h+[\varphi,-\tau (\varphi )]=0.$ Such a metric solves the Hitchin equations (4.4) for the associated ![]() $\mathrm {G}$-Higgs bundle
$\mathrm {G}$-Higgs bundle ![]() $(E(\mathrm {G}),\varphi ).$ Conversely, using an averaging argument, Simpson [Reference SimpsonSim88] showed that, if
$(E(\mathrm {G}),\varphi ).$ Conversely, using an averaging argument, Simpson [Reference SimpsonSim88] showed that, if ![]() $(E,\varphi )$ is a polystable
$(E,\varphi )$ is a polystable ![]() $\mathrm {G}$-Higgs bundle which is a Hodge bundle, then the metric solving the Hitchin equations is compatible with the Hodge bundle reduction. We summarize this in a proposition.
$\mathrm {G}$-Higgs bundle which is a Hodge bundle, then the metric solving the Hitchin equations is compatible with the Hodge bundle reduction. We summarize this in a proposition.
Proposition 4.15 [Reference SimpsonSim88]
A ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair ![]() $(E,\varphi )$ is polystable as a
$(E,\varphi )$ is polystable as a ![]() $(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair if and only if the associated
$(\mathrm {G}_0,\mathfrak {g}_k)$-Higgs pair if and only if the associated ![]() $\mathrm {G}$-Higgs bundle
$\mathrm {G}$-Higgs bundle ![]() $(E(\mathrm {G}),\varphi )$ is polystable as a
$(E(\mathrm {G}),\varphi )$ is polystable as a ![]() $\mathrm {G}$-Higgs bundle. In particular, there is a well-defined map of moduli spaces
$\mathrm {G}$-Higgs bundle. In particular, there is a well-defined map of moduli spaces
whose image consists of ![]() $\mathbb {C}^*$-fixed points, and every
$\mathbb {C}^*$-fixed points, and every ![]() $\mathbb {C}^*$-fixed point in
$\mathbb {C}^*$-fixed point in ![]() ${\mathcal {M}}(\mathrm {G})$ is in the image of such a map for some
${\mathcal {M}}(\mathrm {G})$ is in the image of such a map for some ![]() $(\mathrm {G}_0,\mathfrak {g}_k).$
$(\mathrm {G}_0,\mathfrak {g}_k).$
Remark 4.16 For stable and simple Higgs bundles, the associated type of Hodge bundle is unique.
Remark 4.17 Note that for gradings ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$,
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, ![]() $(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \mathfrak {g}_1)$-pair stability agrees with Higgs bundle stability. This is not true for other gradings. Namely,
$(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \mathfrak {g}_1)$-pair stability agrees with Higgs bundle stability. This is not true for other gradings. Namely, ![]() $(\mathrm {G}_0,\bigoplus _{j\neq 0}\mathfrak {g}_j)$ or
$(\mathrm {G}_0,\bigoplus _{j\neq 0}\mathfrak {g}_j)$ or ![]() $(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \bigoplus _{j>0}\mathfrak {g}_j)$-pair stability does not imply Higgs bundle stability.
$(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \bigoplus _{j>0}\mathfrak {g}_j)$-pair stability does not imply Higgs bundle stability.
Example 4.18 The ![]() $\mathrm {PSL}_2\mathbb {C}$-Higgs bundle
$\mathrm {PSL}_2\mathbb {C}$-Higgs bundle ![]() $(E_\mathrm {T},e)$ from Example 4.4 is polystable. Since
$(E_\mathrm {T},e)$ from Example 4.4 is polystable. Since ![]() $E_\mathrm {T}$ is the frame bundle of
$E_\mathrm {T}$ is the frame bundle of ![]() $K^{-1},$ a metric on
$K^{-1},$ a metric on ![]() $E_\mathrm {T}$ defines a metric on the Riemann surface
$E_\mathrm {T}$ defines a metric on the Riemann surface ![]() $X.$ A solution to the Hitchin equations in this case is equivalent to a metric of constant curvature on
$X.$ A solution to the Hitchin equations in this case is equivalent to a metric of constant curvature on ![]() $X$ (see [Reference HitchinHit87]). As a result, the Higgs bundle
$X$ (see [Reference HitchinHit87]). As a result, the Higgs bundle ![]() $(E_\mathrm {T},e)$ will be referred to as the uniformizing Higgs bundle for
$(E_\mathrm {T},e)$ will be referred to as the uniformizing Higgs bundle for ![]() $X.$
$X.$
4.3 Character varieties and variations of Hodge structure
Given a polystable ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E,\varphi )$, there is a metric
$(E,\varphi )$, there is a metric ![]() $h$ on
$h$ on ![]() $E$ solving the Hitchin equations (4.4). For such a metric
$E$ solving the Hitchin equations (4.4). For such a metric ![]() $h,$ the connection
$h,$ the connection
defines a flat connection on the ![]() $\mathrm {G}^\mathbb {R}$-bundle
$\mathrm {G}^\mathbb {R}$-bundle ![]() $E_h(\mathrm {G}^\mathbb {R})$, where
$E_h(\mathrm {G}^\mathbb {R})$, where ![]() $E_h$ is the
$E_h$ is the ![]() $\mathrm {H}^\mathbb {R}$-bundle associated to the metric
$\mathrm {H}^\mathbb {R}$-bundle associated to the metric ![]() $h.$ As a result, a polystable
$h.$ As a result, a polystable ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle
$\mathrm {G}^\mathbb {R}$-Higgs bundle ![]() $(E,\varphi )$ defines representations
$(E,\varphi )$ defines representations ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ such that
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ such that ![]() $E_h(\mathrm {G}^\mathbb {R})\cong \widetilde X\times _\rho \mathrm {G}^\mathbb {R}$.
$E_h(\mathrm {G}^\mathbb {R})\cong \widetilde X\times _\rho \mathrm {G}^\mathbb {R}$.
Given a representation ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$, a metric
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$, a metric ![]() $h_\rho$ on a flat bundle
$h_\rho$ on a flat bundle ![]() $\widetilde X\times _\rho \mathrm {G}^\mathbb {R}$ can be interpreted as a
$\widetilde X\times _\rho \mathrm {G}^\mathbb {R}$ can be interpreted as a ![]() $\rho$-equivariant map to the Riemannian symmetric space of
$\rho$-equivariant map to the Riemannian symmetric space of ![]() $\mathrm {G}^\mathbb {R}$:
$\mathrm {G}^\mathbb {R}$:
A metric ![]() $h_\rho$ is called harmonic if it is a critical point of the energy function
$h_\rho$ is called harmonic if it is a critical point of the energy function
This makes sense since, for two-dimensional domains, the energy only depends on the conformal structure of the domain. It turns out that a metric ![]() $h$ solves the Hitchin equations (4.4) if and only if the
$h$ solves the Hitchin equations (4.4) if and only if the ![]() $\rho$-equivariant map
$\rho$-equivariant map ![]() $h_\rho :\tilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ is harmonic.
$h_\rho :\tilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ is harmonic.
Remark 4.19 In this correspondence, the Higgs field ![]() $\varphi$ is identified with the
$\varphi$ is identified with the ![]() $(1,0)$-part of the differential of the map
$(1,0)$-part of the differential of the map ![]() $h_\rho$. As a result, for the uniformizing Higgs bundle
$h_\rho$. As a result, for the uniformizing Higgs bundle ![]() $(E_\mathrm {T},e)$, the harmonic metric
$(E_\mathrm {T},e)$, the harmonic metric ![]() $h_\rho :\widetilde X\to \mathbb {H}^2$ is a
$h_\rho :\widetilde X\to \mathbb {H}^2$ is a ![]() $\rho$-equivariant biholomorphism. Thus,
$\rho$-equivariant biholomorphism. Thus, ![]() $X=\mathbb {H}^2/\rho (\pi _1(X))$ and
$X=\mathbb {H}^2/\rho (\pi _1(X))$ and ![]() $\rho$ is the uniformizing representation of the Riemann surface.
$\rho$ is the uniformizing representation of the Riemann surface.
A representation ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ is called reductive if postcomposing
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ is called reductive if postcomposing ![]() $\rho$ with the adjoint representation of
$\rho$ with the adjoint representation of ![]() $\mathrm {G}^\mathbb {R}$ decomposes as a direct sum of irreducible representations. Corlette's theorem [Reference CorletteCor88] (proven by Donaldson [Reference DonaldsonDon87] for
$\mathrm {G}^\mathbb {R}$ decomposes as a direct sum of irreducible representations. Corlette's theorem [Reference CorletteCor88] (proven by Donaldson [Reference DonaldsonDon87] for ![]() $\mathrm {SL}_2\mathbb {C}$) asserts that given a representation
$\mathrm {SL}_2\mathbb {C}$) asserts that given a representation ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$, there exists a
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$, there exists a ![]() $\rho$-equivariant harmonic map
$\rho$-equivariant harmonic map ![]() $h_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ if and only if
$h_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ if and only if ![]() $\rho$ is reductive. Denote the set of reductive representations
$\rho$ is reductive. Denote the set of reductive representations ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ by
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ by ![]() $\operatorname {Hom}^+(\pi _1(X),\mathrm {G}^\mathbb {R})$. The moduli space of
$\operatorname {Hom}^+(\pi _1(X),\mathrm {G}^\mathbb {R})$. The moduli space of ![]() $\mathrm {G}^\mathbb {R}$-conjugacy classes of representations
$\mathrm {G}^\mathbb {R}$-conjugacy classes of representations ![]() $\pi _1(X)$ in
$\pi _1(X)$ in ![]() $\mathrm {G}^\mathbb {R}$ is called the character variety and denoted by
$\mathrm {G}^\mathbb {R}$ is called the character variety and denoted by
Combining Corlette's theorem with the Hitchin–Kobayashi correspondence defines a homeomorphism ![]() ${\mathcal {M}}(\mathrm {G}^\mathbb {R})\cong {\mathcal {R}}(\mathrm {G}^\mathbb {R})$ between the moduli space of
${\mathcal {M}}(\mathrm {G}^\mathbb {R})\cong {\mathcal {R}}(\mathrm {G}^\mathbb {R})$ between the moduli space of ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles on
$\mathrm {G}^\mathbb {R}$-Higgs bundles on ![]() $X$ and the
$X$ and the ![]() $\mathrm {G}^\mathbb {R}$-character variety. This is called the nonabelian Hodge correspondence.
$\mathrm {G}^\mathbb {R}$-character variety. This is called the nonabelian Hodge correspondence.
Let ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a representation and
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a representation and ![]() $\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be a reductive subgroup. We say that
$\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be a reductive subgroup. We say that ![]() $\rho$ factors through
$\rho$ factors through ![]() $\tilde {\mathrm {G}}^\mathbb {R}$ if
$\tilde {\mathrm {G}}^\mathbb {R}$ if ![]() $\rho$ can be written as
$\rho$ can be written as ![]() $\rho :\pi _1(X)\to \tilde {\mathrm {G}}^\mathbb {R}\hookrightarrow \mathrm {G}^\mathbb {R}.$ The following proposition is immediate from the nonabelian Hodge correspondence.
$\rho :\pi _1(X)\to \tilde {\mathrm {G}}^\mathbb {R}\hookrightarrow \mathrm {G}^\mathbb {R}.$ The following proposition is immediate from the nonabelian Hodge correspondence.
Proposition 4.20 Let ![]() $\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be a reductive subgroup with maximal compact
$\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ be a reductive subgroup with maximal compact ![]() $\tilde {\mathrm {H}}^\mathbb {R}<\mathrm {H}^\mathbb {R}$ and let
$\tilde {\mathrm {H}}^\mathbb {R}<\mathrm {H}^\mathbb {R}$ and let ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a reductive representation. The following assertions are equivalent.
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a reductive representation. The following assertions are equivalent.
−
 $\rho$ factors through
$\rho$ factors through  $\tilde {\mathrm {G}}^\mathbb {R}$.
$\tilde {\mathrm {G}}^\mathbb {R}$.− The
 $\rho$-equivariant harmonic map
$\rho$-equivariant harmonic map  $h_\rho$ factors as
$h_\rho$ factors as  $h_\rho :\widetilde X\to \tilde {\mathrm {G}}^\mathbb {R}/\tilde {\mathrm {H}}^\mathbb {R}\hookrightarrow \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$.
$h_\rho :\widetilde X\to \tilde {\mathrm {G}}^\mathbb {R}/\tilde {\mathrm {H}}^\mathbb {R}\hookrightarrow \mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$.− The associated
 $\mathrm {G}^\mathbb {R}$-Higgs bundle reduces to a polystable
$\mathrm {G}^\mathbb {R}$-Higgs bundle reduces to a polystable  $\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle.
$\tilde {\mathrm {G}}^\mathbb {R}$-Higgs bundle.
We now describe the special properties of the representations and harmonic maps arising from ![]() $\mathbb {C}^*$-fixed points in the Higgs bundle moduli space. Let
$\mathbb {C}^*$-fixed points in the Higgs bundle moduli space. Let ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ be a real form of Hodge type with maximal compact
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ be a real form of Hodge type with maximal compact ![]() $\mathrm {H}^\mathbb {R}$ and complexified Cartan decomposition
$\mathrm {H}^\mathbb {R}$ and complexified Cartan decomposition ![]() $\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}.$ Fix a
$\mathfrak {g}=\mathfrak {h}\oplus \mathfrak {m}.$ Fix a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ such that
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ such that ![]() $\mathfrak {g}_{2j}\subset \mathfrak {h}$ and
$\mathfrak {g}_{2j}\subset \mathfrak {h}$ and ![]() $\mathfrak {g}_{2j+1}\subset \mathfrak {m}$ for all
$\mathfrak {g}_{2j+1}\subset \mathfrak {m}$ for all ![]() $j$. Recall that the homogeneous space
$j$. Recall that the homogeneous space ![]() $D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a period domain. The holomorphic tangent bundle decomposes as
$D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a period domain. The holomorphic tangent bundle decomposes as
Definition 4.21 Fix a period domain ![]() $D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$. A variation of Hodge structure over
$D=\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$. A variation of Hodge structure over ![]() $X$ is a pair
$X$ is a pair ![]() $(\rho,f_\rho )$, where
$(\rho,f_\rho )$, where ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ is a representation and
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ is a representation and ![]() $f_\rho :\widetilde X\to D$ is a
$f_\rho :\widetilde X\to D$ is a ![]() $\rho$-equivariant holomorphic map such that
$\rho$-equivariant holomorphic map such that
The following proposition describes the representations and harmonic maps associated to polystable Higgs bundles fixed by the ![]() $\mathbb {C}^*$-action.
$\mathbb {C}^*$-action.
Proposition 4.22 Let ![]() $\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a reductive representation. Then the Higgs bundle associated to
$\rho :\pi _1(X)\to \mathrm {G}^\mathbb {R}$ be a reductive representation. Then the Higgs bundle associated to ![]() $\rho$ is a
$\rho$ is a ![]() $\mathbb {C}^*$-fixed point if and only if
$\mathbb {C}^*$-fixed point if and only if ![]() $\rho$ factors through a reductive subgroup
$\rho$ factors through a reductive subgroup ![]() $\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ of Hodge type, and there is a period domain
$\tilde {\mathrm {G}}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ of Hodge type, and there is a period domain ![]() $\tilde {\mathrm {G}}^\mathbb {R}/\tilde {\mathrm {H}}_0^\mathbb {R}$ such that the associated
$\tilde {\mathrm {G}}^\mathbb {R}/\tilde {\mathrm {H}}_0^\mathbb {R}$ such that the associated ![]() $\rho$-equivariant harmonic map
$\rho$-equivariant harmonic map ![]() $h_\rho :\widetilde X\to \tilde {\mathrm {G}}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ lifts to a variation of Hodge structure
$h_\rho :\widetilde X\to \tilde {\mathrm {G}}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ lifts to a variation of Hodge structure

5. Toledo invariant and Arakelov–Milnor inequality
Let ![]() $\mathrm {G}$ be a complex semisimple Lie group and
$\mathrm {G}$ be a complex semisimple Lie group and ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a ![]() $\mathbb {Z}$-grading with grading element
$\mathbb {Z}$-grading with grading element ![]() $\zeta \in \mathfrak {g}_0$, and let
$\zeta \in \mathfrak {g}_0$, and let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta.$ Consider the PHVS
$\zeta.$ Consider the PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ and recall from (3.1) that the Toledo character
$(\mathrm {G}_0,\mathfrak {g}_1)$ and recall from (3.1) that the Toledo character ![]() $\chi _T:\mathfrak {g}_0\to \mathbb {C}$ is given by
$\chi _T:\mathfrak {g}_0\to \mathbb {C}$ is given by ![]() $\chi _T(x)=B(\zeta,x)B(\gamma,\gamma )$. Recall that the degree of a bundle with respect to a character is defined by (4.3).
$\chi _T(x)=B(\zeta,x)B(\gamma,\gamma )$. Recall that the degree of a bundle with respect to a character is defined by (4.3).
Definition 5.1 Let ![]() $(E,\varphi )$ be a
$(E,\varphi )$ be a ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair and
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair and ![]() $\chi _T:\mathrm {G}_0\to \mathbb {C}^*$ be the Toledo character. Then the Toledo invariant
$\chi _T:\mathrm {G}_0\to \mathbb {C}^*$ be the Toledo character. Then the Toledo invariant ![]() $\tau (E,\varphi )$ is defined by
$\tau (E,\varphi )$ is defined by
Remark 5.2 For the grading ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the canonical real form
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the canonical real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ from Proposition (3.8) is a Hermitian Lie group. For such real forms, a
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ from Proposition (3.8) is a Hermitian Lie group. For such real forms, a ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundle is a
$\mathrm {G}^\mathbb {R}$-Higgs bundle is a ![]() $(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \mathfrak {g}_1)$-Higgs pair. The Toledo invariant of such a Higgs bundle agrees with the Toledo invariant defined above [Reference Biquard, García-Prada and RubioBGR17].
$(\mathrm {G}_0,\mathfrak {g}_{-1}\oplus \mathfrak {g}_1)$-Higgs pair. The Toledo invariant of such a Higgs bundle agrees with the Toledo invariant defined above [Reference Biquard, García-Prada and RubioBGR17].
Recall Definition 3.3 of the Toledo rank ![]() $\operatorname {rk}_{\chi _T}(v)$ of a point
$\operatorname {rk}_{\chi _T}(v)$ of a point ![]() $v\in \mathfrak {g}_1$. We define the Toledo rank
$v\in \mathfrak {g}_1$. We define the Toledo rank ![]() $\operatorname {rk}_T(\varphi )$ of a
$\operatorname {rk}_T(\varphi )$ of a ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E,\varphi )$ to be
$(E,\varphi )$ to be
Theorem 5.3 Let ![]() $\mathrm {G}$ be a complex semisimple Lie group and
$\mathrm {G}$ be a complex semisimple Lie group and ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be a ![]() $\mathbb {Z}$-grading with grading element
$\mathbb {Z}$-grading with grading element ![]() $\zeta \in \mathfrak {g}_0$. Let
$\zeta \in \mathfrak {g}_0$. Let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta$ and
$\zeta$ and ![]() $\alpha =\lambda \zeta$ for
$\alpha =\lambda \zeta$ for ![]() $\lambda \in \mathbb {R}.$ If
$\lambda \in \mathbb {R}.$ If ![]() $(E,\varphi )$ is an
$(E,\varphi )$ is an ![]() $\alpha$-semistable
$\alpha$-semistable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair, then the Toledo invariant
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair, then the Toledo invariant ![]() $\tau (E,\varphi )$ satisfies the inequality
$\tau (E,\varphi )$ satisfies the inequality
Before proving the theorem we list some immediate consequences.
Corollary 5.4 Assume ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS and set
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS and set ![]() $\alpha =\lambda \zeta$. Then the Toledo invariant of a
$\alpha =\lambda \zeta$. Then the Toledo invariant of a ![]() $\alpha$-semistable
$\alpha$-semistable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E,\varphi )$ satisfies
$(E,\varphi )$ satisfies
For the application to Higgs bundles fixed by the ![]() $\mathbb {C}^*$-action we are interested in the case
$\mathbb {C}^*$-action we are interested in the case ![]() $\alpha =0.$
$\alpha =0.$
Corollary 5.5 For ![]() $\alpha =0$, the Toledo invariant
$\alpha =0$, the Toledo invariant ![]() $\tau (E,\varphi )$ of a polystable
$\tau (E,\varphi )$ of a polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-pair satisfies the inequality
$(\mathrm {G}_0,\mathfrak {g}_1)$-pair satisfies the inequality ![]() $-\operatorname {rk}_T(\varphi )(2g-2)\leqslant \tau (E,\varphi )\leqslant 0.$ In particular,
$-\operatorname {rk}_T(\varphi )(2g-2)\leqslant \tau (E,\varphi )\leqslant 0.$ In particular,
Proof. This is a direct application of Theorem 5.3 in the case ![]() $\lambda =0$, for which in fact it is enough to assume the semistability of
$\lambda =0$, for which in fact it is enough to assume the semistability of ![]() $(E,\varphi )$. However, with the extra assumption of polystability, the result can also be deduced from our holomorphic sectional curvature computations in Proposition 3.12, as we shall now explain. By Theorem 4.13 such
$(E,\varphi )$. However, with the extra assumption of polystability, the result can also be deduced from our holomorphic sectional curvature computations in Proposition 3.12, as we shall now explain. By Theorem 4.13 such ![]() $(E,\varphi )$ admits a solution
$(E,\varphi )$ admits a solution ![]() $h$ to the Hitchin equations (4.4), so we have a variation of Hodge structure as studied in § 4.3. In particular, we obtain an equivariant horizontal holomorphic map
$h$ to the Hitchin equations (4.4), so we have a variation of Hodge structure as studied in § 4.3. In particular, we obtain an equivariant horizontal holomorphic map ![]() $f:\tilde X\rightarrow \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$. Denote by
$f:\tilde X\rightarrow \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$. Denote by ![]() $\omega$ the 2-form associated to the Hermitian metric on
$\omega$ the 2-form associated to the Hermitian metric on ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ considered in § 3.3, normalized to have horizontal holomorphic sectional curvature
$\mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ considered in § 3.3, normalized to have horizontal holomorphic sectional curvature ![]() $-1\leqslant K\leqslant - 1/{\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)}$. By the Schwarz lemma, one has
$-1\leqslant K\leqslant - 1/{\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)}$. By the Schwarz lemma, one has
The result will then follow from the identification
where ![]() $F_h$ is the curvature as in (4.4). From (4.4) we have
$F_h$ is the curvature as in (4.4). From (4.4) we have ![]() $\chi _T(F_h)=-\chi _T([\varphi,\varphi ^*])$; locally writing
$\chi _T(F_h)=-\chi _T([\varphi,\varphi ^*])$; locally writing ![]() $\varphi =a\, dz$, we obtain
$\varphi =a\, dz$, we obtain
 \begin{align*} \chi_T(F_h)&=-B(\zeta,[a,a^*])B(\gamma,\gamma)dz\wedge d\bar z\\ &=-B([\zeta,a],a^*)B(\gamma,\gamma)dz\wedge d\bar z \\ &=-B(a,a^*)B(\gamma,\gamma)dz\wedge d\bar z\\ &=-\langle a,a\rangle dz\wedge d\bar z. \end{align*}
\begin{align*} \chi_T(F_h)&=-B(\zeta,[a,a^*])B(\gamma,\gamma)dz\wedge d\bar z\\ &=-B([\zeta,a],a^*)B(\gamma,\gamma)dz\wedge d\bar z \\ &=-B(a,a^*)B(\gamma,\gamma)dz\wedge d\bar z\\ &=-\langle a,a\rangle dz\wedge d\bar z. \end{align*}
On the other hand, ![]() $f^*\omega = \omega (a,\bar a) dz\wedge d\bar z = i \langle a,a \rangle dz\wedge d\bar z$. Therefore
$f^*\omega = \omega (a,\bar a) dz\wedge d\bar z = i \langle a,a \rangle dz\wedge d\bar z$. Therefore ![]() $f^*\omega =-\chi _T(iF_h)$, which completes the proof.
$f^*\omega =-\chi _T(iF_h)$, which completes the proof.
The same argument gives the more precise inequality ![]() $\tau (E,\varphi ) \geqslant -\operatorname {rk}_T(\varphi )(2g-2)$, starting from the holomorphic curvature estimate (3.4).
$\tau (E,\varphi ) \geqslant -\operatorname {rk}_T(\varphi )(2g-2)$, starting from the holomorphic curvature estimate (3.4).
Since the Toledo invariant has discrete values, it is constant on the connected components of the moduli space of polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs ![]() ${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1)$. As a result, we have the following decomposition of
${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1)$. As a result, we have the following decomposition of ![]() ${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1).$
${\mathcal {M}}(\mathrm {G}_0,\mathfrak {g}_1).$
Corollary 5.6 The moduli space of polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs decomposes as
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs decomposes as
where ![]() $(E,\varphi )\in {\mathcal {M}}^\tau (\mathrm {G}_0,\mathfrak {g}_1)$ if and only if
$(E,\varphi )\in {\mathcal {M}}^\tau (\mathrm {G}_0,\mathfrak {g}_1)$ if and only if ![]() $\tau (E,\varphi )=\tau.$
$\tau (E,\varphi )=\tau.$
Remark 5.7 We will discuss the special properties of the space ![]() ${\mathcal {M}}^{\tau }(\mathrm {G}_0,\mathfrak {g}_1)$ for the minimal value
${\mathcal {M}}^{\tau }(\mathrm {G}_0,\mathfrak {g}_1)$ for the minimal value ![]() $\tau =-(2g-2)\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)$ in the next section.
$\tau =-(2g-2)\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)$ in the next section.
Proof of Theorem 5.3 The upper bound follows immediately from stability. Note that ![]() $s=-B(\gamma,\gamma )\zeta$ is in the center of
$s=-B(\gamma,\gamma )\zeta$ is in the center of ![]() $\mathfrak {g}_0$ and has the property that
$\mathfrak {g}_0$ and has the property that ![]() $\operatorname {Ad}(e^{ts})(x)$ is bounded as
$\operatorname {Ad}(e^{ts})(x)$ is bounded as ![]() $t\to \infty$ for all
$t\to \infty$ for all ![]() $x\in \mathfrak {g}_1.$ Since
$x\in \mathfrak {g}_1.$ Since ![]() $s$ is in the center of
$s$ is in the center of ![]() $\mathfrak {g}_0,$ the associated parabolic is all of
$\mathfrak {g}_0,$ the associated parabolic is all of ![]() $\mathrm {G}_0.$ Hence,
$\mathrm {G}_0.$ Hence, ![]() $\alpha$-semistability of
$\alpha$-semistability of ![]() $(E,\varphi )$ implies
$(E,\varphi )$ implies
Since ![]() $-\tau (E,\varphi )=\deg E(-B(\gamma,\gamma )\zeta )$ and
$-\tau (E,\varphi )=\deg E(-B(\gamma,\gamma )\zeta )$ and ![]() $\alpha =\lambda \zeta$ we have
$\alpha =\lambda \zeta$ we have ![]() $\tau (E,\varphi ) \leqslant \lambda B(\gamma,\gamma )B(\zeta,\zeta ).$
$\tau (E,\varphi ) \leqslant \lambda B(\gamma,\gamma )B(\zeta,\zeta ).$
The lower bound is more interesting. For generic ![]() $x\in X$,
$x\in X$, ![]() $\varphi (x)\in \mathfrak {g}_1$ is in a fixed
$\varphi (x)\in \mathfrak {g}_1$ is in a fixed ![]() $\mathrm {G}_0$-orbit. Let
$\mathrm {G}_0$-orbit. Let ![]() $e$ be any element in this orbit and
$e$ be any element in this orbit and ![]() $\{f,h,e\}$ be an associated
$\{f,h,e\}$ be an associated ![]() $\mathfrak {sl}_2$-triple with
$\mathfrak {sl}_2$-triple with ![]() $h\in \mathfrak {g}_0$. Let
$h\in \mathfrak {g}_0$. Let ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be the associated maximal JM-regular PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be the associated maximal JM-regular PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ for
$(\mathrm {G}_0,\mathfrak {g}_1)$ for ![]() $e$ (see Definition 2.17). By Proposition 2.16,
$e$ (see Definition 2.17). By Proposition 2.16, ![]() $e\in \hat \Omega \subset \mathfrak {g}_1$ is in the open
$e\in \hat \Omega \subset \mathfrak {g}_1$ is in the open ![]() $\hat {\mathrm {G}}_0$-orbit. Recall from Proposition 2.21 that
$\hat {\mathrm {G}}_0$-orbit. Recall from Proposition 2.21 that ![]() $e$ defines a parabolic subalgebra
$e$ defines a parabolic subalgebra ![]() $\mathfrak {p}_{0,e}\subset \mathfrak {g}_0$ and a corresponding parabolic subgroup
$\mathfrak {p}_{0,e}\subset \mathfrak {g}_0$ and a corresponding parabolic subgroup ![]() $\mathrm {P}_{0,e}<\mathrm {G}_0$. Since the construction of
$\mathrm {P}_{0,e}<\mathrm {G}_0$. Since the construction of ![]() $\mathrm {P}_{0,e}$ is canonical, we obtain a holomorphic reduction of structure group of
$\mathrm {P}_{0,e}$ is canonical, we obtain a holomorphic reduction of structure group of ![]() $E$ to
$E$ to ![]() $\mathrm {P}_{0,e}$ on the open subset of
$\mathrm {P}_{0,e}$ on the open subset of ![]() $X$ where
$X$ where ![]() $\operatorname {rk}_T(\varphi (x))=\operatorname {rk}_T(e)$. This can be extended to a reduction over all of
$\operatorname {rk}_T(\varphi (x))=\operatorname {rk}_T(e)$. This can be extended to a reduction over all of ![]() $X$. Let
$X$. Let ![]() $E_\sigma$ be the associated
$E_\sigma$ be the associated ![]() $\mathrm {P}_{0,e}$-bundle.
$\mathrm {P}_{0,e}$-bundle.
Set ![]() $\hat \zeta = {h}/{2}$ and write
$\hat \zeta = {h}/{2}$ and write ![]() $\zeta =\hat \zeta +s.$ Recall from Proposition 2.21 that the parabolic subalgebra
$\zeta =\hat \zeta +s.$ Recall from Proposition 2.21 that the parabolic subalgebra ![]() $\mathfrak {p}_{0,e}$ is given by
$\mathfrak {p}_{0,e}$ is given by
By definition of the Toledo character, we have
Thus,
where ![]() $\hat \chi _T:\mathfrak {p}_{0,e}\to \mathbb {C}$ is the character defined by
$\hat \chi _T:\mathfrak {p}_{0,e}\to \mathbb {C}$ is the character defined by ![]() $\hat \chi _T(x)=B(\gamma,\gamma )B(\hat \zeta,x).$
$\hat \chi _T(x)=B(\gamma,\gamma )B(\hat \zeta,x).$
The Levi factor of ![]() $P_{0,e}$ is isomorphic to
$P_{0,e}$ is isomorphic to ![]() $\hat {\mathrm {G}}_0$. Hence, projecting onto the Levi factor defines a holomorphic reduction
$\hat {\mathrm {G}}_0$. Hence, projecting onto the Levi factor defines a holomorphic reduction ![]() $E_{\sigma }(\hat {\mathrm {G}}_0)$ with
$E_{\sigma }(\hat {\mathrm {G}}_0)$ with ![]() $\varphi \in H^0(E_{\sigma }(\hat {\mathrm {G}}_0)(\hat {\mathfrak {g}}_1)\otimes K)$. Recall from Proposition 3.16 that there is a positive integer
$\varphi \in H^0(E_{\sigma }(\hat {\mathrm {G}}_0)(\hat {\mathfrak {g}}_1)\otimes K)$. Recall from Proposition 3.16 that there is a positive integer ![]() $q$ such that the character
$q$ such that the character ![]() $q\cdot \hat \chi _T$ exponentiates to a character of
$q\cdot \hat \chi _T$ exponentiates to a character of ![]() $\hat \chi _{T,q}:\hat {\mathrm {G}}_0\to \mathbb {C}^*$ which has a polynomial relative invariant
$\hat \chi _{T,q}:\hat {\mathrm {G}}_0\to \mathbb {C}^*$ which has a polynomial relative invariant ![]() $F:\hat {\mathfrak {g}}_1\to \mathbb {C}$ of degree
$F:\hat {\mathfrak {g}}_1\to \mathbb {C}$ of degree ![]() $q\cdot \hat \chi _T(\hat \zeta )$. Since
$q\cdot \hat \chi _T(\hat \zeta )$. Since ![]() $\varphi$ is generically in the open
$\varphi$ is generically in the open ![]() $\hat {\mathrm {G}}_0$-orbit of
$\hat {\mathrm {G}}_0$-orbit of ![]() $\hat {\mathfrak {g}}_1,$ applying the relative invariant to the Higgs field defines a nonzero holomorphic section of a line bundle
$\hat {\mathfrak {g}}_1,$ applying the relative invariant to the Higgs field defines a nonzero holomorphic section of a line bundle ![]() $E_\sigma (\hat \chi _{T,q})\otimes K^{q\cdot \hat \chi _T(\hat \zeta )}$:
$E_\sigma (\hat \chi _{T,q})\otimes K^{q\cdot \hat \chi _T(\hat \zeta )}$:
Note that ![]() $\deg _{\hat \chi _T}(E_\sigma )= ({1}/{q})\deg (E_\sigma (\hat \chi _{T,q}))$. Thus, we have
$\deg _{\hat \chi _T}(E_\sigma )= ({1}/{q})\deg (E_\sigma (\hat \chi _{T,q}))$. Thus, we have
We now use the assumption that ![]() $(E,\varphi )$ is
$(E,\varphi )$ is ![]() $\alpha$-semistable for
$\alpha$-semistable for ![]() $\alpha =\lambda \zeta.$ Since
$\alpha =\lambda \zeta.$ Since ![]() $[s,\hat {\mathfrak {g}}_1]=0,$ we have
$[s,\hat {\mathfrak {g}}_1]=0,$ we have ![]() $\hat {\mathfrak {g}}_1\subset \mathfrak {g}_1^s.$ Thus, we have
$\hat {\mathfrak {g}}_1\subset \mathfrak {g}_1^s.$ Thus, we have ![]() $\varphi \in H^0(E_{\sigma }(\hat {\mathfrak {g}}_1^s)\otimes K).$ By the definition of the stability for
$\varphi \in H^0(E_{\sigma }(\hat {\mathfrak {g}}_1^s)\otimes K).$ By the definition of the stability for ![]() $\alpha =\lambda \zeta$, we have
$\alpha =\lambda \zeta$, we have
Combining this with (5.1) and (5.2) gives an inequality for the Toledo invariant:
To finish the proof, recall that ![]() $B(\hat \zeta,s)=0$ and
$B(\hat \zeta,s)=0$ and ![]() $B(\gamma,\gamma )B(\zeta,\hat \zeta )=\operatorname {rk}_T(\varphi ).$ Thus,
$B(\gamma,\gamma )B(\zeta,\hat \zeta )=\operatorname {rk}_T(\varphi ).$ Thus,
and
Hence, we obtain the desired inequality
6. Rigidity results for maximal Hodge bundles and variations of Hodge structure
For this section let ![]() $\mathrm {G}$ be a complex semisimple Lie group with Lie algebra
$\mathrm {G}$ be a complex semisimple Lie group with Lie algebra ![]() $\mathfrak {g}$ and let
$\mathfrak {g}$ and let ![]() $X$ be a compact Riemann surface of genus
$X$ be a compact Riemann surface of genus ![]() $g\geqslant 2$ and canonical bundle
$g\geqslant 2$ and canonical bundle ![]() $K$. Fix a
$K$. Fix a ![]() $\mathbb {Z}$-grading
$\mathbb {Z}$-grading ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ with grading element ![]() $\zeta$ and let
$\zeta$ and let ![]() $\mathrm {G}_0<\mathrm {G}$ be the centralizer of
$\mathrm {G}_0<\mathrm {G}$ be the centralizer of ![]() $\zeta.$
$\zeta.$
We will call a polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E,\varphi )$ maximal if the absolute value of the Toledo invariant is maximized. By Corollary 5.5, the Toledo invariant
$(E,\varphi )$ maximal if the absolute value of the Toledo invariant is maximized. By Corollary 5.5, the Toledo invariant ![]() $\tau (E,\varphi )$ of a polystable
$\tau (E,\varphi )$ of a polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair on
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair on ![]() $X$ satisfies the inequality
$X$ satisfies the inequality
Thus, ![]() $(E,\varphi )$ is maximal if and only if
$(E,\varphi )$ is maximal if and only if ![]() $\tau (E,\varphi )=-\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2).$
$\tau (E,\varphi )=-\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2).$
6.1 The JM-regular case
We start with the JM-regular case. Assume ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS. Fix
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS. Fix ![]() $e\in \Omega$ and let
$e\in \Omega$ and let ![]() $\{f,h,e\}=\{f,2\zeta,e\}$ be the associated
$\{f,h,e\}=\{f,2\zeta,e\}$ be the associated ![]() $\mathfrak {sl}_2$-triple. Let
$\mathfrak {sl}_2$-triple. Let ![]() $\mathrm {S}<\mathrm {G}$ be the connected subgroup with Lie algebra spanned by
$\mathrm {S}<\mathrm {G}$ be the connected subgroup with Lie algebra spanned by ![]() $\{f,h,e\}.$ Note that
$\{f,h,e\}.$ Note that ![]() $\mathrm {S}$ is isomorphic to
$\mathrm {S}$ is isomorphic to ![]() $\mathrm {PSL}_2\mathbb {C}$ or
$\mathrm {PSL}_2\mathbb {C}$ or ![]() $\mathrm {SL}_2\mathbb {C}$ depending on
$\mathrm {SL}_2\mathbb {C}$ depending on ![]() $\mathrm {G}$ and the
$\mathrm {G}$ and the ![]() $\mathfrak {sl}_2$-triple. Finally, let
$\mathfrak {sl}_2$-triple. Finally, let ![]() $\mathrm {C}<\mathrm {G}$ be the reductive group which centralizes the
$\mathrm {C}<\mathrm {G}$ be the reductive group which centralizes the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}.$ Note that
$\{f,h,e\}.$ Note that ![]() $\mathrm {C}=\mathrm {G}_0^e<\mathrm {G}_0$ is also the
$\mathrm {C}=\mathrm {G}_0^e<\mathrm {G}_0$ is also the ![]() $\mathrm {G}_0$-stabilizer of
$\mathrm {G}_0$-stabilizer of ![]() $e$.
$e$.
Let ![]() $\mathrm {T}<\mathrm {S}$ be the connected subgroup with Lie algebra
$\mathrm {T}<\mathrm {S}$ be the connected subgroup with Lie algebra ![]() $\langle h\rangle,$ and note that
$\langle h\rangle,$ and note that ![]() $\mathrm {T}<\mathrm {G}_0.$ Recall the uniformizing Hodge bundle
$\mathrm {T}<\mathrm {G}_0.$ Recall the uniformizing Hodge bundle ![]() $(E_\mathrm {T},e)$ for
$(E_\mathrm {T},e)$ for ![]() $X$ from Examples 4.4 and 4.18. Here
$X$ from Examples 4.4 and 4.18. Here ![]() $E_\mathrm {T}$ is the holomorphic frame bundle of
$E_\mathrm {T}$ is the holomorphic frame bundle of ![]() $K^{-1}$ if
$K^{-1}$ if ![]() $\mathrm {S}=\mathrm {P}\mathrm {SL}_2\mathbb {C}$ and the holomorphic frame bundle of
$\mathrm {S}=\mathrm {P}\mathrm {SL}_2\mathbb {C}$ and the holomorphic frame bundle of ![]() $K^{- {1}/{2}}$ if
$K^{- {1}/{2}}$ if ![]() $\mathrm {S}=\mathrm {SL}_2\mathbb {C}.$ Since
$\mathrm {S}=\mathrm {SL}_2\mathbb {C}.$ Since ![]() $E_\mathrm {T}(\langle e\rangle )\otimes K\cong {\mathcal {O}}$, the Lie algebra element
$E_\mathrm {T}(\langle e\rangle )\otimes K\cong {\mathcal {O}}$, the Lie algebra element ![]() $e$ defines a holomorphic section of
$e$ defines a holomorphic section of ![]() $E_\mathrm {T}(\langle e\rangle ) \otimes K.$ Moreover,
$E_\mathrm {T}(\langle e\rangle ) \otimes K.$ Moreover, ![]() $(E_\mathrm {T},e)$ is polystable, and a solution to the Hitchin equations is equivalent to a metric of constant curvature on
$(E_\mathrm {T},e)$ is polystable, and a solution to the Hitchin equations is equivalent to a metric of constant curvature on ![]() $X.$ Extending the structure group to
$X.$ Extending the structure group to ![]() $\mathrm {G}_0$ defines a maximal polystable
$\mathrm {G}_0$ defines a maximal polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair.
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair.
Proposition 6.1 The ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E_\mathrm {T}(\mathrm {G}_0),e)$ is polystable and maximal.
$(E_\mathrm {T}(\mathrm {G}_0),e)$ is polystable and maximal.
Proof. First note that ![]() $(E,\varphi )=(E_\mathrm {T}(\mathrm {G}_0),e)$ is polystable since
$(E,\varphi )=(E_\mathrm {T}(\mathrm {G}_0),e)$ is polystable since ![]() $(E_\mathrm {T},e)$ polystable. By construction, we have
$(E_\mathrm {T},e)$ polystable. By construction, we have ![]() $\tau (E,\varphi )=-\operatorname {rk}_{T}(\mathrm {G}_0,\mathfrak {g}_1)(2g-2).$
$\tau (E,\varphi )=-\operatorname {rk}_{T}(\mathrm {G}_0,\mathfrak {g}_1)(2g-2).$
Other examples of maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs are given by twisting the above uniformizing Higgs bundle by a holomorphic
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs are given by twisting the above uniformizing Higgs bundle by a holomorphic ![]() $\mathrm {C}$-bundle. Let
$\mathrm {C}$-bundle. Let ![]() $E_\mathrm {C}$ be a holomorphic
$E_\mathrm {C}$ be a holomorphic ![]() $\mathrm {C}$-bundle on
$\mathrm {C}$-bundle on ![]() $X$. Since
$X$. Since ![]() $\mathrm {T}$ and
$\mathrm {T}$ and ![]() $\mathrm {C}$ are commuting subgroups of
$\mathrm {C}$ are commuting subgroups of ![]() $\mathrm {G}_0$, the multiplication map
$\mathrm {G}_0$, the multiplication map ![]() $m:\mathrm {T}\times \mathrm {C}\to \mathrm {G}_0$ is a group homomorphism. Thus, we can form a
$m:\mathrm {T}\times \mathrm {C}\to \mathrm {G}_0$ is a group homomorphism. Thus, we can form a ![]() $\mathrm {G}_0$-bundle
$\mathrm {G}_0$-bundle
This is the principal bundle version of the tensor product of vector bundles, where ![]() $\mathrm {GL}_m\mathbb {C}$ and
$\mathrm {GL}_m\mathbb {C}$ and ![]() $\mathrm {GL}_{n}\mathbb {C}$ are commuting subgroups of
$\mathrm {GL}_{n}\mathbb {C}$ are commuting subgroups of ![]() $\mathrm {GL}_{mn}\mathbb {C}$.
$\mathrm {GL}_{mn}\mathbb {C}$.
As with vector bundles, given metrics ![]() $h_\mathrm {T}$ and
$h_\mathrm {T}$ and ![]() $h_\mathrm {C}$ on
$h_\mathrm {C}$ on ![]() $E_\mathrm {T}$ and
$E_\mathrm {T}$ and ![]() $E_\mathrm {C}$ respectively, there is a metric
$E_\mathrm {C}$ respectively, there is a metric ![]() $h_\mathrm {T}\otimes h_\mathrm {C}$ on
$h_\mathrm {T}\otimes h_\mathrm {C}$ on ![]() $E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$. More specifically, metrics on
$E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$. More specifically, metrics on ![]() $E_\mathrm {T}$ and
$E_\mathrm {T}$ and ![]() $E_\mathrm {C}$ are reductions of structure group to the maximal compact subgroups, say
$E_\mathrm {C}$ are reductions of structure group to the maximal compact subgroups, say ![]() $E_{\mathrm {T}^\mathbb {R}}\subset E_\mathrm {T}$ and
$E_{\mathrm {T}^\mathbb {R}}\subset E_\mathrm {T}$ and ![]() $E_{\mathrm {C}^\mathbb {R}}\subset E_\mathrm {C}$. The metric
$E_{\mathrm {C}^\mathbb {R}}\subset E_\mathrm {C}$. The metric ![]() $h_\mathrm {T}\otimes h_\mathrm {C}$ on
$h_\mathrm {T}\otimes h_\mathrm {C}$ on ![]() $E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ is the reduction of structure group given by
$E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ is the reduction of structure group given by ![]() $E_{\mathrm {T}^\mathbb {R}}\otimes _{\mathrm {G}_0^\mathbb {R}} E_{\mathrm {C}^\mathbb {R}}\subset E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$, where
$E_{\mathrm {T}^\mathbb {R}}\otimes _{\mathrm {G}_0^\mathbb {R}} E_{\mathrm {C}^\mathbb {R}}\subset E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$, where ![]() $\mathrm {G}_0^\mathbb {R}\subset \mathrm {G}_0$ is a maximal compact subgroup containing
$\mathrm {G}_0^\mathbb {R}\subset \mathrm {G}_0$ is a maximal compact subgroup containing ![]() $\mathrm {C}^\mathbb {R}$ and
$\mathrm {C}^\mathbb {R}$ and ![]() $\mathrm {T}^\mathbb {R}.$ Similarly, given connections
$\mathrm {T}^\mathbb {R}.$ Similarly, given connections ![]() $A_\mathrm {T}$ and
$A_\mathrm {T}$ and ![]() $A_\mathrm {C}$ on
$A_\mathrm {C}$ on ![]() $E_\mathrm {T}$ and
$E_\mathrm {T}$ and ![]() $E_\mathrm {C}$ respectively,
$E_\mathrm {C}$ respectively, ![]() $A_\mathrm {T}+A_\mathrm {C}$ defines a connection on
$A_\mathrm {T}+A_\mathrm {C}$ defines a connection on ![]() $E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ and the curvature satisfies
$E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}$ and the curvature satisfies
These formulas make sense because the tensor product is made from the ![]() $\mathrm {T}\times \mathrm {C}$-principal bundle
$\mathrm {T}\times \mathrm {C}$-principal bundle ![]() $E_\mathrm {T}\times E_\mathrm {C}$ by applying the multiplication
$E_\mathrm {T}\times E_\mathrm {C}$ by applying the multiplication ![]() $m:\mathrm {T}\times \mathrm {C}\rightarrow \mathrm {G}_0$, with corresponding Lie algebra morphism
$m:\mathrm {T}\times \mathrm {C}\rightarrow \mathrm {G}_0$, with corresponding Lie algebra morphism ![]() $\mathfrak {t}\oplus \mathfrak {c}\rightarrow \mathfrak {t}+\mathfrak {c}\subset \mathfrak {g}_0$. In the case of the general linear group, this corresponds to first forming the product bundle as a
$\mathfrak {t}\oplus \mathfrak {c}\rightarrow \mathfrak {t}+\mathfrak {c}\subset \mathfrak {g}_0$. In the case of the general linear group, this corresponds to first forming the product bundle as a ![]() $\mathrm {GL}_m\mathbb {C}\times \mathrm {GL}_n\mathbb {C}$-principal bundle and then producing the tensor product as a
$\mathrm {GL}_m\mathbb {C}\times \mathrm {GL}_n\mathbb {C}$-principal bundle and then producing the tensor product as a ![]() $\mathrm {GL}_{mn}\mathbb {C}$-principal bundle by applying the multiplication map
$\mathrm {GL}_{mn}\mathbb {C}$-principal bundle by applying the multiplication map ![]() $\mathrm {GL}_m\mathbb {C}\times \mathrm {GL}_n\mathbb {C}\rightarrow \mathrm {GL}_{mn}\mathbb {C}$ given by
$\mathrm {GL}_m\mathbb {C}\times \mathrm {GL}_n\mathbb {C}\rightarrow \mathrm {GL}_{mn}\mathbb {C}$ given by ![]() $(g,g')\mapsto g\otimes g'$.
$(g,g')\mapsto g\otimes g'$.
Since ![]() $\mathrm {C}$ acts trivially on
$\mathrm {C}$ acts trivially on ![]() $\langle e\rangle,$ we have
$\langle e\rangle,$ we have
Also, since the Lie algebra ![]() $\mathfrak {c}$ is perpendicular to
$\mathfrak {c}$ is perpendicular to ![]() $\zeta$, the Toledo invariant is unchanged:
$\zeta$, the Toledo invariant is unchanged:
Moreover, if ![]() $E_\mathrm {C}$ is a polystable
$E_\mathrm {C}$ is a polystable ![]() $\mathrm {C}$-bundleFootnote 1, then there is a metric
$\mathrm {C}$-bundleFootnote 1, then there is a metric ![]() $h_\mathrm {C}$ on
$h_\mathrm {C}$ on ![]() $E_\mathrm {C}$ whose associated Chern connection is flat (see Remark 4.14). As a result, if
$E_\mathrm {C}$ whose associated Chern connection is flat (see Remark 4.14). As a result, if ![]() $h_\mathrm {T}$ is a metric on
$h_\mathrm {T}$ is a metric on ![]() $E_\mathrm {T}$ solving the Hitchin equations for
$E_\mathrm {T}$ solving the Hitchin equations for ![]() $(E_\mathrm {T},e)$, then
$(E_\mathrm {T},e)$, then ![]() $h_\mathrm {T}\otimes h_\mathrm {C}$ solves the Hitchin equations for the Higgs bundle
$h_\mathrm {T}\otimes h_\mathrm {C}$ solves the Hitchin equations for the Higgs bundle ![]() $(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}(\mathrm {G}),e)$. Hence, if
$(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}(\mathrm {G}),e)$. Hence, if ![]() $E_\mathrm {C}$ is a polystable
$E_\mathrm {C}$ is a polystable ![]() $\mathrm {C}$-bundle, then
$\mathrm {C}$-bundle, then ![]() $(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C},e)$ is a polystable
$(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C},e)$ is a polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair.
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair.
So far, we have shown that there is a well-defined map
from the moduli space ![]() ${\mathcal {N}}(\mathrm {C})$ of polystable
${\mathcal {N}}(\mathrm {C})$ of polystable ![]() $\mathrm {C}$-bundles to the moduli space of polystable
$\mathrm {C}$-bundles to the moduli space of polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs which are maximal. The map
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs which are maximal. The map ![]() $\Psi _e$ from (
$\Psi _e$ from (
) is a moduli space version of a restriction of the global Slodowy slice map from [Reference Collier and SandersCS21] and generalizes a restriction of the Cayley correspondence in the case of a ![]() $\mathbb {Z}$-grading defining a Hermitian group [Reference Biquard, García-Prada and RubioBGR17].
$\mathbb {Z}$-grading defining a Hermitian group [Reference Biquard, García-Prada and RubioBGR17].
Theorem 6.2 The map ![]() $\Psi _e:{\mathcal {N}}(\mathrm {C})\to {\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ from (6.1) defines an isomorphism between the moduli space of polystable
$\Psi _e:{\mathcal {N}}(\mathrm {C})\to {\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ from (6.1) defines an isomorphism between the moduli space of polystable ![]() $\mathrm {C}$-bundles and the moduli space of polystable maximal
$\mathrm {C}$-bundles and the moduli space of polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
Remark 6.3 For classical Lie groups, the centralizers ![]() $\mathrm {C}<\mathrm {G}$ of
$\mathrm {C}<\mathrm {G}$ of ![]() $\mathfrak {sl}_2$-triples are easily described in terms of partitions [Reference Springer and SteinbergSS70] (see [Reference Collingwood and McGovernCM93, Theorem 6.1.3]).
$\mathfrak {sl}_2$-triples are easily described in terms of partitions [Reference Springer and SteinbergSS70] (see [Reference Collingwood and McGovernCM93, Theorem 6.1.3]).
Proof. We first show that ![]() $\Psi _e$ is surjective. Let
$\Psi _e$ is surjective. Let ![]() $(E,\varphi )$ be a polystable maximal
$(E,\varphi )$ be a polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. As above, let
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. As above, let ![]() $E_\mathrm {T}$ be the holomorphic frame bundle of
$E_\mathrm {T}$ be the holomorphic frame bundle of ![]() $K^{-1}$ or
$K^{-1}$ or ![]() $K^{- {1}/{2}}$ if
$K^{- {1}/{2}}$ if ![]() $\mathrm {S}$ is isomorphic to
$\mathrm {S}$ is isomorphic to ![]() $\mathrm {PSL}_2\mathbb {C}$ or
$\mathrm {PSL}_2\mathbb {C}$ or ![]() $\mathrm {SL}_2\mathbb {C}$, respectively. Note that
$\mathrm {SL}_2\mathbb {C}$, respectively. Note that
Since ![]() $(\mathrm {G}_0,\varphi )$ is JM-regular, we have
$(\mathrm {G}_0,\varphi )$ is JM-regular, we have ![]() $\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=\chi _T(\zeta ),$ where
$\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)=\chi _T(\zeta ),$ where ![]() $\zeta = {h}/{2}.$ Also, by Proposition 3.16, a positive multiple of the Toledo character
$\zeta = {h}/{2}.$ Also, by Proposition 3.16, a positive multiple of the Toledo character ![]() $q\cdot \chi _T(x)=q\cdot B(\gamma,\gamma )B(\zeta,x)$ exponentiates to a character
$q\cdot \chi _T(x)=q\cdot B(\gamma,\gamma )B(\zeta,x)$ exponentiates to a character ![]() $\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a polynomial relative invariant
$\chi _{T,q}:\mathrm {G}_0\to \mathbb {C}^*$ which has a polynomial relative invariant ![]() $F:\mathfrak {g}_1\to \mathbb {C}$ of degree
$F:\mathfrak {g}_1\to \mathbb {C}$ of degree ![]() $q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$ As in the proof of Theorem 5.3, applying the relative invariant
$q\cdot \operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1).$ As in the proof of Theorem 5.3, applying the relative invariant ![]() $F$ to the Higgs field defines a nonzero holomorphic section
$F$ to the Higgs field defines a nonzero holomorphic section
The degree of ![]() $E(\chi _{T,q})\otimes K^{q\operatorname {rk}_{T}(\mathrm {G}_0,\mathfrak {g}_1)}$ is
$E(\chi _{T,q})\otimes K^{q\operatorname {rk}_{T}(\mathrm {G}_0,\mathfrak {g}_1)}$ is ![]() $q(\tau (E,\varphi )+\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2))=0.$ Thus,
$q(\tau (E,\varphi )+\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2))=0.$ Thus, ![]() $F(\varphi )$ is nowhere vanishing, and
$F(\varphi )$ is nowhere vanishing, and ![]() $\operatorname {rk}_T(\varphi (x))=\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)$ for all
$\operatorname {rk}_T(\varphi (x))=\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)$ for all ![]() $x\in X.$ That is,
$x\in X.$ That is, ![]() $\varphi (x)$ is in the open orbit
$\varphi (x)$ is in the open orbit ![]() $\Omega$ for all
$\Omega$ for all ![]() $x\in X$.
$x\in X$.
Thus the Higgs field ![]() $\varphi$ is defines a holomorphic section of
$\varphi$ is defines a holomorphic section of ![]() $E(\Omega )\otimes K$. But
$E(\Omega )\otimes K$. But ![]() $\Omega =\mathrm {G}_0/\mathrm {C}$ and
$\Omega =\mathrm {G}_0/\mathrm {C}$ and ![]() $E(\Omega )\otimes K\cong (E_\mathrm {T}^{-1}\otimes _{\mathrm {G}_0} E)(\mathrm {G}_0/\mathrm {C}).$ Thus, the Higgs field defines a holomorphic reduction of structure group of
$E(\Omega )\otimes K\cong (E_\mathrm {T}^{-1}\otimes _{\mathrm {G}_0} E)(\mathrm {G}_0/\mathrm {C}).$ Thus, the Higgs field defines a holomorphic reduction of structure group of ![]() $(E_\mathrm {T}^{-1}\otimes _{\mathrm {G}_0} E)$ to
$(E_\mathrm {T}^{-1}\otimes _{\mathrm {G}_0} E)$ to ![]() $\mathrm {C}.$ Let
$\mathrm {C}.$ Let ![]() $E_\mathrm {C}$ be the resulting holomorphic
$E_\mathrm {C}$ be the resulting holomorphic ![]() $\mathrm {C}$-bundle. Twisting both sides by
$\mathrm {C}$-bundle. Twisting both sides by ![]() $E_\mathrm {T}$, we obtain an isomorphism
$E_\mathrm {T}$, we obtain an isomorphism
By construction, ![]() $\varphi \in H^0((E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C})(\langle e\rangle )\otimes K)$. Since a
$\varphi \in H^0((E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C})(\langle e\rangle )\otimes K)$. Since a ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs ![]() $(E,\varphi )$ is isomorphic to
$(E,\varphi )$ is isomorphic to ![]() $(E,\lambda \varphi )$ for all
$(E,\lambda \varphi )$ for all ![]() $\lambda \in \mathbb {C}^*,$ we can take
$\lambda \in \mathbb {C}^*,$ we can take ![]() $\varphi =e.$
$\varphi =e.$
To complete the proof of surjectivity, we show that if ![]() $(E,\varphi )=(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}),e)$ is a polystable (semistable)
$(E,\varphi )=(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C}),e)$ is a polystable (semistable) ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair, then
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair, then ![]() $E_\mathrm {C}$ is a polystable (semistable) bundle. Suppose that we have a reduction
$E_\mathrm {C}$ is a polystable (semistable) bundle. Suppose that we have a reduction ![]() $(E_{\mathrm {P}'_s},\sigma ')$ of the structure group of
$(E_{\mathrm {P}'_s},\sigma ')$ of the structure group of ![]() $E_\mathrm {C}$ to the parabolic subgroup
$E_\mathrm {C}$ to the parabolic subgroup ![]() $\mathrm {P}'_s\subset \mathrm {C}$ defined by an
$\mathrm {P}'_s\subset \mathrm {C}$ defined by an ![]() $s\in i\mathfrak {c}^\mathbb {R}$, where
$s\in i\mathfrak {c}^\mathbb {R}$, where ![]() $\mathfrak {c}^\mathbb {R}$ is the Lie algebra of the maximal compact subgroup
$\mathfrak {c}^\mathbb {R}$ is the Lie algebra of the maximal compact subgroup ![]() $\mathrm {C}^\mathbb {R}$ of
$\mathrm {C}^\mathbb {R}$ of ![]() $\mathrm {C}$. The element
$\mathrm {C}$. The element ![]() $s$ defines a parabolic subgroup
$s$ defines a parabolic subgroup ![]() $\mathrm {P}_s\subset \mathrm {G}_0$ as well, and, using the map
$\mathrm {P}_s\subset \mathrm {G}_0$ as well, and, using the map ![]() $\mathrm {C}/\mathrm {P}'_s\to \mathrm {G}_0/\mathrm {P}_s$, we obtain from
$\mathrm {C}/\mathrm {P}'_s\to \mathrm {G}_0/\mathrm {P}_s$, we obtain from ![]() $\sigma '$ a reduction
$\sigma '$ a reduction ![]() $\sigma$ of the structure group of
$\sigma$ of the structure group of ![]() $E$ to
$E$ to ![]() $\mathrm {P}_s$, resulting in a
$\mathrm {P}_s$, resulting in a ![]() $\mathrm {P}_s$-bundle
$\mathrm {P}_s$-bundle ![]() $E_{\mathrm {P}_s}$. Since
$E_{\mathrm {P}_s}$. Since ![]() $\mathrm {C}$ stabilizes
$\mathrm {C}$ stabilizes ![]() $e\in \mathfrak {g}_1$, we have
$e\in \mathfrak {g}_1$, we have ![]() $e\in \mathfrak {g}_{1,s}^0$. Since
$e\in \mathfrak {g}_{1,s}^0$. Since ![]() $\langle s,h\rangle =0$, there is no contribution coming from the twisting
$\langle s,h\rangle =0$, there is no contribution coming from the twisting ![]() $E\otimes _{\mathrm {G}_0} E_\mathrm {T}^{-1}$ in the computation of
$E\otimes _{\mathrm {G}_0} E_\mathrm {T}^{-1}$ in the computation of ![]() $\deg E(\sigma, s)$. Hence,
$\deg E(\sigma, s)$. Hence, ![]() $\deg (E)(\sigma,s)=\deg (E_\mathrm {C})(\sigma ',s)$, and (semi)stability of
$\deg (E)(\sigma,s)=\deg (E_\mathrm {C})(\sigma ',s)$, and (semi)stability of ![]() $(E,\varphi )$ implies the (semi)stability of
$(E,\varphi )$ implies the (semi)stability of ![]() $E_\mathrm {C}$. For polystability, one must just check additionally that in the equality case, reduction for the Levi subgroup
$E_\mathrm {C}$. For polystability, one must just check additionally that in the equality case, reduction for the Levi subgroup ![]() $\mathrm {L}_s\subset \mathrm {P}_s$ to an
$\mathrm {L}_s\subset \mathrm {P}_s$ to an ![]() $E_{\mathrm {L}_s}\subset E$ implies reduction for the Levi subgroup
$E_{\mathrm {L}_s}\subset E$ implies reduction for the Levi subgroup ![]() $\mathrm {L}'_s\subset \mathrm {P}'_s$, but it is sufficient to take
$\mathrm {L}'_s\subset \mathrm {P}'_s$, but it is sufficient to take ![]() $E_{\mathrm {L}'_s}=(E_{\mathrm {L}_s}\otimes _{\mathrm {G}_0} E_{\mathrm {T}}^{-1})\cap E_\mathrm {C}$.
$E_{\mathrm {L}'_s}=(E_{\mathrm {L}_s}\otimes _{\mathrm {G}_0} E_{\mathrm {T}}^{-1})\cap E_\mathrm {C}$.
For injectivity, note that two polystable ![]() $\mathrm {C}$-bundles
$\mathrm {C}$-bundles ![]() $E_\mathrm {C}$ and
$E_\mathrm {C}$ and ![]() $E_\mathrm {C}'$ define the same point in
$E_\mathrm {C}'$ define the same point in ![]() ${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ if there is a holomorphic isomorphism of
${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ if there is a holomorphic isomorphism of ![]() $\mathrm {G}_0$-bundles
$\mathrm {G}_0$-bundles
such that ![]() $\Phi ^*e=e.$ Since the
$\Phi ^*e=e.$ Since the ![]() $\mathrm {G}_0$ stabilizer of
$\mathrm {G}_0$ stabilizer of ![]() $e\in \mathfrak {g}_1$ is
$e\in \mathfrak {g}_1$ is ![]() $\mathrm {C},$ we conclude that
$\mathrm {C},$ we conclude that ![]() $\Phi$ induces an isomorphism between
$\Phi$ induces an isomorphism between ![]() $E_\mathrm {C}$ and
$E_\mathrm {C}$ and ![]() $E_\mathrm {C}'.$ Note that injectivity implies that the automorphism group of
$E_\mathrm {C}'.$ Note that injectivity implies that the automorphism group of ![]() $\Psi _e(E_\mathrm {C})$ is equal to the automorphism group of the polystable
$\Psi _e(E_\mathrm {C})$ is equal to the automorphism group of the polystable ![]() $\mathrm {C}$-bundle
$\mathrm {C}$-bundle ![]() $E_\mathrm {C}.$
$E_\mathrm {C}.$
The component count for the moduli space of polystable ![]() $\mathrm {C}$-Higgs bundles is given the number of topologically distinct
$\mathrm {C}$-Higgs bundles is given the number of topologically distinct ![]() $\mathrm {C}$-bundles on
$\mathrm {C}$-bundles on ![]() $X$ which have degree zero with respect to any character
$X$ which have degree zero with respect to any character ![]() $\chi :\mathfrak {c}\to \mathbb {C}.$ For example, when
$\chi :\mathfrak {c}\to \mathbb {C}.$ For example, when ![]() $\mathrm {C}$ is connected and
$\mathrm {C}$ is connected and ![]() $\Gamma <\pi _1(\mathrm {C})$ is the torsion subgroup,
$\Gamma <\pi _1(\mathrm {C})$ is the torsion subgroup, ![]() ${\mathcal {N}}(\mathrm {C})$ has
${\mathcal {N}}(\mathrm {C})$ has ![]() $|\Gamma |$ connected components. As an immediate corollary, we have the following component count.
$|\Gamma |$ connected components. As an immediate corollary, we have the following component count.
Corollary 6.4 We have ![]() $\pi _0({\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1))=\pi _0({\mathcal {N}}(\mathrm {C}))$. In particular, the component count is given by the number of topological degree zero
$\pi _0({\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1))=\pi _0({\mathcal {N}}(\mathrm {C}))$. In particular, the component count is given by the number of topological degree zero ![]() $\mathrm {C}$-bundles on
$\mathrm {C}$-bundles on ![]() $X.$
$X.$
We now use Theorem 6.2 to deduce rigidity results for variations of Hodge structure. Consider the complex linear involution ![]() $\theta :\mathfrak {g}\to \mathfrak {g}$ which is
$\theta :\mathfrak {g}\to \mathfrak {g}$ which is ![]() $(-1)^j\operatorname {Id}$ on each graded factor
$(-1)^j\operatorname {Id}$ on each graded factor ![]() $\mathfrak {g}_j.$ Recall from § 3.2 that a compact real form
$\mathfrak {g}_j.$ Recall from § 3.2 that a compact real form ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ satisfies
$\tau :\mathfrak {g}\to \mathfrak {g}$ satisfies ![]() $\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}.$ Moreover, we can choose such a
$\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}.$ Moreover, we can choose such a ![]() $\tau$ so that the
$\tau$ so that the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ satisfies
$\{f,h,e\}$ satisfies ![]() $f=-\tau (e).$ Let
$f=-\tau (e).$ Let ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ be the associated real form of Hodge type. By construction, the subgroup
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ be the associated real form of Hodge type. By construction, the subgroup ![]() $\mathrm {S}<\mathrm {G}$ defines a subgroup
$\mathrm {S}<\mathrm {G}$ defines a subgroup ![]() $\mathrm {S}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ which is isomorphic to
$\mathrm {S}^\mathbb {R}<\mathrm {G}^\mathbb {R}$ which is isomorphic to ![]() $\mathrm {P}\mathrm {SL}_2\mathbb {R}$ if
$\mathrm {P}\mathrm {SL}_2\mathbb {R}$ if ![]() $\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and isomorphic to
$\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and isomorphic to ![]() $\mathrm {SL}_2\mathbb {R}$ if
$\mathrm {SL}_2\mathbb {R}$ if ![]() $\mathrm {S}\cong \mathrm {SL}_2\mathbb {C}.$ Also by construction, the
$\mathrm {S}\cong \mathrm {SL}_2\mathbb {C}.$ Also by construction, the ![]() $\mathrm {G}^\mathbb {R}$-centralizer of
$\mathrm {G}^\mathbb {R}$-centralizer of ![]() $\mathrm {S}^\mathbb {R}$ is the compact real form
$\mathrm {S}^\mathbb {R}$ is the compact real form ![]() $\mathrm {C}^\mathbb {R}<\mathrm {C}$ of the centralizer of
$\mathrm {C}^\mathbb {R}<\mathrm {C}$ of the centralizer of ![]() $\mathrm {S}.$
$\mathrm {S}.$
Since ![]() $\mathrm {C}^\mathbb {R}$ and
$\mathrm {C}^\mathbb {R}$ and ![]() $\mathrm {S}^\mathbb {R}$ are commuting subgroups of
$\mathrm {S}^\mathbb {R}$ are commuting subgroups of ![]() $\mathrm {G}^\mathbb {R}$, given representations
$\mathrm {G}^\mathbb {R}$, given representations ![]() $\rho _1:\pi _1(X)\to \mathrm {S}^\mathbb {R}$ and
$\rho _1:\pi _1(X)\to \mathrm {S}^\mathbb {R}$ and ![]() $\rho _2:\pi _1(X)\to \mathrm {C}^\mathbb {R}$, we can form a new representation, multiplying the images
$\rho _2:\pi _1(X)\to \mathrm {C}^\mathbb {R}$, we can form a new representation, multiplying the images
Recall that ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular if and only if it arises from an even
$(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular if and only if it arises from an even ![]() $\mathfrak {sl}_2$-triple.
$\mathfrak {sl}_2$-triple.
Theorem 6.5 Let ![]() $\mathrm {G}$ be a complex semisimple Lie group with Lie algebra
$\mathrm {G}$ be a complex semisimple Lie group with Lie algebra ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let ![]() $\{f,h,e\}\subset \mathfrak {g}$ be an even
$\{f,h,e\}\subset \mathfrak {g}$ be an even ![]() $\mathfrak {sl}_2$-triple and
$\mathfrak {sl}_2$-triple and ![]() $\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be the associated
$\mathfrak {g}=\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$ be the associated ![]() $\mathbb {Z}$-grading with grading element
$\mathbb {Z}$-grading with grading element ![]() $ {h}/{2}$, let
$ {h}/{2}$, let ![]() $\mathrm {S}<\mathrm {G}$ be the associated connected subgroup and let
$\mathrm {S}<\mathrm {G}$ be the associated connected subgroup and let ![]() $\mathrm {C}<\mathrm {G}$ be the centralizer of
$\mathrm {C}<\mathrm {G}$ be the centralizer of ![]() $\{f,h,e\}.$ Suppose
$\{f,h,e\}.$ Suppose ![]() $\rho :\pi _1(X)\to \mathrm {G}$ is a reductive representation. The Higgs bundle associated to
$\rho :\pi _1(X)\to \mathrm {G}$ is a reductive representation. The Higgs bundle associated to ![]() $\rho$ is a maximal Hodge bundle of type
$\rho$ is a maximal Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if, up to conjugation,
$(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if, up to conjugation, ![]() $\rho =\rho _u *\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G},$ where
$\rho =\rho _u *\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G},$ where
−
 $\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is (a lift of) the uniformizing representation of
$\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is (a lift of) the uniformizing representation of  $X$, and
$X$, and−
 $\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is any representation into the compact real form of
$\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is any representation into the compact real form of  $\mathrm {C}.$
$\mathrm {C}.$
Remark 6.6 Note that the representations ![]() $\rho =\rho _u*\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G}$ all factor through the canonical real form of Hodge type
$\rho =\rho _u*\rho _\mathrm {C}:\pi _1(X)\to \mathrm {G}$ all factor through the canonical real form of Hodge type ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ associated to the grading
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ associated to the grading ![]() $\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$. Moreover, the
$\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$. Moreover, the ![]() $\mathrm {G}^\mathbb {R}$-centralizer of any such representations is compact since the
$\mathrm {G}^\mathbb {R}$-centralizer of any such representations is compact since the ![]() $\mathrm {G}^\mathbb {R}$-centralizer of
$\mathrm {G}^\mathbb {R}$-centralizer of ![]() $\mathrm {S}^\mathbb {R}$ is
$\mathrm {S}^\mathbb {R}$ is ![]() $\mathrm {C}^\mathbb {R}$, which is compact. As a result, representations associated to maximal Hodge bundles of type
$\mathrm {C}^\mathbb {R}$, which is compact. As a result, representations associated to maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ do not factor through proper parabolic subgroups
$(\mathrm {G}_0,\mathfrak {g}_1)$ do not factor through proper parabolic subgroups ![]() $\mathrm {P}^\mathbb {R}<\mathrm {G}^\mathbb {R}.$
$\mathrm {P}^\mathbb {R}<\mathrm {G}^\mathbb {R}.$
Proof. The proof is immediate from the nonabelian Hodge correspondence and Theorem 6.2. Namely, given an even ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ with associated grading
$\{f,h,e\}$ with associated grading ![]() $\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, every polystable
$\bigoplus _{j\in \mathbb {Z}}\mathfrak {g}_j$, every polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E,\varphi )$ with Toledo invariant
$(E,\varphi )$ with Toledo invariant ![]() $-\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2)$ is isomorphic to
$-\operatorname {rk}_T(\mathrm {G}_0,\mathfrak {g}_1)(2g-2)$ is isomorphic to ![]() $(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C},e)$, where
$(E_\mathrm {T}\otimes _{\mathrm {G}_0} E_\mathrm {C},e)$, where ![]() $(E_\mathrm {T},e)$ is a uniformizing Higgs bundle of
$(E_\mathrm {T},e)$ is a uniformizing Higgs bundle of ![]() $X$ and
$X$ and ![]() $E_\mathrm {C}$ is a polystable
$E_\mathrm {C}$ is a polystable ![]() $\mathrm {C}$-bundle. A solution to the Hitchin equations is given by
$\mathrm {C}$-bundle. A solution to the Hitchin equations is given by ![]() $h_\mathrm {T}\otimes h_\mathrm {C}$, where
$h_\mathrm {T}\otimes h_\mathrm {C}$, where ![]() $h_\mathrm {T}$ solves the Hitchin equations for the uniformizing Higgs bundle
$h_\mathrm {T}$ solves the Hitchin equations for the uniformizing Higgs bundle ![]() $(E_\mathrm {T},e)$ and the Chern connection of
$(E_\mathrm {T},e)$ and the Chern connection of ![]() $h_\mathrm {C}$ is flat. The associated flat connection is then
$h_\mathrm {C}$ is flat. The associated flat connection is then
As a result, the associated representation ![]() $\rho :\pi _1(X)\to \mathrm {G}$ is given by
$\rho :\pi _1(X)\to \mathrm {G}$ is given by ![]() $\rho _u*\rho _\mathrm {C}$, where
$\rho _u*\rho _\mathrm {C}$, where ![]() $\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is the uniformizing representation of
$\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is the uniformizing representation of ![]() $X$ if
$X$ if ![]() $\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and a lift of the uniformizing representation if
$\mathrm {S}\cong \mathrm {PSL}_2\mathbb {C}$ and a lift of the uniformizing representation if ![]() $\mathrm {S}\cong \mathrm {SL}_2\mathbb {C}$ and
$\mathrm {S}\cong \mathrm {SL}_2\mathbb {C}$ and ![]() $\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is a representation into the compact real form of
$\rho _\mathrm {C}:\pi _1(X)\to \mathrm {C}^\mathbb {R}<\mathrm {C}$ is a representation into the compact real form of ![]() $\mathrm {C}.$
$\mathrm {C}.$
Let ![]() $\Sigma$ be a closed topological surface of genus
$\Sigma$ be a closed topological surface of genus ![]() $g\geqslant 2.$ For
$g\geqslant 2.$ For ![]() $\mathrm {S}^\mathbb {R}$ isomorphic to
$\mathrm {S}^\mathbb {R}$ isomorphic to ![]() $\mathrm {PSL}_2\mathbb {R}$ or
$\mathrm {PSL}_2\mathbb {R}$ or ![]() $\mathrm {SL}_2\mathbb {R}$, injective representations
$\mathrm {SL}_2\mathbb {R}$, injective representations ![]() $\rho :\pi _1(\Sigma )\to \mathrm {S}^\mathbb {R}$ with discrete image are called Fuchsian representations. The set of conjugacy classes of Fuchsian representations defines an open and closed set in the character variety
$\rho :\pi _1(\Sigma )\to \mathrm {S}^\mathbb {R}$ with discrete image are called Fuchsian representations. The set of conjugacy classes of Fuchsian representations defines an open and closed set in the character variety ![]() ${\mathcal {R}}(\mathrm {S}^\mathbb {R})$, each connected component of which is identified with the Teichmüller space of the surface
${\mathcal {R}}(\mathrm {S}^\mathbb {R})$, each connected component of which is identified with the Teichmüller space of the surface ![]() $\Sigma$ by the uniformization theorem.
$\Sigma$ by the uniformization theorem.
Corollary 6.7 Suppose ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular and let
$(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular and let ![]() $\rho :\pi _1(\Sigma )\to \mathrm {G}$ be a reductive representation. There exists a Riemann surface structure
$\rho :\pi _1(\Sigma )\to \mathrm {G}$ be a reductive representation. There exists a Riemann surface structure ![]() $X_\rho$ on
$X_\rho$ on ![]() $\Sigma$ such that the Higgs bundle associated to
$\Sigma$ such that the Higgs bundle associated to ![]() $\rho$ is a maximal Hodge bundle of type
$\rho$ is a maximal Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ on
$(\mathrm {G}_0,\mathfrak {g}_1)$ on ![]() $X_\rho$ if and only if
$X_\rho$ if and only if
where ![]() $\rho _{\mathrm {Fuch}}:\pi _1(\Sigma )\to \mathrm {S}^\mathbb {R}$ is a Fuchsian representation and
$\rho _{\mathrm {Fuch}}:\pi _1(\Sigma )\to \mathrm {S}^\mathbb {R}$ is a Fuchsian representation and ![]() $\rho _{\mathrm {C}^\mathbb {R}}:\pi _1(\Sigma )\to \mathrm {C}^\mathbb {R}$ is a representation into the compact real form of
$\rho _{\mathrm {C}^\mathbb {R}}:\pi _1(\Sigma )\to \mathrm {C}^\mathbb {R}$ is a representation into the compact real form of ![]() $\mathrm {C}.$ In particular, for any such representations, the associated Riemann surface
$\mathrm {C}.$ In particular, for any such representations, the associated Riemann surface ![]() $X_\rho$ is unique.
$X_\rho$ is unique.
The following corollary is also immediate from Theorem 6.5.
Corollary 6.8 Suppose ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular. A variation of Hodge structure
$(\mathrm {G}_0,\mathfrak {g}_1)$ is JM-regular. A variation of Hodge structure ![]() $(\rho,f_\rho )$ associated to a Hodge bundle of type
$(\rho,f_\rho )$ associated to a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is maximal if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$ is maximal if and only if ![]() $f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. In particular, the image of
$f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. In particular, the image of ![]() $f_\rho$ is independent of
$f_\rho$ is independent of ![]() $\rho$ and rigid.
$\rho$ and rigid.
6.2 Some explicit examples
We list some explicit examples for ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ JM-regular.
$(\mathrm {G}_0,\mathfrak {g}_1)$ JM-regular.
Example 6.9 When ![]() $\mathrm {G}_0<\mathrm {G}$ is a Cartan subgroup,
$\mathrm {G}_0<\mathrm {G}$ is a Cartan subgroup, ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS associated to a principal
$(\mathrm {G}_0,\mathfrak {g}_1)$ is a JM-regular PHVS associated to a principal ![]() $\mathfrak {sl}_2$-triple. In this case, the group
$\mathfrak {sl}_2$-triple. In this case, the group ![]() $\mathrm {C}$ is the center of
$\mathrm {C}$ is the center of ![]() $\mathrm {G}$. The Higgs bundles
$\mathrm {G}$. The Higgs bundles ![]() $(E_\mathrm {C}\otimes _{\mathrm {G}_0} E_\mathrm {T},e)$ associated to maximal
$(E_\mathrm {C}\otimes _{\mathrm {G}_0} E_\mathrm {T},e)$ associated to maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs are the image of
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs are the image of ![]() $0$ under the Hitchin section [Reference HitchinHit92].
$0$ under the Hitchin section [Reference HitchinHit92].
Example 6.10 For JM-regular PHVSs ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ associated to gradings
$(\mathrm {G}_0,\mathfrak {g}_1)$ associated to gradings ![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the real form
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$, the real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a Hermitian Lie group of tube type (see Example 3.9). In this case, the above results recover the subset of the results in [Reference Biquard, García-Prada and RubioBGR17]. In this case, there is a particular stratum of the boundary of the noncompact Riemannian symmetric space
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ is a Hermitian Lie group of tube type (see Example 3.9). In this case, the above results recover the subset of the results in [Reference Biquard, García-Prada and RubioBGR17]. In this case, there is a particular stratum of the boundary of the noncompact Riemannian symmetric space ![]() $\mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ called the Shilov boundary. The group
$\mathrm {G}^\mathbb {R}/\mathrm {H}^\mathbb {R}$ called the Shilov boundary. The group ![]() $\mathrm {C}^\mathbb {R}$ is isomorphic to the stabilizer of a generic point in the Shilov boundary.
$\mathrm {C}^\mathbb {R}$ is isomorphic to the stabilizer of a generic point in the Shilov boundary.
Example 6.11 We now describe the JM-regular ![]() $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ with
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ with ![]() $q\geqslant p$ from Examples 2.1, 2.5 and 3.9 in more detail. Fix a decomposition
$q\geqslant p$ from Examples 2.1, 2.5 and 3.9 in more detail. Fix a decomposition ![]() $\mathbb {C}^{2p+q}=\mathbb {C}^p\oplus \mathbb {C}^q\oplus \mathbb {C}^p$ with orthogonal structure
$\mathbb {C}^{2p+q}=\mathbb {C}^p\oplus \mathbb {C}^q\oplus \mathbb {C}^p$ with orthogonal structure ![]() $Q(x,y,z)=xz^\mathrm {T} + x^\mathrm {T} z + yy^\mathrm {T}$. Then we may write
$Q(x,y,z)=xz^\mathrm {T} + x^\mathrm {T} z + yy^\mathrm {T}$. Then we may write ![]() $\mathfrak {so}_{2p+q}\mathbb {C}$ as
$\mathfrak {so}_{2p+q}\mathbb {C}$ as

The even ![]() $\mathfrak {sl}_2$-triple is given by
$\mathfrak {sl}_2$-triple is given by

where ![]() $\operatorname {Id}_p$ is the
$\operatorname {Id}_p$ is the ![]() $p\times p$ identity matrix. The
$p\times p$ identity matrix. The ![]() $\mathbb {Z}$-grading is
$\mathbb {Z}$-grading is ![]() $\mathfrak {g}_{-2}\oplus \mathfrak {g}_1\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1\oplus \mathfrak {g}_2$ where the space
$\mathfrak {g}_{-2}\oplus \mathfrak {g}_1\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1\oplus \mathfrak {g}_2$ where the space ![]() $\mathfrak {g}_j$ is the
$\mathfrak {g}_j$ is the ![]() $j$th super block diagonal.
$j$th super block diagonal.
The subgroup ![]() $\mathrm {G}_0<\mathrm {SO}_{2p+q}\mathbb {C}$ is
$\mathrm {G}_0<\mathrm {SO}_{2p+q}\mathbb {C}$ is ![]() $\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ and the
$\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C}$ and the ![]() $\mathrm {G}_0$-stabilizer of
$\mathrm {G}_0$-stabilizer of ![]() $e$ is given by
$e$ is given by

Using the standard representation of ![]() $\mathrm {SO}_{2p+q}\mathbb {C}$, an
$\mathrm {SO}_{2p+q}\mathbb {C}$, an ![]() $\mathrm {SO}_{2p+q}\mathbb {C}$-Higgs bundle is a triple
$\mathrm {SO}_{2p+q}\mathbb {C}$-Higgs bundle is a triple ![]() $(E,Q,\Phi )$, where
$(E,Q,\Phi )$, where ![]() $E$ is a rank
$E$ is a rank ![]() $2p+q$ holomorphic bundle with trivialized determinant bundle,
$2p+q$ holomorphic bundle with trivialized determinant bundle, ![]() $Q$ is an everywhere nondegenerate symmetric bilinear form on
$Q$ is an everywhere nondegenerate symmetric bilinear form on ![]() $E$ and
$E$ and ![]() $\Phi \in H^0(\operatorname {End}(E)\otimes K)$ is a
$\Phi \in H^0(\operatorname {End}(E)\otimes K)$ is a ![]() $K$-twisted endomorphism of
$K$-twisted endomorphism of ![]() $E$ which is skew symmetric with respect to
$E$ which is skew symmetric with respect to ![]() $Q.$ An
$Q.$ An ![]() $\mathrm {SO}_{2p+q}\mathbb {C}$ is a Hodge bundle of type
$\mathrm {SO}_{2p+q}\mathbb {C}$ is a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if
$(\mathrm {G}_0,\mathfrak {g}_1)$ if ![]() $E$ splits holomorphically as
$E$ splits holomorphically as ![]() $E=V\oplus W\oplus V^*$, where
$E=V\oplus W\oplus V^*$, where ![]() $V$ is a rank-
$V$ is a rank-![]() $p$ isotropic subbundle and
$p$ isotropic subbundle and ![]() $W$ is a rank-
$W$ is a rank-![]() $q$ orthogonal subbundle, and with respect to this splitting we have
$q$ orthogonal subbundle, and with respect to this splitting we have
 \begin{equation} \Phi=\begin{pmatrix} 0 & \theta & 0\\0 & 0 & -\theta^\mathrm{T}\\0 & 0 & 0 \end{pmatrix}:V\oplus W\oplus V^*\to(V\oplus W\oplus V^*)\otimes K. \end{equation}
\begin{equation} \Phi=\begin{pmatrix} 0 & \theta & 0\\0 & 0 & -\theta^\mathrm{T}\\0 & 0 & 0 \end{pmatrix}:V\oplus W\oplus V^*\to(V\oplus W\oplus V^*)\otimes K. \end{equation} Such a Higgs bundle is a maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair if and only if ![]() $W$ decomposes holomorphically and orthogonally as
$W$ decomposes holomorphically and orthogonally as ![]() $W=U_p\oplus U_{q-p}$ and
$W=U_p\oplus U_{q-p}$ and ![]() $V=U_p\otimes K^{-1}$ and
$V=U_p\otimes K^{-1}$ and
In this example, the group ![]() $\mathrm {C}=\mathrm {S}(\mathrm {O}_p\mathbb {C}\times \mathrm {O}_{q-p}\mathbb {C})$ and the space of such Higgs bundles is parameterized by the polystable
$\mathrm {C}=\mathrm {S}(\mathrm {O}_p\mathbb {C}\times \mathrm {O}_{q-p}\mathbb {C})$ and the space of such Higgs bundles is parameterized by the polystable ![]() $\mathrm {S}(\mathrm {O}_p\mathbb {C}\times \mathrm {O}_{q-p}\mathbb {C})$ bundle
$\mathrm {S}(\mathrm {O}_p\mathbb {C}\times \mathrm {O}_{q-p}\mathbb {C})$ bundle ![]() $U_p\oplus U_{q-p}.$ These Higgs bundles reduce to
$U_p\oplus U_{q-p}.$ These Higgs bundles reduce to ![]() $\mathrm {SO}(2p,q)$-Higgs bundles and the resulting representations
$\mathrm {SO}(2p,q)$-Higgs bundles and the resulting representations ![]() $\rho :\pi _1(X)\to \mathrm {SO}(2p,q)$ are conjugate to
$\rho :\pi _1(X)\to \mathrm {SO}(2p,q)$ are conjugate to ![]() $\rho _u*\rho _{\mathrm {C}^\mathbb {R}}$ ,where
$\rho _u*\rho _{\mathrm {C}^\mathbb {R}}$ ,where ![]() $\rho _u:\pi _1(X)\to \mathrm {PSL}_2\mathbb {R}$ is the uniformizing representation of
$\rho _u:\pi _1(X)\to \mathrm {PSL}_2\mathbb {R}$ is the uniformizing representation of ![]() $X$ and
$X$ and ![]() $\rho _{\mathrm {C}^\mathbb {R}}:\pi _1(X)\to \mathrm {S}(\mathrm {O}_p\times \mathrm {O}_{q-p})$ is any representation. When
$\rho _{\mathrm {C}^\mathbb {R}}:\pi _1(X)\to \mathrm {S}(\mathrm {O}_p\times \mathrm {O}_{q-p})$ is any representation. When ![]() $p=1,$ this is agrees with Example 6.10 for the Hermitian Lie group
$p=1,$ this is agrees with Example 6.10 for the Hermitian Lie group ![]() $\mathrm {SO}(2,q).$
$\mathrm {SO}(2,q).$
Remark 6.12 For the JM-regular PHVS ![]() $(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p})$ with
$(\mathrm {S}(\mathrm {GL}_p\mathbb {C}\times \mathrm {GL}_q\mathbb {C}\times \mathrm {GL}_p\mathbb {C}),M_{p,q}\oplus M_{q,p})$ with ![]() $q\geqslant p$ from Examples 2.1, 2.5 and 3.9, the moduli space
$q\geqslant p$ from Examples 2.1, 2.5 and 3.9, the moduli space ![]() $\mathrm {SL}_{2p+q}\mathbb {C}$-Higgs bundles which are maximal Hodge bundles of type
$\mathrm {SL}_{2p+q}\mathbb {C}$-Higgs bundles which are maximal Hodge bundles of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ can be described similarly. Namely, they are given by pairs
$(\mathrm {G}_0,\mathfrak {g}_1)$ can be described similarly. Namely, they are given by pairs ![]() $(E,\Phi )$ where
$(E,\Phi )$ where ![]() $E$ is a holomorphic rank-(
$E$ is a holomorphic rank-(![]() $2p+q$) vector bundle with trivialized determinant and
$2p+q$) vector bundle with trivialized determinant and ![]() $\Phi$ is a traceless
$\Phi$ is a traceless ![]() $K$-twisted endomorphism of
$K$-twisted endomorphism of ![]() $E$ such that
$E$ such that ![]() $E=(U_p\otimes K^{-1})\oplus U_p\oplus U_{q-p}\oplus (U_p\otimes K)$,
$E=(U_p\otimes K^{-1})\oplus U_p\oplus U_{q-p}\oplus (U_p\otimes K)$, ![]() $\det (U_p)^3=\det (U_{q-p})$ and
$\det (U_p)^3=\det (U_{q-p})$ and
 \[ \Phi=\begin{pmatrix} 0 & \operatorname{Id}_p & 0 & 0\\0 & 0 & 0 & \operatorname{Id}_p\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0 \end{pmatrix}:E\to E\otimes K. \]
\[ \Phi=\begin{pmatrix} 0 & \operatorname{Id}_p & 0 & 0\\0 & 0 & 0 & \operatorname{Id}_p\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0 \end{pmatrix}:E\to E\otimes K. \]
Example 6.13 There is a class of nilpotent elements called distinguished nilpotents which play an important role in the Bala–Carter theory classification of nilpotent orbits in ![]() $\mathfrak {g}$. A nilpotent
$\mathfrak {g}$. A nilpotent ![]() $e\in \mathfrak {g}$ is distinguished if and only if the centralizer of an associated
$e\in \mathfrak {g}$ is distinguished if and only if the centralizer of an associated ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\mathrm {C}<\mathrm {G}$ is discrete. Such
$\mathrm {C}<\mathrm {G}$ is discrete. Such ![]() $\mathfrak {sl}_2$-triples are necessarily even, and hence the resulting moduli space of maximal JM-regular
$\mathfrak {sl}_2$-triples are necessarily even, and hence the resulting moduli space of maximal JM-regular ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs is discrete. In particular, the associated
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs is discrete. In particular, the associated ![]() $\mathbb {C}^*$-fixed points in the
$\mathbb {C}^*$-fixed points in the ![]() $\mathrm {G}$-Higgs bundle moduli space are isolated.
$\mathrm {G}$-Higgs bundle moduli space are isolated.
The principal ![]() $\mathfrak {sl}_2$-triples are always distinguished and give rise to the isolated fixed points from Example 6.9. In type
$\mathfrak {sl}_2$-triples are always distinguished and give rise to the isolated fixed points from Example 6.9. In type ![]() $\mathrm {A}$, this is the only distinguished nilpotent. However, in all other types there are many distinguished nilpotents. For example, for
$\mathrm {A}$, this is the only distinguished nilpotent. However, in all other types there are many distinguished nilpotents. For example, for ![]() $\mathfrak {g}=\mathfrak {so}_n\mathbb {C}$ a nilpotent is distinguished if and only if it is associated to a partition
$\mathfrak {g}=\mathfrak {so}_n\mathbb {C}$ a nilpotent is distinguished if and only if it is associated to a partition ![]() $n=1\cdot n_1+\cdots +1\cdot n_k,$ where each
$n=1\cdot n_1+\cdots +1\cdot n_k,$ where each ![]() $n_j$ is odd. For
$n_j$ is odd. For ![]() $\mathfrak {g}=\mathfrak {sp}_{2n}\mathbb {C}$ a nilpotent is distinguished if and only if it is associated to a partition
$\mathfrak {g}=\mathfrak {sp}_{2n}\mathbb {C}$ a nilpotent is distinguished if and only if it is associated to a partition ![]() $2n=1\cdot n_1+\cdots +1\cdot n_k$, with each
$2n=1\cdot n_1+\cdots +1\cdot n_k$, with each ![]() $n_j$ even. Moreover, for the Lie group
$n_j$ even. Moreover, for the Lie group ![]() $\mathrm {G}_2$ there are two even
$\mathrm {G}_2$ there are two even ![]() $\mathfrak {sl}_2$-triples and both are distinguished. See [Reference Collingwood and McGovernCM93, §§ 6 & 8] for more details. This means that the moduli space of
$\mathfrak {sl}_2$-triples and both are distinguished. See [Reference Collingwood and McGovernCM93, §§ 6 & 8] for more details. This means that the moduli space of ![]() $\mathrm {G}$-Higgs bundles has isolated fixed points which do not arise from the Hitchin section when
$\mathrm {G}$-Higgs bundles has isolated fixed points which do not arise from the Hitchin section when ![]() $\mathfrak {g}$ is not of type
$\mathfrak {g}$ is not of type ![]() $\mathrm {A}.$
$\mathrm {A}.$
Example 6.14 In [Reference Bradlow, Collier, García-Prada, Gothen and OliveiraBCGGO21], a class of even nilpotents is identified called magical nilpotents. For such even ![]() $\mathfrak {sl}_2$-triples, there is a real form
$\mathfrak {sl}_2$-triples, there is a real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$ such that the associated maximal
$\mathrm {G}^\mathbb {R}<\mathrm {G}$ such that the associated maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs define
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs define ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles which are local minima of the energy function on the moduli space
$\mathrm {G}^\mathbb {R}$-Higgs bundles which are local minima of the energy function on the moduli space ![]() $\mathrm {G}^\mathbb {R}$-Higgs bundles. For such Hodge bundles, the global Slodowy slice map from [Reference Collier and SandersCS21] descends to moduli spaces and describes connected components of the moduli space
$\mathrm {G}^\mathbb {R}$-Higgs bundles. For such Hodge bundles, the global Slodowy slice map from [Reference Collier and SandersCS21] descends to moduli spaces and describes connected components of the moduli space ![]() ${\mathcal {M}}(\mathrm {G}^\mathbb {R})$ with many interesting properties. In particular, the associated components of the character variety
${\mathcal {M}}(\mathrm {G}^\mathbb {R})$ with many interesting properties. In particular, the associated components of the character variety ![]() ${\mathcal {R}}(\mathrm {G}^\mathbb {R})$ define the higher Teichmüller components conjectured by Guichard, Labourie and Wienhard [Reference Guichard, Labourie and WienhardGLW21, Reference Guichard and WienhardGW18]. There are four families of magical nilpotents two of which appear in Examples 6.9 and 6.10.
${\mathcal {R}}(\mathrm {G}^\mathbb {R})$ define the higher Teichmüller components conjectured by Guichard, Labourie and Wienhard [Reference Guichard, Labourie and WienhardGLW21, Reference Guichard and WienhardGW18]. There are four families of magical nilpotents two of which appear in Examples 6.9 and 6.10.
6.3 The non-JM-regular case
We now describe the moduli space of maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs when
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs when ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular. Assume
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular. Assume ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not a JM-regular PHVS. Let
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not a JM-regular PHVS. Let ![]() $\Omega \subset \mathfrak {g}_1$ be the open
$\Omega \subset \mathfrak {g}_1$ be the open ![]() $\mathrm {G}_0$-orbit. For
$\mathrm {G}_0$-orbit. For ![]() $e\in \Omega$ we complete it to an
$e\in \Omega$ we complete it to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ with
$\{f,h,e\}$ with ![]() $h\in \mathfrak {g}_0$ and set
$h\in \mathfrak {g}_0$ and set ![]() $s=\zeta - {h}/{2}$. Recall
$s=\zeta - {h}/{2}$. Recall ![]() $s\neq 0$ exactly when
$s\neq 0$ exactly when ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular. A maximal JM-regular PHVSS
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular. A maximal JM-regular PHVSS ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ for
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ for ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is given by letting
$(\mathrm {G}_0,\mathfrak {g}_1)$ is given by letting ![]() $\hat {\mathrm {G}}_0<\mathrm {G}_0$ be the
$\hat {\mathrm {G}}_0<\mathrm {G}_0$ be the ![]() $\mathrm {G}_0$-centralizer of
$\mathrm {G}_0$-centralizer of ![]() $s$ and
$s$ and ![]() $\hat {\mathfrak {g}}_1=\{x\in \mathfrak {g}_1\,|\,[s,x]=0\}$. Recall also that
$\hat {\mathfrak {g}}_1=\{x\in \mathfrak {g}_1\,|\,[s,x]=0\}$. Recall also that ![]() $s$ determines a parabolic subgroup
$s$ determines a parabolic subgroup ![]() $\mathrm {P}_s<\mathrm {G}_0$ and
$\mathrm {P}_s<\mathrm {G}_0$ and ![]() $\hat {\mathrm {G}}_0<\mathrm {P}_s$ is the Levi subgroup.
$\hat {\mathrm {G}}_0<\mathrm {P}_s$ is the Levi subgroup.
Proposition 6.15 Assume ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular and let
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular and let ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be a maximal JM-regular PHVSS. Then there are no stable
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be a maximal JM-regular PHVSS. Then there are no stable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs which are maximal. Moreover, every maximal polystable
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs which are maximal. Moreover, every maximal polystable ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair with Toledo invariant reduces to a polystable maximal
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair with Toledo invariant reduces to a polystable maximal ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$-Higgs pair.
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$-Higgs pair.
Proof. Let ![]() $(E,\varphi )$ be a polystable maximal
$(E,\varphi )$ be a polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. Since
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. Since ![]() $(E,\varphi )$ is maximal,
$(E,\varphi )$ is maximal, ![]() $\varphi (x)$ is in the open orbit
$\varphi (x)$ is in the open orbit ![]() $\Omega$ for generic
$\Omega$ for generic ![]() $x\in X.$ Let
$x\in X.$ Let ![]() $e\in \Omega$,
$e\in \Omega$, ![]() $\{f,h,e\}$ be an
$\{f,h,e\}$ be an ![]() $\mathfrak {sl}_2$-triple with
$\mathfrak {sl}_2$-triple with ![]() $h\in \mathfrak {g}_0$ and
$h\in \mathfrak {g}_0$ and ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be the associated maximal JM-regular PHVSS of
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$ be the associated maximal JM-regular PHVSS of ![]() $(\mathrm {G}_0,\mathfrak {g}_1).$ Let
$(\mathrm {G}_0,\mathfrak {g}_1).$ Let ![]() $s=\zeta - {h}/{2}$, and
$s=\zeta - {h}/{2}$, and ![]() $\mathrm {P}_s<\mathrm {G}_0$ be the associated parabolic subgroup. As in the proof of Theorem 5.3, the Higgs field defines a reduction of structure group
$\mathrm {P}_s<\mathrm {G}_0$ be the associated parabolic subgroup. As in the proof of Theorem 5.3, the Higgs field defines a reduction of structure group ![]() $\sigma$ of
$\sigma$ of ![]() $E$ to a
$E$ to a ![]() $\mathrm {P}_s$-bundle
$\mathrm {P}_s$-bundle ![]() $E_\sigma$ such that
$E_\sigma$ such that ![]() $\varphi \in H^0(E_\sigma (\mathfrak {g}_{1,s})\otimes K).$ Since
$\varphi \in H^0(E_\sigma (\mathfrak {g}_{1,s})\otimes K).$ Since ![]() $(E,\varphi )$ is maximal, we have
$(E,\varphi )$ is maximal, we have ![]() $\deg E(\sigma,s)=0$. Hence,
$\deg E(\sigma,s)=0$. Hence, ![]() $(E,\varphi )$ is not stable and there is a holomorphic reduction
$(E,\varphi )$ is not stable and there is a holomorphic reduction ![]() $\hat \sigma$ to the Levi subgroup
$\hat \sigma$ to the Levi subgroup ![]() $\hat {\mathrm {G}}_0<\mathrm {P}_s$ with
$\hat {\mathrm {G}}_0<\mathrm {P}_s$ with ![]() $\varphi \in H^0(E_{\hat \sigma }(\hat {\mathfrak {g}}_1)\otimes K.$ Thus,
$\varphi \in H^0(E_{\hat \sigma }(\hat {\mathfrak {g}}_1)\otimes K.$ Thus, ![]() $(E,\varphi )$ reduces to a polystable maximal
$(E,\varphi )$ reduces to a polystable maximal ![]() $(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$-Higgs pair.
$(\hat {\mathrm {G}}_0,\hat {\mathfrak {g}}_1)$-Higgs pair.
Let ![]() $\hat {\mathrm {C}}<\hat {\mathrm {G}}_0$ be the
$\hat {\mathrm {C}}<\hat {\mathrm {G}}_0$ be the ![]() $\hat {\mathrm {G}}_0$-stabilizer of the
$\hat {\mathrm {G}}_0$-stabilizer of the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$. Note that
$\{f,h,e\}$. Note that ![]() $\{f,h,e,s\}\subset \mathfrak {g}$ generates a subalgebra isomorphic to
$\{f,h,e,s\}\subset \mathfrak {g}$ generates a subalgebra isomorphic to ![]() $\mathfrak {gl}_2\mathbb {C}$, and
$\mathfrak {gl}_2\mathbb {C}$, and ![]() $\hat {\mathrm {C}}$ is the
$\hat {\mathrm {C}}$ is the ![]() $\mathrm {G}$-centralizer of the
$\mathrm {G}$-centralizer of the ![]() $\{f,h,e,s\}.$ As in the JM-regular case, extending the structure group of the uniformizing Higgs bundle
$\{f,h,e,s\}.$ As in the JM-regular case, extending the structure group of the uniformizing Higgs bundle ![]() $(E_\mathrm {T},e)$ to
$(E_\mathrm {T},e)$ to ![]() $\mathrm {G}_0$ defines a polystable maximal
$\mathrm {G}_0$ defines a polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair ![]() $(E_\mathrm {T}(\mathrm {G}_0),e)$. Moreover, if
$(E_\mathrm {T}(\mathrm {G}_0),e)$. Moreover, if ![]() $E_{\hat {\mathrm {C}}}$ is a polystable
$E_{\hat {\mathrm {C}}}$ is a polystable ![]() $\hat {\mathrm {C}}$-bundle, then
$\hat {\mathrm {C}}$-bundle, then ![]() $(E_T\otimes _{\mathrm {G}_0} E_{\hat {\mathrm {C}}},e)$ is a polystable maximal
$(E_T\otimes _{\mathrm {G}_0} E_{\hat {\mathrm {C}}},e)$ is a polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. Thus we have a map
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair. Thus we have a map

from the moduli space of polystable ![]() $\hat {\mathrm {C}}$-bundles on
$\hat {\mathrm {C}}$-bundles on ![]() $X$ to the moduli space of maximal
$X$ to the moduli space of maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
Theorem 6.16 If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular, then map
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular, then map ![]() $\hat \Psi _e:{\mathcal {N}}(\hat {\mathrm {C}})\to {\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ from (6.3) defines an isomorphism between the moduli space of polystable
$\hat \Psi _e:{\mathcal {N}}(\hat {\mathrm {C}})\to {\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ from (6.3) defines an isomorphism between the moduli space of polystable ![]() $\hat {\mathrm {C}}$-bundles and the moduli space of polystable maximal
$\hat {\mathrm {C}}$-bundles and the moduli space of polystable maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pairs.
Proof. Surjectivity of the map ![]() $\hat \Psi _e$ follows from Proposition 6.15 and the proof of surjectivity in the JM-regular case. For injectivity, note that two polystable
$\hat \Psi _e$ follows from Proposition 6.15 and the proof of surjectivity in the JM-regular case. For injectivity, note that two polystable ![]() $\hat {\mathrm {C}}$-bundles
$\hat {\mathrm {C}}$-bundles ![]() $E_{\hat {\mathrm {C}}}$ and
$E_{\hat {\mathrm {C}}}$ and ![]() $E'_{\hat {\mathrm {C}}}$ define the same point in
$E'_{\hat {\mathrm {C}}}$ define the same point in ![]() ${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ if there is a holomorphic isomorphism of
${\mathcal {M}}^{\max }(\mathrm {G}_0,\mathfrak {g}_1)$ if there is a holomorphic isomorphism of ![]() $\mathrm {G}_0$-bundles
$\mathrm {G}_0$-bundles
such that ![]() $\Phi ^*e=e.$ Unlike the JM-regular case, the
$\Phi ^*e=e.$ Unlike the JM-regular case, the ![]() $\mathrm {G}_0$-stabilizer of
$\mathrm {G}_0$-stabilizer of ![]() $e$ is not
$e$ is not ![]() $\hat {\mathrm {C}}$. However,
$\hat {\mathrm {C}}$. However, ![]() $E_{\hat {\mathrm {C}}}\otimes _{\mathrm {G}_0} E_\mathrm {T}\cong E_{\hat {\mathrm {C}}}'\otimes _{\mathrm {G}_0} E_\mathrm {T}$ implies that
$E_{\hat {\mathrm {C}}}\otimes _{\mathrm {G}_0} E_\mathrm {T}\cong E_{\hat {\mathrm {C}}}'\otimes _{\mathrm {G}_0} E_\mathrm {T}$ implies that ![]() $\Phi$ acts trivially on
$\Phi$ acts trivially on ![]() $E_\mathrm {T}$. In particular,
$E_\mathrm {T}$. In particular, ![]() $\Phi$ is valued in the
$\Phi$ is valued in the ![]() $\mathrm {G}_0$-centralizer of
$\mathrm {G}_0$-centralizer of ![]() $\{h,e\}$. By the uniqueness part of the Jacobson–Morozov theorem, this is the
$\{h,e\}$. By the uniqueness part of the Jacobson–Morozov theorem, this is the ![]() $\mathrm {G}_0$-centralizer of the
$\mathrm {G}_0$-centralizer of the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}$ which is
$\{f,h,e\}$ which is ![]() $\hat {\mathrm {C}}.$ Hence,
$\hat {\mathrm {C}}.$ Hence, ![]() $\Phi$ induces a holomorphic isomorphism of the
$\Phi$ induces a holomorphic isomorphism of the ![]() $\hat {\mathrm {C}}$-bundles.
$\hat {\mathrm {C}}$-bundles.
The rigidity results for variations of Hodge structure in the JM-regular case have analogues in the non-JM-regular setting. Namely, Consider the Cartan involution ![]() $\theta :\mathfrak {g}\to \mathfrak {g}$ which is
$\theta :\mathfrak {g}\to \mathfrak {g}$ which is ![]() $(-1)^j\operatorname {Id}$ on
$(-1)^j\operatorname {Id}$ on ![]() $\mathfrak {g}_j$ and choose the compact real form
$\mathfrak {g}_j$ and choose the compact real form ![]() $\tau :\mathfrak {g}\to \mathfrak {g}$ such that
$\tau :\mathfrak {g}\to \mathfrak {g}$ such that ![]() $\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ and
$\tau (\mathfrak {g}_j)=\mathfrak {g}_{-j}$ and ![]() $\tau (e)=-f$. Let
$\tau (e)=-f$. Let ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}$,
$\mathrm {G}^\mathbb {R}<\mathrm {G}$, ![]() $\mathrm {S}^\mathbb {R}<\mathrm {S}$,
$\mathrm {S}^\mathbb {R}<\mathrm {S}$, ![]() $\hat {\mathrm {C}}^\mathbb {R}<\hat {\mathrm {C}}$ be the associated real forms. The proof of the following theorem is immediate.
$\hat {\mathrm {C}}^\mathbb {R}<\hat {\mathrm {C}}$ be the associated real forms. The proof of the following theorem is immediate.
Theorem 6.17 Suppose ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular, and
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular, and ![]() $\rho :\pi _1(X)\to \mathrm {G}$ is a reductive representation. The Higgs bundle associated to
$\rho :\pi _1(X)\to \mathrm {G}$ is a reductive representation. The Higgs bundle associated to ![]() $\rho$ is a maximal Hodge bundle of type
$\rho$ is a maximal Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if, up to conjugation,
$(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if, up to conjugation, ![]() $\rho =\rho _u*\rho _{\hat {\mathrm {C}}}:\pi _1(X)\to \mathrm {G}$, where
$\rho =\rho _u*\rho _{\hat {\mathrm {C}}}:\pi _1(X)\to \mathrm {G}$, where
−
 $\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is (a lift of) the uniformizing representation of
$\rho _u:\pi _1(X)\to \mathrm {S}^\mathbb {R}<\mathrm {S}$ is (a lift of) the uniformizing representation of  $X$, and
$X$, and−
 $\rho _{\hat {\mathrm {C}}}:\pi _1(X)\to \hat {\mathrm {C}}^\mathbb {R}<\hat {\mathrm {C}}$ is any representation into the compact real form of
$\rho _{\hat {\mathrm {C}}}:\pi _1(X)\to \hat {\mathrm {C}}^\mathbb {R}<\hat {\mathrm {C}}$ is any representation into the compact real form of  $\hat {\mathrm {C}}.$
$\hat {\mathrm {C}}.$
Remark 6.18 As in the JM-regular case, such representations factor through the real form ![]() $\mathrm {G}^\mathbb {R}<\mathrm {G}.$ However, unlike the JM-regular setting, the
$\mathrm {G}^\mathbb {R}<\mathrm {G}.$ However, unlike the JM-regular setting, the ![]() $\mathrm {G}^\mathbb {R}$-centralizer of these representations is not necessarily compact since
$\mathrm {G}^\mathbb {R}$-centralizer of these representations is not necessarily compact since ![]() $\hat {\mathrm {C}}$ is not the full
$\hat {\mathrm {C}}$ is not the full ![]() $\mathrm {G}$-centralizer of the
$\mathrm {G}$-centralizer of the ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\{f,h,e\}.$
$\{f,h,e\}.$
Note that Corollary 6.8 now holds without the JM-regular assumption.
Corollary 6.19 Consider a PHVS ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$. A variation of Hodge structure
$(\mathrm {G}_0,\mathfrak {g}_1)$. A variation of Hodge structure ![]() $(\rho,f_\rho )$ associated to a maximal Hodge bundle of type
$(\rho,f_\rho )$ associated to a maximal Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if ![]() $f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. If
$f_\rho :\widetilde X\to \mathrm {G}^\mathbb {R}/\mathrm {H}_0^\mathbb {R}$ is a totally geodesic embedding which maximizes the holomorphic sectional curvature. If ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular then
$(\mathrm {G}_0,\mathfrak {g}_1)$ is not JM-regular then ![]() $f_\rho$ factors through a maximal JM-regular subdomain
$f_\rho$ factors through a maximal JM-regular subdomain
Example 6.20 Recall from Examples 2.1 and 2.19 that the PHVS ![]() $(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ with
$(\mathrm {GL}_p\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{p,q})$ with ![]() $q< p$ is not JM-regular and a maximal JM-regular PHVSS is isomorphic to
$q< p$ is not JM-regular and a maximal JM-regular PHVSS is isomorphic to ![]() $(\mathrm {GL}_{q}\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{q,q}).$ Following Example 6.11, an
$(\mathrm {GL}_{q}\mathbb {C}\times \mathrm {GL}_{p-q}\mathbb {C}\times \mathrm {SO}_q\mathbb {C},M_{q,q}).$ Following Example 6.11, an ![]() $\mathrm {SO}_{2p+q}\mathbb {C}$-Higgs bundle
$\mathrm {SO}_{2p+q}\mathbb {C}$-Higgs bundle ![]() $(E,Q,\Phi )$ is a Hodge bundle of type
$(E,Q,\Phi )$ is a Hodge bundle of type ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$ if and only if ![]() $E$ splits holomorphically as
$E$ splits holomorphically as ![]() $V\oplus W\oplus V^*$, where
$V\oplus W\oplus V^*$, where ![]() $V$ is a rank-
$V$ is a rank-![]() $p$ isotropic subbundle and the Higgs field is determined by a holomorphic map
$p$ isotropic subbundle and the Higgs field is determined by a holomorphic map ![]() $\theta :W\to V\otimes K$ as in (6.2). Such a Higgs bundle is a maximal
$\theta :W\to V\otimes K$ as in (6.2). Such a Higgs bundle is a maximal ![]() $(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair if and only if
$(\mathrm {G}_0,\mathfrak {g}_1)$-Higgs pair if and only if ![]() $V$ decomposes holomorphically as
$V$ decomposes holomorphically as ![]() $V=WK^{-1}\oplus V_{q-p}$, where
$V=WK^{-1}\oplus V_{q-p}$, where ![]() $\operatorname {rk}(V_q-p)$ is a rank-(
$\operatorname {rk}(V_q-p)$ is a rank-(![]() $q-p$) degree zero polystable vector bundle and
$q-p$) degree zero polystable vector bundle and
The resulting representation ![]() $\rho :\pi _1(X)\to \mathrm {SO}_{2p+q}\mathbb {C}$ factors through
$\rho :\pi _1(X)\to \mathrm {SO}_{2p+q}\mathbb {C}$ factors through ![]() $\mathrm {SO}(2q,q)\times \mathrm {U}_{p-q}<\mathrm {SO}(2p,q)<\mathrm {SO}_{2p+q}\mathbb {C}.$
$\mathrm {SO}(2q,q)\times \mathrm {U}_{p-q}<\mathrm {SO}(2p,q)<\mathrm {SO}_{2p+q}\mathbb {C}.$
Acknowledgements
We wish to thank Nigel Hitchin and Kang Zuo for very useful discussions. We also want to thank the Institut Henri Poincaré for support under the RIP program in 2017.