Article contents
Arc-smooth functions on closed sets
Published online by Cambridge University Press: 15 March 2019
Abstract
By an influential theorem of Boman, a function  $f$ on an open set
$f$ on an open set 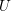 $U$ in
$U$ in 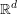 $\mathbb{R}^{d}$ is smooth (
$\mathbb{R}^{d}$ is smooth (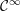 ${\mathcal{C}}^{\infty }$) if and only if it is arc-smooth, that is,
${\mathcal{C}}^{\infty }$) if and only if it is arc-smooth, that is, 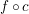 $f\,\circ \,c$ is smooth for every smooth curve
$f\,\circ \,c$ is smooth for every smooth curve 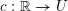 $c:\mathbb{R}\rightarrow U$. In this paper we investigate the validity of this result on closed sets. Our main focus is on sets which are the closure of their interior, so-called fat sets. We obtain an analogue of Boman’s theorem on fat closed sets with Hölder boundary and on fat closed subanalytic sets with the property that every boundary point has a basis of neighborhoods each of which intersects the interior in a connected set. If
$c:\mathbb{R}\rightarrow U$. In this paper we investigate the validity of this result on closed sets. Our main focus is on sets which are the closure of their interior, so-called fat sets. We obtain an analogue of Boman’s theorem on fat closed sets with Hölder boundary and on fat closed subanalytic sets with the property that every boundary point has a basis of neighborhoods each of which intersects the interior in a connected set. If 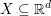 $X\subseteq \mathbb{R}^{d}$ is any such set and
$X\subseteq \mathbb{R}^{d}$ is any such set and 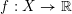 $f:X\rightarrow \mathbb{R}$ is arc-smooth, then
$f:X\rightarrow \mathbb{R}$ is arc-smooth, then 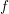 $f$ extends to a smooth function defined on
$f$ extends to a smooth function defined on 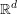 $\mathbb{R}^{d}$. We also get a version of the Bochnak–Siciak theorem on all closed fat subanalytic sets and all closed sets with Hölder boundary: if
$\mathbb{R}^{d}$. We also get a version of the Bochnak–Siciak theorem on all closed fat subanalytic sets and all closed sets with Hölder boundary: if 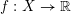 $f:X\rightarrow \mathbb{R}$ is the restriction of a smooth function on
$f:X\rightarrow \mathbb{R}$ is the restriction of a smooth function on 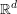 $\mathbb{R}^{d}$ which is real analytic along all real analytic curves in
$\mathbb{R}^{d}$ which is real analytic along all real analytic curves in 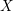 $X$, then
$X$, then 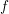 $f$ extends to a holomorphic function on a neighborhood of
$f$ extends to a holomorphic function on a neighborhood of 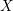 $X$ in
$X$ in 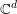 $\mathbb{C}^{d}$. Similar results hold for non-quasianalytic Denjoy–Carleman classes (of Roumieu type). We will also discuss sharpness and applications of these results.
$\mathbb{C}^{d}$. Similar results hold for non-quasianalytic Denjoy–Carleman classes (of Roumieu type). We will also discuss sharpness and applications of these results.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
Footnotes
Supported by FWF-Project P 26735-N25.
References
- 7
- Cited by

