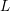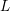Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Perkins, Rudolph Bronson
2014.
Explicit formulae for $$L$$ L -values in positive characteristic.
Mathematische Zeitschrift,
Vol. 278,
Issue. 1-2,
p.
279.
Anglès, Bruno
Ngo Dac, Tuan
and
Tavares Ribeiro, Floric
2016.
Twisted characteristic p zeta functions.
Journal of Number Theory,
Vol. 168,
Issue. ,
p.
180.
Anglès, Bruno
Pellarin, Federico
and
Tavares Ribeiro, Floric
2017.
Anderson-Stark units for 𝔽_{𝕢}[𝜃].
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 3,
p.
1603.
Anglès, Bruno
Ngo Dac, Tuan
and
Tavares Ribeiro, Floric
2017.
Stark units in positive characteristic.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 4,
p.
763.
Pellarin, F.
2017.
A note on certain representations in characteristic p and associated functions.
Journal of Number Theory,
Vol. 176,
Issue. ,
p.
420.
Anglès, Bruno
and
Tavares Ribeiro, Floric
2017.
Arithmetic of function field units.
Mathematische Annalen,
Vol. 367,
Issue. 1-2,
p.
501.
Chang, Chieh‐Yu
El‐Guindy, Ahmad
and
Papanikolas, Matthew A.
2018.
Log‐algebraic identities on Drinfeld modules and special L‐values.
Journal of the London Mathematical Society,
Vol. 97,
Issue. 2,
p.
125.
Green, Nathan
and
Papanikolas, Matthew A.
2018.
Special L-values and shtuka functions for Drinfeld modules on elliptic curves.
Research in the Mathematical Sciences,
Vol. 5,
Issue. 1,
Pellarin, Federico
and
Perkins, Rudolph B.
2018.
Vectorial Drinfeld modular forms over Tate algebras.
International Journal of Number Theory,
Vol. 14,
Issue. 06,
p.
1729.
Goss, David
Anglès, Bruno
Ngo Dac, Tuan
Pellarin, Federico
and
Tavares Ribeiro, Floric
2019.
The digit principle and derivatives of certain L-series.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
81.
Maurischat, Andreas
and
Perkins, Rudolph
2019.
An Integral Digit Derivative Basis for Carlitz Prime Power Torsion Extensions.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
131.
Gezmiş, Oğuz
and
Papanikolas, Matthew A.
2019.
The de Rham isomorphism for Drinfeld modules over Tate algebras.
Journal of Algebra,
Vol. 525,
Issue. ,
p.
454.
Gezmiş, Oğuz
2019.
Taelman L-values for Drinfeld modules over Tate algebras.
Research in the Mathematical Sciences,
Vol. 6,
Issue. 1,
Anglès, Bruno
Ngo Dac, Tuan
and
Tavares Ribeiro, Floric
2020.
On special L-values of t-modules.
Advances in Mathematics,
Vol. 372,
Issue. ,
p.
107313.
Anglès, Bruno
Dac, Tuan Ngo
and
Ribeiro, Floric Tavares
2020.
Recent Developments in the Theory of Anderson Modules.
Acta Mathematica Vietnamica,
Vol. 45,
Issue. 1,
p.
199.
Tavares Ribeiro, Floric
2021.
Arithmetic and Geometry over Local Fields.
Vol. 2275,
Issue. ,
p.
281.
Lara Rodríguez, José Alejandro
and
Thakur, Dinesh S.
2021.
Zeta-like Multizeta Values for higher genus curves.
Journal de Théorie des Nombres de Bordeaux,
Vol. 33,
Issue. 2,
p.
553.
Demeslay, Florent
2022.
A class formula for L-series in positive characteristic.
Annales de l'Institut Fourier,
Vol. 72,
Issue. 3,
p.
1149.
Gezmiş, O
and
Pellarin, F
2022.
Trivial multiple zeta values in Tate algebras.
International Mathematics Research Notices,
Vol. 2022,
Issue. 18,
p.
14319.
Pellarin, F.
and
Perkins, R.
2022.
On twisted A-harmonic sums and Carlitz finite zeta values.
Journal of Number Theory,
Vol. 232,
Issue. ,
p.
355.