Article contents
Around 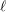 $\ell$ -independence
$\ell$ -independence
Published online by Cambridge University Press: 17 October 2017
Abstract
In this article we study various forms of 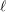 $\ell$ -independence (including the case
$\ell$ -independence (including the case 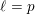 $\ell =p$ ) for the cohomology and fundamental groups of varieties over finite fields and equicharacteristic local fields. Our first result is a strong form of
$\ell =p$ ) for the cohomology and fundamental groups of varieties over finite fields and equicharacteristic local fields. Our first result is a strong form of 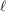 $\ell$ -independence for the unipotent fundamental group of smooth and projective varieties over finite fields. By then proving a certain ‘spreading out’ result we are able to deduce a much weaker form of
$\ell$ -independence for the unipotent fundamental group of smooth and projective varieties over finite fields. By then proving a certain ‘spreading out’ result we are able to deduce a much weaker form of 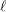 $\ell$ -independence for unipotent fundamental groups over equicharacteristic local fields, at least in the semistable case. In a similar vein, we can also use this to deduce
$\ell$ -independence for unipotent fundamental groups over equicharacteristic local fields, at least in the semistable case. In a similar vein, we can also use this to deduce 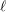 $\ell$ -independence results for the cohomology of smooth and proper varieties over equicharacteristic local fields from the well-known results on
$\ell$ -independence results for the cohomology of smooth and proper varieties over equicharacteristic local fields from the well-known results on 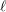 $\ell$ -independence for smooth and proper varieties over finite fields. As another consequence of this ‘spreading out’ result we are able to deduce the existence of a Clemens–Schmid exact sequence for formal semistable families. Finally, by deforming to characteristic
$\ell$ -independence for smooth and proper varieties over finite fields. As another consequence of this ‘spreading out’ result we are able to deduce the existence of a Clemens–Schmid exact sequence for formal semistable families. Finally, by deforming to characteristic 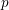 $p$ , we show a similar weak version of
$p$ , we show a similar weak version of 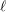 $\ell$ -independence for the unipotent fundamental group of a semistable curve in mixed characteristic.
$\ell$ -independence for the unipotent fundamental group of a semistable curve in mixed characteristic.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
A correction has been issued for this article:
- 3
- Cited by
Linked content
Please note a has been issued for this article.

