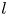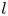1. Introduction
In this paper, we prove new automorphy lifting theorems for Galois representations of unitary type. Thus, we are considering representations ![]() $\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$, where
$\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$, where ![]() $G_F$ is the absolute Galois group of a CM field
$G_F$ is the absolute Galois group of a CM field ![]() $F$ and
$F$ and ![]() $\rho$ is conjugate self-dual, i.e. there is an isomorphism
$\rho$ is conjugate self-dual, i.e. there is an isomorphism ![]() $\rho ^{c} \cong \rho ^{\vee } \otimes \epsilon ^{1-n},$ where
$\rho ^{c} \cong \rho ^{\vee } \otimes \epsilon ^{1-n},$ where ![]() $c \in \operatorname {Aut}(F)$ is complex conjugation. We say in this paper that such a representation is automorphic if there exists a regular algebraic, conjugate self-dual, cuspidal (RACSDC) automorphic representation
$c \in \operatorname {Aut}(F)$ is complex conjugation. We say in this paper that such a representation is automorphic if there exists a regular algebraic, conjugate self-dual, cuspidal (RACSDC) automorphic representation ![]() $\pi$ which is matched with
$\pi$ which is matched with ![]() $\rho$ under the Langlands correspondence. (See § 1.1 below for a more precise formulation.)
$\rho$ under the Langlands correspondence. (See § 1.1 below for a more precise formulation.)
We revisit the context of the paper [Reference ThorneTho15], proving theorems valid in the case that ![]() $\bar {\rho }$ is absolutely reducible, but still satisfies a certain non-degeneracy condition (we say that
$\bar {\rho }$ is absolutely reducible, but still satisfies a certain non-degeneracy condition (we say that ![]() $\bar {\rho }$ is ‘Schur’). The first theorems of this type were proved in the paper [Reference ThorneTho15], under the assumption that
$\bar {\rho }$ is ‘Schur’). The first theorems of this type were proved in the paper [Reference ThorneTho15], under the assumption that ![]() $\bar {\rho }$ has only two irreducible constituents. Our main motivation here is to remove this restriction. Our results are applied to the problem of symmetric power functoriality in [Reference Newton and ThorneNT19], where they are combined with level-raising theorems to establish automorphy of symmetric powers for certain level
$\bar {\rho }$ has only two irreducible constituents. Our main motivation here is to remove this restriction. Our results are applied to the problem of symmetric power functoriality in [Reference Newton and ThorneNT19], where they are combined with level-raising theorems to establish automorphy of symmetric powers for certain level ![]() $1$ Hecke eigenforms congruent to a theta series.
$1$ Hecke eigenforms congruent to a theta series.
We are also able to weaken some other hypotheses in [Reference ThorneTho15], leading to the following result, which is the main theorem of this paper.
Theorem 1.1 (Theorem 6.1) Let ![]() $F$ be an imaginary CM number field with maximal totally real subfield
$F$ be an imaginary CM number field with maximal totally real subfield ![]() $F^{+}$ and let
$F^{+}$ and let ![]() $n \geq 2$ be an integer. Let
$n \geq 2$ be an integer. Let ![]() $l$ be a prime and suppose that
$l$ be a prime and suppose that ![]() $\rho : G_F \rightarrow \mathrm {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is a continuous semisimple representation satisfying the following hypotheses.
$\rho : G_F \rightarrow \mathrm {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is a continuous semisimple representation satisfying the following hypotheses.
(i)
 $\rho ^{c} \cong \rho ^{\vee } \epsilon ^{1-n}$.
$\rho ^{c} \cong \rho ^{\vee } \epsilon ^{1-n}$.(ii)
 $\rho$ is ramified at only finitely many places.
$\rho$ is ramified at only finitely many places.(iii)
 $\rho$ is ordinary of weight
$\rho$ is ordinary of weight  $\lambda$ for some
$\lambda$ for some  $\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(F, {{\bar {{{\mathbb {Q}}}}_l}})}$.
$\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(F, {{\bar {{{\mathbb {Q}}}}_l}})}$.(iv) There is an isomorphism
 $\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each
$\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each  $\bar {\rho }_i$ is absolutely irreducible and satisfies
$\bar {\rho }_i$ is absolutely irreducible and satisfies  $\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$, and
$\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$, and  $\bar {\rho }_i \not \cong \bar {\rho }_j$ if
$\bar {\rho }_i \not \cong \bar {\rho }_j$ if  $i \neq j$.
$i \neq j$.(v) There exists a finite place
 ${{\widetilde {v}}}_0$ of
${{\widetilde {v}}}_0$ of  $F$, prime to
$F$, prime to  $l$, such that
$l$, such that  $\rho |_{G_{F_{{{\widetilde {v}}}_0}}}^{\text {ss}} \cong \oplus _{i=1}^{n} \psi \epsilon ^{n-i}$ for some unramified character
$\rho |_{G_{F_{{{\widetilde {v}}}_0}}}^{\text {ss}} \cong \oplus _{i=1}^{n} \psi \epsilon ^{n-i}$ for some unramified character  $\psi : G_{F_{{{\widetilde {v}}}_0}} \rightarrow \bar {{{\mathbb {Q}}}}_l^{\times }$.
$\psi : G_{F_{{{\widetilde {v}}}_0}} \rightarrow \bar {{{\mathbb {Q}}}}_l^{\times }$.(vi) There exist a RACSDC representation
 $\pi$ of
$\pi$ of  $\mathrm {GL}_n({{\mathbb {A}}}_F)$ and
$\mathrm {GL}_n({{\mathbb {A}}}_F)$ and  $\iota : {{\bar {{{\mathbb {Q}}}}_l}} \to {{\mathbb {C}}}$ such that:
$\iota : {{\bar {{{\mathbb {Q}}}}_l}} \to {{\mathbb {C}}}$ such that:
(a)
 $\pi$ is
$\pi$ is  $\iota$-ordinary;
$\iota$-ordinary;(b)
 $\overline {r_{ \iota }(\pi )}^{\text {ss}} \cong \bar {\rho }^{\text {ss}}$;
$\overline {r_{ \iota }(\pi )}^{\text {ss}} \cong \bar {\rho }^{\text {ss}}$;(c)
 $\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation.
$\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation.
(vii)
 $F(\zeta _l)$ is not contained in
$F(\zeta _l)$ is not contained in  $\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and
$\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and  $F$ is not contained in
$F$ is not contained in  $F^{+}(\zeta _l)$. For each
$F^{+}(\zeta _l)$. For each  $1 \leq i, j \leq {d}$,
$1 \leq i, j \leq {d}$,  $\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and
$\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and  $\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if
$\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if  $i \neq j$. Moreover,
$i \neq j$. Moreover,  $\bar {\rho }^{\text {ss}}$ is primitive (i.e. not induced from any proper subgroup of
$\bar {\rho }^{\text {ss}}$ is primitive (i.e. not induced from any proper subgroup of  $G_F$) and
$G_F$) and  $\bar {\rho }^{\text {ss}}(G_{F})$ has no quotient of order
$\bar {\rho }^{\text {ss}}(G_{F})$ has no quotient of order  $l$.
$l$.(viii)
 $l > 3$ and
$l > 3$ and  $l \nmid n$.
$l \nmid n$.
Then ![]() $\rho$ is automorphic: there exists an
$\rho$ is automorphic: there exists an ![]() $\iota$-ordinary RACSDC automorphic representation
$\iota$-ordinary RACSDC automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$ such that
$\operatorname {GL}_n({{\mathbb {A}}}_F)$ such that ![]() $r_\iota (\Pi ) \cong \rho$.
$r_\iota (\Pi ) \cong \rho$.
Comparing this with [Reference ThorneTho15, Theorem 7.1], we see that we now allow an arbitrary number of irreducible constituents, while also removing the requirement that the individual constituents are adequate (in the sense of [Reference ThorneTho12]) and potentially automorphic. This assumption of potential automorphy was used in [Reference ThorneTho15], together with the Khare–Wintenberger method, to get a handle on the quotient of the universal deformation ring of ![]() $\bar {\rho }$ corresponding to reducible deformations. This made generalizing [Reference ThorneTho15, Theorem 7.1] to the case where more than two irreducible constituents are allowed seem a formidable task: one would want to know that any given direct sum of irreducible constituents of
$\bar {\rho }$ corresponding to reducible deformations. This made generalizing [Reference ThorneTho15, Theorem 7.1] to the case where more than two irreducible constituents are allowed seem a formidable task: one would want to know that any given direct sum of irreducible constituents of ![]() $\bar {\rho }$ was potentially automorphic, and then perhaps use induction on the number of constituents to control the reducible locus.
$\bar {\rho }$ was potentially automorphic, and then perhaps use induction on the number of constituents to control the reducible locus.
The first main innovation in this paper that allows us to bypass this is the observation that by fully exploiting the ‘connectedness dimension’ argument to prove that ![]() $R = {{\mathbb {T}}}$ (which goes back to [Reference Skinner and WilesSW99] and appears in this paper in the proof of Theorem 5.1), one only needs to control the size of the reducible locus in quotients of the universal deformation ring that are known a priori to be finite over the Iwasawa algebra
$R = {{\mathbb {T}}}$ (which goes back to [Reference Skinner and WilesSW99] and appears in this paper in the proof of Theorem 5.1), one only needs to control the size of the reducible locus in quotients of the universal deformation ring that are known a priori to be finite over the Iwasawa algebra ![]() $\Lambda$. This can be done easily by hand using the ‘locally Steinberg’ condition (as in § 3.3).
$\Lambda$. This can be done easily by hand using the ‘locally Steinberg’ condition (as in § 3.3).
The second main innovation is a finer study of the universal deformation ring ![]() $R^{\text {univ}}$ of a (reducible but) Schur residual representation. We show that if the residual representation has
$R^{\text {univ}}$ of a (reducible but) Schur residual representation. We show that if the residual representation has ![]() ${d}$ absolutely irreducible constituents, then there is an action of a group
${d}$ absolutely irreducible constituents, then there is an action of a group ![]() $\mu _2^{d}$ on
$\mu _2^{d}$ on ![]() $R^{\text {univ}}$ and identify the invariant subring
$R^{\text {univ}}$ and identify the invariant subring ![]() $(R^{\text {univ}})^{\mu _2^{d}}$ with the subring topologically generated by the traces of Frobenius elements (which can also be characterized as the image
$(R^{\text {univ}})^{\mu _2^{d}}$ with the subring topologically generated by the traces of Frobenius elements (which can also be characterized as the image ![]() $P$ of the canonical map to
$P$ of the canonical map to ![]() $R^{\text {univ}}$ from the universal pseudodeformation ring). This leads to a neat proof that the map
$R^{\text {univ}}$ from the universal pseudodeformation ring). This leads to a neat proof that the map ![]() $P \to R^{\text {univ}}$ is étale at prime ideals corresponding to irreducible deformations of
$P \to R^{\text {univ}}$ is étale at prime ideals corresponding to irreducible deformations of ![]() $\bar {\rho }$.
$\bar {\rho }$.
We now describe the organization of this paper. Since it is naturally a continuation of [Reference ThorneTho15], we maintain the same notation and use several results and constructions from that paper as black boxes. We begin in §§ 2 and 3 by extending several results from [Reference ThorneTho15] about the relation between deformations and pseudodeformations to the case where ![]() $\bar {\rho }$ is permitted to have more than two irreducible constituents. We also make the above-mentioned study of the dimension of the locus of reducible deformations.
$\bar {\rho }$ is permitted to have more than two irreducible constituents. We also make the above-mentioned study of the dimension of the locus of reducible deformations.
In § 4 we recall from [Reference ThorneTho15] the definition of the unitary group of automorphic forms and Hecke algebras that we use, and state the ![]() ${{\mathbb {T}}}_{{\mathfrak q}} = R_{{\mathfrak p}}$ type result proved in that paper (here
${{\mathbb {T}}}_{{\mathfrak q}} = R_{{\mathfrak p}}$ type result proved in that paper (here ![]() ${{\mathfrak p}}$ denotes a dimension 1, characteristic
${{\mathfrak p}}$ denotes a dimension 1, characteristic ![]() $l$ prime of
$l$ prime of ![]() $R$ with good properties, in particular that the associated representation to
$R$ with good properties, in particular that the associated representation to ![]() $\operatorname {GL}_n(\operatorname {Frac} R / {{\mathfrak p}})$ is absolutely irreducible). In § 5 we carry out the main argument, based on the notion of connectedness dimension, which is described above. Finally, in § 6 we deduce Theorem 1.1, following a simplified version of the argument in [Reference ThorneTho15, § 7] that no longer makes reference to potential automorphy.
$\operatorname {GL}_n(\operatorname {Frac} R / {{\mathfrak p}})$ is absolutely irreducible). In § 5 we carry out the main argument, based on the notion of connectedness dimension, which is described above. Finally, in § 6 we deduce Theorem 1.1, following a simplified version of the argument in [Reference ThorneTho15, § 7] that no longer makes reference to potential automorphy.
1.1 Notation
We use the same notation and normalizations for Galois groups, class field theory, and local Langlands correspondences as in [Reference ThorneTho15, Notation]. Rather than repeat this verbatim here we invite the reader to refer to that paper for more details. We do note the convention that if ![]() $R$ is a ring and
$R$ is a ring and ![]() $P$ is a prime ideal of
$P$ is a prime ideal of ![]() $R$, then
$R$, then ![]() $R_{(P)}$ denotes the localization of
$R_{(P)}$ denotes the localization of ![]() $R$ at
$R$ at ![]() $P$ and
$P$ and ![]() $R_P$ denotes the completion of the localization.
$R_P$ denotes the completion of the localization.
We recall that ![]() ${{\mathbb {Z}}}_n^{+} \subset {{\mathbb {Z}}}^{n}$ denotes the set of tuples
${{\mathbb {Z}}}_n^{+} \subset {{\mathbb {Z}}}^{n}$ denotes the set of tuples ![]() $\lambda = (\lambda _1, \ldots , \lambda _n)$ of integers such that
$\lambda = (\lambda _1, \ldots , \lambda _n)$ of integers such that ![]() $\lambda _1 \geq \cdots \geq \lambda _n$. It is identified in a standard way with the set of highest weights of
$\lambda _1 \geq \cdots \geq \lambda _n$. It is identified in a standard way with the set of highest weights of ![]() $\operatorname {GL}_n$. If
$\operatorname {GL}_n$. If ![]() $F$ is a number field and
$F$ is a number field and ![]() $\lambda = (\lambda _\tau ) \in ({{\mathbb {Z}}}_n^{+})^{\operatorname {Hom}(F, {{\mathbb {C}}})}$, then we write
$\lambda = (\lambda _\tau ) \in ({{\mathbb {Z}}}_n^{+})^{\operatorname {Hom}(F, {{\mathbb {C}}})}$, then we write ![]() $\Xi _\lambda$ for the algebraic representation of
$\Xi _\lambda$ for the algebraic representation of ![]() $\operatorname {GL}_n(F \otimes _{{\mathbb {Q}}} {{\mathbb {C}}}) = \prod _{\tau \in \operatorname {Hom}(F, {{\mathbb {C}}})} \operatorname {GL}_n({{\mathbb {C}}})$ of highest weight
$\operatorname {GL}_n(F \otimes _{{\mathbb {Q}}} {{\mathbb {C}}}) = \prod _{\tau \in \operatorname {Hom}(F, {{\mathbb {C}}})} \operatorname {GL}_n({{\mathbb {C}}})$ of highest weight ![]() $\lambda$. If
$\lambda$. If ![]() $\pi$ is an automorphic representation of
$\pi$ is an automorphic representation of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$, we say that
$\operatorname {GL}_n({{\mathbb {A}}}_F)$, we say that ![]() $\pi$ is regular algebraic of weight
$\pi$ is regular algebraic of weight ![]() $\lambda$ if
$\lambda$ if ![]() $\pi _\infty$ has the same infinitesimal character as the dual
$\pi _\infty$ has the same infinitesimal character as the dual ![]() $\Xi _\lambda ^{\vee }$.
$\Xi _\lambda ^{\vee }$.
Let ![]() $F$ be a CM field (i.e. a totally imaginary quadratic extension of a totally real field
$F$ be a CM field (i.e. a totally imaginary quadratic extension of a totally real field ![]() $F^{+}$). We always write
$F^{+}$). We always write ![]() $c \in \operatorname {Aut}(F)$ for complex conjugation. We say that an automorphic representation
$c \in \operatorname {Aut}(F)$ for complex conjugation. We say that an automorphic representation ![]() $\pi$ of
$\pi$ of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$ is conjugate self-dual if there is an isomorphism
$\operatorname {GL}_n({{\mathbb {A}}}_F)$ is conjugate self-dual if there is an isomorphism ![]() $\pi ^{c} \cong \pi ^{\vee }$. If
$\pi ^{c} \cong \pi ^{\vee }$. If ![]() $\pi$ is a RACSDC automorphic representation of
$\pi$ is a RACSDC automorphic representation of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$ and
$\operatorname {GL}_n({{\mathbb {A}}}_F)$ and ![]() $\iota : \bar {{{\mathbb {Q}}}}_l \to {{\mathbb {C}}}$ is an isomorphism (for some prime
$\iota : \bar {{{\mathbb {Q}}}}_l \to {{\mathbb {C}}}$ is an isomorphism (for some prime ![]() $l$), then there exists an associated Galois representation
$l$), then there exists an associated Galois representation ![]() $r_\iota (\pi ) : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$, characterized up to isomorphism by the requirement of compatibility with the local Langlands correspondence at each finite place of
$r_\iota (\pi ) : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$, characterized up to isomorphism by the requirement of compatibility with the local Langlands correspondence at each finite place of ![]() $F$; see [Reference ThorneTho15, Theorem 2.2] for a reference. We say that a representation
$F$; see [Reference ThorneTho15, Theorem 2.2] for a reference. We say that a representation ![]() $\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is automorphic if there exists a choice of
$\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is automorphic if there exists a choice of ![]() $\iota$ and RACSDC
$\iota$ and RACSDC ![]() $\pi$ such that
$\pi$ such that ![]() $\rho \cong r_\iota (\pi )$.
$\rho \cong r_\iota (\pi )$.
One can define what it means for a RACSDC automorphic representation ![]() $\pi$ to be
$\pi$ to be ![]() $\iota$-ordinary (see [Reference ThorneTho15, Lemma 2.3]; it means that the eigenvalues of certain Hecke operators, a priori
$\iota$-ordinary (see [Reference ThorneTho15, Lemma 2.3]; it means that the eigenvalues of certain Hecke operators, a priori ![]() $l$-adic integers, are in fact
$l$-adic integers, are in fact ![]() $l$-adic units). If
$l$-adic units). If ![]() $\mu \in ({{\mathbb {Z}}}^{n}_+)^{\operatorname {Hom}(F, \bar {{{\mathbb {Q}}}}_l)}$, we say (following [Reference ThorneTho15, Definition 2.5]) that a representation
$\mu \in ({{\mathbb {Z}}}^{n}_+)^{\operatorname {Hom}(F, \bar {{{\mathbb {Q}}}}_l)}$, we say (following [Reference ThorneTho15, Definition 2.5]) that a representation ![]() $\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is ordinary of weight
$\rho : G_F \to \operatorname {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is ordinary of weight ![]() $\mu$ if for each place
$\mu$ if for each place ![]() $v | l$ of
$v | l$ of ![]() $F$, there is an isomorphism
$F$, there is an isomorphism
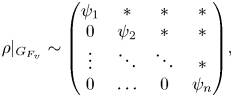 \[ \rho|_{G_{F_v}} \sim \begin{pmatrix} \psi_1 & \ast & \ast & \ast \\ 0 & \psi_2 & \ast & \ast \\ \vdots & \ddots & \ddots & \ast \\ 0 & \ldots & 0 & \psi_n \end{pmatrix}\!, \]
\[ \rho|_{G_{F_v}} \sim \begin{pmatrix} \psi_1 & \ast & \ast & \ast \\ 0 & \psi_2 & \ast & \ast \\ \vdots & \ddots & \ddots & \ast \\ 0 & \ldots & 0 & \psi_n \end{pmatrix}\!, \]
where ![]() $\psi _i : G_{F_v} \rightarrow {{\bar {{{\mathbb {Q}}}}_l}}^{\times }$ is a continuous character satisfying the identity
$\psi _i : G_{F_v} \rightarrow {{\bar {{{\mathbb {Q}}}}_l}}^{\times }$ is a continuous character satisfying the identity
for all ![]() $\sigma$ in a suitable open subgroup of
$\sigma$ in a suitable open subgroup of ![]() $I_{F_v}$. An important result [Reference ThorneTho15, Theorem 2.4] is that if
$I_{F_v}$. An important result [Reference ThorneTho15, Theorem 2.4] is that if ![]() $\pi$ is RACSDC of weight
$\pi$ is RACSDC of weight ![]() $\lambda$ and
$\lambda$ and ![]() $\iota$-ordinary, then
$\iota$-ordinary, then ![]() $r_\iota (\pi )$ is ordinary of weight
$r_\iota (\pi )$ is ordinary of weight ![]() $\iota \lambda$, where by definition
$\iota \lambda$, where by definition ![]() $(\iota \lambda )_\tau = \lambda _{\iota \tau }$.
$(\iota \lambda )_\tau = \lambda _{\iota \tau }$.
2. Determinants
We first give the definition of a determinant from [Reference ChenevierChe14]. We recall that if ![]() $A$ is a ring and
$A$ is a ring and ![]() $M, N$ are
$M, N$ are ![]() $A$-modules, then an
$A$-modules, then an ![]() $A$-polynomial law
$A$-polynomial law ![]() $F : M \to N$ is a natural transformation
$F : M \to N$ is a natural transformation ![]() $F : h_M \to h_N$, where
$F : h_M \to h_N$, where ![]() $h_M : A$-alg
$h_M : A$-alg ![]() $\to$ Sets is the functor
$\to$ Sets is the functor ![]() $h_M(B) = M \otimes _A B$. The
$h_M(B) = M \otimes _A B$. The ![]() $A$-polynomial law
$A$-polynomial law ![]() $F$ is called homogeneous of degree
$F$ is called homogeneous of degree ![]() $n \geq 1$ if for all
$n \geq 1$ if for all ![]() $b \in B$,
$b \in B$, ![]() $x \in M \otimes _A B$, we have
$x \in M \otimes _A B$, we have ![]() $F_B(bx) = b^{n} F_B(x)$.
$F_B(bx) = b^{n} F_B(x)$.
Definition 2.1 Let ![]() $A$ be a ring and let
$A$ be a ring and let ![]() $R$ be an
$R$ be an ![]() $A$-algebra. An
$A$-algebra. An ![]() $A$-valued determinant of
$A$-valued determinant of ![]() $R$ of dimension
$R$ of dimension ![]() $n \geq 1$ is a multiplicative
$n \geq 1$ is a multiplicative ![]() $A$-polynomial law
$A$-polynomial law ![]() $D : R \to A$ which is homogeneous of degree
$D : R \to A$ which is homogeneous of degree ![]() $n$.
$n$.
If ![]() $D$ is a determinant, then there are associated polynomial laws
$D$ is a determinant, then there are associated polynomial laws ![]() $\Lambda _i : R \to A$,
$\Lambda _i : R \to A$, ![]() $i = 0, \ldots , n$, given by the formulae
$i = 0, \ldots , n$, given by the formulae
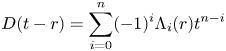 \[ D(t - r) = \sum_{i=0}^{n} (-1)^{i} \Lambda_i(r) t^{n-i} \]
\[ D(t - r) = \sum_{i=0}^{n} (-1)^{i} \Lambda_i(r) t^{n-i} \]
for all ![]() $r \in R \otimes _A B$. We define the characteristic polynomial
$r \in R \otimes _A B$. We define the characteristic polynomial ![]() $A$-polynomial law
$A$-polynomial law ![]() $\chi : R \to R$ by the formula
$\chi : R \to R$ by the formula ![]() $\chi (r) = \sum _{i=0}^{n} (-1)^{i} \Lambda _i(r) r^{n-i}$ (
$\chi (r) = \sum _{i=0}^{n} (-1)^{i} \Lambda _i(r) r^{n-i}$ (![]() $r \in R \otimes _A B$). We write
$r \in R \otimes _A B$). We write ![]() $\operatorname {CH}(D)$ for the two-sided ideal of
$\operatorname {CH}(D)$ for the two-sided ideal of ![]() $R$ generated by the coefficients of
$R$ generated by the coefficients of ![]() $\chi (r_1 t_1 + \cdots + r_m t_m) \in R[t_1, \ldots , t_m]$ for all
$\chi (r_1 t_1 + \cdots + r_m t_m) \in R[t_1, \ldots , t_m]$ for all ![]() $m \ge 1$ and
$m \ge 1$ and ![]() $r_1,\ldots ,r_m \in R$. We have
$r_1,\ldots ,r_m \in R$. We have ![]() $\operatorname {CH}(D) \subseteq \ker (D)$ [Reference ChenevierChe14, Lemma 1.21]. The determinant
$\operatorname {CH}(D) \subseteq \ker (D)$ [Reference ChenevierChe14, Lemma 1.21]. The determinant ![]() $D$ is said to be Cayley–Hamilton if
$D$ is said to be Cayley–Hamilton if ![]() $\operatorname {CH}(D) = 0$, equivalently if
$\operatorname {CH}(D) = 0$, equivalently if ![]() $\chi = 0$ (i.e.
$\chi = 0$ (i.e. ![]() $\chi$ is the zero
$\chi$ is the zero ![]() $A$-polynomial law).
$A$-polynomial law).
We next recall the definition of a generalized matrix algebra [Reference Bellaïche and ChenevierBC09, Definition 1.3.1].
Definition 2.2 Let ![]() $A$ be a ring and let
$A$ be a ring and let ![]() $R$ be an
$R$ be an ![]() $A$-algebra. We say that
$A$-algebra. We say that ![]() $R$ is a generalized matrix algebra of type
$R$ is a generalized matrix algebra of type ![]() $(n_1,\ldots ,n_{d})$ if it is equipped with the following data:
$(n_1,\ldots ,n_{d})$ if it is equipped with the following data:
(i) a family of orthogonal idempotents
 $e_1,\ldots , e_{d}$ with
$e_1,\ldots , e_{d}$ with  $e_1+\cdots +e_{d} = 1$; and
$e_1+\cdots +e_{d} = 1$; and(ii) for each
 $1\le i \le {d}$, an
$1\le i \le {d}$, an  $A$-algebra isomorphism
$A$-algebra isomorphism  $\psi _i \colon e_i R e_i \rightarrow M_{n_i}(A)$
$\psi _i \colon e_i R e_i \rightarrow M_{n_i}(A)$
such that the trace map ![]() $T \colon R \rightarrow A$ defined by
$T \colon R \rightarrow A$ defined by ![]() $T(x) = \sum _{i=1}^{d} \operatorname {tr}\psi _i(e_ix e_i)$ satisfies
$T(x) = \sum _{i=1}^{d} \operatorname {tr}\psi _i(e_ix e_i)$ satisfies ![]() $T(xy) = T(yx)$ for all
$T(xy) = T(yx)$ for all ![]() $x,y \in R$. We refer to the data
$x,y \in R$. We refer to the data ![]() $\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$ as the data of idempotents of
$\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$ as the data of idempotents of ![]() $R$.
$R$.
Construction 2.3 We recall the structure of generalized matrix algebras from [Reference Bellaïche and ChenevierBC09, § 1.3.2]. Let ![]() $R$ be a generalized matrix algebra of type
$R$ be a generalized matrix algebra of type ![]() $(n_1,\ldots ,n_{d})$ with data of idempotents
$(n_1,\ldots ,n_{d})$ with data of idempotents ![]() $\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$. For each
$\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$. For each ![]() $1\le i \le {d}$, let
$1\le i \le {d}$, let ![]() $E_i \in e_i R e_i$ be the unique element such that
$E_i \in e_i R e_i$ be the unique element such that ![]() $\psi _i(E_i)$ is the element of
$\psi _i(E_i)$ is the element of ![]() $M_{n_i}(A)$ whose row
$M_{n_i}(A)$ whose row ![]() $1$, column
$1$, column ![]() $1$ entry is
$1$ entry is ![]() $1$ and all other entries are
$1$ and all other entries are ![]() $0$. We set
$0$. We set ![]() $\mathcal {A}_{i,j} = E_i R E_j$ for each
$\mathcal {A}_{i,j} = E_i R E_j$ for each ![]() $1\le i,j\le {d}$. Note that
$1\le i,j\le {d}$. Note that ![]() $\mathcal {A}_{i,j}\mathcal {A}_{j,k} \subseteq \mathcal {A}_{i,k}$ for each
$\mathcal {A}_{i,j}\mathcal {A}_{j,k} \subseteq \mathcal {A}_{i,k}$ for each ![]() $1\le i,j,k\le {d}$, and the trace map
$1\le i,j,k\le {d}$, and the trace map ![]() $T$ induces an isomorphism
$T$ induces an isomorphism ![]() $\mathcal {A}_{i,i} \cong A$ for each
$\mathcal {A}_{i,i} \cong A$ for each ![]() $1\le i \le {d}$. Via this isomorphism, we will tacitly view
$1\le i \le {d}$. Via this isomorphism, we will tacitly view ![]() $\mathcal {A}_{i,j}\mathcal {A}_{j,i}$ as an ideal in
$\mathcal {A}_{i,j}\mathcal {A}_{j,i}$ as an ideal in ![]() $A$ for each
$A$ for each ![]() $1\le i,j\le {d}$. With this multiplication, there is an isomorphism of
$1\le i,j\le {d}$. With this multiplication, there is an isomorphism of ![]() $A$-algebras
$A$-algebras
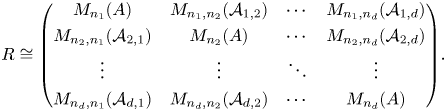 \begin{equation} R \cong \begin{pmatrix} M_{n_1}(A) & M_{n_1,n_2}(\mathcal{A}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{A}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{A}_{2,1}) & M_{n_2}(A) & \cdots & M_{n_2,n_{{d}}}(\mathcal{A}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{A}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{A}_{{{d}},2}) & \cdots & M_{n_{{d}}}(A) \end{pmatrix}\!. \end{equation}
\begin{equation} R \cong \begin{pmatrix} M_{n_1}(A) & M_{n_1,n_2}(\mathcal{A}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{A}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{A}_{2,1}) & M_{n_2}(A) & \cdots & M_{n_2,n_{{d}}}(\mathcal{A}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{A}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{A}_{{{d}},2}) & \cdots & M_{n_{{d}}}(A) \end{pmatrix}\!. \end{equation}The following result of Chenevier allows us to use the above structure when studying determinants.
Theorem 2.4 Let ![]() $A$ be a Henselian local ring with residue field
$A$ be a Henselian local ring with residue field ![]() $k$, let
$k$, let ![]() $R$ be an
$R$ be an ![]() $A$-algebra, and let
$A$-algebra, and let ![]() $D \colon R \rightarrow A$ be a Cayley–Hamilton determinant. Suppose that there exist surjective and pairwise non-conjugate
$D \colon R \rightarrow A$ be a Cayley–Hamilton determinant. Suppose that there exist surjective and pairwise non-conjugate ![]() $k$-algebra homomorphisms
$k$-algebra homomorphisms ![]() $\bar {\rho }_i : R \to M_{n_i}(k)$ such that
$\bar {\rho }_i : R \to M_{n_i}(k)$ such that ![]() $\bar {D} = \prod _{i=1}^{d} (\det \circ \bar {\rho }_i)$, where
$\bar {D} = \prod _{i=1}^{d} (\det \circ \bar {\rho }_i)$, where ![]() $\bar {D} = D \otimes _R k$.
$\bar {D} = D \otimes _R k$.
Then there is a datum of idempotents ![]() $\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$ for which
$\mathcal {E} = \{e_i,\psi _i, 1\le i \le {d}\}$ for which ![]() $R$ is a generalized matrix algebra and such that
$R$ is a generalized matrix algebra and such that ![]() $\psi _i \otimes _A k = \bar {\rho }_i|_{e_i R e_i}$. Any two such data are conjugate by an element of
$\psi _i \otimes _A k = \bar {\rho }_i|_{e_i R e_i}$. Any two such data are conjugate by an element of ![]() $R^{\times }$.
$R^{\times }$.
We note that the assumptions of Theorem 2.4 say that ![]() $D$ is residually split and multiplicity-free, in the sense of [Reference ChenevierChe14, Definition 2.19].
$D$ is residually split and multiplicity-free, in the sense of [Reference ChenevierChe14, Definition 2.19].
Proof. The existence of such a datum of idempotents ![]() $\mathcal {E} = \{e_i,\psi _i,1\le i \le {d}\}$ is contained in [Reference ChenevierChe14, Theorem 2.22] and its proof. The statement that two such data are conjugate is exactly as in [Reference Bellaïche and ChenevierBC09, Lemma 1.4.3]. Namely, if
$\mathcal {E} = \{e_i,\psi _i,1\le i \le {d}\}$ is contained in [Reference ChenevierChe14, Theorem 2.22] and its proof. The statement that two such data are conjugate is exactly as in [Reference Bellaïche and ChenevierBC09, Lemma 1.4.3]. Namely, if ![]() $\mathcal {E}' = \{e_i',\psi _i',1\le i \le {d}\}$ is another such choice, then since
$\mathcal {E}' = \{e_i',\psi _i',1\le i \le {d}\}$ is another such choice, then since ![]() $\operatorname {End}_R(R e_i) \cong M_{n_i}(A) \cong \operatorname {End}_R(R e_i')$ are local rings, the Krull–Schmidt–Azumaya theorem [Reference Curtis and ReinerCR81, Theorem 6.12] (see also [Reference Curtis and ReinerCR81, Remark 6.14 and Chapter 6, Exercise 14]) implies that there is
$\operatorname {End}_R(R e_i) \cong M_{n_i}(A) \cong \operatorname {End}_R(R e_i')$ are local rings, the Krull–Schmidt–Azumaya theorem [Reference Curtis and ReinerCR81, Theorem 6.12] (see also [Reference Curtis and ReinerCR81, Remark 6.14 and Chapter 6, Exercise 14]) implies that there is ![]() $x\in R^{\times }$ such that
$x\in R^{\times }$ such that ![]() $x e_i x^{-1} = e_i'$ for each
$x e_i x^{-1} = e_i'$ for each ![]() $1\le i \le {d}$. By Skolem–Noether, we can adjust
$1\le i \le {d}$. By Skolem–Noether, we can adjust ![]() $x$ by an element of
$x$ by an element of ![]() $(\oplus _{i=1}^{d}e_i R e_i)^{\times }$ so that it further satisfies
$(\oplus _{i=1}^{d}e_i R e_i)^{\times }$ so that it further satisfies ![]() $x\psi _i x^{-1} = \psi _i'$.
$x\psi _i x^{-1} = \psi _i'$.
We now show that the reducibility ideals of [Reference Bellaïche and ChenevierBC09, Proposition 1.5.1] and their basic properties carry over for determinants (so without having to assume that ![]() $n!$ is invertible in
$n!$ is invertible in ![]() $A$).
$A$).
Proposition 2.5 Let ![]() $A$ be a Henselian local ring with residue field
$A$ be a Henselian local ring with residue field ![]() $k$, let
$k$, let ![]() $R$ be an
$R$ be an ![]() $A$-algebra, and let
$A$-algebra, and let ![]() $D \colon R \rightarrow A$ be a determinant. Assume that
$D \colon R \rightarrow A$ be a determinant. Assume that ![]() $\bar {D} = D\otimes _A k \colon R\otimes _A k \rightarrow k$ is split and multiplicity free. Write
$\bar {D} = D\otimes _A k \colon R\otimes _A k \rightarrow k$ is split and multiplicity free. Write ![]() $\bar {D} = \prod _{i=1}^{d} \bar {D}_i$ with each
$\bar {D} = \prod _{i=1}^{d} \bar {D}_i$ with each ![]() $\bar {D}_i$ absolutely irreducible of dimension
$\bar {D}_i$ absolutely irreducible of dimension ![]() $n_i$.
$n_i$.
Let ![]() $\mathcal {P} = (\mathcal {P}_1,\ldots ,\mathcal {P}_s)$ be a partition of
$\mathcal {P} = (\mathcal {P}_1,\ldots ,\mathcal {P}_s)$ be a partition of ![]() $\{1,\ldots ,{d}\}$. There is an ideal
$\{1,\ldots ,{d}\}$. There is an ideal ![]() $I_\mathcal {P}$ of
$I_\mathcal {P}$ of ![]() $A$ such that an ideal
$A$ such that an ideal ![]() $J$ of
$J$ of ![]() $A$ satisfies
$A$ satisfies ![]() $I_\mathcal {P} \subseteq J$ if and only if there are determinants
$I_\mathcal {P} \subseteq J$ if and only if there are determinants ![]() $D_1,\ldots ,D_s \colon R\otimes _A A/J \rightarrow A/J$ such that
$D_1,\ldots ,D_s \colon R\otimes _A A/J \rightarrow A/J$ such that ![]() $D\otimes _A A/J = \prod _{m=1}^{s} D_m$ and
$D\otimes _A A/J = \prod _{m=1}^{s} D_m$ and ![]() $D_m \otimes _A k = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each
$D_m \otimes _A k = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each ![]() $1\le m \le s$. If this property holds, then
$1\le m \le s$. If this property holds, then ![]() $D_1,\ldots ,D_s$ are uniquely determined and satisfy
$D_1,\ldots ,D_s$ are uniquely determined and satisfy ![]() $\ker (D\otimes _A A/J) \subseteq \ker (D_m)$.
$\ker (D\otimes _A A/J) \subseteq \ker (D_m)$.
Moreover, let ![]() $\mathcal {J}$ be a two-sided ideal of
$\mathcal {J}$ be a two-sided ideal of ![]() $R$ with
$R$ with ![]() $\operatorname {CH}(D) \subseteq \mathcal {J} \subseteq \ker (D)$ and let
$\operatorname {CH}(D) \subseteq \mathcal {J} \subseteq \ker (D)$ and let ![]() $\mathcal {A}_{i,j}$ be the
$\mathcal {A}_{i,j}$ be the ![]() $A$-modules as in Construction 2.3 for a choice of data of idempotents as in Theorem 2.4 applied to
$A$-modules as in Construction 2.3 for a choice of data of idempotents as in Theorem 2.4 applied to ![]() $R/\mathcal {J}$. Then
$R/\mathcal {J}$. Then ![]() $I_\mathcal {P} = \sum _{i,j} \mathcal {A}_{i,j}\mathcal {A}_{j,i}$, where the sum is over all pairs
$I_\mathcal {P} = \sum _{i,j} \mathcal {A}_{i,j}\mathcal {A}_{j,i}$, where the sum is over all pairs ![]() $i,j$ not belonging to the same
$i,j$ not belonging to the same ![]() $\mathcal {P}_m\in \mathcal {P}$.
$\mathcal {P}_m\in \mathcal {P}$.
Proof. We follow the proof of [Reference Bellaïche and ChenevierBC09, Proposition 1.5.1] closely. Choose a two-sided ideal ![]() $\mathcal {J}$ of
$\mathcal {J}$ of ![]() $R$ with
$R$ with ![]() $\operatorname {CH}(D) \subseteq \mathcal {J} \subseteq \ker (D)$, and data of idempotents
$\operatorname {CH}(D) \subseteq \mathcal {J} \subseteq \ker (D)$, and data of idempotents ![]() $\mathcal {E}$ for
$\mathcal {E}$ for ![]() $R/\mathcal {J}$ as in Theorem 2.4. We let
$R/\mathcal {J}$ as in Theorem 2.4. We let ![]() $\mathcal {A}_{i,j}$ be as in Construction 2.3 and define
$\mathcal {A}_{i,j}$ be as in Construction 2.3 and define ![]() $I_\mathcal {P} = \sum _{i,j} \mathcal {A}_{i,j}\mathcal {A}_{j,i}$, where the sum is over all pairs
$I_\mathcal {P} = \sum _{i,j} \mathcal {A}_{i,j}\mathcal {A}_{j,i}$, where the sum is over all pairs ![]() $i,j$ not belonging to the same
$i,j$ not belonging to the same ![]() $\mathcal {P}_m\in \mathcal {P}$. Since another such choice of the data of idempotents is conjugate by an element of
$\mathcal {P}_m\in \mathcal {P}$. Since another such choice of the data of idempotents is conjugate by an element of ![]() $(R/\mathcal {J})^{\times }$, the ideal
$(R/\mathcal {J})^{\times }$, the ideal ![]() $I_{\mathcal {P}}$ does not depend on the choice of
$I_{\mathcal {P}}$ does not depend on the choice of ![]() $\mathcal {E}$. To see that it is independent of
$\mathcal {E}$. To see that it is independent of ![]() $\mathcal {J}$, first note that
$\mathcal {J}$, first note that ![]() $D$ further factors through a surjection
$D$ further factors through a surjection ![]() $\psi \colon R/\mathcal {J} \rightarrow R/\ker (D)$. Under this surjection, the data of idempotents
$\psi \colon R/\mathcal {J} \rightarrow R/\ker (D)$. Under this surjection, the data of idempotents ![]() $\mathcal {E}$ is sent to a data of idempotents for
$\mathcal {E}$ is sent to a data of idempotents for ![]() $R/\ker (D)$, and
$R/\ker (D)$, and ![]() $\operatorname {tr}(\psi (\mathcal {A}_{i,j})\psi (\mathcal {A}_{j,i})) = \operatorname {tr}(\mathcal {A}_{i,j}\mathcal {A}_{j,i})$ since
$\operatorname {tr}(\psi (\mathcal {A}_{i,j})\psi (\mathcal {A}_{j,i})) = \operatorname {tr}(\mathcal {A}_{i,j}\mathcal {A}_{j,i})$ since ![]() $\operatorname {tr}\circ \psi = \operatorname {tr}$.
$\operatorname {tr}\circ \psi = \operatorname {tr}$.
We can now replace ![]() $R$ with
$R$ with ![]() $R/\operatorname {CH}(D)$ and assume that
$R/\operatorname {CH}(D)$ and assume that ![]() $D$ is Cayley–Hamilton. Since
$D$ is Cayley–Hamilton. Since ![]() $\operatorname {CH}(D)$ is stable under base change, it suffices to show that
$\operatorname {CH}(D)$ is stable under base change, it suffices to show that ![]() $I_{\mathcal {P}} = 0$ if and only if there are determinants
$I_{\mathcal {P}} = 0$ if and only if there are determinants ![]() $D_1,\ldots ,D_s \colon R\rightarrow A$ such that
$D_1,\ldots ,D_s \colon R\rightarrow A$ such that ![]() $D = \prod _{m=1}^{s} D_m$ and
$D = \prod _{m=1}^{s} D_m$ and ![]() $D_m \otimes _A k_A = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each
$D_m \otimes _A k_A = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each ![]() $1\le m \le s$ and that, if this happens, then
$1\le m \le s$ and that, if this happens, then ![]() $D_1,\ldots ,D_s$ are uniquely determined. Fix a datum of idempotents
$D_1,\ldots ,D_s$ are uniquely determined. Fix a datum of idempotents ![]() $\mathcal {E} = \{e_i,\psi _i,1\le i \le {d}\}$ for
$\mathcal {E} = \{e_i,\psi _i,1\le i \le {d}\}$ for ![]() $R$ as in Theorem 2.4, and let the notation be as in Construction 2.3. For each
$R$ as in Theorem 2.4, and let the notation be as in Construction 2.3. For each ![]() $1\le m \le s$, we set
$1\le m \le s$, we set ![]() $f_m = \sum _{i\in \mathcal {P}_m} e_i$. Then
$f_m = \sum _{i\in \mathcal {P}_m} e_i$. Then ![]() $1 = f_1+\cdots + f_s$ is a decomposition into orthogonal idempotents.
$1 = f_1+\cdots + f_s$ is a decomposition into orthogonal idempotents.
First assume that ![]() $I_{\mathcal {P}} = 0$. Let
$I_{\mathcal {P}} = 0$. Let ![]() $\tilde {D}$ denote the
$\tilde {D}$ denote the ![]() $A$-valued determinant on
$A$-valued determinant on ![]() $R/\ker (D)$ arising from
$R/\ker (D)$ arising from ![]() $D$. Fix
$D$. Fix ![]() $x \in R$, an
$x \in R$, an ![]() $A$-algebra
$A$-algebra ![]() $B$, and
$B$, and ![]() $y \in R\otimes _A B$. If
$y \in R\otimes _A B$. If ![]() $1\le i,j\le {d}$ do not belong to the same
$1\le i,j\le {d}$ do not belong to the same ![]() $\mathcal {P}_m\in \mathcal {P}$, then using the algebra structure as in (1) and the fact that
$\mathcal {P}_m\in \mathcal {P}$, then using the algebra structure as in (1) and the fact that ![]() $\mathcal {A}_{i,j} \mathcal {A}_{j,i} = 0$, we have
$\mathcal {A}_{i,j} \mathcal {A}_{j,i} = 0$, we have ![]() $e_i x e_j y = \sum _{l\ne i} e_i x e_j y e_l$, and [Reference ChenevierChe14, Lemma 1.12(i)] gives
$e_i x e_j y = \sum _{l\ne i} e_i x e_j y e_l$, and [Reference ChenevierChe14, Lemma 1.12(i)] gives
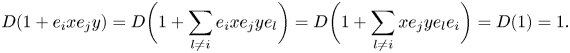 \[ D(1 + e_i x e_ j y) = D\bigg(1+\sum_{l\ne i} e_i x e_j y e_l\bigg) = D\bigg(1+\sum_{l\ne i} x e_j y e_l e_i\bigg) = D(1) = 1. \]
\[ D(1 + e_i x e_ j y) = D\bigg(1+\sum_{l\ne i} e_i x e_j y e_l\bigg) = D\bigg(1+\sum_{l\ne i} x e_j y e_l e_i\bigg) = D(1) = 1. \]
By [Reference ChenevierChe14, Lemma 1.19], ![]() $e_i x e_j \in \ker (D)$ for all
$e_i x e_j \in \ker (D)$ for all ![]() $x\in R$ and all
$x\in R$ and all ![]() $i,j$ that do not belong to the same
$i,j$ that do not belong to the same ![]() $\mathcal {P}_m\in \mathcal {P}$. We then have an isomorphism of
$\mathcal {P}_m\in \mathcal {P}$. We then have an isomorphism of ![]() $A$-algebras
$A$-algebras ![]() $R/\ker (D) \cong \prod _{m=1}^{s} f_m (R/\ker (D)) f_m$ and [Reference ChenevierChe14, Lemma 2.4] gives
$R/\ker (D) \cong \prod _{m=1}^{s} f_m (R/\ker (D)) f_m$ and [Reference ChenevierChe14, Lemma 2.4] gives ![]() $D = \prod _{m=1}^{s} D_m$, where
$D = \prod _{m=1}^{s} D_m$, where ![]() $D_m \colon R \rightarrow A$ is the composite of the surjection
$D_m \colon R \rightarrow A$ is the composite of the surjection ![]() $R \rightarrow f_m (R/\ker (D)) f_m$ with the determinant
$R \rightarrow f_m (R/\ker (D)) f_m$ with the determinant ![]() $\tilde {D}_m \colon f_m (R/\ker (D)) f_m \rightarrow A$ given by
$\tilde {D}_m \colon f_m (R/\ker (D)) f_m \rightarrow A$ given by ![]() $x\mapsto \tilde {D}(x + 1-f_m)$. It is immediate that
$x\mapsto \tilde {D}(x + 1-f_m)$. It is immediate that ![]() $D_m \otimes _A k_A = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each
$D_m \otimes _A k_A = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each ![]() $1\le m \le s$.
$1\le m \le s$.
Now assume that there are determinants ![]() $D_1,\ldots ,D_s \colon R\rightarrow A$ such that
$D_1,\ldots ,D_s \colon R\rightarrow A$ such that ![]() $D = \prod _{m=1}^{s} D_m$ and
$D = \prod _{m=1}^{s} D_m$ and ![]() $D_m \otimes _A k = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each
$D_m \otimes _A k = \prod _{i \in \mathcal {P}_m} \bar {D}_i$ for each ![]() $1\le m \le s$. The determinants
$1\le m \le s$. The determinants ![]() $D_m$ have dimension
$D_m$ have dimension ![]() $d_m := \sum _{i\in \mathcal {P}_m} n_i$. The trace map yields an equality
$d_m := \sum _{i\in \mathcal {P}_m} n_i$. The trace map yields an equality
So, to show that ![]() $I_{\mathcal {P}} = 0$, it suffices to show that
$I_{\mathcal {P}} = 0$, it suffices to show that ![]() $\operatorname {tr}(f_m R f_{m'} R f_m) = 0$ for
$\operatorname {tr}(f_m R f_{m'} R f_m) = 0$ for ![]() $m\ne m'$. For this, it suffices to show that
$m\ne m'$. For this, it suffices to show that ![]() $f_{m'} \in \ker (D_m)$ for any
$f_{m'} \in \ker (D_m)$ for any ![]() $m\ne m'$, since this implies that
$m\ne m'$, since this implies that ![]() $f_m R f_{m'} \in \ker (D_l)$ for any
$f_m R f_{m'} \in \ker (D_l)$ for any ![]() $1\le l\le s$ and hence
$1\le l\le s$ and hence
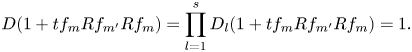 \[ D(1+tf_m R f_{m'} R f_m) = \prod_{l=1}^{s} D_l(1+tf_m R f_{m'} R f_m) = 1. \]
\[ D(1+tf_m R f_{m'} R f_m) = \prod_{l=1}^{s} D_l(1+tf_m R f_{m'} R f_m) = 1. \]
For any idempotent ![]() $f$ of
$f$ of ![]() $R$, we have the determinant
$R$, we have the determinant ![]() $D_{m,f} \colon f R f \rightarrow A$ given by
$D_{m,f} \colon f R f \rightarrow A$ given by ![]() $D_{m,f}(x) = D_m(x+1-f)$. When
$D_{m,f}(x) = D_m(x+1-f)$. When ![]() $f = f_m$,
$f = f_m$,
has dimension ![]() $d_m$. Then [Reference ChenevierChe14, Lemma 2.4(2)] implies that
$d_m$. Then [Reference ChenevierChe14, Lemma 2.4(2)] implies that ![]() $D_{m,1-f_m}$ has dimension
$D_{m,1-f_m}$ has dimension ![]() $0$, i.e. is constant and equal to
$0$, i.e. is constant and equal to ![]() $1$. So, for any
$1$. So, for any ![]() $m\ne m'$, the characteristic polynomial of
$m\ne m'$, the characteristic polynomial of ![]() $f_{m'}$ with respect to
$f_{m'}$ with respect to ![]() $D_m$ is
$D_m$ is
Then ![]() $f_{m'} = f_{m'}^{d_m} \in \operatorname {CH}(D_m) \subseteq \ker (D_m)$, which is what we wanted to prove. This further shows that for each
$f_{m'} = f_{m'}^{d_m} \in \operatorname {CH}(D_m) \subseteq \ker (D_m)$, which is what we wanted to prove. This further shows that for each ![]() $1\le m \le s$, the determinant
$1\le m \le s$, the determinant ![]() $D_m$ is the composite of the surjections
$D_m$ is the composite of the surjections
with the determinant ![]() $D_{f_m} \colon f_m R f_m \rightarrow A$. Since any two choices of the data of idempotents are conjugate under
$D_{f_m} \colon f_m R f_m \rightarrow A$. Since any two choices of the data of idempotents are conjugate under ![]() $R^{\times }$, each
$R^{\times }$, each ![]() $D_m$ is uniquely determined by
$D_m$ is uniquely determined by ![]() $D$.
$D$.
3. Deformations
Galois deformation theory plays an essential role in this paper. The set of results we use is essentially identical to that of [Reference ThorneTho15], with some technical improvements. In this section we recall the notation used in [Reference ThorneTho15], without giving detailed definitions or proofs; we then proceed to prove the new results that we need. Some of the definitions recalled here were first given in [Reference Clozel, Harris and TaylorCHT08] or [Reference GeraghtyGer19], but in order to avoid sending the reader to too many different places we restrict our citations to [Reference ThorneTho15].
We will use exactly the same set-up and notation for deformation theory as in [Reference ThorneTho15]. We recall that this means that we fix at the outset the following objects.
– A CM number field
 $F$, with its totally real subfield
$F$, with its totally real subfield  $F^{+}$.
$F^{+}$.– An odd prime
 $l$ such that each
$l$ such that each  $l$-adic place of
$l$-adic place of  $F^{+}$ splits in
$F^{+}$ splits in  $F$. We write
$F$. We write  $S_l$ for the set of
$S_l$ for the set of  $l$-adic places of
$l$-adic places of  $F^{+}$.
$F^{+}$.– A finite set
 $S$ of finite places of
$S$ of finite places of  $F^{+}$ which split in
$F^{+}$ which split in  $F$. We assume that
$F$. We assume that  $S_l \subset S$ and write
$S_l \subset S$ and write  $F(S)$ for the maximal extension of
$F(S)$ for the maximal extension of  $F$ which is unramified outside
$F$ which is unramified outside  $S$ and set
$S$ and set  $G_{F, S} = \operatorname {Gal}(F(S) / F)$ and
$G_{F, S} = \operatorname {Gal}(F(S) / F)$ and  $G_{F^{+}, S} = \operatorname {Gal}(F(S) / F^{+})$. We fix a choice of complex conjugation
$G_{F^{+}, S} = \operatorname {Gal}(F(S) / F^{+})$. We fix a choice of complex conjugation  $c \in G_{F^{+}, S}$.
$c \in G_{F^{+}, S}$.– For each
 $v \in S$, we fix a choice of place
$v \in S$, we fix a choice of place  ${{\widetilde {v}}}$ of
${{\widetilde {v}}}$ of  $F$ such that
$F$ such that  ${{\widetilde {v}}}|_{F^{+}} = v$, and define
${{\widetilde {v}}}|_{F^{+}} = v$, and define  $\tilde {S} = \{ {{\widetilde {v}}} \mid v \in S \}$.
$\tilde {S} = \{ {{\widetilde {v}}} \mid v \in S \}$.
We also fix the following data.
– A coefficient field
 $K \subset \bar {{{\mathbb {Q}}}}_l$ with ring of integers
$K \subset \bar {{{\mathbb {Q}}}}_l$ with ring of integers  ${{\mathcal {O}}}$, residue field
${{\mathcal {O}}}$, residue field  $k$, and maximal ideal
$k$, and maximal ideal  $\lambda \subset {{\mathcal {O}}}$.
$\lambda \subset {{\mathcal {O}}}$.– A continuous homomorphism
 $\chi : G_{F^{+}, S} \to {{\mathcal {O}}}^{\times }$. We write
$\chi : G_{F^{+}, S} \to {{\mathcal {O}}}^{\times }$. We write  $\bar {\chi } = \chi \text { mod } \lambda$.
$\bar {\chi } = \chi \text { mod } \lambda$.– A continuous homomorphism
 $\bar {r} : G_{F^{+}, S} \to {{\mathcal {G}}}_n(k)$ such that
$\bar {r} : G_{F^{+}, S} \to {{\mathcal {G}}}_n(k)$ such that  $\bar {r}^{-1}({{\mathcal {G}}}_n^{\circ }(k)) = G_{F, S}$. Here
$\bar {r}^{-1}({{\mathcal {G}}}_n^{\circ }(k)) = G_{F, S}$. Here  ${{\mathcal {G}}}_n$ is the algebraic group over
${{\mathcal {G}}}_n$ is the algebraic group over  ${{\mathbb {Z}}}$ defined in [Reference Clozel, Harris and TaylorCHT08, § 2.1]. We follow the convention that if
${{\mathbb {Z}}}$ defined in [Reference Clozel, Harris and TaylorCHT08, § 2.1]. We follow the convention that if  $R : \Gamma \to {{\mathcal {G}}}_n(A)$ is a homomorphism and
$R : \Gamma \to {{\mathcal {G}}}_n(A)$ is a homomorphism and  $\Delta \subset \Gamma$ is a subgroup such that
$\Delta \subset \Gamma$ is a subgroup such that  $R(\Delta ) \subset {{\mathcal {G}}}_n^{0}(A)$, then
$R(\Delta ) \subset {{\mathcal {G}}}_n^{0}(A)$, then  $R|_\Delta$ denotes the composite homomorphism
Thus,
$R|_\Delta$ denotes the composite homomorphism
Thus, \[ \Delta \to {{\mathcal{G}}}_n^{0}(A) = \operatorname{GL}_n(A) \times \operatorname{GL}_1(A) \to \operatorname{GL}_n(A). \]
\[ \Delta \to {{\mathcal{G}}}_n^{0}(A) = \operatorname{GL}_n(A) \times \operatorname{GL}_1(A) \to \operatorname{GL}_n(A). \] $\bar {r}|_{G_{F, S}}$ takes values in
$\bar {r}|_{G_{F, S}}$ takes values in  $\operatorname {GL}_n(k)$.
$\operatorname {GL}_n(k)$.
If ![]() $v \in S_l$, then we write
$v \in S_l$, then we write ![]() $\Lambda _v = {{\mathcal {O}}} [\kern-1pt[ (I^{\text ab}_{F_{{\widetilde {v}}}}(l))^{n} ]\kern-1pt]$, where
$\Lambda _v = {{\mathcal {O}}} [\kern-1pt[ (I^{\text ab}_{F_{{\widetilde {v}}}}(l))^{n} ]\kern-1pt]$, where ![]() $I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ denotes the inertia group in the maximal abelian pro-
$I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ denotes the inertia group in the maximal abelian pro-![]() $l$ extension of
$l$ extension of ![]() $F_{{\widetilde {v}}}$. We set
$F_{{\widetilde {v}}}$. We set ![]() $\Lambda = \hat {\otimes }_v \Lambda _v$, the completed tensor product being over
$\Lambda = \hat {\otimes }_v \Lambda _v$, the completed tensor product being over ![]() ${{\mathcal {O}}}$. A global deformation problem, as defined in [Reference ThorneTho15, § 3], then consists of a tuple
${{\mathcal {O}}}$. A global deformation problem, as defined in [Reference ThorneTho15, § 3], then consists of a tuple
The extra data that we have not defined consists of the choice of a local deformation problem ![]() ${{\mathcal {D}}}_v$ for each
${{\mathcal {D}}}_v$ for each ![]() $v \in S$. We will not need to define any new local deformation problems in this paper, but we recall that the following have been defined in [Reference ThorneTho15]:
$v \in S$. We will not need to define any new local deformation problems in this paper, but we recall that the following have been defined in [Reference ThorneTho15]:
– ‘ordinary deformations’ give rise to a problem
 ${{\mathcal {D}}}_v^{\triangle }$ for each
${{\mathcal {D}}}_v^{\triangle }$ for each  $v \in S_l$ [Reference ThorneTho15, § 3.3.2];
$v \in S_l$ [Reference ThorneTho15, § 3.3.2];– ‘Steinberg deformations’ give rise to a problem
 ${{\mathcal {D}}}_v^{\rm St}$ for each place
${{\mathcal {D}}}_v^{\rm St}$ for each place  $v \in S$ such that
$v \in S$ such that  $q_v \equiv 1 \text { mod }l$ and
$q_v \equiv 1 \text { mod }l$ and  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial;
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial;– ‘
 $\chi _v$-ramified deformations’ give rise to a problem
$\chi _v$-ramified deformations’ give rise to a problem  ${{\mathcal {D}}}_v^{\chi _v}$ for each place
${{\mathcal {D}}}_v^{\chi _v}$ for each place  $v \in S$ such that
$v \in S$ such that  $q_v \equiv 1 \text { mod }l$ and
$q_v \equiv 1 \text { mod }l$ and  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial, given the additional data of a tuple
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial, given the additional data of a tuple  $\chi _v = (\chi _{v, 1}, \ldots , \chi _{v, n})$ of characters
$\chi _v = (\chi _{v, 1}, \ldots , \chi _{v, n})$ of characters  $\chi _{v, i} : k(v)^{\times }(l) \to k^{\times }$;
$\chi _{v, i} : k(v)^{\times }(l) \to k^{\times }$;– ‘unrestricted deformations’ give rise to a problem
 ${{\mathcal {D}}}_v^{\square }$ for any
${{\mathcal {D}}}_v^{\square }$ for any  $v \in S$.
$v \in S$.
If ![]() ${{\mathcal {S}}}$ is a global deformation problem, then we can define (as in [Reference ThorneTho15]) a functor
${{\mathcal {S}}}$ is a global deformation problem, then we can define (as in [Reference ThorneTho15]) a functor ![]() $\operatorname {Def}_{{\mathcal {S}}} : {{\mathcal {C}}}_\Lambda \to \text {Sets}$ of ‘deformations of type
$\operatorname {Def}_{{\mathcal {S}}} : {{\mathcal {C}}}_\Lambda \to \text {Sets}$ of ‘deformations of type ![]() ${{\mathcal {S}}}$’. By definition, if
${{\mathcal {S}}}$’. By definition, if ![]() $A \in {{\mathcal {C}}}_\Lambda$, then
$A \in {{\mathcal {C}}}_\Lambda$, then ![]() $\operatorname {Def}_{{\mathcal {S}}}(A)$ is the set of
$\operatorname {Def}_{{\mathcal {S}}}(A)$ is the set of ![]() $\operatorname {GL}_n(A)$-conjugacy classes of homomorphisms
$\operatorname {GL}_n(A)$-conjugacy classes of homomorphisms ![]() $r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ lifting
$r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ lifting ![]() $\bar {r}$ such that
$\bar {r}$ such that ![]() $\nu \circ r = \chi$ and for each
$\nu \circ r = \chi$ and for each ![]() $v \in S$,
$v \in S$, ![]() $r|_{G_{F_{{\widetilde {v}}}}} \in {{\mathcal {D}}}_v(A)$. If
$r|_{G_{F_{{\widetilde {v}}}}} \in {{\mathcal {D}}}_v(A)$. If ![]() $\bar {r}$ is Schur (see [Reference ThorneTho15, Definition 3.2]), then the functor
$\bar {r}$ is Schur (see [Reference ThorneTho15, Definition 3.2]), then the functor ![]() $\operatorname {Def}_{{\mathcal {S}}}$ is represented by an object
$\operatorname {Def}_{{\mathcal {S}}}$ is represented by an object ![]() $R_{{\mathcal {S}}}^{\rm univ} \in {{\mathcal {C}}}_\Lambda$.
$R_{{\mathcal {S}}}^{\rm univ} \in {{\mathcal {C}}}_\Lambda$.
3.1 An erratum to [Reference ThorneTho15]
We point out an error in [Reference ThorneTho15]. We thank Lue Pan for bringing this to our attention. In [Reference ThorneTho15, Proposition 3.15] it is asserted that the ring ![]() $R_v^{1}$ (representing the deformation problem
$R_v^{1}$ (representing the deformation problem ![]() ${{\mathcal {D}}}_v^{1}$ for
${{\mathcal {D}}}_v^{1}$ for ![]() $v \in R$, defined under the assumptions
$v \in R$, defined under the assumptions ![]() $q_v \equiv 1 \text { mod }l$ and
$q_v \equiv 1 \text { mod }l$ and ![]() $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ trivial) has the property that
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ trivial) has the property that ![]() $R_v^{1} / (\lambda )$ is generically reduced. This is false, even in the case
$R_v^{1} / (\lambda )$ is generically reduced. This is false, even in the case ![]() $n = 2$, as can be seen from the statement of [Reference ShottonSho16, Proposition 5.8] (and noting the identification
$n = 2$, as can be seen from the statement of [Reference ShottonSho16, Proposition 5.8] (and noting the identification ![]() $R_v^{1} / (\lambda ) = R_v^{\chi _v} / (\lambda )$). We offer the following corrected statement.
$R_v^{1} / (\lambda ) = R_v^{\chi _v} / (\lambda )$). We offer the following corrected statement.
Proposition 3.1 Let ![]() $\bar {R}_v^{1}$ denote the nilreduction of
$\bar {R}_v^{1}$ denote the nilreduction of ![]() $R_v^{1}$. Then
$R_v^{1}$. Then ![]() $\bar {R}_v^{1} / (\lambda )$ is generically reduced.
$\bar {R}_v^{1} / (\lambda )$ is generically reduced.
Proof. Let ![]() ${{\mathcal {M}}}$ denote the scheme over
${{\mathcal {M}}}$ denote the scheme over ![]() ${{\mathcal {O}}}$ of pairs of
${{\mathcal {O}}}$ of pairs of ![]() $n \times n$ matrices
$n \times n$ matrices ![]() $(\Phi , \Sigma )$, where
$(\Phi , \Sigma )$, where ![]() $\Phi$ is invertible, the characteristic polynomial of
$\Phi$ is invertible, the characteristic polynomial of ![]() $\Sigma$ equals
$\Sigma$ equals ![]() $(X - 1)^{n}$, and we have
$(X - 1)^{n}$, and we have ![]() $\Phi \Sigma \Phi ^{-1} = \Sigma ^{q_v}$. Then
$\Phi \Sigma \Phi ^{-1} = \Sigma ^{q_v}$. Then ![]() $R_v^{1}$ can be identified with the completed local ring of
$R_v^{1}$ can be identified with the completed local ring of ![]() ${{\mathcal {M}}}$ at the point
${{\mathcal {M}}}$ at the point ![]() $(1_n, 1_n) \in {{\mathcal {M}}}(k)$. By [Reference MatsumuraMat89, Theorem 23.9] (and since
$(1_n, 1_n) \in {{\mathcal {M}}}(k)$. By [Reference MatsumuraMat89, Theorem 23.9] (and since ![]() ${{\mathcal {M}}}$ is excellent), it is enough to show that if
${{\mathcal {M}}}$ is excellent), it is enough to show that if ![]() $\bar {{{\mathcal {M}}}}$ denotes the nilreduction of
$\bar {{{\mathcal {M}}}}$ denotes the nilreduction of ![]() ${{\mathcal {M}}}$, then
${{\mathcal {M}}}$, then ![]() $\bar {{{\mathcal {M}}}} \otimes _{{\mathcal {O}}}k$ is generically reduced.
$\bar {{{\mathcal {M}}}} \otimes _{{\mathcal {O}}}k$ is generically reduced.
Let ![]() ${{\mathcal {M}}}_1, \ldots , {{\mathcal {M}}}_r$ denote the irreducible components of
${{\mathcal {M}}}_1, \ldots , {{\mathcal {M}}}_r$ denote the irreducible components of ![]() ${{\mathcal {M}}}$ with their reduced subscheme structure. According to [Reference ThorneTho12, Lemma 3.15], each
${{\mathcal {M}}}$ with their reduced subscheme structure. According to [Reference ThorneTho12, Lemma 3.15], each ![]() ${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}K$ is non-empty of dimension
${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}K$ is non-empty of dimension ![]() $n^{2}$, while the
$n^{2}$, while the ![]() ${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}k$ are the pairwise-distinct irreducible components of
${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}k$ are the pairwise-distinct irreducible components of ![]() ${{\mathcal {M}}} \otimes _{{\mathcal {O}}}k$ and are all generically reduced. Let
${{\mathcal {M}}} \otimes _{{\mathcal {O}}}k$ and are all generically reduced. Let ![]() $\bar {\eta }_i$ denote the generic point of
$\bar {\eta }_i$ denote the generic point of ![]() ${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}k$. Then
${{\mathcal {M}}}_i \otimes _{{\mathcal {O}}}k$. Then ![]() $\bar {\eta }_i$ admits an open neighbourhood in
$\bar {\eta }_i$ admits an open neighbourhood in ![]() ${{\mathcal {M}}}$ not meeting any
${{\mathcal {M}}}$ not meeting any ![]() ${{\mathcal {M}}}_j$ (
${{\mathcal {M}}}_j$ (![]() $j \neq i$). Consequently, we have an equality of local rings
$j \neq i$). Consequently, we have an equality of local rings ![]() ${{\mathcal {O}}}_{\bar {{{\mathcal {M}}}}, \bar {\eta }_i} = {{\mathcal {O}}}_{{{\mathcal {M}}}_i, \bar {\eta }_i}$, showing that
${{\mathcal {O}}}_{\bar {{{\mathcal {M}}}}, \bar {\eta }_i} = {{\mathcal {O}}}_{{{\mathcal {M}}}_i, \bar {\eta }_i}$, showing that ![]() ${{\mathcal {O}}}_{\bar {{{\mathcal {M}}}}, \bar {\eta }_i} / (\lambda )$ is reduced (in fact, a field). This shows that
${{\mathcal {O}}}_{\bar {{{\mathcal {M}}}}, \bar {\eta }_i} / (\lambda )$ is reduced (in fact, a field). This shows that ![]() $\bar {{{\mathcal {M}}}} \otimes _{{\mathcal {O}}}k$ is generically reduced.
$\bar {{{\mathcal {M}}}} \otimes _{{\mathcal {O}}}k$ is generically reduced.
We now need to explain why this error does not affect the proofs of the two results in [Reference ThorneTho15] which rely on the assertion that ![]() $R_v^{1} / (\lambda )$ is generically reduced. The first of these is [Reference ThorneTho15, Proposition 3.17], which states that the Steinberg deformation ring
$R_v^{1} / (\lambda )$ is generically reduced. The first of these is [Reference ThorneTho15, Proposition 3.17], which states that the Steinberg deformation ring ![]() $R_v^{\rm St}$ has the property that
$R_v^{\rm St}$ has the property that ![]() $R_v^{\rm St} / (\lambda )$ is generically reduced. The proof of this result is still valid if one replaces
$R_v^{\rm St} / (\lambda )$ is generically reduced. The proof of this result is still valid if one replaces ![]() $R_v^{1}$ there with
$R_v^{1}$ there with ![]() $\bar {R}_v^{1}$. Indeed, we need only note that
$\bar {R}_v^{1}$. Indeed, we need only note that ![]() $R_v^{\rm St}$ is
$R_v^{\rm St}$ is ![]() ${{\mathcal {O}}}$-flat (by definition) and reduced (since
${{\mathcal {O}}}$-flat (by definition) and reduced (since ![]() $R_v^{\rm St}[1/l]$ is regular, by [Reference TaylorTay08, Lemma 3.3]). The map
$R_v^{\rm St}[1/l]$ is regular, by [Reference TaylorTay08, Lemma 3.3]). The map ![]() $R_v^{1} \to R_v^{\rm St}$ therefore factors through a surjection
$R_v^{1} \to R_v^{\rm St}$ therefore factors through a surjection ![]() $\bar {R}_v^{1} \to R_v^{\rm St}$.
$\bar {R}_v^{1} \to R_v^{\rm St}$.
The next result is [Reference ThorneTho15, Lemma 3.40(2)], which describes the irreducible components of the localization and completion of a ring ![]() $R^{\infty }$ at a prime ideal
$R^{\infty }$ at a prime ideal ![]() $P_\infty$. The ring
$P_\infty$. The ring ![]() $R^{\infty }$ has
$R^{\infty }$ has ![]() $R_v^{1}$ as a (completed) tensor factor, and the generic reducedness is used to justify an appeal to [Reference ThorneTho15, Proposition 1.6]. Since passing to nilreduction does not change the underlying topological space, one can argue instead with the quotient of
$R_v^{1}$ as a (completed) tensor factor, and the generic reducedness is used to justify an appeal to [Reference ThorneTho15, Proposition 1.6]. Since passing to nilreduction does not change the underlying topological space, one can argue instead with the quotient of ![]() $R^{\infty }$, where
$R^{\infty }$, where ![]() $R_v^{1}$ is replaced by
$R_v^{1}$ is replaced by ![]() $\bar {R}_v^{1}$. The statement of [Reference ThorneTho15, Lemma 3.40] is therefore still valid.
$\bar {R}_v^{1}$. The statement of [Reference ThorneTho15, Lemma 3.40] is therefore still valid.
3.2 Pseudodeformations
In this section, we fix a global deformation problem
such that ![]() $\bar {r}$ is Schur. We write
$\bar {r}$ is Schur. We write ![]() $P_{{\mathcal {S}}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ for the
$P_{{\mathcal {S}}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ for the ![]() $\Lambda$-subalgebra topologically generated by the coefficients of characteristic polynomials of Frobenius elements
$\Lambda$-subalgebra topologically generated by the coefficients of characteristic polynomials of Frobenius elements ![]() $\operatorname {Frob}_w \in G_{F, S}$ (
$\operatorname {Frob}_w \in G_{F, S}$ (![]() $w$ prime to
$w$ prime to ![]() $S$). The subring
$S$). The subring ![]() $P_{{\mathcal {S}}}$ is studied in [Reference ThorneTho15, § 3.4], where it is shown using results of Chenevier that
$P_{{\mathcal {S}}}$ is studied in [Reference ThorneTho15, § 3.4], where it is shown using results of Chenevier that ![]() $P_{{\mathcal {S}}}$ is a complete Noetherian local
$P_{{\mathcal {S}}}$ is a complete Noetherian local ![]() $\Lambda$-algebra and that the inclusion
$\Lambda$-algebra and that the inclusion ![]() $P_{{\mathcal {S}}} \subset R_{{{\mathcal {S}}}}^{\rm univ}$ is a finite ring map (see [Reference ThorneTho15, Proposition 3.29]).
$P_{{\mathcal {S}}} \subset R_{{{\mathcal {S}}}}^{\rm univ}$ is a finite ring map (see [Reference ThorneTho15, Proposition 3.29]).
In fact, more is true, as we now describe. Let ![]() $\bar {B} \in \operatorname {GL}_n(k)$ be the matrix defined by the formula
$\bar {B} \in \operatorname {GL}_n(k)$ be the matrix defined by the formula ![]() $\bar {r}(c) = (\bar {B}, - \chi (c))\jmath \in {{\mathcal {G}}}_n(k)$. Let
$\bar {r}(c) = (\bar {B}, - \chi (c))\jmath \in {{\mathcal {G}}}_n(k)$. Let ![]() $\bar {\rho } = \bar {r}|_{G_{F, S}}$ and suppose that there is a decomposition
$\bar {\rho } = \bar {r}|_{G_{F, S}}$ and suppose that there is a decomposition ![]() $\bar {r}=\oplus _{i=1}^{{d}} \bar {r}_i$ with
$\bar {r}=\oplus _{i=1}^{{d}} \bar {r}_i$ with ![]() $\bar {\rho }_i=\bar {r}_i|_{G_{F,S}}$ absolutely irreducible for each
$\bar {\rho }_i=\bar {r}_i|_{G_{F,S}}$ absolutely irreducible for each ![]() $i$. The representations
$i$. The representations ![]() $\bar {\rho }_i$ are pairwise non-isomorphic, because
$\bar {\rho }_i$ are pairwise non-isomorphic, because ![]() $\bar {r}$ is Schur (see [Reference ThorneTho15, Lemma 3.3]). We recall [Reference ThorneTho15, Lemma 3.1] that to give a lifting
$\bar {r}$ is Schur (see [Reference ThorneTho15, Lemma 3.3]). We recall [Reference ThorneTho15, Lemma 3.1] that to give a lifting ![]() $r:G_{F^{+},S}\rightarrow {{\mathcal {G}}}_n(R)$ of
$r:G_{F^{+},S}\rightarrow {{\mathcal {G}}}_n(R)$ of ![]() $\bar {r}$ with
$\bar {r}$ with ![]() $\nu \circ r = \chi$ is equivalent to giving the following data.
$\nu \circ r = \chi$ is equivalent to giving the following data.
– A representation
 $\rho : G_{F,S}\rightarrow \operatorname {GL}_n(R)$ lifting
$\rho : G_{F,S}\rightarrow \operatorname {GL}_n(R)$ lifting  $\bar {\rho } = \bar {r}|_{G_{F,S}}$.
$\bar {\rho } = \bar {r}|_{G_{F,S}}$.– A matrix
 $B \in \operatorname {GL}_n(R)$ lifting
$B \in \operatorname {GL}_n(R)$ lifting  $\bar {B}$ with
$\bar {B}$ with  $^{t}{}{B} = -\chi (c)B$ and
$^{t}{}{B} = -\chi (c)B$ and  $\chi (\delta )B = \rho (\delta ^{c})B ^{t}{}{\rho }(\delta )$ for all
$\chi (\delta )B = \rho (\delta ^{c})B ^{t}{}{\rho }(\delta )$ for all  $\delta \in G_{F,S}$.
$\delta \in G_{F,S}$.
The equivalence is given by letting ![]() $\rho = r|_{G_{F,S}}$ and
$\rho = r|_{G_{F,S}}$ and ![]() $r(c) = (B,-\chi (c))\jmath$. Conjugating
$r(c) = (B,-\chi (c))\jmath$. Conjugating ![]() $r$ by
$r$ by ![]() $M \in \operatorname {GL}_n(R)$ takes
$M \in \operatorname {GL}_n(R)$ takes ![]() $B$ to
$B$ to ![]() $MB ^{t}{}{M}$. Note that the matrix
$MB ^{t}{}{M}$. Note that the matrix ![]() $B$ defines an isomorphism
$B$ defines an isomorphism ![]() $\chi \otimes \rho ^{\vee } \overset {\sim }{\rightarrow } \rho ^{c}$.
$\chi \otimes \rho ^{\vee } \overset {\sim }{\rightarrow } \rho ^{c}$.
We embed the group ![]() $\mu _2^{{d}}$ in
$\mu _2^{{d}}$ in ![]() $\operatorname {GL}_n({{\mathcal {O}}})$ as block diagonal matrices, the
$\operatorname {GL}_n({{\mathcal {O}}})$ as block diagonal matrices, the ![]() $i$th block being of size
$i$th block being of size ![]() $\dim _k \bar {\rho }_i$. We assume that the global deformation problem
$\dim _k \bar {\rho }_i$. We assume that the global deformation problem ![]() ${{\mathcal {S}}}$ has the property that each local deformation problem
${{\mathcal {S}}}$ has the property that each local deformation problem ![]() ${{\mathcal {D}}}_v \subset {{\mathcal {D}}}_v^{\square }$ is invariant under conjugation by
${{\mathcal {D}}}_v \subset {{\mathcal {D}}}_v^{\square }$ is invariant under conjugation by ![]() $\mu _2^{{d}}$; this is the case for each of the local deformation problems recalled above. With this assumption, the group
$\mu _2^{{d}}$; this is the case for each of the local deformation problems recalled above. With this assumption, the group ![]() $\mu _2^{{d}}$ acts on the ring
$\mu _2^{{d}}$ acts on the ring ![]() $R_{{{\mathcal {S}}}}^{\rm univ}$ by conjugation of the universal deformation and we have the following result.
$R_{{{\mathcal {S}}}}^{\rm univ}$ by conjugation of the universal deformation and we have the following result.
Proposition 3.2
(i) We have an equality
 $P_{{\mathcal {S}}} = (R_{{\mathcal {S}}}^{\text{univ}})^{\mu _2^{{d}}}$.
$P_{{\mathcal {S}}} = (R_{{\mathcal {S}}}^{\text{univ}})^{\mu _2^{{d}}}$.(ii) Let
 ${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text{univ}}$ be a prime ideal and let
${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text{univ}}$ be a prime ideal and let  ${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{\mathcal {S}}}$. Let
${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{\mathcal {S}}}$. Let  $E = \operatorname {Frac} R_{{\mathcal {S}}}^{\text{univ}} / {{\mathfrak p}}$ and suppose that the associated representation
$E = \operatorname {Frac} R_{{\mathcal {S}}}^{\text{univ}} / {{\mathfrak p}}$ and suppose that the associated representation  $\rho _{{\mathfrak p}} = r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E : G_{F, S} \to \operatorname {GL}_n(E)$ is absolutely irreducible. Then
$\rho _{{\mathfrak p}} = r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E : G_{F, S} \to \operatorname {GL}_n(E)$ is absolutely irreducible. Then  $P_{{\mathcal {S}}} \to R_{{\mathcal {S}}}^{\text{univ}}$ is étale at
$P_{{\mathcal {S}}} \to R_{{\mathcal {S}}}^{\text{univ}}$ is étale at  ${{\mathfrak q}}$ and
${{\mathfrak q}}$ and  $\mu _2^{{d}}$ acts transitively on the set of primes of
$\mu _2^{{d}}$ acts transitively on the set of primes of  $R_{{{\mathcal {S}}}}^{\text{univ}}$ above
$R_{{{\mathcal {S}}}}^{\text{univ}}$ above  ${{\mathfrak q}}$.
${{\mathfrak q}}$.
We first establish a preliminary lemma, before proving the proposition.
Lemma 3.3 Let ![]() $R = R_{{{\mathcal {S}}}}^{\text{univ}}/({{\mathfrak m}}_{P_{{{\mathcal {S}}}}})$ and let
$R = R_{{{\mathcal {S}}}}^{\text{univ}}/({{\mathfrak m}}_{P_{{{\mathcal {S}}}}})$ and let ![]() $r: G_{F^{+},S}\rightarrow {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation. Then, after possibly conjugating by an element of
$r: G_{F^{+},S}\rightarrow {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation. Then, after possibly conjugating by an element of ![]() $1+M_n({{\mathfrak m}}_R)$,
$1+M_n({{\mathfrak m}}_R)$, ![]() $r|_{G_{F,S}}$ has (block) diagonal entries given by
$r|_{G_{F,S}}$ has (block) diagonal entries given by ![]() $\bar {\rho }_1,\ldots ,\bar {\rho }_{{d}}$, and the matrix
$\bar {\rho }_1,\ldots ,\bar {\rho }_{{d}}$, and the matrix ![]() $B$ defined above is equal to
$B$ defined above is equal to ![]() $\bar {B}$. (Note we are not asserting that the off-diagonal blocks of
$\bar {B}$. (Note we are not asserting that the off-diagonal blocks of ![]() $r|_{G_{F, S}}$ are zero.)
$r|_{G_{F, S}}$ are zero.)
Proof. We let ![]() $\bar {e}_1,\bar {e}_2,\ldots ,\bar {e}_{{d}} \in M_n(k)$ denote the standard idempotents decomposing
$\bar {e}_1,\bar {e}_2,\ldots ,\bar {e}_{{d}} \in M_n(k)$ denote the standard idempotents decomposing ![]() $\bar {r}|_{G_{F,S}}$ into the block diagonal pieces
$\bar {r}|_{G_{F,S}}$ into the block diagonal pieces ![]() $\bar {\rho }_1,\ldots ,\bar {\rho }_{{d}}$. We let
$\bar {\rho }_1,\ldots ,\bar {\rho }_{{d}}$. We let ![]() ${{\mathcal {A}}} \subset M_n(R)$ denote the image of
${{\mathcal {A}}} \subset M_n(R)$ denote the image of ![]() $R[G_{F,S}]$ under
$R[G_{F,S}]$ under ![]() $r$. The idempotents
$r$. The idempotents ![]() $\bar {e}_i$ lift to orthogonal idempotents
$\bar {e}_i$ lift to orthogonal idempotents ![]() $e_i$ in
$e_i$ in ![]() ${{\mathcal {A}}}$ with
${{\mathcal {A}}}$ with ![]() $e_1 + \cdots + e_{{d}} = 1$ and, after conjugating by an element of
$e_1 + \cdots + e_{{d}} = 1$ and, after conjugating by an element of ![]() $1+M_n({{\mathfrak m}}_R)$, we can assume that the
$1+M_n({{\mathfrak m}}_R)$, we can assume that the ![]() $e_i$ are again the standard idempotents on
$e_i$ are again the standard idempotents on ![]() $R^{n}$. Moreover, applying the first case of the proof of [Reference Bellaïche and ChenevierBC09, Lemma 1.8.2], we can (and do) choose the
$R^{n}$. Moreover, applying the first case of the proof of [Reference Bellaïche and ChenevierBC09, Lemma 1.8.2], we can (and do) choose the ![]() $e_i$ so that they are fixed by the anti-involution
$e_i$ so that they are fixed by the anti-involution ![]() $\star : {{\mathcal {A}}} \to {{\mathcal {A}}}$ given by the formula
$\star : {{\mathcal {A}}} \to {{\mathcal {A}}}$ given by the formula ![]() $M \mapsto B (^{t}{}{M}) B^{-1}$. This implies that the matrix
$M \mapsto B (^{t}{}{M}) B^{-1}$. This implies that the matrix ![]() $B$ is block diagonal. We have
$B$ is block diagonal. We have ![]() $e_i{{\mathcal {A}}}e_i = M_{n_i}(R)$ (see [Reference Bellaïche and ChenevierBC09, Lemma 1.4.3] and [Reference ChenevierChe14, Theorem 2.22]) and,for each
$e_i{{\mathcal {A}}}e_i = M_{n_i}(R)$ (see [Reference Bellaïche and ChenevierBC09, Lemma 1.4.3] and [Reference ChenevierChe14, Theorem 2.22]) and,for each ![]() $i \ne j$, we have
$i \ne j$, we have ![]() $e_i{{\mathcal {A}}}e_j = M_{n_i,n_j}({{\mathcal {A}}}_{i,j})$, where
$e_i{{\mathcal {A}}}e_j = M_{n_i,n_j}({{\mathcal {A}}}_{i,j})$, where ![]() ${{\mathcal {A}}}_{i,j} \subset R$ is an ideal [Reference Bellaïche and ChenevierBC09, Proposition 1.3.8].
${{\mathcal {A}}}_{i,j} \subset R$ is an ideal [Reference Bellaïche and ChenevierBC09, Proposition 1.3.8].
Since ![]() $\det \circ \, r = \det \circ \, \bar {r}$, Proposition 2.5 shows that
$\det \circ \, r = \det \circ \, \bar {r}$, Proposition 2.5 shows that ![]() $\sum _{i \ne j}{{\mathcal {A}}}_{i,j}{{\mathcal {A}}}_{j,i} = 0$. This implies that for each
$\sum _{i \ne j}{{\mathcal {A}}}_{i,j}{{\mathcal {A}}}_{j,i} = 0$. This implies that for each ![]() $i$ the map
$i$ the map
given by
is an algebra homomorphism and we get an ![]() $R$-valued lift of
$R$-valued lift of ![]() $\bar {\rho }_i$. By the uniqueness assertion in Proposition 2.5, the determinant of this lift is equal to
$\bar {\rho }_i$. By the uniqueness assertion in Proposition 2.5, the determinant of this lift is equal to ![]() $\det \circ \bar {\rho }_i$. Since
$\det \circ \bar {\rho }_i$. Since ![]() $\bar {\rho }_i$ is absolutely irreducible, it follows from [Reference ChenevierChe14, Theorem 2.22] that, after conjugating by a block diagonal matrix in
$\bar {\rho }_i$ is absolutely irreducible, it follows from [Reference ChenevierChe14, Theorem 2.22] that, after conjugating by a block diagonal matrix in ![]() $1+M_n({{\mathfrak m}}_R)$, we can assume that the map
$1+M_n({{\mathfrak m}}_R)$, we can assume that the map
is induced by ![]() $\bar {\rho }_i$, which is the desired statement.
$\bar {\rho }_i$, which is the desired statement.
Finally, we consider the matrix ![]() $B$. We have already shown that
$B$. We have already shown that ![]() $B$ is block diagonal. For
$B$ is block diagonal. For ![]() $1\le i \le {{d}}$, we denote the corresponding block of
$1\le i \le {{d}}$, we denote the corresponding block of ![]() $B$ by
$B$ by ![]() $B_i$. It lifts a block
$B_i$. It lifts a block ![]() $\bar {B}_i$ of
$\bar {B}_i$ of ![]() $\bar {B}$. By Schur's lemma, we have
$\bar {B}$. By Schur's lemma, we have ![]() $B_i = \beta _i\bar {B}_i$ for some scalars
$B_i = \beta _i\bar {B}_i$ for some scalars ![]() $\beta _i \in 1+{{\mathfrak m}}_R$. Since
$\beta _i \in 1+{{\mathfrak m}}_R$. Since ![]() $2$ is invertible in
$2$ is invertible in ![]() $R$, we can find
$R$, we can find ![]() $\lambda _i \in 1+{{\mathfrak m}}_R$ with
$\lambda _i \in 1+{{\mathfrak m}}_R$ with ![]() $\lambda _i^{2} = \beta _i^{-1}$. Conjugating
$\lambda _i^{2} = \beta _i^{-1}$. Conjugating ![]() $r$ by the diagonal matrix with
$r$ by the diagonal matrix with ![]() $\lambda _i$ in the
$\lambda _i$ in the ![]() $i$th block puts
$i$th block puts ![]() $r$ into the desired form.
$r$ into the desired form.
Proof of Proposition 3.2 We begin by proving the first part. We again let ![]() $R = R_{{{\mathcal {S}}}}^{\rm univ}/({{\mathfrak m}}_{P_{{{\mathcal {S}}}}})$. By Nakayama's lemma, it suffices to show that
$R = R_{{{\mathcal {S}}}}^{\rm univ}/({{\mathfrak m}}_{P_{{{\mathcal {S}}}}})$. By Nakayama's lemma, it suffices to show that ![]() $R^{\mu _2^{{d}}} = k$. Indeed, the natural map
$R^{\mu _2^{{d}}} = k$. Indeed, the natural map ![]() $(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}/{{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}} \to R^{\mu _2^{{d}}}$ is injective (i.e.
$(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}/{{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}} \to R^{\mu _2^{{d}}}$ is injective (i.e. ![]() $({{\mathfrak m}}_{P_{{{\mathcal {S}}}}}R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}} = {{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}$), since if
$({{\mathfrak m}}_{P_{{{\mathcal {S}}}}}R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}} = {{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}$), since if ![]() $\sum _i m_i x_i$ is
$\sum _i m_i x_i$ is ![]() ${\mu _2^{{d}}}$-invariant, with
${\mu _2^{{d}}}$-invariant, with ![]() $m_i \in {{\mathfrak m}}_{P_{{{\mathcal {S}}}}}$ and
$m_i \in {{\mathfrak m}}_{P_{{{\mathcal {S}}}}}$ and ![]() $x_i \in R_{{{\mathcal {S}}}}^{\rm univ}$, we have
$x_i \in R_{{{\mathcal {S}}}}^{\rm univ}$, we have ![]() $\sum _i m_i x_i = ({1}/{2^{d}})\sum _i m_i\sum _{\sigma \in \mu _2^{d}} \sigma x_i$, which is an element of
$\sum _i m_i x_i = ({1}/{2^{d}})\sum _i m_i\sum _{\sigma \in \mu _2^{d}} \sigma x_i$, which is an element of ![]() ${{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}$. Let
${{\mathfrak m}}_{P_{{{\mathcal {S}}}}}(R_{{{\mathcal {S}}}}^{\rm univ})^{\mu _2^{{d}}}$. Let ![]() $r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation satisfying the conclusion of Lemma 3.3. Then
$r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation satisfying the conclusion of Lemma 3.3. Then ![]() $R$ is a finite
$R$ is a finite ![]() $k$-algebra and is generated as a
$k$-algebra and is generated as a ![]() $k$-algebra by the matrix entries of
$k$-algebra by the matrix entries of ![]() $r$ and hence the matrix entries of
$r$ and hence the matrix entries of ![]() $\rho = r|_{G_{F, S}}$ (because
$\rho = r|_{G_{F, S}}$ (because ![]() $B = \bar {B}$). We recall the ideals
$B = \bar {B}$). We recall the ideals ![]() ${{\mathcal {A}}}_{i,j}\subset R$ appearing in the proof of Lemma 3.3, which are generated by the block
${{\mathcal {A}}}_{i,j}\subset R$ appearing in the proof of Lemma 3.3, which are generated by the block ![]() $(i,j)$ matrix entries of
$(i,j)$ matrix entries of ![]() $\rho$. The conjugate self-duality of
$\rho$. The conjugate self-duality of ![]() $\rho$ is given by
$\rho$ is given by ![]() ${}^{t} \rho (\delta ) = \chi (\delta )\bar {B}^{-1} \rho ((\delta ^{c})^{-1}) \bar {B}$,
${}^{t} \rho (\delta ) = \chi (\delta )\bar {B}^{-1} \rho ((\delta ^{c})^{-1}) \bar {B}$, ![]() $\delta \in G_{F,S}$. Since
$\delta \in G_{F,S}$. Since ![]() $\bar {B}$ is block diagonal, we deduce that
$\bar {B}$ is block diagonal, we deduce that ![]() ${{\mathcal {A}}}_{i,j}= {{\mathcal {A}}}_{j,i}$. Since
${{\mathcal {A}}}_{i,j}= {{\mathcal {A}}}_{j,i}$. Since ![]() $\sum _{i \ne j}{{\mathcal {A}}}_{i,j}{{\mathcal {A}}}_{j,i} = 0$, we see that
$\sum _{i \ne j}{{\mathcal {A}}}_{i,j}{{\mathcal {A}}}_{j,i} = 0$, we see that ![]() ${{\mathcal {A}}}_{i,j}^{2} = 0$ for
${{\mathcal {A}}}_{i,j}^{2} = 0$ for ![]() $i \ne j$. We deduce that
$i \ne j$. We deduce that ![]() $R$ is generated as a
$R$ is generated as a ![]() $k$-module by
$k$-module by ![]() $1 \in R$ and products of the form
$1 \in R$ and products of the form
where ![]() $\emptyset \ne {{\mathcal {P}}} \subset \{(i,j): 1\le i < j \le {{d}}\}$ and
$\emptyset \ne {{\mathcal {P}}} \subset \{(i,j): 1\le i < j \le {{d}}\}$ and ![]() $a_{i,j} \in {{\mathcal {A}}}_{i,j}$ has action of
$a_{i,j} \in {{\mathcal {A}}}_{i,j}$ has action of ![]() $\mu _2^{{d}}$ given by
$\mu _2^{{d}}$ given by ![]() $((-1)^{\alpha _1},\ldots , (-1)^{\alpha _{{d}}})a_{i,j} = (-1)^{\alpha _i+\alpha _j}a_{i,j}$. Suppose that the action of
$((-1)^{\alpha _1},\ldots , (-1)^{\alpha _{{d}}})a_{i,j} = (-1)^{\alpha _i+\alpha _j}a_{i,j}$. Suppose that the action of ![]() $\mu _2^{{d}}$ on
$\mu _2^{{d}}$ on ![]() $a_{{{\mathcal {P}}}}$ is trivial. Then, for each
$a_{{{\mathcal {P}}}}$ is trivial. Then, for each ![]() $1 \le i \le {{d}}$,
$1 \le i \le {{d}}$, ![]() $i$ appears in an even number of elements of
$i$ appears in an even number of elements of ![]() ${{\mathcal {P}}}$. A product
${{\mathcal {P}}}$. A product ![]() $a'_{j_1,j_2} = a_{1,j_1}a_{1,j_2}$ lies in
$a'_{j_1,j_2} = a_{1,j_1}a_{1,j_2}$ lies in ![]() ${{\mathcal {A}}}_{j_1,j_2}$ and the action of
${{\mathcal {A}}}_{j_1,j_2}$ and the action of ![]() $\mu _2^{{d}}$ is given by
$\mu _2^{{d}}$ is given by ![]() $((-1)^{\alpha _1},\ldots ,(-1)^{\alpha _{{d}}})a'_{j_1,j_2} = (-1)^{\alpha _{j_1}+\alpha _{j_2}}a'_{j_1,j_2}$. Since
$((-1)^{\alpha _1},\ldots ,(-1)^{\alpha _{{d}}})a'_{j_1,j_2} = (-1)^{\alpha _{j_1}+\alpha _{j_2}}a'_{j_1,j_2}$. Since ![]() $1$ appears in an even number of elements of
$1$ appears in an even number of elements of ![]() ${{\mathcal {P}}}$, we can ‘pair off’ these elements and rewrite
${{\mathcal {P}}}$, we can ‘pair off’ these elements and rewrite ![]() $a_{{\mathcal {P}}}$ as a product
$a_{{\mathcal {P}}}$ as a product
where ![]() ${{\mathcal {P}}}' \subset \{(i,j): 2\le i < j \le {{d}}\}$ and the action of
${{\mathcal {P}}}' \subset \{(i,j): 2\le i < j \le {{d}}\}$ and the action of ![]() $\mu _2^{{d}}$ on
$\mu _2^{{d}}$ on ![]() $a'_{i,j}$ is given by the same formula as for
$a'_{i,j}$ is given by the same formula as for ![]() $a_{i,j}$. Continuing in this manner, we deduce that
$a_{i,j}$. Continuing in this manner, we deduce that ![]() $a_{{{\mathcal {P}}}}$ is the product of an even number of elements of
$a_{{{\mathcal {P}}}}$ is the product of an even number of elements of ![]() ${{\mathcal {A}}}_{{{d}}-1, {{d}}}$ and thus equals
${{\mathcal {A}}}_{{{d}}-1, {{d}}}$ and thus equals ![]() $0$ since
$0$ since ![]() ${{\mathcal {A}}}_{{{d}}-1, {{d}}}^{2} = 0$.
${{\mathcal {A}}}_{{{d}}-1, {{d}}}^{2} = 0$.
The invariant subring ![]() $R^{\mu _2^{{d}}}$ is equal to the
$R^{\mu _2^{{d}}}$ is equal to the ![]() $k$-submodule of
$k$-submodule of ![]() $R$ generated by
$R$ generated by ![]() $\sum _{\sigma \in \mu _2^{{d}}} \sigma x$, where
$\sum _{\sigma \in \mu _2^{{d}}} \sigma x$, where ![]() $x$ runs over a set of
$x$ runs over a set of ![]() $k$-module generators of
$k$-module generators of ![]() $R$ (since
$R$ (since ![]() $2$ is invertible in
$2$ is invertible in ![]() $k$). It follows from the above calculation that
$k$). It follows from the above calculation that ![]() $R^{\mu _2^{{d}}} = k$.
$R^{\mu _2^{{d}}} = k$.
We now prove the second part. The diagonally embedded subgroup ![]() $\mu _2 \subseteq \mu _2^{{d}}$ acts trivially on
$\mu _2 \subseteq \mu _2^{{d}}$ acts trivially on ![]() $R_{{{\mathcal {S}}}}^{\rm univ}$, so we have an induced action of
$R_{{{\mathcal {S}}}}^{\rm univ}$, so we have an induced action of ![]() $\mu _2^{{d}}/\mu _2$. The first part together with [Sta17, Tag 0BRI] implies that
$\mu _2^{{d}}/\mu _2$. The first part together with [Sta17, Tag 0BRI] implies that ![]() $\mu _2^{{d}} / \mu _2$ acts transitively on the set of primes of
$\mu _2^{{d}} / \mu _2$ acts transitively on the set of primes of ![]() $R_{{{\mathcal {S}}}}^{\rm univ}$ above
$R_{{{\mathcal {S}}}}^{\rm univ}$ above ![]() ${{\mathfrak q}}$. Let
${{\mathfrak q}}$. Let ![]() $R = R_{{{\mathcal {S}}}}^{\rm univ}/{{\mathfrak p}}$ and let
$R = R_{{{\mathcal {S}}}}^{\rm univ}/{{\mathfrak p}}$ and let ![]() $r_{{{\mathfrak p}}} \colon G_{F^{+},S} \rightarrow {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation. By [Sta17, Tag 0BST], to finish the proof if will be enough to show that if
$r_{{{\mathfrak p}}} \colon G_{F^{+},S} \rightarrow {{\mathcal {G}}}_n(R)$ be a representative of the specialization of the universal deformation. By [Sta17, Tag 0BST], to finish the proof if will be enough to show that if ![]() $\sigma \in \mu _2^{{d}}$,
$\sigma \in \mu _2^{{d}}$, ![]() $\sigma ({{\mathfrak p}}) = {{\mathfrak p}}$, and
$\sigma ({{\mathfrak p}}) = {{\mathfrak p}}$, and ![]() $\sigma$ acts as the identity on
$\sigma$ acts as the identity on ![]() $R$, then
$R$, then ![]() $\sigma \in \mu _2$.
$\sigma \in \mu _2$.
If ![]() $\sigma \in \mu _2^{{d}}$ corresponds to the block diagonal matrix
$\sigma \in \mu _2^{{d}}$ corresponds to the block diagonal matrix ![]() $g\in \operatorname {GL}_n({{\mathcal {O}}})$, then these conditions imply that
$g\in \operatorname {GL}_n({{\mathcal {O}}})$, then these conditions imply that ![]() $r_{{{\mathfrak p}}}$ and
$r_{{{\mathfrak p}}}$ and ![]() $g r_{{{\mathfrak p}}} g^{-1}$ are conjugate by an element
$g r_{{{\mathfrak p}}} g^{-1}$ are conjugate by an element ![]() $\gamma \in 1+M_n({{\mathfrak m}}_R)$. Since
$\gamma \in 1+M_n({{\mathfrak m}}_R)$. Since ![]() $r_{{{\mathfrak p}}}|_{G_{F,S}}\otimes E = \rho _{{{\mathfrak p}}}$ is absolutely irreducible, this implies that
$r_{{{\mathfrak p}}}|_{G_{F,S}}\otimes E = \rho _{{{\mathfrak p}}}$ is absolutely irreducible, this implies that ![]() $g\gamma ^{-1}$ is scalar and so
$g\gamma ^{-1}$ is scalar and so ![]() $g$ must also be scalar as
$g$ must also be scalar as ![]() $l>2$; hence,
$l>2$; hence, ![]() $g \in \mu _2$. This completes the proof.
$g \in \mu _2$. This completes the proof.
For each partition ![]() $\{1, \ldots , {{d}}\} = {{\mathcal {P}}}_1 \sqcup {{\mathcal {P}}}_2$ with
$\{1, \ldots , {{d}}\} = {{\mathcal {P}}}_1 \sqcup {{\mathcal {P}}}_2$ with ![]() ${{\mathcal {P}}}_1, {{\mathcal {P}}}_2$ both non-empty, Proposition 2.5 gives an ideal
${{\mathcal {P}}}_1, {{\mathcal {P}}}_2$ both non-empty, Proposition 2.5 gives an ideal ![]() $I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \subset P_{{\mathcal {S}}}$ cutting out the locus where the determinant
$I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \subset P_{{\mathcal {S}}}$ cutting out the locus where the determinant ![]() $\det r|_{G_{F, S}}$ is
$\det r|_{G_{F, S}}$ is ![]() $({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)$-reducible. We write
$({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)$-reducible. We write ![]() $I_{{\mathcal {S}}}^{\rm red} = \prod _{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$, an ideal of
$I_{{\mathcal {S}}}^{\rm red} = \prod _{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$, an ideal of ![]() $P_{{\mathcal {S}}}$.
$P_{{\mathcal {S}}}$.
Lemma 3.4 Let ![]() ${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ be a prime ideal and let
${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ be a prime ideal and let ![]() ${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{{\mathcal {S}}}}$. Let
${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{{\mathcal {S}}}}$. Let ![]() $A = R_{{{\mathcal {S}}}}^{\text {univ}} / {{\mathfrak p}}$,
$A = R_{{{\mathcal {S}}}}^{\text {univ}} / {{\mathfrak p}}$, ![]() $E = \operatorname {Frac} A$. Then
$E = \operatorname {Frac} A$. Then ![]() $\rho _{{\mathfrak p}} = r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E$ is absolutely irreducible if and only if
$\rho _{{\mathfrak p}} = r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E$ is absolutely irreducible if and only if ![]() $I_{{\mathcal {S}}}^{\rm red} \not \subset {{\mathfrak q}}$.
$I_{{\mathcal {S}}}^{\rm red} \not \subset {{\mathfrak q}}$.
Proof. If ![]() $I_{{\mathcal {S}}}^{\rm red} \subset {{\mathfrak q}}$, then
$I_{{\mathcal {S}}}^{\rm red} \subset {{\mathfrak q}}$, then ![]() $I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \subset {{\mathfrak q}}$ for some proper partition
$I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \subset {{\mathfrak q}}$ for some proper partition ![]() $({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)$. Then Proposition 2.5 implies that
$({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)$. Then Proposition 2.5 implies that ![]() $\det r_{{\mathfrak p}}$ admits a decomposition
$\det r_{{\mathfrak p}}$ admits a decomposition ![]() $\det \circ r_{{\mathfrak p}}|_{G_{F,S}} = D_1 D_2$ for two determinants
$\det \circ r_{{\mathfrak p}}|_{G_{F,S}} = D_1 D_2$ for two determinants ![]() $D_i : A[G_{F, S}] \to M_{n_i}(A)$. Then [Reference ChenevierChe14, Corollary 2.13] implies that
$D_i : A[G_{F, S}] \to M_{n_i}(A)$. Then [Reference ChenevierChe14, Corollary 2.13] implies that ![]() $\rho _{{\mathfrak p}}$ is not absolutely irreducible.
$\rho _{{\mathfrak p}}$ is not absolutely irreducible.
Suppose conversely that ![]() $\rho _{{\mathfrak p}}$ is not absolutely irreducible. Let
$\rho _{{\mathfrak p}}$ is not absolutely irreducible. Let ![]() $J_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ denote the image of
$J_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ denote the image of ![]() $I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ in
$I_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ in ![]() $A$. We must show that some
$A$. We must show that some ![]() $J_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ is zero. Let
$J_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)}$ is zero. Let ![]() ${{\mathcal {A}}}$ denote the image of
${{\mathcal {A}}}$ denote the image of ![]() $A[G_{F, S}]$ in
$A[G_{F, S}]$ in ![]() $M_n(A)$ under
$M_n(A)$ under ![]() $r_{{\mathfrak p}}|_{G_{F, S}}$. According to [Reference Bellaïche and ChenevierBC09, Theorem 1.4.4], we can assume that
$r_{{\mathfrak p}}|_{G_{F, S}}$. According to [Reference Bellaïche and ChenevierBC09, Theorem 1.4.4], we can assume that ![]() ${{\mathcal {A}}}$ has the form
${{\mathcal {A}}}$ has the form
 \begin{equation} {{\mathcal{A}}} = \begin{pmatrix} M_{n_1}(A) & M_{n_1,n_2}(\mathcal{A}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{A}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{A}_{2,1}) & M_{n_2}(A) & \cdots & M_{n_2,n_{{d}}}(\mathcal{A}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{A}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{A}_{{{d}},2}) & \cdots & M_{n_{{d}}}(A) \end{pmatrix}\!, \end{equation}
\begin{equation} {{\mathcal{A}}} = \begin{pmatrix} M_{n_1}(A) & M_{n_1,n_2}(\mathcal{A}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{A}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{A}_{2,1}) & M_{n_2}(A) & \cdots & M_{n_2,n_{{d}}}(\mathcal{A}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{A}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{A}_{{{d}},2}) & \cdots & M_{n_{{d}}}(A) \end{pmatrix}\!, \end{equation}
where each ![]() $\mathcal {A}_{i, j}$ is a fractional ideal of
$\mathcal {A}_{i, j}$ is a fractional ideal of ![]() $E$. Consequently,
$E$. Consequently, ![]() ${{\mathcal {A}}} \otimes _A E$ has the form
${{\mathcal {A}}} \otimes _A E$ has the form
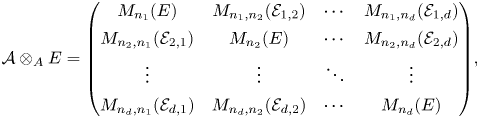 \begin{equation} {{\mathcal{A}}} \otimes_A E= \begin{pmatrix} M_{n_1}(E) & M_{n_1,n_2}(\mathcal{E}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{E}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{E}_{2,1}) & M_{n_2}(E) & \cdots & M_{n_2,n_{{d}}}(\mathcal{E}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{E}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{E}_{{{d}},2}) & \cdots & M_{n_{{d}}}(E) \end{pmatrix}\!, \end{equation}
\begin{equation} {{\mathcal{A}}} \otimes_A E= \begin{pmatrix} M_{n_1}(E) & M_{n_1,n_2}(\mathcal{E}_{1,2}) & \cdots & M_{n_1,n_{{d}}}(\mathcal{E}_{1,{{d}}})\\ M_{n_2,n_1}(\mathcal{E}_{2,1}) & M_{n_2}(E) & \cdots & M_{n_2,n_{{d}}}(\mathcal{E}_{2,{{d}}})\\ \vdots & \vdots & \ddots & \vdots \\ M_{n_{{d}},n_1}(\mathcal{E}_{{{d}},1}) & M_{n_{{d}},n_2}(\mathcal{E}_{{{d}},2}) & \cdots & M_{n_{{d}}}(E) \end{pmatrix}\!, \end{equation}
where each ![]() $\mathcal {E}_{i, j} = \mathcal {A}_{i, j} \otimes _A E$ equals either
$\mathcal {E}_{i, j} = \mathcal {A}_{i, j} \otimes _A E$ equals either ![]() $E$ or
$E$ or ![]() $0$. Let
$0$. Let ![]() $f_i \in M_n(E)$ denote the matrix with 1 in the
$f_i \in M_n(E)$ denote the matrix with 1 in the ![]() $(i, i)$th entry and 0 everywhere else. If
$(i, i)$th entry and 0 everywhere else. If ![]() $\rho _{{\mathfrak p}}$ is not absolutely irreducible, then
$\rho _{{\mathfrak p}}$ is not absolutely irreducible, then ![]() ${{\mathcal {A}}} \otimes _A E$ is a proper subspace of
${{\mathcal {A}}} \otimes _A E$ is a proper subspace of ![]() $M_n(E)$, so there exists
$M_n(E)$, so there exists ![]() $i$ such that
$i$ such that ![]() $({{\mathcal {A}}} \otimes _A E) f_i \subset M_n(E) f_i$ is a proper subspace. Since
$({{\mathcal {A}}} \otimes _A E) f_i \subset M_n(E) f_i$ is a proper subspace. Since ![]() $M_n(E) f_i$ is isomorphic as an
$M_n(E) f_i$ is isomorphic as an ![]() $M_n(E)$-module to the tautological representation
$M_n(E)$-module to the tautological representation ![]() $E^{n}$, this implies that the
$E^{n}$, this implies that the ![]() ${{\mathcal {A}}} \otimes _A E$-module
${{\mathcal {A}}} \otimes _A E$-module ![]() $E^{n}$ admits a proper invariant subspace. After permuting the diagonal blocks, we can assume that this subspace is
$E^{n}$ admits a proper invariant subspace. After permuting the diagonal blocks, we can assume that this subspace is ![]() $E^{n_1 + \cdots + n_s}$ for some
$E^{n_1 + \cdots + n_s}$ for some ![]() $s < {{d}}$ (included as the subspace of
$s < {{d}}$ (included as the subspace of ![]() $E^{n}$ where the last
$E^{n}$ where the last ![]() $n_{s+1} + \cdots + n_{{d}}$ entries are zero). Otherwise said, the spaces
$n_{s+1} + \cdots + n_{{d}}$ entries are zero). Otherwise said, the spaces ![]() $\mathcal {E}_{i, j}$ for
$\mathcal {E}_{i, j}$ for ![]() $i > s$,
$i > s$, ![]() $j \leq s$ are zero. If
$j \leq s$ are zero. If ![]() ${{\mathcal {P}}}_1 = \{ 1, \ldots , s \}$ and
${{\mathcal {P}}}_1 = \{ 1, \ldots , s \}$ and ![]() ${{\mathcal {P}}}_2 = \{ s+1, \ldots , {d}\}$, then this implies that
${{\mathcal {P}}}_2 = \{ s+1, \ldots , {d}\}$, then this implies that ![]() ${{\mathcal {J}}}_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \otimes _A E = 0$ and hence (as
${{\mathcal {J}}}_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} \otimes _A E = 0$ and hence (as ![]() $A$ is a domain)
$A$ is a domain) ![]() ${{\mathcal {J}}}_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} = 0$. This completes the proof.
${{\mathcal {J}}}_{({{\mathcal {P}}}_1, {{\mathcal {P}}}_2)} = 0$. This completes the proof.
Lemma 3.5 Let ![]() ${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ be a prime ideal,
${{\mathfrak p}} \subset R_{{\mathcal {S}}}^{\text {univ}}$ be a prime ideal, ![]() $A = R_{{\mathcal {S}}}^{\text {univ}} / {{\mathfrak p}}$,
$A = R_{{\mathcal {S}}}^{\text {univ}} / {{\mathfrak p}}$, ![]() $E = \operatorname {Frac} A$. Then
$E = \operatorname {Frac} A$. Then ![]() $r_{{\mathfrak p}}\otimes _A E$ is Schur and, if
$r_{{\mathfrak p}}\otimes _A E$ is Schur and, if ![]() $r_{{\mathfrak p}}|_{G_{F, S}} \otimes _A E$ is not absolutely irreducible, then
$r_{{\mathfrak p}}|_{G_{F, S}} \otimes _A E$ is not absolutely irreducible, then ![]() $r_{{\mathfrak p}}$ is equivalent (i.e. conjugate by an element in
$r_{{\mathfrak p}}$ is equivalent (i.e. conjugate by an element in ![]() $1+ M_n({{\mathfrak m}}_A)$) to a type-
$1+ M_n({{\mathfrak m}}_A)$) to a type-![]() ${{\mathcal {S}}}$ lifting of the form
${{\mathcal {S}}}$ lifting of the form ![]() $r_{{\mathfrak p}} = r_1 \oplus r_2$, where
$r_{{\mathfrak p}} = r_1 \oplus r_2$, where ![]() $r_i : G_{F^{+}, S} \to {{\mathcal {G}}}_{m_i}(A)$ and
$r_i : G_{F^{+}, S} \to {{\mathcal {G}}}_{m_i}(A)$ and ![]() $m_1 m_2 \neq 0$.
$m_1 m_2 \neq 0$.
Proof. We argue, as in the proof of Lemma 3.4, using the image ![]() ${{\mathcal {A}}} \subset M_n(A)$ of
${{\mathcal {A}}} \subset M_n(A)$ of ![]() $A[G_{F, S}]$, which is a generalized matrix algebra. Suppose that we are given
$A[G_{F, S}]$, which is a generalized matrix algebra. Suppose that we are given ![]() $G_{F, S}$-invariant subspaces
$G_{F, S}$-invariant subspaces ![]() $E^{n} \supset W_1 \supset W_2$ such that
$E^{n} \supset W_1 \supset W_2$ such that ![]() $W_2$ and
$W_2$ and ![]() $E^{n} / W_1$ are irreducible. We can assume that
$E^{n} / W_1$ are irreducible. We can assume that ![]() ${{\mathcal {A}}}$ has the form (2) and that this decomposition is block upper triangular (perhaps with respect to a coarser partition than
${{\mathcal {A}}}$ has the form (2) and that this decomposition is block upper triangular (perhaps with respect to a coarser partition than ![]() $n = n_1 + \cdots + n_{{d}}$) and moreover than the first block corresponds to
$n = n_1 + \cdots + n_{{d}}$) and moreover than the first block corresponds to ![]() $W_2$, while the last block corresponds to
$W_2$, while the last block corresponds to ![]() $E^{n} / W_1$. In particular,
$E^{n} / W_1$. In particular, ![]() $W_2$ and
$W_2$ and ![]() $E^{n} / W_1$ are even absolutely irreducible. Note that there can be no isomorphism
$E^{n} / W_1$ are even absolutely irreducible. Note that there can be no isomorphism ![]() $W_2^{c \vee }(\nu \circ r_{{\mathfrak p}}) \cong E^{n} / W_1$; if there was, then it would imply an identity of
$W_2^{c \vee }(\nu \circ r_{{\mathfrak p}}) \cong E^{n} / W_1$; if there was, then it would imply an identity of ![]() $A$-valued determinants, which we could reduce modulo
$A$-valued determinants, which we could reduce modulo ![]() ${{\mathfrak m}}_A$ to obtain an identity
${{\mathfrak m}}_A$ to obtain an identity ![]() $\{ \rho _{i} \} = \{ \rho _j \}$ of sets of irreducible constituents of
$\{ \rho _{i} \} = \{ \rho _j \}$ of sets of irreducible constituents of ![]() $\bar {r}|_{G_{F, S}}$. Since these appear with multiplicity 1, this is impossible. This all shows that
$\bar {r}|_{G_{F, S}}$. Since these appear with multiplicity 1, this is impossible. This all shows that ![]() $r_{{\mathfrak p}} \otimes _A E$ is necessarily Schur.
$r_{{\mathfrak p}} \otimes _A E$ is necessarily Schur.
Now suppose that ![]() $r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E$ is not absolutely irreducible. After permuting the diagonal blocks of
$r_{{\mathfrak p}}|_{G_{F, S}}\otimes _A E$ is not absolutely irreducible. After permuting the diagonal blocks of ![]() $\bar {r}$, we can assume that there is some
$\bar {r}$, we can assume that there is some ![]() $1 \leq m \leq {d}$ such that
$1 \leq m \leq {d}$ such that ![]() ${{\mathcal {A}}}_{i, j} = 0$ for
${{\mathcal {A}}}_{i, j} = 0$ for ![]() $i > m$,
$i > m$, ![]() $j \leq m$. The existence of the conjugate self-duality of
$j \leq m$. The existence of the conjugate self-duality of ![]() $r_{{\mathfrak p}}$ implies (cf. [Reference Bellaïche and ChenevierBC09, Lemma 1.8.5]) that
$r_{{\mathfrak p}}$ implies (cf. [Reference Bellaïche and ChenevierBC09, Lemma 1.8.5]) that ![]() ${{\mathcal {A}}}_{j, i} = 0$ in the same range, giving a decomposition
${{\mathcal {A}}}_{j, i} = 0$ in the same range, giving a decomposition ![]() $r_{{\mathfrak p}}|_{G_{F, S}} = \rho _1 \oplus \rho _2$ of representations over
$r_{{\mathfrak p}}|_{G_{F, S}} = \rho _1 \oplus \rho _2$ of representations over ![]() $A$. Since
$A$. Since ![]() $r_{{\mathfrak p}} \otimes _A E$ is Schur, the conjugate self-duality of
$r_{{\mathfrak p}} \otimes _A E$ is Schur, the conjugate self-duality of ![]() $r_{{\mathfrak p}}$ must make
$r_{{\mathfrak p}}$ must make ![]() $\rho _1$ and
$\rho _1$ and ![]() $\rho _2$ orthogonal, showing that
$\rho _2$ orthogonal, showing that ![]() $r_{{\mathfrak p}}$ itself decomposes as
$r_{{\mathfrak p}}$ itself decomposes as ![]() $r_{{\mathfrak p}} = r_1 \oplus r_2$.
$r_{{\mathfrak p}} = r_1 \oplus r_2$.
3.3 Dimension bounds
We now suppose that ![]() $S$ admits a decomposition
$S$ admits a decomposition ![]() $S = S_l \sqcup S(B) \sqcup R \sqcup S_a$, where:
$S = S_l \sqcup S(B) \sqcup R \sqcup S_a$, where:
– for each
 $v \in S(B) \cup R$,
$v \in S(B) \cup R$,  $q_v \equiv 1 \text { mod }l$ and
$q_v \equiv 1 \text { mod }l$ and  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial;
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is trivial;– for each
 $v \in S_a$,
$v \in S_a$,  $q_v \not \equiv 1 \text { mod }l$,
$q_v \not \equiv 1 \text { mod }l$,  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is unramified, and
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is unramified, and  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is scalar. (Then any lifting of
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is scalar. (Then any lifting of  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is unramified.)
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is unramified.)
We consider the global deformation problem
where ![]() $\bar {r}$ is assumed to be Schur. We define quantities
$\bar {r}$ is assumed to be Schur. We define quantities ![]() $d_{F, 0} = d_0$ and
$d_{F, 0} = d_0$ and ![]() $d_{F, l} = d_l$ as follows. Let
$d_{F, l} = d_l$ as follows. Let ![]() $\Delta$ denote the Galois group of the maximal abelian pro-
$\Delta$ denote the Galois group of the maximal abelian pro-![]() $l$ extension of
$l$ extension of ![]() $F$ which is unramified outside
$F$ which is unramified outside ![]() $l$, and let
$l$, and let ![]() $\Delta _0$ denote the Galois group of the maximal abelian pro-
$\Delta _0$ denote the Galois group of the maximal abelian pro-![]() $l$ extension of
$l$ extension of ![]() $F$ which is unramified outside
$F$ which is unramified outside ![]() $l$ and in which each place of
$l$ and in which each place of ![]() $S(B)$ splits completely. We set
$S(B)$ splits completely. We set
and
Lemma 3.6 Suppose that ![]() $d_l > n(n-1)/2 + 1$. Let
$d_l > n(n-1)/2 + 1$. Let ![]() $A \in {{\mathcal {C}}}_\Lambda$ be a finite
$A \in {{\mathcal {C}}}_\Lambda$ be a finite ![]() $\Lambda$-algebra and let
$\Lambda$-algebra and let ![]() $r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a lifting of
$r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a lifting of ![]() $\bar {r}$ of type
$\bar {r}$ of type ![]() ${{\mathcal {S}}}$. Then
${{\mathcal {S}}}$. Then ![]() $\dim A / (I_{{\mathcal {S}}}^{\rm red}, \lambda ) \leq n[F^{+} : {{\mathbb {Q}}}] - d_0$.
$\dim A / (I_{{\mathcal {S}}}^{\rm red}, \lambda ) \leq n[F^{+} : {{\mathbb {Q}}}] - d_0$.
Proof. We can assume without loss of generality that ![]() $A = A / (I_{{\mathcal {S}}}^{\rm red}, \lambda )$ and must show that
$A = A / (I_{{\mathcal {S}}}^{\rm red}, \lambda )$ and must show that ![]() $\dim A \leq [F^{+} : {{\mathbb {Q}}}] - d_0$. Since
$\dim A \leq [F^{+} : {{\mathbb {Q}}}] - d_0$. Since ![]() $A$ is Noetherian and we are interested only in dimension, we can assume moreover that
$A$ is Noetherian and we are interested only in dimension, we can assume moreover that ![]() $A$ is integral. Let
$A$ is integral. Let ![]() $E = \operatorname {Frac}(A)$. Then (Lemma 3.5) we can find a non-trivial partition
$E = \operatorname {Frac}(A)$. Then (Lemma 3.5) we can find a non-trivial partition ![]() $n = n_1 + n_2$ and homomorphisms
$n = n_1 + n_2$ and homomorphisms ![]() $r_i : G_{F^{+}, S} \to {{\mathcal {G}}}_{n_i}(A)$ (
$r_i : G_{F^{+}, S} \to {{\mathcal {G}}}_{n_i}(A)$ (![]() $i = 1, 2$) such that
$i = 1, 2$) such that ![]() $r = r_1 \oplus r_2$.
$r = r_1 \oplus r_2$.
Let ![]() $\bar {E}$ be a choice of algebraic closure of
$\bar {E}$ be a choice of algebraic closure of ![]() $E$. Our condition on
$E$. Our condition on ![]() $d_l$ means that we can appeal to [Reference ThorneTho15, Corollary 3.12] (characterization of
$d_l$ means that we can appeal to [Reference ThorneTho15, Corollary 3.12] (characterization of ![]() $A$-valued points of
$A$-valued points of ![]() ${{\mathcal {D}}}_v^{\triangle }$ for each
${{\mathcal {D}}}_v^{\triangle }$ for each ![]() $v \in S_l$). This result implies the existence for each
$v \in S_l$). This result implies the existence for each ![]() $v \in S_l$ of an increasing filtration
$v \in S_l$ of an increasing filtration
of ![]() $r|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$ by
$r|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$ by ![]() $G_{F_{{\widetilde {v}}}}$-invariant subspaces such that each
$G_{F_{{\widetilde {v}}}}$-invariant subspaces such that each ![]() $\operatorname {Fil}^{i}_v / \operatorname {Fil}^{i-1}_v$ is one dimensional, and the character of
$\operatorname {Fil}^{i}_v / \operatorname {Fil}^{i-1}_v$ is one dimensional, and the character of ![]() $I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ acting on this space is given by composing the universal character
$I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ acting on this space is given by composing the universal character ![]() $\psi _v^{i} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to \Lambda _v^{\times }$ with the homomorphism
$\psi _v^{i} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to \Lambda _v^{\times }$ with the homomorphism
The direct sum decomposition of ![]() $r$ leads to a decomposition
$r$ leads to a decomposition ![]() $r|_{G_{F_{{\widetilde {v}}}}} = r_1|_{G_{F_{{\widetilde {v}}}}} \oplus r_2|_{G_{F_{{\widetilde {v}}}}}$. Let
$r|_{G_{F_{{\widetilde {v}}}}} = r_1|_{G_{F_{{\widetilde {v}}}}} \oplus r_2|_{G_{F_{{\widetilde {v}}}}}$. Let ![]() $F_v^{i} = \operatorname {Fil}_v^{i} \cap r_1|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$ and
$F_v^{i} = \operatorname {Fil}_v^{i} \cap r_1|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$ and ![]() $G_v^{i} = \operatorname {Fil}_v^{i} \cap r_2|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$. Then
$G_v^{i} = \operatorname {Fil}_v^{i} \cap r_2|_{G_{F_{{\widetilde {v}}}}} \otimes _A \bar {E}$. Then ![]() $F_v^{\bullet }$ and
$F_v^{\bullet }$ and ![]() $G_v^{\bullet }$ are increasing filtrations of
$G_v^{\bullet }$ are increasing filtrations of ![]() $\bar {E}^{n_1}$ and
$\bar {E}^{n_1}$ and ![]() $\bar {E}^{n_2}$, respectively, with graded pieces of dimension at most 1. We write
$\bar {E}^{n_2}$, respectively, with graded pieces of dimension at most 1. We write ![]() $\sigma _v$ for the bijection
$\sigma _v$ for the bijection
which is increasing on ![]() $\{ 1, \ldots , n_1 \}$ and
$\{ 1, \ldots , n_1 \}$ and ![]() $\{ 1, \ldots , n_2 \}$ and which has the property that
$\{ 1, \ldots , n_2 \}$ and which has the property that ![]() $\sigma _v( \{ 1, \ldots , n_1 \} )$ is the set of
$\sigma _v( \{ 1, \ldots , n_1 \} )$ is the set of ![]() $i \in \{1, \ldots , n\}$ such that the graded piece
$i \in \{1, \ldots , n\}$ such that the graded piece ![]() $F_v^{i} / F_v^{i-1}$ is non-trivial.
$F_v^{i} / F_v^{i-1}$ is non-trivial.
Let ![]() $\Lambda _{v, 1}$ and
$\Lambda _{v, 1}$ and ![]() $\Lambda _{v, 2}$ denote the analogues of the algebra
$\Lambda _{v, 2}$ denote the analogues of the algebra ![]() $\Lambda _v$ in dimensions
$\Lambda _v$ in dimensions ![]() $n_1$ and
$n_1$ and ![]() $n_2$, respectively. The bijection
$n_2$, respectively. The bijection ![]() $\sigma _v$ determines in an obvious way an isomorphism
$\sigma _v$ determines in an obvious way an isomorphism ![]() $\Lambda _{v, 1} \hat {\otimes } \Lambda _{v, 2} \cong \Lambda _v$. Applying again [Reference ThorneTho15, Corollary 3.12], we see that with this structure on
$\Lambda _{v, 1} \hat {\otimes } \Lambda _{v, 2} \cong \Lambda _v$. Applying again [Reference ThorneTho15, Corollary 3.12], we see that with this structure on ![]() $A$ of
$A$ of ![]() $\Lambda _{v, i}$-algebra, each homomorphism
$\Lambda _{v, i}$-algebra, each homomorphism ![]() $r_i|_{G_{F_{{\widetilde {v}}}}} : G_{F_{{\widetilde {v}}}} \to \operatorname {GL}_{n_i}(A)$ is of type
$r_i|_{G_{F_{{\widetilde {v}}}}} : G_{F_{{\widetilde {v}}}} \to \operatorname {GL}_{n_i}(A)$ is of type ![]() ${{\mathcal {D}}}_v^{\triangle }(A)$. Similarly if we define
${{\mathcal {D}}}_v^{\triangle }(A)$. Similarly if we define ![]() $\Lambda _i = \hat {\otimes }_{v \in S_l} \Lambda _{v, i}$ then the collection of bijections
$\Lambda _i = \hat {\otimes }_{v \in S_l} \Lambda _{v, i}$ then the collection of bijections ![]() $(\sigma _v)_{v \in S_l}$ determines an isomorphism
$(\sigma _v)_{v \in S_l}$ determines an isomorphism ![]() $\Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \cong \Lambda$.
$\Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \cong \Lambda$.
We also define ![]() $\Lambda _{v, 0} = {{\mathcal {O}}} [\kern-1pt[ I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) ]\kern-1pt]$ and
$\Lambda _{v, 0} = {{\mathcal {O}}} [\kern-1pt[ I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) ]\kern-1pt]$ and ![]() $\Lambda _0 = \hat {\otimes }_{v \in S_l} \Lambda _{v, 0}$. Then there are natural maps
$\Lambda _0 = \hat {\otimes }_{v \in S_l} \Lambda _{v, 0}$. Then there are natural maps ![]() $\Lambda _0 \to \Lambda _i$ classifying the characters
$\Lambda _0 \to \Lambda _i$ classifying the characters ![]() $\prod _{j=1}^{n_i} \psi _v^{j} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to \Lambda _{v, i}^{\times }$. Let
$\prod _{j=1}^{n_i} \psi _v^{j} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to \Lambda _{v, i}^{\times }$. Let ![]() $\bar {\chi }_i = \det \bar {r}_i|_{G_{F, S}}$. We get a commutative diagram
$\bar {\chi }_i = \det \bar {r}_i|_{G_{F, S}}$. We get a commutative diagram
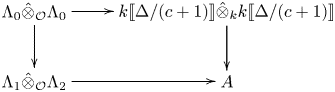
where the map ![]() $k[\kern-1pt[ \Delta / (c+1) ]\kern-1pt] \hat {\otimes }_k k[\kern-1pt[ \Delta / (c+1) ]\kern-1pt] \to A$ classifies the pair of
$k[\kern-1pt[ \Delta / (c+1) ]\kern-1pt] \hat {\otimes }_k k[\kern-1pt[ \Delta / (c+1) ]\kern-1pt] \to A$ classifies the pair of ![]() $A$-valued characters
$A$-valued characters ![]() $(\chi _1, \chi _2) = ( \bar {\chi }_1^{-1} \det r_1|_{G_F}, \bar {\chi }_2^{-1} \det r_2|_{G_F})$ of the group
$(\chi _1, \chi _2) = ( \bar {\chi }_1^{-1} \det r_1|_{G_F}, \bar {\chi }_2^{-1} \det r_2|_{G_F})$ of the group ![]() $\Delta / (c+1)$. The natural map
$\Delta / (c+1)$. The natural map ![]() $\Lambda _{0}/(\lambda ) \to k [\kern-1pt[ \Delta / (c+1) ]\kern-1pt]$ is finite (and dominant). (Note that
$\Lambda _{0}/(\lambda ) \to k [\kern-1pt[ \Delta / (c+1) ]\kern-1pt]$ is finite (and dominant). (Note that ![]() $\det r_1$ and
$\det r_1$ and ![]() $\det r_2$ are unramified at places of
$\det r_2$ are unramified at places of ![]() $S(B) \cup R \cup S_a$ because of our choices of deformation problem.)
$S(B) \cup R \cup S_a$ because of our choices of deformation problem.)
We now use the existence of the places ![]() $S(B)$. For each place
$S(B)$. For each place ![]() $v \in S(B)$, imposing the Steinberg condition on
$v \in S(B)$, imposing the Steinberg condition on ![]() $r_1 \oplus r_2$ determines a relation
$r_1 \oplus r_2$ determines a relation ![]() $\chi _1(\operatorname {Frob}_{{\widetilde {v}}})^{n_2} = \chi _2(\operatorname {Frob}_{{\widetilde {v}}})^{n_1}$ in
$\chi _1(\operatorname {Frob}_{{\widetilde {v}}})^{n_2} = \chi _2(\operatorname {Frob}_{{\widetilde {v}}})^{n_1}$ in ![]() $A$. Let
$A$. Let ![]() ${{\mathcal {E}}}$ denote the quotient of the group
${{\mathcal {E}}}$ denote the quotient of the group ![]() $\Delta / (c+1) \times \Delta / (c+1)$ by the
$\Delta / (c+1) \times \Delta / (c+1)$ by the ![]() ${{\mathbb {Z}}}_l$-submodule generated by the elements
${{\mathbb {Z}}}_l$-submodule generated by the elements ![]() $(n_2 \operatorname {Frob}_{{\widetilde {v}}}, -n_1 \operatorname {Frob}_{{\widetilde {v}}})$ (
$(n_2 \operatorname {Frob}_{{\widetilde {v}}}, -n_1 \operatorname {Frob}_{{\widetilde {v}}})$ (![]() $v \in S(B$)). Then
$v \in S(B$)). Then ![]() $\dim _{{{\mathbb {Q}}}_l} {{\mathcal {E}}}[1/l] = \dim _{{{\mathbb {Q}}}_l} (\Delta / (c+1)\times \Delta / (c+1))[1/l] - d_0$ and we in fact have the following commutative diagram.
$\dim _{{{\mathbb {Q}}}_l} {{\mathcal {E}}}[1/l] = \dim _{{{\mathbb {Q}}}_l} (\Delta / (c+1)\times \Delta / (c+1))[1/l] - d_0$ and we in fact have the following commutative diagram.
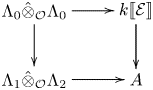
We deduce that the map ![]() $\Lambda \cong \Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \to A$ factors through the quotient
$\Lambda \cong \Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \to A$ factors through the quotient ![]() $\Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \otimes _{\Lambda _{0} \hat {\otimes }_{{\mathcal {O}}} \Lambda _{0}} k[\kern-1pt[ {{\mathcal {E}}} ]\kern-1pt]$ of dimension
$\Lambda _1 \hat {\otimes }_{{\mathcal {O}}} \Lambda _2 \otimes _{\Lambda _{0} \hat {\otimes }_{{\mathcal {O}}} \Lambda _{0}} k[\kern-1pt[ {{\mathcal {E}}} ]\kern-1pt]$ of dimension ![]() $n[F^{+} : {{\mathbb {Q}}}] - d_0$. Using finally that
$n[F^{+} : {{\mathbb {Q}}}] - d_0$. Using finally that ![]() $A$ is a finite
$A$ is a finite ![]() $\Lambda$-algebra, we see that
$\Lambda$-algebra, we see that ![]() $\dim A$ must satisfy the same estimate. This concludes the proof.
$\dim A$ must satisfy the same estimate. This concludes the proof.
Definition 3.7 Let ![]() $A \in {{\mathcal {C}}}_\Lambda$ and let
$A \in {{\mathcal {C}}}_\Lambda$ and let ![]() $r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a homomorphism of type
$r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a homomorphism of type ![]() ${{\mathcal {S}}}$. We say that
${{\mathcal {S}}}$. We say that ![]() $r$ is generic at
$r$ is generic at ![]() $l$ if it satisfies the following two conditions.
$l$ if it satisfies the following two conditions.
– For each
 $v \in S_l$, the universal characters
$v \in S_l$, the universal characters  $\psi ^{v}_{ 1}, \ldots , \psi ^{v}_{n} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to A^{\times }$ are distinct.
$\psi ^{v}_{ 1}, \ldots , \psi ^{v}_{n} : I^{{\text ab}}_{F_{{\widetilde {v}}}}(l) \to A^{\times }$ are distinct.– There exist
 $v \in S_l$ and
$v \in S_l$ and  $\sigma \in I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ such that the elements
$\sigma \in I^{{\text ab}}_{F_{{\widetilde {v}}}}(l)$ such that the elements  $\psi ^{v}_1(\sigma ),\ldots , \psi ^{v}_n(\sigma ) \in A^{\times }$ satisfy no non-trivial
$\psi ^{v}_1(\sigma ),\ldots , \psi ^{v}_n(\sigma ) \in A^{\times }$ satisfy no non-trivial  ${{\mathbb {Z}}}$-linear relation.
${{\mathbb {Z}}}$-linear relation.
We say that ![]() $r$ is generic if it is generic at
$r$ is generic if it is generic at ![]() $l$,
$l$, ![]() $A$ is a domain, and
$A$ is a domain, and ![]() $r|_{G_F} \otimes _A \operatorname {Frac}(A)$ is absolutely irreducible.
$r|_{G_F} \otimes _A \operatorname {Frac}(A)$ is absolutely irreducible.
Lemma 3.8 There exists a countable collection of ideals ![]() $I_i \subset \Lambda /(\lambda )$ (
$I_i \subset \Lambda /(\lambda )$ (![]() $i = 1, 2, \ldots$) with the following properties.
$i = 1, 2, \ldots$) with the following properties.
(i) For each
 $i = 1, 2, \ldots$, we have
$i = 1, 2, \ldots$, we have  $\dim \Lambda / I_i \leq n[F^{+} : {{\mathbb {Q}}}] - d_l$.
$\dim \Lambda / I_i \leq n[F^{+} : {{\mathbb {Q}}}] - d_l$.(ii) Suppose that
 $A \in {{\mathcal {C}}}_\Lambda$ and
$A \in {{\mathcal {C}}}_\Lambda$ and  $r : G_{F^{+}} \to {{\mathcal {G}}}_n(A)$ is a lifting of type
$r : G_{F^{+}} \to {{\mathcal {G}}}_n(A)$ is a lifting of type  ${{\mathcal {S}}}$ which is not generic at
${{\mathcal {S}}}$ which is not generic at  $l$. Then there exists
$l$. Then there exists  $i \geq 1$ such that
$i \geq 1$ such that  $I_i A = 0$.
$I_i A = 0$.
Proof. For each ![]() $v \in S_l$, let
$v \in S_l$, let ![]() $d_v = [ F^{+}_v : {{\mathbb {Q}}}_l]$ and let
$d_v = [ F^{+}_v : {{\mathbb {Q}}}_l]$ and let ![]() $\sigma _{v, 1}, \ldots , \sigma _{v, d_v} \in I^{{\text ab}}_{F_{{{\widetilde {v}}}}}(l)$ be elements which project to a
$\sigma _{v, 1}, \ldots , \sigma _{v, d_v} \in I^{{\text ab}}_{F_{{{\widetilde {v}}}}}(l)$ be elements which project to a ![]() ${{\mathbb {Z}}}_l$-basis of the
${{\mathbb {Z}}}_l$-basis of the ![]() $l$-torsion-free quotient of this finitely generated
$l$-torsion-free quotient of this finitely generated ![]() ${{\mathbb {Z}}}_l$-module.
${{\mathbb {Z}}}_l$-module.
For each ![]() $1 \leq i < j \leq n$ and
$1 \leq i < j \leq n$ and ![]() $v \in S_l$, we define an ideal
$v \in S_l$, we define an ideal ![]() $I(i, j, v) = (\lambda , \psi _v^{i}(\sigma _{v, k}) - \psi _v^{j}(\sigma _{v, k}))_{k = 1, \ldots , d_v}$. Then
$I(i, j, v) = (\lambda , \psi _v^{i}(\sigma _{v, k}) - \psi _v^{j}(\sigma _{v, k}))_{k = 1, \ldots , d_v}$. Then ![]() $\dim \Lambda / I(i, j, v) = n [F^{+} : {{\mathbb {Q}}}] - d_v$ and, if
$\dim \Lambda / I(i, j, v) = n [F^{+} : {{\mathbb {Q}}}] - d_v$ and, if ![]() ${{\mathfrak p}} \subset \Lambda$ is a prime of characteristic
${{\mathfrak p}} \subset \Lambda$ is a prime of characteristic ![]() $l$ which does not contain
$l$ which does not contain ![]() $I(i, j, v)$, then the characters
$I(i, j, v)$, then the characters ![]() $\psi _v^{i} \text { mod } {{\mathfrak p}}$ and
$\psi _v^{i} \text { mod } {{\mathfrak p}}$ and ![]() $\psi _v^{j} \text { mod } {{\mathfrak p}}$ are distinct.
$\psi _v^{j} \text { mod } {{\mathfrak p}}$ are distinct.
Suppose that we are given for each ![]() $v \in S_l$ an
$v \in S_l$ an ![]() $n \times d_v$ matrix
$n \times d_v$ matrix ![]() $A_v$ with integer entries, and with at least one non-zero entry in each column. Then we define an ideal
$A_v$ with integer entries, and with at least one non-zero entry in each column. Then we define an ideal ![]() $J((A_v)_{v \in S_l}) \subset \Lambda$ as the ideal generated by
$J((A_v)_{v \in S_l}) \subset \Lambda$ as the ideal generated by ![]() $\lambda$ and all the elements
$\lambda$ and all the elements
 \[ \prod_{i=1}^{n} \psi_v^{i}(\sigma_{v, j})^{A_{v, i, j}} - 1 \text{ }(v \in S_l, j = 1, \ldots, d_v). \]
\[ \prod_{i=1}^{n} \psi_v^{i}(\sigma_{v, j})^{A_{v, i, j}} - 1 \text{ }(v \in S_l, j = 1, \ldots, d_v). \]
Then ![]() $\dim \Lambda / J((A_v)_{v \in S_l}) = (n-1)[F^{+} : {{\mathbb {Q}}}]$ and, if
$\dim \Lambda / J((A_v)_{v \in S_l}) = (n-1)[F^{+} : {{\mathbb {Q}}}]$ and, if ![]() ${{\mathfrak p}} \subset \Lambda$ is a prime of characteristic
${{\mathfrak p}} \subset \Lambda$ is a prime of characteristic ![]() $l$ not containing any of the ideals
$l$ not containing any of the ideals ![]() $J((A_v)_{v \in S_l})$, then there exist
$J((A_v)_{v \in S_l})$, then there exist ![]() $v \in S_l$ and
$v \in S_l$ and ![]() $1 \leq j \leq d_v$ such that the elements
$1 \leq j \leq d_v$ such that the elements ![]() $\psi _v^{1}(\sigma _{v, j}), \ldots , \psi _v^{n}(\sigma _{v, j}) \in (\Lambda / {{\mathfrak p}})^{\times }$ satisfy no non-trivial
$\psi _v^{1}(\sigma _{v, j}), \ldots , \psi _v^{n}(\sigma _{v, j}) \in (\Lambda / {{\mathfrak p}})^{\times }$ satisfy no non-trivial ![]() ${{\mathbb {Z}}}$-linear relation.
${{\mathbb {Z}}}$-linear relation.
The lemma is completed on taking our countable collection of ideals ![]() $I_i$ to consist of all the ideals
$I_i$ to consist of all the ideals ![]() $I(i, j, v)$ and
$I(i, j, v)$ and ![]() $J((A_v)_{v \in S_l})$ defined above.
$J((A_v)_{v \in S_l})$ defined above.
Combining the previous lemmas, we obtain the following result.
Lemma 3.9 Suppose that ![]() $d_l > n(n-1)/2 + 1$ and that
$d_l > n(n-1)/2 + 1$ and that ![]() $A \in {{\mathcal {C}}}_\Lambda$ is a finite
$A \in {{\mathcal {C}}}_\Lambda$ is a finite ![]() $\Lambda$-algebra such that
$\Lambda$-algebra such that ![]() $\dim A / (\lambda ) > \sup (n[F^{+} : {{\mathbb {Q}}}] - d_0, n[F^{+} : {{\mathbb {Q}}}] - d_l)$. Let
$\dim A / (\lambda ) > \sup (n[F^{+} : {{\mathbb {Q}}}] - d_0, n[F^{+} : {{\mathbb {Q}}}] - d_l)$. Let ![]() $r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a homomorphism of type
$r : G_{F^{+}, S} \to {{\mathcal {G}}}_n(A)$ be a homomorphism of type ![]() ${{\mathcal {S}}}$. Then we can find a prime ideal
${{\mathcal {S}}}$. Then we can find a prime ideal ![]() ${{\mathfrak p}} \subset A$ of dimension 1 and characteristic
${{\mathfrak p}} \subset A$ of dimension 1 and characteristic ![]() $l$ such that, writing
$l$ such that, writing ![]() $r_{{\mathfrak p}} = r \text { mod } {{\mathfrak p}}: G_{F^{+}} \to {{\mathcal {G}}}_n(A / {{\mathfrak p}})$,
$r_{{\mathfrak p}} = r \text { mod } {{\mathfrak p}}: G_{F^{+}} \to {{\mathcal {G}}}_n(A / {{\mathfrak p}})$, ![]() $r_{{\mathfrak p}}$ is generic.
$r_{{\mathfrak p}}$ is generic.
Proof. Replacing ![]() $A$ by
$A$ by ![]() $A / (\lambda )$, we can assume that
$A / (\lambda )$, we can assume that ![]() $A$ is a finite
$A$ is a finite ![]() $\Lambda / (\lambda )$-algebra. Let
$\Lambda / (\lambda )$-algebra. Let ![]() $I_i$ (
$I_i$ (![]() $i = 1, 2, \ldots$) be the countable collection of ideals of
$i = 1, 2, \ldots$) be the countable collection of ideals of ![]() $\Lambda / (\lambda )$ defined in Lemma 3.8. Then
$\Lambda / (\lambda )$ defined in Lemma 3.8. Then ![]() $\dim A / I_i A \leq n [ F^{+} : {{\mathbb {Q}}}] - d_l$ for each
$\dim A / I_i A \leq n [ F^{+} : {{\mathbb {Q}}}] - d_l$ for each ![]() $i = 1, 2, \ldots$. Let
$i = 1, 2, \ldots$. Let ![]() $I_0 = I_{{\mathcal {S}}}^{\rm red} A$; then Lemma 3.6 shows that
$I_0 = I_{{\mathcal {S}}}^{\rm red} A$; then Lemma 3.6 shows that ![]() $\dim A / I_0 \leq n [F^{+} : {{\mathbb {Q}}}] - d_0$.
$\dim A / I_0 \leq n [F^{+} : {{\mathbb {Q}}}] - d_0$.
Applying [Reference ThorneTho15, Lemma 1.9], we can find a prime ideal ![]() ${{\mathfrak p}} \subset A$ of dimension 1 (necessarily of characteristic
${{\mathfrak p}} \subset A$ of dimension 1 (necessarily of characteristic ![]() $l$) such that
$l$) such that ![]() ${{\mathfrak p}}$ does not contain any of the ideals
${{\mathfrak p}}$ does not contain any of the ideals ![]() $I_0$,
$I_0$, ![]() $I_1 A$,
$I_1 A$, ![]() $I_2 A, \ldots$. By construction, the homomorphism
$I_2 A, \ldots$. By construction, the homomorphism ![]() $r_{{\mathfrak p}}$ is then generic.
$r_{{\mathfrak p}}$ is then generic.
4. Automorphic forms and Hecke algebras on unitary groups
4.1 Hecke algebras
We introduce automorphic forms on unitary groups and related Hecke algebras, using exactly the same notation as in [Reference ThorneTho15, § 4]. This means we start with the following data.
– An integer
 $n \geq 1$, an odd prime
$n \geq 1$, an odd prime  $l$, and a totally imaginary CM number field
$l$, and a totally imaginary CM number field  $L$ with totally real subfield
$L$ with totally real subfield  $L^{+}$. We write
$L^{+}$. We write  $S_l$ for the set of
$S_l$ for the set of  $l$-adic places of
$l$-adic places of  $L^{+}$. We assume that
$L^{+}$. We assume that  $L / L^{+}$ is everywhere unramified. (We note that this implies that
$L / L^{+}$ is everywhere unramified. (We note that this implies that  $[L^{+} : {{\mathbb {Q}}}]$ is even. Indeed, the quadratic character of
$[L^{+} : {{\mathbb {Q}}}]$ is even. Indeed, the quadratic character of  $(L^{+})^{\times }\backslash {{\mathbb {A}}}_{L^{+}}^{\times }/\hat {{{\mathcal {O}}}}_{L^{+}}^{\times }$ cutting out
$(L^{+})^{\times }\backslash {{\mathbb {A}}}_{L^{+}}^{\times }/\hat {{{\mathcal {O}}}}_{L^{+}}^{\times }$ cutting out  $L$ has non-trivial restriction to
$L$ has non-trivial restriction to  $(L^{+}_v)^{\times }$ for each
$(L^{+}_v)^{\times }$ for each  $v|\infty$ but is trivial on
$v|\infty$ but is trivial on  $(-1)_{v|\infty } \in (L^{+}_\infty )^{\times }$.)
$(-1)_{v|\infty } \in (L^{+}_\infty )^{\times }$.)– A coefficient field
 $K \subset \bar {{{\mathbb {Q}}}}_l$ which contains the image of all embeddings
$K \subset \bar {{{\mathbb {Q}}}}_l$ which contains the image of all embeddings  $L \hookrightarrow \bar {{{\mathbb {Q}}}}_l$.
$L \hookrightarrow \bar {{{\mathbb {Q}}}}_l$.– A finite set
 $S(B)$ of finite, prime-to-
$S(B)$ of finite, prime-to- $l$ places of
$l$ places of  $L^{+}$ which all split in
$L^{+}$ which all split in  $L$. If
$L$. If  $n$ is even, then we assume that
$n$ is even, then we assume that  $n [ L^{+} : {{\mathbb {Q}}}] / 2 + | S(B) |$ is also even. We allow the possibility that
$n [ L^{+} : {{\mathbb {Q}}}] / 2 + | S(B) |$ is also even. We allow the possibility that  $S(B)$ may be empty. (Since
$S(B)$ may be empty. (Since  $[L^{+}:{{\mathbb {Q}}}]$ is even, we are really just asking that if
$[L^{+}:{{\mathbb {Q}}}]$ is even, we are really just asking that if  $n$ is even, then
$n$ is even, then  $|S(B)|$ is even.)
$|S(B)|$ is even.)
We can then find a central simple algebra ![]() $B$ over
$B$ over ![]() $L$ equipped with an involution
$L$ equipped with an involution ![]() $\dagger$ such that
$\dagger$ such that ![]() $\dim _L B = n^{2}$,
$\dim _L B = n^{2}$, ![]() $B^{\text op} \cong B \otimes _{L, c} L$,
$B^{\text op} \cong B \otimes _{L, c} L$, ![]() $B$ is split outside
$B$ is split outside ![]() $S(B)$,
$S(B)$, ![]() $B$ is a division algebra locally at places
$B$ is a division algebra locally at places ![]() $w | S(B)$ of
$w | S(B)$ of ![]() $L$, and
$L$, and ![]() $\dagger |_L = c$. We can moreover assume that the unitary group
$\dagger |_L = c$. We can moreover assume that the unitary group ![]() $G$ over
$G$ over ![]() $L^{+}$ defined by the formula (
$L^{+}$ defined by the formula (![]() $R$ an
$R$ an ![]() $L^{+}$-algebra)
$L^{+}$-algebra)
has the property that ![]() $G(L^{+} \otimes _{{\mathbb {Q}}} {{\mathbb {R}}})$ is compact and, for each finite place
$G(L^{+} \otimes _{{\mathbb {Q}}} {{\mathbb {R}}})$ is compact and, for each finite place ![]() $v\not \in S(B)$ of
$v\not \in S(B)$ of ![]() $L^{+}$,
$L^{+}$, ![]() $G_{L^{+}}$ is quasi-split (hence unramified).
$G_{L^{+}}$ is quasi-split (hence unramified).
We consider automorphic forms on the group ![]() $G$. To define our Hecke algebras, we need to fix the following additional choices.
$G$. To define our Hecke algebras, we need to fix the following additional choices.
– A finite set
 $R$ of finite places of
$R$ of finite places of  $L^{+}$, disjoint from
$L^{+}$, disjoint from  $S_l \cup S(B)$ and split in
$S_l \cup S(B)$ and split in  $L$, such that for each
$L$, such that for each  $v \in R$,
$v \in R$,  $q_v \equiv 1 \text { mod }l$.
$q_v \equiv 1 \text { mod }l$.– For each
 $v \in R$, we fix a choice of
$v \in R$, we fix a choice of  $n$-tuple of characters
$n$-tuple of characters  $\chi _{v, 1}, \ldots , \chi _{v, n} : k(v)^{\times } \to {{\mathcal {O}}}^{\times }$ which are trivial mod
$\chi _{v, 1}, \ldots , \chi _{v, n} : k(v)^{\times } \to {{\mathcal {O}}}^{\times }$ which are trivial mod  $\varpi$.
$\varpi$.– A finite set
 $T$ of finite places of
$T$ of finite places of  $L^{+}$ split in
$L^{+}$ split in  $L$, containing
$L$, containing  $S_l \cup S(B) \cup R$. For each
$S_l \cup S(B) \cup R$. For each  $v \in T$, we fix a choice of place
$v \in T$, we fix a choice of place  ${{\widetilde {v}}}$ of
${{\widetilde {v}}}$ of  $L$ lying above
$L$ lying above  $v$ and set
$v$ and set  $\tilde {T} = \{ {{\widetilde {v}}} \mid v \in T \}$.
$\tilde {T} = \{ {{\widetilde {v}}} \mid v \in T \}$.
It is also convenient to fix a choice of order ![]() ${{\mathcal {O}}}_B \subset B$ such that
${{\mathcal {O}}}_B \subset B$ such that ![]() ${{\mathcal {O}}}_B^{\dagger } = {{\mathcal {O}}}_B$ and, for each place
${{\mathcal {O}}}_B^{\dagger } = {{\mathcal {O}}}_B$ and, for each place ![]() $v$ of
$v$ of ![]() $L^{+}$ which splits
$L^{+}$ which splits ![]() $v = w w^{c}$ in
$v = w w^{c}$ in ![]() $L$,
$L$, ![]() ${{\mathcal {O}}}_{B_w}$ is a maximal order in
${{\mathcal {O}}}_{B_w}$ is a maximal order in ![]() $B_w$. We use this maximal order
$B_w$. We use this maximal order ![]() ${{\mathcal {O}}}_B$ to extend
${{\mathcal {O}}}_B$ to extend ![]() $G$ to a group scheme over
$G$ to a group scheme over ![]() ${{\mathcal {O}}}_{L^{+}}$. If
${{\mathcal {O}}}_{L^{+}}$. If ![]() $v \in T$, then a choice of isomorphism
$v \in T$, then a choice of isomorphism ![]() ${{\mathcal {O}}}_{B_{{\widetilde {v}}}} \cong M_n({{\mathcal {O}}}_{F_{{\widetilde {v}}}})$ determines an isomorphism
${{\mathcal {O}}}_{B_{{\widetilde {v}}}} \cong M_n({{\mathcal {O}}}_{F_{{\widetilde {v}}}})$ determines an isomorphism ![]() $\iota _{{\widetilde {v}}} : G_{{{\mathcal {O}}}_{F^{+}_v}} \to \operatorname {Res}_{{{\mathcal {O}}}_{F_{{\widetilde {v}}}} / {{\mathcal {O}}}_{F_v^{+}}} \operatorname {GL}_n$ and we fix such a choice.
$\iota _{{\widetilde {v}}} : G_{{{\mathcal {O}}}_{F^{+}_v}} \to \operatorname {Res}_{{{\mathcal {O}}}_{F_{{\widetilde {v}}}} / {{\mathcal {O}}}_{F_v^{+}}} \operatorname {GL}_n$ and we fix such a choice.
Now suppose that we are given an open compact subgroup ![]() $U = \prod _v U_v \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$ which satisfies the following conditions.
$U = \prod _v U_v \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$ which satisfies the following conditions.
– There exists a finite place
 $v \not \in S_l$ of
$v \not \in S_l$ of  $L^{+}$ such that
$L^{+}$ such that  $U_v$ contains no non-trivial elements of finite order (in other words,
$U_v$ contains no non-trivial elements of finite order (in other words,  $U$ is sufficiently small in the terminology of [Reference ThorneTho15]).
$U$ is sufficiently small in the terminology of [Reference ThorneTho15]).– If
 $v \not \in T$ is a finite place of
$v \not \in T$ is a finite place of  $L^{+}$ split in
$L^{+}$ split in  $L$, then
$L$, then  $U_v = G({{\mathcal {O}}}_{L^{+}_v})$.
$U_v = G({{\mathcal {O}}}_{L^{+}_v})$.– If
 $v \in R$, then
$v \in R$, then  $U_v = \iota _{{\widetilde {v}}}^{-1} \operatorname {Iw}({{\widetilde {v}}})$, where
$U_v = \iota _{{\widetilde {v}}}^{-1} \operatorname {Iw}({{\widetilde {v}}})$, where  $\operatorname {Iw}({{\widetilde {v}}}) \subset \operatorname {GL}_n({{\mathcal {O}}}_{F_{{\widetilde {v}}}})$ denotes the standard Iwahori subgroup.
$\operatorname {Iw}({{\widetilde {v}}}) \subset \operatorname {GL}_n({{\mathcal {O}}}_{F_{{\widetilde {v}}}})$ denotes the standard Iwahori subgroup.– If
 $v$ is a finite place of
$v$ is a finite place of  $L^{+}$ inert in
$L^{+}$ inert in  $L$, then
$L$, then  $U_v$ is a hyperspecial maximal compact subgroup of
$U_v$ is a hyperspecial maximal compact subgroup of  $G({L_v^{+}})$.
$G({L_v^{+}})$.
In this case we have defined in [Reference ThorneTho15, Definition 4.2] a Hecke algebra ![]() ${{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$. It is a finite faithful
${{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$. It is a finite faithful ![]() $\Lambda$-algebra, defined as an inverse limit of Hecke algebras which act on spaces of ordinary automorphic forms on
$\Lambda$-algebra, defined as an inverse limit of Hecke algebras which act on spaces of ordinary automorphic forms on ![]() $G$ with coefficients in
$G$ with coefficients in ![]() ${{\mathcal {O}}}$. According to [Reference ThorneTho15, Proposition 4.7], to any maximal ideal
${{\mathcal {O}}}$. According to [Reference ThorneTho15, Proposition 4.7], to any maximal ideal ![]() ${{\mathfrak m}} \subset {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ of residue field
${{\mathfrak m}} \subset {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ of residue field ![]() $k$, one can associate a continuous semisimple representation
$k$, one can associate a continuous semisimple representation ![]() $\bar {\rho }_{{\mathfrak m}} : G_{F, T} \to \operatorname {GL}_n(k)$, uniquely characterized up to
$\bar {\rho }_{{\mathfrak m}} : G_{F, T} \to \operatorname {GL}_n(k)$, uniquely characterized up to ![]() $\operatorname {GL}_n(k)$ conjugacy by a formula for the characteristic polynomials of Frobenius elements in terms of Hecke operators.
$\operatorname {GL}_n(k)$ conjugacy by a formula for the characteristic polynomials of Frobenius elements in terms of Hecke operators.
4.2 Deformation rings
We connect the Hecke algebras defined in the previous section to deformation rings only under the following assumptions (i)–(iii).
(i)
 $T$ has the form
$T$ has the form  $T = S_l \sqcup S(B) \sqcup R \sqcup S_a$, where
$T = S_l \sqcup S(B) \sqcup R \sqcup S_a$, where  $S_a$ is a non-empty set of places of odd residue characteristic which are absolutely unramified and not split in
$S_a$ is a non-empty set of places of odd residue characteristic which are absolutely unramified and not split in  $L(\zeta _l)$. For every
$L(\zeta _l)$. For every  $v \in S_l$,
$v \in S_l$,  $[F_v^{+}:{{\mathbb {Q}}}_l] > n(n-1)/2 + 1$.
$[F_v^{+}:{{\mathbb {Q}}}_l] > n(n-1)/2 + 1$.(ii)
 $U = \prod U_v \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$ is an open compact subgroup such that if
$U = \prod U_v \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$ is an open compact subgroup such that if  $v \in S_a$, then
$v \in S_a$, then  $U_v = \iota _{{\widetilde {v}}}^{-1}( \ker ( \operatorname {GL}_n({{\mathcal {O}}}_{L_{{\widetilde {v}}}}) \to \operatorname {GL}_n(k({{\widetilde {v}}})) ) )$ and, if
$U_v = \iota _{{\widetilde {v}}}^{-1}( \ker ( \operatorname {GL}_n({{\mathcal {O}}}_{L_{{\widetilde {v}}}}) \to \operatorname {GL}_n(k({{\widetilde {v}}})) ) )$ and, if  $v \in S(B)$, then
$v \in S(B)$, then  $U_v$ is the unique maximal compact subgroup of
$U_v$ is the unique maximal compact subgroup of  $G(F_v^{+})$. Since
$G(F_v^{+})$. Since  $S_a$ is non-empty, this forces
$S_a$ is non-empty, this forces  $U$ to be sufficiently small.
$U$ to be sufficiently small.(iii)
 ${{\mathfrak m}} \subset {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ is a maximal ideal of residue field
${{\mathfrak m}} \subset {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ is a maximal ideal of residue field  $k$ such that
$k$ such that  $\bar {\rho }_{{\mathfrak m}} : G_{F, T} \to \operatorname {GL}_n(k)$ satisfies the following conditions:
$\bar {\rho }_{{\mathfrak m}} : G_{F, T} \to \operatorname {GL}_n(k)$ satisfies the following conditions:
– if
 $v \in S_a$, then
$v \in S_a$, then  $\bar {\rho }_{{\mathfrak m}}|_{G_{L_{{\widetilde {v}}}}}$ is unramified and
$\bar {\rho }_{{\mathfrak m}}|_{G_{L_{{\widetilde {v}}}}}$ is unramified and  $\bar {\rho }_{{\mathfrak m}}(\operatorname {Frob}_{{\widetilde {v}}})$ is scalar;
$\bar {\rho }_{{\mathfrak m}}(\operatorname {Frob}_{{\widetilde {v}}})$ is scalar;– if
 $v \in S_l \cup R \cup S(B)$, then
$v \in S_l \cup R \cup S(B)$, then  $\bar {\rho }_{{\mathfrak m}}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation;
$\bar {\rho }_{{\mathfrak m}}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation;– for each
 $v \in S(B) \cup R$,
$v \in S(B) \cup R$,  $q_v \equiv 1 \text { mod }l$;
$q_v \equiv 1 \text { mod }l$;– let
 $\bar {\rho }_{{\mathfrak m}} = \oplus _{i=1}^{d} \bar {\rho }_i$ denote the decomposition into simple constituents. Then each
$\bar {\rho }_{{\mathfrak m}} = \oplus _{i=1}^{d} \bar {\rho }_i$ denote the decomposition into simple constituents. Then each  $\bar {\rho }_i$ is absolutely irreducible, satisfies
$\bar {\rho }_i$ is absolutely irreducible, satisfies  $\bar {\rho }^{c}_i \cong \bar {\rho }_i^{\vee } \otimes \epsilon ^{1-n}$, and, if
$\bar {\rho }^{c}_i \cong \bar {\rho }_i^{\vee } \otimes \epsilon ^{1-n}$, and, if  $i \neq j$, then
$i \neq j$, then  $\bar {\rho }_i \not \cong \bar {\rho }_j$ (equivalently, the maximal ideal
$\bar {\rho }_i \not \cong \bar {\rho }_j$ (equivalently, the maximal ideal  ${{\mathfrak m}}$ is residually Schur in the sense of [Reference ThorneTho15, Definition 4.8]).
${{\mathfrak m}}$ is residually Schur in the sense of [Reference ThorneTho15, Definition 4.8]).
Then [Reference ThorneTho15, Proposition 4.9] ![]() $\bar {\rho }_{{\mathfrak m}}$ extends to a homomorphism
$\bar {\rho }_{{\mathfrak m}}$ extends to a homomorphism ![]() $\bar {r}_{{\mathfrak m}} : G_{L^{+}, T} \to {{\mathcal {G}}}_n(k)$ such that
$\bar {r}_{{\mathfrak m}} : G_{L^{+}, T} \to {{\mathcal {G}}}_n(k)$ such that ![]() $\nu \circ \bar {r}_{{\mathfrak m}} = \epsilon ^{1-n} \delta _{L / L^{+}}^{n}$ and which is Schur. We can consider the global deformation problem
$\nu \circ \bar {r}_{{\mathfrak m}} = \epsilon ^{1-n} \delta _{L / L^{+}}^{n}$ and which is Schur. We can consider the global deformation problem
Then there are ![]() $\Lambda$-algebra homomorphisms
$\Lambda$-algebra homomorphisms ![]() $P_{{{\mathcal {S}}}_\chi } \to R_{{{\mathcal {S}}}_\chi }$ and
$P_{{{\mathcal {S}}}_\chi } \to R_{{{\mathcal {S}}}_\chi }$ and ![]() $P_{{{\mathcal {S}}}_\chi } \to {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})_{{\mathfrak m}}$ (see [Reference ThorneTho15, Proposition 4.13]). We define
$P_{{{\mathcal {S}}}_\chi } \to {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})_{{\mathfrak m}}$ (see [Reference ThorneTho15, Proposition 4.13]). We define ![]() $J_{{{\mathcal {S}}}_\chi } = \ker ( P_{{{\mathcal {S}}}_\chi } \to {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})_{{\mathfrak m}} )$.
$J_{{{\mathcal {S}}}_\chi } = \ker ( P_{{{\mathcal {S}}}_\chi } \to {{\mathbb {T}}}^{T}_\chi (U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})_{{\mathfrak m}} )$.
Theorem 4.1 Let ![]() ${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime ideal of dimension 1 and characteristic
${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime ideal of dimension 1 and characteristic ![]() $l$. Let
$l$. Let ![]() $A = R_{{{\mathcal {S}}}_1}^{\text{univ}} / {{\mathfrak p}}$ and suppose that the following conditions are satisfied.
$A = R_{{{\mathcal {S}}}_1}^{\text{univ}} / {{\mathfrak p}}$ and suppose that the following conditions are satisfied.
(i)
 $J_{{{\mathcal {S}}}_1}R_{{{\mathcal {S}}}_1}^{\text{univ}} \subset {{\mathfrak p}}$.
$J_{{{\mathcal {S}}}_1}R_{{{\mathcal {S}}}_1}^{\text{univ}} \subset {{\mathfrak p}}$.(ii) The representation
 $r_{{\mathfrak p}}$ is generic, in the sense of Definition 3.7.
$r_{{\mathfrak p}}$ is generic, in the sense of Definition 3.7.(iii) For each
 $v \in R$,
$v \in R$,  $r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation and, if
$r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation and, if  $l^{N} || q_v - 1$, then
$l^{N} || q_v - 1$, then  $l^{N} > n$. For each
$l^{N} > n$. For each  $v \in S(B)$,
$v \in S(B)$,  $r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is unramified and
$r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is unramified and  $r_{{\mathfrak p}}(\operatorname {Frob}_{{\widetilde {v}}})$ is a scalar matrix.
$r_{{\mathfrak p}}(\operatorname {Frob}_{{\widetilde {v}}})$ is a scalar matrix.(iv)
 $\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ is primitive.
$\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ is primitive.(v)
 $\zeta _l \not \in L$,
$\zeta _l \not \in L$,  $\bar {r}_{{\mathfrak m}}|_{G_{L^{+}(\zeta _l)}}$ is Schur, and
$\bar {r}_{{\mathfrak m}}|_{G_{L^{+}(\zeta _l)}}$ is Schur, and  $\bar {r}_{{\mathfrak m}}(G_{L, S})$ does not have a quotient of order
$\bar {r}_{{\mathfrak m}}(G_{L, S})$ does not have a quotient of order  $l$.
$l$.(vi)
 $l > 3$ and
$l > 3$ and  $l \nmid n$.
$l \nmid n$.
Let ![]() $Q \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime such that
$Q \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime such that ![]() $Q \subset {{\mathfrak p}}$. Then
$Q \subset {{\mathfrak p}}$. Then ![]() $J_{{{\mathcal {S}}}_1} R_{{{\mathcal {S}}}_1}^{\text{univ}} \subset Q$.
$J_{{{\mathcal {S}}}_1} R_{{{\mathcal {S}}}_1}^{\text{univ}} \subset Q$.
Proof. Let ![]() ${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{{\mathcal {S}}}_1}$. We can assume, after twisting by a character, that
${{\mathfrak q}} = {{\mathfrak p}} \cap P_{{{\mathcal {S}}}_1}$. We can assume, after twisting by a character, that ![]() $\operatorname {Frac} R_{{{\mathcal {S}}}_1}^{\rm univ} / {{\mathfrak p}} = \operatorname {Frac} P_{{{\mathcal {S}}}_1} / {{\mathfrak q}}$. (Apply [Reference ThorneTho15, Lemma 3.38] and [Reference ThorneTho15, Corollary 4.14].)
$\operatorname {Frac} R_{{{\mathcal {S}}}_1}^{\rm univ} / {{\mathfrak p}} = \operatorname {Frac} P_{{{\mathcal {S}}}_1} / {{\mathfrak q}}$. (Apply [Reference ThorneTho15, Lemma 3.38] and [Reference ThorneTho15, Corollary 4.14].)
In the case that ![]() $\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ has two irreducible constituents, the theorem follows on combining [Reference ThorneTho15, Corollary 5.7] (existence of Taylor–Wiles primes under a subset of the hypotheses listed here) and [Reference ThorneTho15, Corollary 4.20] (the assertion
$\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ has two irreducible constituents, the theorem follows on combining [Reference ThorneTho15, Corollary 5.7] (existence of Taylor–Wiles primes under a subset of the hypotheses listed here) and [Reference ThorneTho15, Corollary 4.20] (the assertion ![]() $J_{{{\mathcal {S}}}_1} R_{{{\mathcal {S}}}_1}^{\rm univ} \subset Q$ assuming existence of Taylor–Wiles primes and, in addition, that
$J_{{{\mathcal {S}}}_1} R_{{{\mathcal {S}}}_1}^{\rm univ} \subset Q$ assuming existence of Taylor–Wiles primes and, in addition, that ![]() $\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ has two irreducible constituents).
$\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ has two irreducible constituents).
The proof of [Reference ThorneTho15, Corollary 4.20] can easily be modified to allow ![]() $\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ to have an arbitrary number
$\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ to have an arbitrary number ![]() ${d}$ of irreducible constituents: one just needs to replace the
${d}$ of irreducible constituents: one just needs to replace the ![]() $\mu ^{2}_2$ action there by the
$\mu ^{2}_2$ action there by the ![]() $\mu _2^{{d}}$ action on
$\mu _2^{{d}}$ action on ![]() $R_{{{\mathcal {S}}}_1}^{\rm univ}$ described in § 3.2 and replace the appeal to [Reference ThorneTho15, Proposition 3.29] with an appeal to Proposition 3.2 of this paper. We omit the details.
$R_{{{\mathcal {S}}}_1}^{\rm univ}$ described in § 3.2 and replace the appeal to [Reference ThorneTho15, Proposition 3.29] with an appeal to Proposition 3.2 of this paper. We omit the details.
5. Propagation of potential pro-automorphy
In this section we use Theorem 4.1 (informally, ![]() $R = {{\mathbb {T}}}$ locally at generic primes) to prove our first automorphy lifting theorem for
$R = {{\mathbb {T}}}$ locally at generic primes) to prove our first automorphy lifting theorem for ![]() $l$-adic Galois representations. The argument follows similar lines to [Reference ThorneTho15, § 6]. The main difference is that by making use of Lemma 3.9 we can make do under weaker assumptions. Especially, we do not need an a priori bound on the dimension of the locus of reducible deformations inside
$l$-adic Galois representations. The argument follows similar lines to [Reference ThorneTho15, § 6]. The main difference is that by making use of Lemma 3.9 we can make do under weaker assumptions. Especially, we do not need an a priori bound on the dimension of the locus of reducible deformations inside ![]() $R_{{{\mathcal {S}}}_1}^{\rm univ}$.
$R_{{{\mathcal {S}}}_1}^{\rm univ}$.
Let us take up assumptions (1)–(3) of § 4.2. Thus, we have a CM field ![]() $L$, a unitary group
$L$, a unitary group ![]() $G$, and a set
$G$, and a set ![]() $S = T = S_l \cup R \cup S(B) \cup S_a$ of finite places of
$S = T = S_l \cup R \cup S(B) \cup S_a$ of finite places of ![]() $L^{+}$ split in
$L^{+}$ split in ![]() $L$. We have an open compact subgroup
$L$. We have an open compact subgroup ![]() $U \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$, a maximal ideal
$U \subset G({{\mathbb {A}}}_{L^{+}}^{\infty })$, a maximal ideal ![]() ${{\mathfrak m}}$ of the Hecke algebra
${{\mathfrak m}}$ of the Hecke algebra ![]() ${{\mathbb {T}}}^{S}(U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ of residue field
${{\mathbb {T}}}^{S}(U({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ of residue field ![]() $k$, a deformation problem
$k$, a deformation problem
and a diagram of ![]() $\Lambda$-algebras
$\Lambda$-algebras
We can now state the main theorem of this section.
Theorem 5.1 Let ![]() $r : G_{L^{+}, S} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ be a lifting of
$r : G_{L^{+}, S} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ be a lifting of ![]() $\bar {r}_{{\mathfrak m}}$ of type
$\bar {r}_{{\mathfrak m}}$ of type ![]() ${{\mathcal {S}}}_1$ such that
${{\mathcal {S}}}_1$ such that ![]() $r|_{G_{L, S}}$ is ordinary of weight
$r|_{G_{L, S}}$ is ordinary of weight ![]() $\lambda$ for some
$\lambda$ for some ![]() $\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(L, \bar {{{\mathbb {Q}}}}_l)}$. Suppose that the following conditions hold.
$\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(L, \bar {{{\mathbb {Q}}}}_l)}$. Suppose that the following conditions hold.
(i)
 $\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ is primitive.
$\bar {r}_{{\mathfrak m}}|_{G_{L, S}}$ is primitive.(ii)
 $\zeta _l \not \in L$,
$\zeta _l \not \in L$,  $\bar {r}_{{\mathfrak m}}|_{G_{L^{+}(\zeta _l)}}$ is Schur and
$\bar {r}_{{\mathfrak m}}|_{G_{L^{+}(\zeta _l)}}$ is Schur and  $\bar {r}_{{\mathfrak m}}(G_{L, S})$ does not have a quotient of order
$\bar {r}_{{\mathfrak m}}(G_{L, S})$ does not have a quotient of order  $l$.
$l$.(iii)
 $l > 3$ and
$l > 3$ and  $l \nmid n$.
$l \nmid n$.(iv) Let
 $d_{L, 0}, d_{L, l}$ be as defined in § 3.3. Then
$d_{L, 0}, d_{L, l}$ be as defined in § 3.3. Then  $d_{L, 0} > |R|n(n+1) + 2$ and
$d_{L, 0} > |R|n(n+1) + 2$ and  $d_{L, l} > \sup (|R|n (n+1) + 2, n(n-1)/2 + 1)$.
$d_{L, l} > \sup (|R|n (n+1) + 2, n(n-1)/2 + 1)$.
Then ![]() $r|_{G_{L, S}}$ is automorphic of weight
$r|_{G_{L, S}}$ is automorphic of weight ![]() $\lambda$.
$\lambda$.
We assume the hypotheses of Theorem 5.1 for the rest of § 5. Note that our assumption on ![]() $d_{L,0}$ implies that
$d_{L,0}$ implies that ![]() $S(B)$ is non-empty. In particular, the conclusion of Theorem 5.1 implies, by local–global compatibility at a place in
$S(B)$ is non-empty. In particular, the conclusion of Theorem 5.1 implies, by local–global compatibility at a place in ![]() $S(B)$, that
$S(B)$, that ![]() $r|_{G_{L,S}}$ is absolutely irreducible.
$r|_{G_{L,S}}$ is absolutely irreducible.
Let us say that a soluble CM extension ![]() $M/L$ is good if it is linearly disjoint from the extension of
$M/L$ is good if it is linearly disjoint from the extension of ![]() $L(\zeta _l)$ cut out by
$L(\zeta _l)$ cut out by ![]() $\bar {r}_{{\mathfrak m}}|_{G_{L(\zeta _l)}}$ and every prime above
$\bar {r}_{{\mathfrak m}}|_{G_{L(\zeta _l)}}$ and every prime above ![]() $S_l \cup S_a \cup R$ splits in
$S_l \cup S_a \cup R$ splits in ![]() $M$. (Primes of
$M$. (Primes of ![]() $S(B)$ are not required to split and indeed this possibility plays an important role in the proof; cf. [Reference ThorneTho15, Proposition 6.2].)
$S(B)$ are not required to split and indeed this possibility plays an important role in the proof; cf. [Reference ThorneTho15, Proposition 6.2].)
Lemma 5.2 Let ![]() $M / L$ be a good extension. Then
$M / L$ be a good extension. Then ![]() $\bar {r}_{{\mathfrak m}}|_{G_M}$ is primitive,
$\bar {r}_{{\mathfrak m}}|_{G_M}$ is primitive, ![]() $\zeta _l \not \in M$,
$\zeta _l \not \in M$, ![]() $\bar {r}_{{\mathfrak m}}|_{G_{M^{+}(\zeta _l)}}$ is Schur, and
$\bar {r}_{{\mathfrak m}}|_{G_{M^{+}(\zeta _l)}}$ is Schur, and ![]() $\bar {r}_{{\mathfrak m}}(G_M)$ does not have a quotient of order
$\bar {r}_{{\mathfrak m}}(G_M)$ does not have a quotient of order ![]() $l$.
$l$.
Proof. We take each property in turn. If ![]() $M / L$ is good, then
$M / L$ is good, then ![]() $\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, so this image does not have a quotient of order
$\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, so this image does not have a quotient of order ![]() $l$. Since
$l$. Since ![]() $M / L$ is linearly disjoint from
$M / L$ is linearly disjoint from ![]() $L(\zeta _l)$, we have
$L(\zeta _l)$, we have ![]() $\zeta _l \not \in M$.
$\zeta _l \not \in M$.
To say that ![]() $\bar {r}_{{\mathfrak m}}|_{G_{M^{+}(\zeta _l)}}$ is Schur is to say that
$\bar {r}_{{\mathfrak m}}|_{G_{M^{+}(\zeta _l)}}$ is Schur is to say that ![]() $L \not \subset M^{+}(\zeta _l)$ and, if
$L \not \subset M^{+}(\zeta _l)$ and, if ![]() $\bar {\rho }, \bar {\rho }'$ are two Jordan–Hölder factors of
$\bar {\rho }, \bar {\rho }'$ are two Jordan–Hölder factors of ![]() $\bar {r}_{{\mathfrak m}}|_{G_M}$, then
$\bar {r}_{{\mathfrak m}}|_{G_M}$, then ![]() $\bar {\rho }^{c} \cong \bar {\rho }^{\vee } \otimes \epsilon ^{1-n}$ and
$\bar {\rho }^{c} \cong \bar {\rho }^{\vee } \otimes \epsilon ^{1-n}$ and ![]() $\bar {\rho } \not \cong \bar {\rho }'$. Since
$\bar {\rho } \not \cong \bar {\rho }'$. Since ![]() $\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, the latter property is not disturbed. We show that under our assumptions we in fact have
$\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, the latter property is not disturbed. We show that under our assumptions we in fact have ![]() $M \not \subset M^{+}(\zeta _l)$. It suffices to show that the two extensions
$M \not \subset M^{+}(\zeta _l)$. It suffices to show that the two extensions ![]() $M / M^{+}$ and
$M / M^{+}$ and ![]() $M^{+}(\zeta _l) / M^{+}$ are linearly disjoint. Since these extensions arise from the linearly disjoint extensions
$M^{+}(\zeta _l) / M^{+}$ are linearly disjoint. Since these extensions arise from the linearly disjoint extensions ![]() $L / L^{+}$ and
$L / L^{+}$ and ![]() $L^{+}(\zeta _l) / L^{+}$ by compositum with
$L^{+}(\zeta _l) / L^{+}$ by compositum with ![]() $M^{+}$, it is enough to check that the extensions
$M^{+}$, it is enough to check that the extensions ![]() $M^{+} / L^{+}$ and
$M^{+} / L^{+}$ and ![]() $L(\zeta _l) / L^{+}$ are linearly disjoint or even that
$L(\zeta _l) / L^{+}$ are linearly disjoint or even that ![]() $M^{+} \cap L(\zeta _l) = L^{+}$. This follows from the stronger assertion that
$M^{+} \cap L(\zeta _l) = L^{+}$. This follows from the stronger assertion that ![]() $M \cap L(\zeta _l) = L$.
$M \cap L(\zeta _l) = L$.
Finally, the condition that ![]() $\bar {r}_{{\mathfrak m}}|_{G_M}$ is primitive depends only on the group
$\bar {r}_{{\mathfrak m}}|_{G_M}$ is primitive depends only on the group ![]() $\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, so it is inherited from the corresponding condition for
$\bar {r}_{{\mathfrak m}}(G_M) = \bar {r}_{{\mathfrak m}}(G_L)$, so it is inherited from the corresponding condition for ![]() $\bar {r}_{{\mathfrak m}}$.
$\bar {r}_{{\mathfrak m}}$.
If ![]() $M/L$ is a good extension and
$M/L$ is a good extension and ![]() $X$ (respectively
$X$ (respectively ![]() $\tilde {X}$) is a set of places of
$\tilde {X}$) is a set of places of ![]() $L^{+}$ (respectively
$L^{+}$ (respectively ![]() $L$), then we write
$L$), then we write ![]() $X_M$ (respectively
$X_M$ (respectively ![]() $\tilde {X}_M$) for the set of places of
$\tilde {X}_M$) for the set of places of ![]() $M^{+}$ lying above a place of
$M^{+}$ lying above a place of ![]() $X$ (respectively places of
$X$ (respectively places of ![]() $M$ lying above a place of
$M$ lying above a place of ![]() $\tilde {X}$). We write
$\tilde {X}$). We write ![]() $\Lambda _M = \hat {\otimes }_{v \in S_{l, M}} {{\mathcal {O}}} [\kern-1pt[ I_{M_{{\widetilde {v}}}}^{ab}(l)^{n} ]\kern-1pt]$ for the Iwasawa algebra of
$\Lambda _M = \hat {\otimes }_{v \in S_{l, M}} {{\mathcal {O}}} [\kern-1pt[ I_{M_{{\widetilde {v}}}}^{ab}(l)^{n} ]\kern-1pt]$ for the Iwasawa algebra of ![]() $M$ (so
$M$ (so ![]() $\Lambda _L = \Lambda$). There is a natural surjective homomorphism
$\Lambda _L = \Lambda$). There is a natural surjective homomorphism ![]() $\Lambda _M \to \Lambda$. We can define a deformation problem
$\Lambda _M \to \Lambda$. We can define a deformation problem
 \begin{align*} {{\mathcal{S}}}_{1, M} &= ( M / M^{+}, T_M, \tilde{T}_M, \Lambda_M, \bar{r}_{{\mathfrak m}}|_{G_{M^{+}}}, \epsilon^{1-n} \delta_{M / M^{+}}^{n}, \\ &\quad \ \{ R_v^{\triangle} \}_{v \in S_{l, M}} \cup \{ R_v^{1} \}_{v \in R_M} \cup \{ R_v^{\rm St} \}_{v \in S(B)_M } \cup \{ R_v^{\square} \}_{v \in S_{a, M}} ). \end{align*}
\begin{align*} {{\mathcal{S}}}_{1, M} &= ( M / M^{+}, T_M, \tilde{T}_M, \Lambda_M, \bar{r}_{{\mathfrak m}}|_{G_{M^{+}}}, \epsilon^{1-n} \delta_{M / M^{+}}^{n}, \\ &\quad \ \{ R_v^{\triangle} \}_{v \in S_{l, M}} \cup \{ R_v^{1} \}_{v \in R_M} \cup \{ R_v^{\rm St} \}_{v \in S(B)_M } \cup \{ R_v^{\square} \}_{v \in S_{a, M}} ). \end{align*}
On the automorphic side, we can define an open compact subgroup ![]() $U_M \subset G({{\mathbb {A}}}_{M^{+}}^{\infty })$ with the property that
$U_M \subset G({{\mathbb {A}}}_{M^{+}}^{\infty })$ with the property that ![]() $U_L = U$; see [Reference ThorneTho15, § 4.5] for details. With this choice, it is possible to define a maximal ideal
$U_L = U$; see [Reference ThorneTho15, § 4.5] for details. With this choice, it is possible to define a maximal ideal ![]() ${{\mathfrak m}}_M \subset {{\mathbb {T}}}^{T_M}(U_M({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ with the property that
${{\mathfrak m}}_M \subset {{\mathbb {T}}}^{T_M}(U_M({{\mathfrak l}}^{\infty }), {{\mathcal {O}}})$ with the property that ![]() $\bar {r}_{{{\mathfrak m}}_M} = \bar {r}_{{\mathfrak m}}|_{G_{M^{+}}}$ and then there exists a commutative diagram of
$\bar {r}_{{{\mathfrak m}}_M} = \bar {r}_{{\mathfrak m}}|_{G_{M^{+}}}$ and then there exists a commutative diagram of ![]() $\Lambda _M$-algebras
$\Lambda _M$-algebras
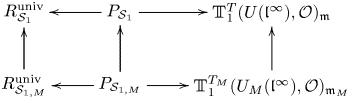
(see [Reference ThorneTho15, Proposition 4.18]). Let ![]() $J_M = J_{{{\mathcal {S}}}_{1, M}} P_{{{\mathcal {S}}}_1}$. Then we have an inclusion
$J_M = J_{{{\mathcal {S}}}_{1, M}} P_{{{\mathcal {S}}}_1}$. Then we have an inclusion ![]() $J_{{{\mathcal {S}}}_{1, M}} P_{{{\mathcal {S}}}_1} \subset J_{{{\mathcal {S}}}_1}$. More generally, if
$J_{{{\mathcal {S}}}_{1, M}} P_{{{\mathcal {S}}}_1} \subset J_{{{\mathcal {S}}}_1}$. More generally, if ![]() $M_1 / M_0 / L$ is a tower of good extensions of
$M_1 / M_0 / L$ is a tower of good extensions of ![]() $L$, then
$L$, then ![]() $J_{M_1} \subset J_{M_0}$. We say that a prime ideal
$J_{M_1} \subset J_{M_0}$. We say that a prime ideal ![]() ${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\rm univ}$ is potentially pro-automorphic if there exists a good extension
${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\rm univ}$ is potentially pro-automorphic if there exists a good extension ![]() $M/L$ such that
$M/L$ such that ![]() $J_MR_{{{\mathcal {S}}}_1}^{\rm univ} \subset {{\mathfrak p}}$.
$J_MR_{{{\mathcal {S}}}_1}^{\rm univ} \subset {{\mathfrak p}}$.
Proposition 5.3 Let ![]() ${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime of dimension 1 and characteristic
${{\mathfrak p}} \subset R_{{{\mathcal {S}}}_1}^{\text{univ}}$ be a prime of dimension 1 and characteristic ![]() $l$ which is potentially pro-automorphic and generic. Suppose further that for each
$l$ which is potentially pro-automorphic and generic. Suppose further that for each ![]() $v \in R$, the restriction
$v \in R$, the restriction ![]() $r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is trivial. Then every minimal prime
$r_{{\mathfrak p}}|_{G_{L_{{\widetilde {v}}}}}$ is trivial. Then every minimal prime ![]() $Q \subset {{\mathfrak p}}$ is potentially pro-automorphic.
$Q \subset {{\mathfrak p}}$ is potentially pro-automorphic.
Proof. The proof is the same as the proof of [Reference ThorneTho15, Proposition 6.2]. We need only replace the reference there to [Reference ThorneTho15, Corollary 4.20] to Theorem 4.1 here.
Proof of Theorem 5.1 For any good extension ![]() $M / L$, the ring
$M / L$, the ring ![]() $R_{{{\mathcal {S}}}_1}^{\text{univ}} / (\lambda , J_M)$ is a finite
$R_{{{\mathcal {S}}}_1}^{\text{univ}} / (\lambda , J_M)$ is a finite ![]() $\Lambda$-algebra. Indeed,
$\Lambda$-algebra. Indeed, ![]() $R_{{{\mathcal {S}}}_{1, M}}^{\rm univ} / (\lambda , J_{{{\mathcal {S}}}_{1, M}})$ is a finite
$R_{{{\mathcal {S}}}_{1, M}}^{\rm univ} / (\lambda , J_{{{\mathcal {S}}}_{1, M}})$ is a finite ![]() $\Lambda _M$-algebra and we can appeal to [Reference ThorneTho15, Lemma 4.16] and [Reference ThorneTho15, Proposition 4.17]. It follows from Lemma 3.9 that any quotient of
$\Lambda _M$-algebra and we can appeal to [Reference ThorneTho15, Lemma 4.16] and [Reference ThorneTho15, Proposition 4.17]. It follows from Lemma 3.9 that any quotient of ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1}/(\lambda , J_M)$ of dimension at least
$R^{\rm univ}_{{{\mathcal {S}}}_1}/(\lambda , J_M)$ of dimension at least ![]() $1 + \sup (n[L^{+} : {{\mathbb {Q}}}] - d_{L, 0}, n[L^{+} : {{\mathbb {Q}}}] - d_{L, l})$ contains a generic, potentially pro-automorphic prime
$1 + \sup (n[L^{+} : {{\mathbb {Q}}}] - d_{L, 0}, n[L^{+} : {{\mathbb {Q}}}] - d_{L, l})$ contains a generic, potentially pro-automorphic prime ![]() ${{\mathfrak p}}$ of dimension 1 and characteristic
${{\mathfrak p}}$ of dimension 1 and characteristic ![]() $l$.
$l$.
Fix a choice of lifting ![]() $r^{\rm univ}_{{{\mathcal {S}}}_1} : G_{L^{+}, S} \to {{\mathcal {G}}}_n(R_{{{\mathcal {S}}}_1}^{\rm univ})$ representing the universal deformation. This induces for each
$r^{\rm univ}_{{{\mathcal {S}}}_1} : G_{L^{+}, S} \to {{\mathcal {G}}}_n(R_{{{\mathcal {S}}}_1}^{\rm univ})$ representing the universal deformation. This induces for each ![]() $v \in R$ a homomorphism
$v \in R$ a homomorphism ![]() $R_v^{1} \rightarrow R^{\rm univ}_{{{\mathcal {S}}}_1}$ and we let
$R_v^{1} \rightarrow R^{\rm univ}_{{{\mathcal {S}}}_1}$ and we let ![]() $J_R$ denote the ideal generated by the images of
$J_R$ denote the ideal generated by the images of ![]() ${{\mathfrak m}}_{R_v^{1}}, v \in R$. The ideal
${{\mathfrak m}}_{R_v^{1}}, v \in R$. The ideal ![]() $J_R$ is independent of the choice of lifting and, for any quotient
$J_R$ is independent of the choice of lifting and, for any quotient ![]() $R_{{{\mathcal {S}}}_1}^{\rm univ}/I$ of characteristic
$R_{{{\mathcal {S}}}_1}^{\rm univ}/I$ of characteristic ![]() $l$, we have
$l$, we have ![]() $\dim R_{{{\mathcal {S}}}_1}^{\rm univ}/(J_R, I) \geq \dim R_{{{\mathcal {S}}}_1}^{\rm univ}/I - |R|n^{2}$ by [Reference MatsumuraMat89, Theorem 15.1] (note that
$\dim R_{{{\mathcal {S}}}_1}^{\rm univ}/(J_R, I) \geq \dim R_{{{\mathcal {S}}}_1}^{\rm univ}/I - |R|n^{2}$ by [Reference MatsumuraMat89, Theorem 15.1] (note that ![]() $R_v^{1}/(\lambda )$ has dimension
$R_v^{1}/(\lambda )$ has dimension ![]() $n^{2}$ [Reference ThorneTho15, Proposition 3.15]). It follows that there exists a generic prime
$n^{2}$ [Reference ThorneTho15, Proposition 3.15]). It follows that there exists a generic prime ![]() ${{\mathfrak p}} \subset R^{\rm univ}_{{{\mathcal {S}}}_1}/(J_R,J_L)$ of dimension 1 and characteristic
${{\mathfrak p}} \subset R^{\rm univ}_{{{\mathcal {S}}}_1}/(J_R,J_L)$ of dimension 1 and characteristic ![]() $l$, since
$l$, since ![]() $\dim R^{\rm univ}_{{{\mathcal {S}}}_1}/(J_R, J_L) \geq n[L^{+} : {{\mathbb {Q}}}] - n^{2} |R| > \sup (n[L^{+} : {{\mathbb {Q}}}] - d_{L, 0}, n[L^{+} : {{\mathbb {Q}}}] - d_{L, l})$ (here we are using assumption (4) in the statement of Theorem 5.1). By Proposition 5.3, any minimal prime
$\dim R^{\rm univ}_{{{\mathcal {S}}}_1}/(J_R, J_L) \geq n[L^{+} : {{\mathbb {Q}}}] - n^{2} |R| > \sup (n[L^{+} : {{\mathbb {Q}}}] - d_{L, 0}, n[L^{+} : {{\mathbb {Q}}}] - d_{L, l})$ (here we are using assumption (4) in the statement of Theorem 5.1). By Proposition 5.3, any minimal prime ![]() $Q \subset {{\mathfrak p}}$ of
$Q \subset {{\mathfrak p}}$ of ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1}$ is potentially pro-automorphic.
$R^{\rm univ}_{{{\mathcal {S}}}_1}$ is potentially pro-automorphic.
We now consider the partition of the set of minimal primes of ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1}$ into two sets
$R^{\rm univ}_{{{\mathcal {S}}}_1}$ into two sets ![]() ${{\mathcal {C}}}_1, {{\mathcal {C}}}_2$, consisting of those primes which respectively are and are not potentially pro-automorphic. We have shown that
${{\mathcal {C}}}_1, {{\mathcal {C}}}_2$, consisting of those primes which respectively are and are not potentially pro-automorphic. We have shown that ![]() ${{\mathcal {C}}}_1$ is non-empty. We claim that
${{\mathcal {C}}}_1$ is non-empty. We claim that ![]() ${{\mathcal {C}}}_2$ is empty. Otherwise, [Reference ThorneTho15, Lemma 3.21] implies the existence of primes
${{\mathcal {C}}}_2$ is empty. Otherwise, [Reference ThorneTho15, Lemma 3.21] implies the existence of primes ![]() $Q_1 \in {{\mathcal {C}}}_1, Q_2 \in {{\mathcal {C}}}_2$ such that
$Q_1 \in {{\mathcal {C}}}_1, Q_2 \in {{\mathcal {C}}}_2$ such that
and hence
The ring ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1}/Q_1$ (and hence each of its quotients) is finite over
$R^{\rm univ}_{{{\mathcal {S}}}_1}/Q_1$ (and hence each of its quotients) is finite over ![]() $\Lambda _L$. Applying Lemma 3.9 and assumption (4) once again, we see that
$\Lambda _L$. Applying Lemma 3.9 and assumption (4) once again, we see that ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1}/(Q_1, Q_2, J_R)$ contains a generic, potentially pro-automorphic prime
$R^{\rm univ}_{{{\mathcal {S}}}_1}/(Q_1, Q_2, J_R)$ contains a generic, potentially pro-automorphic prime ![]() ${{\mathfrak p}}'$ of dimension 1 and characteristic
${{\mathfrak p}}'$ of dimension 1 and characteristic ![]() $l$. Applying Proposition 5.3 to
$l$. Applying Proposition 5.3 to ![]() ${{\mathfrak p}}'$, we deduce that
${{\mathfrak p}}'$, we deduce that ![]() $Q_2$ is potentially pro-automorphic, which is a contradiction.
$Q_2$ is potentially pro-automorphic, which is a contradiction.
Now let ![]() $r : G_{L^{+}, S} \rightarrow {{\mathcal {G}}}_n({{\mathcal {O}}})$ be a lifting of
$r : G_{L^{+}, S} \rightarrow {{\mathcal {G}}}_n({{\mathcal {O}}})$ be a lifting of ![]() $\bar {r}_{{\mathfrak m}}$ which is ordinary of weight
$\bar {r}_{{\mathfrak m}}$ which is ordinary of weight ![]() $\lambda$ and of type
$\lambda$ and of type ![]() ${{\mathcal {S}}}_1$, as in the statement of the theorem. This induces a homomorphism
${{\mathcal {S}}}_1$, as in the statement of the theorem. This induces a homomorphism ![]() $R^{\rm univ}_{{{\mathcal {S}}}_1} \rightarrow {{\mathcal {O}}}$. Let
$R^{\rm univ}_{{{\mathcal {S}}}_1} \rightarrow {{\mathcal {O}}}$. Let ![]() $Q$ be a minimal prime contained inside the kernel of this homomorphism. Then there is a good extension
$Q$ be a minimal prime contained inside the kernel of this homomorphism. Then there is a good extension ![]() $M/L$ such that
$M/L$ such that ![]() $J_M \subset Q$ and so the induced homomorphism
$J_M \subset Q$ and so the induced homomorphism ![]() $R^{\rm univ}_{{{\mathcal {S}}}_{1, M}} \to {{\mathcal {O}}}$ kills
$R^{\rm univ}_{{{\mathcal {S}}}_{1, M}} \to {{\mathcal {O}}}$ kills ![]() $J_{{{\mathcal {S}}}_{1, M}}$, and the map
$J_{{{\mathcal {S}}}_{1, M}}$, and the map ![]() $P_{{{\mathcal {S}}}_{1, M}} \rightarrow {{\mathcal {O}}}$ induced by
$P_{{{\mathcal {S}}}_{1, M}} \rightarrow {{\mathcal {O}}}$ induced by ![]() $r|_{G_{M, S_M}}$ factors through
$r|_{G_{M, S_M}}$ factors through ![]() ${{\mathbb {T}}}^{T_M}_{1}(U_M({{\mathfrak l}}^{\infty }),{{\mathcal {O}}})_{{{\mathfrak m}}_M}$. Using [Reference GeraghtyGer19, Lemma 2.6.4], [Reference Clozel, Harris and TaylorCHT08, Proposition 3.3.2], and [Reference ThorneTho15, Lemma 2.7] (respectively a classicality statement in Hida theory, base change for the unitary group
${{\mathbb {T}}}^{T_M}_{1}(U_M({{\mathfrak l}}^{\infty }),{{\mathcal {O}}})_{{{\mathfrak m}}_M}$. Using [Reference GeraghtyGer19, Lemma 2.6.4], [Reference Clozel, Harris and TaylorCHT08, Proposition 3.3.2], and [Reference ThorneTho15, Lemma 2.7] (respectively a classicality statement in Hida theory, base change for the unitary group ![]() $G_{M^{+}}$, and soluble descent for
$G_{M^{+}}$, and soluble descent for ![]() $\operatorname {GL}_n({{\mathbb {A}}}_M)$), we deduce that the representation
$\operatorname {GL}_n({{\mathbb {A}}}_M)$), we deduce that the representation ![]() $r|_{G_L}$ is automorphic of weight
$r|_{G_L}$ is automorphic of weight ![]() $\lambda$.
$\lambda$.
The following corollary was established in the course of the above proof.
Corollary 5.4 With hypotheses on ![]() $\bar {r}_{{\mathfrak m}}$ as in Theorem 5.1,
$\bar {r}_{{\mathfrak m}}$ as in Theorem 5.1, ![]() $R_{{{\mathcal {S}}}_1}$ is a finite
$R_{{{\mathcal {S}}}_1}$ is a finite ![]() $\Lambda$-algebra.
$\Lambda$-algebra.
6. The end
We are now in a position to state and prove the main theorem of this paper.
Theorem 6.1 Let ![]() $F$ be an imaginary CM number field with maximal totally real subfield
$F$ be an imaginary CM number field with maximal totally real subfield ![]() $F^{+}$ and let
$F^{+}$ and let ![]() $n \geq 2$ be an integer. Let
$n \geq 2$ be an integer. Let ![]() $l$ be a prime and suppose that
$l$ be a prime and suppose that ![]() $\rho : G_F \rightarrow \mathrm {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is a continuous semisimple representation satisfying the following hypotheses.
$\rho : G_F \rightarrow \mathrm {GL}_n(\bar {{{\mathbb {Q}}}}_l)$ is a continuous semisimple representation satisfying the following hypotheses.
(i)
 $\rho ^{c} \cong \rho ^{\vee } \epsilon ^{1-n}$.
$\rho ^{c} \cong \rho ^{\vee } \epsilon ^{1-n}$.(ii)
 $\rho$ is ramified at only finitely many places.
$\rho$ is ramified at only finitely many places.(iii)
 $\rho$ is ordinary of weight
$\rho$ is ordinary of weight  $\lambda$ for some
$\lambda$ for some  $\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(F, {{\bar {{{\mathbb {Q}}}}_l}})}$.
$\lambda \in ({{\mathbb {Z}}}_+^{n})^{\operatorname {Hom}(F, {{\bar {{{\mathbb {Q}}}}_l}})}$.(iv) There is an isomorphism
 $\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each
$\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each  $\bar {\rho }_i$ is absolutely irreducible and satisfies
$\bar {\rho }_i$ is absolutely irreducible and satisfies  $\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$, and
$\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$, and  $\bar {\rho }_i \not \cong \bar {\rho }_j$ if
$\bar {\rho }_i \not \cong \bar {\rho }_j$ if  $i \neq j$.
$i \neq j$.(v) There exists a finite place
 ${{\widetilde {v}}}_0$ of
${{\widetilde {v}}}_0$ of  $F$, prime to
$F$, prime to  $l$, such that
$l$, such that  $\rho |_{G_{F_{{{\widetilde {v}}}_0}}}^{\text {ss}} \cong \oplus _{i=1}^{n} \psi \epsilon ^{n-i}$ for some unramified character
$\rho |_{G_{F_{{{\widetilde {v}}}_0}}}^{\text {ss}} \cong \oplus _{i=1}^{n} \psi \epsilon ^{n-i}$ for some unramified character  $\psi : G_{F_{{{\widetilde {v}}}_0}} \rightarrow \bar {{{\mathbb {Q}}}}_l^{\times }$.
$\psi : G_{F_{{{\widetilde {v}}}_0}} \rightarrow \bar {{{\mathbb {Q}}}}_l^{\times }$.(vi) There exist a RACSDC representation
 $\pi$ of
$\pi$ of  $\mathrm {GL}_n({{\mathbb {A}}}_F)$ and
$\mathrm {GL}_n({{\mathbb {A}}}_F)$ and  $\iota : {{\bar {{{\mathbb {Q}}}}_l}} \to {{\mathbb {C}}}$ such that:
$\iota : {{\bar {{{\mathbb {Q}}}}_l}} \to {{\mathbb {C}}}$ such that:
(a)
 $\pi$ is
$\pi$ is  $\iota$-ordinary;
$\iota$-ordinary;(b)
 $\overline {r_{ \iota }(\pi )}^{\text {ss}} \cong \bar {\rho }^{\text {ss}}$;
$\overline {r_{ \iota }(\pi )}^{\text {ss}} \cong \bar {\rho }^{\text {ss}}$;(c)
 $\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation.
$\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation.
(vii)
 $F(\zeta _l)$ is not contained in
$F(\zeta _l)$ is not contained in  $\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and
$\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and  $F$ is not contained in
$F$ is not contained in  $F^{+}(\zeta _l)$. For each
$F^{+}(\zeta _l)$. For each  $1 \leq i, j \leq {d}$,
$1 \leq i, j \leq {d}$,  $\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and
$\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and  $\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if
$\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if  $i \neq j$. Moreover,
$i \neq j$. Moreover,  $\bar {\rho }^{\text {ss}}$ is primitive and
$\bar {\rho }^{\text {ss}}$ is primitive and  $\bar {\rho }^{\text {ss}}(G_{F})$ has no quotient of order
$\bar {\rho }^{\text {ss}}(G_{F})$ has no quotient of order  $l$.
$l$.(viii)
 $l > 3$ and
$l > 3$ and  $l \nmid n$.
$l \nmid n$.
Then ![]() $\rho$ is automorphic: there exists an
$\rho$ is automorphic: there exists an ![]() $\iota$-ordinary RACSDC automorphic representation
$\iota$-ordinary RACSDC automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$ such that
$\operatorname {GL}_n({{\mathbb {A}}}_F)$ such that ![]() $r_\iota (\Pi ) \cong \rho$.
$r_\iota (\Pi ) \cong \rho$.
Proof. The proof is similar to, and even simpler than, the proof of [Reference ThorneTho15, Theorem 7.1]. We can find a coefficient field ![]() $K \subset \bar {{{\mathbb {Q}}}}_l$ and, after replacing
$K \subset \bar {{{\mathbb {Q}}}}_l$ and, after replacing ![]() $\rho$ by a conjugate, assume that
$\rho$ by a conjugate, assume that ![]() $\rho = r|_{G_F}$, where
$\rho = r|_{G_F}$, where ![]() $r : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ is a homomorphism such that
$r : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ is a homomorphism such that ![]() $\bar {r}$ is Schur and
$\bar {r}$ is Schur and ![]() $\nu \circ r = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$. Similarly, we can assume the existence of a model
$\nu \circ r = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$. Similarly, we can assume the existence of a model ![]() $\rho ' : G_{F} \to \operatorname {GL}_n({{\mathcal {O}}})$ for
$\rho ' : G_{F} \to \operatorname {GL}_n({{\mathcal {O}}})$ for ![]() $r_\iota (\pi )$ which extends to a homomorphism
$r_\iota (\pi )$ which extends to a homomorphism ![]() $r' : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ such that
$r' : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ such that ![]() $\nu \circ r' = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$ and such that
$\nu \circ r' = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$ and such that ![]() $\bar {r}' = \bar {r}$. In fact,
$\bar {r}' = \bar {r}$. In fact, ![]() $\bar {r}|_{G_{F^{+}(\zeta _l)}}$ is Schur. Indeed, making use of assumption 6.1, we just need to check that
$\bar {r}|_{G_{F^{+}(\zeta _l)}}$ is Schur. Indeed, making use of assumption 6.1, we just need to check that ![]() $\bar {r}(G_{F^{+}(\zeta _l)})$ meets both components of
$\bar {r}(G_{F^{+}(\zeta _l)})$ meets both components of ![]() ${{\mathcal {G}}}_n$. This is our assumption that
${{\mathcal {G}}}_n$. This is our assumption that ![]() $F \not \subset F^{+}(\zeta _l)$.
$F \not \subset F^{+}(\zeta _l)$.
After making a preliminary soluble base change, we can assume that the following further conditions are satisfied.
(i)
 $F / F^{+}$ is everywhere unramified and each place of
$F / F^{+}$ is everywhere unramified and each place of  $F^{+}$ dividing
$F^{+}$ dividing  $l$ or above which
$l$ or above which  $\rho$ or
$\rho$ or  $\pi$ is ramified splits in
$\pi$ is ramified splits in  $F$.
$F$.(ii) The place
 ${{\widetilde {v}}}_0$ is split over
${{\widetilde {v}}}_0$ is split over  $F^{+}$. We write
$F^{+}$. We write  $v_0 = {{\widetilde {v}}}_0|_{F^{+}}$.
$v_0 = {{\widetilde {v}}}_0|_{F^{+}}$.(iii) For each place
 $w$ of
$w$ of  $F$ at which
$F$ at which  $\rho$ or
$\rho$ or  $\pi$ is ramified, or which divides
$\pi$ is ramified, or which divides  $l$, the representation
$l$, the representation  $\bar {r}|_{G_{F_w}}$ is trivial.
$\bar {r}|_{G_{F_w}}$ is trivial.(iv) For each prime-to-
 $l$ place
$l$ place  $w$ of
$w$ of  $F$ at which
$F$ at which  $\rho$ or
$\rho$ or  $\pi$ is ramified, we have
$\pi$ is ramified, we have  $q_w \equiv 1 \text { mod }l$ and, if
$q_w \equiv 1 \text { mod }l$ and, if  $l^{N}||(q_w - 1)$, then
$l^{N}||(q_w - 1)$, then  $l^{N} > n$. Moreover,
$l^{N} > n$. Moreover,  $\rho |_{G_{F_w}}$ and
$\rho |_{G_{F_w}}$ and  $\rho '|_{G_{F_w}}$ are unipotently ramified.
$\rho '|_{G_{F_w}}$ are unipotently ramified.
We can find a finite set ![]() $\tilde {X}_0$ of finite places of
$\tilde {X}_0$ of finite places of ![]() $F$ satisfying the following conditions.
$F$ satisfying the following conditions.
–
 $\tilde {X}_0$ does not contain any place at which
$\tilde {X}_0$ does not contain any place at which  $\rho$ or
$\rho$ or  $\pi$ is ramified, or any place dividing
$\pi$ is ramified, or any place dividing  $l$.
$l$.– Let
 $E / F(\zeta _l)$ denote the extension cut out by
$E / F(\zeta _l)$ denote the extension cut out by  $\bar {\rho }|_{G_{F(\zeta _l)}}$. Then, for any Galois subextension
$\bar {\rho }|_{G_{F(\zeta _l)}}$. Then, for any Galois subextension  $E / E'/ F$ with
$E / E'/ F$ with  $\operatorname {Gal}(E'/F)$ simple, there exists a place
$\operatorname {Gal}(E'/F)$ simple, there exists a place  $w \in \tilde {X}_0$ which does not split in
$w \in \tilde {X}_0$ which does not split in  $E'$.
$E'$.–
 $\tilde {X}_0$ contains an absolutely unramified place
$\tilde {X}_0$ contains an absolutely unramified place  ${{\widetilde {v}}}_1$ such that
${{\widetilde {v}}}_1$ such that  $\bar {\rho }(\operatorname {Frob}_{{{\widetilde {v}}}_1})$ is scalar and
$\bar {\rho }(\operatorname {Frob}_{{{\widetilde {v}}}_1})$ is scalar and  $q_{{{\widetilde {v}}}_1} \not \equiv 1 \text { mod }l$.
$q_{{{\widetilde {v}}}_1} \not \equiv 1 \text { mod }l$.
Let ![]() $X_0$ denote the set of places of
$X_0$ denote the set of places of ![]() $F^{+}$ lying below a place of
$F^{+}$ lying below a place of ![]() $\tilde {X}_0$. We write
$\tilde {X}_0$. We write ![]() $v_1 = {{\widetilde {v}}}_1|_{F^{+}}$. If
$v_1 = {{\widetilde {v}}}_1|_{F^{+}}$. If ![]() $L / F$ is any Galois CM extension which is
$L / F$ is any Galois CM extension which is ![]() $\tilde {X}_0$-split, then the analogue of assumption (7) of the theorem (where
$\tilde {X}_0$-split, then the analogue of assumption (7) of the theorem (where ![]() $F$ is replaced by
$F$ is replaced by ![]() $L$ and
$L$ and ![]() $\bar {\rho }$ by
$\bar {\rho }$ by ![]() $\bar {\rho }|_{G_L}$) is satisfied.
$\bar {\rho }|_{G_L}$) is satisfied.
If ![]() $L^{+} / F^{+}$ is a Galois, totally real,
$L^{+} / F^{+}$ is a Galois, totally real, ![]() $X_0$-split extension and
$X_0$-split extension and ![]() $L = L^{+} \cdot F$, then
$L = L^{+} \cdot F$, then ![]() $L / F$ is Galois CM and
$L / F$ is Galois CM and ![]() $\tilde {X}_0$-split. We claim that we can find a soluble, totally real,
$\tilde {X}_0$-split. We claim that we can find a soluble, totally real, ![]() $X_0$-split extension such that the hypotheses of Theorem 5.1 are satisfied for
$X_0$-split extension such that the hypotheses of Theorem 5.1 are satisfied for ![]() $r|_{G_{L^{+}}}$. This will complete the proof: we deduce from Theorem 5.1 that
$r|_{G_{L^{+}}}$. This will complete the proof: we deduce from Theorem 5.1 that ![]() $r|_{G_L} = \rho |_{G_L}$ is automorphic of weight
$r|_{G_L} = \rho |_{G_L}$ is automorphic of weight ![]() $\lambda$ and irreducible. The automorphy of
$\lambda$ and irreducible. The automorphy of ![]() $\rho$ then follows by soluble descent.
$\rho$ then follows by soluble descent.
Let ![]() $\tilde {Y}_0$ denote the set of places
$\tilde {Y}_0$ denote the set of places ![]() ${{\widetilde {v}}} \neq {{\widetilde {v}}}_0, {{\widetilde {v}}}_0^{c}$ of
${{\widetilde {v}}} \neq {{\widetilde {v}}}_0, {{\widetilde {v}}}_0^{c}$ of ![]() $F$ dividing
$F$ dividing ![]() $l$ or at which
$l$ or at which ![]() $\rho$ or
$\rho$ or ![]() $\pi$ is ramified, and let
$\pi$ is ramified, and let ![]() $Y_0$ denote the set of places of
$Y_0$ denote the set of places of ![]() $F^{+}$ lying below a place of
$F^{+}$ lying below a place of ![]() $\tilde {Y}_0$. Then every place of
$\tilde {Y}_0$. Then every place of ![]() $Y_0$ splits in
$Y_0$ splits in ![]() $F$ and
$F$ and ![]() $Y_0 \cap ( X_0 \cup \{ v_0 \} ) = \emptyset$. For any odd integer
$Y_0 \cap ( X_0 \cup \{ v_0 \} ) = \emptyset$. For any odd integer ![]() $\delta \geq 1$, we can find a cyclic totally real extension
$\delta \geq 1$, we can find a cyclic totally real extension ![]() $M_0 / F^{+}$ of degree
$M_0 / F^{+}$ of degree ![]() $\delta$ which is
$\delta$ which is ![]() $X_0 \cup \{ v_0 \}$-split and such that each place
$X_0 \cup \{ v_0 \}$-split and such that each place ![]() $v \in Y_0$ of
$v \in Y_0$ of ![]() $F^{+}$ is totally inert in
$F^{+}$ is totally inert in ![]() $M_0$.
$M_0$.
Let ![]() $M_1$ be a totally real quadratic extension of
$M_1$ be a totally real quadratic extension of ![]() $F^{+}$ which is
$F^{+}$ which is ![]() $X_0 \cup \{ v_0 \} \cup Y_0$-split. We will take
$X_0 \cup \{ v_0 \} \cup Y_0$-split. We will take ![]() $L = F \cdot M_0 \cdot M_1$. We claim that for a suitable choice of odd integer
$L = F \cdot M_0 \cdot M_1$. We claim that for a suitable choice of odd integer ![]() $\delta$, this
$\delta$, this ![]() $L$ will suffice for the application of Theorem 5.1. More precisely, we will apply Theorem 5.1 to the homomorphism
$L$ will suffice for the application of Theorem 5.1. More precisely, we will apply Theorem 5.1 to the homomorphism ![]() $r|_{G_{L^{+}}}$ with the following data.
$r|_{G_{L^{+}}}$ with the following data.
–
 $S_l$ is the set of
$S_l$ is the set of  $l$-adic places of
$l$-adic places of  $L^{+}$.
$L^{+}$.–
 $S(B)$ is the set of places of
$S(B)$ is the set of places of  $L^{+}$ lying above
$L^{+}$ lying above  $v_0$.
$v_0$.–
 $R$ is the set of prime-to-
$R$ is the set of prime-to- $l$ places of
$l$ places of  $L^{+}$ lying above a place of
$L^{+}$ lying above a place of  $Y_0$.
$Y_0$.–
 $S_a$ is the set of places of
$S_a$ is the set of places of  $L^{+}$ lying above
$L^{+}$ lying above  $v_1$.
$v_1$.
Let ![]() $\Delta$ denote the Galois group of the maximal abelian pro-
$\Delta$ denote the Galois group of the maximal abelian pro-![]() $l$ extension of
$l$ extension of ![]() $L$ unramified outside
$L$ unramified outside ![]() $l$, and let
$l$, and let ![]() $\Delta _0$ denote the Galois group of the maximal abelian pro-
$\Delta _0$ denote the Galois group of the maximal abelian pro-![]() $l$ extension of
$l$ extension of ![]() $L$ which is unramified outside
$L$ which is unramified outside ![]() $l$ and which is
$l$ and which is ![]() $S(B)$-split. Then
$S(B)$-split. Then ![]() $\Delta _0$ is naturally a quotient of
$\Delta _0$ is naturally a quotient of ![]() $\Delta$. Let us define
$\Delta$. Let us define
and
In order to complete the proof, we must show that the odd integer ![]() $\delta \geq 1$ can be chosen so that the inequalities
$\delta \geq 1$ can be chosen so that the inequalities
and
are simultaneously satisfied. It follows from [Reference MaireMai02, Proposition 19] that ![]() $d_0 = 2\delta$ (see the proof of [Reference ThorneTho15, Theorem 7.1] for more details). If
$d_0 = 2\delta$ (see the proof of [Reference ThorneTho15, Theorem 7.1] for more details). If ![]() $\delta$ is prime to the absolute residue degrees of all the places of
$\delta$ is prime to the absolute residue degrees of all the places of ![]() $Y_0$, then we will have
$Y_0$, then we will have ![]() $|R| \leq 2 |Y_0|$ and
$|R| \leq 2 |Y_0|$ and ![]() $d_l \geq \delta$. We will therefore be done if we can choose
$d_l \geq \delta$. We will therefore be done if we can choose ![]() $\delta$ to satisfy
$\delta$ to satisfy
and
This is clearly possible and concludes the proof.
We can use the same idea to prove the following finiteness result (compare [Reference ThorneTho12, Theorem 10.2]), which plays a crucial role in some of the level-raising arguments in [Reference Newton and ThorneNT19].
Theorem 6.2 Let ![]() $F$ be a CM field, let
$F$ be a CM field, let ![]() $l$ be a prime, and let
$l$ be a prime, and let ![]() $\iota : \bar {{{\mathbb {Q}}}}_l \to {{\mathbb {C}}}$ be an isomorphism. Let
$\iota : \bar {{{\mathbb {Q}}}}_l \to {{\mathbb {C}}}$ be an isomorphism. Let ![]() $S$ be a finite set of finite places of
$S$ be a finite set of finite places of ![]() $F^{+}$, containing the
$F^{+}$, containing the ![]() $l$-adic ones, and suppose that each place of
$l$-adic ones, and suppose that each place of ![]() $S$ splits in
$S$ splits in ![]() $F$. Choose for each
$F$. Choose for each ![]() $v \in S$ a place
$v \in S$ a place ![]() ${{\widetilde {v}}}$ of
${{\widetilde {v}}}$ of ![]() $F$ lying above
$F$ lying above ![]() $v$ and let
$v$ and let ![]() $\tilde {S}$ denote the set of the
$\tilde {S}$ denote the set of the ![]() ${{\widetilde {v}}}$.
${{\widetilde {v}}}$.
Let ![]() $\pi$ be a RACSDC automorphic representation of
$\pi$ be a RACSDC automorphic representation of ![]() $\operatorname {GL}_n({{\mathbb {A}}}_F)$, and let
$\operatorname {GL}_n({{\mathbb {A}}}_F)$, and let ![]() $K / {{\mathbb {Q}}}_l$ be a coefficient field such that
$K / {{\mathbb {Q}}}_l$ be a coefficient field such that ![]() $r_{\iota }(\pi )$ can be chosen to take values in
$r_{\iota }(\pi )$ can be chosen to take values in ![]() $\operatorname {GL}_n({{\mathcal {O}}})$ and extend it to a homomorphism
$\operatorname {GL}_n({{\mathcal {O}}})$ and extend it to a homomorphism ![]() $r : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ such that
$r : G_{F^{+}} \to {{\mathcal {G}}}_n({{\mathcal {O}}})$ such that ![]() $\nu \circ r = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$. Suppose that the following conditions are satisfied.
$\nu \circ r = \epsilon ^{1-n} \delta _{F / F^{+}}^{n}$. Suppose that the following conditions are satisfied.
(i)
 $\pi$ is
$\pi$ is  $\iota$-ordinary. For each place
$\iota$-ordinary. For each place  $v \in S_l$,
$v \in S_l$,  $\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is the trivial representation.
$\bar {r}|_{G_{F_{{\widetilde {v}}}}}$ is the trivial representation.(ii)
 $\pi$ is unramified outside
$\pi$ is unramified outside  $S$.
$S$.(iii) There exists a place
 $v_0 \nmid l$ of
$v_0 \nmid l$ of  $S$ such that
$S$ such that  $\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation. Moreover,
$\pi _{{{\widetilde {v}}}_0}$ is an unramified twist of the Steinberg representation. Moreover,  $q_{v_0} \equiv 1 \text { mod }l$ and
$q_{v_0} \equiv 1 \text { mod }l$ and  $\bar {r}|_{G_{F_{{{\widetilde {v}}}_0}}}$ is the trivial representation.
$\bar {r}|_{G_{F_{{{\widetilde {v}}}_0}}}$ is the trivial representation.(iv) Let
 $\bar {\rho } = \bar {r}|_{G_{F, S}}$. There is an isomorphism
$\bar {\rho } = \bar {r}|_{G_{F, S}}$. There is an isomorphism  $\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each
$\bar {\rho }^{\text {ss}} \cong \bar {\rho }_1 \oplus \cdots \oplus \bar {\rho }_{d}$, where each  $\bar {\rho }_i$ is absolutely irreducible and satisfies
$\bar {\rho }_i$ is absolutely irreducible and satisfies  $\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$ (in particular,
$\bar {\rho }_i^{c} \cong \bar {\rho }_i^{\vee } \epsilon ^{1-n}$ (in particular,  $\bar {r}$ is Schur and therefore
$\bar {r}$ is Schur and therefore  $\bar {\rho }$ is semisimple).
$\bar {\rho }$ is semisimple).(v)
 $F(\zeta _l)$ is not contained in
$F(\zeta _l)$ is not contained in  $\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and
$\bar {F}^{\ker \rm ad (\bar {\rho }^{\text {ss}})}$ and  $F$ is not contained in
$F$ is not contained in  $F^{+}(\zeta _l)$. For each
$F^{+}(\zeta _l)$. For each  $1 \leq i, j \leq {d}$,
$1 \leq i, j \leq {d}$,  $\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and
$\bar {\rho }_i|_{G_{F(\zeta _l)}}$ is absolutely irreducible and  $\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if
$\bar {\rho }_i|_{G_{F(\zeta _l)}} \not \cong \bar {\rho }_j|_{G_{F(\zeta _l)}}$ if  $i \neq j$. Moreover,
$i \neq j$. Moreover,  $\bar {\rho }$ is primitive and
$\bar {\rho }$ is primitive and  $\bar {\rho }(G_{F})$ has no quotient of order
$\bar {\rho }(G_{F})$ has no quotient of order  $l$.
$l$.(vi)
 $l > 3$ and
$l > 3$ and  $l \nmid n$.
$l \nmid n$.
Define the global deformation problem
Then ![]() $R_{{{\mathcal {S}}}}^{\text{univ}}$ is a finite
$R_{{{\mathcal {S}}}}^{\text{univ}}$ is a finite ![]() $\Lambda$-algebra.
$\Lambda$-algebra.
Proof. Let ![]() $R = S - S_l \cup \{ v_0 \}$,
$R = S - S_l \cup \{ v_0 \}$, ![]() $S(B) = \{ v_0 \}$. If
$S(B) = \{ v_0 \}$. If ![]() $L / F$ is a CM extension, let
$L / F$ is a CM extension, let ![]() $S_L$ denote the set of places of
$S_L$ denote the set of places of ![]() $L^{+}$ above
$L^{+}$ above ![]() $S$,
$S$, ![]() $\tilde {S}_L$ the set of places of
$\tilde {S}_L$ the set of places of ![]() $L$ above
$L$ above ![]() $\tilde {S}$, and define
$\tilde {S}$, and define ![]() $R_L$,
$R_L$, ![]() $\tilde {R}_L$ etc. similarly. If
$\tilde {R}_L$ etc. similarly. If ![]() $L$ satisfies the following conditions:
$L$ satisfies the following conditions:
–
 $\bar {r}|_{L^{+}}$ is Schur;
$\bar {r}|_{L^{+}}$ is Schur;– for each place
 $v \in R_L$,
$v \in R_L$,  $q_v \equiv 1 \text { mod }l$ and
$q_v \equiv 1 \text { mod }l$ and  $\bar {r}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation;
$\bar {r}|_{G_{L_{{\widetilde {v}}}}}$ is the trivial representation;– for each place
 $v \in R$ and each place
$v \in R$ and each place  $w | v$ of
$w | v$ of  $L^{+}$, the induced map
$L^{+}$, the induced map  $R_{L_{{\widetilde {v}}}}^{\square } \to R_{F_{{\widetilde {v}}}}^{\square }$ factors through the quotient
$R_{L_{{\widetilde {v}}}}^{\square } \to R_{F_{{\widetilde {v}}}}^{\square }$ factors through the quotient  $R_{L_{{\widetilde {v}}}}^{\square }\to R_{L_{{\widetilde {v}}}}^{1}$,
$R_{L_{{\widetilde {v}}}}^{\square }\to R_{L_{{\widetilde {v}}}}^{1}$,
then we can define the global deformation problem
and restriction from ![]() $F^{+}$ to
$F^{+}$ to ![]() $L^{+}$ determines a finite morphism
$L^{+}$ determines a finite morphism ![]() $R_{{{\mathcal {S}}}_L}^{\rm univ} \to R_{{{\mathcal {S}}}}^{\rm univ}$. If moreover
$R_{{{\mathcal {S}}}_L}^{\rm univ} \to R_{{{\mathcal {S}}}}^{\rm univ}$. If moreover ![]() $L$ satisfies the conditions of Theorem 5.1, then Corollary 5.4 will imply that
$L$ satisfies the conditions of Theorem 5.1, then Corollary 5.4 will imply that ![]() $R_{{{\mathcal {S}}}_L}^{\rm univ}$ is a finite
$R_{{{\mathcal {S}}}_L}^{\rm univ}$ is a finite ![]() $\Lambda _L$-algebra and hence that
$\Lambda _L$-algebra and hence that ![]() $R_{{{\mathcal {S}}}}^{\rm univ}$ is a finite
$R_{{{\mathcal {S}}}}^{\rm univ}$ is a finite ![]() $\Lambda$-algebra. Such an extension
$\Lambda$-algebra. Such an extension ![]() $L / F$ can be constructed in exactly the same manner as in the proof of Theorem 6.1.
$L / F$ can be constructed in exactly the same manner as in the proof of Theorem 6.1.
Acknowledgements
We would like to thank the organizers of the workshop ‘Deformation Theory, Completed Cohomology, Leopoldt Conjecture and K-theory’ at CIRM in December 2016, where some of the ideas of this paper were first discussed. We also thank the anonymous referee for their helpful comments.
This work was partially conducted during the period that J.A.T. served as a Clay Research Fellow. J.A.T.'s work received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 714405). J.A.T. would like to thank Lue Pan for pointing out an error in [Reference ThorneTho15], which is addressed here in § 3.1.
P.B.A. was supported by Simons Foundation Collaboration Grant 527275 and NSF grant DMS-1902155.