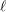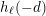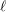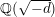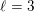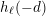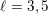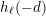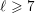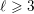Averages and moments associated to class numbers of imaginary quadratic fields

Abstract

For any odd prime $\ell$, let $h_{\ell }(-d)$ denote the $\ell$-part of the class number of the imaginary quadratic field $\mathbb{Q}(\sqrt{-d})$. Nontrivial pointwise upper bounds are known only for $\ell =3$; nontrivial upper bounds for averages of $h_{\ell }(-d)$ have previously been known only for $\ell =3,5$. In this paper we prove nontrivial upper bounds for the average of $h_{\ell }(-d)$ for all primes $\ell \geqslant 7$, as well as nontrivial upper bounds for certain higher moments for all primes $\ell \geqslant 3$.

1 Introduction

Fix an imaginary quadratic field $\mathbb{Q}(\sqrt{-d})$ with square-free $-d<0$ , and let $\text{Cl}(-d)$ be the corresponding class group. The size of the class group, denoted $h(-d)$ , is the class number of $\mathbb{Q}(\sqrt{-d})$ , a fundamental invariant that appears widely in number theory. The divisibility properties of class numbers of quadratic fields are subject to the conjectures known as the Cohen–Lenstra heuristics [CL84], which despite significant attention remain open in most cases. For any prime $\ell \geqslant 2$ , let $h_{\ell }(-d)$ denote the $\ell$ -part of the class number, that is the number of ideal classes in the class group $\text{Cl}(-d)$ whose $\ell$ th power is the principal ideal class. One may obtain a trivial pointwise upper bound for $h_{\ell }(-d)$ by noting that

$$\begin{eqnarray}h_{\ell }(-d)\leqslant h(-d)\ll d^{1/2+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

It is conjectured that

(1.1) $$\begin{eqnarray}h_{\ell }(-d)\ll d^{\unicode[STIX]{x1D700}}\end{eqnarray}$$

for all $d$ and any $\unicode[STIX]{x1D700}>0$ . (Throughout, we will use the convention that all implied constants may depend upon $\ell$ and $\unicode[STIX]{x1D700}$ .)

This conjecture (and a more general version for $\ell$ -torsion in class groups of number fields of any degree) is motivated by the Cohen–Lenstra heuristics [CL84], by counting elliptic curves with fixed conductor  [BS96], by counting number fields of fixed degree and discriminant [Duk98], and by questions on equidistribution of CM-points on Shimura varieties [Zha05]. For $\ell =2$ , the conjecture (1.1) is known by the genus theory of Gauss. For $\ell =3$ the currently best-known upper bound is due to Ellenberg and Venkatesh [EV07]:

(1.2) $$\begin{eqnarray}h_{3}(-d)\ll d^{1/3+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

For primes $\ell \geqslant 5$ , no nontrivial upper bound for $h_{\ell }(-d)$ is known to hold for all  $d$ .

One may also consider averages

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d).\end{eqnarray}$$

In the case $\ell =3$ , Davenport and Heilbronn [DH71] established that

(1.3) $$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{3}(-d)\sim 2\mathop{\sum }_{0<d<X}1,\end{eqnarray}$$

as $X\rightarrow \infty$ , in which both sums are restricted to fundamental discriminants. This asymptotic has recently been refined further to include secondary main terms (see Bhargava et al. [BST13], Taniguchi and Thorne [TT13], and Hough [Hou10]), but for the purposes of this paper it is sufficient that (1.3) provides an upper bound:

(1.4) $$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{3}(-d)\ll X.\end{eqnarray}$$

For $\ell =5$ , the best-known upper bound for the average is due to Soundararajan [Sou00] (also proved by Hough [Hou10]):

(1.5) $$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{5}(-d)\ll X^{5/4+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

For primes $\ell \geqslant 7$ , the literature appears to contain no bound better than the trivial estimate

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)\ll X^{3/2+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

However Soundararajan noted in [Sou00] that he has shown for any prime $\ell \geqslant 3$ that

(1.6) $$\begin{eqnarray}h_{\ell }(-d)\ll d^{1/2-1/2\ell +\unicode[STIX]{x1D700}}\end{eqnarray}$$

for all but one square-free discriminant $d$ in any dyadic range $[X,2X)$ . Summing over $O(\log X)$ dyadic ranges implies the nontrivial average bound

(1.7) $$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)\ll X^{3/2-1/2\ell +\unicode[STIX]{x1D700}}\end{eqnarray}$$

for any $\ell \geqslant 3$ . While this is superseded by (1.4) and (1.5) for $\ell =3$ and $5$ , no improvement has been given hitherto for larger values of $\ell$ .

One can further consider the second moment; motivated by the conjecture (1.1) for the pointwise upper bound for $h_{\ell }(-d)$ , one would expect that

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{2}\ll X^{1+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

For $\ell =3$ and $5$ , one may bound the second moment by applying the best-known pointwise upper bound (respectively (1.2) and (1.6)) to one factor $h_{\ell }(-d)$ , and then applying the best-known average upper bound to the remaining sum (respectively (1.4) and (1.5)). For $\ell \geqslant 7$ , it is advantageous to apply Soundararajan’s result (1.6) to both factors of $h_{\ell }(-d)$ . This approach results in the following upper bounds for the second moment:

(1.8) $$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{2}\ll \left\{\begin{array}{@{}ll@{}}X^{4/3+\unicode[STIX]{x1D700}}\quad & \ell =3,\\ X^{33/20+\unicode[STIX]{x1D700}}\quad & \ell =5,\\ X^{2-1/\ell +\unicode[STIX]{x1D700}}\quad & \ell \geqslant 7,\;\text{prime.}\end{array}\right.\end{eqnarray}$$

More generally, for any real number $k\geqslant 1$ , known results lead to bounds for the $k$ th moment of the form

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{k}\ll \left\{\begin{array}{@{}ll@{}}X^{1+(k-1)/3+\unicode[STIX]{x1D700}}\quad & \ell =3,\\ X^{5/4+(k-1)(2/5)+\unicode[STIX]{x1D700}}+X^{k/2+\unicode[STIX]{x1D700}}\quad & \ell =5,\\ X^{1+k((\ell -1)/2\ell )+\unicode[STIX]{x1D700}}+X^{k/2+\unicode[STIX]{x1D700}}\quad & \ell \geqslant 7,\;\text{prime.}\end{array}\right.\end{eqnarray}$$

1.1 Statement of the theorems

The purpose of this paper is to improve on these bounds for the averages and moments of $h_{\ell }(-d)$ for $d$ square-free and $\ell$ an odd prime. (For the rest of this paper the notations $d$ and $\ell$ are reserved for square-free integers and odd primes respectively.)

Theorem 1.1. For each prime $\ell \geqslant 5$ ,

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)\ll X^{3/2-3/(2\ell +2)+\unicode[STIX]{x1D700}},\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ .

This recaptures Soundararajan’s result (1.5) for $\ell =5$ and improves on the bound (1.7) for all primes $\ell \geqslant 7$ . (Since Davenport and Heilbronn’s result (1.3) is best possible, our work provides no new information for the average of $h_{3}(-d)$ .)

We also consider higher moments. First we consider the moments of $h_{3}(-d)$ , for which our main result is the following.

Theorem 1.2.

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{3}(-d)^{4}\ll X^{11/6+\unicode[STIX]{x1D700}}\quad \text{for any }\unicode[STIX]{x1D700}>0.\end{eqnarray}$$

It may be surprising to see the fourth moment here, but it turns out to give the best results of its type, as we shall see.

By the reflection principle of Scholz [Sch32], $\log _{3}h_{3}(-d)$ and $\log _{3}h_{3}(+3d)$ differ by at most one. Thus the corresponding bound for the $3$ -part of the class number of real quadratic fields follows as a corollary, making an identical improvement over previously known bounds as in the imaginary case.

Corollary 1.3.

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{3}(d)^{4}\ll X^{11/6+\unicode[STIX]{x1D700}}\quad \text{for any }\unicode[STIX]{x1D700}>0.\end{eqnarray}$$

Nontrivial bounds for other moments are also an immediate corollary. For $1\leqslant k<4$ one merely uses Hölder’s inequality in conjunction with (1.4), while for $k>4$ one just applies (1.2) in combination with Theorem 1.2.

Corollary 1.4. For all real $k\in [1,4]$ , and for any $\unicode[STIX]{x1D700}>0$ ,

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{0<d<X}h_{3}(-d)^{k} & \ll & \displaystyle X^{(5k+13)/18+\unicode[STIX]{x1D700}},\nonumber\\ \displaystyle \mathop{\sum }_{0<d<X}h_{3}(d)^{k} & \ll & \displaystyle X^{(5k+13)/18+\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$

For all real $k\geqslant 4$ , and for any $\unicode[STIX]{x1D700}>0$ ,

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{0<d<X}h_{3}(-d)^{k} & \ll & \displaystyle X^{(2k+3)/6+\unicode[STIX]{x1D700}},\nonumber\\ \displaystyle \mathop{\sum }_{0<d<X}h_{3}(d)^{k} & \ll & \displaystyle X^{(2k+3)/6+\unicode[STIX]{x1D700}}.\nonumber\end{eqnarray}$$

In particular, for any $\unicode[STIX]{x1D700}>0$ ,

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{3}(-d)^{2}\ll X^{23/18+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

This final bound improves on (1.8); we note that $23/18=1.2777\ldots \,$ .

We next consider higher moments for $h_{\ell }(-d)$ for primes $\ell \geqslant 5$ . Theorem 1.1 combined with (1.6) implies that, for any real $k\geqslant 1$ ,

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{k}\ll X^{3/2-3/(2\ell +2)+(k-1)(1/2-1/2\ell )+\unicode[STIX]{x1D700}}+X^{k/2+\unicode[STIX]{x1D700}},\end{eqnarray}$$

where the last term arises from the possible exceptions to (1.6). For purposes of comparison, we rewrite this as

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{k}\ll X^{1+k((\ell -1)/2\ell )-(2\ell -1)/(2\ell (\ell +1))+\unicode[STIX]{x1D700}}+X^{k/2+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

We will improve on this for all real $1<k<(2\ell ^{2}+1)/(\ell +1)$ .

Theorem 1.5. For any prime $\ell \geqslant 5$ , all real $k\geqslant 1$ , and any $\unicode[STIX]{x1D700}>0$ ,

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{k}\ll \left\{\begin{array}{@{}ll@{}}X^{1+k((\ell -2)/(2\ell +2))+\unicode[STIX]{x1D700}}\quad & \text{if }1\leqslant k\leqslant {\displaystyle \frac{\ell ^{2}-1}{2\ell -1}},\\ X^{1+k((\ell -1)/2\ell )-((\ell -1)/2\ell )+\unicode[STIX]{x1D700}}\quad & \text{if }{\displaystyle \frac{\ell ^{2}-1}{2\ell -1}}\leqslant k\leqslant \ell +1,\\ X^{k/2+\unicode[STIX]{x1D700}}\quad & \text{if }k\geqslant \ell +1.\end{array}\right.\end{eqnarray}$$

In particular, we single out the consequence of Theorem 1.5 for the second moment (noting that $k=2$ lies in the first case of the theorem for $\ell \geqslant 5$ ).

Corollary 1.6. For any prime $\ell \geqslant 5$ , for any $\unicode[STIX]{x1D700}>0$ ,

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)^{2}\ll X^{2-3/(\ell +1)+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

This improves on (1.8) in every case. Theorem 1.1 may of course be deduced from the above corollary via the Cauchy–Schwarz inequality. However we have stated and proved Theorem 1.1 separately since it is, in effect, used in the proof of Theorem 1.5.

Our approach is to develop an unconditional upper bound for $h_{\ell }(-d)$ that holds for almost all $d$ , by using the relation between $h_{\ell }(-d)$ and small split primes in $\mathbb{Q}(\sqrt{-d})$ . The original observation of this relation is credited to Soundararajan (and to Michel in a related context) in the work of Helfgott and Venkatesh [HV06] and Ellenberg and Venkatesh [EV07], and has been used in [HV06], for example, to prove a bound for $h_{3}(-d)$ for all $d$ , conditional on the Generalized Riemann Hypothesis. Here we prove an unconditional version, at the cost that it only holds for ‘almost all’ $d$ . To treat higher moments, we combine this with upper bounds for the number of simultaneous representations of integers by certain polynomials; this counting problem is similar to computations performed in [Sou00] and [HB07]. Finally, we remark that the methods of § 6 may also be applied to prove upper bounds for mixed averages of the form

$$\begin{eqnarray}\mathop{\sum }_{0<d<X}h_{\ell }(-d)h_{\ell ^{\prime }}(-d)\end{eqnarray}$$

for distinct odd primes $\ell ,\ell ^{\prime }$ ; we leave the details to the interested reader.

We reiterate that throughout this paper we consider sums over $0<d<X$ to be restricted to square-free integers, and $\ell$ represents an odd prime. We will frequently combine factors of size $X^{\unicode[STIX]{x1D700}}$ for various $\unicode[STIX]{x1D700}$ ; in all cases $\unicode[STIX]{x1D700}$ may be taken to be an arbitrarily small real number, so we re-define it wherever appropriate so that the total factor remains represented by $X^{\unicode[STIX]{x1D700}}$ . We also use the notation $A\ll B$ to indicate that there is a constant $c$ , possibly depending on certain allowable parameters such as $\ell$ or $\unicode[STIX]{x1D700}$ , such that $|A|\leqslant c|B|$ , and similarly for $A\gg B$ .

2 An unconditional pointwise upper bound

Our starting point is the following unconditional pointwise upper bound for $h_{\ell }(-d)$ .

Proposition 2.1. Fix any prime $\ell \geqslant 3$ and real parameters ${\textstyle \frac{1}{4}}X^{1/2\ell }\leqslant Z\leqslant X$ . There exists a small exceptional set $E(Z;X)\subset [X,2X)$ such that for all square-free $d\in [X,2X)\setminus E(Z;X)$ ,

$$\begin{eqnarray}h_{\ell }(-d)\ll X^{\unicode[STIX]{x1D700}}\{d^{1/2}Z^{-1}+d^{1/2}Z^{-2}S_{\ell }(d;Z)\},\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ , where $S_{\ell }(d;Z)$ is the cardinality of the set of pairs of primes $p,p^{\prime }$ satisfying

$$\begin{eqnarray}Z\leqslant p\neq p^{\prime }<2Z\end{eqnarray}$$

for which there exist $u,v\in \mathbb{Z}\setminus \{0\}$ with $(v,pp^{\prime })=1$ such that

$$\begin{eqnarray}4(pp^{\prime })^{\ell }=u^{2}+dv^{2}.\end{eqnarray}$$

Moreover, the exceptional set satisfies

(2.1) $$\begin{eqnarray}\#E(Z;X)\ll X^{\unicode[STIX]{x1D700}^{\prime }}\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}^{\prime }>0$ .

Corollary 2.2. Fix any $\unicode[STIX]{x1D700}^{\prime }>0$ . For all $d\in [X,2X)$ apart from at most $O(X^{\unicode[STIX]{x1D700}^{\prime }})$ exceptions,

$$\begin{eqnarray}h_{\ell }(-d)\ll d^{1/2-1/2\ell +\unicode[STIX]{x1D700}}\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ .

This corollary, which we will prove at the end of § 2, gives a weak form of Soundararajan’s result concerning the bound (1.6).

It is clear from Proposition 2.1 that an understanding of $S_{\ell }(d;Z)$ , both in terms of its average over $d$ and its second moment, will yield corresponding information for $h_{\ell }(-d)$ . Our two main technical results are for the average and second moment of $S_{\ell }(d;Z)$ .

Proposition 2.3. For any prime $\ell \geqslant 3$ and $X^{1/2\ell }\leqslant Z\leqslant X$ ,

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z)\ll X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{\ell +2}X^{-1/2}\}\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ .

Proposition 2.4. For $\ell =3$ and $X^{1/6}\leqslant Z\leqslant X$ ,

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{3}(d;Z)^{2}\ll X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{12}X^{-3/2}\}\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ . For any prime $\ell \geqslant 5$ and $X^{1/2\ell }\leqslant Z\leqslant X$ ,

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z)^{2}\ll X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{2\ell +4}X^{-1}\}\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ .

We include the case $\ell \geqslant 5$ in Proposition 2.4 as it requires little extra effort, but we will not make use of it: while it does result in a nontrivial upper bound for the second moment of $h_{\ell }(-d)$ , a stronger result may be obtained by applying Proposition 2.3 directly.

In the remainder of this section, we prove Proposition 2.1 and its corollary. We prove Propositions 2.3 and 2.4 in §§ 3 and 4, respectively. Finally, in §§ 5 and 6 we record the consequences of these results for averages and moments of $h_{\ell }(-d)$ .

2.1 Proof of Proposition 2.1

Fix a prime $\ell \geqslant 3$ and a square-free integer $X\leqslant d<2X$ . Let $H=\text{Cl}(-d)$ be the class group of $\mathbb{Q}(\sqrt{-d})$ , with class number $h(-d)=\#\text{Cl}(-d)$ . Let $H_{\ell }$ denote the maximal elementary abelian $\ell$ -group in $H$ , with $h_{\ell }(-d)=\#H_{\ell }$ . Since

(2.2) $$\begin{eqnarray}\#H/H_{\ell }=\frac{h(-d)}{h_{\ell }(-d)},\end{eqnarray}$$

in order to show that $h_{\ell }(-d)$ is small it suffices to show that there are many cosets of $H_{\ell }$ in $H$ . Let $\unicode[STIX]{x1D712}_{d}(\cdot )$ denote the quadratic character associated to $\mathbb{Q}(\sqrt{-d})$ . Picking a prime $p\nmid 2d$ such that $\unicode[STIX]{x1D712}_{d}(p)=1$ , it follows that $p$ splits in $\mathbb{Q}(\sqrt{-d})$ as $\mathfrak{p}\mathfrak{p}^{\unicode[STIX]{x1D70E}}$ , say, where $\unicode[STIX]{x1D70E}$ is the nontrivial Galois automorphism of $\mathbb{Q}(\sqrt{-d})$ . Suppose that two distinct primes $p,p^{\prime }$ split in this manner as $\mathfrak{p}\mathfrak{p}^{\unicode[STIX]{x1D70E}}$ and $\mathfrak{p}^{\prime }{\mathfrak{p}^{\prime }}^{\unicode[STIX]{x1D70E}}$ respectively, and suppose that $\mathfrak{p}$ and $\mathfrak{p}^{\prime }$ represent the same class in $H/H_{\ell }$ , so that $\mathfrak{p}H_{\ell }=\mathfrak{p}^{\prime }H_{\ell }$ . It follows that $\mathfrak{p}^{-1}\mathfrak{p}^{\prime }\in H_{\ell }$ , so that $(\mathfrak{p}^{-1}\mathfrak{p}^{\prime })^{\ell }$ is a principal ideal. Thus $(\mathfrak{p}^{\unicode[STIX]{x1D70E}}\mathfrak{p}^{\prime })^{\ell }$ is also a principal ideal, say

(2.3) $$\begin{eqnarray}(\mathfrak{p}^{\unicode[STIX]{x1D70E}}\mathfrak{p}^{\prime })^{\ell }=\biggl(\frac{u+v\sqrt{-d}}{2}\biggr),\end{eqnarray}$$

for some $u,v\in \mathbb{Z}$ . Hence taking norms, it follows that

(2.4) $$\begin{eqnarray}4(pp^{\prime })^{\ell }=u^{2}+dv^{2}.\end{eqnarray}$$

Note that we may require that $\gcd (v,pp^{\prime })=1$ (and in particular that $v\neq 0$ ). For supposing that $p\mid v$ , say, then by (2.4) we see that also $p\mid u$ so that $p\mid ((u+v\sqrt{-d})/2)$ . Hence $\mathfrak{p}\mid ((u+v\sqrt{-d})/2)$ , which by (2.3) implies that $\mathfrak{p}\mid (\mathfrak{p}^{\unicode[STIX]{x1D70E}}\mathfrak{p}^{\prime })^{\ell }$ . Since $p$ is unramified this would then imply that $\mathfrak{p}\mid \mathfrak{p}^{\prime }$ , which contradicts the fact that $p\neq p^{\prime }$ . A similar argument shows that we may require that $u\neq 0$ .

We will show that for all but a small number of ‘exceptional’ $d$ there are many primes $p,p^{\prime }$ that split in this manner, while also showing there can only be few solutions $(u,v)$ to (2.4) with $\gcd (v,pp^{\prime })=1$ and $u,v$ in an appropriate range. This forces there to be many distinct cosets of $H_{\ell }$ in $H$ , and provides an upper bound for $h_{\ell }(-d)$ , as long as $d$ is not exceptional.

We first fix $X\leqslant d<2X$ and count the number of primes $p$ that split appropriately, with

$$\begin{eqnarray}Z\leqslant p<2Z\end{eqnarray}$$

for some parameter $Z$ with ${\textstyle \frac{1}{4}}X^{1/2\ell }\leqslant Z\leqslant X$ (to be chosen precisely in applications). We see that

$$\begin{eqnarray}\#\{Z\leqslant p<2Z:\unicode[STIX]{x1D712}_{d}(p)=1\}=\frac{1}{2}\mathop{\sum }_{Z\leqslant p<2Z}(1+\unicode[STIX]{x1D712}_{d}(p))+O(\unicode[STIX]{x1D714}(d)),\end{eqnarray}$$

where the last term reflects the contribution of the primes that divide $d$ , and contributes no more than $O(\log X)=O(\log Z)$ . We now separate the two terms within the sum over $p$ and apply the prime number theorem, obtaining

$$\begin{eqnarray}\#\{Z\leqslant p<2Z:\unicode[STIX]{x1D712}_{d}(p)=1\}={\textstyle \frac{1}{2}}Z(\log Z)^{-1}+{\textstyle \frac{1}{2}}M(d;Z)+O(Z(\log Z)^{-2}),\end{eqnarray}$$

say, where

$$\begin{eqnarray}M(d;Z)=\mathop{\sum }_{Z\leqslant p<2Z}\unicode[STIX]{x1D712}_{d}(p).\end{eqnarray}$$

Thus the number of split primes in this range is at least of order $Z(\log Z)^{-1}$ , unless we have $|M(d;Z)|\geqslant {\textstyle \frac{1}{4}}Z(\log Z)^{-1}$ ; we will show this exceptional scenario can occur for only a small number of $d$ .

Given a character $\unicode[STIX]{x1D712}$ , set

$$\begin{eqnarray}V(\unicode[STIX]{x1D712})=\biggl(\mathop{\sum }_{Z\leqslant p<2Z}\unicode[STIX]{x1D712}(p)\biggr)^{4\ell }.\end{eqnarray}$$

Upon unfolding the product, we see that this is a character sum of the form

$$\begin{eqnarray}\mathop{\sum }_{Z^{4\ell }\leqslant n<(2Z)^{4\ell }}a_{n}\unicode[STIX]{x1D712}(n)\end{eqnarray}$$

for some coefficients $|a_{n}|\ll d(n)^{4\ell }\ll Z^{\unicode[STIX]{x1D700}}$ . Now we note that with the particular choice $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{d}$ ,

(2.5) $$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}|M(d;Z)|^{8\ell }=\mathop{\sum }_{X\leqslant d<2X}|V(\unicode[STIX]{x1D712}_{d})|^{2}.\end{eqnarray}$$

By positivity, we can enlarge the sum on the right-hand side of (2.5) to include all primitive characters modulo $d$ and apply the large sieve (see, for example, [Dav00, Theorem 4, ch. 27]), to obtain

(2.6) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{X\leqslant d<2X}|M(d;Z)|^{8\ell } & {\leqslant} & \displaystyle \mathop{\sum }_{X\leqslant d<2X}\;\sum ^{\ast }_{\unicode[STIX]{x1D712}\;(\text{mod}\;d)}|V(\unicode[STIX]{x1D712})|^{2}\nonumber\\ \displaystyle & \ll & \displaystyle (X^{2}+Z^{4\ell })\biggl(\mathop{\sum }_{Z^{4\ell }\leqslant n<(2Z)^{4\ell }}|a_{n}|^{2}\biggr)\nonumber\\ \displaystyle & \ll & \displaystyle Z^{4\ell +2\unicode[STIX]{x1D700}}(X^{2}+Z^{4\ell })\ll Z^{8\ell +2\unicode[STIX]{x1D700}},\end{eqnarray}$$

since $X^{1/2\ell }\ll Z$ by assumption. Let $E(Z;X)$ denote the exceptional set,

(2.7) $$\begin{eqnarray}E(Z;X)=\{X\leqslant d<2X:|M(d;Z)|\geqslant {\textstyle \frac{1}{4}}Z(\log Z)^{-1}\}.\end{eqnarray}$$

Then we may conclude from (2.6) that the exceptional set is small:

$$\begin{eqnarray}\#E(Z;X)\ll X^{\unicode[STIX]{x1D700}},\end{eqnarray}$$

for any $\unicode[STIX]{x1D700}>0$ .

We now fix a $d$ with $X\leqslant d<2X$ such that $d\not \in E(X,Z)$ ; the above argument shows that there are at least of order $Z(\log Z)^{-1}$ split primes for this $d$ . In particular, summing over all cosets of $H_{\ell }$ in $H$ shows that, for this $d$ ,

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{C\in H/H_{\ell }}\#\{Z\leqslant p<2Z:\unicode[STIX]{x1D712}_{d}(p)=1,p=\mathfrak{p}\mathfrak{p}^{\unicode[STIX]{x1D70E}},\mathfrak{p}\in C\}\,=\,\#\{Z\leqslant p<2Z:\unicode[STIX]{x1D712}_{d}(p)=1\}\,\gg \,Z(\log Z)^{-1}. & & \displaystyle \nonumber\end{eqnarray}$$

On the other hand, applying the Cauchy–Schwarz inequality to the left-hand side shows that

(2.8) $$\begin{eqnarray}(\#H/H_{\ell })^{1/2}(S_{\ell }^{(1)}(d;Z))^{1/2}\gg Z(\log Z)^{-1},\end{eqnarray}$$

where we define

$$\begin{eqnarray}S_{\ell }^{(1)}(d;Z)=\mathop{\sum }_{C\in H/H_{\ell }}\#\{Z\leqslant p<2Z:\unicode[STIX]{x1D712}_{d}(p)=1,p=\mathfrak{p}\mathfrak{p}^{\unicode[STIX]{x1D70E}},\mathfrak{p}\in C\}^{2}.\end{eqnarray}$$

By the above discussion, we know that

(2.9) $$\begin{eqnarray}S_{\ell }^{(1)}(d;Z)\ll \#\{Z\leqslant p,p^{\prime }<2Z:4(pp^{\prime })^{\ell }=u^{2}+dv^{2}\;\text{for some }u,v\in \mathbb{Z}\},\end{eqnarray}$$

where in the case that $p\neq p^{\prime }$ we may impose the additional conditions that $u,v\neq 0$ and $(v,pp^{\prime })=1$ . Combining (2.8) and (2.2), we may conclude that

$$\begin{eqnarray}h_{\ell }(-d)\ll d^{1/2+\unicode[STIX]{x1D700}}Z^{-2}(\log Z)^{2}S_{\ell }^{(1)}(d;Z),\end{eqnarray}$$

still under the assumption that $d$ is not exceptional. Finally, we write

$$\begin{eqnarray}S_{\ell }^{(1)}(d;Z)=S_{\ell }^{(0)}(d;Z)+S_{\ell }(d;Z),\end{eqnarray}$$

where $S_{\ell }^{(0)}(d;Z)$ is the contribution to the set (2.9) from pairs $p=p^{\prime }$ and $S_{\ell }(d;Z)$ is the contribution from pairs $p\neq p^{\prime }$ . Trivially, $S_{\ell }^{(0)}(d;Z)\ll Z$ , and we see that Proposition 2.1 holds.

To deduce the corollary we take $Z={\textstyle \frac{1}{4}}X^{1/2\ell }$ , and note that any pairs of primes $p,p^{\prime }$ counted by $S_{\ell }(d;Z)$ would satisfy

$$\begin{eqnarray}X\leqslant d\leqslant u^{2}+dv^{2}=4(pp^{\prime })^{\ell }\leqslant 4(4Z^{2})^{\ell }=4^{1-\ell }X<X.\end{eqnarray}$$

Thus $S_{\ell }(d;Z)$ must vanish, so that $h_{\ell }(-d)\ll X^{\unicode[STIX]{x1D700}}d^{1/2}Z^{-1}\ll d^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}$ unless $d$ lies in $E(Z;X)$ . The result then follows.

3 Proof of Proposition 2.3

Define the parameters

(3.1) $$\begin{eqnarray}W=Z^{2},\quad U=2^{\ell +1}Z^{\ell },\quad V=2^{\ell +1}Z^{\ell }X^{-1/2}.\end{eqnarray}$$

Note that $V\geqslant 2$ as long as

$$\begin{eqnarray}Z\geqslant X^{1/2\ell },\end{eqnarray}$$

which we henceforward assume. Note also that up to a constant factor (accounting for changing signs of $u,v$ ), we may express $S_{\ell }(d;Z)$ as the quantity

$$\begin{eqnarray}\#\{Z\leqslant p\neq p^{\prime }<2Z:4(pp^{\prime })^{\ell }=u^{2}+dv^{2}\;\text{for some }u,v\geqslant 1\text{ with }(v,pp^{\prime })=1\}.\end{eqnarray}$$

Furthermore, for any $X\leqslant d<2X$ , any triple $w=pp^{\prime }$ , $u,v$ considered in the set above certainly satisfies $W\leqslant w<4W$ , $1\leqslant u\leqslant U$ , $1\leqslant v\leqslant V$ .

We wish to bound $S_{\ell }(d;Z)$ on average over $d$ ; for this we note that

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ X\leqslant d<2X \\ d\not \in E(Z;X)}}S_{\ell }(d;Z) & \ll & \displaystyle \#\{\!W\leqslant w<4W,1\leqslant u\leqslant U,1\leqslant v\leqslant V:\gcd (v,w)=1,\nonumber\\ \displaystyle & & \displaystyle v^{2}\mid (4w^{\ell }-u^{2}),(4w^{\ell }-u^{2})/v^{2}\in [X,2X)\!\}.\nonumber\end{eqnarray}$$

It is convenient to work with dyadic ranges; thus for any parameter $1\leqslant V_{0}\leqslant V/2$ , define

$$\begin{eqnarray}\displaystyle N(Z,X;V_{0}) & = & \displaystyle \#\{\!W\leqslant w<4W,1\leqslant u\leqslant U,V_{0}\leqslant v<2V_{0}:\gcd (v,w)=1,\nonumber\\ \displaystyle & & \displaystyle v^{2}\mid (4w^{\ell }-u^{2}),(4w^{\ell }-u^{2})/v^{2}\in [X,2X)\!\}.\nonumber\end{eqnarray}$$

Then certainly

$$\begin{eqnarray}\mathop{\sum }_{\substack{ X\leqslant d<2X \\ d\not \in E(Z;X)}}S_{\ell }(d;Z)\ll \mathop{\sum }_{0\leqslant j\leqslant \log _{2}(V)-1}N(Z,X;2^{j})=\mathop{\sum }_{\substack{ V_{0}\leqslant V/2 \\ \text{dyadic}}}N(Z,X;V_{0}).\end{eqnarray}$$

We turn to bounding an individual term $N(Z,X;V_{0})$ . We first fix $w$ and $v$ and let

$$\begin{eqnarray}M(w;v)=\#\{u\;(\text{mod}\;v^{2}):u^{2}\equiv 4w^{\ell }\;(\text{mod}\;v^{2})\}.\end{eqnarray}$$

Lemma 3.1. For any coprime $w$ and $v$ ,

(3.2) $$\begin{eqnarray}M(w;v)\leqslant 2^{\unicode[STIX]{x1D714}(v)+1}\ll v^{\unicode[STIX]{x1D700}},\end{eqnarray}$$

where $\unicode[STIX]{x1D714}(v)$ denotes the number of distinct prime divisors of $v$ .

Proof. This is proved in a standard fashion. Writing $v=q_{1}^{r_{1}}\cdots q_{s}^{r_{s}}$ in its prime decomposition, it suffices by the Chinese Remainder Theorem to count $M(w;q_{i}^{r_{i}})$ for each $q_{i}$ . Since $(w,v)=1$ we may assume that $(w,q_{i})=1$ ; we also assume for the moment that $q_{i}$ is odd. Then $M(w;q_{i}^{r_{i}})$ will be nonzero only if $w$ is a quadratic residue modulo $q_{i}$ , in which case $u$ can lie in at most two residue classes modulo $q_{i}$ ; since $q_{i}$ is odd, each solution modulo $q_{i}$ lifts uniquely to a solution modulo $q_{i}^{2r_{i}}$ . Thus we see that in this case

$$\begin{eqnarray}M(w;q_{i}^{r_{i}})\leqslant 2.\end{eqnarray}$$

If $q_{i}=2$ then the relevant congruence has solutions only if $2\mid u$ , in which case we may equivalently count solutions to $(u/2)^{2}\equiv w^{\ell }\;(\text{mod}\;q_{i}^{2r_{i}-2})$ . However if $n$ is odd, a congruence $x^{2}\equiv n\;(\text{mod}\;2^{r})$ has at most four solutions. We may therefore conclude that $M(w;q_{i}^{r_{i}})\leqslant 4$ , thus proving (3.2).◻

Applying Lemma 3.1 directly to count solutions $u\leqslant U$ to $u^{2}\equiv 4w^{\ell }\;(\text{mod}\;v^{2})$ would lead to the upper bound

(3.3) $$\begin{eqnarray}N(Z,X;V_{0})\ll WV_{0}^{1+\unicode[STIX]{x1D700}}(UV_{0}^{-2}+1).\end{eqnarray}$$

But then summing over all dyadic ranges with $1\leqslant V_{0}\leqslant V/2$ would not allow us to take advantage of the decay with respect to $V_{0}$ in (3.3). Thus we return to the definition of $N(Z,X;V_{0})$ and utilize the additional piece of information that

$$\begin{eqnarray}X\leqslant \frac{4w^{\ell }-u^{2}}{v^{2}}<2X,\end{eqnarray}$$

which we rewrite as

(3.4) $$\begin{eqnarray}v^{2}X\leqslant 4w^{\ell }-u^{2}<2v^{2}X.\end{eqnarray}$$

We will conclude from this that $u$ must lie within a short interval around $2w^{\ell /2}$ ; precisely, we write

$$\begin{eqnarray}\biggl(\frac{u}{2w^{\ell /2}}\biggr)^{2}=1+E,\end{eqnarray}$$

in which (3.4) shows that

$$\begin{eqnarray}|E|\leqslant \frac{2Xv^{2}}{4w^{\ell }}\leqslant \frac{8XV_{0}^{2}}{4W^{\ell }}=\frac{2XV_{0}^{2}}{Z^{2\ell }}=2^{2\ell +3}\frac{V_{0}^{2}}{V^{2}}.\end{eqnarray}$$

Thus $E\ll 1$ whence $\sqrt{1+E}=1+O(E)$ . It follows that

$$\begin{eqnarray}u=2w^{\ell /2}+O(w^{\ell /2}E)=2w^{\ell /2}+O(W^{\ell /2}V_{0}^{2}V^{-2}).\end{eqnarray}$$

Thus for each fixed $w,v$ , in order to be counted by $N(Z,X;V_{0})$ , $u$ must lie in an interval $I_{w}$ around $2w^{\ell /2}$ of length $O(W^{\ell /2}V_{0}^{2}V^{-2})$ . We apply this information along with the bound (3.2) to conclude that for each fixed $w,v$ considered in $N(Z,X;V_{0})$ ,

$$\begin{eqnarray}\#\{u\in I_{w}:u^{2}\equiv 4w^{\ell }\;(\text{mod}\;v^{2})\}\ll V_{0}^{\unicode[STIX]{x1D700}}\biggl(\frac{W^{\ell /2}V_{0}^{2}V^{-2}}{V_{0}^{2}}+1\biggr)=V_{0}^{\unicode[STIX]{x1D700}}(W^{\ell /2}V^{-2}+1).\end{eqnarray}$$

As a consequence,

$$\begin{eqnarray}\displaystyle N(Z,X;V_{0}) & \ll & \displaystyle \mathop{\sum }_{\substack{ W\leqslant w<4W,V_{0}\leqslant v<2V_{0} \\ (v,w)=1}}\#\{u\in I_{w}:u^{2}\equiv 4w^{\ell }\;(\text{mod}\;v^{2})\}\nonumber\\ \displaystyle & \ll & \displaystyle WV_{0}^{1+\unicode[STIX]{x1D700}}(W^{\ell /2}V^{-2}+1).\nonumber\end{eqnarray}$$

(This improves upon (3.3) by effectively replacing $V_{0}^{-2}$ by $V^{-2}$ ; observe that up to constant factors, $U$ is the same size as $W^{\ell /2}$ .) Summing over dyadic regions then shows

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ V_{0}\leqslant V/2 \\ \text{dyadic}}}N(Z,X;V_{0}) & \ll & \displaystyle W^{1+\ell /2}V^{-1+\unicode[STIX]{x1D700}}+WV^{1+\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{\ell +2}X^{-1/2}\},\nonumber\end{eqnarray}$$

which proves Proposition 2.3.

4 Proof of Proposition 2.4

We define a quantity $R_{\ell }(d;Z)$ according to the parameters $U,V,W$ given in (3.1) as follows: set $R_{\ell }(d;Z)=0$ if $d$ is not square-free, and for $d$ square-free let $R_{\ell }(d;Z)$ be the number of triples $(w,u,v)\in \mathbb{N}^{3}$ satisfying

$$\begin{eqnarray}\displaystyle & W\leqslant w<4W,\quad u\leqslant U,\quad v\leqslant V,\quad \gcd (w,v)=1, & \displaystyle \nonumber\\ \displaystyle & w=p_{1}p_{2}\quad \text{with }p_{1}\not =p_{2}\in [Z,2Z), & \displaystyle \nonumber\end{eqnarray}$$

and

$$\begin{eqnarray}4w^{\ell }=u^{2}+dv^{2}.\end{eqnarray}$$

Recall also the quantity $S_{\ell }(d;Z)$ defined in Proposition 2.1. Upon letting $w=p_{1}p_{2}$ , we observe that (up to signs) any tuple $p_{1},p_{2},u,v$ contributing to $S_{\ell }(d;Z)$ must have $W\leqslant w<4W$ , $1\leqslant u\leqslant U$ , $1\leqslant v\leqslant V$ , so that $S_{\ell }(d;Z)\ll R_{\ell }(d;Z)$ . Thus we may write

(4.1) $$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z)^{2}\ll \mathop{\sum }_{X\leqslant d<2X}R_{\ell }(d;Z)+\mathop{\sum }_{X\leqslant d<2X}R_{\ell }(d;Z)(R_{\ell }(d;Z)-1).\end{eqnarray}$$

The advantage of separating the terms in this fashion is that in the second term on the right-hand side we may now count only distinct tuples $(u,v,w)\neq (u^{\prime },v^{\prime },w^{\prime })$ in $R_{\ell }(d;Z)$ .

We note that for $X^{1/2\ell }\leqslant Z\leqslant X$ the first term on the right-hand side of (4.1) satisfies

(4.2) $$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}R_{\ell }(d;Z)\ll \mathop{\sum }_{\substack{ V_{0}\leqslant V/2 \\ \text{dyadic}}}N(Z,X;V_{0})\ll X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{\ell +2}X^{-1/2}\},\end{eqnarray}$$

by Proposition 2.3. The main remaining task is to treat

$$\begin{eqnarray}T_{\ell }=T_{\ell }(Z;X):=\mathop{\sum }_{X\leqslant d<2X}R_{\ell }(d;Z)(R_{\ell }(d;Z)-1).\end{eqnarray}$$

We will prove the following proposition.

Proposition 4.1. For $X^{1/2\ell }\leqslant Z\leqslant X$ ,

(4.3) $$\begin{eqnarray}T_{\ell }\ll Z^{2\ell +4}X^{\unicode[STIX]{x1D700}-1}.\end{eqnarray}$$

Moreover when $\ell =3$ and $X^{1/6}\leqslant Z\leqslant X$ we have

(4.4) $$\begin{eqnarray}T_{3}\ll X^{\unicode[STIX]{x1D700}}(Z^{7}X^{-1/2}+Z^{12}X^{-3/2}).\end{eqnarray}$$

Combining (4.2) and (4.3), we see that

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z)^{2}\ll X^{\unicode[STIX]{x1D700}}(Z^{2}X^{1/2}+Z^{\ell +2}X^{-1/2}+Z^{2\ell +4}X^{-1}).\end{eqnarray}$$

Note that

$$\begin{eqnarray}Z^{\ell +2}X^{-1/2}\leqslant Z^{2\ell +4}X^{-1}\end{eqnarray}$$

for $Z\geqslant X^{1/(2\ell )}$ , so that under this assumption

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z)^{2}\ll X^{\unicode[STIX]{x1D700}}(Z^{2}X^{1/2}+Z^{2\ell +4}X^{-1}).\end{eqnarray}$$

This suffices for Proposition 2.4 for $\ell \geqslant 5$ . For $\ell =3$ we improve on this; from (4.2) and (4.4) we obtain

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}S_{3}(d;Z)^{2}\ll X^{\unicode[STIX]{x1D700}}(Z^{2}X^{1/2}+Z^{5}X^{-1/2}+Z^{7}X^{-1/2}+Z^{12}X^{-3/2}).\end{eqnarray}$$

However

$$\begin{eqnarray}Z^{5}X^{-1/2}\leqslant Z^{7}X^{-1/2}=\{Z^{2}X^{1/2}\}^{1/2}\{Z^{12}X^{-3/2}\}^{1/2}\leqslant Z^{2}X^{1/2}+Z^{12}X^{-3/2},\end{eqnarray}$$

whence the case $\ell =3$ of Proposition 2.4 also follows.

4.1 Proof of Proposition 4.1: a first bound for $T_{\ell }$

We now prove (4.3). We recall the parameters $U,V,W$ of (3.1) and note that $T_{\ell }$ is at most the number of 6-tuples $(w_{1},w_{2},u_{1},u_{2},v_{1},v_{2})$ in the ranges

$$\begin{eqnarray}W\leqslant w_{1},w_{2}<4W,\quad 1\leqslant u_{1},u_{2}\leqslant U,\quad 1\leqslant v_{1},v_{2}\leqslant V\end{eqnarray}$$

that satisfy the conditions

(4.5) $$\begin{eqnarray}\displaystyle & (u_{1},v_{1},w_{1})\neq (u_{2},v_{2},w_{2}), & \displaystyle\end{eqnarray}$$

(4.6) $$\begin{eqnarray}\displaystyle & \gcd (w_{1},v_{1})=\gcd (w_{2},v_{2})=1, & \displaystyle\end{eqnarray}$$

(4.7) $$\begin{eqnarray}\displaystyle & v_{1}^{2}\mid (4w_{1}^{\ell }-u_{1}^{2})\quad \text{and}\quad v_{2}^{2}\mid (4w_{2}^{\ell }-u_{2}^{2}), & \displaystyle\end{eqnarray}$$

(4.8) $$\begin{eqnarray}\displaystyle & v_{1}^{2}(4w_{2}^{\ell }-u_{2}^{2})=v_{2}^{2}(4w_{1}^{\ell }-u_{1}^{2})\neq 0. & \displaystyle\end{eqnarray}$$

We will obtain a first upper bound for $T_{\ell }$ by following the approach of [Sou00], ignoring the divisibility conditions (4.7); note that we are also now ignoring the fact that each of $w_{1},w_{2}$ is a product of two distinct primes. We claim that for tuples satisfying the above conditions,

(4.9) $$\begin{eqnarray}v_{1}^{2}w_{2}^{\ell }-v_{2}^{2}w_{1}^{\ell }\neq 0.\end{eqnarray}$$

To prove this we recall that $\gcd (w_{i},v_{i})=1$ for $i=1,2$ , whence $v_{1}^{2}w_{2}^{\ell }=v_{2}^{2}w_{1}^{\ell }$ would imply that $v_{1}=v_{2}$ and $w_{1}=w_{2}$ , and hence $u_{1}=u_{2}$ . This would then contradict (4.5).

We now observe that once $v_{1},v_{2},w_{1},w_{2}$ are fixed then $u_{1},u_{2}$ are fixed up to $X^{\unicode[STIX]{x1D700}}$ choices. For indeed, fixing $v_{1},v_{2},w_{1},w_{2}$ in (4.8) gives

(4.10) $$\begin{eqnarray}4(v_{2}^{2}w_{1}^{\ell }-v_{1}^{2}w_{2}^{\ell })=(v_{2}u_{1}-v_{1}u_{2})(v_{2}u_{1}+v_{1}u_{2}).\end{eqnarray}$$

The left-hand side is a nonzero integer by (4.9), so that $u_{1},u_{2}$ are fixed up to $X^{\unicode[STIX]{x1D700}}$ choices. Thus we obtain

$$\begin{eqnarray}T_{\ell }\ll W^{2}V^{2}X^{\unicode[STIX]{x1D700}}\ll Z^{2\ell +4}X^{-1+\unicode[STIX]{x1D700}},\end{eqnarray}$$

which is the bound given in (4.3).

4.2 Proof of Proposition 4.1: a second bound for $T_{\ell }$

We may obtain the alternative upper bound (4.4) for $T_{\ell }$ by following the method of [HB07], but with the addition of certain technical considerations because in the present case the variables $v_{i}$ are not restricted to be primes. Although it is easy enough to do this for general odd primes $\ell$ we shall confine our attention to $\ell =3$ , since this is the only case we shall use.

First we consider the contribution to $T_{3}$ arising from the case in which $\gcd (w_{1},w_{2})\not =1$ . We write $T_{3}^{0}$ for the number of 6-tuples of this type. Since each of $w_{1}$ and $w_{2}$ is a product of two primes in the interval $[Z,2Z)$ this can happen only when there is at least one prime $p\in [Z,2Z)$ dividing both of $w_{1}$ and $w_{2}$ . The number of possible pairs $w_{1},w_{2}$ is thus $O(Z^{3})$ . We now follow the argument of § 4.1. There are $O(V^{2})$ pairs $v_{1},v_{2}$ , and the factorization (4.10) shows that there are $O(X^{\unicode[STIX]{x1D700}})$ possibilities for $u_{1},u_{2}$ once $w_{1},w_{2},v_{1},v_{2}$ are fixed. It follows that

$$\begin{eqnarray}T_{3}^{0}\ll Z^{3}V^{2}X^{\unicode[STIX]{x1D700}}.\end{eqnarray}$$

From now on we assume that $\gcd (w_{1},w_{2})=1$ . For each integer $1\leqslant \unicode[STIX]{x1D6FF}\leqslant V$ , we will let $T_{3}(\unicode[STIX]{x1D6FF})$ denote the contribution to $T_{3}$ from triples $(u_{1},v_{1},w_{1})$ and $(u_{2},v_{2},w_{2})$ with $w_{1},w_{2}$ coprime, such that $\gcd (v_{1},v_{2})=\unicode[STIX]{x1D6FF}$ . We will prove the following proposition.

Proposition 4.2. For each integer $1\leqslant \unicode[STIX]{x1D6FF}\leqslant V$ ,

$$\begin{eqnarray}T_{3}(\unicode[STIX]{x1D6FF})\ll X^{\unicode[STIX]{x1D700}}(W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}+V^{3}U\unicode[STIX]{x1D6FF}^{-3}+WV\unicode[STIX]{x1D6FF}^{-1}).\end{eqnarray}$$

From this we conclude that

$$\begin{eqnarray}\displaystyle T_{3} & \ll & \displaystyle T_{3}^{0}+\mathop{\sum }_{\unicode[STIX]{x1D6FF}=1}^{V}T_{3}(\unicode[STIX]{x1D6FF})\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}\biggl\{Z^{3}V^{2}+\mathop{\sum }_{\unicode[STIX]{x1D6FF}=1}^{V}(W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}+V^{3}U\unicode[STIX]{x1D6FF}^{-3}+WV\unicode[STIX]{x1D6FF}^{-1})\biggr\}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}(Z^{3}V^{2}+VW^{2}+V^{3}U+WV)\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}(Z^{3}V^{2}+VW^{2}+V^{3}U),\nonumber\end{eqnarray}$$

since clearly $WV\ll VW^{2}$ . Upon recalling the parameter definitions (3.1) this shows that

$$\begin{eqnarray}T_{3}\ll X^{\unicode[STIX]{x1D700}}\{Z^{9}X^{-1}+Z^{7}X^{-1/2}+Z^{12}X^{-3/2}\}.\end{eqnarray}$$

This provides the second bound for $T_{3}$ given in Proposition 4.1, since $Z\geqslant X^{1/6}$ .

Proof of Proposition 4.2 . To prove Proposition 4.2, we fix $\unicode[STIX]{x1D6FF}$ and write $v_{i}=\unicode[STIX]{x1D6FF}y_{i}$ for $i=1,2$ so that $\gcd (y_{1},y_{2})=1$ . We first isolate solutions $(u_{1},v_{1},w_{1})$ and $(u_{2},v_{2},w_{2})$ that contribute to $T_{3}(\unicode[STIX]{x1D6FF})$ such that $y_{1},y_{2}$ satisfy a relation

(4.11) $$\begin{eqnarray}y_{1}^{2}\unicode[STIX]{x1D707}_{2}^{3}=y_{2}^{2}\unicode[STIX]{x1D707}_{1}^{3}\end{eqnarray}$$

for some integers $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$ . Given a relation of the form (4.11), we may divide both sides by $\gcd (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})^{3}$ to obtain an equivalent relation

$$\begin{eqnarray}y_{1}^{2}\unicode[STIX]{x1D706}_{2}^{3}=y_{2}^{2}\unicode[STIX]{x1D706}_{1}^{3}\end{eqnarray}$$

in which $(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})=1$ and $(y_{1},y_{2})=1$ . This implies that for each $i=1,2$ ,

(4.12) $$\begin{eqnarray}y_{i}^{2}=\unicode[STIX]{x1D706}_{i}^{3}.\end{eqnarray}$$

This implies that $y_{i}$ is itself a perfect cube, say $y_{i}=s_{i}^{3}$ . We recall from (4.10) that once $v_{1},v_{2},w_{1},w_{2}$ are fixed, $u_{1},u_{2}$ are fixed up to $X^{\unicode[STIX]{x1D700}}$ choices. Thus we count how many $v_{1},v_{2}\leqslant V$ with $\gcd (v_{1},v_{2})=\unicode[STIX]{x1D6FF}$ are of the type (4.12) by noting that there are at most $O((V\unicode[STIX]{x1D6FF}^{-1})^{1/3})$ choices for each $s_{i}$ . We bound the number of choices for $w_{1},w_{2}$ trivially by $O(W^{2})$ , and conclude that the contribution to $T_{3}(\unicode[STIX]{x1D6FF})$ of solutions for which a relation of the form (4.11) holds is at most

(4.13) $$\begin{eqnarray}\ll W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}X^{\unicode[STIX]{x1D700}}.\end{eqnarray}$$

We now proceed to count the remaining contribution to $T_{3}(\unicode[STIX]{x1D6FF})$ ; we may assume from now on that no relation of the form (4.11) holds for $y_{1}$ and $y_{2}$ . Define

(4.14) $$\begin{eqnarray}k=y_{2}u_{1}+y_{1}u_{2}.\end{eqnarray}$$

Note that if $\unicode[STIX]{x1D6FF},w_{1},w_{2},y_{1},y_{2}$ and $k$ are fixed, then $u_{1},u_{2}$ are fixed uniquely by (4.10). Thus we will count the number of solutions $w_{1},w_{2}$ contributing to $T_{3}(\unicode[STIX]{x1D6FF})$ for each fixed $y_{1},y_{2},k$ .

Recalling the definition of $y_{1},y_{2}$ we see that the condition (4.8) now becomes

$$\begin{eqnarray}y_{1}^{2}(4w_{2}^{\ell }-u_{2}^{2})=y_{2}^{2}(4w_{1}^{\ell }-u_{1}^{2})\neq 0,\end{eqnarray}$$

and since $\gcd (y_{1},y_{2})=1$ , this implies a system of congruences

(4.15) $$\begin{eqnarray}\displaystyle 4y_{2}^{2}w_{1}^{3} & \equiv & \displaystyle k^{2}\;(\text{mod}\;y_{1}),\end{eqnarray}$$

(4.16) $$\begin{eqnarray}\displaystyle 4y_{1}^{2}w_{2}^{3} & \equiv & \displaystyle k^{2}\;(\text{mod}\;y_{2}),\end{eqnarray}$$

(4.17) $$\begin{eqnarray}\displaystyle 4y_{2}^{2}w_{1}^{3} & \equiv & \displaystyle 4y_{1}^{2}w_{2}^{3}\;(\text{mod}\;k).\end{eqnarray}$$

We first reduce this to a similar system of congruences with square-free moduli. For $i=1,2$ let $q_{i}$ denote the odd square-free kernel of $y_{i}$ , that is

$$\begin{eqnarray}q_{i}=\mathop{\prod }_{\substack{ p\mid y_{i} \\ p>2}}p.\end{eqnarray}$$

The congruence (4.15) implies that $4y_{2}^{2}w_{1}^{3}\equiv k^{2}\;(\text{mod}\;q_{1})$ . Since $(4y_{2},q_{1})=1$ this congruence may be re-written as $w_{1}^{3}\equiv a_{1}\;(\text{mod}\;q_{1})$ for some constant $a_{1}$ determined by $y_{2}$ and $k$ . A similar observation applies to (4.16). Next, we define

$$\begin{eqnarray}r=\mathop{\prod }_{\substack{ p\mid k \\ p>2}}p\end{eqnarray}$$

to be the odd square-free kernel of $k$ , and deduce from (4.17) an analogous congruence modulo $r$ . It follows that any solutions $w_{1},w_{2}$ of the system (4.15)–(4.17) must satisfy the congruences

(4.18) $$\begin{eqnarray}\displaystyle w_{1}^{3} & \equiv & \displaystyle a_{1}\;(\text{mod}\;q_{1}),\end{eqnarray}$$

(4.19) $$\begin{eqnarray}\displaystyle w_{2}^{3} & \equiv & \displaystyle a_{2}\;(\text{mod}\;q_{2}),\end{eqnarray}$$

(4.20) $$\begin{eqnarray}\displaystyle y_{2}^{2}w_{1}^{3} & \equiv & \displaystyle y_{1}^{2}w_{2}^{3}\;(\text{mod}\;r)\end{eqnarray}$$

for some constant $a_{1}$ determined by $y_{2},k\;(\text{mod}\;q_{1})$ and some constant $a_{2}$ determined by $y_{1},k\;(\text{mod}\;q_{2})$ .

Certainly $(q_{1},q_{2})=1$ . In addition, we note that $(y_{1},r)=1$ and $(y_{2},r)=1$ . For indeed, if some odd prime $p$ satisfies $p\mid k$ and $p\mid y_{1}$ , then by (4.14) it follows that $p\mid u_{1}$ , since by construction $(y_{1},y_{2})=1$ . However, by the condition $v_{1}^{2}\mid (4w_{1}^{3}-u_{1}^{2})$ , this would imply that $p\mid w_{1}$ , which contradicts the fact that $(v_{1},w_{1})=1$ . The fact that $(y_{2},r)=1$ may be shown similarly. As a consequence of these observations,

(4.21) $$\begin{eqnarray}(q_{1},q_{2})=1,\quad (q_{1},r)=1,\quad (q_{2},r)=1.\end{eqnarray}$$

The next step is to note that the conditions (4.18)–(4.20) may be interpreted as lattice conditions.

Lemma 4.3. The congruence (4.18) requires that $w_{1}$ lies in one of at most $3^{\unicode[STIX]{x1D714}(q_{1})}$ residue classes modulo $q_{1}$ , and similarly (4.19) requires that $w_{2}$ lies in one of at most $3^{\unicode[STIX]{x1D714}(q_{2})}$ residue classes modulo $q_{2}$ .

Furthermore, there exists a collection of at most $3^{\unicode[STIX]{x1D714}(r)}$ lattices $\unicode[STIX]{x1D6EC}_{i}\subset \mathbb{Z}^{2}$ of determinant $r$ , such that any coprime pair $(w_{1},w_{2})$ satisfying (4.20) must lie in $\unicode[STIX]{x1D6EC}_{i}$ for some $i$ . Conversely any pair $(w_{1},w_{2})$ in any of the lattices $\unicode[STIX]{x1D6EC}_{i}$ will satisfy (4.20).

Proof. To prove this, we first consider the congruence (4.18). Fix a prime divisor $p\mid q_{1}$ ; then $w_{1}$ can only be a solution to (4.18) if

(4.22) $$\begin{eqnarray}w_{1}^{3}\equiv a_{1}\;(\text{mod}\;p).\end{eqnarray}$$

There are at most three residue classes modulo $p$ in which a solution $w_{1}$ to (4.22) may lie. We may conclude that $w_{1}$ lies in one of at most $3^{\unicode[STIX]{x1D714}(q_{1})}$ residue classes modulo $q_{1}$ . A similar argument applies to (4.19), establishing that $w_{2}$ may lie in at most $3^{\unicode[STIX]{x1D714}(q_{2})}$ residue classes modulo $q_{2}$ .

We now turn to (4.20). Since $(y_{1},r)=1$ and $(w_{1},w_{2})=1$ we must have $(w_{1},r)=1$ . (Indeed, otherwise, if we suppose $p$ is a prime factor of both $w_{1}$ and $r$ , we would see in (4.20) that $p\mid y_{1}^{2}w_{2}^{3}$ , but since $(w_{1},w_{2})=1$ we cannot have $p\mid w_{2}$ , so we would conclude $p\mid y_{1}$ . This would in turn contradict that fact we previously proved that $(y_{1},r)=1$ .) Using the fact that $(w_{1},r)=1$ we see that (4.20) implies

(4.23) $$\begin{eqnarray}w^{3}\equiv a\;(\text{mod}\;r),\end{eqnarray}$$

where $w\equiv w_{2}w_{1}^{-1}\;(\text{mod}\;r)$ and $a\equiv (y_{2}y_{1}^{-1})^{2}\;(\text{mod}\;r)$ is coprime to $r$ . Now, just as with our analysis of (4.18), we see that there is a collection of at most $3^{\unicode[STIX]{x1D714}(r)}$ residue classes $w\equiv b_{i}\;(\text{mod}\;r)$ in which $w$ must lie. This leads to a corresponding collection of lattice conditions $w_{2}\equiv b_{i}w_{1}\;(\text{mod}\;r)$ which, taken together, are equivalent to (4.23). Finally we note that the resulting lattice of pairs $(w_{1},w_{2})$ has a basis $\{(1,b_{i}),(0,r)\}$ , so that its determinant is just $r$ . This completes the proof of the lemma.◻

4.3 Counting lattice points

Since $q_{1},q_{2},r$ are coprime in pairs, we may conclude from Lemma 4.3 that $(w_{1},w_{2})$ must lie in one of at most $3^{\unicode[STIX]{x1D714}(q_{1})+\unicode[STIX]{x1D714}(q_{2})+\unicode[STIX]{x1D714}(r)}$ lattice cosets of the form $(c_{1},c_{2})+\unicode[STIX]{x1D6EC}$ , where $\unicode[STIX]{x1D6EC}$ is a lattice with $\det (\unicode[STIX]{x1D6EC})=q_{1}q_{2}r$ . We note that the total number of lattices is $\ll X^{\unicode[STIX]{x1D700}}$ , since under the assumption $Z\leqslant X$ , we have $v_{i}\leqslant V\ll X^{5/2}$ and $k\leqslant 2UV\ll X^{11/2}$ . We now fix one of these lattices, which we will denote by $\unicode[STIX]{x1D6EC}$ , and its corresponding shift $(c_{1},c_{2})$ . Note that we may choose $(c_{1},c_{2})$ such that $W\leqslant c_{i}<4W$ for $i=1,2$ , since otherwise $w_{1},w_{2}$ would lie outside the desired range $W\leqslant w_{1},w_{2}<4W$ . We now write $(z_{1},z_{2})=(w_{1},w_{2})-(c_{1},c_{2})$ , and proceed to count the number of

$$\begin{eqnarray}(z_{1},z_{2})\in \unicode[STIX]{x1D6EC},\quad |z_{i}|<3W.\end{eqnarray}$$

Let $\unicode[STIX]{x1D706}_{1}\leqslant \unicode[STIX]{x1D706}_{2}$ be the successive minima of $\unicode[STIX]{x1D6EC}$ , so that the standard Minkowski inequalities show that $\det (\unicode[STIX]{x1D6EC})\ll \unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}\ll \det (\unicode[STIX]{x1D6EC})$ (see, for example, Davenport [Dav58, Eqn (5)]). We note that in our particular case,

(4.24) $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}\ll \sqrt{\det (\unicode[STIX]{x1D6EC})}\ll \sqrt{q_{1}q_{2}r}\ll V^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}.\end{eqnarray}$$

Here we have used the fact that $q_{i}\leqslant y_{i}\leqslant V\unicode[STIX]{x1D6FF}^{-1}$ for $i=1,2$ and hence $r\leqslant k\ll UV\unicode[STIX]{x1D6FF}^{-1}$ . Moreover, by Lemma 1 of Davenport [Dav58], the number of lattice points in $\unicode[STIX]{x1D6EC}$ with $|(z_{1},z_{2})|\leqslant x$ is (up to a constant) at most $(1+x/\unicode[STIX]{x1D706}_{1})(1+x/\unicode[STIX]{x1D706}_{2}).$ Thus the number of allowable $z_{1},z_{2}$ in our case is

$$\begin{eqnarray}\displaystyle & & \displaystyle \ll (1+W/\unicode[STIX]{x1D706}_{1})(1+W/\unicode[STIX]{x1D706}_{2})\nonumber\\ \displaystyle & & \displaystyle \ll 1+W^{2}/\det (\unicode[STIX]{x1D6EC})+W/\unicode[STIX]{x1D706}_{1}\nonumber\\ \displaystyle & & \displaystyle \ll 1+W^{2}/(q_{1}q_{2}r)+W/\unicode[STIX]{x1D706}_{1}.\nonumber\end{eqnarray}$$

Thus we have

(4.25) $$\begin{eqnarray}T_{3}(\unicode[STIX]{x1D6FF})\ll X^{\unicode[STIX]{x1D700}}\mathop{\sum }_{y_{1},y_{2},k}\biggl(1+\frac{W^{2}}{q_{1}q_{2}r}+\frac{W}{\unicode[STIX]{x1D706}_{1}}\biggr),\end{eqnarray}$$

where we recall that $q_{i}$ is the odd square-free kernel of $y_{i}$ and for each triple $y_{1},y_{2},k$ we take $\unicode[STIX]{x1D706}_{1}$ to be the smallest value from all the corresponding lattices $\unicode[STIX]{x1D6EC}$ . Recall that $y_{1},y_{2}\leqslant V\unicode[STIX]{x1D6FF}^{-1}$ and $k\leqslant 2UV\unicode[STIX]{x1D6FF}^{-1}$ . Then we see that the contribution of the first term in (4.25) to $T_{3}(\unicode[STIX]{x1D6FF})$ is at most

(4.26) $$\begin{eqnarray}\ll X^{\unicode[STIX]{x1D700}}V^{3}U\unicode[STIX]{x1D6FF}^{-3}.\end{eqnarray}$$

The contribution to $T_{3}(\unicode[STIX]{x1D6FF})$ from the second term in (4.25) is

(4.27) $$\begin{eqnarray}\ll X^{\unicode[STIX]{x1D700}}W^{2}\biggl(\mathop{\sum }_{y_{1}\leqslant V\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{q_{1}}\biggr)\biggl(\mathop{\sum }_{y_{2}\leqslant V\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{q_{2}}\biggr)\biggl(\mathop{\sum }_{k\leqslant 2UV\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{r}\biggr).\end{eqnarray}$$

To bound each internal sum we apply the following minor variant of [HB07, Lemma 1].

Lemma 4.4. Given an integer $k$ , let $k^{\ast }$ denote its odd square-free kernel. For any fixed integer $\unicode[STIX]{x1D705}\leqslant K$ ,

$$\begin{eqnarray}\#\{k\leqslant K:k^{\ast }=\unicode[STIX]{x1D705}\}\ll K^{\unicode[STIX]{x1D700}}.\end{eqnarray}$$

We defer the proof of this lemma until § 4.4, and merely apply it now to (4.27); for example the first sum is bounded by

$$\begin{eqnarray}\mathop{\sum }_{y_{1}\leqslant V\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{q_{1}}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D708}\leqslant V\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{\unicode[STIX]{x1D708}}\#\{v\leqslant V\unicode[STIX]{x1D6FF}^{-1}:v^{\ast }=\unicode[STIX]{x1D708}\}\ll V^{\unicode[STIX]{x1D700}}\mathop{\sum }_{\unicode[STIX]{x1D708}\leqslant V\unicode[STIX]{x1D6FF}^{-1}}\frac{1}{\unicode[STIX]{x1D708}}\ll V^{\unicode[STIX]{x1D700}}.\end{eqnarray}$$

One may handle the second and third sums in (4.27) similarly, and deduce that the second term in (4.25) is $O(W^{2}X^{\unicode[STIX]{x1D700}})$ overall. Since $W^{2}\leqslant W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}$ for $\unicode[STIX]{x1D6FF}\leqslant V$ we see that this error is dominated by (4.13).

Finally, the contribution, say $T_{3}^{\prime }(\unicode[STIX]{x1D6FF})$ , of the third term in (4.25) may be bounded by following the same argument as in [HB07], which we sketch for completeness. For each triple $y_{1},y_{2},k$ , let $\unicode[STIX]{x1D6EC}$ be the lattice to which $\unicode[STIX]{x1D706}_{1}$ corresponds, and let $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})$ be the shortest nonzero vector in $\unicode[STIX]{x1D6EC}$ , so that $\unicode[STIX]{x1D706}_{1}$ is the length of $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})$ . Then

$$\begin{eqnarray}T_{3}^{\prime }(\unicode[STIX]{x1D6FF})\ll X^{\unicode[STIX]{x1D700}}W\mathop{\sum }_{\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}}\frac{\#\{y_{1},y_{2},k\}}{\sqrt{|\unicode[STIX]{x1D707}_{1}|^{2}+|\unicode[STIX]{x1D707}_{2}|^{2}}},\end{eqnarray}$$

where we count the number of $y_{1},y_{2},k$ that generate a lattice in which $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})$ is a vector of minimal length. We note by (4.24) that

(4.28) $$\begin{eqnarray}\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\ll V^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}.\end{eqnarray}$$

Since $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})$ lies in the lattice $\unicode[STIX]{x1D6EC}$ , then by construction

(4.29) $$\begin{eqnarray}q_{1}\mid \unicode[STIX]{x1D707}_{1},\quad q_{2}\mid \unicode[STIX]{x1D707}_{2}\end{eqnarray}$$

and

(4.30) $$\begin{eqnarray}r\mid (y_{2}^{2}\unicode[STIX]{x1D707}_{1}^{3}-y_{1}^{2}\unicode[STIX]{x1D707}_{2}^{3}),\end{eqnarray}$$

as described in Lemma 4.3.

We first consider the case where both $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$ are nonzero. By (4.29), once $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$ are fixed, they determine at most $X^{\unicode[STIX]{x1D700}}$ values of $q_{1},q_{2}$ and hence at most $X^{\unicode[STIX]{x1D700}}$ values for $y_{1},y_{2}$ by Lemma 4.4. If $y_{2}^{2}\unicode[STIX]{x1D707}_{1}^{3}-y_{1}^{2}\unicode[STIX]{x1D707}_{2}^{3}$ is nonzero, then it determines at most $X^{\unicode[STIX]{x1D700}}$ values for $r$ by (4.30) and hence at most $X^{\unicode[STIX]{x1D700}}$ values for $k$ . On the other hand, if

(4.31) $$\begin{eqnarray}y_{2}^{2}\unicode[STIX]{x1D707}_{1}^{3}=y_{1}^{2}\unicode[STIX]{x1D707}_{2}^{3},\end{eqnarray}$$

then $y_{1},y_{2}$ would satisfy a relation of the form (4.11); pairs $y_{1},y_{2}$ of this type have already been treated, and are excluded from the contribution we are currently calculating. We therefore see that the contribution to $T_{3}^{\prime }(\unicode[STIX]{x1D6FF})$ from $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$ both nonzero is

$$\begin{eqnarray}T_{3}^{\prime }(\unicode[STIX]{x1D6FF})\ll X^{4\unicode[STIX]{x1D700}}W\mathop{\sum }_{\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}}\frac{1}{\sqrt{|\unicode[STIX]{x1D707}_{1}|^{2}+|\unicode[STIX]{x1D707}_{2}|^{2}}}.\end{eqnarray}$$

To bound the sum, we begin by focusing on a fixed dyadic range

$$\begin{eqnarray}{\textstyle \frac{1}{2}}B<\sqrt{|\unicode[STIX]{x1D707}_{1}|^{2}+|\unicode[STIX]{x1D707}_{2}|^{2}}\leqslant B,\end{eqnarray}$$

for any appropriate $B\geqslant 1$ ; we note that the restriction (4.28) implies that $B\ll V^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}.$ There are $O(B^{2})$ pairs $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$ , each of which contribute $O(B^{-1})$ to the sum. Summing over dyadic $B\ll V^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}$ therefore produces a total contribution of $\ll X^{\unicode[STIX]{x1D700}}WV^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}$ to $T_{3}^{\prime }(\unicode[STIX]{x1D6FF})$ .

On the other hand if $\unicode[STIX]{x1D707}_{1}$ vanishes, then there are $V\unicode[STIX]{x1D6FF}^{-1}$ choices for $y_{1}$ and $O(X^{2\unicode[STIX]{x1D700}})$ choices for $q_{2},r$ , hence $O(X^{4\unicode[STIX]{x1D700}})$ choices for $y_{2},k$ . (In particular, (4.31) cannot occur, since it would force $\unicode[STIX]{x1D707}_{1}=\unicode[STIX]{x1D707}_{2}=0$ .) Thus the contribution from these terms to $T_{3}^{\prime }(\unicode[STIX]{x1D6FF})$ is

$$\begin{eqnarray}\ll X^{5\unicode[STIX]{x1D700}}VW\unicode[STIX]{x1D6FF}^{-1}\mathop{\sum }_{\unicode[STIX]{x1D707}_{2}\ll V^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}}\frac{1}{|\unicode[STIX]{x1D707}_{2}|}\ll X^{6\unicode[STIX]{x1D700}}VW\unicode[STIX]{x1D6FF}^{-1}.\end{eqnarray}$$

The case where $\unicode[STIX]{x1D707}_{2}$ vanishes may be treated by an analogous argument. We may conclude that

$$\begin{eqnarray}T_{3}^{\prime }(\unicode[STIX]{x1D6FF})\ll X^{\unicode[STIX]{x1D700}}(WV^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}+VW\unicode[STIX]{x1D6FF}^{-1}).\end{eqnarray}$$

Combining this with the contributions (4.13) and (4.26) shows that

$$\begin{eqnarray}T_{3}(\unicode[STIX]{x1D6FF})\ll X^{\unicode[STIX]{x1D700}}(W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}+V^{3}U\unicode[STIX]{x1D6FF}^{-3}+WV^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2}+VW\unicode[STIX]{x1D6FF}^{-1}).\end{eqnarray}$$

Since

$$\begin{eqnarray}\displaystyle WV^{3/2}U^{1/2}\unicode[STIX]{x1D6FF}^{-3/2} & = & \displaystyle \{W^{2}\}^{1/2}\{V^{3}U\unicode[STIX]{x1D6FF}^{-3}\}^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \{W^{2}V^{2/3}\unicode[STIX]{x1D6FF}^{-2/3}\}^{1/2}\{V^{3}U\unicode[STIX]{x1D6FF}^{-3}\}^{1/2}\nonumber\end{eqnarray}$$

for $\unicode[STIX]{x1D6FF}\leqslant V$ , the third term above is dominated by the first two, so that Proposition 4.2 follows.◻

4.4 Proof of Lemma 4.4

We now prove Lemma 4.4, in the following more general form. Given any finite set ${\mathcal{P}}$ of primes (possibly empty), let

$$\begin{eqnarray}k({\mathcal{P}})=\mathop{\prod }_{\substack{ p\mid k \\ p\not \in {\mathcal{P}}}}p.\end{eqnarray}$$

Consider the set $\{k\leqslant K:k({\mathcal{P}})=\unicode[STIX]{x1D705}\}$ for a fixed positive integer $\unicode[STIX]{x1D705}$ . The set is empty unless $\unicode[STIX]{x1D705}\leqslant K$ is square-free and satisfies $(\unicode[STIX]{x1D705},\prod _{p\in {\mathcal{P}}}p)=1$ , which we now assume. Then for any $\unicode[STIX]{x1D702}>0$ ,

$$\begin{eqnarray}\displaystyle \#\{k\leqslant K:k({\mathcal{P}})=\unicode[STIX]{x1D705}\} & {\leqslant} & \displaystyle \mathop{\sum }_{\substack{ k=1 \\ k({\mathcal{P}})=\unicode[STIX]{x1D705}}}^{K}\biggl(\frac{K}{k}\biggr)^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle K^{\unicode[STIX]{x1D702}}\mathop{\sum }_{\substack{ k=1 \\ k({\mathcal{P}})=\unicode[STIX]{x1D705}}}^{\infty }k^{-\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle K^{\unicode[STIX]{x1D702}}\mathop{\prod }_{p\in {\mathcal{P}}}\biggl(\mathop{\sum }_{e=0}^{\infty }p^{-e\unicode[STIX]{x1D702}}\biggr)\mathop{\prod }_{p\mid \unicode[STIX]{x1D705}}\biggl(\mathop{\sum }_{e=1}^{\infty }p^{-e\unicode[STIX]{x1D702}}\biggr).\nonumber\end{eqnarray}$$

Setting $A(\unicode[STIX]{x1D702})=\sum _{e=0}^{\infty }2^{-e\unicode[STIX]{x1D702}}$ we then see that

$$\begin{eqnarray}\#\{k\leqslant K:k({\mathcal{P}})=\unicode[STIX]{x1D705}\}\leqslant K^{\unicode[STIX]{x1D702}}A(\unicode[STIX]{x1D702})^{\unicode[STIX]{x1D714}(\unicode[STIX]{x1D705})+\#{\mathcal{P}}}\leqslant K^{\unicode[STIX]{x1D702}}A(\unicode[STIX]{x1D702})^{(\#{\mathcal{P}}+1)\unicode[STIX]{x1D714}(\unicode[STIX]{x1D705})}.\end{eqnarray}$$

Upon recalling that $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D705})\ll (\log 3\unicode[STIX]{x1D705})(\log \log 3\unicode[STIX]{x1D705})^{-1}$ and $\unicode[STIX]{x1D705}\leqslant K$ we may conclude that

$$\begin{eqnarray}\#\{k\leqslant K:k({\mathcal{P}})=\unicode[STIX]{x1D705}\}\ll _{\unicode[STIX]{x1D702}}K^{(\#{\mathcal{P}}+2)\unicode[STIX]{x1D702}}\end{eqnarray}$$

for any $\unicode[STIX]{x1D702}>0$ , which proves Lemma 4.4.◻

5 Average of $h_{\ell }(-d)$

We now turn to applications of the key propositions. We first apply Proposition 2.1 to derive a nontrivial upper bound for the average of $h_{\ell }(-d)$ . Fix a dyadic region $X\leqslant d<2X$ and assume that $X^{1/(2\ell )}\leqslant Z\leqslant X$ . Then Proposition 2.1 implies that

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{X\leqslant d<2X}h_{\ell }(-d)\ll X^{\unicode[STIX]{x1D700}}\biggl\{X^{1/2}\#E(Z;X)+X^{3/2}Z^{-1}+X^{1/2}Z^{-2}\mathop{\sum }_{\substack{ X\leqslant d<2X \\ d\not \in E(Z;X)}}S_{\ell }(d;Z)\biggr\}. & & \displaystyle \nonumber\end{eqnarray}$$

We apply the upper bound (2.1) to the exceptional set $E(Z;X)$ and Proposition 2.3 to the average of $S_{\ell }(d;Z)$ to conclude that

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}h_{\ell }(-d)\ll X^{\unicode[STIX]{x1D700}}\{X^{3/2}Z^{-1}+X+Z^{\ell }\}.\end{eqnarray}$$

It is optimal to choose $Z=X^{3/(2\ell +2)}$ , resulting in

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}h_{\ell }(-d)\ll X^{3/2-3/(2\ell +2)+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

Summing over $O(\log X)$ dyadic intervals to cover the full range $0<d<X$ then yields the result of Theorem 1.1.

6 Higher moments of $h_{\ell }(-d)$

We now consider higher moments. For any odd prime $\ell$ , define for any real $H\geqslant 1$ the set

$$\begin{eqnarray}A_{\ell }(H;X)=\{X\leqslant d<2X:h_{\ell }(-d)>H\},\end{eqnarray}$$

with corresponding counting function

$$\begin{eqnarray}N_{\ell }(H;X)=\#A_{\ell }(H;X).\end{eqnarray}$$

We also define for any $\frac{1}{4}X^{1/2\ell }\leqslant Z\leqslant X$ the set

$$\begin{eqnarray}A_{\ell }^{0}(H,Z;X)=\{X\leqslant d<2X:h_{\ell }(-d)>H\}\setminus E(Z;X),\end{eqnarray}$$

where $E(Z;X)$ is as usual the exceptional set provided by Proposition 2.1. We define the corresponding counting function

$$\begin{eqnarray}N_{\ell }^{0}(H,Z;X)=\#A_{\ell }^{0}(H,Z;X).\end{eqnarray}$$

We note that for any fixed choice of $Z$ in the above range,

(6.1) $$\begin{eqnarray}N_{\ell }(H;X)\leqslant \#E(Z;X)+N_{\ell }^{0}(H,Z;X)\ll X^{\unicode[STIX]{x1D700}}+N_{\ell }^{0}(H,Z;X).\end{eqnarray}$$

6.1 The case $\ell =3$

Restricting to the case $\ell =3$ , we see that (1.4) implies that

(6.2) $$\begin{eqnarray}N_{3}(H;X)\ll XH^{-1}.\end{eqnarray}$$

We also note that $A_{3}(H;X)$ is empty by (1.2) unless $H\leqslant X^{1/3+\unicode[STIX]{x1D700}}$ for some small $\unicode[STIX]{x1D700}>0$ . In general we have the following.

Proposition 6.1. For $1\leqslant H\leqslant X^{1/3+\unicode[STIX]{x1D700}}$ ,

$$\begin{eqnarray}N_{3}(H;X)\ll X^{\unicode[STIX]{x1D700}}(X^{1/2}+X^{7/2}H^{-10}).\end{eqnarray}$$

Proof. To prove this we consider $A_{3}^{0}(H,Z;X)$ with the choice $Z=X^{1/2+2\unicode[STIX]{x1D700}}H^{-1}$ ; note in particular $Z\geqslant X^{1/6}$ when $H\leqslant X^{1/3+\unicode[STIX]{x1D700}}$ . Moreover we will have

$$\begin{eqnarray}h_{3}(-d)>H\gg d^{1/2+\unicode[STIX]{x1D700}}Z^{-1}\end{eqnarray}$$

for all $d$ in $A_{3}^{0}(H,Z;X),$ whence Proposition 2.1 shows that

$$\begin{eqnarray}h_{3}(-d)\ll d^{1/2+\unicode[STIX]{x1D700}}Z^{-2}S_{3}(d;Z).\end{eqnarray}$$

We therefore have

$$\begin{eqnarray}S_{3}(d;Z)\gg d^{-1/2-\unicode[STIX]{x1D700}}Z^{2}h_{3}(-d)\gg X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}h_{3}(-d)>X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H,\end{eqnarray}$$

for all $d\in A_{3}^{0}(H,Z;X)$ . This leads to the bound

$$\begin{eqnarray}N_{3}^{0}(H;X)(X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H)^{2}\ll \mathop{\sum }_{d\in A_{3}^{0}(H,Z;X)}S_{3}(d;Z)^{2}\ll \mathop{\sum }_{X\leqslant d<2X}S_{3}(d;Z)^{2}.\end{eqnarray}$$

We can now apply the case $\ell =3$ of Proposition 2.4 to obtain

$$\begin{eqnarray}N_{3}^{0}(H,Z;X)(X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H)^{2}\ll X^{\unicode[STIX]{x1D700}}\{Z^{2}X^{1/2}+Z^{12}X^{-3/2}\},\end{eqnarray}$$

so that

$$\begin{eqnarray}N_{3}^{0}(H,Z;X)\ll X^{3\unicode[STIX]{x1D700}}H^{-2}\{Z^{-2}X^{3/2}+Z^{8}X^{-1/2}\}\ll X^{19\unicode[STIX]{x1D700}}\{X^{1/2}+X^{7/2}H^{-10}\}\end{eqnarray}$$

in view of our choice of $Z$ . This is sufficient to prove Proposition 6.1, by (6.1).◻

Proof of Theorem 1.2.

We may now derive Theorem 1.2 from Proposition 6.1. It will suffice to consider a dyadic range $X\leqslant d<2X$ . Then

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{X\leqslant d<2X}h_{3}(-d)^{k} & \ll & \displaystyle \mathop{\sum }_{\substack{ H\leqslant X^{1/3+\unicode[STIX]{x1D700}} \\ \text{dyadic}}}\mathop{\sum }_{\substack{ X\leqslant d<2X \\ H<h_{3}(-d)\leqslant 2H}}h_{3}(-d)^{k}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\substack{ H\leqslant X^{1/3+\unicode[STIX]{x1D700}} \\ \text{dyadic}}}N_{3}(H;X)(2H)^{k}.\nonumber\end{eqnarray}$$

In view of (6.2) we have

$$\begin{eqnarray}N_{3}(H;X)(2H)^{k}\ll XH^{k-1}.\end{eqnarray}$$

On the other hand, Proposition 6.1 yields

$$\begin{eqnarray}N_{3}(H;X)(2H)^{k}\ll X^{\unicode[STIX]{x1D700}}(X^{1/2}H^{k}+X^{7/2}H^{k-10}).\end{eqnarray}$$

In particular for $k=4$ we deduce that

$$\begin{eqnarray}\displaystyle N_{3}(H;X)(2H)^{4} & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}\min \{XH^{3},X^{1/2}H^{4}+X^{7/2}H^{-6}\}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}\min \{XH^{3},X^{1/2}H^{4}\}+\min \{XH^{3},X^{7/2}H^{-6}\}.\nonumber\end{eqnarray}$$

For $H\leqslant X^{1/3+\unicode[STIX]{x1D700}}$ the first term is at most

$$\begin{eqnarray}X^{1/2}H^{4}\leqslant X^{11/6+4\unicode[STIX]{x1D700}}\end{eqnarray}$$

while the second term is at most

$$\begin{eqnarray}\{XH^{3}\}^{2/3}\{X^{7/2}H^{-6}\}^{1/3}=X^{11/6}.\end{eqnarray}$$

It follows that $N_{3}(H;X)(2H)^{4}\ll X^{11/6+4\unicode[STIX]{x1D700}}$ , whence

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}h_{3}(-d)^{4}\ll X^{11/6+5\unicode[STIX]{x1D700}}.\end{eqnarray}$$

This suffices to prove Theorem 1.2. ◻

As noted in the introduction, one can deduce estimates for other moments from the fourth moment. The reader may check that a direct application of the methods of this section to the general moment only reproduces these consequences of the special case $k=4$ .

6.2 The case $\ell \geqslant 5$

We now consider the $k$ th moment of $h_{\ell }(-d)$ for primes $\ell \geqslant 5$ and any real $k\geqslant 1$ . By Corollary 2.2 we see that

$$\begin{eqnarray}N_{\ell }(H;X)\ll X^{\unicode[STIX]{x1D700}}\quad \text{if }H\geqslant X^{1/2-1/2\ell +\unicode[STIX]{x1D700}}.\end{eqnarray}$$

We also record the trivial bound

(6.3) $$\begin{eqnarray}N_{\ell }(H;X)\ll X,\end{eqnarray}$$

valid for all $H$ . In addition, we claim the following.

Proposition 6.2. For any prime $\ell \geqslant 3$ and $1\leqslant H\leqslant X^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}$ ,

$$\begin{eqnarray}N_{\ell }(H;X)\ll X^{\unicode[STIX]{x1D700}}(XH^{-1}+X^{\ell /2}H^{-(\ell +1)}).\end{eqnarray}$$

With Proposition 6.2 in hand, we will prove the following.

Proposition 6.3. For any prime $\ell \geqslant 5$ and any real number $k\geqslant 1$ ,

$$\begin{eqnarray}\mathop{\sum }_{X\leqslant d<2X}h_{\ell }(-d)^{k}\ll X^{\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D700}},\end{eqnarray}$$

where

$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\max \{\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}\}\end{eqnarray}$$

and

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{1} & = & \displaystyle 1+k\biggl(\frac{\ell -2}{2\ell +2}\biggr),\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}_{2} & = & \displaystyle 1+k\biggl(\frac{\ell -1}{2\ell }\biggr)-\biggl(\frac{\ell -1}{2\ell }\biggr),\nonumber\\ \displaystyle \unicode[STIX]{x1D70E}_{3} & = & \displaystyle \frac{k}{2}.\nonumber\end{eqnarray}$$

We note that the maximum is $\unicode[STIX]{x1D70E}_{1}$ in the range $1\leqslant k\leqslant (\ell ^{2}-1)/(2\ell -1)$ ; it is $\unicode[STIX]{x1D70E}_{2}$ in the range $(\ell ^{2}-1)/(2\ell -1)\leqslant k\leqslant \ell +1$ ; and it is $\unicode[STIX]{x1D70E}_{3}$ for $k\geqslant \ell +1$ . This leads immediately to the statement of Theorem 1.5. We note that Proposition 6.2 does not imply any new results in the case of $h_{3}(-d)$ .

Proof of Proposition 6.2.

The proof of Proposition 6.2 follows similar lines to that of Proposition 6.1. As before we set $Z=X^{1/2+2\unicode[STIX]{x1D700}}H^{-1}$ , so that $Z\geqslant X^{1/(2\ell )}$ for $H\leqslant X^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}$ . We deduce that

$$\begin{eqnarray}S_{\ell }(d;Z)\gg d^{-1/2-\unicode[STIX]{x1D700}}Z^{2}h_{\ell }(-d)\gg X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}h_{\ell }(-d)>X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H,\end{eqnarray}$$

again under the assumption that $d\in A_{\ell }^{0}(H,Z;X)$ . As a result,

$$\begin{eqnarray}N_{\ell }^{0}(H,Z;X)X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H\ll \mathop{\sum }_{d\in A_{\ell }^{0}(H,Z;Z)}S_{\ell }(d;Z)\ll \mathop{\sum }_{X\leqslant d<2X}S_{\ell }(d;Z).\end{eqnarray}$$

Upon applying Proposition 2.3 we obtain

$$\begin{eqnarray}N_{\ell }^{0}(H,Z;X)X^{-1/2-\unicode[STIX]{x1D700}}Z^{2}H\ll X^{\unicode[STIX]{x1D700}}(Z^{2}X^{1/2}+Z^{\ell +2}X^{-1/2}),\end{eqnarray}$$

so that

$$\begin{eqnarray}N_{\ell }^{0}(H,Z;X)\ll X^{2\unicode[STIX]{x1D700}}(XH^{-1}+Z^{\ell }H^{-1})\ll X^{(2+2\ell )\unicode[STIX]{x1D700}}(XH^{-1}+X^{\ell /2}H^{-(\ell +1)}),\end{eqnarray}$$

upon recalling the choice of $Z$ . This is sufficient to prove Proposition 6.2, by (6.1).◻

Proof of Proposition 6.3.

We turn finally to Proposition 6.3, for which we initially fix any real number $k\geqslant 1$ . We have already observed that $N_{\ell }(H;X)\ll X^{\unicode[STIX]{x1D700}}$ if

$$\begin{eqnarray}X^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}\leqslant H\leqslant X^{1/2+\unicode[STIX]{x1D700}},\end{eqnarray}$$

which shows that for such $H$ ,

(6.4) $$\begin{eqnarray}N_{\ell }(H;X)H^{k}\ll X^{k/2+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

Thus we now instead assume that

(6.5) $$\begin{eqnarray}H\leqslant X^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}.\end{eqnarray}$$

Then by the trivial bound (6.3) and Proposition 6.2 we have

$$\begin{eqnarray}\displaystyle N_{\ell }(H;X)H^{k} & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}\min \{XH^{k},XH^{k-1}+X^{\ell /2}H^{k-\ell -1}\}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}(XH^{k-1}+\min \{XH^{k},X^{\ell /2}H^{k-\ell -1}\}).\nonumber\end{eqnarray}$$

Under (6.5), the first term is $\ll X^{\unicode[STIX]{x1D70E}_{2}}$ . As long as $k\leqslant \ell +1$ , the second term is largest when $XH^{k}=X^{\ell /2}H^{k-\ell -1}$ , namely when

$$\begin{eqnarray}H=X^{(\ell -2)/(2\ell +2)}=X^{1/2-3/(2\ell +2)}.\end{eqnarray}$$

We may conclude that if $k\leqslant \ell +1$ and $H\leqslant X^{1/2-1/(2\ell )+\unicode[STIX]{x1D700}}$ then

$$\begin{eqnarray}N_{\ell }(H;X)H^{k}\ll X^{\unicode[STIX]{x1D700}}(X^{\unicode[STIX]{x1D70E}_{1}}+X^{\unicode[STIX]{x1D70E}_{2}}),\end{eqnarray}$$

with the notation of Proposition 6.3. On the other hand, if $k\geqslant \ell +1$ then

$$\begin{eqnarray}X^{\ell /2}H^{k-\ell -1}\leqslant X^{\ell /2}H^{k-\ell }\leqslant X^{\ell /2}(X^{1/2})^{k-\ell }=X^{k/2}.\end{eqnarray}$$

Thus $N_{\ell }(H;X)H^{k}\ll X^{\unicode[STIX]{x1D700}}(X^{\unicode[STIX]{x1D70E}_{2}}+X^{k/2})$ in this case; note that the second term dominates in the range $k\geqslant \ell +1$ . To conclude, we have

(6.6) $$\begin{eqnarray}N_{\ell }(H;X)H^{k}\ll X^{\unicode[STIX]{x1D700}}(X^{\unicode[STIX]{x1D70E}_{1}}+X^{\unicode[STIX]{x1D70E}_{2}}+X^{\unicode[STIX]{x1D70E}_{3}})\end{eqnarray}$$

for all $k\geqslant 1$ .

Combining (6.4) and (6.6) shows that

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{X\leqslant d<2X}h_{\ell }(-d)^{k} & \ll & \displaystyle \mathop{\sum }_{\substack{ H\ll X^{1/2+\unicode[STIX]{x1D700}} \\ \text{dyadic}}}\mathop{\sum }_{\substack{ X\leqslant d<2X \\ H<h_{\ell }(-d)\leqslant 2H}}h_{\ell }(-d)^{k}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\substack{ H\ll X^{1/2+\unicode[STIX]{x1D700}} \\ \text{dyadic}}}N_{\ell }(H;X)(2H)^{k}\nonumber\\ \displaystyle & \ll & \displaystyle X^{\unicode[STIX]{x1D700}}(X^{\unicode[STIX]{x1D70E}_{1}}+X^{\unicode[STIX]{x1D70E}_{2}}+X^{\unicode[STIX]{x1D70E}_{3}}).\nonumber\end{eqnarray}$$

We note that $k/2\leqslant \max \{\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}\}$ in the range $k\leqslant \ell +1$ . This proves Proposition 6.3, and hence Theorem 1.5.◻

The reader may verify that a similar computation based on Proposition 2.4 yields no improvements.