Hostname: page-component-6bf8c574d5-mcfzb Total loading time: 0 Render date: 2025-03-07T02:22:39.915Z Has data issue: false hasContentIssue false
  • English
  • Français

The Baum–Connes conjecture localised at the unit element of a discrete group

Part of: Fiber spaces and bundles Partial differential equations on manifolds; differential operators Selfadjoint operator algebras $K$-theory and operator algebras Higher algebraic $K$-theory

Published online by Cambridge University Press:  14 January 2021

Paolo Antonini ,
Sara Azzali  and
Georges Skandalis
Paolo Antonini
Affiliation:
Scuola Internazionale Superiore di Studi Avanzati, via Bonomea, 265, 34136Trieste, Italypantonin@sissa.it
Sara Azzali
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstrasse 55, 20146Hamburg, Germanysara.azzali@uni-hamburg.de
Georges Skandalis
Affiliation:
Université de Paris and Sorbonne Université, CNRS, IMJ-PRG, F-75006Paris, Franceskandalis@math.univ-paris-diderot.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a Baum–Connes assembly map localised at the unit element of a discrete group 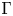$\Gamma$. This morphism, called 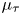$\mu _\tau$, is defined in 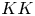$KK$-theory with coefficients in 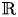$\mathbb {R}$ by means of the action of the idempotent 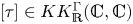$[\tau ]\in KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ canonically associated to the group trace of 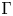$\Gamma$. We show that the corresponding 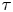$\tau$-Baum–Connes conjecture is weaker than the classical version, but still implies the strong Novikov conjecture. The right-hand side of 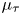$\mu _\tau$ is functorial with respect to the group 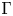$\Gamma$.

Keywords

assembly mapsNovikov conjectureequivariant Kasparov theoryclassifying spaces

MSC classification

Primary: 19K35: Kasparov theory ($KK$-theory) 46L80: $K$-theory and operator algebras (including cyclic theory)
Secondary: 58J22: Exotic index theories 55R40: Homology of classifying spaces, characteristic classes 19D55: $K$-theory and homology; cyclic homology and cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2536 - 2559
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Paolo Antonini was partially supported by the grant H2020-MSCA-RISE-2015-691246-QUANTUM DYNAMICS; Sara Azzali acknowledges support by the DFG grant Secondary invariants for foliations within the Priority Programme SPP 2026 ‘Geometry at Infinity’.

References

Antonini, P., Azzali, S. and Skandalis, G., Flat bundles, von Neumann algebras and $K$-theory with ${\mathbin {{\mathbb {R}}}}/\mathbb {Z}$-coefficients, J. K-Theory 13 (2014), 275–303.CrossRefGoogle Scholar
Antonini, P., Azzali, S. and Skandalis, G., Bivariant $K$-theory with ${\mathbin {{\mathbb {R}}}}/\mathbin {\mathbb {Z}}$-coefficients and rho classes of unitary representations, J. Funct. Anal. 270 (2016), 447–481.Google Scholar
Antonini, P., Buss, A., Engel, A. and Siebenand, T., Strong Novikov conjecture for low degree cohomology and exotic group $C^*$-algebras, Preprint (2020), arXiv:1905.07730v2 [math.OA].CrossRefGoogle Scholar
Arzhantseva, G. and Delzant, T., Examples of random groups, 2008, available at http://irma.math.unistra.fr/delzant/random.pdf.Google Scholar
Baum, P. and Connes, A., Geometric $K$-theory for Lie groups and foliations, Enseign. Math. 46 (2000), 3–42.Google Scholar
Baum, P., Connes, A. and Higson, N., Classifying space for proper actions and K-theory of group $C^*$-algebras, Contemporary Mathematics, vol. 167 (American Mathematical Society, Providence, RI, 1994), 240–291.Google Scholar
Buss, A., Echterhoff, S. and Willett, R., The minimal exact crossed product, Doc. Math. 23 (2018), 2043–2077 (after publication, the authors added an erratum in the arXiv version arXiv:1804.02725v3 explaining some gaps).Google Scholar
Baum, P., Guentner, E. and Willett, R., Expanders, exact crossed products, and the Baum–Connes conjecture, Ann. K-Theory 1 (2016), 155–208.CrossRefGoogle Scholar
Burghelea, D., The cyclic homology of the group rings, Comment. Math. Helv. 60 (1985), 354–365.CrossRefGoogle Scholar
Coulon, R., On the geometry of burnside quotients of torsion free hyperbolic groups, Internat. J. Algebra Comput. 24 (2014), 251–345.CrossRefGoogle Scholar
Cuntz, J., $K$-theoretic amenability for discrete groups, J. Reine Angew. Math. 344 (1983), 180–195.Google Scholar
El Morsli, D., Semi-exactitude du bifoncteur de Kasparov pour les actions moyennables, Thèse, Université de la Méditerranée (2006), http://iml.univ-mrs.fr/theses/files/el_morsli-these.pdf.Google Scholar
Gong, S., Wu, J. and Yu, G., The Novikov conjecture, the group of volume preserving diffeomorphisms and Hilbert-Hadamard spaces, Preprint (2018), arXiv:1811.02086 [math.KT].Google Scholar
Gromov, M., Random walks in random groups, Geom. Funct. Anal. 13 (2003), 73–146.CrossRefGoogle Scholar
Gomez Aparicio, M. P., Julg, P. and Valette, A., The Baum–Connes conjecture: an extended survey, in Advances in noncommutative geometry (Springer, 2019).Google Scholar
Higson, N., Lafforgue, V. and Skandalis, G., Counterexample to the Baum–Connes conjecture, Geom. Funct. Anal. 12 (2002), 330–354.CrossRefGoogle Scholar
Kaad, J. and Proietti, V., Index theory on the Miščenko bundle, Kyoto J. Math., to appear. Preprint (2018), arXiv:1807.05757 [math.KT].Google Scholar
Kasparov, G., The operator $K$-functor and extensions of $C^*$-algebras, Math. USSR Izv. 16 (1981), 513–572.CrossRefGoogle Scholar
Kasparov, G., Equivariant $KK$-theory and the Novikov conjecture, Invent. Math. 91 (1988), 147–202.CrossRefGoogle Scholar
Lafforgue, V., La conjecture de Baum–Connes à coefficients pour les groupes hyperboliques, J. Noncommut. Geom. 6 (2012), 1–197.CrossRefGoogle Scholar
Mishchenko, A. S. and Fomenko, A. T., The index of elliptic operators over $C^*$-algebras, Math. USSR Izv. 15 (1980), 87–112.Google Scholar
Osajda, D., Small cancellation labellings of some infinite graphs and applications, Preprint (2014), arXiv:1406.5015v3.Google Scholar
Skandalis, G., Exact sequences for the Kasparov groups of graded algebras, Canad. J. Math. 13 (1985), 255–263.Google Scholar
Skandalis, G., On the group of extensions relative to a semifinite factor, J. Operator Theory 37 (1985), 193–216.Google Scholar
Skandalis, G., Une notion de nuclearité en $K$-théorie, K-Theory 1 (1988), 549–573.CrossRefGoogle Scholar
Valette, A., Introduction to the Baum–Connes conjecture, Lectures in Mathematics ETH Zürich (Birkhäuser, Basel, 2002).Google Scholar