Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Warnaar, S. Ole
2009.
A Selberg integral for the Lie algebra An.
Acta Mathematica,
Vol. 203,
Issue. 2,
p.
269.
Rosengren, Hjalmar
2009.
An Izergin–Korepin-type identity for the 8VSOS model, with applications to alternating sign matrices.
Advances in Applied Mathematics,
Vol. 43,
Issue. 2,
p.
137.
Warnaar, S. Ole
2010.
The sl3 Selberg integral.
Advances in Mathematics,
Vol. 224,
Issue. 2,
p.
499.
Lascoux, Alain
and
Warnaar, S. Ole
2011.
Branching rules for symmetric functions and sln basic hypergeometric series.
Advances in Applied Mathematics,
Vol. 46,
Issue. 1-4,
p.
424.
Cai, Tommy Wuxing
and
Jing, Naihuan
2014.
A generalization of Newton's identity and Macdonald functions.
Journal of Combinatorial Theory, Series A,
Vol. 125,
Issue. ,
p.
342.
Betea, D.
Wheeler, M.
and
Zinn-Justin, P.
2015.
Refined Cauchy/Littlewood identities and six-vertex model partition functions: II. Proofs and new conjectures.
Journal of Algebraic Combinatorics,
Vol. 42,
Issue. 2,
p.
555.
Aggarwal, Amol
2015.
Correlation functions of the Schur process through Macdonald difference operators.
Journal of Combinatorial Theory, Series A,
Vol. 131,
Issue. ,
p.
88.
Wheeler, Michael
and
Zinn-Justin, Paul
2016.
Refined Cauchy/Littlewood identities and six-vertex model partition functions: III. Deformed bosons.
Advances in Mathematics,
Vol. 299,
Issue. ,
p.
543.
Duval, Antoine
and
Pasquier, Vincent
2016.
q-bosons, Toda lattice, Pieri rules and Baxterq-operator.
Journal of Physics A: Mathematical and Theoretical,
Vol. 49,
Issue. 15,
p.
154006.
Betea, D.
and
Wheeler, M.
2016.
Refined Cauchy and Littlewood identities, plane partitions and symmetry classes of alternating sign matrices.
Journal of Combinatorial Theory, Series A,
Vol. 137,
Issue. ,
p.
126.
Cuenca, Cesar
2018.
Interpolation Macdonald operators at infinity.
Advances in Applied Mathematics,
Vol. 101,
Issue. ,
p.
15.
Galleas, W
2019.
Domain-wall boundaries through non-diagonal twists in the six-vertex model.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2019,
Issue. 2,
p.
023101.
Gatica, Jessica
Jones, Miles
and
Lapointe, Luc
2019.
Pieri Rules for the Jack Polynomials in Superspace and the 6-Vertex Model.
Annales Henri Poincaré,
Vol. 20,
Issue. 4,
p.
1051.
Cantini, Luigi
Colomo, Filippo
and
Pronko, Andrei G.
2020.
Integral Formulas and Antisymmetrization Relations for the Six-Vertex Model.
Annales Henri Poincaré,
Vol. 21,
Issue. 3,
p.
865.
Colomo, F.
Di Giulio, G.
and
Pronko, A.G.
2021.
Six-vertex model on a finite lattice: Integral representations for nonlocal correlation functions.
Nuclear Physics B,
Vol. 972,
Issue. ,
p.
115535.
Albion, Seamus P.
Rains, Eric M.
and
Warnaar, S. Ole
2021.
AFLT-type Selberg integrals.
Communications in Mathematical Physics,
Vol. 388,
Issue. 2,
p.
735.
Petrov, Leonid
2021.
Refined Cauchy identity for spin Hall–Littlewood symmetric rational functions.
Journal of Combinatorial Theory, Series A,
Vol. 184,
Issue. ,
p.
105519.
Rimányi, Richárd
and
Varchenko, Alexander
2022.
The $${{\mathbb {F}}}_p$$-Selberg Integral.
Arnold Mathematical Journal,
Vol. 8,
Issue. 1,
p.
39.
Saenz, Axel
Tracy, Craig A.
and
Widom, Harold
2022.
Toeplitz Operators and Random Matrices.
Vol. 289,
Issue. ,
p.
9.
Aprile, Francesco
and
Heslop, Paul
2023.
Superconformal Blocks in Diverse Dimensions and BC Symmetric Functions.
Communications in Mathematical Physics,
Vol. 402,
Issue. 2,
p.
995.

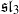 basic hypergeometric series
basic hypergeometric series