Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jiang, Dihua
and
Zhang, Lei
2021.
Relative Trace Formulas.
p.
253.
Gourevitch, Dmitry
Sayag, Eitan
and
Karshon, Ido
2021.
Annihilator varieties of distinguished modules of reductive Lie algebras.
Forum of Mathematics, Sigma,
Vol. 9,
Issue. ,
Loeffler, David
2021.
Gross–Prasad periods for reducible representations.
Forum Mathematicum,
Vol. 33,
Issue. 5,
p.
1169.
Haan, Jaeho
2022.
The local Gan-Gross-Prasad conjecture for U(n + 1)×U(n): A non-generic case.
Journal of Number Theory,
Vol. 233,
Issue. ,
p.
1.
Yang, Chang
2022.
Linear periods for unitary representations.
Mathematische Zeitschrift,
Vol. 302,
Issue. 4,
p.
2253.
Prasad, Dipendra
and
Raghunathan, Ravi
2022.
Relations between cusp forms sharing Hecke eigenvalues.
Representation Theory of the American Mathematical Society,
Vol. 26,
Issue. 34,
p.
1063.
Chan, Kei Yuen
2022.
Restriction for general linear groups: The local non-tempered Gan–Gross–Prasad conjecture (non-Archimedean case).
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 783,
p.
49.
Gan, Wee Teck
Gross, Benedict H.
and
Prasad, Dipendra
2023.
Twisted GGP problems and conjectures.
Compositio Mathematica,
Vol. 159,
Issue. 9,
p.
1916.
Liu, Gang
Oshima, Yoshiki
and
Yu, Jun
2023.
Restriction of irreducible unitary representations of 𝑆𝑝𝑖𝑛(𝑁,1) to parabolic subgroups.
Representation Theory of the American Mathematical Society,
Vol. 27,
Issue. 24,
p.
887.
Chan, Kei Yuen
2023.
Ext-multiplicity theorem for standard representations of $$(\textrm{GL}_{n+1},\textrm{GL}_n)$$.
Mathematische Zeitschrift,
Vol. 303,
Issue. 2,
Asgari, Mahdi
and
Choiy, Kwangho
2024.
Representations of the p-adic GSpin4 and GSpin6 and the adjoint L-function.
Journal of Number Theory,
Vol. 265,
Issue. ,
p.
76.
Haan, Jaeho
2024.
Regularized periods and the global Gan–Gross–Prasad conjecture: the case of $$U(n+2r) \times U(n)$$.
Mathematische Annalen,
Vol. 389,
Issue. 4,
p.
4149.
Chan, Kei Yuen
2024.
On the Product Functor on Inner forms of the General Linear Group Over A Non-Archimedean Local Field.
Transformation Groups,
Chen, Cheng
Jiang, Dihua
Liu, Dongwen
and
Zhang, Lei
2024.
Arithmetic branching law and generic 𝐿-packets.
Representation Theory of the American Mathematical Society,
Vol. 28,
Issue. 8,
p.
328.
Liu, Baiying
and
Lo, Chi-Heng
2024.
On the Weak Local Arthur Packets Conjecture for Split Classical Groups.
International Mathematics Research Notices,
Vol. 2024,
Issue. 14,
p.
10708.
Aizenbud, Avraham
and
Gourevitch, Dmitry
2024.
Finite Multiplicities Beyond Spherical Spaces.
International Mathematics Research Notices,
Vol. 2024,
Issue. 7,
p.
5894.
Qadri, Mohammed Saad
2025.
Non-tempered Ext Branching Laws for the p-adic General Linear Group.
International Mathematics Research Notices,
Vol. 2025,
Issue. 1,
Suzuki, Miyu
2025.
A reformulation of the conjecture of Prasad and Takloo-Bighash.
Journal of Algebra,
Vol. 680,
Issue. ,
p.
174.
Ørsted, Bent
and
Speh, Birgit
2025.
Symmetry in Geometry and Analysis, Volume 2.
Vol. 358,
Issue. ,
p.
457.
Gourevitch, Dmitry
2025.
Symmetry in Geometry and Analysis, Volume 3.
Vol. 359,
Issue. ,
p.
15.
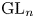 ${{\rm GL}}_n$ and all classical groups over both local fields and global fields. It plays a role for all the branching problems studied in Gan et al. [Symplectic local root numbers, central critical L-values and restriction problems in the representation theory of classical groups. Sur les conjectures de Gross et Prasad. I, Astérisque 346 (2012), 1–109] including Bessel models and Fourier–Jacobi models.
${{\rm GL}}_n$ and all classical groups over both local fields and global fields. It plays a role for all the branching problems studied in Gan et al. [Symplectic local root numbers, central critical L-values and restriction problems in the representation theory of classical groups. Sur les conjectures de Gross et Prasad. I, Astérisque 346 (2012), 1–109] including Bessel models and Fourier–Jacobi models.

