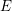 $E$-theory
$E$-theoryPublished online by Cambridge University Press: 13 March 2017
We prove that the 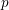 $p$-completed Brown–Peterson spectrum is a retract of a product of Morava
$p$-completed Brown–Peterson spectrum is a retract of a product of Morava 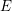 $E$-theory spectra. As a consequence, we generalize results of Kashiwabara and of Ravenel, Wilson and Yagita from spaces to spectra and deduce that the notion of a good group is determined by Brown–Peterson cohomology. Furthermore, we show that rational factorizations of the Morava
$E$-theory spectra. As a consequence, we generalize results of Kashiwabara and of Ravenel, Wilson and Yagita from spaces to spectra and deduce that the notion of a good group is determined by Brown–Peterson cohomology. Furthermore, we show that rational factorizations of the Morava 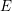 $E$-theory of certain finite groups hold integrally up to bounded torsion with height-independent exponent, thereby lifting these factorizations to the rationalized Brown–Peterson cohomology of such groups.
$E$-theory of certain finite groups hold integrally up to bounded torsion with height-independent exponent, thereby lifting these factorizations to the rationalized Brown–Peterson cohomology of such groups.