Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T11:43:12.382Z Has data issue: false hasContentIssue false
  • English
  • Français

C1 actions on manifolds by lattices in Lie groups

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory Lie groups

Published online by Cambridge University Press:  13 May 2022

Aaron Brown ,
Danijela Damjanović  and
Zhiyuan Zhang
Aaron Brown
Affiliation:
Northwestern University, Evanston, IL 60208, USA awb@northwestern.edu
Danijela Damjanović
Affiliation:
Department of Mathematics, Kungliga Tekniska högskolan, Lindstedtsvägen 25, SE-100 44 Stockholm, Sweden ddam@kth.se
Zhiyuan Zhang
Affiliation:
Institut Galilée, Université Paris 13, CNRS UMR, 7539, 93430 Villetaneuse, France zhiyuan.zhang@math.univ-paris13.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study Zimmer's conjecture for 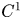$C^{1}$ actions of lattice subgroup of a higher-rank simple Lie group with finite center on compact manifolds. We show that when the rank of an uniform lattice is larger than the dimension of the manifold, then the action factors through a finite group. For lattices in 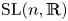${\rm SL}(n, {{\mathbb {R}}})$, the dimensional bound is sharp.

Keywords

lattice actionsZimmer's conjecturerigidity

MSC classification

Primary: 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 22E40: Discrete subgroups of Lie groups
Secondary: 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 3 , March 2022 , pp. 529 - 549
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Brown was supported by NSF No.1752675. Damjanović was supported by Swedish Research Council grant VR2015-04644. Zhang was supported by the National Science Foundation under Grant No. DMS-1638352.

References

Avila, A. and Viana, M., Extremal Lyapunov exponents: an invariance principle and applications, Invent. Math. 181 (2010), 115–189.10.1007/s00222-010-0243-1CrossRefGoogle Scholar
Brown, A., Fisher, D. and Hurtado, S., Zimmer's conjecture: Subexponential growth, measure rigidity, and strong property (T), Ann. of Math. (2), to appear. Preprint (2016), arXiv:1608.04995.Google Scholar
Brown, A., Fisher, D. and Hurtado, S., Zimmer's conjecture for actions of $\mathrm {SL}(m, \mathbb {Z})$, Invent. Math. 221 (2020), 1001–1060.10.1007/s00222-020-00962-xCrossRefGoogle Scholar
Brown, A., Fisher, D. and Hurtado, S., Zimmer's conjecture for non-uniform lattices and escape of mass, Preprint (2021), arXiv:2105.14541.Google Scholar
Brown, A., Rodriguez Hertz, F. and Wang, Z., Invariant measures and measurable projective factors for actions of higher-rank lattices on manifolds, Ann. of Math. (2), to appear. Preprint (2016), arXiv:1609.05565.Google Scholar
Brown, A., Rodriguez Hertz, F. and Wang, Z., Smooth ergodic theory of $\mathbb {Z}^ d$-actions, Preprint (2016), arXiv:1610.09997.Google Scholar
Burger, M. and Monod, N., Continuous bounded cohomology and applications to rigidity theory, Geom. Funct. Anal. 12 (2002), 219–280.10.1007/s00039-002-8245-9CrossRefGoogle Scholar
Cantat, S., Progrès récents concernant le programme de Zimmer [d'après A. Brown, D. Fisher, et S. Hurtado], in Séminaire Bourbaki, Vol. 2017–2018, Exposé 1136, Astérisque, vol. 414 (Société Mathmatique de France, 2019).Google Scholar
Cornfield, P., Fomin, S. V. and Sinai, Y. G., Ergodic theory, Grundlehren der Mathematischen Wissenschaften (Comprehensive Studies in Mathematics), vol. 245 (Springer, New York, NY, 1892).Google Scholar
de Laat, T. and de la Salle, M., Strong property (T) for higher-rank simple Lie groups, Proc. Lond. Math. Soc. (3) 111 (2015), 936–966.CrossRefGoogle Scholar
de la Salle, M., Strong property (T) for higher rank lattices, Acta Math. 223 (2019), 151–193.10.4310/ACTA.2019.v223.n1.a3CrossRefGoogle Scholar
Einsiedler, M. and Katok, A., Rigidity of measures: the high entropy case and non-commuting foliations: Probability in mathematics, Israel J. Math. 148 (2005), 169–238.10.1007/BF02775436CrossRefGoogle Scholar
Farb, B. and Shalen, P., Real-analytic actions of lattices, Invent. Math. 135 (1999), 273–296.10.1007/s002220050286CrossRefGoogle Scholar
Fisher, D., Groups acting on manifolds: around the Zimmer program, in Geometry, rigidity, and group actions, Chicago Lectures in Mathematics (The University of Chicago Press, Chicago, IL, 2011), 72–157.Google Scholar
Fisher, D., Recent progress in the Zimmer program, Preprint (2017), arXiv:1711.07089.Google Scholar
Fisher, D. and Margulis, G. A., Local rigidity for cocycles, in Lectures on geometry and topology held in honor of Calabi, Lawson, Siu, and Uhlenbeck, Surveys in Differential Geometry, vol. 8 (International Press, Somerville, MA, 2003), 191–234.Google Scholar
Franks, J. and Handel, M., Distortion elements in group actions on surfaces, Duke Math. J. 131 (2006), 441–468.CrossRefGoogle Scholar
Ghys, É., Actions de réseaux sur le cercle, Invent. Math. 137 (1999), 199–231.10.1007/s002220050329CrossRefGoogle Scholar
Hu, H., Some ergodic properties of commuting diffeomorphisms, Ergodic Theory Dynam. Systems 13 (1993), 73–100.10.1017/S0143385700007215CrossRefGoogle Scholar
Katok, A. and Rodriguez Hertz, F., Measure and cocycle rigidity for certain nonuniformly hyperbolic actions of higher-rank abelian groups, J. Mod. Dyn. 4 (2010), 487–515.CrossRefGoogle Scholar
Knapp, A. W., Lie groups beyond an introduction, Progress in Mathematics, vol. 140, second edition (Birkhauser, Boston, MA, 2002).Google Scholar
Lafforgue, V., Un renforcement de la propriété (T), Duke Math. J. 143 (2008), 559–602.10.1215/00127094-2008-029CrossRefGoogle Scholar
Ledrappier, F., Proprieites ergodiques des mesures de Sinai, Publ. Math. Inst. Hautes Études Sci. 59 (1984), 163–188.10.1007/BF02698772CrossRefGoogle Scholar
Ledrappier, F., Positivity of the exponent for stationary sequences of matrices, in Lyapunov exponents (Bremen, 1984), Lecture Notes in Mathematics, vol. 1186, (Springer, Berlin, 1986), 56–73.10.1007/BFb0076833CrossRefGoogle Scholar
Ledrappier, F. and Strelcyn, J.-M., A proof of the estimation from below in Pesin's entropy formula, Ergodic Theory Dynam. Systems 2 (1982), 203–219.10.1017/S0143385700001528CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S., The metric entropy of diffeomorphisms. I. Characterization of measures satisfying Pesin's entropy formula, Ann. of Math. (2) 122 (1985), 509–539.10.2307/1971328CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S., The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension, Ann. of Math. (2) 122 (1985), 540–574.10.2307/1971329CrossRefGoogle Scholar
Lifschitz, L. and Witte Morris, D., Bounded generation and lattices that cannot act on the line, Pure Appl. Math. Q. 4 (2008), 99–126.10.4310/PAMQ.2008.v4.n1.a4CrossRefGoogle Scholar
Lubotzky, A., Mozes, S. and Raghunathan, M. S., The word and Riemannian metrics on lattices of semisimple groups, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 5–53.CrossRefGoogle Scholar
Maleshich, Ĭ., The Hilbert-Smith conjecture for Hölder actions, Uspekhi Mat. Nauk 52 (1997), 173–174; MR 1480156 (99d:57026).Google Scholar
Mãné, R., A proof of Pesin's formula, Ergodic Theory Dynam. Systems 1 (1981), 95–102.CrossRefGoogle Scholar
Margulis, G. A., Discrete subgroups of semisimple Lie groups, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 17 (Springer, Berlin, 1991).10.1007/978-3-642-51445-6CrossRefGoogle Scholar
Margulis, G. A. and Tomanov, G. M., Invariant measures for actions of unipotent groups over local fields on homogeneous spaces, Invent. Math. 116 (1994), 347–392.CrossRefGoogle Scholar
Moore, C. C., Ergodicity of flows on homogeneous spaces, Amer. J. Math. 88 (1966), 154–178.CrossRefGoogle Scholar
Mostow, G. D., Strong rigidity of locally symmetric spaces, Annals of Mathematics Studies, vol. 78 (Princeton University Press, Princeton, NJ, 1973).Google Scholar
Newmann, M. H. A., A theorem on periodic transformations of spaces, Quart. J. Math. 2 (1931), 1–8.CrossRefGoogle Scholar
Polterovich, L., Growth of maps, distortion in groups and symplectic geometry, Invent. Math. 150 (2002), 655–686.CrossRefGoogle Scholar
Repovs̆, D. and S̆c̆epin, E. V., A proof of the Hilbert-Smith conjecture for actions by Lipschitz maps, Math. Ann. 308 (1997), 361–364.Google Scholar
Selberg, A., On discontinuous groups in higher-dimensional symmetric spaces, in Contributions to function theory, Internat. colloq. function theory, Bombay, 1960 (Tata Institute of Fundamental Research, Bombay, 1960), 147–164.Google Scholar
Smith, P. A., Transformations of finite period, III: Newman's theorem, Ann. of Math. (2) 42 (1941), 446–458.10.2307/1968910CrossRefGoogle Scholar
Stuck, G., Low dimensional actions of semisimple groups, Israel J. Math. 76 (1991), 27–71.10.1007/BF02782843CrossRefGoogle Scholar
Weil, A., On discrete subgroups of Lie groups. II, Ann. of Math. (2) 75 (1962), 578–602.10.2307/1970212CrossRefGoogle Scholar
Witte Morris, D., Arithmetic groups of higher Q-rank cannot act on 1-manifolds, Proc. Amer. Math. Soc. 122 (1994), 333–340.Google Scholar
Ye, S., Euler characteristics and actions of automorphism groups of free groups, Algebr. Geom. Topol. 18 (2018), 1195–1204.10.2140/agt.2018.18.1195CrossRefGoogle Scholar
Zimmer, R. J., Strong rigidity for ergodic actions of semisimple Lie groups, Ann. of Math. (2) 112 (1980), 511–529.CrossRefGoogle Scholar
Zimmer, R. J., Ergodic theory and semisimple groups (Birkhäuser, Basel, 1984); MR 0776417 (86j:22014).10.1007/978-1-4684-9488-4CrossRefGoogle Scholar
Zimmer, R. J. and Witte Morris, D., Ergodic theory, groups, and geometry, CBMS Regional Conference Series in Mathematics, vol. 109 (American Mathematical Society, Providence, RI, 2008).10.1090/cbms/109CrossRefGoogle Scholar