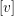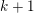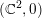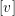Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hahn, David
and
Peters, Han
2021.
A polynomial automorphism with a wandering Fatou component.
Advances in Mathematics,
Vol. 382,
Issue. ,
p.
107650.
Astorg, Matthieu
Boc Thaler, Luka
and
Peters, Han
2023.
Wandering domains arising from Lavaurs maps with siegel disks.
Analysis & PDE,
Vol. 16,
Issue. 1,
p.
35.
Rong, Feng
2023.
A note on attracting domains for holomorphic maps in ℂ2 tangent to the identity.
International Journal of Mathematics,
Vol. 34,
Issue. 09,
Mongodi, Samuele
and
Ruggiero, Matteo
2023.
Birational properties of tangent to the identity germs without non‐degenerate singular directions.
Journal of the London Mathematical Society,
Vol. 107,
Issue. 4,
p.
1242.
LÓPEZ-HERNANZ, LORENA
and
ROSAS, RUDY
2025.
A flower theorem in dimension two.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 10,
p.
3223.