Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T07:35:45.709Z Has data issue: false hasContentIssue false
  • English
  • Français

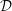Characters of equivariant ${\mathcal{D}}$ -modules on spaces of matrices

Part of: Special varieties Commutative algebra: Homological methods (Co)homology theory

Published online by Cambridge University Press:  28 June 2016

Claudiu Raicu
Claudiu Raicu*
Affiliation:
Department of Mathematics, University of Notre Dame, 255 Hurley, Notre Dame, IN 46556, USA email craicu@nd.edu Institute of Mathematics ‘Simion Stoilow’ of the Romanian Academy, Sector 1, 21 Calea Grivitei str., PO Box 1-764, Bucharest, Romania
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

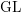We compute the characters of the simple $\text{GL}$ -equivariant holonomic 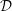${\mathcal{D}}$ -modules on the vector spaces of general, symmetric, and skew-symmetric matrices. We realize some of these 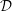${\mathcal{D}}$ -modules explicitly as subquotients in the pole order filtration associated to the 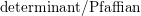$\text{determinant}/\text{Pfaffian}$ of a generic matrix, and others as local cohomology modules. We give a direct proof of a conjecture of Levasseur in the case of general and skew-symmetric matrices, and provide counterexamples in the case of symmetric matrices. The character calculations are used in subsequent work with Weyman to describe the 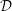${\mathcal{D}}$ -module composition factors of local cohomology modules with determinantal and Pfaffian support.

Keywords

equivariant D-modulesrank stratificationslocal cohomology

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 13D45: Local cohomology 14M12: Determinantal varieties
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 9 , September 2016 , pp. 1935 - 1965
Copyright
© The Author 2016 

References

Borel, A., Grivel, P.-P., Kaup, B., Haefliger, A., Malgrange, B. and Ehlers, F., AlgebraicD-modules, Perspectives in Mathematics, vol. 2 (Academic Press, Boston, MA, 1987); MR 882000 89g:32014).Google Scholar
Braden, T. and Grinberg, M., Perverse sheaves on rank stratifications , Duke Math. J. 96 (1999), 317–362, doi:10.1215/S0012-7094-99-09609-6; MR 1666554 (2000f:14031).Google Scholar
Coutinho, S. C. and Levcovitz, D., D-modules and étale morphisms , Comm. Algebra 29 (2001), 1487–1497, doi:10.1081/AGB-100002114; MR 1853107 (2002m:14014).CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry, available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977); MR 0463157 (57 #3116).CrossRefGoogle Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, Boston, MA, 2008); MR 2357361 (2008k:32022).CrossRefGoogle Scholar
Kashiwara, M., B-functions and holonomic systems. Rationality of roots of B-functions , Invent. Math. 38 (1976–1977), 33–53; MR 0430304 (55 #3309).Google Scholar
Kempf, G., The Grothendieck–Cousin complex of an induced representation , Adv. Math. 29 (1978), 310–396, doi:10.1016/0001-8708(78)90021-X; MR 509802 (80g:14042).CrossRefGoogle Scholar
Kimura, T., Introduction to prehomogeneous vector spaces, Translations of Mathematical Monographs, vol. 215 (American Mathematical Society, Providence, RI, 2003); MR 1944442 (2003k:11180).Google Scholar
Levasseur, T., Radial components, prehomogeneous vector spaces, and rational Cherednik algebras , Int. Math. Res. Not. IMRN 3 (2009), 462–511, doi:10.1093/imrn/rnn137; MR 2482122 (2010g:22028).Google Scholar
Macdonald, I. G., Symmetric functions and Hall polynomials, second edition, Oxford Mathematical Monographs (The Clarendon Press–Oxford University Press, New York, 1995), with contributions by A. Zelevinsky; MR 1354144 (96h:05207).Google Scholar
MacPherson, R. and Vilonen, K., Elementary construction of perverse sheaves , Invent. Math. 84 (1986), 403–435, doi:10.1007/BF01388812; MR 833195 (87m:32028).Google Scholar
Nang, P., On a class of holonomic D-modules on M n (ℂ) related to the action of GL n (ℂ) × GL n (ℂ) , Adv. Math. 218 (2008), 635–648, doi:10.1016/j.aim.2008.01.001; MR 2414315 (2009c:14028).Google Scholar
Nang, P., On the classification of regular holonomic D-modules on skew-symmetric matrices , J. Algebra 356 (2012), 115–132, doi:10.1016/j.jalgebra.2012.01.021; MR 2891125.Google Scholar
Raicu, C., Characters of equivariant ${\mathcal{D}}$ -modules on Veronese cones, Trans. Amer. Math. Soc. (2016), doi:10.1090/tran/6713.Google Scholar
Raicu, C. and Weyman, J., Local cohomology with support in generic determinantal ideals , Algebra Number Theory 8 (2014), 1231–1257, doi:10.2140/ant.2014.8.1231; MR 3263142.CrossRefGoogle Scholar
Raicu, C. and Weyman, J., Local cohomology with support in ideals of symmetric minors and Pfaffians, J. Lond. Math. Soc. (2), to appear. Preprint (2015), arXiv:1509.03954.Google Scholar
Raicu, C., Weyman, J. and Witt, E. E., Local cohomology with support in ideals of maximal minors and sub-maximal Pfaffians , Adv. Math. 250 (2014), 596–610, doi:10.1016/j.aim.2013.10.005; MR 3122178.Google Scholar
Saito, M., ${\mathcal{D}}$ -modules generated by rational powers of holomorphic functions, Preprint (2015), arXiv:1507.01877.Google Scholar
Van den Bergh, M., Local cohomology of modules of covariants , Adv. Math. 144 (1999), 161–220, doi:10.1006/aima.1998.1809; MR 1695237 (2000d:14051).CrossRefGoogle Scholar
Vilonen, K., Intersection homology D-module on local complete intersections with isolated singularities , Invent. Math. 81 (1985), 107–114, doi:10.1007/BF01388774; MR 796193 (87f:32023).Google Scholar
Walther, U., Survey on the D-module f s , in Commutative algebra and noncommutative algebraic geometry, Vol. 1, Mathematical Sciences Research Institute Publications, vol. 67 (Cambridge University Presss, Cambridge, 2015), 391–430, with an appendix by A. Leykin.Google Scholar
Weyman, J., Cohomology of vector bundles and syzygies, Cambridge Tracts in Mathematics, vol. 149 (Cambridge University Press, Cambridge, 2003); MR 1988690 (2004d:13020).Google Scholar