Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:08:26.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of algebraic solutions of irregular Garnier systems

Part of: Differential equations in the complex domain

Published online by Cambridge University Press:  14 April 2020

Karamoko Diarra  and
Frank Loray
Karamoko Diarra
Affiliation:
DER de Mathématiques et d’Informatique, FAST, Université des Sciences, des Techniques et des Technologies de Bamako, BP: E 3206, Mali email karamoko.diarra@gmail.com
Frank Loray
Affiliation:
Univ Rennes, CNRS, IRMAR – UMR 6625, F-35000 Rennes, France email frank.loray@univ-rennes1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that algebraic solutions of Garnier systems in the irregular case are of two types. The classical ones come from isomonodromic deformations of linear equations with diagonal or dihedral differential Galois group; we give a complete list in the rank-2 case (two indeterminates). The pull-back ones come from deformations of coverings over a fixed degenerate hypergeometric equation; we provide a complete list when the differential Galois group is 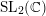$\text{SL}_{2}(\mathbb{C})$. As a byproduct, we obtain a complete list of algebraic solutions for the rank-2 irregular Garnier systems.

Keywords

ordinary differential equationsisomonodromic deformationsHurwitz spaces

MSC classification

Primary: 34M55: Painlevé and other special equations; classification, hierarchies; 34M56: Isomonodromic deformations 34M03: Linear equations and systems
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 5 , May 2020 , pp. 881 - 907
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank CNRS, Université de Rennes 1, Henri Lebesgue Center and ANR-16-CE40-0008 project ‘Foliage’ for financial support. We also thank the Simons Foundation’s project NLAGA which invited the two of us to Dakar, where we started working on this subject. We finally thank Hiroyuki Kawamuko and Yousuke Ohyama for helpful discussions on the subject.

References

Allegretti, D. G. L. and Bridgeland, T., The monodromy of meromorphic projective structures, Preprint (2018), arXiv:1802.02505.Google Scholar
Andreev, F. V. and Kitaev, A. V., Transformations RS 42(3) of the ranks ⩽4 and algebraic solutions of the sixth Painlevé equation, Comm. Math. Phys. 228 (2002), 151–176.CrossRefGoogle Scholar
Andreev, F. V. and Kitaev, A. V., Some examples of RS 32(3)-transformations of ranks 5 and 6 as the higher order transformations for the hypergeometric function, Ramanujan J. 7 (2003), 455–476.CrossRefGoogle Scholar
Boalch, P., The fifty-two icosahedral solutions to Painlevé VI, J. Reine Angew. Math. 596 (2006), 183–214.Google Scholar
Boalch, P., Six results on Painlevé VI, in Théories asymptotiques et équations de Painlevé, Séminaires et Congrès, vol. 14 (Société Mathématique de France, Paris, 2006), 1–20.Google Scholar
Boalch, P., Some explicit solutions to the Riemann–Hilbert problem, in Differential equations and quantum groups, IRMA Lectures in Mathematics and Theoretical Physics, vol. 9 (European Mathematical Society, Zürich, 2007), 85–112.Google Scholar
Boalch, P., Higher genus icosahedral Painlevé curves, Funkcial. Ekvac. 50 (2007), 19–32.CrossRefGoogle Scholar
Boalch, P., Towards a non-linear Schwarz’s list, in The many facets of geometry (Oxford University Press, Oxford, 2010), 210–236.CrossRefGoogle Scholar
Boalch, P., Simply-laced isomonodromy systems, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 1–68.CrossRefGoogle Scholar
Boalch, P., Geometry and braiding of Stokes data; fission and wild character varieties, Ann. of Math. (2) 179 (2014), 301–365.CrossRefGoogle Scholar
Bolibruch, A. A., Malek, S. and Mitschi, C., On the generalized Riemann–Hilbert problem with irregular singularities, Expo. Math. 24 (2006), 235–272.CrossRefGoogle Scholar
Calligaris, P. and Mazzocco, M., Finite orbits of the pure braid group on the monodromy of the 2-variable Garnier system, J. Integrable Syst. 3 (2018), xyy005.Google Scholar
Cantat, S. and Loray, F., Dynamics on character varieties and Malgrange irreducibility of Painlevé VI equation, Ann. Inst. Fourier (Grenoble) 59 (2009), 2927–2978.CrossRefGoogle Scholar
Chekhov, L. and Mazzocco, M., Colliding holes in Riemann surfaces and quantum cluster algebras, Nonlinearity 31 (2018), 54–107.CrossRefGoogle Scholar
Chekhov, L., Mazzocco, M. and Rubtsov, V. N., Painlevé monodromy manifolds, decorated character varieties, and cluster algebras, Int. Math. Res. Not. IMRN 2017 (2017), 7639–7691.Google Scholar
Corlette, K. and Simpson, C., On the classification of rank-two representations of quasiprojective fundamental groups, Compos. Math. 144 (2008), 1271–1331.CrossRefGoogle Scholar
Cousin, G., Un exemple de feuilletage modulaire déduit d’une solution algébrique de l’équation de Painlevé VI, Ann. Inst. Fourier (Grenoble) 64 (2014), 699–737.CrossRefGoogle Scholar
Cousin, G., Algebraic isomonodromic deformations of logarithmic connections on the Riemann sphere and finite braid group orbits on character varieties, Math. Ann. 367 (2017), 965–1005.CrossRefGoogle Scholar
Cousin, G. and Heu, V., Algebraic isomonodromic deformations and the mapping class group, J. Inst. Math. Jussieu, to appear. Preprint (2016), arXiv:1612.05779.Google Scholar
Cousin, G. and Moussard, D., Finite braid group orbits in Aff(ℂ)-character varieties of the punctured sphere, Int. Math. Res. Not. IMRN 2018 (2018), 3388–3442.CrossRefGoogle Scholar
Diarra, K., Construction et classification de certaines solutions algébriques des systèmes de Garnier, Bull. Braz. Math. Soc. 44 (2013), 129–154.CrossRefGoogle Scholar
Diarra, K. and Loray, F., Classification of algebraic solutions of irregular Garnier systems, Preprint (2018), arXiv:1808.09190.Google Scholar
Doran, C. F., Algebraic and geometric isomonodromic deformations, J. Differential Geom. 59 (2001), 33–85.CrossRefGoogle Scholar
Dubrovin, B., Geometry of 2D topological field theories, in Integrable systems and quantum groups, Lecture Notes in Mathematics, vol. 1620 (Springer, 1995), 120–348.Google Scholar
Dubrovin, B. and Mazzocco, M., Monodromy of certain Painlevé-VI transcendents and reflection groups, Invent. Math. 141 (2000), 55–147.CrossRefGoogle Scholar
Dubrovin, B. and Mazzocco, M., Canonical structure and symmetries of the Schlesinger equations, Comm. Math. Phys. 271 (2007), 289–373.CrossRefGoogle Scholar
Fuchs, R., Über Lineare Homogene Differentialgleichungen Zweiter Ordnung mit drei im Endlichen gelegenen wesentlichen singulären Stellen, Math. Ann. 63 (1907), 301–321.CrossRefGoogle Scholar
Garnier, R., Sur des équations différentielles du troisième ordre dont l’intégrale générale est uniforme et sur une classe d’équations nouvelles d’ordre supérieur dont l’intégrale générale a ses points critiques fixes, Ann. Sci. Éc. Norm. Supér. 3 (1912), 1–126.Google Scholar
Girand, A., A new two-parameter family of isomonodromic deformations over the five punctured sphere, Bull. Soc. Math. France 144 (2016), 339–368.CrossRefGoogle Scholar
Heu, V., Universal isomonodromic deformations of meromorphic rank 2 connections on curves, Ann. Inst. Fourier (Grenoble) 60 (2010), 515–549.CrossRefGoogle Scholar
Hitchin, N. J., Twistor spaces, Einstein metrics and isomonodromic deformations, J. Differential Geom. 42 (1995), 30–112.CrossRefGoogle Scholar
Hitchin, N. J., Poncelet polygons and the Painlevé equations, in Geometry and analysis (Bombay, 1992) (Tata Institute of Fundamental Research, Bombay, 1995), 151–185.Google Scholar
Inaba, M., Moduli space of irregular singular parabolic connections of generic ramified type on a smooth projective curve, Preprint (2016), arXiv:1606.02369.Google Scholar
Inaba, M., Iwasaki, K. and Saito, M.-H., Dynamics of the sixth Painlevé equation, in Théories asymptotiques et équations de Painlevé, Séminaires et Congrès, vol. 14 (Société Mathématique de France, Paris, 2006), 103–167.Google Scholar
Inaba, M. and Saito, M.-H., Moduli of unramified irregular singular parabolic connections on a smooth projective curve, Kyoto J. Math. 53 (2013), 433–482.CrossRefGoogle Scholar
Jimbo, M., Miwa, T. and Ueno, K., Monodromy preserving deformation of linear ordinary differential equations with rational coefficients. I. General theory and 𝜏-function, Physica D 2 (1981), 306–352.Google Scholar
Kato, M., Mano, T. and Sekiguchi, J., Flat structure and potential vector fields related with algebraic solutions to Painlevé VI equation, Opuscula Math. 38 (2018), 201–252.CrossRefGoogle Scholar
Kawamuko, H., Rational solutions of the fourth Painlevé equation in two variables, Funkcial. Ekvac. 46 (2003), 1–21.CrossRefGoogle Scholar
Kawamuko, H., On the Garnier system of half-integer type in two variables, Funkcial. Ekvac. 52 (2009), 181–201.CrossRefGoogle Scholar
Kawamuko, H., On algebraic solutions of G (3, 2) and G (5/2, 1, 1), in Exact WKB analysis and microlocal analysis, RIMS Kôkyûroku Bessatsu, vol. B37 (Research Institute of Mathematical Sciences (RIMS), Kyoto, 2013), 99–111.Google Scholar
Kimura, H., The degeneration of the two-dimensional Garnier system and the polynomial Hamiltonian structure, Ann. Mat. Pura Appl. 155 (1989), 25–74.CrossRefGoogle Scholar
Kitaev, A. V., Special functions of isomonodromy type, rational transformations of the spectral parameter, and algebraic solutions of the sixth Painlevé equation, St. Petersburg Math. J. 14 (2003), 453–465.Google Scholar
Kitaev, A. V., Quadratic transformations for the third and fifth Painlevé equations, J. Math. Sci. (N. Y.) 136 (2006), 3586–3595.CrossRefGoogle Scholar
Kitaev, A. V., Grothendieck’s dessins d’enfants, their deformations, and algebraic solutions of the sixth Painlevé and Gauss hypergeometric equations, St. Petersburg Math. J. 17 (2006), 169–206.CrossRefGoogle Scholar
Kitaev, A. V., Remarks towards a classification of RS 42(3)-transformations and algebraic solutions of the sixth Painlevé equation, in Théories asymptotiques et équations de Painlevé, Séminaires et Congrès, vol. 14 (Société Mathématique de France, Paris, 2006), 199–227.Google Scholar
Klimes, M., The wild monodromy of the Painlevé V equation and its action on the wild character variety: an approach of confluence, Preprint (2016), arXiv:1609.05185.Google Scholar
Komyo, A., A family of flat connections on the projective space having dihedral monodromy and algebraic Garnier solutions, Ann. Fac. Sci. Toulouse Math., to appear. Preprint (2018), arXiv:1806.00970.Google Scholar
Krichever, I. M., Isomonodromy equations on algebraic curves, canonical transformations and Whitham equations, Mosc. Math. J. 2 (2002), 717–752.CrossRefGoogle Scholar
Lins Neto, A., Some examples for the Poincaré and Painlevé problems, Ann. Sci. Éc. Norm. Supér. 35 (2002), 231–266.CrossRefGoogle Scholar
Lisovyy, O. and Tykhyy, Y., Algebraic solutions of the sixth Painlevé equation, J. Geom. Phys. 85 (2014), 124–163.CrossRefGoogle Scholar
Loray, F., Pereira, J. V. and Touzet, F., Representations of quasiprojective groups, flat connections and transversely projective foliations, J. Éc. Polytech. Math. 3 (2016), 263–308.CrossRefGoogle Scholar
Loray, F., van der Put, M. and Ulmer, F., The Lamé family of connections on the projective line, Ann. Fac. Sci. Toulouse Math. 17 (2008), 371–409.CrossRefGoogle Scholar
Malgrange, B., Sur les déformations isomonodromiques. I. Singularités régulières. II. Singularités irrégulières, Progress in Mathematics, vol. 37 (Birkhäuser, Boston, MA, 1983), 401–438.Google Scholar
Martinet, J. and Ramis, J.-P., Théorie de Galois différentielle et resommation, in Computer algebra and differential equations, Computers & Mathematics with Applications (Academic Press, London, 1990), 117–214.Google Scholar
Mazzocco, M., Rational solutions of the Painlevé VI equation, J. Phys. A 34 (2001), 2281–2294.CrossRefGoogle Scholar
Mazzocco, M., Picard and Chazy solutions to the Painlevé VI equation, Math. Ann. 321 (2001), 157–195.CrossRefGoogle Scholar
Ohyama, Y. and Okumura, S., R. Fuchs’ problem of the Painlevé equations from the first to the fifth, in Algebraic and geometric aspects of integrable systems and random matrices, Contemporary Mathematics, vol. 593 (American Mathematical Society, Providence, RI, 2013), 163–178.Google Scholar
Okamoto, K., Studies on the Painlevé equations. I. Sixth Painlevé equation PVI, Ann. Mat. Pura Appl. 146 (1987), 337–381.CrossRefGoogle Scholar
Paul, E. and Ramis, J.-P., Dynamics on wild character varieties, SIGMA Symmetry Integrability Geom. Methods Appl. 11 (2015), Paper 068.Google Scholar
Suzuki, T., Classical solutions of the degenerate Garnier system and their coalescence structures, J. Phys. A 39 (2006), 12103–12113.CrossRefGoogle Scholar
Umemura, H., Irreducibility of the first differential equation of Painlevé, Nagoya Math. J. 117 (1990), 231–252.Google Scholar
van der Put, M. and Saito, M.-H., Moduli spaces for linear differential equations and the Painlevé equations, Ann. Inst. Fourier (Grenoble) 59 (2009), 2611–2667.CrossRefGoogle Scholar
Vidunas, R. and Kitaev, A. V., Quadratic transformations of the sixth Painlevé equation with application to algebraic solutions, Math. Nachr. 280 (2007), 1834–1855.CrossRefGoogle Scholar
Vidunas, R. and Kitaev, A. V., Computation of highly ramified coverings, Math. Comp. 78 (2009), 2371–2395.CrossRefGoogle Scholar
Watanabe, H., Birational canonical transformations and classical solutions of the sixth Painlevé equation, Ann. Sc. Norm. Super. Pisa Cl. Sci. 27 (1998), 379–425.Google Scholar