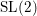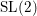Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kerr, Matt
and
Robles, Colleen
2017.
Variations of Hodge structure and orbits in flag varieties.
Advances in Mathematics,
Vol. 315,
Issue. ,
p.
27.
Robles, Colleen
2017.
Surveys on Recent Developments in Algebraic Geometry.
Vol. 95,
Issue. ,
p.
267.
Han, Xiayimei
Robles, Colleen
and
Clingher, Adrian
2020.
Hodge Representations.
Experimental Results,
Vol. 1,
Issue. ,
Grimm, Thomas W.
2021.
Moduli space holography and the finiteness of flux vacua.
Journal of High Energy Physics,
Vol. 2021,
Issue. 10,
Bönisch, Kilian
Duhr, Claude
Fischbach, Fabian
Klemm, Albrecht
and
Nega, Christoph
2022.
Feynman integrals in dimensional regularization and extensions of Calabi-Yau motives.
Journal of High Energy Physics,
Vol. 2022,
Issue. 9,
Grimm, Thomas W.
Monnee, Jeroen
and
van de Heisteeg, Damian
2022.
Bulk reconstruction in moduli space holography.
Journal of High Energy Physics,
Vol. 2022,
Issue. 5,
Grimm, Thomas W.
and
Monnee, Jeroen
2023.
Bi-Yang-Baxter models and Sl(2)-orbits.
Journal of High Energy Physics,
Vol. 2023,
Issue. 11,
Grimm, Thomas W.
and
Monnee, Jeroen
2024.
Finiteness theorems and counting conjectures for the flux landscape.
Journal of High Energy Physics,
Vol. 2024,
Issue. 8,
Bastian, Brice
Grimm, Thomas W.
and
van de Heisteeg, Damian
2025.
Modeling General Asymptotic Calabi–Yau Periods.
Fortschritte der Physik,
Vol. 73,
Issue. 7,