Article contents
Classification of irreversible and reversible Pimsner operator algebras
Published online by Cambridge University Press: 13 January 2021
Abstract
Since their inception in the 1930s by von Neumann, operator algebras have been used to shed light on many mathematical theories. Classification results for self-adjoint and non-self-adjoint operator algebras manifest this approach, but a clear connection between the two has been sought since their emergence in the late 1960s. We connect these seemingly separate types of results by uncovering a hierarchy of classification for non-self-adjoint operator algebras and 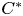 $C^{*}$-algebras with additional
$C^{*}$-algebras with additional 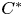 $C^{*}$-algebraic structure. Our approach naturally applies to algebras arising from
$C^{*}$-algebraic structure. Our approach naturally applies to algebras arising from 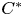 $C^{*}$-correspondences to resolve self-adjoint and non-self-adjoint isomorphism problems in the literature. We apply our strategy to completely elucidate this newly found hierarchy for operator algebras arising from directed graphs.
$C^{*}$-correspondences to resolve self-adjoint and non-self-adjoint isomorphism problems in the literature. We apply our strategy to completely elucidate this newly found hierarchy for operator algebras arising from directed graphs.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
Footnotes
The first author was supported by NSF grant DMS-1900916 and by the European Union's Horizon 2020 Marie Sklodowska-Curie grant No 839412. The second author was supported by the DFF-Research Project 2 ‘Automorphisms and Invariants of Operator Algebras’, no. 7014-00145B, and by the DNRF through the Centre for Symmetry and Deformation (DNRF92). The third author was supported by a Negev fellowship, a Minerva fellowship programme, an ISF grant no. 476/16 and the DFG through SFB 878 and EXC 2044 Mathematics Münster: Dynamics–Geometry–Structure.
References
- 6
- Cited by


