Article contents
Composite quasianalytic functions
Published online by Cambridge University Press: 17 August 2018
Abstract
We prove two main results on Denjoy–Carleman classes: (1) a composite function theorem which asserts that a function 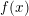 $f(x)$ in a quasianalytic Denjoy–Carleman class
$f(x)$ in a quasianalytic Denjoy–Carleman class 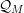 ${\mathcal{Q}}_{M}$, which is formally composite with a generically submersive mapping
${\mathcal{Q}}_{M}$, which is formally composite with a generically submersive mapping 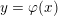 $y=\unicode[STIX]{x1D711}(x)$ of class
$y=\unicode[STIX]{x1D711}(x)$ of class 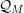 ${\mathcal{Q}}_{M}$, at a single given point in the source (or in the target) of
${\mathcal{Q}}_{M}$, at a single given point in the source (or in the target) of 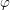 $\unicode[STIX]{x1D711}$ can be written locally as
$\unicode[STIX]{x1D711}$ can be written locally as 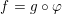 $f=g\circ \unicode[STIX]{x1D711}$, where
$f=g\circ \unicode[STIX]{x1D711}$, where 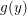 $g(y)$ belongs to a shifted Denjoy–Carleman class
$g(y)$ belongs to a shifted Denjoy–Carleman class 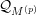 ${\mathcal{Q}}_{M^{(p)}}$; (2) a statement on a similar loss of regularity for functions definable in the
${\mathcal{Q}}_{M^{(p)}}$; (2) a statement on a similar loss of regularity for functions definable in the  $o$-minimal structure given by expansion of the real field by restricted functions of quasianalytic class
$o$-minimal structure given by expansion of the real field by restricted functions of quasianalytic class 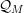 ${\mathcal{Q}}_{M}$. Both results depend on an estimate for the regularity of a
${\mathcal{Q}}_{M}$. Both results depend on an estimate for the regularity of a 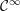 ${\mathcal{C}}^{\infty }$ solution
${\mathcal{C}}^{\infty }$ solution 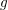 $g$ of the equation
$g$ of the equation 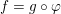 $f=g\circ \unicode[STIX]{x1D711}$, with
$f=g\circ \unicode[STIX]{x1D711}$, with 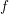 $f$ and
$f$ and 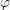 $\unicode[STIX]{x1D711}$ as above. The composite function result depends also on a quasianalytic continuation theorem, which shows that the formal assumption at a given point in (1) propagates to a formal composition condition at every point in a neighbourhood.
$\unicode[STIX]{x1D711}$ as above. The composite function result depends also on a quasianalytic continuation theorem, which shows that the formal assumption at a given point in (1) propagates to a formal composition condition at every point in a neighbourhood.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 2
- Cited by

