Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T05:05:41.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructibilité et modération uniformes en cohomologie étale

Part of: Number theory: Connections with logic Singularities (Co)homology theory Birational geometry

Published online by Cambridge University Press:  19 March 2019

Fabrice Orgogozo Open the ORCID record for Fabrice Orgogozo [Opens in a new window]
Fabrice Orgogozo*
Affiliation:
CMLS, École polytechnique, CNRS, Université Paris-Saclay, 91128 Palaiseau Cedex, France email Fabrice.Orgogozo+math@normalesup.org
Get access Rights & Permissions [Opens in a new window]

Abstract

Soient 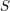$S$ un schéma nœthérien et 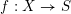$f:X\rightarrow S$ un morphisme propre. D’après SGA 4 XIV, pour tout faisceau constructible 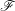$\mathscr{F}$ de 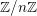$\mathbb{Z}/n\mathbb{Z}$-modules sur 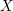$X$, les faisceaux de 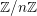$\mathbb{Z}/n\mathbb{Z}$-modules 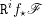$\mathtt{R}^{i}f_{\star }\mathscr{F}$, obtenus par image directe (pour la topologie étale), sont également constructibles : il existe une stratification 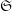$\mathfrak{S}$ de 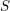$S$ telle que ces faisceaux soient localement constants constructibles sur les strates. À la suite de travaux de N. Katz et G. Laumon, ou L. Illusie, dans le cas particulier où 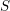$S$ est génériquement de caractéristique nulle ou bien les faisceaux 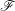$\mathscr{F}$ sont constants (de torsion inversible sur 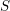$S$), on étudie ici la dépendance de 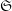$\mathfrak{S}$ en 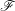$\mathscr{F}$. On montre qu’une condition naturelle de constructibilité et modération « uniforme » satisfaite par les faisceaux constants, introduite par O. Gabber, est stable par les foncteurs 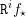$\mathtt{R}^{i}f_{\star }$. Si 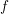$f$ n’est pas supposé propre, ce résultat subsiste sous réserve de modération à l’infini, relativement à 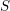$S$. On démontre aussi l’existence de bornes uniformes sur les nombres de Betti, qui s’appliquent notamment pour les fibres des faisceaux 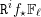$\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, où 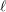$\ell$ parcourt les nombres premiers inversibles sur 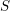$S$.

Let 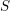$S$ be a Noetherian scheme and 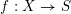$f:X\rightarrow S$ a proper morphism. By SGA 4 XIV, for any constructible sheaf 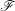$\mathscr{F}$ of 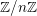$\mathbb{Z}/n\mathbb{Z}$-modules on 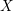$X$, the sheaves of 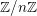$\mathbb{Z}/n\mathbb{Z}$-modules 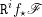$\mathtt{R}^{i}f_{\star }\mathscr{F}$ obtained by direct image (for the étale topology) are themselves constructible, that is, there is a stratification 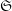$\mathfrak{S}$ of 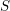$S$ on whose strata these sheaves are locally constant constructible. After previous work of N. Katz and G. Laumon, or L. Illusie, on the special case in which 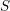$S$ is generically of characteristic zero or the sheaves 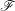$\mathscr{F}$ are constant (with invertible torsion on 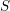$S$), here we study the dependency of 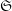$\mathfrak{S}$ on 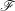$\mathscr{F}$. We show that a natural ‘uniform’ tameness and constructibility condition satisfied by constant sheaves, which was introduced by O. Gabber, is stable under the functors 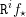$\mathtt{R}^{i}f_{\star }$. If 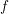$f$ is not proper, this result still holds assuming tameness at infinity, relative to 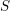$S$. We also prove the existence of uniform bounds on Betti numbers, in particular for the stalks of the sheaves 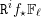$\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, where 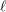$\ell$ ranges through all prime numbers invertible on 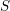$S$.

Keywords

étale cohomologyconstructible sheafstratificationtamenesscohomological descentalterationultraproduct

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies
Secondary: 14E22: Ramification problems 32S60: Stratifications; constructible sheaves; intersection cohomology 14E15: Global theory and resolution of singularities 11U07: Ultraproducts
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 4 , April 2019 , pp. 711 - 757
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Sigles

Éléments de mathématique

N. Bourbaki, Éléments de mathématique. Algèbre. Ch. 1–3 (1970), Ch. 4–7 (1981), Ch. 8 (2012), Ch. 9 (1959), Ch. 10 (1980) (Springer, 1959–2012).Google Scholar
N. Bourbaki, Éléments de mathématique. Topologie générale. Ch. 1–4 (1971), Ch. 5–10 (1974) (Springer, 1971–1974).Google Scholar

Éléments de géométrie algébrique

A. Grothendieck, Éléments de géométrie algébrique. I. Le langage des schémas, Grundlehren der mathematischen Wissenschaften, vol. 166, edited in collaboration with J. Dieudonné (Springer, 1971).Google Scholar
A. Grothendieck, Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes, Publications mathématiques de l’IHÉS 8 (1961), 5–222. Edited in collaboration with J. Dieudonné.10.1007/BF02699291Google Scholar

Séminaires de géométrie algébrique

Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1). Séminaire de géométrie algébrique du Bois-Marie, 1960–1961 , in Documents mathématiques, vol. 3 (Société Mathématique de France, 2003). Updated and annotated reprint of Lecture Notes in Mathematics, vol. 224 (Springer, 1971).Google Scholar
M. Raynaud, Propreté cohomologique des faisceaux d’ensembles et des faisceaux en groupes non commutatifs, in SGA 1.Google Scholar
A. Grothendieck, M. Artin and J.-L. Verdier, Théorie des topos et cohomologie étale des schémas (SGA 4). Séminaire de géométrie algébrique du Bois-Marie, 1963–1964, Lecture Notes in Mathematics, vols 269, 270, 305 (Springer, 1972–1973).Google Scholar
M. Artin, Faisceaux constructibles. Cohomologie d’une courbe algébrique, in SGA 4.Google Scholar
B. Saint-Donat, Technique de descente cohomologique, in SGA 4.Google Scholar
A. Grothendieck, Foncteurs fibres, supports, étude cohomologique des morphismes finis, in SGA 4.Google Scholar
M. Artin, Comparaison avec la cohomologique classique: cas d’un schéma lisse, in SGA 4.Google Scholar
M. Artin, Théorème de finitude pour un morphisme propre; dimension cohomologique des schémas algébriques affines, in SGA 4.Google Scholar
M. Artin, Théorème de changement de base par un morphisme lisse, et applications, in SGA 4.Google Scholar
P. Deligne, Cohomologie étale (SGA 4½). Séminaire de Géométrie Algébrique du Bois-Marie, Lecture Notes in Mathematics, vol. 569, in collaboration with J.-F. Boutot, A. Grothendieck, L. Illusie and J.-L. Verdier (Springer, 1977).Google Scholar
P. Deligne, Théorèmes de finitude en cohomologie $\ell$ -adique, in SGA 4½.Google Scholar
L. Illusie, Appendix to [Th. finitude].Google Scholar
A. Grothendieck, Cohomologie  $\ell$ -adique et fonctions L (SGA 5), Séminaire de géometrie algébrique du Bois-Marie, 1965–1966, Lecture Notes in Mathematics, vol. 589 (Springer, 1977).Google Scholar
L. Illusie, Complexes dualisants, in SGA 5.Google Scholar
J.-P. Jouanolou, Cohomologie  $\ell$ -adique, in SGA 5.Google Scholar
A. Grothendieck, Formule d’Euler-Poincaré en cohomologie étale, in SGA 5.Google Scholar
A. Grothendieck, P. Deligne and N. M. Katz, Groupes de monodromie en géométrie algébrique (SGA 7), Séminaire de géométrie algébrique du Bois-Marie, 1967–1969, Lecture Notes in Mathematics, vols 288, 340 in collaboration with M. Raynaud and D. S. Rim (Springer, 1972).Google Scholar
P. Deligne, Résumé des premiers exposés de A. Grothendieck, in SGA 7.Google Scholar
P. Deligne, Le formalisme des cycles évanescents, in SGA 7.Google Scholar

Séminaire sur les travaux de Gabber

L. Illusie, Y. Laszlo and F. Orgogozo, Travaux de Gabber sur l’uni-formisation locale et la cohomologie étale des schémas quasi-excellents. Séminaire à l’École polytechnique 2006–2008, Astérisque vol. 363–364, in collaboration with F. Déglise, A. Moreau, V. Pilloni, M. Raynaud, J. Riou, B. Stroh, M. Temkin and W. Zheng (Société Mathématique de France, 2014).Google Scholar
F. Orgogozo, Topologies adaptées à l’uniformisation locale, in STG.Google Scholar
L. Illusie, Log régularité, actions très modérées, in STG.Google Scholar
F. Orgogozo, Démonstration du théorème d’uniformisation locale (faible), in STG.Google Scholar
F. Orgogozo, Descente cohomologique orientée, in STG.Google Scholar
W. Zheng, On hyper base change, in STG.Google Scholar
F. Orgogozo, Le théorème de finitude, in STG.Google Scholar
V. Pilloni and B. Stroh, Théorème de Lefschetz affine, in STG.Google Scholar
J. Riou, Classes de Chern, morphismes de Gysin, pureté absolue, in STG.Google Scholar
J. Riou, Dualité, in STG.Google Scholar
Illusie, L., Cohomological dimension: first results, in STG.Google Scholar

Autres références

Artin, E., Geometric algebra (Interscience Publishers, 1957).Google Scholar
Beilinson, A. A., Bernstein, J., Deligne, P. and Gabber, O., Faisceaux pervers , in Astérisque, vol. 100, Analyse et topologie sur les espaces singuliers I (Société Mathématique de France, 1982).Google Scholar
Berthelot, P., Altérations de variétés algébriques (d’après A. J. de Jong) , in Séminaire Bourbaki, Astérisque, vol. 241, (1997), 273–311; exp. no 815.Google Scholar
Bhargava, M. and Satriano, M., On a notion of ‘Galois closure’ for extensions of rings , J. Eur. Math. Soc. (JEMS) 16 (2014), 1881–1913.10.4171/JEMS/478Google Scholar
Böckle, G., Gajda, W. and Petersen, S., Independence of ℓ-adic representations of geometric Galois groups , J. Reine Angew. Math. 736 (2018), 69–93.10.1515/crelle-2015-0024Google Scholar
Borel, A. and collaborators, Intersection cohomology, Progress in Mathematics, vol. 50 (Birkhäuser, Boston, 1984).10.1007/978-0-8176-4765-0Google Scholar
Brünjes, L. and Serpé, C., Etale and motivic cohomology and ultraproducts of schemes, Preprint (2008), arXiv:0807.1007.Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations , Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.10.1007/BF02698644Google Scholar
de Jong, A. J., Families of curves and alterations , Ann. Inst. Fourier 47 (1997), 599–621.10.5802/aif.1575Google Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L , in Modular functions of one variable, II (Anvers, 1972), Lecture Notes in Mathematics, vol. 349 (Springer, 1973), 501–597.10.1007/978-3-540-37855-6_7Google Scholar
Deligne, P., La conjecture de Weil. I , Publ. Math. Inst. Hautes Études Sci. 43 (1974a), 273–307.10.1007/BF02684373Google Scholar
Deligne, P., Théorie de Hodge. III , Publ. Math. Inst. Hautes Études Sci. 44 (1974b), 5–77.10.1007/BF02685881Google Scholar
Deligne, P., La conjecture de Weil. II , Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.10.1007/BF02684780Google Scholar
Fouvry, É. and Katz, N. M., A general stratification theorem for exponential sums, and applications , J. Reine Angew. Math. 540 (2001), 115–166.Google Scholar
Gabber, O., Sur la torsion dans la cohomologie ℓ-adique d’une variété , C. R. Acad. Sci. Paris Sér. I Math. 297 (1983), 179–182.Google Scholar
Gabber, O. and Loeser, F., Faisceaux pervers ℓ-adiques sur un tore , Duke Math. J. 83 (1996), 501–606.10.1215/S0012-7094-96-08317-9Google Scholar
Gabber, O. and Ramero, L., Foundations for almost ring theory, Preprint (2016),arXiv:math/0409584v11.Google Scholar
Gillet, H. and Soulé, C., Motivic weight complexes for arithmetic varieties , J. Algebra 322 (2009), 3088–3141.Google Scholar
Igusa, J., Fibre systems of Jacobian varieties. III. Fibre systems of elliptic curves , Amer. J. Math. 81 (1959), 453–476.10.2307/2372751Google Scholar
Illusie, L., Théorie de Brauer et caractéristique d’Euler-Poincaré (d’après P. Deligne), Astérisque, vol. 82 (Société Mathématique de France, 1981), 161–172.Google Scholar
Illusie, L., An overview of the work of K. Fujiwara, K. Kato, and C. Nakayama on logarithmic étale cohomology, Astérisque, vol. 279 (Société Mathématique de France, 2002), 271–322.Google Scholar
Illusie, L., On semistable reduction and the calculation of nearby cycles, Geometric aspects of Dwork theory, vol. II (de Gruyter, 2004), 785–803.Google Scholar
Illusie, L., Constructibilité générique et uniformité en $\ell$ , Preprint (2010), unpublished.Google Scholar
Kato, F., Log smooth deformation and moduli of log smooth curves , Internat. J. Math. 11 (2000), 215–232.10.1142/S0129167X0000012XGoogle Scholar
Kato, K., Toric singularities , Amer. J. Math. 116 (1994), 1073–1099.Google Scholar
Kato, K. and Saito, T., Ramification theory for varieties over a local field , Publ. Math. Inst. Hautes Études Sci. 117 (2013), 1–178.10.1007/s10240-013-0048-zGoogle Scholar
Katz, N. M., Gauss sums, Kloosterman sums, and monodromy groups, Annals of Mathematics Studies, vol. 116 (Princeton University Press, 1988).Google Scholar
Katz, N. M., Exponential sums and differential equations, Annals of Mathematics Studies, vol. 124 (Princeton University Press, 1990).10.1515/9781400882434Google Scholar
Katz, N. M., Sums of Betti numbers in arbitrary characteristic , Finite Fields and Their Applications 7 (2001), 29–44.10.1006/ffta.2000.0303Google Scholar
Katz, N. M. and Laumon, G., Transformation de Fourier et majoration de sommes exponentielles , Publ. Math. Inst. Hautes Études Sci. 62 (1985), 361–418.Google Scholar
Katz, N. M. and Messing, W., Some consequences of the Riemann hypothesis for varieties over finite fields , Invent. Math. 23 (1974), 73–77.10.1007/BF01405203Google Scholar
Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, American Mathematical Society Colloquium Publications, vol. 45 (American Mathematical Society, 1999).Google Scholar
Kleiman, S. L., Algebraic cycles and the Weil conjectures , in Dix exposés sur la cohomologie des schémas, Advanced Studies in Pure Mathematics, vol. 3 (North-Holland, 1968), 359–386.Google Scholar
Laumon, G., Vanishing cycles over a base of dimension ⩾1 , in Algebraic geometry (Tokyo/Kyoto, 1982), Lecture Notes in Mathematics, vol. 1016 (Springer, 1983), 143–150.Google Scholar
Laumon, G., Transformation de Fourier, constantes d’équations fonctionnelles et conjecture de Weil , Publ. Math. Inst. Hautes Études Sci. 65 (1987), 131–210.10.1007/BF02698937Google Scholar
Lombardi, H. and Quitté, C., Algèbre commutative (Méthodes constructives), Mathématiques en devenir (Calvage & Mounet, 2011).Google Scholar
Madore, D. and Orgogozo, F., Calculabilité de la cohomologie étale modulo ℓ , Algebra & Number Theory 9–7 (2015), 1647–1739.10.2140/ant.2015.9.1647Google Scholar
Mochizuki, S., The geometry of the compactification of the Hurwitz scheme , Publ. Res. Inst. Math. Sci. 31 (1995), 355–441.Google Scholar
Mochizuki, S., Extending families of curves over log regular schemes , J. Reine Angew. Math. 511 (1999), 43–71.Google Scholar
Ogg, A. P., Cohomology of abelian varieties over function fields , Ann. of Math. (2) 76 (1962), 185–212.Google Scholar
Orgogozo, F., Altérations et groupe fondamental premier à p , Bull. Soc. Math. France 131 (2003), 123–147.10.24033/bsmf.2438Google Scholar
Orgogozo, F., Modifications et cycles proches sur une base générale , Int. Math. Res. Not. IMRN (2006), Art. ID 25315, 38.10.1155/IMRN/2006/25315Google Scholar
Pink, R., Lettre to N. Katz (26 May 1995), unpublished.Google Scholar
Šafarevič, I. R., Principal homogeneous spaces defined over a function field (Russian) , Trudy Mat. Inst. Steklov. 64 (1961), 316–346; Engl. Transl. in Amer. Math. Soc. Transl. (2) 37 (1964).Google Scholar
Saito, T., Log smooth extension of a family of curves and semi-stable reduction , J. Algebraic Geom. 13 (2004), 287–321.10.1090/S1056-3911-03-00338-2Google Scholar
Serre, J.-P., Corps locaux, Publications de l’Université de Nancago, no. VIII, second edition (Hermann, 1968).Google Scholar
Serre, J.-P., Bounds for the orders of the finite subgroups of G (k) , in Group representation theory (EPFL Press, 2007), 405–450.Google Scholar
Serre, J.-P., Un critère d’indépendance pour une famille de représentations ℓ-adiques , Comment. Math. Helv. 88 (2013), 541–554.10.4171/CMH/295Google Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu, 2019.Google Scholar
Steinberg, R., Lectures on Chevalley groups, University Lecture Series, vol. 66 (American Mathematical Society, Providence, RI, 2016).10.1090/ulect/066Google Scholar
Suh, J., Symmetry and parity in Frobenius action on cohomology , Compos. Math. 148 (2012), 295–303.Google Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories , in The Grothendieck Festschrift III, Progress in Mathematics, vol. 88 (Birkhäuser, 1990), 247–435.10.1007/978-0-8176-4576-2_10Google Scholar
Tomašić, I., A new Weil cohomology theory , Bull. Lond. Math. Soc. 36 (2004), 663–670.Google Scholar
Umezaki, N., A uniform bound for the order of monodromy , Math. Res. Lett. 23 (2016), 929–937.Google Scholar
Yu, J.-K., Report, Princeton University, February 1995. Cited in [ KS99 ].Google Scholar
Zalesskiĭ, A. E. and Serëžkin, V. N., Linear groups generated by transvections (Russian) , Izv. Akad. Nauk SSSR Ser. Mat. 40 (1976), 26–49, 221; Engl. Transl. in Math. USSR-Izv. 10 (1976) no. 1, 25–46.Google Scholar