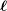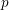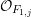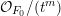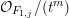1 Introduction
It was pointed out to us by Zheng that the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1] is invalid. The problem is in the final step of the proof on p. 237, where we showed that there was an exact sequence
 $$\begin{eqnarray}0\rightarrow H_{\ell }^{i+n}(X)\rightarrow H_{\ell }^{i+n}(X_{0})\rightarrow H_{\ell }^{i+n}(X_{1})\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{\ell }^{i+n}(X)\rightarrow H_{\ell }^{i+n}(X_{0})\rightarrow H_{\ell }^{i+n}(X_{1})\rightarrow \cdots\end{eqnarray}$$ and claimed to deduce  $\ell$-independence of
$\ell$-independence of 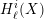 $H_{\ell }^{i}(X)$ from
$H_{\ell }^{i}(X)$ from  $\ell$-independence of all the other terms
$\ell$-independence of all the other terms 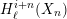 $H_{\ell }^{i+n}(X_{n})$. Of course, this deduction does not work, since there might be infinitely many such other terms.
$H_{\ell }^{i+n}(X_{n})$. Of course, this deduction does not work, since there might be infinitely many such other terms.
In their paper [Reference Lu and ZhengLZ19], Lu and Zheng provide (amongst other things) an alternative proof of this  $\ell$-independence result, at least for
$\ell$-independence result, at least for  $\ell \neq p$, see Theorem 1.4(2). In this corrigendum we will explain how to fix the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1] by instead proving a stronger version of [Reference Chiarellotto and LazdaCL18, Corollary 5.5] where the semistable hypothesis is removed. In particular, this includes the case
$\ell \neq p$, see Theorem 1.4(2). In this corrigendum we will explain how to fix the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1] by instead proving a stronger version of [Reference Chiarellotto and LazdaCL18, Corollary 5.5] where the semistable hypothesis is removed. In particular, this includes the case 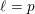 $\ell =p$.
$\ell =p$.
Notation and conventions
We will use notation from [Reference Chiarellotto and LazdaCL18] freely.
2 Log structures
We begin with a general result on semistable reduction and log schemes. Let 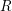 $R$ be a complete discrete valuation ring (DVR) with perfect residue field
$R$ be a complete discrete valuation ring (DVR) with perfect residue field  $k$,
$k$,  $\unicode[STIX]{x1D70B}$ a uniformiser for
$\unicode[STIX]{x1D70B}$ a uniformiser for  $R$, and let
$R$, and let 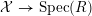 ${\mathcal{X}}\rightarrow \text{Spec}(R)$ be a strictly semistable scheme. That is,
${\mathcal{X}}\rightarrow \text{Spec}(R)$ be a strictly semistable scheme. That is,  ${\mathcal{X}}$ is Zariski locally étale over
${\mathcal{X}}$ is Zariski locally étale over 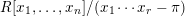 $R[x_{1},\ldots ,x_{n}]/(x_{1}\cdots x_{r}-\unicode[STIX]{x1D70B})$ for some
$R[x_{1},\ldots ,x_{n}]/(x_{1}\cdots x_{r}-\unicode[STIX]{x1D70B})$ for some  $n,r$. There is a natural log structure
$n,r$. There is a natural log structure  ${\mathcal{M}}_{{\mathcal{X}}}$ on
${\mathcal{M}}_{{\mathcal{X}}}$ on 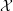 ${\mathcal{X}}$ given by functions invertible outside the special fibre
${\mathcal{X}}$ given by functions invertible outside the special fibre  $X$, and we let
$X$, and we let 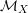 ${\mathcal{M}}_{X}$ denote the pull-back of this log structure to
${\mathcal{M}}_{X}$ denote the pull-back of this log structure to  $X$. We will also write
$X$. We will also write 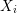 $X_{i}$ for the reduction of
$X_{i}$ for the reduction of  ${\mathcal{X}}$ modulo
${\mathcal{X}}$ modulo  $\unicode[STIX]{x1D70B}^{i+1}$, and
$\unicode[STIX]{x1D70B}^{i+1}$, and  $k^{\times }$ for
$k^{\times }$ for 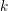 $k$ equipped with the log structure pulled back from the canonical log structure
$k$ equipped with the log structure pulled back from the canonical log structure  $R^{\times }$ on
$R^{\times }$ on  $R$.
$R$.
Proposition 2.1 (Illusie, Nakayama [Reference NakayamaNak98, Appendix A.4]).
If  ${\mathcal{X}},{\mathcal{X}}^{\prime }$ are strictly semistable schemes over
${\mathcal{X}},{\mathcal{X}}^{\prime }$ are strictly semistable schemes over 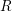 $R$, and
$R$, and  $g:X_{1}\rightarrow X_{1}^{\prime }$ is an isomorphism between their mod
$g:X_{1}\rightarrow X_{1}^{\prime }$ is an isomorphism between their mod  $\unicode[STIX]{x1D70B}^{2}$-reductions, then
$\unicode[STIX]{x1D70B}^{2}$-reductions, then  $g$ induces a canonical isomorphism
$g$ induces a canonical isomorphism 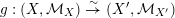 $g:(X,{\mathcal{M}}_{X})\overset{{\sim}}{\rightarrow }(X^{\prime },{\mathcal{M}}_{X^{\prime }})$ of log schemes over
$g:(X,{\mathcal{M}}_{X})\overset{{\sim}}{\rightarrow }(X^{\prime },{\mathcal{M}}_{X^{\prime }})$ of log schemes over  $k^{\times }$.
$k^{\times }$.
Sketch of proof.
Use  $g$ to identify
$g$ to identify  $X_{1}$ and
$X_{1}$ and  $X_{1}^{\prime }$, and thus
$X_{1}^{\prime }$, and thus 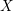 $X$ and
$X$ and  $X^{\prime }$. Let
$X^{\prime }$. Let 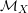 ${\mathcal{M}}_{X}$ and
${\mathcal{M}}_{X}$ and 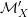 ${\mathcal{M}}_{X}^{\prime }$ be the log structures on
${\mathcal{M}}_{X}^{\prime }$ be the log structures on 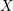 $X$ coming from
$X$ coming from  ${\mathcal{X}}$ and
${\mathcal{X}}$ and 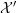 ${\mathcal{X}}^{\prime }$ respectively.
${\mathcal{X}}^{\prime }$ respectively.
Near a closed point of  $X$ let
$X$ let  $X^{(1)},\ldots ,X^{(r)}$ be the irreducible components of
$X^{(1)},\ldots ,X^{(r)}$ be the irreducible components of  $X$, and pick
$X$, and pick  $x_{1},\ldots ,x_{r}\in {\mathcal{O}}_{{\mathcal{X}}}$ such that
$x_{1},\ldots ,x_{r}\in {\mathcal{O}}_{{\mathcal{X}}}$ such that 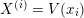 $X^{(i)}=V(x_{i})$. Similarly pick
$X^{(i)}=V(x_{i})$. Similarly pick 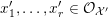 $x_{1}^{\prime },\ldots ,x_{r}^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}$ such that
$x_{1}^{\prime },\ldots ,x_{r}^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}$ such that 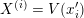 $X^{(i)}=V(x_{i}^{\prime })$. Let
$X^{(i)}=V(x_{i}^{\prime })$. Let 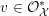 $v\in {\mathcal{O}}_{{\mathcal{X}}}^{\ast }$ and
$v\in {\mathcal{O}}_{{\mathcal{X}}}^{\ast }$ and  $v^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}^{\ast }$ be such that
$v^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}^{\ast }$ be such that  $x_{1}\cdots x_{r}=v\unicode[STIX]{x1D70B}$ and
$x_{1}\cdots x_{r}=v\unicode[STIX]{x1D70B}$ and 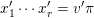 $x_{1}^{\prime }\cdots x_{r}^{\prime }=v^{\prime }\unicode[STIX]{x1D70B}$. Then in a neighbourhood of
$x_{1}^{\prime }\cdots x_{r}^{\prime }=v^{\prime }\unicode[STIX]{x1D70B}$. Then in a neighbourhood of  $p$ the morphisms
$p$ the morphisms  $({\mathcal{X}},{\mathcal{M}}_{{\mathcal{X}}})\rightarrow \text{Spec}(R^{\times })$ and
$({\mathcal{X}},{\mathcal{M}}_{{\mathcal{X}}})\rightarrow \text{Spec}(R^{\times })$ and  $({\mathcal{X}}^{\prime },{\mathcal{M}}_{{\mathcal{X}}^{\prime }})\rightarrow \text{Spec}(R^{\times })$ can be described by the following diagrams:
$({\mathcal{X}}^{\prime },{\mathcal{M}}_{{\mathcal{X}}^{\prime }})\rightarrow \text{Spec}(R^{\times })$ can be described by the following diagrams:

Pulling back to 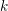 $k$, we see that the morphisms
$k$, we see that the morphisms 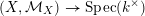 $(X,{\mathcal{M}}_{X})\rightarrow \text{Spec}(k^{\times })$ and
$(X,{\mathcal{M}}_{X})\rightarrow \text{Spec}(k^{\times })$ and  $(X,{\mathcal{M}}_{X}^{\prime })\rightarrow \text{Spec}(k^{\times })$ can be described by the diagrams
$(X,{\mathcal{M}}_{X}^{\prime })\rightarrow \text{Spec}(k^{\times })$ can be described by the diagrams

and

respectively, again in a neighbourhood of 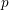 $p$. Since
$p$. Since  $V(x_{i})=V(x_{i}^{\prime })$ inside
$V(x_{i})=V(x_{i}^{\prime })$ inside  $X_{1}$, we must have
$X_{1}$, we must have 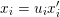 $x_{i}=u_{i}x_{i}^{\prime }$ for some
$x_{i}=u_{i}x_{i}^{\prime }$ for some 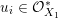 $u_{i}\in {\mathcal{O}}_{X_{1}}^{\ast }$, and so we can define an isomorphism
$u_{i}\in {\mathcal{O}}_{X_{1}}^{\ast }$, and so we can define an isomorphism
 $$\begin{eqnarray}{\mathcal{M}}_{X}\overset{{\sim}}{\rightarrow }{\mathcal{M}}_{X}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{X}\overset{{\sim}}{\rightarrow }{\mathcal{M}}_{X}^{\prime }\end{eqnarray}$$of log structures by mapping
 $$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto (uu_{1}^{a_{1}}\cdots u_{r}^{a_{r}},a_{1},\ldots ,a_{r}).\end{eqnarray}$$
$$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto (uu_{1}^{a_{1}}\cdots u_{r}^{a_{r}},a_{1},\ldots ,a_{r}).\end{eqnarray}$$ This is checked to be a morphism of log structures over  $k^{\times }$ by using the above local descriptions. Note that any other choice
$k^{\times }$ by using the above local descriptions. Note that any other choice 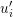 $u_{i}^{\prime }$ must satisfy
$u_{i}^{\prime }$ must satisfy  $(u_{i}-u_{i}^{\prime })x_{i}^{\prime }=0$ in
$(u_{i}-u_{i}^{\prime })x_{i}^{\prime }=0$ in 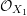 ${\mathcal{O}}_{X_{1}}$, and hence we must have
${\mathcal{O}}_{X_{1}}$, and hence we must have 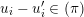 $u_{i}-u_{i}^{\prime }\in (\unicode[STIX]{x1D70B})$. In particular, the above isomorphism does not depend on the choice of
$u_{i}-u_{i}^{\prime }\in (\unicode[STIX]{x1D70B})$. In particular, the above isomorphism does not depend on the choice of  $u_{i}$. By a similar argument, neither does it depend on the choice of
$u_{i}$. By a similar argument, neither does it depend on the choice of 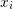 $x_{i}$ and
$x_{i}$ and  $x_{i}^{\prime }$, and so it glues to give a global isomorphism
$x_{i}^{\prime }$, and so it glues to give a global isomorphism 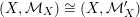 $(X,{\mathcal{M}}_{X})\cong (X,{\mathcal{M}}_{X}^{\prime })$ of log schemes over
$(X,{\mathcal{M}}_{X})\cong (X,{\mathcal{M}}_{X}^{\prime })$ of log schemes over 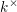 $k^{\times }$.◻
$k^{\times }$.◻
We will need to extend this result to cover morphisms between strictly semistable schemes over different bases. So suppose that  $R\rightarrow S$ is a finite morphism of complete DVRs, with induced residue field extension
$R\rightarrow S$ is a finite morphism of complete DVRs, with induced residue field extension  $k\rightarrow k_{S}$. Let
$k\rightarrow k_{S}$. Let  $\unicode[STIX]{x1D70B}_{S}$ be a uniformiser for
$\unicode[STIX]{x1D70B}_{S}$ be a uniformiser for  $S$, and let
$S$, and let 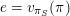 $e=v_{\unicode[STIX]{x1D70B}_{S}}(\unicode[STIX]{x1D70B})$. We do not assume that the induced extension
$e=v_{\unicode[STIX]{x1D70B}_{S}}(\unicode[STIX]{x1D70B})$. We do not assume that the induced extension 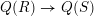 $Q(R)\rightarrow Q(S)$ of fraction fields is separable.
$Q(R)\rightarrow Q(S)$ of fraction fields is separable.
Suppose that we have strictly semistable schemes  ${\mathcal{X}},{\mathcal{X}}^{\prime }$ over
${\mathcal{X}},{\mathcal{X}}^{\prime }$ over  $R$ and
$R$ and  ${\mathcal{Y}},{\mathcal{Y}}^{\prime }$ over
${\mathcal{Y}},{\mathcal{Y}}^{\prime }$ over  $S$, and a pair of commutative diagrams
$S$, and a pair of commutative diagrams

As before, let us write  $Y_{j}$ for the reduction of
$Y_{j}$ for the reduction of  ${\mathcal{Y}}$ modulo
${\mathcal{Y}}$ modulo  $\unicode[STIX]{x1D70B}_{S}^{j+1}$. Suppose that we have isomorphisms
$\unicode[STIX]{x1D70B}_{S}^{j+1}$. Suppose that we have isomorphisms
 $$\begin{eqnarray}g_{Y}:Y_{e}\overset{{\sim}}{\rightarrow }Y_{e}^{\prime },\quad g_{X}:X_{1}\overset{{\sim}}{\rightarrow }X_{1}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}g_{Y}:Y_{e}\overset{{\sim}}{\rightarrow }Y_{e}^{\prime },\quad g_{X}:X_{1}\overset{{\sim}}{\rightarrow }X_{1}^{\prime }\end{eqnarray}$$ of  $S$- and
$S$- and  $R$-schemes respectively such that the diagram
$R$-schemes respectively such that the diagram

commutes. Then by Proposition 2.1 we obtain isomorphisms
 $$\begin{eqnarray}g_{Y}:(Y,{\mathcal{M}}_{Y})\overset{{\sim}}{\rightarrow }(Y^{\prime },{\mathcal{M}}_{Y^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}g_{Y}:(Y,{\mathcal{M}}_{Y})\overset{{\sim}}{\rightarrow }(Y^{\prime },{\mathcal{M}}_{Y^{\prime }})\end{eqnarray}$$ of log schemes over  $k_{S}^{\times }$, as well as
$k_{S}^{\times }$, as well as
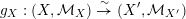 $$\begin{eqnarray}g_{X}:(X,{\mathcal{M}}_{X})\overset{{\sim}}{\rightarrow }(X^{\prime },{\mathcal{M}}_{X^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}g_{X}:(X,{\mathcal{M}}_{X})\overset{{\sim}}{\rightarrow }(X^{\prime },{\mathcal{M}}_{X^{\prime }})\end{eqnarray}$$ of log schemes over  $k^{\times }$. The above commutative diagrams of strictly semistable schemes induce commutative diagrams
$k^{\times }$. The above commutative diagrams of strictly semistable schemes induce commutative diagrams
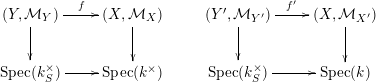
of log schemes. Note that the morphism of punctured points along the bottom of each square is given by
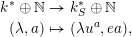 $$\begin{eqnarray}\displaystyle k^{\ast }\oplus \mathbb{N} & \rightarrow & \displaystyle k_{S}^{\ast }\oplus \mathbb{N}\nonumber\\ \displaystyle (\unicode[STIX]{x1D706},a) & \mapsto & \displaystyle (\unicode[STIX]{x1D706}u^{a},ea),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k^{\ast }\oplus \mathbb{N} & \rightarrow & \displaystyle k_{S}^{\ast }\oplus \mathbb{N}\nonumber\\ \displaystyle (\unicode[STIX]{x1D706},a) & \mapsto & \displaystyle (\unicode[STIX]{x1D706}u^{a},ea),\nonumber\end{eqnarray}$$ where  $u\in S^{\ast }$ is such that
$u\in S^{\ast }$ is such that  $\unicode[STIX]{x1D70B}=u\unicode[STIX]{x1D70B}_{S}^{e}$.
$\unicode[STIX]{x1D70B}=u\unicode[STIX]{x1D70B}_{S}^{e}$.
Proposition 2.2. The diagram
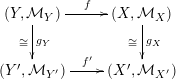
of log schemes commutes.
Proof. Let us use  $g$ to identify
$g$ to identify 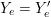 $Y_{e}=Y_{e}^{\prime }$ and
$Y_{e}=Y_{e}^{\prime }$ and 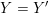 $Y=Y^{\prime }$, and let
$Y=Y^{\prime }$, and let 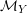 ${\mathcal{M}}_{Y}$ and
${\mathcal{M}}_{Y}$ and  ${\mathcal{M}}_{Y}^{\prime }$ be the log structures on
${\mathcal{M}}_{Y}^{\prime }$ be the log structures on 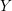 $Y$ coming from
$Y$ coming from 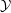 ${\mathcal{Y}}$ and
${\mathcal{Y}}$ and 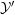 ${\mathcal{Y}}^{\prime }$ respectively. Similarly identify
${\mathcal{Y}}^{\prime }$ respectively. Similarly identify 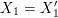 $X_{1}=X_{1}^{\prime }$ and
$X_{1}=X_{1}^{\prime }$ and  $X=X^{\prime }$, and let
$X=X^{\prime }$, and let 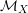 ${\mathcal{M}}_{X}$ and
${\mathcal{M}}_{X}$ and 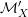 ${\mathcal{M}}_{X}^{\prime }$ be the log structures on
${\mathcal{M}}_{X}^{\prime }$ be the log structures on  $X$ coming from
$X$ coming from  ${\mathcal{X}}$ and
${\mathcal{X}}$ and  ${\mathcal{X}}^{\prime }$ respectively.
${\mathcal{X}}^{\prime }$ respectively.
Locally on 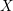 $X$ and
$X$ and 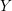 $Y$, choose functions
$Y$, choose functions 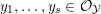 $y_{1},\ldots ,y_{s}\in {\mathcal{O}}_{{\mathcal{Y}}}$,
$y_{1},\ldots ,y_{s}\in {\mathcal{O}}_{{\mathcal{Y}}}$,  $y_{1}^{\prime },\ldots ,y_{s}^{\prime }\in {\mathcal{O}}_{{\mathcal{Y}}^{\prime }}$ cutting out the irreducible components of
$y_{1}^{\prime },\ldots ,y_{s}^{\prime }\in {\mathcal{O}}_{{\mathcal{Y}}^{\prime }}$ cutting out the irreducible components of  $Y$, and functions
$Y$, and functions  $x_{1},\ldots ,x_{r}\in {\mathcal{O}}_{{\mathcal{X}}}$ and
$x_{1},\ldots ,x_{r}\in {\mathcal{O}}_{{\mathcal{X}}}$ and 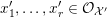 $x_{1}^{\prime },\ldots ,x_{r}^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}$ cutting out the irreducible components of
$x_{1}^{\prime },\ldots ,x_{r}^{\prime }\in {\mathcal{O}}_{{\mathcal{X}}^{\prime }}$ cutting out the irreducible components of  $X$. Write
$X$. Write
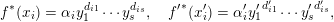 $$\begin{eqnarray}f^{\ast }(x_{i})=\unicode[STIX]{x1D6FC}_{i}y_{1}^{d_{i1}}\cdots y_{s}^{d_{is}},\quad {f^{\prime }}^{\ast }(x_{i}^{\prime })=\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}^{\prime }}\cdots {y_{s}^{\prime }}^{d_{is}^{\prime }},\end{eqnarray}$$
$$\begin{eqnarray}f^{\ast }(x_{i})=\unicode[STIX]{x1D6FC}_{i}y_{1}^{d_{i1}}\cdots y_{s}^{d_{is}},\quad {f^{\prime }}^{\ast }(x_{i}^{\prime })=\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}^{\prime }}\cdots {y_{s}^{\prime }}^{d_{is}^{\prime }},\end{eqnarray}$$ since both  $d_{ij}$ and
$d_{ij}$ and  $d_{ij}^{\prime }$ are given by the multiplicity of the
$d_{ij}^{\prime }$ are given by the multiplicity of the 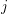 $j$th irreducible component of
$j$th irreducible component of  $Y$ in the scheme theoretic preimage of the
$Y$ in the scheme theoretic preimage of the  $i$th irreducible component of
$i$th irreducible component of 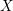 $X$ inside
$X$ inside 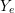 $Y_{e}$, we must have
$Y_{e}$, we must have  $d_{ij}=d_{ij}^{\prime }$. Moreover, since
$d_{ij}=d_{ij}^{\prime }$. Moreover, since  $V(f^{\ast }(x_{i}))\subset V(\unicode[STIX]{x1D70B}_{S}^{e})=V(y_{1}^{e}\cdots y_{s}^{e})$ we must have
$V(f^{\ast }(x_{i}))\subset V(\unicode[STIX]{x1D70B}_{S}^{e})=V(y_{1}^{e}\cdots y_{s}^{e})$ we must have 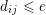 $d_{ij}\leqslant e$ for all
$d_{ij}\leqslant e$ for all 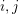 $i,j$.
$i,j$.
Now choose  $u_{i}\in {\mathcal{O}}_{X_{1}}^{\ast }$ such that
$u_{i}\in {\mathcal{O}}_{X_{1}}^{\ast }$ such that 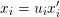 $x_{i}=u_{i}x_{i}^{\prime }$, and
$x_{i}=u_{i}x_{i}^{\prime }$, and 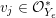 $v_{j}\in {\mathcal{O}}_{Y_{e}}^{\ast }$ such that
$v_{j}\in {\mathcal{O}}_{Y_{e}}^{\ast }$ such that  $y_{j}=v_{j}y_{j}^{\prime }$. Then the isomorphisms of log structures induced by
$y_{j}=v_{j}y_{j}^{\prime }$. Then the isomorphisms of log structures induced by 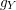 $g_{Y}$ and
$g_{Y}$ and  $g_{X}$ are given by
$g_{X}$ are given by
 $$\begin{eqnarray}\displaystyle {\mathcal{M}}_{Y}={\mathcal{O}}_{Y}^{\ast }\oplus \mathbb{N}^{s} & \rightarrow & \displaystyle {\mathcal{M}}_{Y}^{\prime }={\mathcal{O}}_{Y}^{\ast }\oplus \mathbb{N}^{s}\nonumber\\ \displaystyle (v,b_{1},\ldots ,b_{s}) & \mapsto & \displaystyle (vv_{1}^{b_{1}}\cdots v_{s}^{b_{s}},b_{1},\ldots ,b_{s})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{Y}={\mathcal{O}}_{Y}^{\ast }\oplus \mathbb{N}^{s} & \rightarrow & \displaystyle {\mathcal{M}}_{Y}^{\prime }={\mathcal{O}}_{Y}^{\ast }\oplus \mathbb{N}^{s}\nonumber\\ \displaystyle (v,b_{1},\ldots ,b_{s}) & \mapsto & \displaystyle (vv_{1}^{b_{1}}\cdots v_{s}^{b_{s}},b_{1},\ldots ,b_{s})\nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle {\mathcal{M}}_{X}={\mathcal{O}}_{X}^{\ast }\oplus \mathbb{N}^{r} & \rightarrow & \displaystyle {\mathcal{M}}_{X}^{\prime }={\mathcal{O}}_{X}^{\ast }\oplus \mathbb{N}^{r}\nonumber\\ \displaystyle (u,a_{1},\ldots ,a_{r}) & \mapsto & \displaystyle (uu_{1}^{a_{1}}\cdots u_{r}^{a_{r}},a_{1},\ldots ,a_{r})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{X}={\mathcal{O}}_{X}^{\ast }\oplus \mathbb{N}^{r} & \rightarrow & \displaystyle {\mathcal{M}}_{X}^{\prime }={\mathcal{O}}_{X}^{\ast }\oplus \mathbb{N}^{r}\nonumber\\ \displaystyle (u,a_{1},\ldots ,a_{r}) & \mapsto & \displaystyle (uu_{1}^{a_{1}}\cdots u_{r}^{a_{r}},a_{1},\ldots ,a_{r})\nonumber\end{eqnarray}$$ respectively, and the morphisms  ${\mathcal{M}}_{X}\rightarrow {\mathcal{M}}_{Y}$ and
${\mathcal{M}}_{X}\rightarrow {\mathcal{M}}_{Y}$ and  ${\mathcal{M}}_{X}^{\prime }\rightarrow {\mathcal{M}}_{Y}^{\prime }$ are defined by
${\mathcal{M}}_{X}^{\prime }\rightarrow {\mathcal{M}}_{Y}^{\prime }$ are defined by
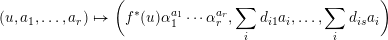 $$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)\unicode[STIX]{x1D6FC}_{1}^{a_{1}}\cdots \unicode[STIX]{x1D6FC}_{r}^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)\unicode[STIX]{x1D6FC}_{1}^{a_{1}}\cdots \unicode[STIX]{x1D6FC}_{r}^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$and
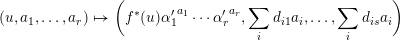 $$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u){\unicode[STIX]{x1D6FC}_{1}^{\prime }}^{a_{1}}\cdots {\unicode[STIX]{x1D6FC}_{r}^{\prime }}^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u){\unicode[STIX]{x1D6FC}_{1}^{\prime }}^{a_{1}}\cdots {\unicode[STIX]{x1D6FC}_{r}^{\prime }}^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$respectively. Hence in the diagram
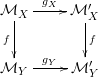
the composite  $f\circ g_{X}$ is given by
$f\circ g_{X}$ is given by
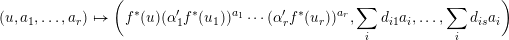 $$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)(\unicode[STIX]{x1D6FC}_{1}^{\prime }f^{\ast }(u_{1}))^{a_{1}}\cdots (\unicode[STIX]{x1D6FC}_{r}^{\prime }f^{\ast }(u_{r}))^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)(\unicode[STIX]{x1D6FC}_{1}^{\prime }f^{\ast }(u_{1}))^{a_{1}}\cdots (\unicode[STIX]{x1D6FC}_{r}^{\prime }f^{\ast }(u_{r}))^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr)\end{eqnarray}$$ and the composite 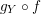 $g_{Y}\circ f$ is given by
$g_{Y}\circ f$ is given by
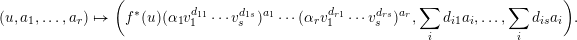 $$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)(\unicode[STIX]{x1D6FC}_{1}v_{1}^{d_{11}}\cdots v_{s}^{d_{1s}})^{a_{1}}\cdots (\unicode[STIX]{x1D6FC}_{r}v_{1}^{d_{r1}}\cdots v_{s}^{d_{rs}})^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}(u,a_{1},\ldots ,a_{r})\mapsto \biggl(f^{\ast }(u)(\unicode[STIX]{x1D6FC}_{1}v_{1}^{d_{11}}\cdots v_{s}^{d_{1s}})^{a_{1}}\cdots (\unicode[STIX]{x1D6FC}_{r}v_{1}^{d_{r1}}\cdots v_{s}^{d_{rs}})^{a_{r}},\mathop{\sum }_{i}d_{i1}a_{i},\ldots ,\mathop{\sum }_{i}d_{is}a_{i}\biggr).\end{eqnarray}$$ We thus need to show that  $\unicode[STIX]{x1D6FC}_{i}^{\prime }f^{\ast }(u_{i})=\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}$ in
$\unicode[STIX]{x1D6FC}_{i}^{\prime }f^{\ast }(u_{i})=\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}$ in 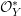 ${\mathcal{O}}_{Y}^{\ast }$ for all
${\mathcal{O}}_{Y}^{\ast }$ for all  $i$. But now we write
$i$. But now we write
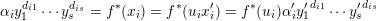 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}y_{1}^{d_{i1}}\cdots y_{s}^{d_{is}}=f^{\ast }(x_{i})=f^{\ast }(u_{i}x_{i}^{\prime })=f^{\ast }(u_{i})\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}y_{1}^{d_{i1}}\cdots y_{s}^{d_{is}}=f^{\ast }(x_{i})=f^{\ast }(u_{i}x_{i}^{\prime })=f^{\ast }(u_{i})\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}\end{eqnarray}$$ in  ${\mathcal{O}}_{Y_{e}}$ and so deduce that
${\mathcal{O}}_{Y_{e}}$ and so deduce that
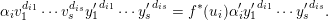 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}=f^{\ast }(u_{i})\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}=f^{\ast }(u_{i})\unicode[STIX]{x1D6FC}_{i}^{\prime }{y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}.\end{eqnarray}$$ We deduce that the difference 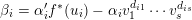 $\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FC}_{i}^{\prime }f^{\ast }(u_{i})-\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}$ annihilates
$\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FC}_{i}^{\prime }f^{\ast }(u_{i})-\unicode[STIX]{x1D6FC}_{i}v_{1}^{d_{i1}}\cdots v_{s}^{d_{is}}$ annihilates  ${y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}$ inside
${y_{1}^{\prime }}^{d_{i1}}\cdots {y_{s}^{\prime }}^{d_{is}}$ inside  ${\mathcal{O}}_{Y_{e}}$, and since each
${\mathcal{O}}_{Y_{e}}$, and since each  $d_{ij}\leqslant e$ we deduce that in fact
$d_{ij}\leqslant e$ we deduce that in fact  $\unicode[STIX]{x1D6FD}_{i}$ annihilates
$\unicode[STIX]{x1D6FD}_{i}$ annihilates  $\unicode[STIX]{x1D70B}_{S}^{e}$, and therefore must lie in
$\unicode[STIX]{x1D70B}_{S}^{e}$, and therefore must lie in  $(\unicode[STIX]{x1D70B}_{S})$. Hence
$(\unicode[STIX]{x1D70B}_{S})$. Hence  $\unicode[STIX]{x1D6FD}_{i}=0$ in
$\unicode[STIX]{x1D6FD}_{i}=0$ in  ${\mathcal{O}}_{Y}$ and the proof is complete.◻
${\mathcal{O}}_{Y}$ and the proof is complete.◻
3 Functoriality of comparison isomorphisms
We will also need to know that the comparison isomorphisms [Reference Chiarellotto and LazdaCL18, Propositions 5.3, 5.4] are compatible with morphisms of semistable schemes over different bases. So let us suppose that we are again in the above set-up, where we have a commutative diagram
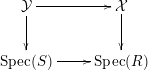
of strictly semistable schemes  ${\mathcal{Y}}$ and
${\mathcal{Y}}$ and  ${\mathcal{X}}$ over
${\mathcal{X}}$ over  $S$ and
$S$ and  $R$ respectively, with
$R$ respectively, with  $S$ the integral closure of
$S$ the integral closure of  $R$ in some finite extension of its fraction field. Let us assume that
$R$ in some finite extension of its fraction field. Let us assume that 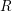 $R$, and hence
$R$, and hence  $S$, is of equicharacteristic
$S$, is of equicharacteristic  $p>0$, with fraction fields
$p>0$, with fraction fields 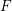 $F$ and
$F$ and 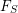 $F_{S}$ respectively, whose absolute Galois groups we will denote by
$F_{S}$ respectively, whose absolute Galois groups we will denote by  $G_{F}$ and
$G_{F}$ and 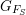 $G_{F_{S}}$. Fix an embedding
$G_{F_{S}}$. Fix an embedding  $F^{\text{sep}}{\hookrightarrow}F_{S}^{\text{sep}}$ of separable closures; note that this sends
$F^{\text{sep}}{\hookrightarrow}F_{S}^{\text{sep}}$ of separable closures; note that this sends  $F^{\text{tame}}$ into
$F^{\text{tame}}$ into  $F_{S}^{\text{tame}}$ and induces an injective homomorphism
$F_{S}^{\text{tame}}$ and induces an injective homomorphism  $G_{F_{S}}\rightarrow G_{F}$ with finite cokernel.
$G_{F_{S}}\rightarrow G_{F}$ with finite cokernel.
Let  ${\mathcal{X}}^{\times }$ and
${\mathcal{X}}^{\times }$ and 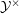 ${\mathcal{Y}}^{\times }$ denote these semistable schemes endowed with their canonical log structures, and
${\mathcal{Y}}^{\times }$ denote these semistable schemes endowed with their canonical log structures, and  $X^{\times }$ and
$X^{\times }$ and  $Y^{\times }$ the corresponding log special fibres. We therefore have a commutative diagram
$Y^{\times }$ the corresponding log special fibres. We therefore have a commutative diagram
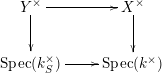
of log schemes. For every finite subextension  $F\subset L\subset F^{\text{tame}}$, let
$F\subset L\subset F^{\text{tame}}$, let 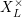 $X_{L}^{\times }$ denote the corresponding base change of
$X_{L}^{\times }$ denote the corresponding base change of 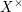 $X^{\times }$, and
$X^{\times }$, and  $X^{\times ,\text{tame}}$ the inverse limit of the étale topoi of all such
$X^{\times ,\text{tame}}$ the inverse limit of the étale topoi of all such  $X_{L}^{\times }$; we have
$X_{L}^{\times }$; we have  $Y^{\times ,\text{tame}}$ defined entirely similarly. Via the embedding
$Y^{\times ,\text{tame}}$ defined entirely similarly. Via the embedding  $F^{\text{tame}}{\hookrightarrow}F_{S}^{\text{tame}}$ this induces a
$F^{\text{tame}}{\hookrightarrow}F_{S}^{\text{tame}}$ this induces a  $G_{F_{S}}$-equivariant morphism of topoi
$G_{F_{S}}$-equivariant morphism of topoi
 $$\begin{eqnarray}Y^{\times ,\text{tame}}\rightarrow X^{\times ,\text{tame}}\end{eqnarray}$$
$$\begin{eqnarray}Y^{\times ,\text{tame}}\rightarrow X^{\times ,\text{tame}}\end{eqnarray}$$ and hence a  $G_{F_{S}}$-equivariant morphism
$G_{F_{S}}$-equivariant morphism
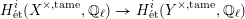 $$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(X^{\times ,\text{tame}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(X^{\times ,\text{tame}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\end{eqnarray}$$ in cohomology, for any 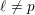 $\ell \neq p$. On the other hand we have a natural
$\ell \neq p$. On the other hand we have a natural  $G_{F_{S}}$-equivariant map
$G_{F_{S}}$-equivariant map
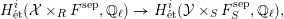 $$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}\times _{R}F^{\text{sep}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell }),\end{eqnarray}$$
$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}\times _{R}F^{\text{sep}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell }),\end{eqnarray}$$and by [Reference NakayamaNak98, Proposition 4.2] equivariant isomorphisms
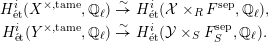 $$\begin{eqnarray}\displaystyle H_{\acute{\text{e}}\text{t}}^{i}(X^{\times ,\text{tame}},\mathbb{Q}_{\ell }) & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}\times _{R}F^{\text{sep}},\mathbb{Q}_{\ell }),\nonumber\\ \displaystyle H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell }) & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\acute{\text{e}}\text{t}}^{i}(X^{\times ,\text{tame}},\mathbb{Q}_{\ell }) & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}\times _{R}F^{\text{sep}},\mathbb{Q}_{\ell }),\nonumber\\ \displaystyle H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell }) & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell }).\nonumber\end{eqnarray}$$Proposition 3.1. The diagram
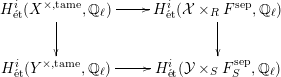
commutes.
Proof. Consider the commutative diagram
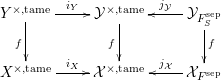
of topoi as in [Reference NakayamaNak98, §3], where  ${\mathcal{Y}}^{\times ,\text{tame}}$ and
${\mathcal{Y}}^{\times ,\text{tame}}$ and  ${\mathcal{X}}^{\times ,\text{tame}}$ are defined by ‘base change’ along
${\mathcal{X}}^{\times ,\text{tame}}$ are defined by ‘base change’ along  $F_{S}\rightarrow F_{S}^{\text{tame}}$ and
$F_{S}\rightarrow F_{S}^{\text{tame}}$ and  $F\rightarrow F^{\text{tame}}$ respectively. Then the isomorphism
$F\rightarrow F^{\text{tame}}$ respectively. Then the isomorphism
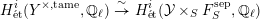 $$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\overset{{\sim}}{\rightarrow }H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\overset{{\sim}}{\rightarrow }H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell })\end{eqnarray}$$is given as the composite
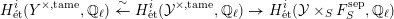 $$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\overset{{\sim}}{\leftarrow }H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}^{\times ,\text{tame}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{i}(Y^{\times ,\text{tame}},\mathbb{Q}_{\ell })\overset{{\sim}}{\leftarrow }H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}^{\times ,\text{tame}},\mathbb{Q}_{\ell })\rightarrow H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{Y}}\times _{S}F_{S}^{\text{sep}},\mathbb{Q}_{\ell })\end{eqnarray}$$ using the proper base change theorem in log-étale cohomology [Reference NakayamaNak97, Theorem 5.1], and there is a similar statement for  ${\mathcal{X}}$. The claim then follows simply from commutativity of the above diagram of log schemes.◻
${\mathcal{X}}$. The claim then follows simply from commutativity of the above diagram of log schemes.◻
We will also need a version of this result for  $p$-adic cohomology. Write
$p$-adic cohomology. Write  $W=W(k)$,
$W=W(k)$,  $W_{S}=W(k_{S})$, let
$W_{S}=W(k_{S})$, let  $K=W[1/p]$,
$K=W[1/p]$,  $K_{S}=W_{S}[1/p]$, and let
$K_{S}=W_{S}[1/p]$, and let 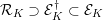 ${\mathcal{R}}_{K}\supset {\mathcal{E}}_{K}^{\dagger }\subset {\mathcal{E}}_{K}$, and
${\mathcal{R}}_{K}\supset {\mathcal{E}}_{K}^{\dagger }\subset {\mathcal{E}}_{K}$, and 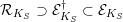 ${\mathcal{R}}_{K_{S}}\supset {\mathcal{E}}_{K_{S}}^{\dagger }\subset {\mathcal{E}}_{K_{S}}$ denote copies of the Robba ring, the bounded Robba ring and the Amice ring over
${\mathcal{R}}_{K_{S}}\supset {\mathcal{E}}_{K_{S}}^{\dagger }\subset {\mathcal{E}}_{K_{S}}$ denote copies of the Robba ring, the bounded Robba ring and the Amice ring over  $K$ and
$K$ and 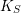 $K_{S}$ respectively. Lift the extension
$K_{S}$ respectively. Lift the extension  $F\rightarrow F_{S}$ to a finite flat morphism
$F\rightarrow F_{S}$ to a finite flat morphism 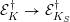 ${\mathcal{E}}_{K}^{\dagger }\rightarrow {\mathcal{E}}_{K_{S}}^{\dagger }$ which extends to finite flat morphisms
${\mathcal{E}}_{K}^{\dagger }\rightarrow {\mathcal{E}}_{K_{S}}^{\dagger }$ which extends to finite flat morphisms  ${\mathcal{R}}_{K}\rightarrow {\mathcal{R}}_{K_{S}}$ and
${\mathcal{R}}_{K}\rightarrow {\mathcal{R}}_{K_{S}}$ and  ${\mathcal{E}}_{K}\rightarrow {\mathcal{E}}_{K_{S}}$. Then, as above, the morphism of log schemes
${\mathcal{E}}_{K}\rightarrow {\mathcal{E}}_{K_{S}}$. Then, as above, the morphism of log schemes 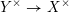 $Y^{\times }\rightarrow X^{\times }$ induces a morphism
$Y^{\times }\rightarrow X^{\times }$ induces a morphism
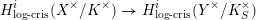 $$\begin{eqnarray}H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\rightarrow H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\rightarrow H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\end{eqnarray}$$ in log crystalline cohomology, and the morphism  ${\mathcal{Y}}_{F_{S}}\rightarrow {\mathcal{X}}_{F}$ induces a morphism
${\mathcal{Y}}_{F_{S}}\rightarrow {\mathcal{X}}_{F}$ induces a morphism
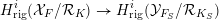 $$\begin{eqnarray}H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})\rightarrow H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})\rightarrow H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\end{eqnarray}$$in Robba-ring valued rigid cohomology. Then following [Reference Chiarellotto and LazdaCL18, Proposition 5.4] we can construct isomorphisms
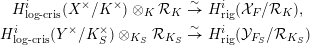 $$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\otimes _{K}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\otimes _{K_{S}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\otimes _{K}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\otimes _{K_{S}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\nonumber\end{eqnarray}$$ as follows. Let  $t$ denote a co-ordinate on
$t$ denote a co-ordinate on  ${\mathcal{E}}_{K}^{\dagger }$ and
${\mathcal{E}}_{K}^{\dagger }$ and 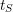 $t_{S}$ a co-ordinate on
$t_{S}$ a co-ordinate on  ${\mathcal{E}}_{K_{S}}^{\dagger }$ such that
${\mathcal{E}}_{K_{S}}^{\dagger }$ such that  $t\in W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$. Write
$t\in W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$. Write  $S_{K}=K\otimes W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ and
$S_{K}=K\otimes W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ and  $S_{K_{S}}=K_{S}\otimes W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$. Equip
$S_{K_{S}}=K_{S}\otimes W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$. Equip  $W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ (respectively
$W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ (respectively  $W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$) with the log structure defined by the ideal
$W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$) with the log structure defined by the ideal 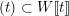 $(t)\subset W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ (respectively
$(t)\subset W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ (respectively  $(t_{S})\subset W\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$) and define the log-crystalline cohomology groups
$(t_{S})\subset W\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7}$) and define the log-crystalline cohomology groups
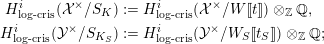 $$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K}) & := & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7})\otimes _{\mathbb{Z}}\mathbb{Q},\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}}) & := & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7})\otimes _{\mathbb{Z}}\mathbb{Q};\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K}) & := & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7})\otimes _{\mathbb{Z}}\mathbb{Q},\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}}) & := & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/W_{S}\unicode[STIX]{x27E6}t_{S}\unicode[STIX]{x27E7})\otimes _{\mathbb{Z}}\mathbb{Q};\nonumber\end{eqnarray}$$ these are naturally endowed with the extra structure of 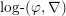 $\text{log}\text{-}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules over
$\text{log}\text{-}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules over 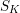 $S_{K}$ and
$S_{K}$ and  $S_{K_{S}}$ respectively. Moreover, we have isomorphisms of
$S_{K_{S}}$ respectively. Moreover, we have isomorphisms of  $\unicode[STIX]{x1D711}$-modules
$\unicode[STIX]{x1D711}$-modules
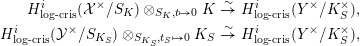 $$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K})\otimes _{S_{K},t\mapsto 0}K & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times }),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}})\otimes _{S_{K_{S}},t_{S}\mapsto 0}K_{S} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K})\otimes _{S_{K},t\mapsto 0}K & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times }),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}})\otimes _{S_{K_{S}},t_{S}\mapsto 0}K_{S} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times }),\nonumber\end{eqnarray}$$ by smooth and proper base change in log-crystalline cohomology, as well as isomorphisms of  $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules
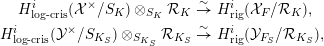 $$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K})\otimes _{S_{K}}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}})\otimes _{S_{K_{S}}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{X}}^{\times }/S_{K})\otimes _{S_{K}}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}({\mathcal{Y}}^{\times }/S_{K_{S}})\otimes _{S_{K_{S}}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}}),\nonumber\end{eqnarray}$$ by [Reference Lazda and PálLP16, Proposition 5.45]. It therefore follows from the logarithmic form of Dwork’s trick [Reference KedlayaKed10, Corollary 17.2.4] that the  $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules  $H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})$ and
$H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})$ and 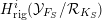 $H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})$ are unipotent, that there are isomorphisms
$H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})$ are unipotent, that there are isomorphisms
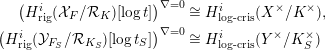 $$\begin{eqnarray}\displaystyle \left(H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})[\log t]\right)^{\unicode[STIX]{x1D6FB}=0} & \cong & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times }),\nonumber\\ \displaystyle \left(H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})[\log t_{S}]\right)^{\unicode[STIX]{x1D6FB}=0} & \cong & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K})[\log t]\right)^{\unicode[STIX]{x1D6FB}=0} & \cong & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times }),\nonumber\\ \displaystyle \left(H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})[\log t_{S}]\right)^{\unicode[STIX]{x1D6FB}=0} & \cong & \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\nonumber\end{eqnarray}$$ and moreover the connection 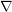 $\unicode[STIX]{x1D6FB}$ on the rigid cohomology groups appearing on the left-hand side can be completely recovered from the monodromy operator
$\unicode[STIX]{x1D6FB}$ on the rigid cohomology groups appearing on the left-hand side can be completely recovered from the monodromy operator 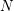 $N$ on the right-hand side. This allows us to construct isomorphisms of
$N$ on the right-hand side. This allows us to construct isomorphisms of 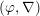 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$-modules
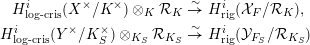 $$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\otimes _{K}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\otimes _{K_{S}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(X^{\times }/K^{\times })\otimes _{K}{\mathcal{R}}_{K} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{X}}_{F}/{\mathcal{R}}_{K}),\nonumber\\ \displaystyle H_{\text{log}\text{-}\text{cris}}^{i}(Y^{\times }/K_{S}^{\times })\otimes _{K_{S}}{\mathcal{R}}_{K_{S}} & \overset{{\sim}}{\rightarrow } & \displaystyle H_{\text{rig}}^{i}({\mathcal{Y}}_{F_{S}}/{\mathcal{R}}_{K_{S}})\nonumber\end{eqnarray}$$ where the left-hand side is endowed a natural connection coming from 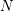 $N$; for more details see, for example, [Reference MarmoraMar08, §3.2].
$N$; for more details see, for example, [Reference MarmoraMar08, §3.2].
Proposition 3.2. The diagram
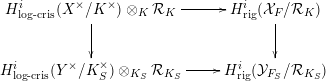
commutes.
Proof. Given the construction of the horizontal isomorphisms outlined above, it suffices to show that the diagram
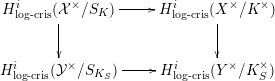
of log-crystalline cohomology groups commutes, which as in Proposition 3.1 simply follows from functoriality of log-crystalline cohomology. ◻
4 Cohomology and global approximations
Now suppose that 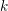 $k$ is a finite field,
$k$ is a finite field, 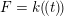 $F=k(\!(t)\!)$, and
$F=k(\!(t)\!)$, and 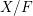 $X/F$ is a smooth and proper variety.
$X/F$ is a smooth and proper variety.
Definition 4.1. We say that 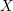 $X$ is globally defined if there exist a smooth curve
$X$ is globally defined if there exist a smooth curve  $C/k$, a
$C/k$, a  $k$-valued point
$k$-valued point  $c\in C(k)$, a smooth and proper morphism
$c\in C(k)$, a smooth and proper morphism  $\mathbf{X}\rightarrow (C\setminus \{c\})$ and an isomorphism
$\mathbf{X}\rightarrow (C\setminus \{c\})$ and an isomorphism 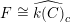 $F\cong \widehat{k(C)}_{c}$ such that
$F\cong \widehat{k(C)}_{c}$ such that  $\mathbf{X}_{F}\cong X$.
$\mathbf{X}_{F}\cong X$.
We will prove the following strengthened version of [Reference Chiarellotto and LazdaCL18, Corollary 5.5].
Theorem 4.2. For any smooth and proper variety  $X/F$ there exists a globally defined smooth and proper variety
$X/F$ there exists a globally defined smooth and proper variety  $Z/F$ such that
$Z/F$ such that
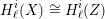 $$\begin{eqnarray}H_{\ell }^{i}(X)\cong H_{\ell }^{i}(Z)\end{eqnarray}$$
$$\begin{eqnarray}H_{\ell }^{i}(X)\cong H_{\ell }^{i}(Z)\end{eqnarray}$$ for all  $\ell$ (including
$\ell$ (including  $\ell =p$).
$\ell =p$).
Once we have shown this, the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1] can then be completed using [Reference Chiarellotto and LazdaCL18, Proposition 5.8], exactly as in the proof of [Reference Chiarellotto and LazdaCL18, Theorem 5.1].
To prove Theorem 4.2, first of all choose a proper and flat model  ${\mathcal{X}}$ for
${\mathcal{X}}$ for  $X$ over the ring of integers
$X$ over the ring of integers  ${\mathcal{O}}_{F}$. By [Reference de JongdJ96, Theorem 6.5] we may choose an alteration
${\mathcal{O}}_{F}$. By [Reference de JongdJ96, Theorem 6.5] we may choose an alteration  ${\mathcal{X}}_{0}\rightarrow {\mathcal{X}}$ and a finite extension
${\mathcal{X}}_{0}\rightarrow {\mathcal{X}}$ and a finite extension 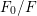 $F_{0}/F$ such that
$F_{0}/F$ such that  ${\mathcal{X}}_{0}$ is strictly semistable over
${\mathcal{X}}_{0}$ is strictly semistable over  ${\mathcal{O}}_{F_{0}}$.
${\mathcal{O}}_{F_{0}}$.
Next, we take the fibre product  ${\mathcal{X}}_{0}\times _{{\mathcal{X}}}{\mathcal{X}}_{0}$, and let
${\mathcal{X}}_{0}\times _{{\mathcal{X}}}{\mathcal{X}}_{0}$, and let 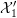 ${\mathcal{X}}_{1}^{\prime }$ denote the disjoint union of the reduced, irreducible components of
${\mathcal{X}}_{1}^{\prime }$ denote the disjoint union of the reduced, irreducible components of  ${\mathcal{X}}_{0}\times _{{\mathcal{X}}}{\mathcal{X}}_{0}$ which are flat over
${\mathcal{X}}_{0}\times _{{\mathcal{X}}}{\mathcal{X}}_{0}$ which are flat over 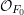 ${\mathcal{O}}_{F_{0}}$, or equivalently which map surjectively to
${\mathcal{O}}_{F_{0}}$, or equivalently which map surjectively to 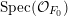 $\text{Spec}({\mathcal{O}}_{F_{0}})$. Once more applying [Reference de JongdJ96, Theorem 6.5] to each of the connected components of
$\text{Spec}({\mathcal{O}}_{F_{0}})$. Once more applying [Reference de JongdJ96, Theorem 6.5] to each of the connected components of 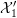 ${\mathcal{X}}_{1}^{\prime }$ in turn enables us to produce:
${\mathcal{X}}_{1}^{\prime }$ in turn enables us to produce:
– a 2-truncated augmented simplicial scheme
which is a proper hypercover after base changing to $$\begin{eqnarray}{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\rightarrow {\mathcal{X}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\rightarrow {\mathcal{X}}\end{eqnarray}$$ $F$;
$F$;– a collection
 $F_{1,1},\ldots ,F_{1,s}$ of finite field extensions of
$F_{1,1},\ldots ,F_{1,s}$ of finite field extensions of  $F_{0}$
$F_{0}$
such that  ${\mathcal{X}}_{1}$ is a disjoint union of schemes
${\mathcal{X}}_{1}$ is a disjoint union of schemes  ${\mathcal{X}}_{1,j}$, for
${\mathcal{X}}_{1,j}$, for  $1\leqslant j\leqslant s$, proper and strictly semistable over
$1\leqslant j\leqslant s$, proper and strictly semistable over  $\text{Spec}({\mathcal{O}}_{F_{1,j}})$.
$\text{Spec}({\mathcal{O}}_{F_{1,j}})$.
Let 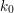 $k_{0}$ denote the residue field of
$k_{0}$ denote the residue field of  $F_{0}$,
$F_{0}$,  $k_{1,j}$ the residue field of
$k_{1,j}$ the residue field of  $F_{1,j}$, and consider the intermediate extensions
$F_{1,j}$, and consider the intermediate extensions
 $$\begin{eqnarray}F\subset F_{0}^{\text{un}}\subset F_{0}^{s}\subset F_{0}\subset F_{1,j}^{\text{un}}\subset F_{1,j}^{s}\subset F_{1,j},\end{eqnarray}$$
$$\begin{eqnarray}F\subset F_{0}^{\text{un}}\subset F_{0}^{s}\subset F_{0}\subset F_{1,j}^{\text{un}}\subset F_{1,j}^{s}\subset F_{1,j},\end{eqnarray}$$ where  $F_{0}^{\text{un}}/F$ and
$F_{0}^{\text{un}}/F$ and 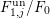 $F_{1,j}^{\text{un}}/F_{0}$ are separable and unramified,
$F_{1,j}^{\text{un}}/F_{0}$ are separable and unramified, 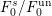 $F_{0}^{s}/F_{0}^{\text{un}}$ and
$F_{0}^{s}/F_{0}^{\text{un}}$ and 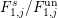 $F_{1,j}^{s}/F_{1,j}^{\text{un}}$ are separable and totally ramified, and
$F_{1,j}^{s}/F_{1,j}^{\text{un}}$ are separable and totally ramified, and  $F_{0}/F_{0}^{s}$ and
$F_{0}/F_{0}^{s}$ and  $F_{1,j}/F_{1,j}^{s}$ are totally inseparable, of degree
$F_{1,j}/F_{1,j}^{s}$ are totally inseparable, of degree 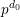 $p^{d_{0}}$ and
$p^{d_{0}}$ and 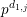 $p^{d_{1,j}}$ respectively. Let
$p^{d_{1,j}}$ respectively. Let  $t$ denote a uniformiser for
$t$ denote a uniformiser for 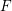 $F$,
$F$,  $t_{0}$ one for
$t_{0}$ one for  $F_{0}^{s}$, and let
$F_{0}^{s}$, and let  $P_{0}$ be the minimal polynomial of
$P_{0}$ be the minimal polynomial of 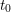 $t_{0}$ over
$t_{0}$ over 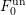 $F_{0}^{\text{un}}$. Then
$F_{0}^{\text{un}}$. Then 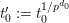 $t_{0}^{\prime }:=t_{0}^{1/p^{d_{0}}}$ is a uniformiser for
$t_{0}^{\prime }:=t_{0}^{1/p^{d_{0}}}$ is a uniformiser for  ${\mathcal{O}}_{F_{0}}$. Similarly, let
${\mathcal{O}}_{F_{0}}$. Similarly, let 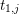 $t_{1,j}$ be a uniformiser for
$t_{1,j}$ be a uniformiser for  $F_{1,j}^{s}$, and
$F_{1,j}^{s}$, and  $P_{1,j}$ the minimal polynomial of
$P_{1,j}$ the minimal polynomial of  $t_{1,j}$ over
$t_{1,j}$ over  $F_{1,j}^{\text{un}}$. Then
$F_{1,j}^{\text{un}}$. Then  $t_{1,j}^{\prime }:=t_{1,j}^{1/p^{d_{1,j}}}$ is a uniformiser for
$t_{1,j}^{\prime }:=t_{1,j}^{1/p^{d_{1,j}}}$ is a uniformiser for  ${\mathcal{O}}_{F_{1,j}}$.
${\mathcal{O}}_{F_{1,j}}$.
Now choose a finitely generated sub- $k$-algebra
$k$-algebra  $R\subset {\mathcal{O}}_{F}$, containing
$R\subset {\mathcal{O}}_{F}$, containing  $t$, such that there exists a proper, flat scheme
$t$, such that there exists a proper, flat scheme  ${\mathcal{Y}}\rightarrow \text{Spec}(R)$ whose base change to
${\mathcal{Y}}\rightarrow \text{Spec}(R)$ whose base change to 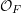 ${\mathcal{O}}_{F}$ is exactly
${\mathcal{O}}_{F}$ is exactly  ${\mathcal{X}}$. By [Reference SpivakovskySpi99, Theorem 10.1], we may at any point increase
${\mathcal{X}}$. By [Reference SpivakovskySpi99, Theorem 10.1], we may at any point increase  $R$ to ensure that it is in fact smooth over
$R$ to ensure that it is in fact smooth over 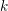 $k$. Next, enlarge
$k$. Next, enlarge 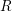 $R$ so that
$R$ so that  $R_{0}^{\text{un}}:=R\,\otimes _{k}\,k_{0}\subset {\mathcal{O}}_{F_{0}^{\text{un}}}$ contains all the coefficients of the minimal (Eisenstein) polynomial
$R_{0}^{\text{un}}:=R\,\otimes _{k}\,k_{0}\subset {\mathcal{O}}_{F_{0}^{\text{un}}}$ contains all the coefficients of the minimal (Eisenstein) polynomial 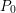 $P_{0}$ of
$P_{0}$ of 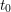 $t_{0}$, and let
$t_{0}$, and let 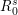 $R_{0}^{s}$ denote the corresponding finite flat extension
$R_{0}^{s}$ denote the corresponding finite flat extension 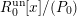 $R_{0}^{\text{un}}[x]/(P_{0})$ of
$R_{0}^{\text{un}}[x]/(P_{0})$ of  $R_{0}^{\text{un}}$. We can thus consider
$R_{0}^{\text{un}}$. We can thus consider  $R_{0}^{s}\subset {\mathcal{O}}_{F_{0}^{s}}$ as a subring containing
$R_{0}^{s}\subset {\mathcal{O}}_{F_{0}^{s}}$ as a subring containing 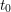 $t_{0}$, and we set
$t_{0}$, and we set 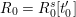 $R_{0}=R_{0}^{s}[t_{0}^{\prime }]$. Hence we have
$R_{0}=R_{0}^{s}[t_{0}^{\prime }]$. Hence we have 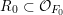 $R_{0}\subset {\mathcal{O}}_{F_{0}}$ such that
$R_{0}\subset {\mathcal{O}}_{F_{0}}$ such that
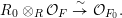 $$\begin{eqnarray}R_{0}\otimes _{R}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{0}\otimes _{R}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{0}}.\end{eqnarray}$$ Note also that  $R_{0}$ is finite and flat over
$R_{0}$ is finite and flat over 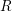 $R$; after localising
$R$; after localising  $R$ within
$R$ within  ${\mathcal{O}}_{F}$ we may in fact assume that
${\mathcal{O}}_{F}$ we may in fact assume that  $R_{0}$ is finite free over
$R_{0}$ is finite free over  $R$.
$R$.
Next we enlarge  $R$ so that there exists a proper and flat morphism
$R$ so that there exists a proper and flat morphism 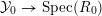 ${\mathcal{Y}}_{0}\rightarrow \text{Spec}(R_{0})$ whose base change to
${\mathcal{Y}}_{0}\rightarrow \text{Spec}(R_{0})$ whose base change to  ${\mathcal{O}}_{F_{0}}$ is
${\mathcal{O}}_{F_{0}}$ is  ${\mathcal{X}}_{0}$. Again, by further enlarging
${\mathcal{X}}_{0}$. Again, by further enlarging  $R$ we may in addition assume that the map
$R$ we may in addition assume that the map  ${\mathcal{X}}_{0}\rightarrow {\mathcal{X}}$ arises from a proper surjective map
${\mathcal{X}}_{0}\rightarrow {\mathcal{X}}$ arises from a proper surjective map
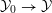 $$\begin{eqnarray}{\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}\end{eqnarray}$$ of 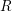 $R$-schemes, and moreover that there exists an open cover of
$R$-schemes, and moreover that there exists an open cover of  ${\mathcal{Y}}_{0}$ by schemes which are étale over
${\mathcal{Y}}_{0}$ by schemes which are étale over 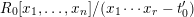 $R_{0}[x_{1},\ldots ,x_{n}]/(x_{1}\cdots x_{r}-t_{0}^{\prime })$ for some
$R_{0}[x_{1},\ldots ,x_{n}]/(x_{1}\cdots x_{r}-t_{0}^{\prime })$ for some  $n,r$. In other words,
$n,r$. In other words, 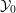 ${\mathcal{Y}}_{0}$ is ‘strictly
${\mathcal{Y}}_{0}$ is ‘strictly 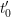 $t_{0}^{\prime }$-semistable’.
$t_{0}^{\prime }$-semistable’.
We now repeat this process to produce further finite free extensions 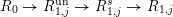 $R_{0}\rightarrow R_{1,j}^{\text{un}}\rightarrow R_{1,j}^{s}\rightarrow R_{1,j}$ for all
$R_{0}\rightarrow R_{1,j}^{\text{un}}\rightarrow R_{1,j}^{s}\rightarrow R_{1,j}$ for all  $j$, and an injection
$j$, and an injection  $R_{1,j}\subset {\mathcal{O}}_{F_{1,j}}$ containing the image of
$R_{1,j}\subset {\mathcal{O}}_{F_{1,j}}$ containing the image of 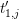 $t_{1,j}^{\prime }$ such that
$t_{1,j}^{\prime }$ such that
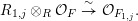 $$\begin{eqnarray}R_{1,j}\otimes _{R}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{1,j}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{1,j}\otimes _{R}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{1,j}}.\end{eqnarray}$$ We can also find proper, strictly  $t_{1,j}^{\prime }$-semistable schemes
$t_{1,j}^{\prime }$-semistable schemes 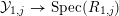 ${\mathcal{Y}}_{1,j}\rightarrow \text{Spec}(R_{1,j})$ whose base change to
${\mathcal{Y}}_{1,j}\rightarrow \text{Spec}(R_{1,j})$ whose base change to  ${\mathcal{O}}_{F_{1,j}}$ is
${\mathcal{O}}_{F_{1,j}}$ is  ${\mathcal{X}}_{1,j}$, so that setting
${\mathcal{X}}_{1,j}$, so that setting 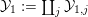 ${\mathcal{Y}}_{1}:=\coprod _{j}{\mathcal{Y}}_{1,j}$ (and again, possibly increasing
${\mathcal{Y}}_{1}:=\coprod _{j}{\mathcal{Y}}_{1,j}$ (and again, possibly increasing 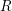 $R$), we obtain a 2-truncated augmented simplicial scheme
$R$), we obtain a 2-truncated augmented simplicial scheme
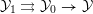 $$\begin{eqnarray}{\mathcal{Y}}_{1}\rightrightarrows {\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}_{1}\rightrightarrows {\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}\end{eqnarray}$$ which becomes a proper hypercover over a dense open subscheme of 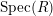 $\text{Spec}(R)$, and whose base change to
$\text{Spec}(R)$, and whose base change to 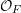 ${\mathcal{O}}_{F}$ is exactly our original 2-truncated augmented simplicial scheme
${\mathcal{O}}_{F}$ is exactly our original 2-truncated augmented simplicial scheme
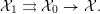 $$\begin{eqnarray}{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\rightarrow {\mathcal{X}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\rightarrow {\mathcal{X}}.\end{eqnarray}$$ Let  $\unicode[STIX]{x1D704}:R{\hookrightarrow}{\mathcal{O}}_{F}$ denote the canonical inclusion, and
$\unicode[STIX]{x1D704}:R{\hookrightarrow}{\mathcal{O}}_{F}$ denote the canonical inclusion, and 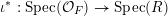 $\unicode[STIX]{x1D704}^{\ast }:\text{Spec}({\mathcal{O}}_{F})\rightarrow \text{Spec}(R)$ the induced morphism of schemes. Note that since
$\unicode[STIX]{x1D704}^{\ast }:\text{Spec}({\mathcal{O}}_{F})\rightarrow \text{Spec}(R)$ the induced morphism of schemes. Note that since 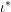 $\unicode[STIX]{x1D704}^{\ast }$ maps the generic point of
$\unicode[STIX]{x1D704}^{\ast }$ maps the generic point of  $\text{Spec}({\mathcal{O}}_{F})$ to that of
$\text{Spec}({\mathcal{O}}_{F})$ to that of  $\text{Spec}(R)$, the map
$\text{Spec}(R)$, the map  ${\mathcal{Y}}\rightarrow \text{Spec}(R)$ is generically smooth. We may thus choose an open subset
${\mathcal{Y}}\rightarrow \text{Spec}(R)$ is generically smooth. We may thus choose an open subset 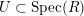 $U\subset \text{Spec}(R)$ such that
$U\subset \text{Spec}(R)$ such that 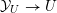 ${\mathcal{Y}}_{U}\rightarrow U$ is smooth, and such that the base change of
${\mathcal{Y}}_{U}\rightarrow U$ is smooth, and such that the base change of 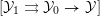 $[{\mathcal{Y}}_{1}\rightrightarrows {\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}]$ to
$[{\mathcal{Y}}_{1}\rightrightarrows {\mathcal{Y}}_{0}\rightarrow {\mathcal{Y}}]$ to  $U$ is a proper hypercover.
$U$ is a proper hypercover.
Lemma 4.3. For any  $n\geqslant 0$ there exists a smooth curve
$n\geqslant 0$ there exists a smooth curve  $C/k$, a rational point
$C/k$, a rational point  $c\in C(k)$, a uniformiser
$c\in C(k)$, a uniformiser  $t_{c}$ at
$t_{c}$ at  $c$, and a locally closed immersion
$c$, and a locally closed immersion  $C\rightarrow \text{Spec}(R)$ such that
$C\rightarrow \text{Spec}(R)$ such that  $C\setminus \{c\}\subset U$, and the induced map
$C\setminus \{c\}\subset U$, and the induced map
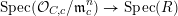 $$\begin{eqnarray}\text{Spec}({\mathcal{O}}_{C,c}/\mathfrak{m}_{c}^{n})\rightarrow \text{Spec}(R)\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}({\mathcal{O}}_{C,c}/\mathfrak{m}_{c}^{n})\rightarrow \text{Spec}(R)\end{eqnarray}$$ agrees with the modulo  $t^{n}$-reduction of
$t^{n}$-reduction of  $\unicode[STIX]{x1D704}^{\ast }$ via the isomorphism
$\unicode[STIX]{x1D704}^{\ast }$ via the isomorphism
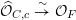 $$\begin{eqnarray}\widehat{{\mathcal{O}}}_{C,c}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{O}}}_{C,c}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F}\end{eqnarray}$$ sending  $t_{c}$ to
$t_{c}$ to  $t$.
$t$.
Proof. Since 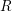 $R$ is smooth, we may choose étale co-ordinates around the image
$R$ is smooth, we may choose étale co-ordinates around the image  $\unicode[STIX]{x1D704}^{\ast }(s)$ of the closed point of
$\unicode[STIX]{x1D704}^{\ast }(s)$ of the closed point of 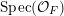 $\text{Spec}({\mathcal{O}}_{F})$ under
$\text{Spec}({\mathcal{O}}_{F})$ under  $\unicode[STIX]{x1D704}^{\ast }$. This induces an étale map
$\unicode[STIX]{x1D704}^{\ast }$. This induces an étale map  $\text{Spec}(R)\rightarrow \mathbb{A}_{k}^{n}$ for some
$\text{Spec}(R)\rightarrow \mathbb{A}_{k}^{n}$ for some  $n$, and it is a simple exercise to prove the corresponding claim for
$n$, and it is a simple exercise to prove the corresponding claim for 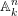 $\mathbb{A}_{k}^{n}$. We then just take the pull-back to
$\mathbb{A}_{k}^{n}$. We then just take the pull-back to  $\text{Spec}(R)$.◻
$\text{Spec}(R)$.◻
The canonical inclusion  $\unicode[STIX]{x1D704}$ induces similar inclusions
$\unicode[STIX]{x1D704}$ induces similar inclusions
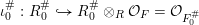 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{0}^{\#}:R_{0}^{\#}{\hookrightarrow}R_{0}^{\#}\otimes _{R}{\mathcal{O}}_{F}={\mathcal{O}}_{F_{0}^{\#}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{0}^{\#}:R_{0}^{\#}{\hookrightarrow}R_{0}^{\#}\otimes _{R}{\mathcal{O}}_{F}={\mathcal{O}}_{F_{0}^{\#}}\end{eqnarray}$$ for  $\#\in \{\text{un},s,\emptyset \}$, as well as
$\#\in \{\text{un},s,\emptyset \}$, as well as
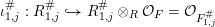 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{1,j}^{\#}:R_{1,j}^{\#}{\hookrightarrow}R_{1,j}^{\#}\otimes _{R}{\mathcal{O}}_{F}={\mathcal{O}}_{F_{1,j}^{\#}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{1,j}^{\#}:R_{1,j}^{\#}{\hookrightarrow}R_{1,j}^{\#}\otimes _{R}{\mathcal{O}}_{F}={\mathcal{O}}_{F_{1,j}^{\#}}\end{eqnarray}$$ for all 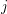 $j$, and again for
$j$, and again for  $\#\in \{\text{un},s,\emptyset \}$. We will need the following form of Krasner’s lemma [Sta18,
§0BU9].
$\#\in \{\text{un},s,\emptyset \}$. We will need the following form of Krasner’s lemma [Sta18,
§0BU9].
Lemma 4.4. Let 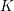 $K$ be a local field, with ring of integers
$K$ be a local field, with ring of integers  ${\mathcal{O}}_{K}$, and let
${\mathcal{O}}_{K}$, and let 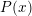 $P(x)$ be an Eisenstein polynomial over
$P(x)$ be an Eisenstein polynomial over  ${\mathcal{O}}_{K}$. Let
${\mathcal{O}}_{K}$. Let 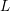 $L$ be the corresponding finite totally ramified extension, and let
$L$ be the corresponding finite totally ramified extension, and let 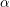 $\unicode[STIX]{x1D6FC}$ be a root of
$\unicode[STIX]{x1D6FC}$ be a root of  $P$ in
$P$ in 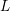 $L$. Then for any
$L$. Then for any  $m\geqslant 1$ there exists an
$m\geqslant 1$ there exists an 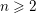 $n\geqslant 2$ such that any
$n\geqslant 2$ such that any  $Q(x)\in {\mathcal{O}}_{K}[x]$ congruent to
$Q(x)\in {\mathcal{O}}_{K}[x]$ congruent to  $P$ modulo
$P$ modulo  $\mathfrak{m}_{K}^{n}$ is Eisenstein, and
$\mathfrak{m}_{K}^{n}$ is Eisenstein, and  $L$ contains a root
$L$ contains a root 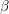 $\unicode[STIX]{x1D6FD}$ of
$\unicode[STIX]{x1D6FD}$ of  $Q$ such that
$Q$ such that  $L=K(\unicode[STIX]{x1D6FD})$ and
$L=K(\unicode[STIX]{x1D6FD})$ and  $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D6FD}$ modulo
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D6FD}$ modulo  $\mathfrak{m}_{L}^{m}$.
$\mathfrak{m}_{L}^{m}$.
We will use this as follows: given  $n_{1}\geqslant \max _{j}\{[F_{1,j}:F]\}$ Lemma 4.4 shows that there exists some
$n_{1}\geqslant \max _{j}\{[F_{1,j}:F]\}$ Lemma 4.4 shows that there exists some  $n_{0}\geqslant \max \left\{2,[F_{0}:F]\right\}$ such that any polynomial
$n_{0}\geqslant \max \left\{2,[F_{0}:F]\right\}$ such that any polynomial  $Q_{1,j}$ with coefficients in
$Q_{1,j}$ with coefficients in  ${\mathcal{O}}_{F_{1,j}^{\text{un}}}$ which agrees with the minimal polynomial
${\mathcal{O}}_{F_{1,j}^{\text{un}}}$ which agrees with the minimal polynomial 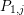 $P_{1,j}$ of
$P_{1,j}$ of 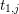 $t_{1,j}$ modulo
$t_{1,j}$ modulo 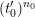 $(t_{0}^{\prime })^{n_{0}}$ is Eisenstein, and has a root in
$(t_{0}^{\prime })^{n_{0}}$ is Eisenstein, and has a root in  ${\mathcal{O}}_{F_{1,j}^{s}}$ which agrees with
${\mathcal{O}}_{F_{1,j}^{s}}$ which agrees with  $t_{1,j}$ modulo
$t_{1,j}$ modulo 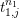 $t_{1,j}^{n_{1}}$. Applying the lemma again shows the existence of some
$t_{1,j}^{n_{1}}$. Applying the lemma again shows the existence of some 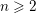 $n\geqslant 2$ such that any polynomial
$n\geqslant 2$ such that any polynomial 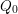 $Q_{0}$ with coefficients in
$Q_{0}$ with coefficients in  ${\mathcal{O}}_{F_{0}^{\text{un}}}$ which agrees with
${\mathcal{O}}_{F_{0}^{\text{un}}}$ which agrees with 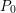 $P_{0}$ modulo
$P_{0}$ modulo  $t^{n}$ is Eisenstein, and has a root in
$t^{n}$ is Eisenstein, and has a root in 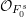 ${\mathcal{O}}_{F_{0}^{s}}$ which agrees with
${\mathcal{O}}_{F_{0}^{s}}$ which agrees with  $t_{0}$ modulo
$t_{0}$ modulo  $t_{0}^{n_{0}}$. Now choose a
$t_{0}^{n_{0}}$. Now choose a 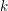 $k$-algebra homomorphism
$k$-algebra homomorphism 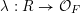 $\unicode[STIX]{x1D706}:R\rightarrow {\mathcal{O}}_{F}$ as provided by Lemma 4.3, that is, factoring through the local ring of some smooth point on a curve inside
$\unicode[STIX]{x1D706}:R\rightarrow {\mathcal{O}}_{F}$ as provided by Lemma 4.3, that is, factoring through the local ring of some smooth point on a curve inside 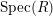 $\text{Spec}(R)$ and agreeing with
$\text{Spec}(R)$ and agreeing with  $\unicode[STIX]{x1D704}$ modulo
$\unicode[STIX]{x1D704}$ modulo 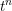 $t^{n}$.
$t^{n}$.
Since  $\unicode[STIX]{x1D706}$ is a
$\unicode[STIX]{x1D706}$ is a 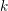 $k$-algebra homomorphism, we have a canonical isomorphism
$k$-algebra homomorphism, we have a canonical isomorphism  $R_{0}^{\text{un}}\otimes _{R,\unicode[STIX]{x1D706}}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{0}^{\text{un}}}$, which therefore induces a homomorphism
$R_{0}^{\text{un}}\otimes _{R,\unicode[STIX]{x1D706}}{\mathcal{O}}_{F}\overset{{\sim}}{\rightarrow }{\mathcal{O}}_{F_{0}^{\text{un}}}$, which therefore induces a homomorphism
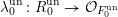 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{\text{un}}:R_{0}^{\text{un}}\rightarrow {\mathcal{O}}_{F_{0}^{\text{un}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{\text{un}}:R_{0}^{\text{un}}\rightarrow {\mathcal{O}}_{F_{0}^{\text{un}}}\end{eqnarray}$$ extending 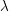 $\unicode[STIX]{x1D706}$ and which agrees with
$\unicode[STIX]{x1D706}$ and which agrees with 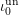 $\unicode[STIX]{x1D704}_{0}^{\text{un}}$ modulo
$\unicode[STIX]{x1D704}_{0}^{\text{un}}$ modulo  $t^{n}$. Now let
$t^{n}$. Now let  $Q_{0}=\unicode[STIX]{x1D706}_{0}^{\text{un}}(P_{0})$ denote the image under
$Q_{0}=\unicode[STIX]{x1D706}_{0}^{\text{un}}(P_{0})$ denote the image under  $\unicode[STIX]{x1D706}_{0}^{\text{un}}$ of the minimal polynomial
$\unicode[STIX]{x1D706}_{0}^{\text{un}}$ of the minimal polynomial 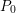 $P_{0}$ of
$P_{0}$ of 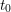 $t_{0}$; this is therefore a monic polynomial with coefficients in
$t_{0}$; this is therefore a monic polynomial with coefficients in  ${\mathcal{O}}_{F_{0}^{\text{un}}}$, which agrees with
${\mathcal{O}}_{F_{0}^{\text{un}}}$, which agrees with  $P_{0}$ modulo
$P_{0}$ modulo  $t^{n}$. Thus it is also Eisenstein, and by the choice of
$t^{n}$. Thus it is also Eisenstein, and by the choice of  $n$ we know that
$n$ we know that  ${\mathcal{O}}_{F_{0}^{s}}$ contains a root of
${\mathcal{O}}_{F_{0}^{s}}$ contains a root of  $\unicode[STIX]{x1D706}_{0}^{\text{un}}(P_{0})$ which is congruent to
$\unicode[STIX]{x1D706}_{0}^{\text{un}}(P_{0})$ which is congruent to 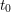 $t_{0}$ modulo
$t_{0}$ modulo 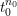 $t_{0}^{n_{0}}$ and generates
$t_{0}^{n_{0}}$ and generates  ${\mathcal{O}}_{F_{0}^{s}}$ as an
${\mathcal{O}}_{F_{0}^{s}}$ as an  ${\mathcal{O}}_{F_{0}^{\text{un}}}$-algebra. This then allows us to extend
${\mathcal{O}}_{F_{0}^{\text{un}}}$-algebra. This then allows us to extend  $\unicode[STIX]{x1D706}_{0}^{\text{un}}$ to a homomorphism
$\unicode[STIX]{x1D706}_{0}^{\text{un}}$ to a homomorphism
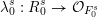 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{s}:R_{0}^{s}\rightarrow {\mathcal{O}}_{F_{0}^{s}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{s}:R_{0}^{s}\rightarrow {\mathcal{O}}_{F_{0}^{s}}\end{eqnarray}$$ which agrees with  $\unicode[STIX]{x1D704}_{0}^{s}$ modulo
$\unicode[STIX]{x1D704}_{0}^{s}$ modulo  $t_{0}^{n_{0}}$, and since
$t_{0}^{n_{0}}$, and since 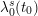 $\unicode[STIX]{x1D706}_{0}^{s}(t_{0})$ generates
$\unicode[STIX]{x1D706}_{0}^{s}(t_{0})$ generates  ${\mathcal{O}}_{F_{0}^{s}}$ as an
${\mathcal{O}}_{F_{0}^{s}}$ as an  ${\mathcal{O}}_{F_{0}^{\text{un}}}$-algebra, we deduce that the diagram
${\mathcal{O}}_{F_{0}^{\text{un}}}$-algebra, we deduce that the diagram
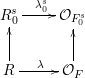
is coCartesian. We can then extend this to a homomorphism
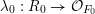 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}:R_{0}\rightarrow {\mathcal{O}}_{F_{0}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}:R_{0}\rightarrow {\mathcal{O}}_{F_{0}}\end{eqnarray}$$ agreeing with 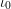 $\unicode[STIX]{x1D704}_{0}$ modulo
$\unicode[STIX]{x1D704}_{0}$ modulo  $(t_{0}^{\prime })^{n_{0}}$, and forming a similar coCartesian diagram to
$(t_{0}^{\prime })^{n_{0}}$, and forming a similar coCartesian diagram to 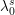 $\unicode[STIX]{x1D706}_{0}^{s}$. We now play exactly the same game for all of the
$\unicode[STIX]{x1D706}_{0}^{s}$. We now play exactly the same game for all of the 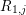 $R_{1,j}$, to produce
$R_{1,j}$, to produce  $\unicode[STIX]{x1D706}_{1,j}:R_{1,j}\rightarrow {\mathcal{O}}_{F_{1,j}}$ extending all other
$\unicode[STIX]{x1D706}_{1,j}:R_{1,j}\rightarrow {\mathcal{O}}_{F_{1,j}}$ extending all other  $\unicode[STIX]{x1D706}_{0}$ and all previous
$\unicode[STIX]{x1D706}_{0}$ and all previous 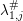 $\unicode[STIX]{x1D706}_{1,j}^{\#}$, which agree with
$\unicode[STIX]{x1D706}_{1,j}^{\#}$, which agree with  $\unicode[STIX]{x1D704}_{1,j}$ modulo
$\unicode[STIX]{x1D704}_{1,j}$ modulo  $(t_{1,j}^{\prime })^{n_{1,j}}$, and which form coCartesian diagrams
$(t_{1,j}^{\prime })^{n_{1,j}}$, and which form coCartesian diagrams
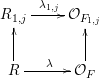
Now let  ${\mathcal{Z}}$ be the base change of
${\mathcal{Z}}$ be the base change of  ${\mathcal{Y}}$ to
${\mathcal{Y}}$ to  ${\mathcal{O}}_{F}$ via
${\mathcal{O}}_{F}$ via  $\unicode[STIX]{x1D706}$; note that the generic fibre
$\unicode[STIX]{x1D706}$; note that the generic fibre  ${\mathcal{Z}}_{F}$ is globally defined by construction. Similarly define
${\mathcal{Z}}_{F}$ is globally defined by construction. Similarly define  ${\mathcal{Z}}_{0}$ to be the base change of
${\mathcal{Z}}_{0}$ to be the base change of  ${\mathcal{Y}}_{0}$ to
${\mathcal{Y}}_{0}$ to  ${\mathcal{O}}_{F_{0}}$ via
${\mathcal{O}}_{F_{0}}$ via  $\unicode[STIX]{x1D706}_{0}$,
$\unicode[STIX]{x1D706}_{0}$,  ${\mathcal{Z}}_{1,j}$ the base change of
${\mathcal{Z}}_{1,j}$ the base change of  ${\mathcal{Y}}_{1,j}$ to
${\mathcal{Y}}_{1,j}$ to  ${\mathcal{O}}_{F_{1,j}}$ via
${\mathcal{O}}_{F_{1,j}}$ via  $\unicode[STIX]{x1D706}_{1,j}$, and
$\unicode[STIX]{x1D706}_{1,j}$, and 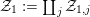 ${\mathcal{Z}}_{1}:=\coprod _{j}{\mathcal{Z}}_{1,j}$, so we have a 2-truncated augmented simplicial scheme
${\mathcal{Z}}_{1}:=\coprod _{j}{\mathcal{Z}}_{1,j}$, so we have a 2-truncated augmented simplicial scheme
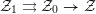 $$\begin{eqnarray}{\mathcal{Z}}_{1}\rightrightarrows {\mathcal{Z}}_{0}\rightarrow {\mathcal{Z}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{1}\rightrightarrows {\mathcal{Z}}_{0}\rightarrow {\mathcal{Z}}\end{eqnarray}$$ over  ${\mathcal{O}}_{F}$, which gives a proper hypercover after base changing to
${\mathcal{O}}_{F}$, which gives a proper hypercover after base changing to  $F$. For any
$F$. For any  $m\geqslant 2$ we can therefore take
$m\geqslant 2$ we can therefore take  $n_{1}\geqslant m\max _{j}\{[F_{1,j}:F]\}$ to ensure:
$n_{1}\geqslant m\max _{j}\{[F_{1,j}:F]\}$ to ensure:
–
 ${\mathcal{Z}}_{0}$ is a proper and strictly semistable scheme over
${\mathcal{Z}}_{0}$ is a proper and strictly semistable scheme over  ${\mathcal{O}}_{F_{0}}$, and each
${\mathcal{O}}_{F_{0}}$, and each  ${\mathcal{Z}}_{1,j}$ is a proper and strictly semistable scheme over
${\mathcal{Z}}_{1,j}$ is a proper and strictly semistable scheme over  ${\mathcal{O}}_{F_{1,j}}$;
${\mathcal{O}}_{F_{1,j}}$;– there is an isomorphism
of 2-truncated simplicial schemes, such that $$\begin{eqnarray}\left[{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\right]\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }\left[{\mathcal{Z}}_{1}\rightrightarrows {\mathcal{Z}}_{0}\right]\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$is in fact an isomorphism of
$$\begin{eqnarray}\left[{\mathcal{X}}_{1}\rightrightarrows {\mathcal{X}}_{0}\right]\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }\left[{\mathcal{Z}}_{1}\rightrightarrows {\mathcal{Z}}_{0}\right]\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$is in fact an isomorphism of $$\begin{eqnarray}{\mathcal{X}}_{0}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{0}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{0}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{0}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$ ${\mathcal{O}}_{F_{0}}/(t^{m})$-schemes, and is obtained as a disjoint union of isomorphisms
${\mathcal{O}}_{F_{0}}/(t^{m})$-schemes, and is obtained as a disjoint union of isomorphisms $$\begin{eqnarray}{\mathcal{X}}_{1}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{1}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$of
$$\begin{eqnarray}{\mathcal{X}}_{1}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{1}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$of $$\begin{eqnarray}{\mathcal{X}}_{1,j}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{1,j}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{1,j}\otimes {\mathcal{O}}_{F}/t^{m}\overset{{\sim}}{\rightarrow }{\mathcal{Z}}_{1,j}\otimes {\mathcal{O}}_{F}/t^{m}\end{eqnarray}$$ ${\mathcal{O}}_{F_{1,j}}/(t^{m})$-schemes.
${\mathcal{O}}_{F_{1,j}}/(t^{m})$-schemes.
Thus if we let 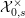 ${\mathcal{X}}_{0,s}^{\times }$ and
${\mathcal{X}}_{0,s}^{\times }$ and  ${\mathcal{Z}}_{0,s}^{\times }$ denote the log schemes over
${\mathcal{Z}}_{0,s}^{\times }$ denote the log schemes over  $k_{0}^{\times }$ given by the special fibres of
$k_{0}^{\times }$ given by the special fibres of  ${\mathcal{X}}_{0}$ and
${\mathcal{X}}_{0}$ and  ${\mathcal{Z}}_{0}$, and
${\mathcal{Z}}_{0}$, and  ${\mathcal{X}}_{1,s}^{\times }$ and
${\mathcal{X}}_{1,s}^{\times }$ and  ${\mathcal{Z}}_{1,s}^{\times }$ the log schemes over
${\mathcal{Z}}_{1,s}^{\times }$ the log schemes over  $\coprod _{j=1}^{s}\text{Spec}(k_{1,j}^{\times })$ given by the special fibres of
$\coprod _{j=1}^{s}\text{Spec}(k_{1,j}^{\times })$ given by the special fibres of 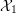 ${\mathcal{X}}_{1}$ and
${\mathcal{X}}_{1}$ and  ${\mathcal{Z}}_{1}$, then by Proposition 2.2 there is an isomorphism
${\mathcal{Z}}_{1}$, then by Proposition 2.2 there is an isomorphism
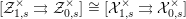 $$\begin{eqnarray}[{\mathcal{Z}}_{1,s}^{\times }\rightrightarrows {\mathcal{Z}}_{0,s}^{\times }]\cong [{\mathcal{X}}_{1,s}^{\times }\rightrightarrows {\mathcal{X}}_{0,s}^{\times }]\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{Z}}_{1,s}^{\times }\rightrightarrows {\mathcal{Z}}_{0,s}^{\times }]\cong [{\mathcal{X}}_{1,s}^{\times }\rightrightarrows {\mathcal{X}}_{0,s}^{\times }]\end{eqnarray}$$ of 2-truncated simplicial log schemes over 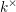 $k^{\times }$. Now by [Reference Chiarellotto and LazdaCL18, Propositions 5.3, 5.4] there are isomorphisms
$k^{\times }$. Now by [Reference Chiarellotto and LazdaCL18, Propositions 5.3, 5.4] there are isomorphisms
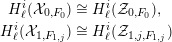 $$\begin{eqnarray}\displaystyle H_{\ell }^{i}({\mathcal{X}}_{0,F_{0}}) & \cong & \displaystyle H_{\ell }^{i}({\mathcal{Z}}_{0,F_{0}}),\nonumber\\ \displaystyle H_{\ell }^{i}({\mathcal{X}}_{1,F_{1,j}}) & \cong & \displaystyle H_{\ell }^{i}({\mathcal{Z}}_{1,j,F_{1,j}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\ell }^{i}({\mathcal{X}}_{0,F_{0}}) & \cong & \displaystyle H_{\ell }^{i}({\mathcal{Z}}_{0,F_{0}}),\nonumber\\ \displaystyle H_{\ell }^{i}({\mathcal{X}}_{1,F_{1,j}}) & \cong & \displaystyle H_{\ell }^{i}({\mathcal{Z}}_{1,j,F_{1,j}})\nonumber\end{eqnarray}$$ between the cohomology of the generic fibres of  ${\mathcal{X}}_{0},{\mathcal{X}}_{1,j}$ and
${\mathcal{X}}_{0},{\mathcal{X}}_{1,j}$ and 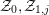 ${\mathcal{Z}}_{0},{\mathcal{Z}}_{1,j}$, as Weil–Deligne representations over
${\mathcal{Z}}_{0},{\mathcal{Z}}_{1,j}$, as Weil–Deligne representations over  $F_{0}$ and
$F_{0}$ and  $F_{1,j}$ respectively. If we define the category
$F_{1,j}$ respectively. If we define the category
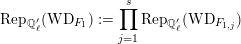 $$\begin{eqnarray}\text{Rep}_{\mathbb{Q}_{\ell }^{\prime }}(\text{WD}_{F_{1}}):=\mathop{\prod }_{j=1}^{s}\text{Rep}_{\mathbb{ Q}_{\ell }^{\prime }}(\text{WD}_{F_{1,j}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Rep}_{\mathbb{Q}_{\ell }^{\prime }}(\text{WD}_{F_{1}}):=\mathop{\prod }_{j=1}^{s}\text{Rep}_{\mathbb{ Q}_{\ell }^{\prime }}(\text{WD}_{F_{1,j}})\end{eqnarray}$$ of Weil–Deligne representations over  $F_{1}:=\prod _{j}F_{1,j}$ to be the product of the categories of Weil–Deligne representations over each
$F_{1}:=\prod _{j}F_{1,j}$ to be the product of the categories of Weil–Deligne representations over each  $F_{1,j}$, then by Propositions 3.1 and 3.2, the diagram
$F_{1,j}$, then by Propositions 3.1 and 3.2, the diagram
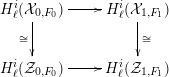
(with horizontal arrows given by the differences of the two pullback maps) commutes via the restriction functor from Weil–Deligne representations over  $F_{0}$ to Weil–Deligne representations over
$F_{0}$ to Weil–Deligne representations over  $F_{1}$.
$F_{1}$.
Let 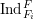 $\text{Ind}_{F_{i}}^{F}$ denote a right adjoint to the restriction functor from Weil–Deligne representations over
$\text{Ind}_{F_{i}}^{F}$ denote a right adjoint to the restriction functor from Weil–Deligne representations over 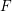 $F$ to those over
$F$ to those over 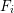 $F_{i}$: on the separable part this is the normal induction of representations, on the inseparable part it is a quasi-inverse to Frobenius pull-back, and
$F_{i}$: on the separable part this is the normal induction of representations, on the inseparable part it is a quasi-inverse to Frobenius pull-back, and  $\text{Ind}_{F_{1}}^{F}=\bigoplus _{j}\text{Ind}_{F_{1,j}}^{F}$. We therefore have a commutative diagram
$\text{Ind}_{F_{1}}^{F}=\bigoplus _{j}\text{Ind}_{F_{1,j}}^{F}$. We therefore have a commutative diagram

and, in particular, the kernels of both horizontal maps are isomorphic as Weil–Deligne representations over  $F$. The proof of Theorem 4.2 now boils down to the following claim.
$F$. The proof of Theorem 4.2 now boils down to the following claim.
Proposition 4.5. Let 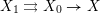 $X_{1}\rightrightarrows X_{0}\rightarrow X$ be a 2-truncated semisimplicial proper hypercover of a smooth and proper
$X_{1}\rightrightarrows X_{0}\rightarrow X$ be a 2-truncated semisimplicial proper hypercover of a smooth and proper 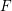 $F$-variety
$F$-variety  $X$, such that there exist finite field extensions
$X$, such that there exist finite field extensions  $F_{0}/F$ and
$F_{0}/F$ and 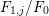 $F_{1,j}/F_{0}$ for
$F_{1,j}/F_{0}$ for  $1\leqslant j\leqslant s$, with
$1\leqslant j\leqslant s$, with  $X_{0}$ smooth over
$X_{0}$ smooth over  $F_{0}$, and
$F_{0}$, and 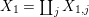 $X_{1}=\coprod _{j}X_{1,j}$ with
$X_{1}=\coprod _{j}X_{1,j}$ with  $X_{1,j}$ smooth over
$X_{1,j}$ smooth over 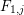 $F_{1,j}$. If we set
$F_{1,j}$. If we set 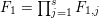 $F_{1}=\prod _{j=1}^{s}F_{1,j}$, then
$F_{1}=\prod _{j=1}^{s}F_{1,j}$, then
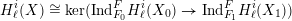 $$\begin{eqnarray}H_{\ell }^{i}(X)\cong \text{ker}(\text{Ind}_{F_{0}}^{F}H_{\ell }^{i}(X_{0})\rightarrow \text{Ind}_{F_{1}}^{F}H_{\ell }^{i}(X_{1}))\end{eqnarray}$$
$$\begin{eqnarray}H_{\ell }^{i}(X)\cong \text{ker}(\text{Ind}_{F_{0}}^{F}H_{\ell }^{i}(X_{0})\rightarrow \text{Ind}_{F_{1}}^{F}H_{\ell }^{i}(X_{1}))\end{eqnarray}$$ for all primes  $\ell$.
$\ell$.
Proof. By taking  $\widetilde{F}_{1}/F$ a sufficiently large finite extension such that all of the
$\widetilde{F}_{1}/F$ a sufficiently large finite extension such that all of the 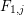 $F_{1,j}$ embed into
$F_{1,j}$ embed into 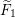 $\widetilde{F}_{1}$ and applying [Reference de JongdJ96, Theorem 4.1], we can extend
$\widetilde{F}_{1}$ and applying [Reference de JongdJ96, Theorem 4.1], we can extend  $X_{1}\rightrightarrows X_{0}\rightarrow X$ to a full proper hypercover
$X_{1}\rightrightarrows X_{0}\rightarrow X$ to a full proper hypercover  $X_{\bullet }\rightarrow X$ such that for
$X_{\bullet }\rightarrow X$ such that for 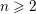 $n\geqslant 2$ there exists a finite extension
$n\geqslant 2$ there exists a finite extension  $F_{n}/\widetilde{F}_{1}$ with
$F_{n}/\widetilde{F}_{1}$ with 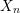 $X_{n}$ smooth over
$X_{n}$ smooth over  $F_{n}$. Now applying [Reference Chiarellotto and LazdaCL18, Lemma 6.4] we can see that the terms in
$F_{n}$. Now applying [Reference Chiarellotto and LazdaCL18, Lemma 6.4] we can see that the terms in  $i$th column of the resulting spectral sequence have to be ‘quasi-pure’ of weight
$i$th column of the resulting spectral sequence have to be ‘quasi-pure’ of weight  $i$. Therefore the spectral sequence degenerates exactly as in the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1], and the proposition follows.◻
$i$. Therefore the spectral sequence degenerates exactly as in the proof of [Reference Chiarellotto and LazdaCL18, Theorem 6.1], and the proposition follows.◻
We now deduce from the proposition that  $H_{\ell }^{i}(X)\cong H_{\ell }^{i}({\mathcal{Z}}_{F})$ as Weil–Deligne representations for all
$H_{\ell }^{i}(X)\cong H_{\ell }^{i}({\mathcal{Z}}_{F})$ as Weil–Deligne representations for all  $i,\ell$, and by construction
$i,\ell$, and by construction 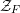 ${\mathcal{Z}}_{F}$ is globally defined. This completes the proof of Theorem 4.2
${\mathcal{Z}}_{F}$ is globally defined. This completes the proof of Theorem 4.2
Remark 4.6. Note the use of the finite field hypothesis (via a weight argument) in the proof of Proposition 4.5. It might be possible to relax the assumption to  $k$ perfect using a more sophisticated argument.
$k$ perfect using a more sophisticated argument.
Acknowledgements
Both authors would like to thank W. Zheng for pointing out the error in [Reference Chiarellotto and LazdaCL18], as well as L. Illusie for useful discussions concerning log structures, in particular the proof of Proposition 2.1. We would also like to thank the anonymous referee for a careful reading of an earlier version of the manuscript, in particular for correcting a mistake in our use of alterations.