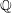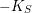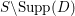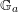Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marquand, Lisa
and
Won, Joonyeong
2018.
Cylinders in rational surfaces.
European Journal of Mathematics,
Vol. 4,
Issue. 3,
p.
1161.
Cheltsov, Ivan
Dubouloz, Adrien
and
Park, Jihun
2018.
Super-rigid affine Fano varieties.
Compositio Mathematica,
Vol. 154,
Issue. 11,
p.
2462.
Dubouloz, Adrien
and
Kishimoto, Takashi
2019.
Deformations of $$\mathbb {A}^1$$-cylindrical varieties.
Mathematische Annalen,
Vol. 373,
Issue. 3-4,
p.
1135.
PARK, JIHUN
2022.
$$ {\mathbbm{G}}_a $$-ACTIONS ON THE COMPLEMENTS OF HYPERSURFACES.
Transformation Groups,
Vol. 27,
Issue. 2,
p.
651.
Belousov, Grigory
2023.
Birational Geometry, Kähler–Einstein Metrics and Degenerations.
Vol. 409,
Issue. ,
p.
17.
Sawahara, Masatomo
2023.
Notes on cylinders in smooth projective surfaces.
Geometriae Dedicata,
Vol. 217,
Issue. 1,
SAWAHARA, MASATOMO
2023.
CYLINDERS IN WEAK DEL PEZZO FIBRATIONS.
Transformation Groups,
Vol. 28,
Issue. 1,
p.
413.
Arzhantsev, I.
and
the author
2023.
Automorphisms of algebraic varieties and infinite transitivity.
St. Petersburg Mathematical Journal,
Vol. 34,
Issue. 2,
p.
143.
Sawahara, Masatomo
2024.
Cylinders in canonical del Pezzo fibrations.
Annales de l'Institut Fourier,
Vol. 74,
Issue. 1,
p.
1.
Sawahara, Masatomo
2025.
Cylindrical ample divisors on Du Val del Pezzo surfaces.
Forum Mathematicum,