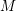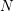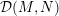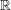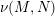Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Meinrenken, Eckhard
2021.
Euler-like vector fields, normal forms, and isotropic embeddings.
Indagationes Mathematicae,
Vol. 32,
Issue. 1,
p.
224.
Yi, Zelin
2021.
Lefschetz fixed point formula: Non-isometry case.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 12,
p.
5393.
Dang, Nguyen Viet
and
Wrochna, Michał
2022.
Dynamical residues of Lorentzian spectral zeta functions.
Journal de l’École polytechnique — Mathématiques,
Vol. 9,
Issue. ,
p.
1245.
Kotov, Alexei
Laurent-Gengoux, Camille
and
Salnikov, Vladimir
2023.
Normal forms of Z-graded Q-manifolds.
Journal of Geometry and Physics,
Vol. 191,
Issue. ,
p.
104908.
Loizides, Yiannis
and
Meinrenken, Eckhard
2023.
Differential geometry of weightings.
Advances in Mathematics,
Vol. 424,
Issue. ,
p.
109072.
Frejlich, Pedro
and
Mărcuţ, Ioan
2024.
Normal forms for principal Poisson Hamiltonian spaces.
Indagationes Mathematicae,
Vol. 35,
Issue. 2,
p.
288.
Haj Saeedi Sadegh, Ahmad Reza
Liu, Shiqi
Loizides, Yiannis
and
Sanchez, Jesus
2024.
A fixed-point formula for Dirac operators on Lie groupoids.
Journal of Functional Analysis,
Vol. 287,
Issue. 11,
p.
110624.
Schüßler, Andreas
2025.
On the real projective blowup of Poisson structures.
Differential Geometry and its Applications,
Vol. 101,
Issue. ,
p.
102293.