Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:53:12.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Derived subalgebras of centralisers and finite 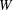$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  09 July 2014

Alexander Premet  and
Lewis Topley
Alexander Premet
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK email Alexander.Premet@manchester.ac.uk
Lewis Topley
Affiliation:
Department of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK email Lewis.Topley@uea.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 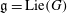$\mathfrak{g}=\mbox{Lie}(G)$ be the Lie algebra of a simple algebraic group 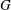$G$ over an algebraically closed field of characteristic 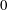$0$. Let $e$ be a nilpotent element of 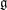$\mathfrak{g}$ and let 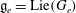$\mathfrak{g}_e=\mbox{Lie}(G_e)$ where 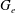$G_e$ stands for the stabiliser of $e$ in $G$. For 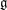$\mathfrak{g}$ classical, we give an explicit combinatorial formula for the codimension of 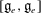$[\mathfrak{g}_e,\mathfrak{g}_e]$ in 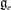$\mathfrak{g}_e$ and use it to determine those 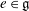$e\in \mathfrak{g}$ for which the largest commutative quotient 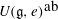$U(\mathfrak{g},e)^{\mbox{ab}}$ of the finite 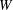$W$-algebra 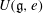$U(\mathfrak{g},e)$ is isomorphic to a polynomial algebra. It turns out that this happens if and only if $e$ lies in a unique sheet of 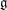$\mathfrak{g}$. The nilpotent elements with this property are called non-singular in the paper. Confirming a recent conjecture of Izosimov, we prove that a nilpotent element 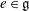$e\in \mathfrak{g}$ is non-singular if and only if the maximal dimension of the geometric quotients 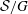$\mathcal{S}/G$, where 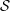$\mathcal{S}$ is a sheet of 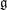$\mathfrak{g}$ containing $e$, coincides with the codimension of 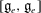$[\mathfrak{g}_e,\mathfrak{g}_e]$ in 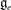$\mathfrak{g}_e$ and describe all non-singular nilpotent elements in terms of partitions. We also show that for any nilpotent element $e$ in a classical Lie algebra 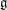$\mathfrak{g}$ the closed subset of Specm  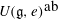$U(\mathfrak{g},e)^{\mbox{ab}}$ consisting of all points fixed by the natural action of the component group of 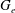$G_e$ is isomorphic to an affine space. Analogues of these results for exceptional Lie algebras are also obtained and applications to the theory of primitive ideals are given.

Keywords

simple Lie algebranilpotent elementprimitive idealfinite W-algebra

MSC classification

Secondary: 17B35: Universal enveloping (super)algebras 17B20: Simple, semisimple, reductive (super)algebras 17B63: Poisson algebras
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 9 , September 2014 , pp. 1485 - 1548
Copyright
© The Author(s) 2014 

References

Barbasch, D. and Vogan, D. A., Unipotent representations of complex semisimple groups, Ann. of Math. (2) 121 (1985), 41–110.Google Scholar
Blanc, P. and Brylinski, J.-L., Cyclic homology and the Selberg principle, J. Funct. Anal. 109 (1992), 289–330.Google Scholar
Borho, W., Primitive vollprime Ideale in der Enhüllenden von so(5, ℂ), J. Algebra 43 (1976), 619–654.Google Scholar
Borho, W., Über Schichten halbeinfacher Lie-Algebren, Invent. Math. 65 (1981), 283–317.Google Scholar
Borho, W., Gabriel, P. and Rentschler, R., Primideale in Einhüllenden auflösbarer Lie-Algebren, Lecture Notes in Mathematics, vol. 357 (Springer, Berlin, 1973).CrossRefGoogle Scholar
Borho, W. and Joseph, A., Sheets and topology of primitive spectra for semisimple Lie algebras, J. Algebra 244 (2001), 76–167; Corrigendum 259 (2003), 310–311.Google Scholar
Borho, W. and Kraft, H., Über Bahnen und deren Deformationen bei linearen Aktionen reduktiver Gruppen, Comment. Math. Helv. 54 (1979), 61–104.Google Scholar
Bourbaki, N., Groupes et algèbres de Lie, Chapitres IV, V, VI (Hermann, Paris, 1968).Google Scholar
Brundan, J., Mœglin’s theorem and Goldie rank polynomials in Cartan type A, Compositio Math. 147 (2011), 11741–11771.Google Scholar
Brundan, J., Goodwin, S. M. and Kleshchev, A., Highest weight theory for finite W-algebras, Int. Math. Res. Not. 15 (2008), Art. ID rnn051.Google Scholar
Brundan, J. and Kleshchev, A., Shifted Yangians and finite W-algebras, Adv. Math. 200 (2006), 136–195.Google Scholar
Brylinski, R., Dixmier algebras for classical complex nilpotent orbits via Kraft–Procesi models I, Progress in Mathematics, vol. 213 (Birkhäuser, Boston, 2003), 49–67.Google Scholar
Carter, R. W., Finite groups of Lie type—conjugacy classes and complex characters, 2nd edition (Wiley, New York, 1985).Google Scholar
Collingwood, D. H. and McGovern, W., Nilpotent orbits in semisimple Lie algebras (Van Nostrand Reinhold, New York, 1993).Google Scholar
Conze, N., Algèbres d’opérateurs différentiels et quotients des algèbres enveloppantes, Bull. Soc. Math. France 102 (1974), 379–415.Google Scholar
de Graaf, W. A. and Elashvili, A., Induced nilpotent orbits of the simple Lie algebras of exceptional type, Georgian Math. J. 2 (2009), 257–278.Google Scholar
de Graaf, W. A., Computations with nilpotent orbits in SLA, Preprint (2013), arXiv:1301.1149v1 [math.RA].Google Scholar
Dixmier, J., Algèbres enveloppantes (Gauthier-Villars, Paris, 1974).Google Scholar
Elashvili, A. G., Sheets of the exceptional Lie algebras, Studies in Algebra (Tbilisi University Press, Tbilisi, 1984), 171–194 (in Russian).Google Scholar
Elashvili, A. G. and Grélaud, G., Classification des éléments nilpotents compacts des algèbres de Lie simples, C. R. Acad. Sci. Paris, Série I 317 (1993), 445–447.Google Scholar
Fu, B., Extremal contractions, stratified Mukai flops and Springer maps, Adv. Math. 213 (2007), 165–182.Google Scholar
Fu, B., On ℚ-factorial terminalizations of nilpotent orbits, J. Math. Pures Appl. 93 (2010), 623–635.Google Scholar
Gan, W. L. and Ginzburg, V., Quantization of Slodowy slices, Int. Math. Res. Not. 5 (2002), 243–255.Google Scholar
Ginzburg, V., Harish–Chandra bimodules for quantized Slodowy slices, Represent. Theory 13 (2009), 236–271.Google Scholar
Goodwin, S. M., Röhrle, G. and Ubly, G., On 1-dimensional representations of finite W-algebras associated to simple Lie algebras of exceptional type, LMS J. Comput. Math. 13 (2010), 357–369.Google Scholar
Im Hof, A., The Sheets of a Classical Lie Algebra, PhD thesis, University of Basel, 2005, available at http://edoc.unibas.ch.Google Scholar
Izosimov, A., The derived algebra of a stabilizer, families of coadjoint orbits and sheets, Preprint (2012), arXiv:1202.1135v2 [math.RT].Google Scholar
Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren (Springer, Berlin, 1983).CrossRefGoogle Scholar
Jantzen, J. C., Nilpotent orbits in representation theory, in Representation and Lie theory, Progress in Mathematics, vol. 228, ed. Orsted, B. (Birkhäuser, Boston, 2004), 1–211.Google Scholar
Joseph, A., The minimal orbit in a semisimple Lie algebra and its associated maximal ideal, Ann. Sci. Éc. Norm. Supér. 9 (1976), 1–30.Google Scholar
Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra I, II, J. Algebra 65 (1980), 269–306.CrossRefGoogle Scholar
Joseph, A., On the associated variety of a primitive ideal, J. Algebra 93 (1985), 509–523.Google Scholar
Joseph, A., A surjectivity theorem for rigid highest weight modules, Invent. Math. 92 (1985), 567–596.Google Scholar
Katsylo, P. I., Sections of sheets in a reductive algebraic Lie algebra, Math. USSR-Izv. 20 (1983), 449–458.Google Scholar
Kempken, G., Induced conjugacy classes in classical Lie algebras, Abh. Math. Semin. Univ. Hambg. 53 (1983), 53–83.CrossRefGoogle Scholar
Kraft, H. and Procesi, C., On the geometry of conjugacy classes in classical groups, Comment. Math. Helv. 57 (1982), 539–602.Google Scholar
Lawther, R. and Testerman, D. M., Centres of centralizers of unipotent elements in simple algebraic groups, Preprint (2007), 301pp.Google Scholar
Lawther, R. and Testerman, D. M., Centres of centralizers of unipotent elements in simple algebraic groups, Mem. Amer. Math. Soc. 210 (2011), 188 pp.Google Scholar
Losev, I., Quantized symplectic actions and W-algebras, J. Amer. Math. Soc. 23 (2010), 35–59.CrossRefGoogle Scholar
Losev, I., Quantizations of nilpotent orbits vs 1-dimensional representations of W-algebras, Preprint (2010), arXiv:1004.1669v1 [math.RT].Google Scholar
Losev, I., 1-dimensional representations and parabolic induction for W-algebras, Adv. Math. 226 (2011), 4841–4883.Google Scholar
Losev, I., Finite-dimensional representations of W-algebras, Duke Math. J. 159 (2011), 99–143.Google Scholar
Losev, I., Dimensions of irreducible modules over W-algebras and Goldie ranks, Preprint (2012), arXiv:1209.1083v2 [math.RT].Google Scholar
Lusztig, G. and Spaltenstein, N., Induced unipotent classes, J. Lond. Math. Soc. (2) 19 (1979), 41–52.Google Scholar
Matsumura, H., Commutative ring theory, 2nd edition (Cambridge University Press, Cambridge, 1989); translated from the Japanese by Miles Reid.Google Scholar
McGovern, W. M., Completely prime primitive ideals and quantization, Mem. Amer. Math. Soc. 108(519) (1994), 67 pp.Google Scholar
Mœglin, C., Idéaux complètement premiers de l’algèbre enveloppante de gln(ℂ), J. Algebra 106 (1987), 287–366.Google Scholar
Mœglin, C., Modèle de Whittaker et idéaux primitifs complètement premiers dans les algèbres enveloppantes des algèbres de Lie semi-simples complexes II, Math. Scand. 63 (1988), 5–35.CrossRefGoogle Scholar
Moreau, A., On the dimension of the sheets of a reductive Lie algebra, J. Lie Theory 18 (2008), 671–696.Google Scholar
Moreau, A., Corrigendum to ‘On the dimension of the sheets of a reductive Lie algebra’, J. Lie Theory 23 (2013), 1075–1083.Google Scholar
Namikawa, Y., Induced nilpotent orbits and birational geometry, Adv. Math. 222 (2009), 547–564.Google Scholar
Panyushev, D. I., On reachable elements and the boundary of nilpotent orbits in simple Lie algebras, Bull. Sci. Math. 128 (2004), 859–870.Google Scholar
Premet, A., Special transverse slices and their enveloping algebras, Adv. Math. 170 (2002), 1–55; with an appendix by S. Skryabin.Google Scholar
Premet, A., Nilpotent orbits in good characteristic and the Kempf–Rousseau theory, J. Algebra 260 (2003), 338–366.Google Scholar
Premet, A., Enveloping algebras of Slodowy slices and the Joseph ideal, J. Eur. Math. Soc. (JEMS) 9 (2007), 487–543.Google Scholar
Premet, A., Commutative quotients of finite W-algebras, Adv. Math. 225 (2010), 269–306.Google Scholar
Premet, A., Enveloping algebras of Slodowy slices and Goldie rank, Transform. Groups 16 (2011), 857–888.CrossRefGoogle Scholar
Premet, A., Multiplicity-free primitive ideals associated with rigid nilpotent orbits, Transform. Groups 19 (2014), 569–641.CrossRefGoogle Scholar
Shafarevich, I. R., Basic algebraic geometry 1. Varieties in projective space, 2nd edition (Springer, Berlin, 1994); translated from the 1988 Russian edition and with notes by Miles Reid.Google Scholar
Spaltenstein, N., Classes unipotentes et sous-groupes de Borel, Lecture Notes in Mathematics, vol. 946 (Springer, Berlin, 1982).Google Scholar
Tauvel, P. and Yu, R., Lie algebras and algebraic groups (Springer, Berlin, 2005).Google Scholar
Topley, L., Invariants of centralisers in positive characteristic, J. Algebra 399 (2014), 1021–1055.Google Scholar
Yakimova, O., The centralisers of nilpotent elements in classical Lie algebras, Funct. Anal. Appl. 40 (2006), 42–51.Google Scholar
Yakimova, O., On the derived algebra of a centraliser, Bull. Sci. Math. 134 (2010), 579–587.Google Scholar