Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T09:00:37.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimensional reduction in cohomological Donaldson–Thomas theory

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  08 February 2022

Tasuki Kinjo
Tasuki Kinjo*
Affiliation:
Graduate School of Mathematical Science, The University of Tokyo, 3-8-1 Komaba, Meguroku, Tokyo 153-8914, Japan tasuki.kinjo@ipmu.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

For oriented 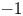$-1$-shifted symplectic derived Artin stacks, Ben-Bassat, Brav, Bussi and Joyce introduced certain perverse sheaves on them which can be regarded as sheaf-theoretic categorifications of the Donaldson–Thomas invariants. In this paper, we prove that the hypercohomology of the above perverse sheaf on the 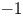$-1$-shifted cotangent stack over a quasi-smooth derived Artin stack is isomorphic to the Borel–Moore homology of the base stack up to a certain shift of degree. This is a global version of the dimensional reduction theorem due to Davison. We give two applications of our main theorem. Firstly, we apply it to the study of the cohomological Donaldson–Thomas invariants for local surfaces. Secondly, regarding our main theorem as a version of the Thom isomorphism theorem for dual obstruction cones, we propose a sheaf-theoretic construction of the virtual fundamental classes for quasi-smooth derived Artin stacks.

Keywords

cohomological Donaldson–Thomas theoryshifted symplectic geometryvirtual fundamental classes

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 1 , January 2022 , pp. 123 - 167
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by WINGS-FMSP.

References

Amorim, L. and Ben-Bassat, O., Perversely categorified Lagrangian correspondences, Adv. Theor. Math. Phys. 21 (2017), 289–381.10.4310/ATMP.2017.v21.n2.a1CrossRefGoogle Scholar
Aranha, D. and Pstrgowski, P., The intrinsic normal cone for Artin stacks, Preprint (2019), arXiv:1909.07478.Google Scholar
Behrend, K., Bryan, J. and Szendröi, B., Motivic degree zero Donaldson-Thomas invariants, Invent. Math. 192 (2013), 111–160.10.1007/s00222-012-0408-1CrossRefGoogle Scholar
Behrend, K. and Fantechi, B., The intrinsic normal cone, Invent. Math. 128 (1997), 45–88.CrossRefGoogle Scholar
Ben-Bassat, O., Brav, C., Bussi, V. and Joyce, D., A ‘Darboux Theorem’ for shifted symplectic structures on derived Artin stacks, with applications, Geom. Topol. 19 (2015), 1287–1359.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., Projectivity of the Witt vector affine Grassmannian, Invent. Math. 209 (2017), 329–423.10.1007/s00222-016-0710-4CrossRefGoogle Scholar
Borisov, D. and Joyce, D., Virtual fundamental classes for moduli spaces of sheaves on Calabi-Yau four-folds, Geom. Topol. 21 (2017), 3231–3311.CrossRefGoogle Scholar
Bozec, T., Calaque, D. and Scherotzke, S., Relative critical loci and quiver moduli, Preprint (2020), arXiv:2006.01069.Google Scholar
Brav, C., Bussi, V., Dupont, D., Joyce, D. and Szeondröi, B., Symmetries and stabilization for sheaves of vanishing cycles, J. Singul. 11 (2015), 85–151.Google Scholar
Brav, C., Bussi, V. and Joyce, D., A Darboux theorem for derived schemes with shifted symplectic structure, J. Amer. Math. Soc. 32 (2019), 399–443.10.1090/jams/910CrossRefGoogle Scholar
Brav, C. and Dyckerhoff, T., Relative Calabi-Yau structures, Compos. Math. 155 (2019), 372–412.10.1112/S0010437X19007024CrossRefGoogle Scholar
Brav, C. and Dyckerhoff, T., Relative Calabi-Yau structures II: Shifted Lagrangians in the moduli of objects, Selecta Math. 27 (2021), 63.CrossRefGoogle Scholar
Calaque, D., Shifted cotangent stacks are shifted symplectic, Ann. Fac. Sci. Toulouse Math. (6) 28 (2019), 67–90.CrossRefGoogle Scholar
Cao, Y. and Leung, C. L., Donaldson-Thomas theory for Calabi-Yau 4-folds, Preprint (2014), arXiv:1407.7659.Google Scholar
Davison, B., The integrality conjecture and the cohomology of preprojective stacks, Preprint (2016), arXiv:1602.02110.Google Scholar
Davison, B., The critical CoHA of a quiver with potential, Q. J. Math. 68 (2017), 635–703.CrossRefGoogle Scholar
Davison, B. and Meinhardt, S., Cohomological Donaldson-Thomas theory of a quiver with potential and quantum enveloping algebras, Invent. Math. 221 (2020), 777–871.CrossRefGoogle Scholar
Dimca, A., Sheaves in topology, Universitext (Springer, Berlin, 2004).CrossRefGoogle Scholar
Ikeda, A. and Qiu, Y., $q$-stability conditions on Calabi–Yau-$\mathbb {X}$ categories and twisted periods, Preprint (2018), arXiv:1807.00469.Google Scholar
Joyce, D., A classical model for derived critical loci, J. Differential Geom. 101 (2015), 289–367.CrossRefGoogle Scholar
Joyce, D. and Upmeier, M., Orientation data for moduli spaces of coherent sheaves over Calabi–Yau 3-folds, Adv. Math. 381 (2021), 107627.CrossRefGoogle Scholar
Kapranov, M. and Vasserot, E., The cohomological Hall algebra of a surface and factorization cohomology, Preprint (2019), arXiv:1901.07641.Google Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der Mathematischen Wissenschaften, vol. 292 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Khan, A., Virtual fundamental classes of derived stacks I, Preprint (2019), arXiv:1909.01332.Google Scholar
Kinjo, T., Virtual classes via vanishing cycles, Preprint (2021), arXiv:2109.06468.Google Scholar
Knudsen, F. and Mumford, D., The projectivity of the moduli space of stable curves. I. Preliminaries on ‘det’ and ‘Div’, Math. Scand. 39 (1976), 19–55.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson-Thomas invariants, Commun. Number Theory Phys. 5 (2011), 231–352.10.4310/CNTP.2011.v5.n2.a1CrossRefGoogle Scholar
Kresh, A., Cycle groups for Artin stacks, Invent. Math. 138 (1999), 495–536.CrossRefGoogle Scholar
Laszlo, Y. and Olsson, M., The six operations for sheaves on Artin stacks I: Finite coefficients, Publ. Math. Inst. Hautes Études Sci. 107 (2008), 109–168.10.1007/s10240-008-0011-6CrossRefGoogle Scholar
Laszlo, Y. and Olsson, M., Perverse $t$-structure on Artin stacks, Math. Z. 261 (2009), 737–748.CrossRefGoogle Scholar
Massey, D., Natural commuting of vanishing cycles and the Verdier dual, Pacific J. Math. 284 (2016), 431–437.CrossRefGoogle Scholar
Oh, J. and Thomas, R., Counting sheaves on Calabi-Yau 4-folds, I, Preprint (2020), arXiv:2009.05542.Google Scholar
Olsson, M., Sheaves on Artin stacks, J. Reine Angew. Math. 603 (2007), 55–112, https://math.berkeley.edu/molsson/qcohrevised.pdf.Google Scholar
Pantev, T., Toën, B., Vaquié, M. and Vezzosi, G., Shifted symplectic structures, Publ. Math. Inst. Hautes Études Sci. 117 (2013), 271–328.CrossRefGoogle Scholar
Schürman, J., Topology of singular spaces and constructible sheaves, Monografie Matematyczne, vol. 63 (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
Schwede, S. and Shipley, B., Stable model categories are categories of modules, Topology 42 (2003), 103–153.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks project (2020), https://stacks.math.columbia.edu.Google Scholar
Sun, S., Generic base change, Artin's comparison theorem, and the decomposition theorem for complex Artin stacks, J. Algebraic Geom. 26 (2017), 513–555.10.1090/jag/683CrossRefGoogle Scholar
Szendröi, B., Non-commutative Donaldson-Thomas theory and the conifold, Geom. Topol. 12 (2008), 1171–1202.CrossRefGoogle Scholar
Thomas, R., A holomorphic Casson invariant for Calabi-Yau 3-folds, and bundles on K3 fibrations, J. Differential Geom. 54 (2000), 367–438.CrossRefGoogle Scholar
Toda, Y., On categorical Donaldson–Thomas theory for local surfaces, Preprint (2019), arXiv:abs/1907.09076.Google Scholar
Toën, B. and Vaquié, M., Moduli of objects in dg-categories, Ann. Sci. Éc Norm. Supér. (4) 40 (2007), 387–444.CrossRefGoogle Scholar
Toën, B. and Vezzosi, G., Algebres simpliciales $S^{1}$-équivariantes, théorie de de Rham et théoremes HKR multiplicatifs, Compos. Math. 147 (2011), 1979–2000.CrossRefGoogle Scholar