Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T16:29:11.143Z Has data issue: false hasContentIssue false
  • English
  • Français

The diminished base locus is not always closed

Part of: Birational geometry

Published online by Cambridge University Press:  15 September 2014

John Lesieutre
John Lesieutre*
Affiliation:
Department of Mathematics, MIT, 77 Massachusetts Avenue, Cambridge, MA 02139, USA email johnl@math.mit.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

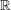We exhibit a pseudoeffective $\mathbb{R}$-divisor 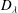${D}_{\lambda }$ on the blow-up of 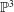${\mathbb{P}}^{3}$ at nine very general points which lies in the closed movable cone and has negative intersections with a set of curves whose union is Zariski dense. It follows that the diminished base locus 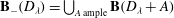${\boldsymbol{B}}_{-}({D}_{\lambda })={\bigcup }_{A\,\text{ample}}\boldsymbol{B}({D}_{\lambda }+A)$ is not closed and that 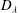${D}_{\lambda }$ does not admit a Zariski decomposition in even a very weak sense. By a similar method, we construct an 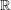$\mathbb{R}$-divisor on the family of blow-ups of 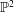${\mathbb{P}}^{2}$ at ten distinct points, which is nef on a very general fiber but fails to be nef over countably many prime divisors in the base.

Keywords

diminished base locusZariski decompositionCremona transformations

MSC classification

Secondary: 14E07: Birational automorphisms, Cremona group and generalizations 14E30: Minimal model program (Mori theory, extremal rays)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 10 , October 2014 , pp. 1729 - 1741
Copyright
© The Author 2014 

References

Bayraktar, T., Green currents for meromorphic maps of compact Kähler manifolds, J. Geom. Anal. (2012), 1–29.Google Scholar
Bedford, E. and Kim, K., On the degree growth of birational mappings in higher dimension, J. Geom. Anal. 14 (2004), 567–596.Google Scholar
Bedford, E. and Kim, K., Periodicities in linear fractional recurrences: degree growth of birational surface maps, Michigan Math. J. 54 (2006), 647–670.Google Scholar
Birkhoff, G., Linear transformations with invariant cones, Amer. Math. Monthly 74 (1967), 274–276.Google Scholar
Birkar, C., On existence of log minimal models and weak Zariski decompositions, Math. Ann. 354 (2012), 787–799.CrossRefGoogle Scholar
Coble, A. B., Algebraic geometry and theta functions, American Mathematical Society Colloquium Publications, vol. 10 (American Mathematical Society, Providence, RI, 1982); (Reprint of the 1929 edition).Google Scholar
Dolgachev, I. and Ortland, D., Point sets in projective spaces and theta functions, Astérisque, vol. 165 (Société de Mathématique de France, Paris, 1988).Google Scholar
Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M., Asymptotic invariants of base loci, Ann. Inst. Fourier (Grenoble) 56 (2006), 1701–1734.Google Scholar
Langer, A., On positivity and semistability of vector bundles in finite and mixed characteristics, J. Ramanujan Math. Soc. 28A (2013), 287–309.Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I (Springer, Berlin, 2004).CrossRefGoogle Scholar
Laface, A. and Ugaglia, L., On a class of special linear systems of ℙ3, Trans. Amer. Math. Soc. 358 (2006), 5485–5500.Google Scholar
Laface, A. and Ugaglia, L., Elementary (−1)-curves of ℙ3, Comm. Algebra 35 (2007), 313–324.Google Scholar
McMullen, C.T., Dynamics on blowups of the projective plane, Publ. Math. Inst. Hautes Études Sci. (2007), 49–89.Google Scholar
Mukai, S., Counterexample to Hilbert’s fourteenth problem for the 3-dimensional additive group, RIMS Kyoto Preprint 1343 (2001).Google Scholar
Nagata, M., On rational surfaces. II, Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 33 (1960/1961), 271–293.Google Scholar
Nakayama, N., Zariski-decomposition and Abundance, MSJ Memoirs, vol. 14 (Mathematical Society of Japan, Tokyo, 2004).Google Scholar
Prokhorov, Y. G., On the Zariski decomposition problem, Tr. Mat. Inst. Steklova 240 (2003), no. Biratsion. Geom. Linein. Sist. Konechno Porozhdennye Algebry, 43–72.Google Scholar
Perroni, F. and Zhang, D-Q, Pseudo-automorphisms of positive entropy on the blowups of products of projective spaces, Math. Ann. (2013), 1–21.Google Scholar