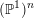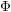Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ghioca, Dragos
and
Nguyen, Khoa
2018.
A dynamical variant of the Pink–Zilber
conjecture.
Algebra & Number Theory,
Vol. 12,
Issue. 7,
p.
1749.
Xie, Junyi
2018.
Algebraic dynamics of the lifts of Frobenius.
Algebra & Number Theory,
Vol. 12,
Issue. 7,
p.
1715.
Benedetto, Robert
Ingram, Patrick
Jones, Rafe
Manes, Michelle
Silverman, Joseph
and
Tucker, Thomas
2019.
Current trends and open problems in arithmetic dynamics.
Bulletin of the American Mathematical Society,
Vol. 56,
Issue. 4,
p.
611.
Bell, Jason P.
and
Ghioca, Dragos
2019.
Periodic subvarieties of semiabelian varieties and annihilators of irreducible representations.
Advances in Mathematics,
Vol. 349,
Issue. ,
p.
459.
Huang, Keping
2020.
A Gap Principle for Subvarieties with Finitely Many Periodic Points.
Canadian Mathematical Bulletin,
Vol. 63,
Issue. 2,
p.
382.
GHIOCA, DRAGOS
and
TUCKER, THOMAS J.
2021.
A REFORMULATION OF THE DYNAMICAL MANIN–MUMFORD CONJECTURE.
Bulletin of the Australian Mathematical Society,
Vol. 103,
Issue. 1,
p.
154.
Bridy, Andrew
Doyle, John R.
Ghioca, Dragos
Hsia, Liang-Chung
and
Tucker, Thomas J.
2021.
A question for iterated Galois groups in arithmetic dynamics.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 2,
p.
401.
Xie, Junyi
2022.
The existence of Zariski dense orbits for endomorphisms of projective surfaces.
Journal of the American Mathematical Society,
Vol. 38,
Issue. 1,
p.
1.
Peng, Wayne
2023.
Unlikely intersection problems for restricted lifts of a p-th power.
Journal of Number Theory,
Vol. 249,
Issue. ,
p.
21.
Mavraki, Niki Myrto
Schmidt, Harry
and
Wilms, Robert
2023.
Height coincidences in products of the projective line.
Mathematische Zeitschrift,
Vol. 304,
Issue. 2,
Pakovich, Fedor
2023.
Invariant curves for endomorphisms of $${{\mathbb {P}}}^1\times {{\mathbb {P}}}^1$$.
Mathematische Annalen,
Vol. 385,
Issue. 1-2,
p.
259.
Xie, Junyi
2024.
Algebraicity Criteria, Invariant Subvarieties and Transcendence Problems from Arithmetic Dynamics.
Peking Mathematical Journal,
Vol. 7,
Issue. 1,
p.
345.
Carter, Annie
Lalín, Matilde
Manes, Michelle
and
Miller, Alison Beth
2024.
Research Directions in Number Theory.
Vol. 33,
Issue. ,
p.
219.
Mavraki, Niki Myrto
and
Schmidt, Harry
2025.
On the dynamical Bogomolov conjecture for families of split rational maps.
Duke Mathematical Journal,
Vol. 174,
Issue. 5,
DeMarco, Laura
and
Mavraki, Niki Myrto
2025.
Geometry of PCF parameters in spaces of quadratic polynomials.
Algebra & Number Theory,
Vol. 19,
Issue. 11,
p.
2163.