Hostname: page-component-7b9c58cd5d-dlb68 Total loading time: 0 Render date: 2025-03-15T08:29:53.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic singularities on log symplectic manifolds and Feigin–Odesskii Poisson brackets

Part of: Singularities Surfaces and higher-dimensional varieties Symplectic geometry, contact geometry

Published online by Cambridge University Press:  13 March 2017

Brent Pym
Brent Pym*
Affiliation:
Mathematical Institute and Jesus College, University of Oxford, Woodstock Road, Oxford OX2 6GG, UK email pym@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A log symplectic manifold is a complex manifold equipped with a complex symplectic form that has simple poles on a hypersurface. The possible singularities of such a hypersurface are heavily constrained. We introduce the notion of an elliptic point of a log symplectic structure, which is a singular point at which a natural transversality condition involving the modular vector field is satisfied, and we prove a local normal form for such points that involves the simple elliptic surface singularities 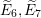$\widetilde{E}_{6},\widetilde{E}_{7}$ and 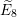$\widetilde{E}_{8}$. Our main application is to the classification of Poisson brackets on Fano fourfolds. For example, we show that Feigin and Odesskii’s Poisson structures of type 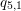$q_{5,1}$ are the only log symplectic structures on projective four-space whose singular points are all elliptic.

Keywords

Poisson structureelliptic curveFano manifoldhypersurface singularitylogarithmic differential form

MSC classification

Primary: 53D17: Poisson manifolds; Poisson groupoids and algebroids 32S25: Surface and hypersurface singularities 32S65: Singularities of holomorphic vector fields and foliations 14J45: Fano varieties
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 4 , April 2017 , pp. 717 - 744
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleksandrov, A. G., Nonisolated Saito singularities , Mat. Sb. (N.S.) 137(179) (1988), 554–567, 576; MR 981525 (90b:32024).Google Scholar
Aleksandrov, A. G., Nonisolated hypersurface singularities , in Theory of singularities and its applications, Advances in Soviet Mathematics, vol. 1 (American Mathematical Society, Providence, RI, 1990), 211–246; MR 1089679 (92b:32039).Google Scholar
Atiyah, M. and Hitchin, N., The geometry and dynamics of magnetic monopoles, M. B. Porter Lectures (Princeton University Press, Princeton, NJ, 1988); MR 934202 (89k:53067).CrossRefGoogle Scholar
Barlet, D., Le faisceau 𝜔 X ⋅ sur un espace analytique X de dimension pure , in Fonctions de plusieurs variables complexes, III (Sém. François Norguet, 1975–1977), Lecture Notes in Mathematics, vol. 670 (Springer, Berlin, 1978), 187–204; MR 521919 (80i:32037).Google Scholar
Bartocci, C. and Macrí, E., Classification of Poisson surfaces , Commun. Contemp. Math. 7 (2005), 89–95; MR 2129789 (2005m:14064).Google Scholar
Bondal, A. I., Non-commutative deformations and Poisson brackets on projective spaces, Preprint (1993), Max-Planck Institute Report no. 93-67.Google Scholar
Bottacin, F., Poisson structures on Hilbert schemes of points of a surface and integrable systems , Manuscripta Math. 97 (1998), 517–527; MR 1660136 (99m:14003).Google Scholar
Buchsbaum, D. A. and Eisenbud, D., Algebra structures for finite free resolutions, and some structure theorems for ideals of codimension 3 , Amer. J. Math. 99 (1977), 447–485; MR 0453723 (56 #11983).CrossRefGoogle Scholar
Bursztyn, H. and Radko, O., Gauge equivalence of Dirac structures and symplectic groupoids , Ann. Inst. Fourier (Grenoble) 53 (2003), 309–337; MR 1973074 (2004d:53101).Google Scholar
Castro-Jiménez, F. J., Narváez-Macarro, L. and Mond, D., Cohomology of the complement of a free divisor , Trans. Amer. Math. Soc. 348 (1996), 3037–3049; MR 1363009 (96k:32072).Google Scholar
Cavalcanti, G. R., Examples and counter-examples of log-symplectic manifolds, Preprint (2013), arXiv:1303.6420.Google Scholar
Cavalcanti, G. R. and Gualtieri, M., Stable generalized complex structures, Preprint (2015), arXiv:1503.06357.Google Scholar
Cerveau, D. and Lins Neto, A., Irreducible components of the space of holomorphic foliations of degree two in CP(n), n⩾3 , Ann. of Math. (2) 143 (1996), 577–612; MR 1394970 (97i:32039).Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, Berlin, 1970); MR 0417174 (54 #5232).Google Scholar
Dongho, J., Logarithmic Poisson cohomology: example of calculation and application to prequantization , Ann. Fac. Sci. Toulouse Math. (6) 21 (2012), 623–650; MR 3052027.Google Scholar
Druel, S., Structures de Poisson sur les variétés algébriques de dimension 3 , Bull. Soc. Math. France 127 (1999), 229–253; MR 1708651 (2000h:14013).Google Scholar
Ellingsrud, G. and Laksov, D., The normal bundle of elliptic space curves of degree 5 , in 18th Scandinavian Congress of Mathematicians (Aarhus, 1980), Progress in Mathematics, vol. 11 (Birkhäuser, Boston, MA, 1981), 258–287; MR 633362 (83h:14006).Google Scholar
Eriksen, E. and Gustavsen, T. S., Lie–Rinehart cohomology and integrable connections on modules of rank one , J. Algebra 322 (2009), 4283–4294; MR 2558865 (2011d:13040).Google Scholar
Etingof, P. and Ginzburg, V., Noncommutative del Pezzo surfaces and Calabi–Yau algebras , J. Eur. Math. Soc. (JEMS) 12 (2010), 1371–1416; MR 2734346 (2012d:16082).Google Scholar
Feĭgin, B. L. and Odesskiĭ, A. V., Sklyanin’s elliptic algebras , Funktsional. Anal. i Prilozhen. 23 (1989), 45–54; 96; MR 1026987 (91e:16037).Google Scholar
Feĭgin, B. L. and Odesskiĭ, A. V., Vector bundles on an elliptic curve and Sklyanin algebras , in Topics in quantum groups and finite-type invariants, American Mathematical Society Translations, Series 2, vol. 185 (American Mathematical Society, Providence, RI, 1998), 65–84; MR 1736164 (2001f:14063).Google Scholar
Goto, R., Unobstructed deformations of generalized complex structures induced by C ∞ logarithmic symplectic structures and logarithmic Poisson structures , in Geometry and topology of manifolds, Springer Proceedings in Mathematics & Statistics, vol. 154, eds Futaki, A., Miyaoka, R., Tang, Z. and Zhang, W. (Springer, Tokyo, 2016).Google Scholar
Goto, R., Rozansky–Witten invariants of log symplectic manifolds , in Integrable systems, topology, and physics (Tokyo, 2000), Contemporary Mathematics, vol. 309 (American Mathematical Society, Providence, RI, 2002), 69–84; MR 1953353 (2004b:53065).Google Scholar
Graf v. Bothmer, H.-C. and Hulek, K, Geometric syzygies of elliptic normal curves and their secant varieties , Manuscripta Math. 113 (2004), 35–68; MR 2135560 (2006b:14009).Google Scholar
Gualtieri, M. and Li, S., Symplectic groupoids of log symplectic manifolds , Int. Math. Res. Not. IMRN (2014), 3022–3074; MR 3214314.Google Scholar
Gualtieri, M., Li, S., Pelayo, A. and Ratiu, T., The tropical momentum map: a classification of toric log symplectic manifolds , Math. Ann. (2016), doi:10.1007/s00208-016-1427-9.Google Scholar
Guillemin, V., Miranda, E. and Pires, A. R., Symplectic and Poisson geometry on b-manifolds , Adv. Math. 264 (2014), 864–896; MR 3250302.Google Scholar
Guillemin, V., Miranda, E., Pires, A. R. and Scott, G., Toric actions on b-symplectic manifolds , Int. Math. Res. Not. IMRN (2015), 5818–5848.Google Scholar
Gualtieri, M. and Pym, B., Poisson modules and degeneracy loci , Proc. Lond. Math. Soc. (3) 107 (2013), 627–654; MR 3100779.Google Scholar
Hartshorne, R., Stable reflexive sheaves , Math. Ann. 254 (1980), 121–176; MR 597077 (82b:14011).Google Scholar
Hulek, K., Projective geometry of elliptic curves , in Algebraic geometry—open problems (Ravello, 1982), Lecture Notes in Mathematics, vol. 997 (Springer, Berlin, 1983), 228–266; MR 714752 (85g:14035).Google Scholar
Ingalls, C., Quantizable orders over surfaces , J. Algebra 207 (1998), 616–656; MR 1644207 (99h:14045).Google Scholar
Lima, R. and Vitório Pereira, J., A characterization of diagonal Poisson structures , Bull. Lond. Math. Soc. 46 (2014), 1203–1217; MR 3291256.Google Scholar
Loray, F., Vitório Pereira, J. and Touzet, F., Foliations with trivial canonical bundle on Fano 3-folds , Math. Nachr. 286 (2013), 921–940; MR 3066408.Google Scholar
Mărcuţ, I. and Osorno Torres, B., Deformations of log-symplectic structures , J. Lond. Math. Soc. (2) 90 (2014), 197–212; MR 3245143.Google Scholar
Mărcuţ, I. and Osorno Torres, B., On cohomological obstructions for the existence of log-symplectic structures , J. Symplectic Geom. 12 (2014), 863–866; MR 3333030.Google Scholar
Nevins, T. A. and Stafford, J. T., Sklyanin algebras and Hilbert schemes of points , Adv. Math. 210 (2007), 405–478; MR 2303228 (2008f:14002).Google Scholar
Nest, R. and Tsygan, B., Formal deformations of symplectic manifolds with boundary , J. Reine Angew. Math. 481 (1996), 27–54; MR 1421945 (98f:58093).Google Scholar
Polishchuk, A., Algebraic geometry of Poisson brackets , J. Math. Sci. (N.Y.) 84 (1997), 1413–1444; Algebraic geometry, 7. MR 1465521 (98d:58065).Google Scholar
Polishchuk, A., Poisson structures and birational morphisms associated with bundles on elliptic curves , Int. Math. Res. Not. IMRN (1998), 683–703; MR 1636545 (99f:14014).Google Scholar
Radko, O., A classification of topologically stable Poisson structures on a compact surface , J. Symplectic Geom. 1 (2002), 523–542.Google Scholar
Ran, Z., Deformations of holomorphic pseudo-symplectic Poisson manifolds , Adv. Math. 304 (2017), 1156–1175.Google Scholar
Saito, K., Quasihomogene isolierte Singularitäten von Hyperflächen , Invent. Math. 14 (1971), 123–142; MR 0294699 (45 #3767).Google Scholar
Saito, K., Theory of logarithmic differential forms and logarithmic vector fields , J. Fac. Sci. Univ. Tokyo Sect. IA Math. 27 (1980), 265–291; MR 586450 (83h:32023).Google Scholar
Terao, H., Arrangements of hyperplanes and their freeness. I , J. Fac. Sci. Univ. Tokyo Sect. IA Math. 27 (1980), 293–312; MR 586451 (84i:32016a).Google Scholar
Weinstein, A., The local structure of Poisson manifolds , J. Differential Geom. 18 (1983), 523–557; MR 723816 (86i:58059).CrossRefGoogle Scholar
Weinstein, A., The modular automorphism group of a Poisson manifold , J. Geom. Phys. 23 (1997), 379–394; MR 1484598 (98k:58095).Google Scholar