Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T23:45:09.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic Springer theory

Part of: Curves Lie groups

Published online by Cambridge University Press:  08 April 2015

David Ben-Zvi  and
David Nadler
David Ben-Zvi
Affiliation:
Department of Mathematics, University of Texas, Austin, TX 78712-0257, USA email benzvi@math.utexas.edu
David Nadler
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA email nadler@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce an elliptic version of the Grothendieck–Springer sheaf and establish elliptic analogues of the basic results of Springer theory. From a geometric perspective, our constructions specialize geometric Eisenstein series to the resolution of degree-zero, semistable 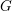$G$-bundles by degree-zero 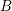$B$-bundles over an elliptic curve 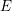$E$. From a representation theory perspective, they produce a full embedding of representations of the elliptic or double affine Weyl group into perverse sheaves with nilpotent characteristic variety on the moduli of 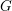$G$-bundles over 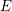$E$. The resulting objects are principal series examples of elliptic character sheaves, objects expected to play the role of character sheaves for loop groups.

Keywords

Springer theoryprincipal bundles on elliptic curves

MSC classification

Primary: 22E57: Geometric Langlands program
Secondary: 14H60: Vector bundles on curves and their moduli
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 8 , August 2015 , pp. 1568 - 1584
Copyright
© The Authors 2015 

References

Arinkin, D. and Gaitsgory, D., Singular support of coherent sheaves and the geometric Langlands conjecture, Selecta Math. (N.S.) 21 (2015), 1–199.CrossRefGoogle Scholar
Atiyah, M., Vector bundles over an elliptic curve, Proc. Lond. Math. Soc. (3) 7 (1957), 414–452.CrossRefGoogle Scholar
Baranovsky, V. and Ginzburg, V., Conjugacy classes in loop groups and G-bundles on elliptic curves, Int. Math. Res. Not. IMRN 15 (1996), 734–751.Google Scholar
Ben-Zvi, D. and Nadler, D., The character theory of a complex group, Preprint (2009),arXiv:0904.1247.Google Scholar
Ben-Zvi, D., Nadler, D. and Preygel, A., A spectral incarnation of affine character sheaves, Preprint (2013), arXiv:1312.7163.Google Scholar
Ben-Zvi, D. and Nevins, T., From solitons to many-body systems, Pure Appl. Math. Q. 4 (2008), Special Issue: in honor of Fedor Bogomolov, Part 1, 319–361.CrossRefGoogle Scholar
Bezrukavnikov, R., Noncommutative counterparts of the Springer resolution, in International Congress of Mathematicians, vol. II (European Mathematical Society, Zürich, 2006), 1119–1144.Google Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra, Preprint (2012),arXiv:1209.0403.Google Scholar
Borho, W. and MacPherson, R., Représentations des groupes de Weyl et homologie d’intersection pour les variétés nilpotentes, C. R. Acad. Sci. Paris Sér. I Math. 292 (1981), 707–710.Google Scholar
Braverman, A. and Gaitsgory, D., Geometric Eisenstein series, Invent. Math. 150 (2002), 287–384.CrossRefGoogle Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, 1997).Google Scholar
de Cataldo, M. A. and Migliorini, L., The decomposition theorem, perverse sheaves and the topology of algebraic maps, Bull. Amer. Math. Soc. (N.S.) 4 (2009), 535–633.CrossRefGoogle Scholar
Etingof, P., Frenkel, I. and Kirillov , A. Jr, Spherical functions on affine Lie groups, Duke Math. J. 80 (1995), 59–90.CrossRefGoogle Scholar
Friedman, R. and Morgan, J., Principal G-bundles over elliptic curves, Math. Res. Lett. 5 (1998), 97–118.CrossRefGoogle Scholar
Friedman, R., Morgan, J. and Witten, E., Vector bundles and F theory, Comm. Math. Phys. 187 (1997), 679–743.CrossRefGoogle Scholar
Ginzburg, V., Intégrales sur les orbites nilpotentes et représentations des groupes de Weyl, C. R. Acad. Sci. Paris Sèr. I Math. 296 (1983), 249–252.Google Scholar
Ginzburg, V., Admissible modules on a symmetric space, in Orbites unipotentes et représentations, III, Astérisque, vol. 173–174 (Société Mathématique de France, Paris, 1989), 9–10, 199–255.Google Scholar
Ginzburg, V., Isospectral commuting variety, the Harish-Chandra D-module, and principal nilpotent pairs, Duke Math. J. 161 (2012), 2023–2111.CrossRefGoogle Scholar
Gunningham, S., Categorified harmonic analysis on complex reductive groups, PhD thesis, Northwestern University (2013).Google Scholar
Hotta, R. and Kashiwara, M., The invariant holonomic system on a semisimple Lie algebra, Invent. Math. 75 (1984), 327–358.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., A topological approach to Springer’s representations, Adv. Math. 38 (1980), 222–228.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne-Langlands conjecture for Hecke algebras, Invent. Math. 87 (1987), 153–215.CrossRefGoogle Scholar
Laszlo, Y., About G-bundles over elliptic curves, Ann. Inst. Fourier (Grenoble) 48 (1998), 413–424.CrossRefGoogle Scholar
Laumon, G., Faisceaux automorphes liés aux séries d’Eisenstein, in Automorphic forms, Shimura varieties, and L-functions, Vol. I (Ann Arbor, MI, 1988), Perspectives in Mathematics vol. 10 (Academic Press, Boston, 1990), 227–281.Google Scholar
Lusztig, G., Green polynomials and singularities of unipotent classes, Adv. Math. 42 (1981), 169–178.CrossRefGoogle Scholar
Lusztig, G., Character sheaves I, Adv. Math. 56 (1985), 193–237.CrossRefGoogle Scholar
Mirković, I. and Vilonen, K., Characteristic varieties of character sheaves, Invent. Math. 93 (1988), 405–418.CrossRefGoogle Scholar
Nadler, D., Springer theory via the Hitchin fibration, Compositio Math. 147 (2011), 1635–1670.CrossRefGoogle Scholar
Ngô, B. C., Le lemme fondamental pour les algèbres de Lie, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 1–169.CrossRefGoogle Scholar
Ramanathan, A., Stable principal bundles on a compact Rieman surface, Math. Ann. 213 (1975), 129–152.CrossRefGoogle Scholar
Ramanathan, A., Moduli for principal bundles over algebraic curves, I and II, Proc. Indian Acad. Sci. Math. Sci. 106 (1996), 301–328; 421–449.CrossRefGoogle Scholar
Rider, L., Formality for the nilpotent cone and a derived Springer correspondence, Adv. Math. 235 (2013), 208–236.CrossRefGoogle Scholar
Schiffmann, O., Spherical Hall algebras of curves and Harder-Narasimhan stratas, J. Korean Math. Soc. 48 (2011), 953–967.CrossRefGoogle Scholar
Schiffmann, O., On the Hall algebra of an elliptic curve, II, Duke Math. J. 161 (2012), 1711–1750.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E., The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials, Compositio Math. 147 (2011), 188–234.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E., Hall algebras of curves, commuting varieties and Langlands duality, Math. Ann. 353 (2012), 1399–1451.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E., The elliptic Hall algebra and the equivariant K-theory of the Hilbert scheme of A2, Duke Math. J. 162 (2013), 279–366.CrossRefGoogle Scholar
Springer, T. A., Trigonometric sums, Green functions of finite groups and representations of Weyl groups, Invent. Math. 36 (1976), 173–207.CrossRefGoogle Scholar
Springer, T. A., A construction of representations of Weyl groups, Invent. Math. 44 (1978), 279–293.CrossRefGoogle Scholar
Springer, T. A., Quelques applications de la cohomologie d’intersection, in Séminar Bourbaki, Vol. 24 (1981–1982), Astérisque, vol. 92–93 (Société Mathématique de France, Paris, 1982), 249–273.Google Scholar