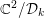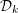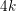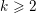Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Foscolo, Lorenzo
2020.
Lectures and Surveys on G2-Manifolds and Related Topics.
Vol. 84,
Issue. ,
p.
173.
Schroers, B J
and
Singer, M A
2021.
Dk Gravitational Instantons as Superpositions of Atiyah–Hitchin and Taub–NUT Geometries.
The Quarterly Journal of Mathematics,
Vol. 72,
Issue. 1-2,
p.
277.
Ozuch, Tristan
2022.
Noncollapsed degeneration of Einstein
4–manifolds, II.
Geometry & Topology,
Vol. 26,
Issue. 4,
p.
1529.
Ozuch, Tristan
2024.
Integrability of Einstein deformations and desingularizations.
Communications on Pure and Applied Mathematics,
Vol. 77,
Issue. 1,
p.
177.