Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T09:20:06.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois symmetries of knot spaces

Part of: Differential topology Homotopy groups

Published online by Cambridge University Press:  29 April 2021

Pedro Boavida de Brito  and
Geoffroy Horel
Pedro Boavida de Brito
Affiliation:
Department of Mathematics, IST, Universidade de Lisboa, Av. Rovisco Pais, 1049–001 Lisboa, Portugalpedrobbrito@tecnico.ulisboa.pt
Geoffroy Horel
Affiliation:
Université Sorbonne Paris Nord, LAGA, CNRS, UMR 7539, F-93430, Villetaneuse, Francehorel@math.univ-paris13.fr École Normale Supérieure, DMA, CNRS, UMR 8553, 45 rue d'Ulm, 75230Paris Cedex 05, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We exploit the Galois symmetries of the little disks operads to show that many differentials in the Goodwillie–Weiss spectral sequences approximating the homology and homotopy of knot spaces vanish at a prime 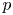$p$. Combined with recent results on the relationship between embedding calculus and finite-type theory, we deduce that the 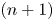$(n+1)$th Goodwillie–Weiss approximation is a 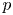$p$-local universal Vassiliev invariant of degree 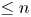$\leq n$ for every 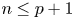$n \leq p + 1$.

Keywords

finite-type invariantsmanifold calculusspaces of knotslittle disks operad

MSC classification

Primary: 57R40: Embeddings 55Q99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 5 , May 2021 , pp. 997 - 1021
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We gratefully acknowledge the support through: grant SFRH/BPD/99841/2014 and project MAT-PUR/31089/2017, funded by Fundação para a Ciência e Tecnologia; projects ANR-14-CE25-0008 SAT, ANR-16-CE40-0003 ChroK, ANR-18-CE40-0017 PerGAMo, funded by Agence Nationale pour la Recherche.

References

Arone, G., Lambrechts, P., Turchin, V. and Volić, I., Coformality and rational homotopy groups of spaces of long knots, Math. Res. Lett. 15 (2008), 1–15.CrossRefGoogle Scholar
Bar-Natan, D., On the Vassiliev knot invariants, Topology 34 (1995), 423–472.CrossRefGoogle Scholar
Boavida de Brito, P. and Horel, G., On the formality of the little disks operad in positive characteristic, J. London Math. Soc. (2021), https://doi.org/10.1112/jlms.12442.CrossRefGoogle Scholar
Boavida de Brito, P. and Weiss, M., Spaces of smooth embeddings and configuration categories, J. Topol. 11 (2018), 65–143.CrossRefGoogle Scholar
Boavida de Brito, P. and Weiss, M. S., The configuration category of a product, Proc. Amer. Math. Soc. 146 (2018), 4497–4512.CrossRefGoogle Scholar
Bousfield, A. K., The localization of spaces with respect to homology, Topology 14 (1975), 133–150.CrossRefGoogle Scholar
Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, vol. 304 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Budney, R., Conant, J., Koytcheff, R. and Sinha, D., Embedding calculus knot invariants are of finite type, Algebr. Geom. Topol. 17 (2017), 1701–1742.CrossRefGoogle Scholar
Budney, R., Conant, J., Scannell, K. P. and Sinha, D., New perspectives on self-linking, Adv. Math. 191 (2005), 78–113.CrossRefGoogle Scholar
Cisinski, D. and Moerdijk, I., Dendroidal sets and simplicial operads, J. Topol. 6 (2013), 705–756.CrossRefGoogle Scholar
Conant, J., Homotopy approximations to the space of knots, Feynman diagrams, and a conjecture of Scannell and Sinha, Amer. J. Math. 130 (2008), 341–357.CrossRefGoogle Scholar
Conant, J. and Teichner, P., Grope cobordism and Feynman diagrams, Math. Ann. 328 (2004), 135–171.CrossRefGoogle Scholar
Drinfel'd, V. G., On quasitriangular quasi-Hopf algebras and on a group that is closely connected with $\textrm {Gal}(\bar {\textbf {Q}}/\textbf {Q})$, Algebra i Analiz 2 (1990), 149–181.Google Scholar
Dwyer, W. and Hess, K., Long knots and maps between operads, Geom. Topol. 16 (2012), 919–955.CrossRefGoogle Scholar
Furusho, H., Galois action on knots I: Action of the absolute Galois group, Quantum Topol. 8 (2017), 295–360.CrossRefGoogle Scholar
Goodwillie, T. G. and Klein, J. R., Multiple disjunction for spaces of smooth embeddings, J. Topol. 8 (2015), 651–674.CrossRefGoogle Scholar
Goodwillie, T. G. and Weiss, M., Embeddings from the point of view of immersion theory. II, Geom. Topol. 3 (1999), 103–118.CrossRefGoogle Scholar
Göppl, F., A spectral sequence for spaces of maps between operads, Preprint (2018), arXiv:1810.05589.Google Scholar
Gusarov, M., On n-equivalence of knots and invariants of finite degree, in Topology of manifolds and varieties, Advances in Soviet Mathematics, vol. 18 (American Mathematical Society, Providence, RI, 1994), 173–192.CrossRefGoogle Scholar
Horel, G., Groupe de galois et espace des noeuds, in SMF 2018: Congrès de la SMF, Séminaires et Congrès, vol. 33 (Société Mathématique de France, Paris, 2019), 273–282.Google Scholar
Kassel, C. and Turaev, V., Chord diagram invariants of tangles and graphs, Duke Math. J. 92 (1998), 497–552.CrossRefGoogle Scholar
Kosanović, D., Embedding calculus and grope cobordism of knots, Preprint (2020), arXiv:2010.05120.Google Scholar
Lambrechts, P., Turchin, V. and Volić, I., The rational homology of spaces of long knots in codimension $>2$, Geom. Topol. 14 (2010), 2151–2187.CrossRefGoogle Scholar
Muro, F., Homotopy theory of non-symmetric operads. II: Change of base category and left properness, Algebr. Geom. Topol. 14 (2014), 229–281.CrossRefGoogle Scholar
Shi, Y., Goodwillie's cosimplicial model for the space of long knots and its applications, Preprint (2020), arXiv:2012.04036.Google Scholar
Sinha, D., Operads and knot spaces, J. Amer. Math. Soc. 19 (2006), 461–486.CrossRefGoogle Scholar
Sinha, D. P., The topology of spaces of knots: cosimplicial models, Amer. J. Math. 131 (2009), 945–980.CrossRefGoogle Scholar
Turchin, V., Delooping totalization of a multiplicative operad, J. Homotopy Relat. Struct. 9 (2014), 349–418.10.1007/s40062-013-0032-9CrossRefGoogle Scholar
Vasil'ev, V. A., Complements of discriminants of smooth maps: topology and applications (revised edition), in Translations of Mathematical Monographs, vol. 98 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Volić, I., Finite type knot invariants and the calculus of functors, Compos. Math. 142 (2006), 222–250.CrossRefGoogle Scholar