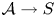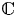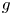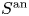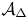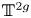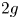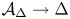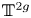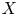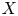1. Introduction
Let ![]() $S$ be an irreducible variety over
$S$ be an irreducible variety over ![]() $\mathbb {C}$, and let
$\mathbb {C}$, and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g$, namely a proper smooth group scheme whose fibers are abelian varieties.
$g$, namely a proper smooth group scheme whose fibers are abelian varieties.
For any ![]() $s \in S(\mathbb {C})$, there exists an open neighborhood
$s \in S(\mathbb {C})$, there exists an open neighborhood ![]() $\Delta \subseteq S^{\mathrm {an}}$ of
$\Delta \subseteq S^{\mathrm {an}}$ of ![]() $s$ with a real-analytic map, which we call the Betti map,
$s$ with a real-analytic map, which we call the Betti map,
where ![]() $\mathbb {T}^{2g}$ is the real torus of dimension
$\mathbb {T}^{2g}$ is the real torus of dimension ![]() $2g$. The precise definition will be given in (4.2), but we give a brief explanation here: up to shrinking
$2g$. The precise definition will be given in (4.2), but we give a brief explanation here: up to shrinking ![]() $\Delta$ we may assume that it is simply-connected. Then one can define a basis
$\Delta$ we may assume that it is simply-connected. Then one can define a basis ![]() $\omega _1(s),\ldots ,\omega _{2g}(s)$ of the period lattice of each fiber
$\omega _1(s),\ldots ,\omega _{2g}(s)$ of the period lattice of each fiber ![]() $s \in \Delta$ as holomorphic functions of
$s \in \Delta$ as holomorphic functions of ![]() $s$. Now each fiber
$s$. Now each fiber ![]() $\mathcal {A}_s = \pi _S^{-1}(s)$ can be identified with the complex torus
$\mathcal {A}_s = \pi _S^{-1}(s)$ can be identified with the complex torus ![]() $\mathbb {C}^g/\mathbb {Z} \omega _1(s)\oplus \cdots \oplus \mathbb {Z}\omega _{2g}(s)$, and each point
$\mathbb {C}^g/\mathbb {Z} \omega _1(s)\oplus \cdots \oplus \mathbb {Z}\omega _{2g}(s)$, and each point ![]() $x \in \mathcal {A}_s(\mathbb {C})$ can be expressed as the class of
$x \in \mathcal {A}_s(\mathbb {C})$ can be expressed as the class of ![]() $\sum _{i=1}^{2g}b_i(x) \omega _i(s)$ for real numbers
$\sum _{i=1}^{2g}b_i(x) \omega _i(s)$ for real numbers ![]() $b_1(x),\ldots ,b_{2g}(x)$. Then
$b_1(x),\ldots ,b_{2g}(x)$. Then ![]() $b_{\Delta }(x)$ is defined to be the class of the
$b_{\Delta }(x)$ is defined to be the class of the ![]() $2g$-tuple
$2g$-tuple ![]() $(b_1(x),\ldots ,b_{2g}(x)) \in \mathbb {R}^{2g}$ modulo
$(b_1(x),\ldots ,b_{2g}(x)) \in \mathbb {R}^{2g}$ modulo ![]() $\mathbb {Z}^{2g}$.
$\mathbb {Z}^{2g}$.
Through the introduction, let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$ such that
$\mathcal {A}$ such that ![]() $\pi _S(X) = S$.
$\pi _S(X) = S$.
The goal of this paper is to compute the generic rank of ![]() $b_{\Delta }|_{X \cap \mathcal {A}_{\Delta }}$. We also systematically study the link between this rank and the relative Manin–Mumford conjecture, reducing the latter to a simpler conjecture on unlikely intersections.
$b_{\Delta }|_{X \cap \mathcal {A}_{\Delta }}$. We also systematically study the link between this rank and the relative Manin–Mumford conjecture, reducing the latter to a simpler conjecture on unlikely intersections.
First of all, ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x$ must be an even number for each
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x$ must be an even number for each ![]() $x \in X^{\mathrm {sm}}(\mathbb {C})$, as each
$x \in X^{\mathrm {sm}}(\mathbb {C})$, as each ![]() $\omega _i(s)$ is holomorphic. So the question becomes giving a characterization for
$\omega _i(s)$ is holomorphic. So the question becomes giving a characterization for
Also it can be shown that ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$ does not depend on the choice of
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$ does not depend on the choice of ![]() $\Delta$ by Sard's theorem; see the end of § 4 for a detailed explanation.
$\Delta$ by Sard's theorem; see the end of § 4 for a detailed explanation.
There is a naive bound for ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$ as follows. Let
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$ as follows. Let ![]() $\mathfrak {A}_g$ be the universal abelian variety over the moduli space
$\mathfrak {A}_g$ be the universal abelian variety over the moduli space ![]() $\mathbb {A}_g$ of abelian varieties. We have the following modular map.
$\mathbb {A}_g$ of abelian varieties. We have the following modular map.

It is not hard to show that ![]() $b_{\Delta }$ factors through
$b_{\Delta }$ factors through ![]() $\iota$. So
$\iota$. So ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \min (\dim \iota (X), g)$.
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \min (\dim \iota (X), g)$.
The question to characterize (1.1) was explicitly asked and systematically studied for the first time in [Reference André, Corvaja and ZannierACZ20]. The submersivity problem, i.e. ![]() $l=g$, was solved in [Reference André, Corvaja and ZannierACZ20] for all
$l=g$, was solved in [Reference André, Corvaja and ZannierACZ20] for all ![]() $\mathcal {A}/S$ with
$\mathcal {A}/S$ with ![]() $\mathrm {End}(\mathcal {A}/S) = \mathbb {Z}$ and
$\mathrm {End}(\mathcal {A}/S) = \mathbb {Z}$ and ![]() $\dim \iota _S(S) \ge g$. A clear connection to functional transcendence (André's independence of abelian logarithms [Reference AndréAnd92] and the pure Ax–Schanuel theorem [Reference Mok, Pila and TsimermanMPT19]) was presented.
$\dim \iota _S(S) \ge g$. A clear connection to functional transcendence (André's independence of abelian logarithms [Reference AndréAnd92] and the pure Ax–Schanuel theorem [Reference Mok, Pila and TsimermanMPT19]) was presented.
In our paper we completely solve the generic rank problem by giving a criterion (equivalent condition) to (1.1) for each ![]() $l$ in simple terms of the geometry of
$l$ in simple terms of the geometry of ![]() $X$. Our approach is independent of [Reference André, Corvaja and ZannierACZ20]. It uses functional transcendence (in a different vein, the mixed Ax–Schanuel theorem [Reference GaoGao20]), combined with a finiteness result [Reference GaoGao20, Theorem 1.4]. Here let us state the criterion in an equivalent (but simpler formulated) way: give a criterion to
$X$. Our approach is independent of [Reference André, Corvaja and ZannierACZ20]. It uses functional transcendence (in a different vein, the mixed Ax–Schanuel theorem [Reference GaoGao20]), combined with a finiteness result [Reference GaoGao20, Theorem 1.4]. Here let us state the criterion in an equivalent (but simpler formulated) way: give a criterion to ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2l$ for each
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2l$ for each ![]() $l$.
$l$.
The following notation will be used throughout the paper. Denote by ![]() $\mathcal {A}_X$ the translate of an abelian subscheme of
$\mathcal {A}_X$ the translate of an abelian subscheme of ![]() $\mathcal {A} \rightarrow S$ by a torsion section (up to a finite covering of
$\mathcal {A} \rightarrow S$ by a torsion section (up to a finite covering of ![]() $S$), which contains
$S$), which contains ![]() $X$, minimal for this property. Then
$X$, minimal for this property. Then ![]() $\mathcal {A}_X \rightarrow S$ itself is an abelian scheme (up to taking a finite covering of
$\mathcal {A}_X \rightarrow S$ itself is an abelian scheme (up to taking a finite covering of ![]() $S$), whose relative dimension we denote by
$S$), whose relative dimension we denote by ![]() $g_X$.
$g_X$.
Theorem 1.1 For each ![]() $l$, we have the following.
$l$, we have the following.
(i) (Criterion to (1.1))
 $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2 l$ if and only if the following condition holds: there exists an abelian subscheme
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2 l$ if and only if the following condition holds: there exists an abelian subscheme  $\mathcal {B}$ of
$\mathcal {B}$ of  $\mathcal {A}_X \rightarrow S$ (of relative dimension
$\mathcal {A}_X \rightarrow S$ (of relative dimension  $g_{\mathcal {B}}$) such that for the quotient abelian scheme
$g_{\mathcal {B}}$) such that for the quotient abelian scheme  $p_{\mathcal {B}} \colon \mathcal {A}_X \rightarrow \mathcal {A}_X/\mathcal {B}$ and the modular map
$p_{\mathcal {B}} \colon \mathcal {A}_X \rightarrow \mathcal {A}_X/\mathcal {B}$ and the modular map  $\iota _{/\mathcal {B}} \colon \mathcal {A}_X/\mathcal {B} \rightarrow \mathfrak {A}_{g_X - g_{\mathcal {B}}}$, we have
$\iota _{/\mathcal {B}} \colon \mathcal {A}_X/\mathcal {B} \rightarrow \mathfrak {A}_{g_X - g_{\mathcal {B}}}$, we have  $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < l - g_{\mathcal {B}}$.
(1.3)
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < l - g_{\mathcal {B}}$.
(1.3)
(ii) There exists a Zariski closed subset
 $X_{<2l}$ of
$X_{<2l}$ of  $X^{\mathrm {sm}}$ such that
$X^{\mathrm {sm}}$ such that  $\{x \in X^{\mathrm {sm}}(\mathbb {C}) : \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x < 2l\} = X_{<2l}(\mathbb {C}) \cap \mathcal {A}_{\Delta }$.
$\{x \in X^{\mathrm {sm}}(\mathbb {C}) : \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x < 2l\} = X_{<2l}(\mathbb {C}) \cap \mathcal {A}_{\Delta }$.
Part (ii) says that the locus where the Betti rank decreases with respect to the generic one is defined by algebraic equations. This is not obvious a priori, and not even the fact that this locus is complex analytic is obvious (left as an open issue in [Reference Corvaja, Masser and ZannierCMZ18]).
In fact we can prove more: we are able to write the locus of ![]() $X$ where
$X$ where ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{X\cap \mathcal {A}_{\Delta }})_x$ is smaller than
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{X\cap \mathcal {A}_{\Delta }})_x$ is smaller than ![]() $2l$ for each
$2l$ for each ![]() $l$ (Theorem 1.7).
$l$ (Theorem 1.7).
This geometric criterion to detect the Betti rank can be simplified in some cases, e.g.
See Definition A.1 for the definition of ![]() $\langle X \rangle _{\mathrm {gen-sp}}$ and Corollary A.4 for the statement.
$\langle X \rangle _{\mathrm {gen-sp}}$ and Corollary A.4 for the statement.
Betti map was first studied and used in [Reference ZannierZan12]. Then it was used to study the relative Manin–Mumford conjecture by Bertrand, Corvaja, Masser, Pillay, and Zannier in a series of works [Reference Masser and ZannierMZ12, Reference Masser and ZannierMZ14, Reference Masser and ZannierMZ15, Reference Bertrand, Masser, Pillay and ZannierBMPZ16, Reference Corvaja, Masser and ZannierCMZ18, Reference Masser and ZannierMZ18], to prove the geometric Bogomolov conjecture over char ![]() $0$ by Gao and Habegger [Reference Gao and HabeggerGH19] and Cantat, Gao, Habegger and Xie [Reference Cantat, Gao, Habegger and XieCGHX20] with (1.1) for
$0$ by Gao and Habegger [Reference Gao and HabeggerGH19] and Cantat, Gao, Habegger and Xie [Reference Cantat, Gao, Habegger and XieCGHX20] with (1.1) for ![]() $l = \dim X - \dim S$, and to prove the denseness of torsion points on sections of Lagrangian fibrations by Voisin [Reference VoisinVoi18] using André, Corvaja and Zannier's result [Reference André, Corvaja and ZannierACZ20] on (1.1) for
$l = \dim X - \dim S$, and to prove the denseness of torsion points on sections of Lagrangian fibrations by Voisin [Reference VoisinVoi18] using André, Corvaja and Zannier's result [Reference André, Corvaja and ZannierACZ20] on (1.1) for ![]() $l = g \le 4$.
$l = g \le 4$.
1.1 Two applications
We see two applications of Theorem 1.1 in this subsection.
As shown by [Reference Dimitrov, Gao and HabeggerDGH20, Theorem 1.6], in some number theory and algebro-geometric applications, it is particularly important to understand when (1.1) holds for ![]() $l = \dim X$, namely
$l = \dim X$, namely
As ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \min (\dim \iota (X), g)$ always holds, (1.5) requires
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \min (\dim \iota (X), g)$ always holds, (1.5) requires ![]() $\iota |_X$ to be generically finite and that
$\iota |_X$ to be generically finite and that ![]() $\dim X \le g$. But in applications we often need to handle
$\dim X \le g$. But in applications we often need to handle ![]() $X$ with
$X$ with ![]() $\dim X >g$.
$\dim X >g$.
Because of this problem, our main result towards (1.5) is in the following philosophy. Instead of proving (1.5) for ![]() $X$, we raise
$X$, we raise ![]() $X$ to a large enough fibered power so that (1.5) holds for this fibered power. In this process we need to put some extra assumptions on
$X$ to a large enough fibered power so that (1.5) holds for this fibered power. In this process we need to put some extra assumptions on ![]() $X$.
$X$.
Let us explain this in detail. For any integer ![]() $m \ge 1$, let
$m \ge 1$, let ![]() $\mathcal {A}^{[m]} = \mathcal {A}\times _S \cdots \times _S \mathcal {A}$ (
$\mathcal {A}^{[m]} = \mathcal {A}\times _S \cdots \times _S \mathcal {A}$ (![]() $m$-copies),
$m$-copies), ![]() $X^{[m]} = X \times _S \cdots \times _S X$ (
$X^{[m]} = X \times _S \cdots \times _S X$ (![]() $m$-copies) and
$m$-copies) and ![]() $b^{[m]}_{\Delta } = (b_{\Delta }, \ldots , b_{\Delta }) \colon \mathcal {A}^{[m]}_{\Delta } \rightarrow \mathbb {T}^{2mg}$. Let
$b^{[m]}_{\Delta } = (b_{\Delta }, \ldots , b_{\Delta }) \colon \mathcal {A}^{[m]}_{\Delta } \rightarrow \mathbb {T}^{2mg}$. Let ![]() $\mathscr {D}_m^{\mathcal {A}} \colon \mathcal {A}^{[m+1]} \rightarrow \mathcal {A}^{[m]}$ be the
$\mathscr {D}_m^{\mathcal {A}} \colon \mathcal {A}^{[m+1]} \rightarrow \mathcal {A}^{[m]}$ be the ![]() $m$th Faltings–Zhang map fiberwise defined by
$m$th Faltings–Zhang map fiberwise defined by ![]() $(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$.
$(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$.
We start with the following example. Let ![]() $\mathbb {M}_g$ be the moduli space of curves of genus
$\mathbb {M}_g$ be the moduli space of curves of genus ![]() $g$. Up to taking a finite covering, we have a universal curve
$g$. Up to taking a finite covering, we have a universal curve ![]() $\mathfrak {C}_g \rightarrow \mathbb {M}_g$. Let
$\mathfrak {C}_g \rightarrow \mathbb {M}_g$. Let ![]() $\mathbb {A}_g$ be the moduli space of principally polarized abelian varieties of dimension
$\mathbb {A}_g$ be the moduli space of principally polarized abelian varieties of dimension ![]() $g$. Up to taking a finite covering, we have a universal abelian variety
$g$. Up to taking a finite covering, we have a universal abelian variety ![]() $\pi \colon \mathfrak {A}_g \rightarrow \mathbb {A}_g$. Then we have the following diagram.
$\pi \colon \mathfrak {A}_g \rightarrow \mathbb {A}_g$. Then we have the following diagram.

By abuse of notation denote by ![]() $\mathbb {M}_g$ the image of the bottom arrow.
$\mathbb {M}_g$ the image of the bottom arrow.
Let ![]() $S$ be an irreducible variety with a generically finite (not necessarily dominant) morphism
$S$ be an irreducible variety with a generically finite (not necessarily dominant) morphism ![]() $S \rightarrow \mathbb {M}_g$ such that
$S \rightarrow \mathbb {M}_g$ such that ![]() $\mathfrak {C}_g \times _{\mathbb {M}_g} S \rightarrow S$ admits a section
$\mathfrak {C}_g \times _{\mathbb {M}_g} S \rightarrow S$ admits a section ![]() $\epsilon$. Take
$\epsilon$. Take ![]() $\mathcal {A} = \mathfrak {A}_g \times _{\mathbb {A}_g} S$, and let
$\mathcal {A} = \mathfrak {A}_g \times _{\mathbb {A}_g} S$, and let ![]() ${\mathfrak {C}_S = \mathfrak {C}_g \times _{\mathcal {M}_g}S}$. We have the fiberwise Abel–Jacobi embedding
${\mathfrak {C}_S = \mathfrak {C}_g \times _{\mathcal {M}_g}S}$. We have the fiberwise Abel–Jacobi embedding ![]() $j_{\epsilon } \colon \mathfrak {C}_S \hookrightarrow \mathrm {Jac}(\mathfrak {C}_S)$ via
$j_{\epsilon } \colon \mathfrak {C}_S \hookrightarrow \mathrm {Jac}(\mathfrak {C}_S)$ via ![]() $\epsilon$, and by abuse of notation denote by
$\epsilon$, and by abuse of notation denote by ![]() $\mathfrak {C}_S$ the image of
$\mathfrak {C}_S$ the image of ![]() $\mathfrak {C}_S$ under
$\mathfrak {C}_S$ under ![]() $\iota \circ j_{\epsilon }$. Denote by
$\iota \circ j_{\epsilon }$. Denote by ![]() $\mathfrak {C}_S-\mathfrak {C}_S = \mathscr {D}_1^{\mathcal {A}}(\mathfrak {C}_S)$.
$\mathfrak {C}_S-\mathfrak {C}_S = \mathscr {D}_1^{\mathcal {A}}(\mathfrak {C}_S)$.
Theorem 1.2 Let ![]() $S$,
$S$, ![]() $\mathcal {A}$, and
$\mathcal {A}$, and ![]() $\mathfrak {C}_S$ be as above. For any
$\mathfrak {C}_S$ be as above. For any ![]() $m \ge 1$, we have the following:
$m \ge 1$, we have the following:
(i)
 $\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathfrak {C}_S^{[m]}}) = 2 \dim (\mathfrak {C}_S^{[m]})$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathfrak {C}_S^{[m]}}) = 2 \dim (\mathfrak {C}_S^{[m]})$ for all  $m \ge \dim S$ if
$m \ge \dim S$ if  $g \ge 2$;
$g \ge 2$;(ii)
 $\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{(\mathfrak {C}_S - \mathfrak {C}_S)^{[m]}}) = 2 \dim (\mathfrak {C}_S - \mathfrak {C}_S)^{[m]}$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{(\mathfrak {C}_S - \mathfrak {C}_S)^{[m]}}) = 2 \dim (\mathfrak {C}_S - \mathfrak {C}_S)^{[m]}$ for all  $m \ge \dim S$ if
$m \ge \dim S$ if  $g \ge 3$.
$g \ge 3$.
Theorem 1.2 is a particular case of part (i) of the following Theorem 1.3 (applied to ![]() $\iota = \mathrm {id}$,
$\iota = \mathrm {id}$, ![]() $X = \mathfrak {C}_S$ and
$X = \mathfrak {C}_S$ and ![]() $X = \mathfrak {C}_S - \mathfrak {C}_S$), which is the general result towards (1.5).
$X = \mathfrak {C}_S - \mathfrak {C}_S$), which is the general result towards (1.5).
Theorem 1.3 Assume that ![]() $\iota |_X$ is generically finite. Assume furthermore that
$\iota |_X$ is generically finite. Assume furthermore that ![]() $X$ satisfies the following:
$X$ satisfies the following:
(a) we have
 $\dim X > \dim S$;
$\dim X > \dim S$;(b) there exists
 $s \in S$ such that no proper subgroup of
$s \in S$ such that no proper subgroup of  $\mathcal {A}_s$ contains
$\mathcal {A}_s$ contains  $X_s$;
$X_s$;(c) we have
 $X + \mathcal {A}' \not \subseteq X$ for any non-isotrivial abelian subscheme
$X + \mathcal {A}' \not \subseteq X$ for any non-isotrivial abelian subscheme  $\mathcal {A}'$ of
$\mathcal {A}'$ of  $\mathcal {A} \rightarrow S$.
$\mathcal {A} \rightarrow S$.
Then we have the following:
(i)
 $\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{X^{[m]}}) = 2 \dim X^{[m]}$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{X^{[m]}}) = 2 \dim X^{[m]}$ for all  $m \ge \dim S$;
$m \ge \dim S$;(ii)
 $\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})}) = 2 \dim \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})}) = 2 \dim \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$ for all  $m \ge \dim X$.
$m \ge \dim X$.
This theorem follows directly from Theorem 10.1, applied to ![]() $r=t=0$. In practice, the bound for
$r=t=0$. In practice, the bound for ![]() $m$ can often be improved; see Remark A.5 for some cases for Theorems 1.2 and 1.2′. Hypothesis (a) is crucial: if
$m$ can often be improved; see Remark A.5 for some cases for Theorems 1.2 and 1.2′. Hypothesis (a) is crucial: if ![]() $X$ is the image of a multi-section of
$X$ is the image of a multi-section of ![]() $\mathcal {A} \rightarrow S$, then
$\mathcal {A} \rightarrow S$, then ![]() $X^{[m]}$ is contained in the diagonal of
$X^{[m]}$ is contained in the diagonal of ![]() $\mathcal {A} \rightarrow \mathcal {A}^{[m]}$, so essentially no new objects are constructed with the operations.
$\mathcal {A} \rightarrow \mathcal {A}^{[m]}$, so essentially no new objects are constructed with the operations.
We close this subsection with the following result, which is a direct corollary of part (ii) of Theorem 1.3 applied to ![]() $\iota = \mathrm {id}$ and
$\iota = \mathrm {id}$ and ![]() $X = \mathfrak {C}_S$.
$X = \mathfrak {C}_S$.
Theorem 1.2′ Under the notation of Theorem 1.2. Let ![]() $\mathscr {D}_m := \mathscr {D}_m^{\mathfrak {A}_g}$, namely
$\mathscr {D}_m := \mathscr {D}_m^{\mathfrak {A}_g}$, namely
 \[ \mathscr{D}_m \colon \underbrace{\mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \cdots \times_{\mathbb{A}_{g}} \mathfrak{A}_{g}}_{(m+1)\text{-copies}} \rightarrow \underbrace{\mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \cdots \times_{\mathbb{A}_{g}} \mathfrak{A}_{g}}_{m\text{-coplies}} \]
\[ \mathscr{D}_m \colon \underbrace{\mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \cdots \times_{\mathbb{A}_{g}} \mathfrak{A}_{g}}_{(m+1)\text{-copies}} \rightarrow \underbrace{\mathfrak{A}_{g} \times_{\mathbb{A}_{g}} \cdots \times_{\mathbb{A}_{g}} \mathfrak{A}_{g}}_{m\text{-coplies}} \]
fiberwise defined by ![]() $(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$. Assume
$(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$. Assume ![]() $g \ge 2$. Then we have
$g \ge 2$. Then we have ![]() $\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathscr {D}_m(\mathfrak {C}_S^{[m+1]})}) = 2 \dim \mathscr {D}_m(\mathfrak {C}_S^{[m+1]})$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b^{[m]}_{\Delta }|_{\mathscr {D}_m(\mathfrak {C}_S^{[m+1]})}) = 2 \dim \mathscr {D}_m(\mathfrak {C}_S^{[m+1]})$ for all ![]() $m \ge \dim (\mathfrak {C}_S) = 1 + \dim S$.
$m \ge \dim (\mathfrak {C}_S) = 1 + \dim S$.
Theorem 1.2′ will be applied in [Reference Dimitrov, Gao and HabeggerDGH20], as an important step, to prove: for a smooth projective curve ![]() $C$ of genus
$C$ of genus ![]() $g \ge 2$ defined over a number field
$g \ge 2$ defined over a number field ![]() $K$,
$K$, ![]() $\#C(K)$ is bounded only in terms of
$\#C(K)$ is bounded only in terms of ![]() $g$,
$g$, ![]() $[K:\mathbb {Q}]$ and the Mordell–Weil rank.
$[K:\mathbb {Q}]$ and the Mordell–Weil rank.
Our second application is to answer a question of André, Corvaja and Zannier (ACZ) [Reference André, Corvaja and ZannierACZ20].
ACZ question. Assume that ![]() $\mathcal {A}/S$ has no fixed part over any finite covering of
$\mathcal {A}/S$ has no fixed part over any finite covering of ![]() $S$ and that
$S$ and that ![]() $\mathbb {Z} X = \cup _{N \in \mathbb {Z}}\{[N]x : x\in X(\mathbb {C})\}$ is Zariski dense in
$\mathbb {Z} X = \cup _{N \in \mathbb {Z}}\{[N]x : x\in X(\mathbb {C})\}$ is Zariski dense in ![]() $\mathcal {A}$. Does (1.1) hold for
$\mathcal {A}$. Does (1.1) hold for ![]() $l = \min (\dim \iota (X), g)$?
$l = \min (\dim \iota (X), g)$?
Many cases of this question were proved to be true when ![]() $\dim \iota _S(S) \ge g$ in [Reference André, Corvaja and ZannierACZ20], e.g. when
$\dim \iota _S(S) \ge g$ in [Reference André, Corvaja and ZannierACZ20], e.g. when ![]() $g\le 3$ or any
$g\le 3$ or any ![]() $\mathcal {A}/S$ with
$\mathcal {A}/S$ with ![]() $\mathrm {End}(\mathcal {A}/S) = \mathbb {Z}$.
$\mathrm {End}(\mathcal {A}/S) = \mathbb {Z}$.
We hereby answer the ACZ question: it has a positive answer in many cases, but may be false in general.
Theorem 1.4 We have the following.
(i) The ACZ question has a positive answer if the following hold:
(a) either
 $\mathcal {A} \rightarrow S$ is geometrically simple;
$\mathcal {A} \rightarrow S$ is geometrically simple;(b) or each Hodge generic curve
 $C \subseteq \iota _S(S)$ satisfies the following property:
$C \subseteq \iota _S(S)$ satisfies the following property:  $\iota (\mathcal {A})|_C := \pi ^{-1}(C) \rightarrow C$ has no fixed part over any finite covering of
$\iota (\mathcal {A})|_C := \pi ^{-1}(C) \rightarrow C$ has no fixed part over any finite covering of  $C$.
$C$.
(ii) There exist a closed irreducible subvariety
 $S \subseteq \mathbb {A}_4$ of dimension
$S \subseteq \mathbb {A}_4$ of dimension  $4$ and a section
$4$ and a section  $\xi$ of
$\xi$ of  $\mathfrak {A}_4|_S \rightarrow S$ such that
$\mathfrak {A}_4|_S \rightarrow S$ such that  $\mathfrak {A}_4|_S \rightarrow S$ has no fixed part over any finite covering of
$\mathfrak {A}_4|_S \rightarrow S$ has no fixed part over any finite covering of  $S$,
$S$,  $\mathbb {Z}\xi$ is Zariski dense in
$\mathbb {Z}\xi$ is Zariski dense in  $\mathfrak {A}_4|_S$, and
$\mathfrak {A}_4|_S$, and  $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\xi (S)\cap \mathcal {A}_{\Delta }})_x < 8$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\xi (S)\cap \mathcal {A}_{\Delta }})_x < 8$ for all  $x \in \xi (S)$.
$x \in \xi (S)$.
Part (i) is Theorem 9.2; see Remark 9.3 for (i)(b). Part (i)(a) for ![]() $l = g$, combined with [Reference André, Corvaja and ZannierACZ20, Proposition 2.1.1], shows that [Reference VoisinVoi18, Theorem 0.3] holds without the dimension assumption because by Lemma 4.5 of [Reference VoisinVoi18] the abelian scheme in question is geometrically simple. Part (ii) is constructed in Example 9.4; it is closely related to [Reference André, Corvaja and ZannierACZ20, Remark 6.2.1]. Note that this counterexample is the simplest one: in this example
$l = g$, combined with [Reference André, Corvaja and ZannierACZ20, Proposition 2.1.1], shows that [Reference VoisinVoi18, Theorem 0.3] holds without the dimension assumption because by Lemma 4.5 of [Reference VoisinVoi18] the abelian scheme in question is geometrically simple. Part (ii) is constructed in Example 9.4; it is closely related to [Reference André, Corvaja and ZannierACZ20, Remark 6.2.1]. Note that this counterexample is the simplest one: in this example ![]() $\mathcal {A}/S$ has maximal variation and
$\mathcal {A}/S$ has maximal variation and ![]() $X$ is the image of a section, and by [Reference André, Corvaja and ZannierACZ20, Theorem 2.3.1] no such examples exist for
$X$ is the image of a section, and by [Reference André, Corvaja and ZannierACZ20, Theorem 2.3.1] no such examples exist for ![]() $g \le 3$.
$g \le 3$.
1.2 The  $t$th degeneracy locus
$t$th degeneracy locus
Our method to study the generic rank of the Betti map is to translate the problem into studying the ![]() $t$th degeneracy locus defined below. Let us explain it in this subsection. Recall our abelian scheme
$t$th degeneracy locus defined below. Let us explain it in this subsection. Recall our abelian scheme ![]() $\pi _S \colon \mathcal {A} \rightarrow S$.
$\pi _S \colon \mathcal {A} \rightarrow S$.
Definition 1.5 A closed irreducible subvariety ![]() $Z$ of
$Z$ of ![]() $\mathcal {A}$ is called a generically special subvariety of sg type of
$\mathcal {A}$ is called a generically special subvariety of sg type of ![]() $\mathcal {A}$ if there exists a finite covering
$\mathcal {A}$ if there exists a finite covering ![]() $S' \rightarrow S$, inducing a morphism
$S' \rightarrow S$, inducing a morphism ![]() $\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that
$\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that ![]() $Z = \rho (\sigma ' + \sigma _0' + \mathcal {B}')$, where
$Z = \rho (\sigma ' + \sigma _0' + \mathcal {B}')$, where ![]() $\mathcal {B}'$ is an abelian subscheme of
$\mathcal {B}'$ is an abelian subscheme of ![]() $\mathcal {A}'/S'$,
$\mathcal {A}'/S'$, ![]() $\sigma '$ is a torsion section of
$\sigma '$ is a torsion section of ![]() $\mathcal {A}'/S'$, and
$\mathcal {A}'/S'$, and ![]() $\sigma _0'$ is a constant section of
$\sigma _0'$ is a constant section of ![]() $\mathcal {A}'/S'$.
$\mathcal {A}'/S'$.
We briefly explain the meaning of constant section here. Let ![]() $C' \times S'$ be the largest constant abelian subscheme of
$C' \times S'$ be the largest constant abelian subscheme of ![]() $\mathcal {A}'/S'$. We say that a section
$\mathcal {A}'/S'$. We say that a section ![]() $\sigma _0' \colon S' \rightarrow \mathcal {A}'$ is a constant section if there exists
$\sigma _0' \colon S' \rightarrow \mathcal {A}'$ is a constant section if there exists ![]() $c' \in C'(\mathbb {C})$ such that
$c' \in C'(\mathbb {C})$ such that ![]() $\sigma _0$ is the composite of
$\sigma _0$ is the composite of ![]() $S' \rightarrow C' \times S'$,
$S' \rightarrow C' \times S'$, ![]() $s' \mapsto (c',s')$, and the inclusion
$s' \mapsto (c',s')$, and the inclusion ![]() $C' \times S' \subseteq \mathcal {A}'$.
$C' \times S' \subseteq \mathcal {A}'$.
Definition 1.5 is closely related to the generically special subvarieties defined in [Reference Gao and HabeggerGH19, Definition 1.2]. See Appendix A for some discussion.
For any locally closed irreducible subvariety ![]() $Y$ of
$Y$ of ![]() $\mathcal {A}$, denote by
$\mathcal {A}$, denote by ![]() $\langle Y \rangle _{\mathrm {sg}}$ the smallest generically special subvariety of sg type of
$\langle Y \rangle _{\mathrm {sg}}$ the smallest generically special subvariety of sg type of ![]() $\mathcal {A}|_{\pi _S(Y)} = \pi _S^{-1}(\pi _S(Y))$, which contains
$\mathcal {A}|_{\pi _S(Y)} = \pi _S^{-1}(\pi _S(Y))$, which contains ![]() $Y$.
$Y$.
Definition 1.6 Let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$. For any
$\mathcal {A}$. For any ![]() $t \in \mathbb {Z}$, define the
$t \in \mathbb {Z}$, define the ![]() $t{\rm th}$ degeneracy locus of
$t{\rm th}$ degeneracy locus of ![]() $X$, denoted by
$X$, denoted by ![]() $X^{\mathrm {deg}}(t)$, to be the union of positive dimensional closed irreducible subvarieties
$X^{\mathrm {deg}}(t)$, to be the union of positive dimensional closed irreducible subvarieties ![]() $Y \subseteq X$ such that
$Y \subseteq X$ such that ![]() $\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi _S(Y) < \dim Y + t$. When
$\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi _S(Y) < \dim Y + t$. When ![]() $t = 0$, we abbreviate
$t = 0$, we abbreviate ![]() $X^{\mathrm {deg}}(0)$ as
$X^{\mathrm {deg}}(0)$ as ![]() $X^{\mathrm {deg}}$. We say that
$X^{\mathrm {deg}}$. We say that ![]() $X$ is degenerate if
$X$ is degenerate if ![]() $X^{\mathrm {deg}}$ is Zariski dense in
$X^{\mathrm {deg}}$ is Zariski dense in ![]() $X$.
$X$.
Note that ![]() $X^{\mathrm {deg}} = X$ clearly holds if
$X^{\mathrm {deg}} = X$ clearly holds if ![]() $X$ is a multi-section and
$X$ is a multi-section and ![]() $g < \dim S$.
$g < \dim S$.
The locus on which ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x$ is smaller than expected is precisely
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)_x$ is smaller than expected is precisely ![]() $X^{\mathrm {deg}}(t)$ for some
$X^{\mathrm {deg}}(t)$ for some ![]() $t \le 0$. More precisely we have the following result (recall the modular map
$t \le 0$. More precisely we have the following result (recall the modular map ![]() $\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (2.1) and the naive bound
$\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (2.1) and the naive bound ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \dim \iota (X)$).
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2 \dim \iota (X)$).
Theorem 1.7 Let ![]() $x \in X^{\mathrm {sm}}(\mathbb {C}) \cap \mathcal {A}_{\Delta }$. Then for each integer
$x \in X^{\mathrm {sm}}(\mathbb {C}) \cap \mathcal {A}_{\Delta }$. Then for each integer ![]() $l \le \dim \iota (X)$, we have
$l \le \dim \iota (X)$, we have
This is not yet satisfactory as the ![]() $X^{\mathrm {deg}}(t)$ thus defined is a priori a complicated subset of
$X^{\mathrm {deg}}(t)$ thus defined is a priori a complicated subset of ![]() $X$. However we show that they are all Zariski closed in
$X$. However we show that they are all Zariski closed in ![]() $X$.
$X$.
Theorem 1.8 The set ![]() $X^{\mathrm {deg}}(t)$ is Zariski closed in
$X^{\mathrm {deg}}(t)$ is Zariski closed in ![]() $X$ for each
$X$ for each ![]() $t \in \mathbb {Z}$.
$t \in \mathbb {Z}$.
Both theorems will be proved in § 9. Before the treatment of the general case, we will prove, for the case ![]() $X \subseteq \mathfrak {A}_g$, Theorem 1.7 in § 6 and Theorem 1.8 in § 7. Note that Theorem 1.1(ii) follows directly from Theorems 1.7 and 1.8.
$X \subseteq \mathfrak {A}_g$, Theorem 1.7 in § 6 and Theorem 1.8 in § 7. Note that Theorem 1.1(ii) follows directly from Theorems 1.7 and 1.8.
1.3 Relation with the relative Manin–Mumford conjecture
Another application of the ![]() $t$th degeneracy locus is for the relative Manin–Mumford conjecture. In this application we need to take
$t$th degeneracy locus is for the relative Manin–Mumford conjecture. In this application we need to take ![]() $t = 1$. Let us state the result.
$t = 1$. Let us state the result.
Denote by ![]() $\mathcal {A}_{\mathrm {tor}}$ the set of points
$\mathcal {A}_{\mathrm {tor}}$ the set of points ![]() $x \in \mathcal {A}(\mathbb {C})$ such that
$x \in \mathcal {A}(\mathbb {C})$ such that ![]() $[N]x$ lies in the zero section of
$[N]x$ lies in the zero section of ![]() $\mathcal {A} \rightarrow S$ for some integer
$\mathcal {A} \rightarrow S$ for some integer ![]() $N$. Zannier [Reference ZannierZan12] proposed the following relative Manin–Mumford conjecture.
$N$. Zannier [Reference ZannierZan12] proposed the following relative Manin–Mumford conjecture.
Relative Manin–Mumford Conjecture. Assume that ![]() $\mathbb {Z} X:= \bigcup _{N \in \mathbb {Z}}\{[N]x: x \in X(\mathbb {C})\}$ is Zariski dense in
$\mathbb {Z} X:= \bigcup _{N \in \mathbb {Z}}\{[N]x: x \in X(\mathbb {C})\}$ is Zariski dense in ![]() $\mathcal {A}$. If
$\mathcal {A}$. If ![]() $(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then
$(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then ![]() $\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
$\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
In this paper we will reduce this conjecture to another simpler conjecture.
Conjecture 1.9 Assume ![]() $S$ is a locally closed irreducible subvariety of
$S$ is a locally closed irreducible subvariety of ![]() $\mathbb {A}_g$ defined over
$\mathbb {A}_g$ defined over ![]() $\bar {\mathbb {Q}}$ and
$\bar {\mathbb {Q}}$ and ![]() $\mathcal {A} = \mathfrak {A}_g \times _{\mathbb {A}_g} S$. Assume
$\mathcal {A} = \mathfrak {A}_g \times _{\mathbb {A}_g} S$. Assume ![]() $X$ is defined over
$X$ is defined over ![]() $\bar {\mathbb {Q}}$. If
$\bar {\mathbb {Q}}$. If ![]() $(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then
$(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then ![]() $X^{\mathrm {deg}}(1) = X$.
$X^{\mathrm {deg}}(1) = X$.
Proposition 1.10 Conjecture 1.9 implies the relative Manin–Mumford conjecture.
A more precise version of this reduction is Proposition 11.2.
Proposition 1.10 suggests that there is a strong link between the Betti map and the relative Manin–Mumford conjecture. The existence of such a link already appeared in previous works on the relative Manin–Mumford conjecture: the Betti coordinate played a key role in the proofs of many particular cases of the conjecture by Masser and Zannier [Reference Masser and ZannierMZ12, Reference Masser and ZannierMZ14, Reference Masser and ZannierMZ15] and Corvaja, Masser and Zannier [Reference Corvaja, Masser and ZannierCMZ18] (pencils of abelian surfaces, first over ![]() $\bar {\mathbb {Q}}$ then over
$\bar {\mathbb {Q}}$ then over ![]() $\mathbb {C}$; passing from
$\mathbb {C}$; passing from ![]() $\bar {\mathbb {Q}}$ to
$\bar {\mathbb {Q}}$ to ![]() $\mathbb {C}$ is highly non-trivial as it enlarges the base), Bertrand, Masser, Pillay and Zannier [Reference Bertrand, Masser, Pillay and ZannierBMPZ16] (semi-abelian surfaces), and Masser and Zannier [Reference Masser and ZannierMZ18] (any abelian scheme over a curve). See also [Reference ZannierZan14].
$\mathbb {C}$ is highly non-trivial as it enlarges the base), Bertrand, Masser, Pillay and Zannier [Reference Bertrand, Masser, Pillay and ZannierBMPZ16] (semi-abelian surfaces), and Masser and Zannier [Reference Masser and ZannierMZ18] (any abelian scheme over a curve). See also [Reference ZannierZan14].
1.4 Outline of the paper
In § 2 we set up some convention of the paper. In § 3 we recall the universal abelian variety and define the Betti map for this case. In § 4 we define the Betti map for a general abelian scheme. These are the basic setting up of the paper.
In § 5 we explain in details our main tools to study the Betti map. There are two parts. The first part §§ 5.1 and 5.2 is to introduce the functional transcendence theorem (mixed Ax–Schanuel), and the second part §§ 5.3 and 5.4 is Deligne and Pink's language of mixed Shimura varieties.
Sections 6–8 are the core of this paper. In these sections we prove the main results on the Betti rank (Theorems 1.7, 1.8, and 1.1) for the case ![]() $X \subseteq \mathfrak {A}_g$. In § 6 we use the weak mixed Ax–Schanuel theorem to transfer the problem of the generic rank of the Betti map into studying the
$X \subseteq \mathfrak {A}_g$. In § 6 we use the weak mixed Ax–Schanuel theorem to transfer the problem of the generic rank of the Betti map into studying the ![]() $t$th degeneracy locus for some particular
$t$th degeneracy locus for some particular ![]() $t$, and hence prove Theorem 1.7 for
$t$, and hence prove Theorem 1.7 for ![]() $X \subseteq \mathfrak {A}_g$. In § 7 we use the finiteness result [Reference GaoGao20, Theorem 1.4] to prove the Zariski closedness of the
$X \subseteq \mathfrak {A}_g$. In § 7 we use the finiteness result [Reference GaoGao20, Theorem 1.4] to prove the Zariski closedness of the ![]() $t$th degeneracy locus (Theorem 1.8) for
$t$th degeneracy locus (Theorem 1.8) for ![]() $X \subseteq \mathfrak {A}_g$. The proof in this section will also be used in § 8, where the criterion to check whether
$X \subseteq \mathfrak {A}_g$. The proof in this section will also be used in § 8, where the criterion to check whether ![]() $X$ is degenerate is proved for
$X$ is degenerate is proved for ![]() $X \subseteq \mathfrak {A}_g$. Combined with results in §§ 6 and 7 this proves Theorem 1.1 for
$X \subseteq \mathfrak {A}_g$. Combined with results in §§ 6 and 7 this proves Theorem 1.1 for ![]() $X \subseteq \mathfrak {A}_g$.
$X \subseteq \mathfrak {A}_g$.
Then ultimate versions of the main results on the Betti rank (Theorems 1.7, 1.8, and 1.1) are proved in § 9. As we shall see they are not hard to be deduced from the case ![]() $X \subseteq \mathfrak {A}_g$. The end of this section sees its application to the ACZ question and proves Theorem 1.4.
$X \subseteq \mathfrak {A}_g$. The end of this section sees its application to the ACZ question and proves Theorem 1.4.
Then in § 10 we prove Theorem 1.3, claiming that the Betti map attains the maximal rank if we raise ![]() $X$ to a large enough fibered power, for
$X$ to a large enough fibered power, for ![]() $X$ satisfying some mild properties.
$X$ satisfying some mild properties.
In § 11 we reduce the relative Manin–Mumford conjecture to a simpler conjecture involving the first degeneracy locus.
In Appendix A we further simplify the formula of the Betti rank when the base takes some simple form.
2. Convention and notation
2.1 Convention on abelian schemes
Let ![]() $g \ge 1$ be an integer. Let
$g \ge 1$ be an integer. Let ![]() $S$ be an irreducible variety over
$S$ be an irreducible variety over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g$. Since level structures are not important in this paper, we will use the following abuse of notation through the whole paper.
$g$. Since level structures are not important in this paper, we will use the following abuse of notation through the whole paper.
(i) We say that a subvariety
 $\mathcal {B}$ of
$\mathcal {B}$ of  $\mathcal {A}$ is an abelian subscheme of
$\mathcal {A}$ is an abelian subscheme of  $\mathcal {A} \rightarrow S$ if there exists a finite covering
$\mathcal {A} \rightarrow S$ if there exists a finite covering  $S' \rightarrow S$, inducing a morphism
$S' \rightarrow S$, inducing a morphism  $\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that
$\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that  $\mathcal {B} = \rho (\mathcal {B}')$ where
$\mathcal {B} = \rho (\mathcal {B}')$ where  $\mathcal {B}'$ is an abelian subscheme of
$\mathcal {B}'$ is an abelian subscheme of  $\mathcal {A}'/S'$ in the usual sense.Footnote 1
$\mathcal {A}'/S'$ in the usual sense.Footnote 1(ii) We say that
 $\sigma$ is a section of
$\sigma$ is a section of  $\mathcal {A} \rightarrow S$ if there exists a finite covering
$\mathcal {A} \rightarrow S$ if there exists a finite covering  $S' \rightarrow S$, inducing a morphism
$S' \rightarrow S$, inducing a morphism  $\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that
$\rho \colon \mathcal {A}' = \mathcal {A} \times _S S' \rightarrow \mathcal {A}$, such that  $\sigma = \rho \circ \sigma '$ where
$\sigma = \rho \circ \sigma '$ where  $\sigma ' \colon S' \rightarrow \mathcal {A}'$ is a section of
$\sigma ' \colon S' \rightarrow \mathcal {A}'$ is a section of  $\mathcal {A}' \rightarrow S'$ in the usual sense.Footnote 2 Denote by
$\mathcal {A}' \rightarrow S'$ in the usual sense.Footnote 2 Denote by  $\sigma (S) := (\rho \circ \sigma ')(S')$.
$\sigma (S) := (\rho \circ \sigma ')(S')$.(iii) In (ii), call
 $\sigma$ a torsion section if
$\sigma$ a torsion section if  $\sigma '(s')$ is a torsion point on
$\sigma '(s')$ is a torsion point on  $\mathcal {A}'_{s'}$ for each
$\mathcal {A}'_{s'}$ for each  $s' \in S'(\mathbb {C})$; call
$s' \in S'(\mathbb {C})$; call  $\sigma$ a constant section if
$\sigma$ a constant section if  $\sigma '$ is the composite of
$\sigma '$ is the composite of  $S' \rightarrow C' \times S'$,
$S' \rightarrow C' \times S'$,  $s' \mapsto (c',s')$, and the inclusion
$s' \mapsto (c',s')$, and the inclusion  $C' \times S' \subseteq \mathcal {A}'$, where
$C' \times S' \subseteq \mathcal {A}'$, where  $C' \times S'$ is a constant abelian subscheme of
$C' \times S'$ is a constant abelian subscheme of  $\mathcal {A}' \rightarrow S'$.
$\mathcal {A}' \rightarrow S'$.
The following definition is convenient to study constant sections.
Definition 2.1 An abelian scheme ![]() $\mathcal {C} \rightarrow S$ (of relative dimension
$\mathcal {C} \rightarrow S$ (of relative dimension ![]() $g$) is said to be isotrivial if one of the following equivalent conditions holds:
$g$) is said to be isotrivial if one of the following equivalent conditions holds:
(i) the fibers
 $\mathcal {C}_s$ are isomorphic to each other for all
$\mathcal {C}_s$ are isomorphic to each other for all  $s \in S(\mathbb {C})$;
$s \in S(\mathbb {C})$;(ii) there exists a finite covering
 $S' \rightarrow S$ such that
$S' \rightarrow S$ such that  $\mathcal {C} \times _S S'$ is a constant abelian scheme, namely
$\mathcal {C} \times _S S'$ is a constant abelian scheme, namely  $\mathcal {C} \times _S S' = C \times S'$ for some abelian variety
$\mathcal {C} \times _S S' = C \times S'$ for some abelian variety  $C$ over
$C$ over  $\mathbb {C}$;
$\mathbb {C}$;(iii) the image of the modular map
 $S \rightarrow \mathbb {A}_g$ induced by
$S \rightarrow \mathbb {A}_g$ induced by  $\mathcal {C} \rightarrow S$ is a point.
$\mathcal {C} \rightarrow S$ is a point.
In particular, the zero section of any abelian scheme ![]() $\mathcal {A} \rightarrow S$ is an isotrivial abelian subscheme. If
$\mathcal {A} \rightarrow S$ is an isotrivial abelian subscheme. If ![]() $\dim S = 0$, then
$\dim S = 0$, then ![]() $\mathcal {A} \rightarrow S$ is isotrivial.
$\mathcal {A} \rightarrow S$ is isotrivial.
Since the sum of two isotrivial abelian subschemes of ![]() $\mathcal {A} \rightarrow S$ is isotrivial, we can define the largest isotrivial abelian subscheme of
$\mathcal {A} \rightarrow S$ is isotrivial, we can define the largest isotrivial abelian subscheme of ![]() $\mathcal {A} \rightarrow S$, which we denote by
$\mathcal {A} \rightarrow S$, which we denote by ![]() $\mathcal {C}$. Then any constant section of
$\mathcal {C}$. Then any constant section of ![]() $\mathcal {A} \rightarrow S$ (defined above) has image in
$\mathcal {A} \rightarrow S$ (defined above) has image in ![]() $\mathcal {C}$.
$\mathcal {C}$.
2.2 Modular map
When ![]() $g = 0$, let
$g = 0$, let ![]() $\mathfrak {A}_0$ and
$\mathfrak {A}_0$ and ![]() $\mathbb {A}_0$ be a point. When
$\mathbb {A}_0$ be a point. When ![]() $g \ge 1$. Let
$g \ge 1$. Let ![]() $D = \mathrm {diag}(d_1,\ldots ,d_g)$ be a
$D = \mathrm {diag}(d_1,\ldots ,d_g)$ be a ![]() $g \times g$ diagonal matrix with
$g \times g$ diagonal matrix with ![]() $d_1, \ldots , d_g$ positive integers such that
$d_1, \ldots , d_g$ positive integers such that ![]() $d_1|\cdots |d_g$.
$d_1|\cdots |d_g$.
For any integer ![]() $N \ge 3$, let
$N \ge 3$, let ![]() $\mathbb {A}_{g,D}(N)$ denote the moduli space of abelian varieties of dimension
$\mathbb {A}_{g,D}(N)$ denote the moduli space of abelian varieties of dimension ![]() $g$ with polarization of type
$g$ with polarization of type ![]() $D$ and with level-
$D$ and with level-![]() $N$-structure. Then
$N$-structure. Then ![]() $\mathbb {A}_{g,D}(N)$ is a fine moduli space, and hence admits a universal family
$\mathbb {A}_{g,D}(N)$ is a fine moduli space, and hence admits a universal family ![]() $\pi \colon \mathfrak {A}_{g,D}(N) \rightarrow \mathbb {A}_{g,D}(N)$. Since level structure is not important for our purpose, we shall drop the ‘
$\pi \colon \mathfrak {A}_{g,D}(N) \rightarrow \mathbb {A}_{g,D}(N)$. Since level structure is not important for our purpose, we shall drop the ‘![]() $(N)$’ in the rest of the paper. When there is no ambiguity about the polarization type, we also drop the ‘
$(N)$’ in the rest of the paper. When there is no ambiguity about the polarization type, we also drop the ‘![]() $D$’ and simply use the notation
$D$’ and simply use the notation ![]() $\pi \colon \mathfrak {A}_g \rightarrow \mathbb {A}_g$.
$\pi \colon \mathfrak {A}_g \rightarrow \mathbb {A}_g$.
It is known that any abelian scheme ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ can be equipped with a polarization of type
$\pi _S \colon \mathcal {A} \rightarrow S$ can be equipped with a polarization of type ![]() $D$ for some
$D$ for some ![]() $D = \mathrm {diag}(d_1,\ldots ,d_g)$, with
$D = \mathrm {diag}(d_1,\ldots ,d_g)$, with ![]() $d_1, \ldots , d_g$ positive integers such that
$d_1, \ldots , d_g$ positive integers such that ![]() $d_1|\cdots |d_g$; see [Reference Genestier and NgôGN09, § 2.1]. Thus up to taking a finite covering of
$d_1|\cdots |d_g$; see [Reference Genestier and NgôGN09, § 2.1]. Thus up to taking a finite covering of ![]() $S$ and the associated base change of
$S$ and the associated base change of ![]() $\mathcal {A} \rightarrow S$, we have the following modular map.
$\mathcal {A} \rightarrow S$, we have the following modular map.

Then ![]() $\mathcal {A} \rightarrow S$ is isotrivial if and only if
$\mathcal {A} \rightarrow S$ is isotrivial if and only if ![]() $\iota _S(S)$ is a point. In particular, if
$\iota _S(S)$ is a point. In particular, if ![]() $S \subseteq \mathbb {A}_g$, then
$S \subseteq \mathbb {A}_g$, then ![]() $\mathfrak {A}_g \times _{\mathbb {A}_g}S$ is isotrivial if and only if
$\mathfrak {A}_g \times _{\mathbb {A}_g}S$ is isotrivial if and only if ![]() $S$ is a point.
$S$ is a point.
3. Universal abelian variety and Betti map
We recall some facts on the universal abelian variety in this section. Let ![]() $D = \mathrm {diag}(d_1,\ldots ,d_g)$ be a
$D = \mathrm {diag}(d_1,\ldots ,d_g)$ be a ![]() $g \times g$ diagonal matrix with
$g \times g$ diagonal matrix with ![]() $d_1,\ldots ,d_g$ positive integers such that
$d_1,\ldots ,d_g$ positive integers such that ![]() $d_1|\cdots |d_g$.
$d_1|\cdots |d_g$.
3.1 Uniformizing space of  $\mathbb {A}_g$
$\mathbb {A}_g$
Let ![]() $\mathfrak {H}_g^+$ be the Siegel upper half space
$\mathfrak {H}_g^+$ be the Siegel upper half space
It is well-known that the uniformization of ![]() $\mathbb {A}_g := \mathbb {A}_{g,D}$ in the category of complex varieties is given by
$\mathbb {A}_g := \mathbb {A}_{g,D}$ in the category of complex varieties is given by
Let us take a closer look at this uniformization.
Let ![]() $\mathrm {Sp}_{2g}$ be the
$\mathrm {Sp}_{2g}$ be the ![]() $\mathbb {Q}$-group
$\mathbb {Q}$-group
and let ![]() $\mathrm {GSp}_{2g}$ be the image of
$\mathrm {GSp}_{2g}$ be the image of ![]() $\mathbb {G}_{\mathrm {m}} \times \mathrm {Sp}_{2g}$ under the central isogeny
$\mathbb {G}_{\mathrm {m}} \times \mathrm {Sp}_{2g}$ under the central isogeny ![]() $\mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_{2g} \rightarrow \mathrm {GL}_{2g}$. Then
$\mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_{2g} \rightarrow \mathrm {GL}_{2g}$. Then ![]() $\mathrm {GSp}_{2g}(\mathbb {R})^+$, the connected component of
$\mathrm {GSp}_{2g}(\mathbb {R})^+$, the connected component of ![]() $\mathrm {GSp}_{2g}(\mathbb {R})$ containing the identity, acts on
$\mathrm {GSp}_{2g}(\mathbb {R})$ containing the identity, acts on ![]() $\mathfrak {H}_g^+$ by the formula
$\mathfrak {H}_g^+$ by the formula
It is known that the action of ![]() $\mathrm {GSp}_{2g}^{\mathrm {der}}(\mathbb {R}) = \mathrm {Sp}_{2g}(\mathbb {R})$ on
$\mathrm {GSp}_{2g}^{\mathrm {der}}(\mathbb {R}) = \mathrm {Sp}_{2g}(\mathbb {R})$ on ![]() $\mathfrak {H}_g^+$ thus defined is transitive, and the uniformization (3.1) is obtained by identifying
$\mathfrak {H}_g^+$ thus defined is transitive, and the uniformization (3.1) is obtained by identifying ![]() $(\mathbb {A}_g)^{\mathrm {an}}$ with the quotient space
$(\mathbb {A}_g)^{\mathrm {an}}$ with the quotient space ![]() $\Gamma _{\mathrm {GSp}_{2g}}\backslash \mathfrak {H}_g^+$ for a suitable congruence group
$\Gamma _{\mathrm {GSp}_{2g}}\backslash \mathfrak {H}_g^+$ for a suitable congruence group ![]() $\Gamma _{\mathrm {Sp}_{2g}}$ of
$\Gamma _{\mathrm {Sp}_{2g}}$ of ![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$.
$\mathrm {Sp}_{2g}(\mathbb {Z})$.
3.2 Uniformizing space of  $\mathfrak {A}_g$
$\mathfrak {A}_g$
To obtain the uniformization of ![]() $\mathfrak {A}_g$, let us construct the following complex space
$\mathfrak {A}_g$, let us construct the following complex space ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$:
$\mathcal {X}_{2g,\mathrm {a}}^+$:
(i) as a semi-algebraic space,
 $\mathcal {X}_{2g,\mathrm {a}}^+ = \mathbb {R}^{2g} \times \mathfrak {H}_g^+$;
$\mathcal {X}_{2g,\mathrm {a}}^+ = \mathbb {R}^{2g} \times \mathfrak {H}_g^+$;(ii) the complex structure of
 $\mathcal {X}_{2g,\mathrm {a}}^+$ is the one given by
(3.2)
$\mathcal {X}_{2g,\mathrm {a}}^+$ is the one given by
(3.2) \begin{equation} \begin{array}{cccc} \mathcal{X}_{2g,\mathrm{a}}^+ = & \mathbb{R}^g \times \mathbb{R}^g \times \mathfrak{H}_g^+ & \xrightarrow{\sim} & \mathbb{C}^g \times \mathfrak{H}_g^+, \\ & (a,b,Z) & \mapsto & (Da+Zb, Z) \end{array}. \end{equation}
\begin{equation} \begin{array}{cccc} \mathcal{X}_{2g,\mathrm{a}}^+ = & \mathbb{R}^g \times \mathbb{R}^g \times \mathfrak{H}_g^+ & \xrightarrow{\sim} & \mathbb{C}^g \times \mathfrak{H}_g^+, \\ & (a,b,Z) & \mapsto & (Da+Zb, Z) \end{array}. \end{equation}
The uniformization of ![]() $\mathfrak {A}_g$ in the category of complex varieties is then given by
$\mathfrak {A}_g$ in the category of complex varieties is then given by
Similar to the discussion on ![]() $\textbf {u}_G$, there exists a
$\textbf {u}_G$, there exists a ![]() $\mathbb {Q}$-group, which we call
$\mathbb {Q}$-group, which we call ![]() $P_{2g,\mathrm {a}}$ such that
$P_{2g,\mathrm {a}}$ such that ![]() $P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {R})$ acts transitively on
$P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {R})$ acts transitively on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ and
$\mathcal {X}_{2g,\mathrm {a}}^+$ and ![]() $\textbf {u}$ is obtained by identifying
$\textbf {u}$ is obtained by identifying ![]() $(\mathfrak {A}_g)^{\mathrm {an}}$ with the quotient space
$(\mathfrak {A}_g)^{\mathrm {an}}$ with the quotient space ![]() $\Gamma \backslash \mathcal {X}_{2g,\mathrm {a}}^+$ for a suitable congruence subgroup
$\Gamma \backslash \mathcal {X}_{2g,\mathrm {a}}^+$ for a suitable congruence subgroup ![]() $\Gamma = \mathbb {Z}^{2g} \rtimes \Gamma _{\mathrm {Sp}_{2g}}$ of
$\Gamma = \mathbb {Z}^{2g} \rtimes \Gamma _{\mathrm {Sp}_{2g}}$ of ![]() $P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$. Let us briefly explain this.
$P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$. Let us briefly explain this.
Use ![]() $V_{2g}$ to denote the
$V_{2g}$ to denote the ![]() $\mathbb {Q}$-vector group of dimension
$\mathbb {Q}$-vector group of dimension ![]() $2g$. Then the natural action of
$2g$. Then the natural action of ![]() $\mathrm {GSp}_{2g}$ on
$\mathrm {GSp}_{2g}$ on ![]() $V_{2g}$ defines a
$V_{2g}$ defines a ![]() $\mathbb {Q}$-group
$\mathbb {Q}$-group
The action of ![]() $P_{2g,\mathrm {a}}(\mathbb {R})^+$ on
$P_{2g,\mathrm {a}}(\mathbb {R})^+$ on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ is defined as follows: for any
$\mathcal {X}_{2g,\mathrm {a}}^+$ is defined as follows: for any ![]() $(v,h) \in P_{2g,\mathrm {a}}(\mathbb {R})^+ = V_{2g}(\mathbb {R}) \rtimes \mathrm {GSp}_{2g}(\mathbb {R})^+$ and any
$(v,h) \in P_{2g,\mathrm {a}}(\mathbb {R})^+ = V_{2g}(\mathbb {R}) \rtimes \mathrm {GSp}_{2g}(\mathbb {R})^+$ and any ![]() $(v',x) \in \mathcal {X}_{2g,\mathrm {a}}^+$, we have
$(v',x) \in \mathcal {X}_{2g,\mathrm {a}}^+$, we have
where ![]() $\mathrm {GSp}_{2g}(\mathbb {R})^+$ acts on
$\mathrm {GSp}_{2g}(\mathbb {R})^+$ acts on ![]() $\mathbb {R}^{2g}$ as above (3.2).
$\mathbb {R}^{2g}$ as above (3.2).
The natural projection of complex spaces ![]() $\tilde {\pi } \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {H}_g^+$ is equivariant with respect to the natural projection of groups
$\tilde {\pi } \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {H}_g^+$ is equivariant with respect to the natural projection of groups ![]() $P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$. Hence by abuse of notation we also denote by
$P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$. Hence by abuse of notation we also denote by ![]() $\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$.
$\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$.
3.3 Betti map
We define the Betti map in this section. We will start by defining the universal uniformized Betti map on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$, and then descend it to
$\mathcal {X}_{2g,\mathrm {a}}^+$, and then descend it to ![]() $\mathcal {A}_{\mathfrak {H}_g^+}$, the pullback of
$\mathcal {A}_{\mathfrak {H}_g^+}$, the pullback of ![]() $\mathfrak {A}_g / \mathbb {A}_g$ under
$\mathfrak {A}_g / \mathbb {A}_g$ under ![]() $\textbf {u}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$. Note that
$\textbf {u}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$. Note that ![]() $\mathcal {A}_{\mathfrak {H}_g^+}$ is a family of abelian varieties over
$\mathcal {A}_{\mathfrak {H}_g^+}$ is a family of abelian varieties over ![]() $\mathfrak {H}_g^+$.
$\mathfrak {H}_g^+$.
Recall that ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ is defined to be
$\mathcal {X}_{2g,\mathrm {a}}^+$ is defined to be ![]() $\mathbb {R}^{2g} \times \mathfrak {H}_g^+$ with the complex structure determined by (3.2). The universal uniformized Betti map
$\mathbb {R}^{2g} \times \mathfrak {H}_g^+$ with the complex structure determined by (3.2). The universal uniformized Betti map ![]() $\tilde {b}$ is defined to be the natural projection
$\tilde {b}$ is defined to be the natural projection
Then ![]() $\tilde {b}$ is semi-algebraic. For the complex structure on
$\tilde {b}$ is semi-algebraic. For the complex structure on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ given by (3.2), it is clear that
$\mathcal {X}_{2g,\mathrm {a}}^+$ given by (3.2), it is clear that ![]() $\tilde {b}^{-1}(r)$ is complex analytic for each
$\tilde {b}^{-1}(r)$ is complex analytic for each ![]() $r \in \mathbb {R}^{2g}$.
$r \in \mathbb {R}^{2g}$.
Recall that ![]() $(\mathfrak {A}_g)^{\mathrm {an}} \simeq \Gamma \backslash \mathcal {X}_{2g,\mathrm {a}}^+$ as complex spaces for a suitable congruence subgroup
$(\mathfrak {A}_g)^{\mathrm {an}} \simeq \Gamma \backslash \mathcal {X}_{2g,\mathrm {a}}^+$ as complex spaces for a suitable congruence subgroup ![]() $\Gamma = \mathbb {Z}^{2g} \rtimes \Gamma _{\mathrm {Sp}_{2g}}$ of
$\Gamma = \mathbb {Z}^{2g} \rtimes \Gamma _{\mathrm {Sp}_{2g}}$ of ![]() $P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$. The family of abelian varieties
$P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$. The family of abelian varieties ![]() $\mathcal {A}_{\mathfrak {H}_g^+}$ defined as at the beginning of this subsection can be identified with the quotient space
$\mathcal {A}_{\mathfrak {H}_g^+}$ defined as at the beginning of this subsection can be identified with the quotient space ![]() $(\mathbb {Z}^{2g} \rtimes \{1\}) \backslash \mathcal {X}_{2g,\mathrm {a}}^+$. Now taking quotient by
$(\mathbb {Z}^{2g} \rtimes \{1\}) \backslash \mathcal {X}_{2g,\mathrm {a}}^+$. Now taking quotient by ![]() $\mathbb {Z}^{2g}$ on both sides of (3.5), we obtain the universal Betti map
$\mathbb {Z}^{2g}$ on both sides of (3.5), we obtain the universal Betti map
where ![]() $\mathbb {T}^{2g}$ denotes the real torus of dimension
$\mathbb {T}^{2g}$ denotes the real torus of dimension ![]() $2g$. By the discussion below (3.5), we have the following properties for
$2g$. By the discussion below (3.5), we have the following properties for ![]() $\tilde {b}$ and
$\tilde {b}$ and ![]() $b$.
$b$.
(i) Both
 $\tilde {b}$ and
$\tilde {b}$ and  $b$ are real-analytic, and
$b$ are real-analytic, and  $\tilde {b}$ is moreover semi-algebraic.
$\tilde {b}$ is moreover semi-algebraic.(ii) For each
 $r \in \mathbb {R}^{2g}$, resp. each
$r \in \mathbb {R}^{2g}$, resp. each  $t \in \mathbb {T}^{2g}$, we have that
$t \in \mathbb {T}^{2g}$, we have that  $\tilde {b}^{-1}(r)$, resp.
$\tilde {b}^{-1}(r)$, resp.  $b^{-1}(t)$, is complex analytic.
$b^{-1}(t)$, is complex analytic.(iii) For each
 $\tau \in \mathfrak {H}_g^+$, the restriction
$\tau \in \mathfrak {H}_g^+$, the restriction  $b|_{(\mathcal {A}_{\mathfrak {H}_g^+})_{\tau }}$ is a group isomorphism.
$b|_{(\mathcal {A}_{\mathfrak {H}_g^+})_{\tau }}$ is a group isomorphism.
We summarize our notation regarding the uniformizations in the following diagram:

with the uniformization ![]() ${\mathbf {u}}$ from (3.3) and the uniformization
${\mathbf {u}}$ from (3.3) and the uniformization ![]() ${\mathbf {u}}_G$ from (3.1).
${\mathbf {u}}_G$ from (3.1).
4. Betti map on arbitrary abelian schemes
The goal of this section is to extend the definition of Betti map to an arbitrary abelian scheme. Moreover we choose to work on the original abelian scheme instead of on the pullback to the universal covering.
Let ![]() $S$ be an irreducible quasi-projective variety over
$S$ be an irreducible quasi-projective variety over ![]() $\mathbb {C}$, and let
$\mathbb {C}$, and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g$. Then up to replacing
$g$. Then up to replacing ![]() $S$ by a finite covering and
$S$ by a finite covering and ![]() $\mathcal {A} \rightarrow S$ by the corresponding base change, we have the following diagram.
$\mathcal {A} \rightarrow S$ by the corresponding base change, we have the following diagram.

Let ![]() $\Delta _0$ be a simply-connected open subset in
$\Delta _0$ be a simply-connected open subset in ![]() $\mathbb {A}_g^{\mathrm {an}}$. Fix a component of
$\mathbb {A}_g^{\mathrm {an}}$. Fix a component of ![]() $\tilde {\Delta }_0$ of
$\tilde {\Delta }_0$ of ![]() ${\mathbf {u}}_G^{-1}(\Delta _0)$ under the uniformization
${\mathbf {u}}_G^{-1}(\Delta _0)$ under the uniformization ![]() ${\mathbf {u}}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$. The fact that
${\mathbf {u}}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$. The fact that ![]() $\Delta _0$ is simply-connected implies that
$\Delta _0$ is simply-connected implies that ![]() ${\mathbf {u}}_G|_{\tilde {\Delta }_0}$ is an isomorphism in the category of complex spaces. Thus the universal Betti map (3.6) induces a map
${\mathbf {u}}_G|_{\tilde {\Delta }_0}$ is an isomorphism in the category of complex spaces. Thus the universal Betti map (3.6) induces a map ![]() $b_{\Delta _0} \colon \mathfrak {A}_g|_{\Delta _0} \rightarrow \mathbb {T}^{2g}$ by identifying
$b_{\Delta _0} \colon \mathfrak {A}_g|_{\Delta _0} \rightarrow \mathbb {T}^{2g}$ by identifying ![]() $\mathfrak {A}_g|_{\Delta _0} = \pi ^{-1}(\Delta _0)$ with
$\mathfrak {A}_g|_{\Delta _0} = \pi ^{-1}(\Delta _0)$ with ![]() $\mathcal {A}_{\mathfrak {H}_g^+}|_{\tilde {\Delta }_0}$.
$\mathcal {A}_{\mathfrak {H}_g^+}|_{\tilde {\Delta }_0}$.
For any ![]() $s \in S(\mathbb {C})$, we can find a
$s \in S(\mathbb {C})$, we can find a ![]() $\Delta _0$ as above such that
$\Delta _0$ as above such that ![]() $\iota _S(s) \in \Delta _0$. Let
$\iota _S(s) \in \Delta _0$. Let ![]() $\Delta$ be a component of
$\Delta$ be a component of ![]() $\iota _S^{-1}(\Delta _0)$, which contains
$\iota _S^{-1}(\Delta _0)$, which contains ![]() $s$. Let
$s$. Let ![]() $\mathcal {A}_{\Delta } = \pi _S^{-1}(\Delta )$. Define
$\mathcal {A}_{\Delta } = \pi _S^{-1}(\Delta )$. Define
to be the composite of ![]() $\iota$ and
$\iota$ and ![]() $b_{\Delta _0}$. The following properties of
$b_{\Delta _0}$. The following properties of ![]() $b_{\Delta }$ follow from the properties of the universal Betti map listed below (3.6).
$b_{\Delta }$ follow from the properties of the universal Betti map listed below (3.6).
(i) The map
 $b_{\Delta }$ is real-analytic.
$b_{\Delta }$ is real-analytic.(ii) For each
 $t \in \mathbb {T}^{2g}$, we have that
$t \in \mathbb {T}^{2g}$, we have that  $b_{\Delta }^{-1}(t)$, is complex analytic.
$b_{\Delta }^{-1}(t)$, is complex analytic.(iii) For each
 $s \in \Delta$, the restriction
$s \in \Delta$, the restriction  $b_{\Delta }|_{\mathcal {A}_s}$ is a group isomorphism.
$b_{\Delta }|_{\mathcal {A}_s}$ is a group isomorphism.
Note that ![]() $b_{\Delta }$ is not unique as we can choose different components of
$b_{\Delta }$ is not unique as we can choose different components of ![]() $\mathbf {u}_G^{-1}(\Delta _0)$. But
$\mathbf {u}_G^{-1}(\Delta _0)$. But ![]() $b_{\Delta }$ is unique up to
$b_{\Delta }$ is unique up to ![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$ because
$\mathrm {Sp}_{2g}(\mathbb {Z})$ because ![]() $\mathbb {A}_g \simeq \Gamma _{\mathrm {GSp}_{2g}} \backslash \mathfrak {H}_g^+$ for some congruence subgroup
$\mathbb {A}_g \simeq \Gamma _{\mathrm {GSp}_{2g}} \backslash \mathfrak {H}_g^+$ for some congruence subgroup ![]() $\Gamma _{\mathrm {GSp}_{2g}}$ of
$\Gamma _{\mathrm {GSp}_{2g}}$ of ![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$.
$\mathrm {Sp}_{2g}(\mathbb {Z})$.
The Betti map factors through the universal abelian variety by definition. Thus to study the generic rank of the Betti map, it often suffices to consider the subvarieties of ![]() $\mathfrak {A}_g$.
$\mathfrak {A}_g$.
Before moving on, let us see another way to define the Betti map. Let ![]() $\mathbf {u}_S \colon \tilde {S} \rightarrow S^{\mathrm {an}}$ be the universal covering, and let
$\mathbf {u}_S \colon \tilde {S} \rightarrow S^{\mathrm {an}}$ be the universal covering, and let ![]() $\mathcal {A}_{\tilde {S}}$ be the pullback of
$\mathcal {A}_{\tilde {S}}$ be the pullback of ![]() $\mathcal {A} \rightarrow S$ under
$\mathcal {A} \rightarrow S$ under ![]() $\mathbf {u}_S$. Then the modular map
$\mathbf {u}_S$. Then the modular map ![]() $\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ induces a natural morphism
$\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ induces a natural morphism ![]() $\tilde {\iota } \colon \mathcal {A}_{\tilde {S}} \rightarrow \mathcal {A}_{\mathfrak {H}_g^+}$; see (3.6) for notation. Then one can define
$\tilde {\iota } \colon \mathcal {A}_{\tilde {S}} \rightarrow \mathcal {A}_{\mathfrak {H}_g^+}$; see (3.6) for notation. Then one can define ![]() $b_{\tilde {S}} \colon \mathcal {A}_{\tilde {S}} \rightarrow \mathbb {T}^{2g}$ to be
$b_{\tilde {S}} \colon \mathcal {A}_{\tilde {S}} \rightarrow \mathbb {T}^{2g}$ to be ![]() $\tilde {\iota }$ composed with the universal Betti map (3.6). Note that
$\tilde {\iota }$ composed with the universal Betti map (3.6). Note that ![]() $b_{\tilde {S}}$ is uniquely determined, contrary to
$b_{\tilde {S}}$ is uniquely determined, contrary to ![]() $b_{\Delta }$. Now
$b_{\Delta }$. Now ![]() $b_{\Delta }$ (4.2) can be obtained as follows: identify
$b_{\Delta }$ (4.2) can be obtained as follows: identify ![]() $\mathcal {A}_{\Delta }$ and
$\mathcal {A}_{\Delta }$ and ![]() $\mathcal {A}_{\tilde {\Delta }}$ by identifying
$\mathcal {A}_{\tilde {\Delta }}$ by identifying ![]() $\Delta$ with a component
$\Delta$ with a component ![]() $\tilde {\Delta }$ of
$\tilde {\Delta }$ of ![]() $\mathbf {u}_S^{-1}(\Delta )$, then
$\mathbf {u}_S^{-1}(\Delta )$, then ![]() $b_{\Delta }$ is
$b_{\Delta }$ is ![]() $b_{\tilde {S}}$ restricted to
$b_{\tilde {S}}$ restricted to ![]() $\mathcal {A}_{\Delta }$.
$\mathcal {A}_{\Delta }$.
Now we are able to prove some easy properties of the Betti rank. Let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$ with
$\mathcal {A}$ with ![]() $\pi _S(X) = S$. Then
$\pi _S(X) = S$. Then ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) := \max _{x \in X^{\mathrm {sm}}(\mathbb {C})\cap \mathcal {A}_{\Delta }}(\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)_x)$ satisfies the following:
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) := \max _{x \in X^{\mathrm {sm}}(\mathbb {C})\cap \mathcal {A}_{\Delta }}(\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)_x)$ satisfies the following:
(i) it is at most
 $2\min (\dim \iota (X), g)$ as
$2\min (\dim \iota (X), g)$ as  $b_{\Delta }$ factors through
$b_{\Delta }$ factors through  $\iota$;
$\iota$;(ii) it is even by property (ii) above;
(iii) it does not depend on the choice of
 $\Delta$: take a complex analytic irreducible component
$\Delta$: take a complex analytic irreducible component  $\hat {X}$ of the inverse image of
$\hat {X}$ of the inverse image of  $X^{\mathrm {sm}}$ under
$X^{\mathrm {sm}}$ under  $\mathcal {A}_{\tilde {S}} \rightarrow \mathcal {A}$, then
$\mathcal {A}_{\tilde {S}} \rightarrow \mathcal {A}$, then  $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = \mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}})$. As
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = \mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}})$. As  $\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}$ is open (and hence has positive Lebesgue measure) in
$\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}$ is open (and hence has positive Lebesgue measure) in  $\hat {X}$, we have
$\hat {X}$, we have  $\mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}}) = \mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X}})$ by Sard's theorem. The conclusion then follows.
$\mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X} \cap \mathcal {A}_{\tilde {\Delta }}}) = \mathrm {rank}_{\mathbb {R}}({d}b_{\tilde {S}}|_{\hat {X}})$ by Sard's theorem. The conclusion then follows.
5. Bi-algebraic system associated with  $\mathfrak {A}_g$
$\mathfrak {A}_g$
The goal of this section is to give some further background knowledge on the universal abelian varieties, which will serve as our main tools to study the Betti map. There are two parts. The first part §§ 5.1 and 5.2 is to introduce the functional transcendence theorem (called weak Ax–Schanuel), and the second part §§ 5.3 and 5.4 is Deligne and Pink's language of mixed Shimura varieties.Footnote 3
5.1 Generically special subvarieties of sg type and bi-algebraic subvarieties
The goal of this subsection is to explain the relation between generically special subvarieties of sg type (see Definition 1.5) and bi-algebraic subvarieties of ![]() $\mathfrak {A}_g$.
$\mathfrak {A}_g$.
Let us start with defining bi-algebraic subvarieties of ![]() $\mathfrak {A}_g$. Recall the uniformization
$\mathfrak {A}_g$. Recall the uniformization ![]() $\mathbf {u} \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {A}_g$. By [Reference GaoGao17b, § 4]
$\mathbf {u} \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {A}_g$. By [Reference GaoGao17b, § 4] ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ can be embedded as an open, in the usual topology, semi-algebraic subset of a complex flag variety (hence algebraic)
$\mathcal {X}_{2g,\mathrm {a}}^+$ can be embedded as an open, in the usual topology, semi-algebraic subset of a complex flag variety (hence algebraic) ![]() $\mathcal {X}_{2g,\mathrm {a}}^\vee$.
$\mathcal {X}_{2g,\mathrm {a}}^\vee$.
Definition 5.1 (i) A subset ![]() $\tilde {Y}$ of
$\tilde {Y}$ of ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ is said to be irreducible algebraic if it is a complex analytic irreducible component of
$\mathcal {X}_{2g,\mathrm {a}}^+$ is said to be irreducible algebraic if it is a complex analytic irreducible component of ![]() $\mathcal {X}_{2g,\mathrm {a}}^+ \cap W$ for some algebraic subvariety
$\mathcal {X}_{2g,\mathrm {a}}^+ \cap W$ for some algebraic subvariety ![]() $W$ of
$W$ of ![]() $\mathcal {X}_{2g,\mathrm {a}}^\vee$.
$\mathcal {X}_{2g,\mathrm {a}}^\vee$.
(ii) An irreducible subvariety ![]() $Y$ of
$Y$ of ![]() $\mathfrak {A}_g$ is said to be bi-algebraic if one (and hence any) complex analytic irreducible component
$\mathfrak {A}_g$ is said to be bi-algebraic if one (and hence any) complex analytic irreducible component ![]() $\tilde {Y}$ of
$\tilde {Y}$ of ![]() ${\mathbf {u}}^{-1}(Y)$ is algebraic.
${\mathbf {u}}^{-1}(Y)$ is algebraic.
It is not hard to show that the intersection of two bi-algebraic subvarieties of ![]() $\mathfrak {A}_g$ is a finite union of irreducible bi-algebraic subvarieties of
$\mathfrak {A}_g$ is a finite union of irreducible bi-algebraic subvarieties of ![]() $\mathfrak {A}_g$. Hence for any subset
$\mathfrak {A}_g$. Hence for any subset ![]() $Z$ of
$Z$ of ![]() $\mathfrak {A}_g$, there exists a smallest bi-algebraic subvariety
$\mathfrak {A}_g$, there exists a smallest bi-algebraic subvariety ![]() $\mathfrak {A}_g$ which contains
$\mathfrak {A}_g$ which contains ![]() $Z$. We use
$Z$. We use ![]() $Z^{\mathrm {biZar}}$ to denote it. Note that
$Z^{\mathrm {biZar}}$ to denote it. Note that ![]() $Z^{\mathrm {biZar}} \supseteq Z^{\mathrm {Zar}}$.
$Z^{\mathrm {biZar}} \supseteq Z^{\mathrm {Zar}}$.
Remark 5.2 There is a canonical way to endow ![]() $\mathfrak {H}_g^+$ with an algebraic structure, which is compatible with
$\mathfrak {H}_g^+$ with an algebraic structure, which is compatible with ![]() $\tilde {\pi } \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {H}_g^+$ and the algebraic structure on
$\tilde {\pi } \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathfrak {H}_g^+$ and the algebraic structure on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ defined above; see [Reference GaoGao17b, § 4]. Then it is clear that for any
$\mathcal {X}_{2g,\mathrm {a}}^+$ defined above; see [Reference GaoGao17b, § 4]. Then it is clear that for any ![]() $F$ bi-algebraic in
$F$ bi-algebraic in ![]() $\mathfrak {A}_g$, we have that
$\mathfrak {A}_g$, we have that ![]() $\pi (F)$ is bi-algebraic in
$\pi (F)$ is bi-algebraic in ![]() $\mathbb {A}_g$.
$\mathbb {A}_g$.
Bi-algebraic subvarieties of ![]() $\mathfrak {A}_g$ are closely related to generically special subvarieties of sg type defined in Definition 1.5 by the following proposition.
$\mathfrak {A}_g$ are closely related to generically special subvarieties of sg type defined in Definition 1.5 by the following proposition.
Proposition 5.3 [Gao17a, Proposition 3.3] Let ![]() $B$ be an irreducible subvariety of
$B$ be an irreducible subvariety of ![]() $\mathbb {A}_g$. Denote by
$\mathbb {A}_g$. Denote by ![]() $\mathfrak {A}_g|_B = \pi ^{-1}(B)$. Then we have
$\mathfrak {A}_g|_B = \pi ^{-1}(B)$. Then we have
The following equivalent form of Proposition 5.3 is more practical for our use.
Corollary 5.4 Let ![]() $Y$ be an irreducible subvariety of
$Y$ be an irreducible subvariety of ![]() $\mathfrak {A}_g$. Then
$\mathfrak {A}_g$. Then ![]() $\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of
$\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of ![]() $(\mathfrak {A}_g|_{\pi (Y)}) \cap Y^{\mathrm {biZar}}$. In particular,
$(\mathfrak {A}_g|_{\pi (Y)}) \cap Y^{\mathrm {biZar}}$. In particular, ![]() $\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) = \dim Y^{\mathrm {biZar}} - \dim \pi (Y)^{\mathrm {biZar}}$.
$\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) = \dim Y^{\mathrm {biZar}} - \dim \pi (Y)^{\mathrm {biZar}}$.
Proof. First note that ![]() $(\mathfrak {A}_g|_{\pi (Y)}) \cap Y^{\mathrm {biZar}}$ is equidimensional. So the ‘In particular’ part follows from the main part and the fact that
$(\mathfrak {A}_g|_{\pi (Y)}) \cap Y^{\mathrm {biZar}}$ is equidimensional. So the ‘In particular’ part follows from the main part and the fact that ![]() $\pi (Y)^{\mathrm {biZar}} = \pi (Y^{\mathrm {biZar}})$ (Remark 5.2).
$\pi (Y)^{\mathrm {biZar}} = \pi (Y^{\mathrm {biZar}})$ (Remark 5.2).
Let ![]() $B = \pi (Y)$. Proposition 5.3 implies that each irreducible component of
$B = \pi (Y)$. Proposition 5.3 implies that each irreducible component of ![]() $(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}}$ is a generically special subvariety of sg type of
$(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}}$ is a generically special subvariety of sg type of ![]() $\mathfrak {A}_g|_B$. Hence
$\mathfrak {A}_g|_B$. Hence ![]() $\langle Y \rangle _{\mathrm {sg}} \subseteq W$, where
$\langle Y \rangle _{\mathrm {sg}} \subseteq W$, where ![]() $W$ is an irreducible component of
$W$ is an irreducible component of ![]() $(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}}$.
$(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}}$.
For the other inclusion, since ![]() $\langle Y \rangle _{\mathrm {sg}}$ is a generically special subvariety of sg type of
$\langle Y \rangle _{\mathrm {sg}}$ is a generically special subvariety of sg type of ![]() $\mathfrak {A}_g|_B$, we have by Proposition 5.3 that
$\mathfrak {A}_g|_B$, we have by Proposition 5.3 that ![]() $\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of
$\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of ![]() $(\mathfrak {A}_g|_B) \cap F$ for some irreducible bi-algebraic subvariety
$(\mathfrak {A}_g|_B) \cap F$ for some irreducible bi-algebraic subvariety ![]() $F$ of
$F$ of ![]() $\mathfrak {A}_g$. Then
$\mathfrak {A}_g$. Then ![]() $Y \subseteq \langle Y \rangle _{\mathrm {sg}} \subseteq F$. Hence
$Y \subseteq \langle Y \rangle _{\mathrm {sg}} \subseteq F$. Hence ![]() $Y^{\mathrm {biZar}} \subseteq F$. Thus
$Y^{\mathrm {biZar}} \subseteq F$. Thus ![]() $(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}} \subseteq (\mathfrak {A}_g|_B) \cap F$.
$(\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}} \subseteq (\mathfrak {A}_g|_B) \cap F$.
In summary, we have ![]() $\langle Y \rangle _{\mathrm {sg}} \subseteq W \subseteq (\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}} \subseteq (\mathfrak {A}_g|_B) \cap F$, and that
$\langle Y \rangle _{\mathrm {sg}} \subseteq W \subseteq (\mathfrak {A}_g|_B) \cap Y^{\mathrm {biZar}} \subseteq (\mathfrak {A}_g|_B) \cap F$, and that ![]() $\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of
$\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of ![]() $(\mathfrak {A}_g|_B) \cap F$. So
$(\mathfrak {A}_g|_B) \cap F$. So ![]() $W = \langle Y \rangle _{\mathrm {sg}}$ and we are done.
$W = \langle Y \rangle _{\mathrm {sg}}$ and we are done.
5.2 Weak Ax–Schanuel for  $\mathfrak {A}_g$
$\mathfrak {A}_g$
One of the most important tools we use to study the Betti map is the following weak Ax–Schanuel theorem for ![]() $\mathfrak {A}_g$ [Reference GaoGao20, Theorem 1.1 or Theorem 3.5].
$\mathfrak {A}_g$ [Reference GaoGao20, Theorem 1.1 or Theorem 3.5].
Theorem 5.5 Let ![]() $\tilde {Z}$ be a complex analytic irreducible subset of
$\tilde {Z}$ be a complex analytic irreducible subset of ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$. Then
$\mathcal {X}_{2g,\mathrm {a}}^+$. Then
where ![]() $\tilde {Z}^{\mathrm {Zar}}$ means the smallest irreducible algebraic subset of
$\tilde {Z}^{\mathrm {Zar}}$ means the smallest irreducible algebraic subset of ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ which contains
$\mathcal {X}_{2g,\mathrm {a}}^+$ which contains ![]() $\tilde {Z}$.
$\tilde {Z}$.
5.3 A quick introduction to Shimura varieties
We gather some notation and facts on Shimura varieties. We will need the knowledge (only) for the proofs in §§ 7 and 8.
Recall that in § 3.1, we have associated a reductive ![]() $\mathbb {Q}$-group
$\mathbb {Q}$-group ![]() $\mathrm {GSp}_{2g}$ and a complex space
$\mathrm {GSp}_{2g}$ and a complex space ![]() $\mathfrak {H}_g^+$ to the moduli space
$\mathfrak {H}_g^+$ to the moduli space ![]() $\mathbb {A}_g$. In other words, we have associated a pair
$\mathbb {A}_g$. In other words, we have associated a pair ![]() $(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$ to
$(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$ to ![]() $\mathbb {A}_g$, where:
$\mathbb {A}_g$, where:
•
 $\mathrm {GSp}_{2g}$ is a reductive
$\mathrm {GSp}_{2g}$ is a reductive  $\mathbb {Q}$-group;
$\mathbb {Q}$-group;•
 $\mathfrak {H}_g^+$ is a complex space on which
$\mathfrak {H}_g^+$ is a complex space on which  $\mathrm {GSp}_{2g}(\mathbb {R})^+$ acts transitively;
$\mathrm {GSp}_{2g}(\mathbb {R})^+$ acts transitively;• as a complex space,
 $\mathbb {A}_g$ is the quotient of
$\mathbb {A}_g$ is the quotient of  $\mathfrak {H}_g^+$ by a congruence subgroup of
$\mathfrak {H}_g^+$ by a congruence subgroup of  $\mathrm {GSp}_{2g}^{\mathrm {der}}(\mathbb {Z})$.
$\mathrm {GSp}_{2g}^{\mathrm {der}}(\mathbb {Z})$.
This pair ![]() $(\mathrm {GSp}_{2g},\mathfrak {H}_g^+)$ is a special case of pure Shimura datum, and the third bullet point makes
$(\mathrm {GSp}_{2g},\mathfrak {H}_g^+)$ is a special case of pure Shimura datum, and the third bullet point makes ![]() $\mathbb {A}_g$ a pure Shimura variety. In general, a pure Shimura datum is a pair
$\mathbb {A}_g$ a pure Shimura variety. In general, a pure Shimura datum is a pair ![]() $(G,\mathcal {X}_G^+)$ such that
$(G,\mathcal {X}_G^+)$ such that ![]() $G$ is a reductive
$G$ is a reductive ![]() $\mathbb {Q}$-group and
$\mathbb {Q}$-group and ![]() $\mathcal {X}_G^+$ is a complex space on which
$\mathcal {X}_G^+$ is a complex space on which ![]() $G^{\mathrm {der}}(\mathbb {R})^+$ acts transitively (along with some other properties). A pure Shimura variety is a quotient space
$G^{\mathrm {der}}(\mathbb {R})^+$ acts transitively (along with some other properties). A pure Shimura variety is a quotient space ![]() $\Gamma _G \backslash \mathcal {X}_G^+$ for some congruence subgroup
$\Gamma _G \backslash \mathcal {X}_G^+$ for some congruence subgroup ![]() $\Gamma _G$ of
$\Gamma _G$ of ![]() $G^{\mathrm {der}}(\mathbb {Z})$.
$G^{\mathrm {der}}(\mathbb {Z})$.
Next we turn to the universal abelian variety ![]() $\mathfrak {A}_g$. In § 3.2 we have associated with it a
$\mathfrak {A}_g$. In § 3.2 we have associated with it a ![]() $\mathbb {Q}$-group
$\mathbb {Q}$-group ![]() $P_{2g,\mathrm {a}}$ and a complex space
$P_{2g,\mathrm {a}}$ and a complex space ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$. Note that
$\mathcal {X}_{2g,\mathrm {a}}^+$. Note that ![]() $P_{2g,\mathrm {a}}$ is not a reductive group. Nevertheless we have the following properties for the pair
$P_{2g,\mathrm {a}}$ is not a reductive group. Nevertheless we have the following properties for the pair ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$:
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$:
•
 $P_{2g,\mathrm {a}}$ is a
$P_{2g,\mathrm {a}}$ is a  $\mathbb {Q}$-group, whose unipotent radical is a vector group;
$\mathbb {Q}$-group, whose unipotent radical is a vector group;•
 $\mathcal {X}_{2g,\mathrm {a}}^+$ is a complex space on which
$\mathcal {X}_{2g,\mathrm {a}}^+$ is a complex space on which  $P_{2g,\mathrm {a}}(\mathbb {R})^+$ acts transitively;
$P_{2g,\mathrm {a}}(\mathbb {R})^+$ acts transitively;• as a complex space,
 $\mathfrak {A}_g$ is the quotient of
$\mathfrak {A}_g$ is the quotient of  $\mathcal {X}_{2g,\mathrm {a}}^+$ by a congruence subgroup of
$\mathcal {X}_{2g,\mathrm {a}}^+$ by a congruence subgroup of  $P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$.
$P_{2g,\mathrm {a}}^{\mathrm {der}}(\mathbb {Z})$.
This makes the pair ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ a mixed Shimura datum of Kuga type, and the third bullet point makes
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ a mixed Shimura datum of Kuga type, and the third bullet point makes ![]() $\mathfrak {A}_g$ a mixed Shimura variety of Kuga type. In general a mixed Shimura datum of Kuga type is a pair
$\mathfrak {A}_g$ a mixed Shimura variety of Kuga type. In general a mixed Shimura datum of Kuga type is a pair ![]() $(P,\mathcal {X}^+)$ such that
$(P,\mathcal {X}^+)$ such that ![]() $P$ is a
$P$ is a ![]() $\mathbb {Q}$-group whose unipotent radical is a vector group, and
$\mathbb {Q}$-group whose unipotent radical is a vector group, and ![]() $\mathcal {X}^+$ is a complex space on which
$\mathcal {X}^+$ is a complex space on which ![]() $P(\mathbb {R})^+$ acts transitively (along with some other properties). A mixed Shimura variety of Kuga type is a quotient space
$P(\mathbb {R})^+$ acts transitively (along with some other properties). A mixed Shimura variety of Kuga type is a quotient space ![]() $\Gamma \backslash \mathcal {X}^+$ for some congruence subgroup
$\Gamma \backslash \mathcal {X}^+$ for some congruence subgroup ![]() $\Gamma$ of
$\Gamma$ of ![]() $P^{\mathrm {der}}(\mathbb {Z})$.
$P^{\mathrm {der}}(\mathbb {Z})$.
It is worth pointing out that any pure Shimura datum is a mixed Shimura datum of Kuga type (such that the unipotent radical of the underlying group is trivial). Given two mixed Shimura data of Kuga type ![]() $(Q,\mathcal {Y}^+)$ and
$(Q,\mathcal {Y}^+)$ and ![]() $(P,\mathcal {X}^+)$, a map
$(P,\mathcal {X}^+)$, a map ![]() $f \colon (Q,\mathcal {Y}^+) \rightarrow (P,\mathcal {X}^+)$ is called a Shimura morphism if
$f \colon (Q,\mathcal {Y}^+) \rightarrow (P,\mathcal {X}^+)$ is called a Shimura morphism if ![]() $f$ is a group homomorphism on the underlying groups and is a holomorphic morphism on the underlying complex spaces, and that
$f$ is a group homomorphism on the underlying groups and is a holomorphic morphism on the underlying complex spaces, and that ![]() $f(q \cdot \tilde {y}) = f(q) \cdot f(\tilde {y})$ for any
$f(q \cdot \tilde {y}) = f(q) \cdot f(\tilde {y})$ for any ![]() $q \in Q(\mathbb {R})^+$ and any
$q \in Q(\mathbb {R})^+$ and any ![]() $\tilde {y} \in \mathcal {Y}^+$. For a Shimura morphism
$\tilde {y} \in \mathcal {Y}^+$. For a Shimura morphism ![]() $f$ of this form, we say that
$f$ of this form, we say that ![]() $(f(Q), f(\mathcal {Y}^+))$ is a mixed Shimura subdatum of
$(f(Q), f(\mathcal {Y}^+))$ is a mixed Shimura subdatum of ![]() $(P,\mathcal {X}^+)$. Applying the discussion to
$(P,\mathcal {X}^+)$. Applying the discussion to ![]() $(P,\mathcal {X}^+) = (P_{2g,\mathrm {a}} , \mathcal {X}_{2g,\mathrm {a}}^+)$, we get the definition of mixed Shimura subdata of
$(P,\mathcal {X}^+) = (P_{2g,\mathrm {a}} , \mathcal {X}_{2g,\mathrm {a}}^+)$, we get the definition of mixed Shimura subdata of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$. Applying the discussion to
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$. Applying the discussion to ![]() $(G,\mathcal {X}_G^+) = (\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$, we get the definition of Shimura subdata of
$(G,\mathcal {X}_G^+) = (\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$, we get the definition of Shimura subdata of ![]() $(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$.
$(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$.
It is known that for each mixed Shimura subdatum ![]() $(Q,\mathcal {Y}^+)$ of
$(Q,\mathcal {Y}^+)$ of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$, the unipotent radical of
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$, the unipotent radical of ![]() $Q$ is
$Q$ is ![]() $V_{2g} \cap Q$ by weight reasons; see [Reference GaoGao17b, Proposition 2.9].
$V_{2g} \cap Q$ by weight reasons; see [Reference GaoGao17b, Proposition 2.9].
Define the special subvarieties of ![]() $\mathfrak {A}_g$ to be the subvarieties of the form
$\mathfrak {A}_g$ to be the subvarieties of the form ![]() ${\mathbf {u}}(\mathcal {Y}^+)$ where
${\mathbf {u}}(\mathcal {Y}^+)$ where ![]() $\mathcal {Y}^+$ is the underlying space of some mixed Shimura subdatum
$\mathcal {Y}^+$ is the underlying space of some mixed Shimura subdatum ![]() $(Q,\mathcal {Y}^+)$ of
$(Q,\mathcal {Y}^+)$ of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$. Define the special subvarieties of
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$. Define the special subvarieties of ![]() $\mathbb {A}_g$ to be the subvarieties of the form
$\mathbb {A}_g$ to be the subvarieties of the form ![]() ${\mathbf {u}}_G(\mathcal {Y}_G^+)$, where
${\mathbf {u}}_G(\mathcal {Y}_G^+)$, where ![]() $\mathcal {Y}_G^+$ is the underlying space of some Shimura subdatum
$\mathcal {Y}_G^+$ is the underlying space of some Shimura subdatum ![]() $(H, \mathcal {Y}_G^+)$ of
$(H, \mathcal {Y}_G^+)$ of ![]() $(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$.
$(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$.
Let us end this subsection by the following proposition on the geometric meaning of special subvarieties of ![]() $\mathfrak {A}_g$ and beyond. Recall the notation
$\mathfrak {A}_g$ and beyond. Recall the notation ![]() $\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$ at the end of § 3.2 and the uniformizations (see (3.7)).
$\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$ at the end of § 3.2 and the uniformizations (see (3.7)).

Proposition 5.6 Let ![]() $M$ be a special subvariety of
$M$ be a special subvariety of ![]() $\mathfrak {A}_g$. Then
$\mathfrak {A}_g$. Then ![]() $M_G := \pi (M)$ is a special subvariety of
$M_G := \pi (M)$ is a special subvariety of ![]() $\mathbb {A}_g$, and
$\mathbb {A}_g$, and ![]() $M$ is the translate of an abelian subscheme of
$M$ is the translate of an abelian subscheme of ![]() $\mathfrak {A}_g|_{M_G} \rightarrow M_G$ by a torsion section. Conversely all special subvarieties of
$\mathfrak {A}_g|_{M_G} \rightarrow M_G$ by a torsion section. Conversely all special subvarieties of ![]() $\mathfrak {A}_g$ are obtained in this way.
$\mathfrak {A}_g$ are obtained in this way.
More precisely, if ![]() $M$ is associated with the mixed Shimura subdatum of Kuga type
$M$ is associated with the mixed Shimura subdatum of Kuga type ![]() $(Q,\mathcal {Y}^+)$ of
$(Q,\mathcal {Y}^+)$ of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ (namely
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ (namely ![]() $M = {\mathbf {u}}(\mathcal {Y}^+)$), then the relative dimension of
$M = {\mathbf {u}}(\mathcal {Y}^+)$), then the relative dimension of ![]() $M \rightarrow M_G$ is
$M \rightarrow M_G$ is
5.4 Quotient by a normal group
In §§ 7 and 8, we need the geometric interpretation of the operation of taking the quotient mixed Shimura varieties of Kuga type. We explain this in the current subsection.
The setting is as follows. Let ![]() $(Q,\mathcal {Y}^+)$ be a mixed Shimura subdatum of
$(Q,\mathcal {Y}^+)$ be a mixed Shimura subdatum of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$, and let
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$, and let ![]() $M = {\mathbf {u}}(\mathcal {Y}^+)$ be the associated special subvariety of
$M = {\mathbf {u}}(\mathcal {Y}^+)$ be the associated special subvariety of ![]() $\mathfrak {A}_g$. Take a normal subgroup
$\mathfrak {A}_g$. Take a normal subgroup ![]() $N$ of
$N$ of ![]() $Q$. Pink [Reference PinkPin89, 2.9] constructed the quotient mixed Shimura datum
$Q$. Pink [Reference PinkPin89, 2.9] constructed the quotient mixed Shimura datum ![]() $(Q,\mathcal {Y}^+)/N$ whose underlying group is
$(Q,\mathcal {Y}^+)/N$ whose underlying group is ![]() $Q/N$.
$Q/N$.
By Proposition 5.6, ![]() $M_G := \pi (M)$ is a special subvariety of
$M_G := \pi (M)$ is a special subvariety of ![]() $\mathbb {A}_g$. Let
$\mathbb {A}_g$. Let ![]() $(G_Q, \mathcal {Y}_{G_Q}^+)$ be the pure Shimura subdatum of
$(G_Q, \mathcal {Y}_{G_Q}^+)$ be the pure Shimura subdatum of ![]() $(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$ in Proposition 5.6, then
$(\mathrm {GSp}_{2g}, \mathfrak {H}_g^+)$ in Proposition 5.6, then ![]() $M_G = {\mathbf {u}}_G(\mathcal {Y}_{G_Q}^+)$.
$M_G = {\mathbf {u}}_G(\mathcal {Y}_{G_Q}^+)$.
Let ![]() $V_Q = V_{2g} \cap Q$ and
$V_Q = V_{2g} \cap Q$ and ![]() $V_N = V_{2g} \cap N$. We explained above (5.1) that
$V_N = V_{2g} \cap N$. We explained above (5.1) that ![]() $V_Q$ is the unipotent radical of
$V_Q$ is the unipotent radical of ![]() $Q$. Since
$Q$. Since ![]() $N \lhd Q$, group theory implies that
$N \lhd Q$, group theory implies that ![]() $V_N$ is the unipotent radical of
$V_N$ is the unipotent radical of ![]() $N$. Let
$N$. Let ![]() $G_N = N/V_N$, then
$G_N = N/V_N$, then ![]() $G_N$ is a normal subgroup of
$G_N$ is a normal subgroup of ![]() $G_Q$.
$G_Q$.
Proposition 5.6 says that ![]() $\pi |_M \colon M \rightarrow M_G$ itself is an abelian scheme of relative dimension
$\pi |_M \colon M \rightarrow M_G$ itself is an abelian scheme of relative dimension ![]() $g_Q = \frac{1}{2}\dim (V_{2g} \cap Q)$. Let
$g_Q = \frac{1}{2}\dim (V_{2g} \cap Q)$. Let ![]() $\epsilon \colon M_G \rightarrow M$ be the zero section.Footnote 4 It induces a Levi decomposition
$\epsilon \colon M_G \rightarrow M$ be the zero section.Footnote 4 It induces a Levi decomposition ![]() $Q = V_Q \rtimes G_Q$ and a semi-algebraic isomorphism
$Q = V_Q \rtimes G_Q$ and a semi-algebraic isomorphism
such that ![]() ${\mathbf {u}}(\{0\} \times \mathcal {Y}_{G_Q}^+) = \epsilon (M_G)$. In the rest of this subsection, we shall use this identification of
${\mathbf {u}}(\{0\} \times \mathcal {Y}_{G_Q}^+) = \epsilon (M_G)$. In the rest of this subsection, we shall use this identification of ![]() $\mathcal {Y}^+$ with
$\mathcal {Y}^+$ with ![]() $V_Q(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+$.
$V_Q(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+$.
Deligne [Reference DeligneDel71, Rappel 4.4.3] proved that ![]() $\mathcal {Y}^+ \rightarrow \mathcal {Y}^+_{G_Q}$ is a variation of Hodge structure of type
$\mathcal {Y}^+ \rightarrow \mathcal {Y}^+_{G_Q}$ is a variation of Hodge structure of type ![]() $(-1,0)+(0,-1)$.
$(-1,0)+(0,-1)$.
We have ![]() $V_N \lhd Q$ since
$V_N \lhd Q$ since ![]() $N\lhd Q$ and
$N\lhd Q$ and ![]() $V_N$ is the unipotent radical of
$V_N$ is the unipotent radical of ![]() $N$. The reductive group
$N$. The reductive group ![]() $G_Q$, as a subgroup of
$G_Q$, as a subgroup of ![]() $\mathrm {GSp}_{2g}$, acts on
$\mathrm {GSp}_{2g}$, acts on ![]() $V_{2g}$. Now
$V_{2g}$. Now ![]() $V_N \lhd Q$ implies that
$V_N \lhd Q$ implies that ![]() $V_N$ is a
$V_N$ is a ![]() $G_Q$-submodule of
$G_Q$-submodule of ![]() $V_{2g}$, so
$V_{2g}$, so ![]() $V_N$ is a sub-Hodge structure of
$V_N$ is a sub-Hodge structure of ![]() $V_Q$. Thus
$V_Q$. Thus ![]() $V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+ \rightarrow \mathcal {Y}^+_{G_Q}$ is a subvariation of Hodge structure of
$V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+ \rightarrow \mathcal {Y}^+_{G_Q}$ is a subvariation of Hodge structure of ![]() $\mathcal {Y}^+ \rightarrow \mathcal {Y}^+_{G_Q}$. Thus
$\mathcal {Y}^+ \rightarrow \mathcal {Y}^+_{G_Q}$. Thus ![]() ${\mathbf {u}}(V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+)$ is an abelian subscheme of
${\mathbf {u}}(V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+)$ is an abelian subscheme of ![]() $M \rightarrow M_G$ by [Reference DeligneDel71, Rappel 4.4.3].
$M \rightarrow M_G$ by [Reference DeligneDel71, Rappel 4.4.3].
The quotient ![]() $\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N$ can be constructed in two steps. First we take the quotient
$\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N$ can be constructed in two steps. First we take the quotient ![]() $(Q_0,\mathcal {Y}_0^+) := (Q,\mathcal {Y}^+)/V_N$, and then we take
$(Q_0,\mathcal {Y}_0^+) := (Q,\mathcal {Y}^+)/V_N$, and then we take ![]() $(Q', \mathcal {Y}^{\prime +}) := (Q_0,\mathcal {Y}_0^+)/G_N$.
$(Q', \mathcal {Y}^{\prime +}) := (Q_0,\mathcal {Y}_0^+)/G_N$.
The geometric meaning of the quotient ![]() $\tilde {p}_0 \colon (Q,\mathcal {Y}^+) \rightarrow (Q_0,\mathcal {Y}_0^+) = (Q,\mathcal {Y}^+)/V_N$ is as follows. We have the following commutative diagram (where
$\tilde {p}_0 \colon (Q,\mathcal {Y}^+) \rightarrow (Q_0,\mathcal {Y}_0^+) = (Q,\mathcal {Y}^+)/V_N$ is as follows. We have the following commutative diagram (where ![]() $\Gamma _0 = \tilde {p}_0(\Gamma \cap Q(\mathbb {R}))$):
$\Gamma _0 = \tilde {p}_0(\Gamma \cap Q(\mathbb {R}))$):

such that ![]() $M_0 \rightarrow M_G$ is the abelian scheme obtained by taking the quotient of
$M_0 \rightarrow M_G$ is the abelian scheme obtained by taking the quotient of ![]() $M \rightarrow M_G$ by
$M \rightarrow M_G$ by ![]() ${\mathbf {u}}(V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+)$. Let
${\mathbf {u}}(V_N(\mathbb {R}) \times \mathcal {Y}_{G_Q}^+)$. Let ![]() $g_N = \frac{1}{2} \dim V_N$, then the relative dimension of
$g_N = \frac{1}{2} \dim V_N$, then the relative dimension of ![]() $M_0 \rightarrow M_G$ is
$M_0 \rightarrow M_G$ is ![]() $g_Q - g_N$.
$g_Q - g_N$.
To explain the quotient ![]() $\tilde {p}' \colon (Q_0, \mathcal {Y}_0^+) \rightarrow (Q', \mathcal {Y}^{\prime +}) = (Q_0,\mathcal {Y}_0^+)/G_N$, we need the following preliminary. We know that
$\tilde {p}' \colon (Q_0, \mathcal {Y}_0^+) \rightarrow (Q', \mathcal {Y}^{\prime +}) = (Q_0,\mathcal {Y}_0^+)/G_N$, we need the following preliminary. We know that ![]() $G_N$ is a normal subgroup of
$G_N$ is a normal subgroup of ![]() $G_Q$. We take for granted that we can do the operation
$G_Q$. We take for granted that we can do the operation ![]() $(G_Q, \mathcal {Y}_{G_Q}^+)/G_N$ for pure Shimura datum, and this quotient gives a morphism
$(G_Q, \mathcal {Y}_{G_Q}^+)/G_N$ for pure Shimura datum, and this quotient gives a morphism ![]() $p_{G_N} \colon M_G \rightarrow M'_G$.Footnote 5
$p_{G_N} \colon M_G \rightarrow M'_G$.Footnote 5
For each ![]() $y'_G \in M'_G$, the inverse image
$y'_G \in M'_G$, the inverse image ![]() $(p_{G_N})^{-1}(y'_G)$ equals
$(p_{G_N})^{-1}(y'_G)$ equals ![]() ${\mathbf {u}}_G(G_N(\mathbb {R})^+\tilde {y}_G)$ for some
${\mathbf {u}}_G(G_N(\mathbb {R})^+\tilde {y}_G)$ for some ![]() $\tilde {y}_G \in \mathcal {Y}_{G_Q}^+$. So the connected algebraic monodromy group of
$\tilde {y}_G \in \mathcal {Y}_{G_Q}^+$. So the connected algebraic monodromy group of ![]() $(p_{G_N})^{-1}(y'_G)$ is
$(p_{G_N})^{-1}(y'_G)$ is ![]() $G_N^{\mathrm {der}}$. Since
$G_N^{\mathrm {der}}$. Since ![]() $N \lhd Q$, we have
$N \lhd Q$, we have ![]() $G_N = N/V_N \lhd Q/V_N$. Hence
$G_N = N/V_N \lhd Q/V_N$. Hence ![]() $G_N$ acts trivially on
$G_N$ acts trivially on ![]() $V_Q/V_N$. So
$V_Q/V_N$. So ![]() $M_0|_{(p_{G_N})^{-1}(y'_G)} \rightarrow (p_{G_N})^{-1}(y'_G)$ is an isotrivial abelian scheme by Deligne's theorem of the fixed part [Reference DeligneDel71, Corollaire 4.1.2]. We have the following commutative diagram:
$M_0|_{(p_{G_N})^{-1}(y'_G)} \rightarrow (p_{G_N})^{-1}(y'_G)$ is an isotrivial abelian scheme by Deligne's theorem of the fixed part [Reference DeligneDel71, Corollaire 4.1.2]. We have the following commutative diagram:

where ![]() $\pi '$ is an abelian scheme (of relative dimension
$\pi '$ is an abelian scheme (of relative dimension ![]() $g_Q - g_N$) such that each closed fiber of
$g_Q - g_N$) such that each closed fiber of ![]() $M_0|_{(p_{G_N})^{-1}(y'_G)} \rightarrow (p_{G_N})^{-1}(y'_G)$ is the abelian variety
$M_0|_{(p_{G_N})^{-1}(y'_G)} \rightarrow (p_{G_N})^{-1}(y'_G)$ is the abelian variety ![]() $(\pi ')^{-1}(y'_G)$. In other words, the lower box is an intermediate step of the following modular map.
$(\pi ')^{-1}(y'_G)$. In other words, the lower box is an intermediate step of the following modular map.

We end this subsection by summarizing the quotient ![]() $\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N$ (after taking the uniformizations) in the following commutative diagram:
$\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N$ (after taking the uniformizations) in the following commutative diagram:

where each vertical arrow is an abelian scheme, with the left one of relative dimension ![]() $g_Q$ and the other three of relative dimension
$g_Q$ and the other three of relative dimension ![]() $g_Q - g_N$. Moreover
$g_Q - g_N$. Moreover ![]() $M_0|_{p_{G_N}^{-1}(b')}$ is isotrivial for any
$M_0|_{p_{G_N}^{-1}(b')}$ is isotrivial for any ![]() $b' \in M'_G$ by the discussion above (
$b' \in M'_G$ by the discussion above (
). And for any ![]() $x' \in M'$, we have that
$x' \in M'$, we have that ![]() $p_N^{-1}(x')$ is the translate of an abelian subscheme of
$p_N^{-1}(x')$ is the translate of an abelian subscheme of ![]() $M|_{\pi (p_N^{-1}(x'))} \rightarrow \pi (p_N^{-1}(x'))$ of relative dimension
$M|_{\pi (p_N^{-1}(x'))} \rightarrow \pi (p_N^{-1}(x'))$ of relative dimension ![]() $g_Q - (g_Q - g_N) = g_N$ by a constant section.
$g_Q - (g_Q - g_N) = g_N$ by a constant section.
6. From Betti map to the  $t$th degeneracy locus
$t$th degeneracy locus
In §§ 6–8 we will prove Theorem 1.1 for ![]() $X \subseteq \mathfrak {A}_g$. It is arranged as follows: § 6 transfers the study of the generic rank of the Betti map to the
$X \subseteq \mathfrak {A}_g$. It is arranged as follows: § 6 transfers the study of the generic rank of the Betti map to the ![]() $t$th degenerate locus of
$t$th degenerate locus of ![]() $X$ for some particular
$X$ for some particular ![]() $t$, § 7 proves the Zariski closedness of the
$t$, § 7 proves the Zariski closedness of the ![]() $t$th degenerate locus
$t$th degenerate locus ![]() $X^{\mathrm {deg}}(t)$, and § 8 gives the criterion to
$X^{\mathrm {deg}}(t)$, and § 8 gives the criterion to ![]() $X^{\mathrm {deg}}(t) = X$.
$X^{\mathrm {deg}}(t) = X$.
Let us fix the notation. Recall the uniformizations (5.1)

and the uniformized universal Betti map ![]() $\tilde {b} \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathbb {R}^{2g}$ defined in (3.5). Let
$\tilde {b} \colon \mathcal {X}_{2g,\mathrm {a}}^+ \rightarrow \mathbb {R}^{2g}$ defined in (3.5). Let ![]() $X$ be an irreducible subvariety of
$X$ be an irreducible subvariety of ![]() $\mathfrak {A}_g$. Fix a complex analytic irreducible component
$\mathfrak {A}_g$. Fix a complex analytic irreducible component ![]() $\tilde {X}$ of
$\tilde {X}$ of ![]() ${\mathbf {u}}^{-1}(X)$.
${\mathbf {u}}^{-1}(X)$.
Proposition 6.1 Let ![]() $d = \dim X$. For any integer
$d = \dim X$. For any integer ![]() $l \in \{1,\ldots ,d\}$, let
$l \in \{1,\ldots ,d\}$, let
Then ![]() $X^{\mathrm {deg}}(l-d) \cap X^{\mathrm {sm}}(\mathbb {C}) \subseteq {\mathbf {u}}(\tilde {X}_{<2l}) \subseteq X^{\mathrm {deg}}(l-d)$, where
$X^{\mathrm {deg}}(l-d) \cap X^{\mathrm {sm}}(\mathbb {C}) \subseteq {\mathbf {u}}(\tilde {X}_{<2l}) \subseteq X^{\mathrm {deg}}(l-d)$, where ![]() $X^{\mathrm {deg}}(l-d)$ is defined in Definition 1.6.
$X^{\mathrm {deg}}(l-d)$ is defined in Definition 1.6.
In particular, if ![]() $\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} < 2l$ for all
$\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} < 2l$ for all ![]() $\tilde {x} \in \tilde {X}$ with
$\tilde {x} \in \tilde {X}$ with ![]() ${\mathbf {u}}(\tilde {x}) \in X^{\mathrm {sm}}(\mathbb {C})$, then
${\mathbf {u}}(\tilde {x}) \in X^{\mathrm {sm}}(\mathbb {C})$, then ![]() $X^{\mathrm {deg}}(l-d)$ is Zariski dense in
$X^{\mathrm {deg}}(l-d)$ is Zariski dense in ![]() $X$.
$X$.
Proof. The ‘In particular’ part of the proposition follows directly from the main statement by letting ![]() $x$ run over all points in
$x$ run over all points in ![]() $X^{\mathrm {sm}}(\mathbb {C})$.
$X^{\mathrm {sm}}(\mathbb {C})$.
Let us prove ![]() $X^{\mathrm {deg}}(l-d) \cap X^{\mathrm {sm}}(\mathbb {C}) \subseteq {\mathbf {u}}(\tilde {X}_{<2l})$. Suppose not, then there exists some
$X^{\mathrm {deg}}(l-d) \cap X^{\mathrm {sm}}(\mathbb {C}) \subseteq {\mathbf {u}}(\tilde {X}_{<2l})$. Suppose not, then there exists some ![]() $\tilde {x} \in \tilde {X}$ such that
$\tilde {x} \in \tilde {X}$ such that ![]() ${\mathbf {u}}(\tilde {x}) \in X^{\mathrm {deg}} \cap X^{\mathrm {sm}}(\mathbb {C})$ and
${\mathbf {u}}(\tilde {x}) \in X^{\mathrm {deg}} \cap X^{\mathrm {sm}}(\mathbb {C})$ and ![]() $\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} = 2 l$. By definition of
$\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} = 2 l$. By definition of ![]() $X^{\mathrm {deg}}(l-d)$, the point
$X^{\mathrm {deg}}(l-d)$, the point ![]() ${\mathbf {u}}(\tilde {x})$ lies in a subvariety
${\mathbf {u}}(\tilde {x})$ lies in a subvariety ![]() $Y$ of
$Y$ of ![]() $X$ such that
$X$ such that ![]() $\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) < \dim Y + (l-d)$, where
$\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) < \dim Y + (l-d)$, where ![]() $\langle Y \rangle _{\mathrm {sg}}$ is defined above Definition 1.6.
$\langle Y \rangle _{\mathrm {sg}}$ is defined above Definition 1.6.
Let ![]() $\tilde {Y}$ be a complex analytic irreducible component of
$\tilde {Y}$ be a complex analytic irreducible component of ![]() ${\mathbf {u}}^{-1}(Y)$ with
${\mathbf {u}}^{-1}(Y)$ with ![]() $\tilde {x} \in \tilde {Y} \subseteq \tilde {X}$. Observe that
$\tilde {x} \in \tilde {Y} \subseteq \tilde {X}$. Observe that ![]() $\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} \le \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {Y}})_{\tilde {x}} + 2 (\dim X - \dim Y)$. So
$\mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} \le \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {Y}})_{\tilde {x}} + 2 (\dim X - \dim Y)$. So ![]() $2l - 2(d-\dim Y) = \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} - 2(\dim X - \dim Y) \le \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {Y}})_{\tilde {x}}$. So for
$2l - 2(d-\dim Y) = \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {X}})_{\tilde {x}} - 2(\dim X - \dim Y) \le \mathrm {rank}_{\mathbb {R}}(\tilde {b}|_{\tilde {Y}})_{\tilde {x}}$. So for ![]() $\widetilde {\langle Y \rangle _{\mathrm {sg}}}$ a complex analytic irreducible component of
$\widetilde {\langle Y \rangle _{\mathrm {sg}}}$ a complex analytic irreducible component of ![]() ${\mathbf {u}}^{-1}(\langle Y \rangle _{\mathrm {sg}})$, which contains
${\mathbf {u}}^{-1}(\langle Y \rangle _{\mathrm {sg}})$, which contains ![]() $\tilde {Y}$, we have
$\tilde {Y}$, we have
 \begin{align*} \mathrm{rank}_{\mathbb{R}}(\tilde{b}|_{\widetilde{\langle Y \rangle_{\mathrm{sg}}}})_{\tilde{x}} & = 2(\dim \langle Y \rangle_{\mathrm{sg}} - \dim \pi(Y)) \\ & < 2l - 2(d-\dim Y) \quad \text{ by choice of }Y \\ & \le \mathrm{rank}_{\mathbb{R}}(\tilde{b}|_{\tilde{Y}})_{\tilde{x}}. \end{align*}
\begin{align*} \mathrm{rank}_{\mathbb{R}}(\tilde{b}|_{\widetilde{\langle Y \rangle_{\mathrm{sg}}}})_{\tilde{x}} & = 2(\dim \langle Y \rangle_{\mathrm{sg}} - \dim \pi(Y)) \\ & < 2l - 2(d-\dim Y) \quad \text{ by choice of }Y \\ & \le \mathrm{rank}_{\mathbb{R}}(\tilde{b}|_{\tilde{Y}})_{\tilde{x}}. \end{align*}
But this cannot happen as ![]() $\tilde {Y} \subseteq \widetilde {\langle Y \rangle _{\mathrm {sg}}}$.
$\tilde {Y} \subseteq \widetilde {\langle Y \rangle _{\mathrm {sg}}}$.
Next we prove the other inclusion ![]() ${\mathbf {u}}(\tilde {X}_{<2l}) \subseteq X^{\mathrm {deg}}(t)$. Take any
${\mathbf {u}}(\tilde {X}_{<2l}) \subseteq X^{\mathrm {deg}}(t)$. Take any ![]() $\tilde {x} \in \tilde {X}_{<2l}$. Set
$\tilde {x} \in \tilde {X}_{<2l}$. Set ![]() $r = \tilde {b}(\tilde {x}) \in \mathbb {R}^{2g}$. By assumption of the proposition, we have
$r = \tilde {b}(\tilde {x}) \in \mathbb {R}^{2g}$. By assumption of the proposition, we have
In the rest of the proof, we identify ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ as the semi-algebraic space
$\mathcal {X}_{2g,\mathrm {a}}^+$ as the semi-algebraic space ![]() $\mathbb {R}^{2g} \times \mathfrak {H}_g^+$ with the complex structure defined by (3.2). In particular,
$\mathbb {R}^{2g} \times \mathfrak {H}_g^+$ with the complex structure defined by (3.2). In particular, ![]() $\tilde {b}^{-1}(r) = \{r\} \times \mathfrak {H}_g^+$. Property (ii) of the Betti map (below (3.6)) implies that
$\tilde {b}^{-1}(r) = \{r\} \times \mathfrak {H}_g^+$. Property (ii) of the Betti map (below (3.6)) implies that ![]() $\tilde {b}^{-1}(r) \cap \tilde {X}$ is complex analytic. Then by (6.1), there exists a complex analytic irreducible subset
$\tilde {b}^{-1}(r) \cap \tilde {X}$ is complex analytic. Then by (6.1), there exists a complex analytic irreducible subset ![]() $\tilde {W}$ in
$\tilde {W}$ in ![]() $\mathfrak {H}_g^+$ of dimension
$\mathfrak {H}_g^+$ of dimension ![]() $\ge d-l + 1$ such that
$\ge d-l + 1$ such that
Hence it suffices to prove the following assertion: ![]() $Y = ({\mathbf {u}}(\{r\} \times \tilde {W}))^{\mathrm {Zar}}$ satisfies
$Y = ({\mathbf {u}}(\{r\} \times \tilde {W}))^{\mathrm {Zar}}$ satisfies
Apply weak Ax–Schanuel for ![]() $\mathfrak {A}_g$, namely Theorem 5.5, to
$\mathfrak {A}_g$, namely Theorem 5.5, to ![]() $\{r\} \times \tilde {W}$. Then we get
$\{r\} \times \tilde {W}$. Then we get
On the other hand we have
where the last inclusion holds because ![]() $\mathbf {u}_G(\tilde {W})\subseteq \pi (Y)$ by definition of
$\mathbf {u}_G(\tilde {W})\subseteq \pi (Y)$ by definition of ![]() $Y$.
$Y$.
Let us temporarily assume ![]() $(\{r\} \times \tilde {W})^{\mathrm {Zar}} = \{r\} \times \tilde {W}^{\mathrm {Zar}}$ and finish the proof. Then from (6.3) and (6.4) we get
$(\{r\} \times \tilde {W})^{\mathrm {Zar}} = \{r\} \times \tilde {W}^{\mathrm {Zar}}$ and finish the proof. Then from (6.3) and (6.4) we get
Thus
where the first equality follows from Corollary 5.4. Therefore (6.2) holds since ![]() $\dim \tilde {W} \ge d-l+1$.
$\dim \tilde {W} \ge d-l+1$.
It remains to prove ![]() $(\{r\} \times \tilde {W})^{\mathrm {Zar}} = \{r\} \times \tilde {W}^{\mathrm {Zar}}$. First note that
$(\{r\} \times \tilde {W})^{\mathrm {Zar}} = \{r\} \times \tilde {W}^{\mathrm {Zar}}$. First note that ![]() $\{r\} \times \tilde {W}^{\mathrm {Zar}}$ is semi-algebraic and complex analytic. Then it is a general fact that
$\{r\} \times \tilde {W}^{\mathrm {Zar}}$ is semi-algebraic and complex analytic. Then it is a general fact that ![]() $\{r\} \times \tilde {W}^{\mathrm {Zar}}$ is algebraic in
$\{r\} \times \tilde {W}^{\mathrm {Zar}}$ is algebraic in ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$; see [Reference Klingler, Ullmo and YafaevKUY16, (the proof of) Lemma B.1]. Thus
$\mathcal {X}_{2g,\mathrm {a}}^+$; see [Reference Klingler, Ullmo and YafaevKUY16, (the proof of) Lemma B.1]. Thus ![]() $(\{r\} \times \tilde {W})^{\mathrm {Zar}} \subseteq \{r\} \times \tilde {W}^{\mathrm {Zar}}$. Remark 5.2 says that the algebraic structures on
$(\{r\} \times \tilde {W})^{\mathrm {Zar}} \subseteq \{r\} \times \tilde {W}^{\mathrm {Zar}}$. Remark 5.2 says that the algebraic structures on ![]() $\mathcal {X}_{2g,\mathrm {a}}^+$ and
$\mathcal {X}_{2g,\mathrm {a}}^+$ and ![]() $\mathfrak {H}_g^+$ are compatible under
$\mathfrak {H}_g^+$ are compatible under ![]() $\tilde {\pi }$, so
$\tilde {\pi }$, so ![]() $\tilde {\pi }|_{(\{r\} \times \tilde {W})^{\mathrm {Zar}}} \colon (\{r\} \times \tilde {W})^{\mathrm {Zar}} \rightarrow \tilde {W}^{\mathrm {Zar}}$ is dominant. Now we can conclude.
$\tilde {\pi }|_{(\{r\} \times \tilde {W})^{\mathrm {Zar}}} \colon (\{r\} \times \tilde {W})^{\mathrm {Zar}} \rightarrow \tilde {W}^{\mathrm {Zar}}$ is dominant. Now we can conclude.
7. Zariski closeness of the  $t$th degeneracy locus
$t$th degeneracy locus
The goal of this section is to prove Theorem 1.8 for ![]() $X \subseteq \mathfrak {A}_g$. Let
$X \subseteq \mathfrak {A}_g$. Let ![]() $X$ be an irreducible subvariety of
$X$ be an irreducible subvariety of ![]() $\mathfrak {A}_g$. Through the whole section we fix a
$\mathfrak {A}_g$. Through the whole section we fix a ![]() $t \in \mathbb {Z}$. Let
$t \in \mathbb {Z}$. Let ![]() $X^{\mathrm {deg}}(t)$ be the
$X^{\mathrm {deg}}(t)$ be the ![]() $t$th degeneracy locus of
$t$th degeneracy locus of ![]() $X$ defined in Definition 1.6.
$X$ defined in Definition 1.6.
Theorem 7.1 The subset ![]() $X^{\mathrm {deg}}(t)$ is Zariski closed in
$X^{\mathrm {deg}}(t)$ is Zariski closed in ![]() $X$.
$X$.
Combined with Proposition 6.1, this theorem proves part (ii) of Theorem 1.1 for ![]() $X \subseteq \mathfrak {A}_g$.
$X \subseteq \mathfrak {A}_g$.
Our proof of Theorem 7.1 is inspired by Daw and Ren's work [Reference Daw and RenDR18, § 7] on the anomalous subvarieties in a pure Shimura variety.
7.1 Weakly optimal subvariety
To prove Theorem 7.1, we need the following definition of weakly optimal subvarieties. The notion was first introduced by Habegger and Pila [Reference Habegger and PilaHP16] to study the Zilber–Pink conjecture for abelian varieties and product of modular curves.
Definition 7.2 (i) For any irreducible subvariety ![]() $Z$ of
$Z$ of ![]() $\mathfrak {A}_g$, define the weakly defect to be
$\mathfrak {A}_g$, define the weakly defect to be ![]() $\delta _{\mathrm {ws}}(Z) = \dim Z^{\mathrm {biZar}} - \dim Z$.
$\delta _{\mathrm {ws}}(Z) = \dim Z^{\mathrm {biZar}} - \dim Z$.
(ii) A closed irreducible subvariety ![]() $Z$ of
$Z$ of ![]() $X$ is said to be weakly optimal if the following condition holds:
$X$ is said to be weakly optimal if the following condition holds: ![]() $Z \subsetneq Z' \subseteq X$ with
$Z \subsetneq Z' \subseteq X$ with ![]() $Z'$ irreducible closed in
$Z'$ irreducible closed in ![]() $X$
$X$ ![]() $\Rightarrow$
$\Rightarrow$ ![]() $\delta _{\mathrm {ws}}(Z') > \delta _{\mathrm {ws}}(Z)$.
$\delta _{\mathrm {ws}}(Z') > \delta _{\mathrm {ws}}(Z)$.
Weakly optimal subvarieties of ![]() $X$ are closely related to
$X$ are closely related to ![]() $X^{\mathrm {deg}}(t)$ by the following lemmas.
$X^{\mathrm {deg}}(t)$ by the following lemmas.
Lemma 7.3 ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t \Leftrightarrow \delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$.
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t \Leftrightarrow \delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$.
Proof. The condition ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ can be rewritten to be
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ can be rewritten to be
By Corollary 5.4, we have ![]() $\dim Z^{\mathrm {biZar}} = (\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z)) + \dim \pi (Z)^{\mathrm {biZar}}$. Hence the inequality above becomes
$\dim Z^{\mathrm {biZar}} = (\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z)) + \dim \pi (Z)^{\mathrm {biZar}}$. Hence the inequality above becomes ![]() $\delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$.
$\delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$.
Lemma 7.4 Assume a closed irreducible subvariety ![]() $Z \subseteq X$ satisfies
$Z \subseteq X$ satisfies ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property. Then
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property. Then ![]() $Z$ is weakly optimal.
$Z$ is weakly optimal.
Proof. For any ![]() $Z \subseteq Z' \subseteq X$ with
$Z \subseteq Z' \subseteq X$ with ![]() $Z'$ irreducible closed in
$Z'$ irreducible closed in ![]() $X$, if
$X$, if ![]() $\delta _{\mathrm {ws}}(Z') \le \delta _{\mathrm {ws}}(Z)$, then we have
$\delta _{\mathrm {ws}}(Z') \le \delta _{\mathrm {ws}}(Z)$, then we have
where the second inequality follows from Lemma 7.3 (applied to ![]() $Z$). Applying Lemma 7.3 to
$Z$). Applying Lemma 7.3 to ![]() $Z'$, we get
$Z'$, we get ![]() $\dim \langle Z' \rangle _{\mathrm {sg}} - \dim \pi (Z') < \dim Z' + t$. The maximality of
$\dim \langle Z' \rangle _{\mathrm {sg}} - \dim \pi (Z') < \dim Z' + t$. The maximality of ![]() $Z$ then implies
$Z$ then implies ![]() $Z = Z'$. So
$Z = Z'$. So ![]() $Z$ is weakly optimal.
$Z$ is weakly optimal.
Thus ![]() $X^{\mathrm {deg}}(t)$ is the union of some weakly optimal subvarieties. We will show that this union is finite. The key point is the following finiteness theorem concerning weakly optimal subvarieties [Reference GaoGao20, Theorem 1.4]. See § 5.3 for notation.
$X^{\mathrm {deg}}(t)$ is the union of some weakly optimal subvarieties. We will show that this union is finite. The key point is the following finiteness theorem concerning weakly optimal subvarieties [Reference GaoGao20, Theorem 1.4]. See § 5.3 for notation.
Theorem 7.5 There exists a finite set ![]() $\Sigma$ consisting of elements of the form
$\Sigma$ consisting of elements of the form ![]() $((Q,\mathcal {Y}^+),N)$, where
$((Q,\mathcal {Y}^+),N)$, where ![]() $(Q,\mathcal {Y}^+)$ is a mixed Shimura subdatum of Kuga type of
$(Q,\mathcal {Y}^+)$ is a mixed Shimura subdatum of Kuga type of ![]() $(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ and
$(P_{2g,\mathrm {a}}, \mathcal {X}_{2g,\mathrm {a}}^+)$ and ![]() $N$ is a connected normal subgroup of
$N$ is a connected normal subgroup of ![]() $Q$ whose reductive part is semi-simple, such that the following property holds. If a closed irreducible subvariety
$Q$ whose reductive part is semi-simple, such that the following property holds. If a closed irreducible subvariety ![]() $Z$ of
$Z$ of ![]() $X$ is weakly optimal, then there exists
$X$ is weakly optimal, then there exists ![]() $((Q,\mathcal {Y}^+),N) \in \Sigma$ such that
$((Q,\mathcal {Y}^+),N) \in \Sigma$ such that ![]() $Z^{\mathrm {biZar}} = {\mathbf {u}}(N(\mathbb {R})^+\tilde {y})$ for some
$Z^{\mathrm {biZar}} = {\mathbf {u}}(N(\mathbb {R})^+\tilde {y})$ for some ![]() $\tilde {y} \in \mathcal {Y}^+$.
$\tilde {y} \in \mathcal {Y}^+$.
7.2 An auxiliary proposition
Let ![]() $X$ be as in Theorem 7.1.
$X$ be as in Theorem 7.1.
Let ![]() $Z$ be a positive dimensional closed irreducible subvariety
$Z$ be a positive dimensional closed irreducible subvariety ![]() $X$ such that
$X$ such that ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property. Then
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property. Then ![]() $Z$ is weakly optimal by Lemma 7.4. So Theorem 7.5 gives a finite set
$Z$ is weakly optimal by Lemma 7.4. So Theorem 7.5 gives a finite set ![]() $\Sigma$ and a
$\Sigma$ and a ![]() $((Q,\mathcal {Y}^+),N) \in \Sigma$ such that
$((Q,\mathcal {Y}^+),N) \in \Sigma$ such that ![]() $Z^{\mathrm {biZar}} = {\mathbf {u}}(N(\mathbb {R})^+\tilde {y})$ for some
$Z^{\mathrm {biZar}} = {\mathbf {u}}(N(\mathbb {R})^+\tilde {y})$ for some ![]() $\tilde {y} \in \mathcal {Y}^+$. Recall that
$\tilde {y} \in \mathcal {Y}^+$. Recall that ![]() $N$ is a connected normal subgroup of
$N$ is a connected normal subgroup of ![]() $Q$ whose reductive part is semi-simple. Note that
$Q$ whose reductive part is semi-simple. Note that ![]() $N \not = 1$ since
$N \not = 1$ since ![]() $Z$ has positive dimension.
$Z$ has positive dimension.
Consider the operation of taking quotient mixed Shimura datum ![]() $\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N =: (Q', \mathcal {Y}^{\prime +})$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type.
$\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N =: (Q', \mathcal {Y}^{\prime +})$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type.

We refer to (5.4) for the geometric meaning of ![]() $p_N \colon M \rightarrow M'$ and notation.
$p_N \colon M \rightarrow M'$ and notation.
For any integer ![]() $h$, define
$h$, define
Then ![]() $E_h$ is Zariski closed in
$E_h$ is Zariski closed in ![]() $X$.
$X$.
Proposition 7.6 For ![]() $g_N = \frac{1}{2}\dim (V_{2g} \cap N)$ as in (5.4):
$g_N = \frac{1}{2}\dim (V_{2g} \cap N)$ as in (5.4):
(i) we have
 $Z \subseteq E_{g_N - t}$;
$Z \subseteq E_{g_N - t}$;(ii) we have
 $E_{g_N - t} \subseteq X^{\mathrm {deg}}(t)$.
$E_{g_N - t} \subseteq X^{\mathrm {deg}}(t)$.
Proof. (i) Recall that ![]() $Z$ satisfies
$Z$ satisfies ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$. Therefore
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$. Therefore ![]() $\delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$ by Lemma 7.3. Hence
$\delta _{\mathrm {ws}}(Z) < \dim \pi (Z)^{\mathrm {biZar}} + t$ by Lemma 7.3. Hence
By construction we know that ![]() $Z^{\mathrm {biZar}}$ is a fiber of
$Z^{\mathrm {biZar}}$ is a fiber of ![]() $p_N$. Hence as a morphism,
$p_N$. Hence as a morphism, ![]() $Z^{\mathrm {biZar}} \rightarrow \pi (Z)^{\mathrm {biZar}}$ is an abelian scheme of relative dimension
$Z^{\mathrm {biZar}} \rightarrow \pi (Z)^{\mathrm {biZar}}$ is an abelian scheme of relative dimension ![]() $g_N$ by the discussion below (5.4). So the inequality above becomes
$g_N$ by the discussion below (5.4). So the inequality above becomes ![]() $\dim Z > g_N - t$. As
$\dim Z > g_N - t$. As ![]() $Z \subseteq X \cap M$, we have that
$Z \subseteq X \cap M$, we have that ![]() $Z \subseteq E_{g_N - t}$ by definition of
$Z \subseteq E_{g_N - t}$ by definition of ![]() $E_{g_N - t}$.
$E_{g_N - t}$.
(ii) For any ![]() $x \in E_{g_N - t}$, there exists a component
$x \in E_{g_N - t}$, there exists a component ![]() $Y$ of
$Y$ of ![]() $(p_N|_{X\cap M})^{-1}(p_N(x))$ containing
$(p_N|_{X\cap M})^{-1}(p_N(x))$ containing ![]() $x$ such that
$x$ such that ![]() $\dim Y > g_N - t$. Let
$\dim Y > g_N - t$. Let ![]() $x' = p_N(x)$.
$x' = p_N(x)$.
By (5.4) and the discussion below, ![]() $p_N^{-1}(x') \rightarrow \pi (p_N^{-1}(x'))$ is an abelian scheme of relative dimension
$p_N^{-1}(x') \rightarrow \pi (p_N^{-1}(x'))$ is an abelian scheme of relative dimension ![]() $g_N$.
$g_N$.
Proposition 5.3 says that as a morphism, ![]() $Y^{\mathrm {biZar}} \rightarrow \pi (Y)^{\mathrm {biZar}}$ is an abelian scheme. Since
$Y^{\mathrm {biZar}} \rightarrow \pi (Y)^{\mathrm {biZar}}$ is an abelian scheme. Since ![]() $p_N^{-1}(x')$ is bi-algebraic [Reference GaoGao17b, Corollary 8.3] and
$p_N^{-1}(x')$ is bi-algebraic [Reference GaoGao17b, Corollary 8.3] and ![]() $Y \subseteq p_N^{-1}(x')$, we have
$Y \subseteq p_N^{-1}(x')$, we have ![]() $Y^{\mathrm {biZar}} \subseteq p_N^{-1}(x')$. Thus the relative dimension of the abelian scheme
$Y^{\mathrm {biZar}} \subseteq p_N^{-1}(x')$. Thus the relative dimension of the abelian scheme ![]() $Y^{\mathrm {biZar}} \rightarrow \pi (Y)^{\mathrm {biZar}}$ is at most
$Y^{\mathrm {biZar}} \rightarrow \pi (Y)^{\mathrm {biZar}}$ is at most ![]() $g_N$. So
$g_N$. So
Hence ![]() $\delta _{\mathrm {ws}}(Y) < \dim \pi (Y)^{\mathrm {biZar}} + t$. Thus
$\delta _{\mathrm {ws}}(Y) < \dim \pi (Y)^{\mathrm {biZar}} + t$. Thus ![]() $\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) < \dim Y + t$ by Lemma 7.3, and hence
$\dim \langle Y \rangle _{\mathrm {sg}} - \dim \pi (Y) < \dim Y + t$ by Lemma 7.3, and hence ![]() $Y \subseteq X^{\mathrm {deg}}(t)$ by definition. By varying
$Y \subseteq X^{\mathrm {deg}}(t)$ by definition. By varying ![]() $x \in E_h$, we get the conclusion.
$x \in E_h$, we get the conclusion.
7.3 Proof of Theorem 7.1
Now we are ready to prove Theorem 7.1. Let ![]() $X$ be as in Theorem 7.1. Let
$X$ be as in Theorem 7.1. Let ![]() $\Sigma$ be the finite set in Theorem 7.5.
$\Sigma$ be the finite set in Theorem 7.5.
For any positive dimensional closed irreducible subvariety ![]() $Z$ of
$Z$ of ![]() $X$ such that
$X$ such that ![]() $\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property, we obtain some
$\dim \langle Z \rangle _{\mathrm {sg}} - \dim \pi (Z) < \dim Z + t$ and is maximal for this property, we obtain some ![]() $((Q,\mathcal {Y}^+),N) \in \Sigma$ from which we can construct a Zariski closed subset
$((Q,\mathcal {Y}^+),N) \in \Sigma$ from which we can construct a Zariski closed subset ![]() $E_{g_N - t}$ of
$E_{g_N - t}$ of ![]() $X$ such that
$X$ such that ![]() $Z \subseteq E_{g_N - t}$ by (i) of Proposition 7.6. Since
$Z \subseteq E_{g_N - t}$ by (i) of Proposition 7.6. Since ![]() $\Sigma$ is a finite set, we have finitely many such
$\Sigma$ is a finite set, we have finitely many such ![]() $E_{g_N - t}$. By definition of
$E_{g_N - t}$. By definition of ![]() $X^{\mathrm {deg}}(t)$, we then have that
$X^{\mathrm {deg}}(t)$, we then have that ![]() $X^{\mathrm {deg}}(t)$ is contained in the union of these
$X^{\mathrm {deg}}(t)$ is contained in the union of these ![]() $E_{g_N - t}$, which is a Zariski closed subset of
$E_{g_N - t}$, which is a Zariski closed subset of ![]() $X$.
$X$.
Conversely by (ii) of Proposition 7.6, each such ![]() $E_{g_N - t}$ is contained in
$E_{g_N - t}$ is contained in ![]() $X^{\mathrm {deg}}(t)$.
$X^{\mathrm {deg}}(t)$.
Hence ![]() $X^{\mathrm {deg}}(t)$ is the union of these
$X^{\mathrm {deg}}(t)$ is the union of these ![]() $E_{g_N - t}$. This is a finite union with each member being a closed subset of
$E_{g_N - t}$. This is a finite union with each member being a closed subset of ![]() $X$. Hence
$X$. Hence ![]() $X^{\mathrm {deg}}(t)$ is Zariski closed in
$X^{\mathrm {deg}}(t)$ is Zariski closed in ![]() $X$.
$X$.
8. Criterion of degenerate subvarieties
Let ![]() $X$ be an irreducible subvariety of
$X$ be an irreducible subvariety of ![]() $\mathfrak {A}_g$. Through the whole section we fix a
$\mathfrak {A}_g$. Through the whole section we fix a ![]() $t \in \mathbb {Z}$. Let
$t \in \mathbb {Z}$. Let ![]() $X^{\mathrm {deg}}(t)$ be the
$X^{\mathrm {deg}}(t)$ be the ![]() $t$th degeneracy locus of
$t$th degeneracy locus of ![]() $X$ defined in Definition 1.6.
$X$ defined in Definition 1.6.
The goal of this section is to prove the criterion for ![]() $X = X^{\mathrm {deg}}(t)$, and hence part (i) of Theorem 1.1 for
$X = X^{\mathrm {deg}}(t)$, and hence part (i) of Theorem 1.1 for ![]() $X \subseteq \mathfrak {A}_g$ in view of Proposition 6.1 and Theorem 7.1.
$X \subseteq \mathfrak {A}_g$ in view of Proposition 6.1 and Theorem 7.1.
For notation let ![]() $B = \pi (X)$, let
$B = \pi (X)$, let ![]() $\mathcal {A}_X$ be the translate of an abelian subscheme of
$\mathcal {A}_X$ be the translate of an abelian subscheme of ![]() $\mathfrak {A}_g|_B \rightarrow B$ by a torsion section, which contains
$\mathfrak {A}_g|_B \rightarrow B$ by a torsion section, which contains ![]() $X$, minimal for this property. Then
$X$, minimal for this property. Then ![]() $\mathcal {A}_X \rightarrow B$ itself is an abelian scheme (up to taking a finite covering of
$\mathcal {A}_X \rightarrow B$ itself is an abelian scheme (up to taking a finite covering of ![]() $B$), whose relative dimension we denote by
$B$), whose relative dimension we denote by ![]() $g_X$.
$g_X$.
For any abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}_X \rightarrow B$ whose relative dimension we denote by
$\mathcal {A}_X \rightarrow B$ whose relative dimension we denote by ![]() $g_{\mathcal {B}}$, we obtain the following diagram:
$g_{\mathcal {B}}$, we obtain the following diagram:

where ![]() $p_{\mathcal {B}}$ is taking the quotient abelian scheme, and the right box is the modular map.
$p_{\mathcal {B}}$ is taking the quotient abelian scheme, and the right box is the modular map.
Theorem 8.1 Assume either ![]() $t \le 0$, or
$t \le 0$, or ![]() $t = 1$ and
$t = 1$ and ![]() $\mathcal {A}_X = \mathfrak {A}_g|_B$. Then
$\mathcal {A}_X = \mathfrak {A}_g|_B$. Then ![]() $X = X^{\mathrm {deg}}(t)$ if and only if the following condition holds: there exists an abelian subscheme
$X = X^{\mathrm {deg}}(t)$ if and only if the following condition holds: there exists an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}_X \rightarrow B$ (whose relative dimension we denote by
$\mathcal {A}_X \rightarrow B$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that for the map
$g_{\mathcal {B}}$) such that for the map ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ constructed above, we have
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ constructed above, we have ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < \dim X - g_{\mathcal {B}} + t$ and that
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < \dim X - g_{\mathcal {B}} + t$ and that ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite.
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite.
Note that when ![]() $t \le 0$, the condition
$t \le 0$, the condition ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite is redundant. This is because in this case,
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite is redundant. This is because in this case, ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < \dim X - g_{\mathcal {B}} + t$ implies
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < \dim X - g_{\mathcal {B}} + t$ implies ![]() $\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) < \dim X$, and hence
$\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) < \dim X$, and hence ![]() $\iota _{/\mathcal {B}}\circ p_{\mathcal {B}}$ is not generically finite.
$\iota _{/\mathcal {B}}\circ p_{\mathcal {B}}$ is not generically finite.
8.1 Auxiliary proposition
We start by proving the following auxiliary proposition.
Proposition 8.2 We have ![]() $X = X^{\mathrm {deg}}(t)$ if and only if there exist:
$X = X^{\mathrm {deg}}(t)$ if and only if there exist:
• a special subvariety
 $M_*$ of
$M_*$ of  $\mathfrak {A}_g$, associated with
$\mathfrak {A}_g$, associated with  $(Q_*,\mathcal {Y}^+_*)$, which contains
$(Q_*,\mathcal {Y}^+_*)$, which contains  $X$;
$X$;• a non-trivial connected normal subgroup
 $N_*$ of
$N_*$ of  $Q_*$ whose reductive part is semi-simple;
$Q_*$ whose reductive part is semi-simple;
such that the following condition holds: for the operation of taking quotient mixed Shimura datum ![]() $\tilde {p}_{N_*} \colon (Q_*,\mathcal {Y}_*^+) \rightarrow (Q_*,\mathcal {Y}_*^+)/N_*$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type
$\tilde {p}_{N_*} \colon (Q_*,\mathcal {Y}_*^+) \rightarrow (Q_*,\mathcal {Y}_*^+)/N_*$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type

we have ![]() $\dim X - \dim p_{N_*}(X) > g_{N_*} - t$, where
$\dim X - \dim p_{N_*}(X) > g_{N_*} - t$, where ![]() $g_{N_*} = \frac{1}{2} \dim (V_{2g} \cap N_*)$.
$g_{N_*} = \frac{1}{2} \dim (V_{2g} \cap N_*)$.
Proof. We prove ![]() $\Leftarrow$. Let
$\Leftarrow$. Let ![]() $E_{g_{N_*} - t} = \{ x \in X : \dim _x (p_{N_*}|_{X})^{-1}(p_{N_*}(x)) > g_{N_*} - t\}$ as defined in (7.2). Then
$E_{g_{N_*} - t} = \{ x \in X : \dim _x (p_{N_*}|_{X})^{-1}(p_{N_*}(x)) > g_{N_*} - t\}$ as defined in (7.2). Then ![]() $X = E_{g_{N_*} - t}$ as
$X = E_{g_{N_*} - t}$ as ![]() $\dim X - \dim p_{N_*}(X) > g_{N_*} - t$. Note that (7.1) and (8.2) have the same shape. Hence
$\dim X - \dim p_{N_*}(X) > g_{N_*} - t$. Note that (7.1) and (8.2) have the same shape. Hence ![]() $X = X^{\mathrm {deg}}(t)$ by (ii) of Proposition 7.6.
$X = X^{\mathrm {deg}}(t)$ by (ii) of Proposition 7.6.
Now let us prove ![]() $\Rightarrow$. By the proof of Theorem 7.1 (§ 7.3), we have that
$\Rightarrow$. By the proof of Theorem 7.1 (§ 7.3), we have that ![]() $X^{\mathrm {deg}}(t)$ is a finite union of some Zariski closed subsets
$X^{\mathrm {deg}}(t)$ is a finite union of some Zariski closed subsets ![]() $E_{g_{N_*} - t}$ of
$E_{g_{N_*} - t}$ of ![]() $X$. Now
$X$. Now ![]() $X = E_{g_{N_*} - t}$ for some
$X = E_{g_{N_*} - t}$ for some ![]() $E_{g_{N_*} - t}$ since
$E_{g_{N_*} - t}$ since ![]() $X= X^{\mathrm {deg}}(t)$.
$X= X^{\mathrm {deg}}(t)$.
Recall the definition of ![]() $E_{g_{N_*} - t}$ as in (7.2):
$E_{g_{N_*} - t}$ as in (7.2): ![]() $E_{g_{N_*} - t} = \{ x \in X : \dim _x (p_{N_*}|_{X \cap M_*})^{-1}(p_{N_*}(x)) > g_{N_*} - t\}$ for some mixed Shimura subdatum of Kuga type
$E_{g_{N_*} - t} = \{ x \in X : \dim _x (p_{N_*}|_{X \cap M_*})^{-1}(p_{N_*}(x)) > g_{N_*} - t\}$ for some mixed Shimura subdatum of Kuga type ![]() $(Q_*,\mathcal {Y}_*^+)$ of
$(Q_*,\mathcal {Y}_*^+)$ of ![]() $(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$ and a non-trivial connected normal subgroup
$(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$ and a non-trivial connected normal subgroup ![]() $N_*$ of
$N_*$ of ![]() $Q_*$ whose reductive part is semi-simple, with
$Q_*$ whose reductive part is semi-simple, with ![]() $g_{N_*} = \frac{1}{2}\dim (V_{2g} \cap N_*)$.
$g_{N_*} = \frac{1}{2}\dim (V_{2g} \cap N_*)$.
By definition of ![]() $E_{g_{N_*} - t}$, it is contained in
$E_{g_{N_*} - t}$, it is contained in ![]() $X \cap M_*$. Hence
$X \cap M_*$. Hence ![]() $X = E_{g_{N_*} - t} \subseteq M_*$.
$X = E_{g_{N_*} - t} \subseteq M_*$.
Now that each fiber of ![]() $p_{N_*}|_X$ has dimension
$p_{N_*}|_X$ has dimension ![]() $> g_{N_*}-t$, we have
$> g_{N_*}-t$, we have ![]() $\dim X - \dim p_{N_*}(X) > g_{N_*} - t$.
$\dim X - \dim p_{N_*}(X) > g_{N_*} - t$.
8.2 Theorem 8.1 in terms of mixed Shimura variety
In this subsection, we prove Theorem 8.1 in terms of mixed Shimura variety. Then we translate it into the desired geometric description in the next subsection.
Let ![]() $M$ be the smallest special subvariety of
$M$ be the smallest special subvariety of ![]() $\mathfrak {A}_g$, which contains
$\mathfrak {A}_g$, which contains ![]() $X$. Assume that
$X$. Assume that ![]() $M$ is associated with the mixed Shimura subdatum of Kuga type
$M$ is associated with the mixed Shimura subdatum of Kuga type ![]() $(Q,\mathcal {Y}^+)$ of
$(Q,\mathcal {Y}^+)$ of ![]() $(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$.
$(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$.
Proposition 8.3 Assume either ![]() $t \le 0$, or
$t \le 0$, or ![]() $t = 1$ and
$t = 1$ and ![]() $M = \mathfrak {A}_g|_{\pi (M)}$. Then
$M = \mathfrak {A}_g|_{\pi (M)}$. Then ![]() $X = X^{\mathrm {deg}}(t)$ if and only if there exists a non-trivial connected normal subgroup
$X = X^{\mathrm {deg}}(t)$ if and only if there exists a non-trivial connected normal subgroup ![]() $N$ of
$N$ of ![]() $Q$ whose reductive part is semi-simple, such that the following condition holds: For the operation of taking quotient Shimura datum
$Q$ whose reductive part is semi-simple, such that the following condition holds: For the operation of taking quotient Shimura datum ![]() $\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N =: (Q', \mathcal {Y}^{\prime +})$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type
$\tilde {p}_N \colon (Q,\mathcal {Y}^+) \rightarrow (Q,\mathcal {Y}^+)/N =: (Q', \mathcal {Y}^{\prime +})$ discussed in § 5.4 and the induced morphism on the corresponding mixed Shimura varieties of Kuga type

we have ![]() $\dim X - \dim p_N(X) > g_N - t$, where
$\dim X - \dim p_N(X) > g_N - t$, where ![]() $g_N = \frac{1}{2} \dim (V_{2g} \cap N)$.
$g_N = \frac{1}{2} \dim (V_{2g} \cap N)$.
Proof of Proposition 8.3 We use Proposition 8.2. First ![]() $\Leftarrow$ of Proposition 8.3 follows directly from
$\Leftarrow$ of Proposition 8.3 follows directly from ![]() $\Leftarrow$ of Proposition 8.2.
$\Leftarrow$ of Proposition 8.2.
Let us prove ![]() $\Rightarrow$ of Proposition 8.3. Let
$\Rightarrow$ of Proposition 8.3. Let ![]() $M_*$,
$M_*$, ![]() $(Q_*,\mathcal {Y}^+_*)$,
$(Q_*,\mathcal {Y}^+_*)$, ![]() $N_*$ and
$N_*$ and ![]() $g_{N_*}$ be as in
$g_{N_*}$ be as in ![]() $\Rightarrow$ of Proposition 8.2.
$\Rightarrow$ of Proposition 8.2.
Set ![]() $N$ to be the identity component of
$N$ to be the identity component of ![]() $Q \cap N_*$. Since
$Q \cap N_*$. Since ![]() $X \subseteq M_*$ and
$X \subseteq M_*$ and ![]() $M$ is the smallest special subvariety of
$M$ is the smallest special subvariety of ![]() $\mathfrak {A}_g$, which contains
$\mathfrak {A}_g$, which contains ![]() $X$, we have
$X$, we have ![]() $M \subseteq M_*$. Hence we may assume
$M \subseteq M_*$. Hence we may assume ![]() $(Q,\mathcal {Y}^+) \subseteq (Q_*,\mathcal {Y}_*^+)$. Let
$(Q,\mathcal {Y}^+) \subseteq (Q_*,\mathcal {Y}_*^+)$. Let ![]() $N = Q \cap N_*$, then
$N = Q \cap N_*$, then ![]() $N \lhd Q$. Replacing
$N \lhd Q$. Replacing ![]() $N$ by
$N$ by ![]() $N \cap \tilde {\pi }^{-1}(\tilde {\pi }(N)^{\mathrm {der}})$, we may and do assume that the reductive part of
$N \cap \tilde {\pi }^{-1}(\tilde {\pi }(N)^{\mathrm {der}})$, we may and do assume that the reductive part of ![]() $N$ is semi-simple; here
$N$ is semi-simple; here ![]() $\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$.
$\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$.
Let us temporarily assume
and finish the proof by showing that this ![]() $N$ can be taken as the desired connected normal subgroup of
$N$ can be taken as the desired connected normal subgroup of ![]() $Q$. We need to prove the following:
$Q$. We need to prove the following:
(i)
 $\dim X - \dim p_N(X) > g_N - t$ for
$\dim X - \dim p_N(X) > g_N - t$ for  $g_N = \frac{1}{2} \dim (V_{2g} \cap N)$;
$g_N = \frac{1}{2} \dim (V_{2g} \cap N)$;(ii)
 $N$ is a non-trivial group.
$N$ is a non-trivial group.
For (i), we have ![]() $g_N \le g_{N_*}$ since
$g_N \le g_{N_*}$ since ![]() $N < N_*$. So
$N < N_*$. So ![]() $\dim X - \dim p_N(X) = \dim X - \dim p_{N_*}(X) > g_{N_*} - t \ge g_N - t$.
$\dim X - \dim p_N(X) = \dim X - \dim p_{N_*}(X) > g_{N_*} - t \ge g_N - t$.
For (ii), suppose ![]() $N$ is trivial. Then
$N$ is trivial. Then ![]() $p_N = \mathrm {id}_M$ and thus
$p_N = \mathrm {id}_M$ and thus ![]() $\dim p_N(X) = \dim X$. So
$\dim p_N(X) = \dim X$. So ![]() $\dim p_{N_*}(X) = \dim X$. Hence
$\dim p_{N_*}(X) = \dim X$. Hence ![]() $p_{N_*}|_X$ is generically finite. So
$p_{N_*}|_X$ is generically finite. So ![]() $X= E_{g_{N_*}-t}$ implies that
$X= E_{g_{N_*}-t}$ implies that ![]() $g_{N_*} - t < 0$. But then
$g_{N_*} - t < 0$. But then ![]() $g_{N_*} = 0$ and
$g_{N_*} = 0$ and ![]() $t = 1$ as
$t = 1$ as ![]() $t \le 1$. Hence
$t \le 1$. Hence ![]() $N_*$ is reductive. It can be viewed as a subgroup of
$N_*$ is reductive. It can be viewed as a subgroup of ![]() $\mathrm {Sp}_{2g}$ via
$\mathrm {Sp}_{2g}$ via ![]() $\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$. Now
$\tilde {\pi } \colon P_{2g,\mathrm {a}} \rightarrow \mathrm {GSp}_{2g}$. Now ![]() $N_* \lhd Q_*$ implies that the subgroup
$N_* \lhd Q_*$ implies that the subgroup ![]() $N_*$ of
$N_*$ of ![]() $\mathrm {Sp}_{2g}$ acts trivially on
$\mathrm {Sp}_{2g}$ acts trivially on ![]() $V_{2g} \cap Q_*$. By our hypothesis on
$V_{2g} \cap Q_*$. By our hypothesis on ![]() $X$ (note that
$X$ (note that ![]() $t = 1$ now) and Proposition 5.6, we have
$t = 1$ now) and Proposition 5.6, we have ![]() $M = \mathfrak {A}_g|_{\pi (M)}$. Hence
$M = \mathfrak {A}_g|_{\pi (M)}$. Hence ![]() $V_{2g} \cap Q = V_{2g}$. Thus
$V_{2g} \cap Q = V_{2g}$. Thus ![]() $V_{2g} \cap Q_* = V_{2g}$ since
$V_{2g} \cap Q_* = V_{2g}$ since ![]() $Q \subseteq Q_*$. But the only connected subgroup of
$Q \subseteq Q_*$. But the only connected subgroup of ![]() $\mathrm {Sp}_{2g}$ acting trivially on
$\mathrm {Sp}_{2g}$ acting trivially on ![]() $V_{2g}$ is
$V_{2g}$ is ![]() $1$. Hence
$1$. Hence ![]() $N_*$ is trivial, contradicting to the choice of
$N_*$ is trivial, contradicting to the choice of ![]() $N_*$. Thus
$N_*$. Thus ![]() $N$ is non-trivial. Hence this
$N$ is non-trivial. Hence this ![]() $N$ can be taken as the desired connected normal subgroup of
$N$ can be taken as the desired connected normal subgroup of ![]() $Q$.
$Q$.
Now it remains to prove (8.4). Each fiber of ![]() $\tilde {p}_N$ is of the form
$\tilde {p}_N$ is of the form ![]() $N(\mathbb {R})^+\tilde {y}$ for some
$N(\mathbb {R})^+\tilde {y}$ for some ![]() $\tilde {y} \in \mathcal {Y}^+$, and each fiber of
$\tilde {y} \in \mathcal {Y}^+$, and each fiber of ![]() $\tilde {p}_{N_*}$ is of the form
$\tilde {p}_{N_*}$ is of the form ![]() $N_*(\mathbb {R})^+\tilde {y}_*$ for some
$N_*(\mathbb {R})^+\tilde {y}_*$ for some ![]() $\tilde {y}_* \in \mathcal {Y}^+_*$. As
$\tilde {y}_* \in \mathcal {Y}^+_*$. As ![]() $\mathcal {Y}^+ \subseteq \mathcal {Y}^+_*$, we can take
$\mathcal {Y}^+ \subseteq \mathcal {Y}^+_*$, we can take ![]() $\tilde {y}_* = \tilde {y} \in \mathcal {Y}^+$. By definition of
$\tilde {y}_* = \tilde {y} \in \mathcal {Y}^+$. By definition of ![]() $N$, we have
$N$, we have ![]() $N(\mathbb {R})^+\tilde {y} = Q(\mathbb {R})^+ \tilde {y} \cap N_*(\mathbb {R})^+ \tilde {y} = \mathcal {Y}^+ \cap N_*(\mathbb {R})^+\tilde {y}$.
$N(\mathbb {R})^+\tilde {y} = Q(\mathbb {R})^+ \tilde {y} \cap N_*(\mathbb {R})^+ \tilde {y} = \mathcal {Y}^+ \cap N_*(\mathbb {R})^+\tilde {y}$.
Denote by ![]() $\tilde {X}$ a complex analytic irreducible component of
$\tilde {X}$ a complex analytic irreducible component of ![]() $\mathbf {u}^{-1}(X)$, which is contained in
$\mathbf {u}^{-1}(X)$, which is contained in ![]() $\mathcal {Y}^+$. Then by the previous paragraph, each fiber of
$\mathcal {Y}^+$. Then by the previous paragraph, each fiber of ![]() $\tilde {p}_N|_{\tilde {X}}$ is of the form
$\tilde {p}_N|_{\tilde {X}}$ is of the form ![]() $N(\mathbb {R})^+\tilde {y} \cap \tilde {X}$, and each fiber of
$N(\mathbb {R})^+\tilde {y} \cap \tilde {X}$, and each fiber of ![]() $\tilde {p}_{N_*}|_{\tilde {X}}$ is of the form
$\tilde {p}_{N_*}|_{\tilde {X}}$ is of the form ![]() $N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$. The last sentence of last paragraph says
$N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$. The last sentence of last paragraph says ![]() $N(\mathbb {R})^+\tilde {y} \cap \tilde {X} = \mathcal {Y}^+ \cap N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$, which furthermore equals
$N(\mathbb {R})^+\tilde {y} \cap \tilde {X} = \mathcal {Y}^+ \cap N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$, which furthermore equals ![]() $N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$ since
$N_*(\mathbb {R})^+\tilde {y} \cap \tilde {X}$ since ![]() $\tilde {X} \subseteq \mathcal {Y}^+$. Thus the fibers of
$\tilde {X} \subseteq \mathcal {Y}^+$. Thus the fibers of ![]() $\tilde {p}_N|_{\tilde {X}}$ and
$\tilde {p}_N|_{\tilde {X}}$ and ![]() $\tilde {p}_{N_*}|_{\tilde {X}}$ have the same dimensions. Hence the fibers of
$\tilde {p}_{N_*}|_{\tilde {X}}$ have the same dimensions. Hence the fibers of ![]() $p_N|_X$ and
$p_N|_X$ and ![]() $p_{N_*}|_X$ have the same dimensions. Thus (8.4) holds. Now we are done.
$p_{N_*}|_X$ have the same dimensions. Thus (8.4) holds. Now we are done.
8.3 Proof of Theorem 8.1
Let ![]() $M$ be the smallest special subvariety of
$M$ be the smallest special subvariety of ![]() $\mathfrak {A}_g$, which contains
$\mathfrak {A}_g$, which contains ![]() $X$. Assume that
$X$. Assume that ![]() $M$ is associated with the mixed Shimura subdatum of Kuga type
$M$ is associated with the mixed Shimura subdatum of Kuga type ![]() $(Q,\mathcal {Y}^+)$ of
$(Q,\mathcal {Y}^+)$ of ![]() $(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$. Denote by
$(P_{2g,\mathrm {a}},\mathcal {X}_{2g,\mathrm {a}}^+)$. Denote by ![]() $V_Q = V_{2g} \cap Q$ and
$V_Q = V_{2g} \cap Q$ and ![]() $G_Q = \tilde {\pi }(Q)$ the reductive part of
$G_Q = \tilde {\pi }(Q)$ the reductive part of ![]() $Q$. Let
$Q$. Let ![]() $g_Q = \frac{1}{2}\dim V_Q$.
$g_Q = \frac{1}{2}\dim V_Q$.
Special subvarieties of ![]() $\mathfrak {A}_g$ are described in Proposition 5.6. Hence the smallest special subvariety
$\mathfrak {A}_g$ are described in Proposition 5.6. Hence the smallest special subvariety ![]() $M$ of
$M$ of ![]() $\mathfrak {A}_g$, which contains
$\mathfrak {A}_g$, which contains ![]() $X$ can be described as follows:
$X$ can be described as follows:
• let
 $M_G$ be the smallest special subvariety of
$M_G$ be the smallest special subvariety of  $\mathbb {A}_g$, which contains
$\mathbb {A}_g$, which contains  $\pi (X)$;
$\pi (X)$;• let
 $M$ be the translate of an abelian subscheme of
$M$ be the translate of an abelian subscheme of  $\mathfrak {A}_g|_{M_G} \rightarrow M_G$ by a torsion section which contains
$\mathfrak {A}_g|_{M_G} \rightarrow M_G$ by a torsion section which contains  $X$, minimal for this property.
$X$, minimal for this property.
Then ![]() $M \rightarrow M_G$ itself is an abelian scheme of relative dimension
$M \rightarrow M_G$ itself is an abelian scheme of relative dimension ![]() $g_Q$.
$g_Q$.
![]() $\Rightarrow$ of Theorem 8.1. Apply
$\Rightarrow$ of Theorem 8.1. Apply ![]() $\Rightarrow$ of Proposition 8.3. Then we obtain a non-trivial connected normal subgroup
$\Rightarrow$ of Proposition 8.3. Then we obtain a non-trivial connected normal subgroup ![]() $N$ of
$N$ of ![]() $Q$ whose reductive part is semi-simple, such that for the quotient Shimura morphism
$Q$ whose reductive part is semi-simple, such that for the quotient Shimura morphism ![]() $p_N \colon M \rightarrow M'$, we have (
$p_N \colon M \rightarrow M'$, we have (![]() $g_N = \frac{1}{2}\dim (V_{2g}\cap N)$)
$g_N = \frac{1}{2}\dim (V_{2g}\cap N)$)
Recall the geometric meaning of ![]() $p_N$ (5.4):
$p_N$ (5.4):

The morphism ![]() $p_0$ is taking the quotient of
$p_0$ is taking the quotient of ![]() $M \rightarrow M_G$ by the abelian subscheme
$M \rightarrow M_G$ by the abelian subscheme ![]() $\operatorname {Ker}(p_0)^{\circ }$ (which has relative dimension
$\operatorname {Ker}(p_0)^{\circ }$ (which has relative dimension ![]() $g_N$). For each
$g_N$). For each ![]() $b' \in M_G'$, the abelian scheme
$b' \in M_G'$, the abelian scheme ![]() $M_0|_{p_{G_N}^{-1}(b')} \rightarrow p_{G_N}^{-1}(b')$ is isotrivial.
$M_0|_{p_{G_N}^{-1}(b')} \rightarrow p_{G_N}^{-1}(b')$ is isotrivial.
Take ![]() $\mathcal {B} = \operatorname {Ker}(p_0)^{\circ } \cap \mathcal {A}_X$. Then
$\mathcal {B} = \operatorname {Ker}(p_0)^{\circ } \cap \mathcal {A}_X$. Then ![]() $\mathcal {B}$ is an abelian subscheme of
$\mathcal {B}$ is an abelian subscheme of ![]() $\mathcal {A}_X \rightarrow B$ of relative dimension
$\mathcal {A}_X \rightarrow B$ of relative dimension ![]() $g_N$, namely
$g_N$, namely ![]() $g_{\mathcal {B}} = g_N$. Now we can construct the maps in (8.1). We have
$g_{\mathcal {B}} = g_N$. Now we can construct the maps in (8.1). We have ![]() $\mathcal {A}_X = M|_B$,
$\mathcal {A}_X = M|_B$, ![]() $p_{\mathcal {B}} = p_0|_{\mathcal {A}_X}$,
$p_{\mathcal {B}} = p_0|_{\mathcal {A}_X}$, ![]() $\pi _{/\mathcal {B}} = \pi _0|_{M_0|_B}$,
$\pi _{/\mathcal {B}} = \pi _0|_{M_0|_B}$, ![]() $\iota _{/\mathcal {B}} = (i \circ p')|_{M_0|_B}$ and
$\iota _{/\mathcal {B}} = (i \circ p')|_{M_0|_B}$ and ![]() $\iota _{/\mathcal {B},G} = (i_G \circ p_{G_N})|_B$. Thus
$\iota _{/\mathcal {B},G} = (i_G \circ p_{G_N})|_B$. Thus
where the first inequality follows from ![]() $X \subseteq M|_B$ and the second inequality follows from (8.5). Thus it suffices to prove that
$X \subseteq M|_B$ and the second inequality follows from (8.5). Thus it suffices to prove that ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite.
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite.
Suppose ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is generically finite. Then
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is generically finite. Then ![]() $g_N = 0$,
$g_N = 0$, ![]() $p_{\mathcal {B}} = \mathrm {id}_{\mathcal {A}_X}$ and
$p_{\mathcal {B}} = \mathrm {id}_{\mathcal {A}_X}$ and ![]() $\iota _{/\mathcal {B}}$ is generically finite. Hence
$\iota _{/\mathcal {B}}$ is generically finite. Hence ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = \dim X$. But then
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = \dim X$. But then ![]() $\dim X < \dim X - g_{\mathcal {B}} + t = \dim X + t$. When
$\dim X < \dim X - g_{\mathcal {B}} + t = \dim X + t$. When ![]() $t \le 0$ this cannot hold. Hence
$t \le 0$ this cannot hold. Hence ![]() $t = 1$ and
$t = 1$ and ![]() $\mathcal {A}_X = \mathfrak {A}_g|_B$ by our hypothesis. Hence
$\mathcal {A}_X = \mathfrak {A}_g|_B$ by our hypothesis. Hence ![]() $M = \mathfrak {A}_g|_{M_G}$.
$M = \mathfrak {A}_g|_{M_G}$.
Since ![]() $g_N = 0$, we have
$g_N = 0$, we have ![]() $p_0 = \mathrm {id}_M$ and
$p_0 = \mathrm {id}_M$ and ![]() $M_0 = M = \mathfrak {A}_g|_{M_G}$. For each
$M_0 = M = \mathfrak {A}_g|_{M_G}$. For each ![]() $b' \in M_G'$, the abelian scheme
$b' \in M_G'$, the abelian scheme ![]() $\mathfrak {A}_g|_{p_{G_N}^{-1}(b')} \rightarrow p_{G_N}^{-1}(b')$ is isotrivial. So
$\mathfrak {A}_g|_{p_{G_N}^{-1}(b')} \rightarrow p_{G_N}^{-1}(b')$ is isotrivial. So ![]() $\dim p_{G_N}^{-1}(b') = 0$; see the end of § 2. Hence
$\dim p_{G_N}^{-1}(b') = 0$; see the end of § 2. Hence ![]() $p_{G_N}$ is generically finite, and so is
$p_{G_N}$ is generically finite, and so is ![]() $p'$. Thus
$p'$. Thus ![]() $\dim M = \dim M'$. This contradicts our choice of
$\dim M = \dim M'$. This contradicts our choice of ![]() $N$ (non-trivial connected).
$N$ (non-trivial connected).
![]() $\Leftarrow$ of Theorem 8.1. Before moving on, let me point out that if
$\Leftarrow$ of Theorem 8.1. Before moving on, let me point out that if ![]() $t \le 0$, then this implication follows rather easily from Proposition 6.1 and Theorem 7.1 because we can translate it into studying the generic rank of the Betti map. However the argument below works also for
$t \le 0$, then this implication follows rather easily from Proposition 6.1 and Theorem 7.1 because we can translate it into studying the generic rank of the Betti map. However the argument below works also for ![]() $t =1$.
$t =1$.
Hodge theory says that: (1) every abelian subscheme of ![]() $\mathcal {A}_X \rightarrow B$ is the intersection of an abelian subscheme of
$\mathcal {A}_X \rightarrow B$ is the intersection of an abelian subscheme of ![]() $M \rightarrow M_G$ with
$M \rightarrow M_G$ with ![]() $\mathfrak {A}_g|_B$ (in particular
$\mathfrak {A}_g|_B$ (in particular ![]() $\mathcal {A}_X = M \cap \mathfrak {A}_g|_B = M|_B$ and
$\mathcal {A}_X = M \cap \mathfrak {A}_g|_B = M|_B$ and ![]() $g_X = g_Q$); (2) the abelian subschemes of
$g_X = g_Q$); (2) the abelian subschemes of ![]() $M \rightarrow M_G$ are in one-to-one correspondence to
$M \rightarrow M_G$ are in one-to-one correspondence to ![]() $G_Q$-submodules of
$G_Q$-submodules of ![]() $V_Q$. See [Reference DeligneDel71, 4.4.1–4.4.3].
$V_Q$. See [Reference DeligneDel71, 4.4.1–4.4.3].
Assume that ![]() $\mathcal {B} = \mathfrak {B} \cap \mathfrak {A}_g|_B$ where
$\mathcal {B} = \mathfrak {B} \cap \mathfrak {A}_g|_B$ where ![]() $\mathfrak {B}$ is an abelian subscheme of
$\mathfrak {B}$ is an abelian subscheme of ![]() $M \rightarrow M_G$, and that
$M \rightarrow M_G$, and that ![]() $\mathfrak {B}$ corresponds to the
$\mathfrak {B}$ corresponds to the ![]() $G_Q$-submodule
$G_Q$-submodule ![]() $V_N$ of
$V_N$ of ![]() $V_Q$. Let
$V_Q$. Let ![]() $g_N = \frac{1}{2}\dim V_N$, then
$g_N = \frac{1}{2}\dim V_N$, then ![]() $\mathfrak {B} \rightarrow M_G$ has relative dimension
$\mathfrak {B} \rightarrow M_G$ has relative dimension ![]() $g_N$. Hence
$g_N$. Hence ![]() $g_{\mathcal {B}} = g_N$.
$g_{\mathcal {B}} = g_N$.
Taking the quotient, we get the following.

In particular, ![]() $\pi _{/\mathfrak {B}}$ is an abelian scheme of relative dimension
$\pi _{/\mathfrak {B}}$ is an abelian scheme of relative dimension ![]() $g_Q-g_N$. It induces the following modular map.
$g_Q-g_N$. It induces the following modular map.

By definition of ![]() $\iota _{/\mathfrak {B},G}$,
$\iota _{/\mathfrak {B},G}$, ![]() $(M/\mathfrak {B})|_{\iota _{/\mathfrak {B},G}^{-1}(a)}$ is an isotrivial abelian scheme for each
$(M/\mathfrak {B})|_{\iota _{/\mathfrak {B},G}^{-1}(a)}$ is an isotrivial abelian scheme for each ![]() $a \in \mathbb {A}_{g_Q-g_N}$.
$a \in \mathbb {A}_{g_Q-g_N}$.
Modular interpretation of Shimura varieties implies that ![]() $\iota _{/\mathfrak {B},G}$ is a Shimura morphism, namely
$\iota _{/\mathfrak {B},G}$ is a Shimura morphism, namely ![]() $\iota _{/\mathfrak {B},G}$ is induced by some
$\iota _{/\mathfrak {B},G}$ is induced by some ![]() $\tilde {\iota }_{/\mathfrak {B},G} \colon (G_Q,\tilde {\pi }(\mathcal {Y}^+)) \rightarrow (\mathrm {GSp}_{2(g_Q-g_N)}, \mathfrak {H}_{g_Q-g_N}^+)$. Denote by
$\tilde {\iota }_{/\mathfrak {B},G} \colon (G_Q,\tilde {\pi }(\mathcal {Y}^+)) \rightarrow (\mathrm {GSp}_{2(g_Q-g_N)}, \mathfrak {H}_{g_Q-g_N}^+)$. Denote by ![]() $H$ the kernel of
$H$ the kernel of ![]() $\tilde {\iota }_{/\mathfrak {B},G}$ on the underlying groups, then
$\tilde {\iota }_{/\mathfrak {B},G}$ on the underlying groups, then ![]() $H \lhd G_Q$. Replace
$H \lhd G_Q$. Replace ![]() $H$ by
$H$ by ![]() $H^{\mathrm {der}}$, then
$H^{\mathrm {der}}$, then ![]() $H \lhd G_Q^{\mathrm {der}}$.
$H \lhd G_Q^{\mathrm {der}}$.
Each fiber of ![]() $\tilde {\iota }_{/\mathfrak {B},G}$ on the underlying spaces is of the form
$\tilde {\iota }_{/\mathfrak {B},G}$ on the underlying spaces is of the form ![]() $H(\mathbb {R})^+\tilde {y}_G$ for some
$H(\mathbb {R})^+\tilde {y}_G$ for some ![]() $\tilde {y}_G \in \tilde {\pi }(\mathcal {Y}^+)$. Hence each fiber of
$\tilde {y}_G \in \tilde {\pi }(\mathcal {Y}^+)$. Hence each fiber of ![]() $\iota _{/\mathcal {B},G}$ is of the form
$\iota _{/\mathcal {B},G}$ is of the form ![]() $\mathbf {u}_G(H(\mathbb {R})^+\tilde {y}_G)$ for some
$\mathbf {u}_G(H(\mathbb {R})^+\tilde {y}_G)$ for some ![]() $\tilde {y}_G \in \tilde {\pi }(\mathcal {Y}^+)$, where
$\tilde {y}_G \in \tilde {\pi }(\mathcal {Y}^+)$, where ![]() $\mathbf {u}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$ is the uniformization. Thus the connected algebraic monodromy group of
$\mathbf {u}_G \colon \mathfrak {H}_g^+ \rightarrow \mathbb {A}_g$ is the uniformization. Thus the connected algebraic monodromy group of ![]() $\iota _{/\mathfrak {B},G}^{-1}(a)$ is
$\iota _{/\mathfrak {B},G}^{-1}(a)$ is ![]() $H$ for each
$H$ for each ![]() $a \in \mathbb {A}_{g_Q-g_N}$. By Deligne's theorem of the fixed part [Reference DeligneDel71, Corollaire 4.1.2],
$a \in \mathbb {A}_{g_Q-g_N}$. By Deligne's theorem of the fixed part [Reference DeligneDel71, Corollaire 4.1.2], ![]() $H$ acts trivially on
$H$ acts trivially on ![]() $V_Q/V_N \simeq V_{2(g_Q-g_N)}$ because
$V_Q/V_N \simeq V_{2(g_Q-g_N)}$ because ![]() $(M/\mathfrak {B})|_{\iota _{/\mathfrak {B},G}^{-1}(a)}$ is isotrivial.
$(M/\mathfrak {B})|_{\iota _{/\mathfrak {B},G}^{-1}(a)}$ is isotrivial.
The zero section of the abelian scheme ![]() $M \rightarrow M_G$ gives rise to a Levi decomposition
$M \rightarrow M_G$ gives rise to a Levi decomposition ![]() $Q = V_Q \rtimes G_Q$. Let
$Q = V_Q \rtimes G_Q$. Let ![]() $N = V_N \rtimes H$. Then
$N = V_N \rtimes H$. Then ![]() $N$ is a connected normal subgroup of
$N$ is a connected normal subgroup of ![]() $Q$ whose reductive part is semi-simple. Moreover the quotient morphism
$Q$ whose reductive part is semi-simple. Moreover the quotient morphism ![]() $p_N$ is precisely
$p_N$ is precisely ![]() $\iota _{/\mathcal {B}} \circ p_{\mathfrak {B}}$, namely the geometric interpretation (5.4) for this
$\iota _{/\mathcal {B}} \circ p_{\mathfrak {B}}$, namely the geometric interpretation (5.4) for this ![]() $N$ becomes the following.
$N$ becomes the following.

Note that (8.1) is precisely (
8.6) restricted to ![]() $B \subseteq M_G$.
$B \subseteq M_G$.
If ![]() $N = 1$, then
$N = 1$, then ![]() $p_N = \mathrm {id}_M$. This contradicts
$p_N = \mathrm {id}_M$. This contradicts ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ being not generically finite. Hence
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ being not generically finite. Hence ![]() $N$ is non-trivial.
$N$ is non-trivial.
Note that ![]() $X \subseteq M|_B$. Thus the inequality in
$X \subseteq M|_B$. Thus the inequality in ![]() $\Leftarrow$ of Theorem 8.1 becomes
$\Leftarrow$ of Theorem 8.1 becomes ![]() $\dim p_N(X) < \dim X - g_N + t$. Now it suffices to apply
$\dim p_N(X) < \dim X - g_N + t$. Now it suffices to apply ![]() $\Leftarrow$ of Proposition 8.3 to this
$\Leftarrow$ of Proposition 8.3 to this ![]() $N$.
$N$.
9. Summary on the generic rank of the Betti map
In this section, we go back to the general setting and prove the main results concerning the Betti rank. First of all let us recall the setting up.
Let ![]() $S$ be an irreducible quasi-projective variety over
$S$ be an irreducible quasi-projective variety over ![]() $\mathbb {C}$, and let
$\mathbb {C}$, and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g\ge 1$. Recall the following modular map (4.1).
$g\ge 1$. Recall the following modular map (4.1).

Let ![]() $b_{\Delta } \colon \mathcal {A}_{\Delta } \rightarrow \mathbb {T}^{2g}$ be as defined in (4.2) where
$b_{\Delta } \colon \mathcal {A}_{\Delta } \rightarrow \mathbb {T}^{2g}$ be as defined in (4.2) where ![]() $\Delta$ is some open subset of
$\Delta$ is some open subset of ![]() $S^{\mathrm {an}}$.
$S^{\mathrm {an}}$.
Let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$ dominant to
$\mathcal {A}$ dominant to ![]() $S$. Assume that
$S$. Assume that ![]() $\iota |_X \colon X \rightarrow \iota (X)$ has relative dimension
$\iota |_X \colon X \rightarrow \iota (X)$ has relative dimension ![]() $r \ge 0$. Then for each
$r \ge 0$. Then for each ![]() $x \in X(\mathbb {C})$, we have
$x \in X(\mathbb {C})$, we have
9.1 Proof of Theorem 1.8
Fix ![]() $t \in \mathbb {Z}$. We proved that
$t \in \mathbb {Z}$. We proved that ![]() $\iota (X)^{\mathrm {deg}}(t)$ is Zariski closed in
$\iota (X)^{\mathrm {deg}}(t)$ is Zariski closed in ![]() $\iota (X)$ for each
$\iota (X)$ for each ![]() $t$ in Theorem 7.1. Thus Theorem 1.8 follows immediately from the below lemma.
$t$ in Theorem 7.1. Thus Theorem 1.8 follows immediately from the below lemma.
Lemma 9.1  $X^\mathrm {deg}(t) = \begin {cases} \iota ^{-1}\big ( \iota (X)^{\mathrm {deg}}(t+r) \big ) & \text {if}\ t+r \le 0 \text { or } r=0, \\ X & \text {otherwise.} \end {cases}$
$X^\mathrm {deg}(t) = \begin {cases} \iota ^{-1}\big ( \iota (X)^{\mathrm {deg}}(t+r) \big ) & \text {if}\ t+r \le 0 \text { or } r=0, \\ X & \text {otherwise.} \end {cases}$
Proof. First let us make the following observation: for any ![]() $Y \subseteq \mathcal {A}$ irreducible, we have that
$Y \subseteq \mathcal {A}$ irreducible, we have that ![]() $\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of
$\langle Y \rangle _{\mathrm {sg}}$ is an irreducible component of ![]() $\iota ^{-1}(\langle \iota (Y) \rangle _{\mathrm {sg}})$. So
$\iota ^{-1}(\langle \iota (Y) \rangle _{\mathrm {sg}})$. So
![]() $\text {Case } t+r \le 0\text { or }r=0$. For
$\text {Case } t+r \le 0\text { or }r=0$. For ![]() $\subseteq$, take
$\subseteq$, take ![]() $Y \subseteq X^{\mathrm {deg}}(t)$ irreducible such that
$Y \subseteq X^{\mathrm {deg}}(t)$ irreducible such that ![]() $\dim Y > 0$ and
$\dim Y > 0$ and
As ![]() $\iota |_X$ has relative dimension
$\iota |_X$ has relative dimension ![]() $r$, we have
$r$, we have ![]() $\dim \iota (Y) \ge \dim Y - r$. So (9.2) implies
$\dim \iota (Y) \ge \dim Y - r$. So (9.2) implies
If ![]() $t+r \le 0$, then the inequality above further implies
$t+r \le 0$, then the inequality above further implies ![]() $0 < \dim \iota (Y)$. If
$0 < \dim \iota (Y)$. If ![]() $r=0$, then
$r=0$, then ![]() $\iota$ is generically finite and hence
$\iota$ is generically finite and hence ![]() $\dim \iota (Y) = \dim Y >0$. Hence in either case, we have
$\dim \iota (Y) = \dim Y >0$. Hence in either case, we have ![]() $\iota (Y) \subseteq \iota (X)^{\mathrm {deg}}(t+r)$. This proves
$\iota (Y) \subseteq \iota (X)^{\mathrm {deg}}(t+r)$. This proves ![]() $\subseteq$.
$\subseteq$.
For ![]() $\supseteq$, conversely take
$\supseteq$, conversely take ![]() $Y' \subseteq \iota (X)^{\mathrm {deg}}(t+r)$ irreducible such that
$Y' \subseteq \iota (X)^{\mathrm {deg}}(t+r)$ irreducible such that ![]() $\dim Y' >0$ and
$\dim Y' >0$ and
Let ![]() $Y$ be an irreducible component of
$Y$ be an irreducible component of ![]() $\iota |_X^{-1}(Y')$. Then
$\iota |_X^{-1}(Y')$. Then ![]() $Y' = \iota (Y)$. So
$Y' = \iota (Y)$. So ![]() $\dim Y \ge \dim Y' + r >0$ by (9.1). By (9.2) we have then
$\dim Y \ge \dim Y' + r >0$ by (9.1). By (9.2) we have then
Hence ![]() $Y \subseteq X^{\mathrm {deg}}(t)$. This proves
$Y \subseteq X^{\mathrm {deg}}(t)$. This proves ![]() $\supseteq$.
$\supseteq$.
Case t + r > 0 and r > 0. Let ![]() $x \in X(\mathbb {C})$. Let
$x \in X(\mathbb {C})$. Let ![]() $Y$ be the irreducible component of
$Y$ be the irreducible component of ![]() $\iota |_X^{-1}(\iota (x))$, which contains
$\iota |_X^{-1}(\iota (x))$, which contains ![]() $x$. Then
$x$. Then ![]() $\dim Y \ge r > 0$.
$\dim Y \ge r > 0$.
For ![]() $B:= \pi _S(\iota ^{-1}(\iota (x))) = \iota _S^{-1}(\pi (\iota (x)))$, we have that
$B:= \pi _S(\iota ^{-1}(\iota (x))) = \iota _S^{-1}(\pi (\iota (x)))$, we have that ![]() $\iota ^{-1}(\iota (x))$ is a constant section of
$\iota ^{-1}(\iota (x))$ is a constant section of ![]() $\mathcal {A}|_B \rightarrow B$. Thus
$\mathcal {A}|_B \rightarrow B$. Thus ![]() $\dim \pi _S(Y) = \dim Y \ge r$, and
$\dim \pi _S(Y) = \dim Y \ge r$, and ![]() $\langle Y \rangle _{\mathrm {sg}} = Y$. Hence
$\langle Y \rangle _{\mathrm {sg}} = Y$. Hence
So ![]() $Y \subseteq X^{\mathrm {deg}}(-r+1)$. Thus
$Y \subseteq X^{\mathrm {deg}}(-r+1)$. Thus ![]() $X \subseteq X^{\mathrm {deg}}(-r+1)$.
$X \subseteq X^{\mathrm {deg}}(-r+1)$.
But ![]() $t \ge -r+1$ since
$t \ge -r+1$ since ![]() $t+r>0$. So
$t+r>0$. So ![]() $X^{\mathrm {deg}}(-r+1) \subseteq X^{\mathrm {deg}}(t)$ by definition. So we are done.
$X^{\mathrm {deg}}(-r+1) \subseteq X^{\mathrm {deg}}(t)$ by definition. So we are done.
9.2 Proof of Theorem 1.7
Fix ![]() $x \in X^{\mathrm {sm}}(\mathbb {C})$. Then
$x \in X^{\mathrm {sm}}(\mathbb {C})$. Then
Apply Proposition 6.1 to ![]() $\iota (X)$, then we have
$\iota (X)$, then we have
Since ![]() $l \le \dim \iota (X)$, we have
$l \le \dim \iota (X)$, we have
by Lemma 9.1, because ![]() $\dim X = \dim \iota (X) + r$. We are done by the three equivalences above.
$\dim X = \dim \iota (X) + r$. We are done by the three equivalences above.
9.3 Proof of Theorem 1.1
Part (ii) follows immediately from Theorems 1.7 and 1.8. So it remains to prove part (i).
The implication ![]() $\Leftarrow$ is clear: the generic rank of the Betti map on
$\Leftarrow$ is clear: the generic rank of the Betti map on ![]() $(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$ has the trivial upper bound
$(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$ has the trivial upper bound ![]() $2 \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$, and thus
$2 \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$, and thus ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2g_{\mathcal {B}} + 2 \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < 2l$.Footnote 6
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) \le 2g_{\mathcal {B}} + 2 \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) < 2l$.Footnote 6
Let us prove ![]() $\Rightarrow$. If
$\Rightarrow$. If ![]() $l > \dim \iota (X)$, then
$l > \dim \iota (X)$, then ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2l$ always holds. Take
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2l$ always holds. Take ![]() $\mathcal {B}$ to be the zero section of
$\mathcal {B}$ to be the zero section of ![]() $\mathcal {A}_X \rightarrow S$. Then
$\mathcal {A}_X \rightarrow S$. Then ![]() $g_{\mathcal {B}} =0$. Thus
$g_{\mathcal {B}} =0$. Thus
It suffices then to consider the case ![]() $l \le \dim \iota (X)$. By Theorem 1.7, we have
$l \le \dim \iota (X)$. By Theorem 1.7, we have
Set ![]() $B = \iota _S(S) = \pi (\iota (X))$. Apply Theorem 8.1 (and the discussion below) to
$B = \iota _S(S) = \pi (\iota (X))$. Apply Theorem 8.1 (and the discussion below) to ![]() $\iota (X)$ and
$\iota (X)$ and ![]() $t = l - \dim \iota (X) \le 0$. We thus obtain an abelian subscheme
$t = l - \dim \iota (X) \le 0$. We thus obtain an abelian subscheme ![]() $\mathcal {B}'$ of
$\mathcal {B}'$ of ![]() $\mathcal {A}_{\iota (X)} \rightarrow B$ (of relative dimension
$\mathcal {A}_{\iota (X)} \rightarrow B$ (of relative dimension ![]() $g_{\mathcal {B}'}$), such that
$g_{\mathcal {B}'}$), such that ![]() $\dim (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X)) < \dim \iota (X) - g_{\mathcal {B}'}$ for the following.
$\dim (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X)) < \dim \iota (X) - g_{\mathcal {B}'}$ for the following.

Observe ![]() $\mathcal {A}_X=\iota ^{-1}(\mathcal {A}_{\iota (X)})$ (so
$\mathcal {A}_X=\iota ^{-1}(\mathcal {A}_{\iota (X)})$ (so ![]() $g_X = g_{\iota (X)}$). Set
$g_X = g_{\iota (X)}$). Set ![]() $\mathcal {B} = \iota ^{-1}(\mathcal {B}')$. Then
$\mathcal {B} = \iota ^{-1}(\mathcal {B}')$. Then ![]() $\mathcal {B}$ is an abelian subscheme of
$\mathcal {B}$ is an abelian subscheme of ![]() $\mathcal {A}_X \rightarrow S$; its relative dimension
$\mathcal {A}_X \rightarrow S$; its relative dimension ![]() $g_{\mathcal {B}}$ equals
$g_{\mathcal {B}}$ equals ![]() $g_{\mathcal {B}'}$. The following diagram commutes.
$g_{\mathcal {B}'}$. The following diagram commutes.

Thus ![]() $(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X))$. So
$(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X))$. So ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = \dim (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X)) < \dim \iota (X) - g_{\mathcal {B}'} \le \dim X - g_{\mathcal {B}}$.
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) = \dim (\iota _{/\mathcal {B}'}\circ p_{\mathcal {B}'})(\iota (X)) < \dim \iota (X) - g_{\mathcal {B}'} \le \dim X - g_{\mathcal {B}}$.
9.4 A question of André, Corvaja and Zannier
In this subsection we apply the previous results to study a conjecture of André, Corvaja and Zannier.
Let ![]() $\xi$ be a section of
$\xi$ be a section of ![]() $\mathcal {A} \rightarrow S$. Denote by
$\mathcal {A} \rightarrow S$. Denote by ![]() $b_{\Delta }|_{\xi }$ the composite
$b_{\Delta }|_{\xi }$ the composite ![]() $b_{\Delta } \circ \xi \colon \Delta \rightarrow \mathcal {A}_{\Delta } \rightarrow \mathbb {T}^{2g}$.
$b_{\Delta } \circ \xi \colon \Delta \rightarrow \mathcal {A}_{\Delta } \rightarrow \mathbb {T}^{2g}$.
Theorem 9.2 Assume that ![]() $\mathbb {Z} \xi$ is Zariski dense in
$\mathbb {Z} \xi$ is Zariski dense in ![]() $\mathcal {A}$. Assume, furthermore, the following:
$\mathcal {A}$. Assume, furthermore, the following:
(i) either
 $\mathcal {A}/S$ is geometrically simple;
$\mathcal {A}/S$ is geometrically simple;(ii) or each Hodge generic curve
 $C \subseteq \iota _S(S)$ satisfies the following property:
$C \subseteq \iota _S(S)$ satisfies the following property:  $\iota (\mathcal {A}) \times _{\iota _S(S)} C = \pi ^{-1}(C) \rightarrow C$ has no fixed part over any finite covering of
$\iota (\mathcal {A}) \times _{\iota _S(S)} C = \pi ^{-1}(C) \rightarrow C$ has no fixed part over any finite covering of  $C$.Footnote 7
$C$.Footnote 7
Then ![]() $\max _{s \in \Delta } \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_{\xi })_s = 2 \min (\dim \iota (\xi (S)), g)$.
$\max _{s \in \Delta } \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_{\xi })_s = 2 \min (\dim \iota (\xi (S)), g)$.
Remark 9.3 If ![]() $\mathcal {A}/S$ is isotrivial, then hypothesis (ii) holds automatically since
$\mathcal {A}/S$ is isotrivial, then hypothesis (ii) holds automatically since ![]() $\iota _S(S)$ is a point. In general hypothesis (ii) can be checked in the following way. Let
$\iota _S(S)$ is a point. In general hypothesis (ii) can be checked in the following way. Let ![]() $G_B$ be the connected algebraic monodromy group of
$G_B$ be the connected algebraic monodromy group of ![]() $\iota _S(S)$. Then hypothesis (ii) is equivalent to: for any non-trivial connected normal subgroup
$\iota _S(S)$. Then hypothesis (ii) is equivalent to: for any non-trivial connected normal subgroup ![]() $H$ of
$H$ of ![]() $G_B$, the only element of
$G_B$, the only element of ![]() $V_{2g}$ stable under
$V_{2g}$ stable under ![]() $H$ is
$H$ is ![]() $0$. It holds for example when
$0$. It holds for example when ![]() $\mathcal {A} \rightarrow S$ has no fixed part and
$\mathcal {A} \rightarrow S$ has no fixed part and ![]() $G_B$ is a simple group.
$G_B$ is a simple group.
Proof. Let ![]() $X = \xi (S)$ and
$X = \xi (S)$ and ![]() $d = \dim \iota (X)$. Then
$d = \dim \iota (X)$. Then ![]() $\max _{s \in \Delta } \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_{\xi })_s = \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$.
$\max _{s \in \Delta } \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_{\xi })_s = \mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X)$.
Since ![]() $\mathbb {Z}\xi$ is Zariski dense in
$\mathbb {Z}\xi$ is Zariski dense in ![]() $\mathcal {A}$, we have
$\mathcal {A}$, we have ![]() $\mathcal {A}_X = \mathcal {A}$ where
$\mathcal {A}_X = \mathcal {A}$ where ![]() $\mathcal {A}_X$ is defined above Theorem 1.1.
$\mathcal {A}_X$ is defined above Theorem 1.1.
Assume ![]() $\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2 \min (d,g)$. Applying Theorem 1.1(i) to
$\mathrm {rank}_{\mathbb {R}} ({d}b_{\Delta }|_X) < 2 \min (d,g)$. Applying Theorem 1.1(i) to ![]() $l = \min (d,g)$, we get an abelian subscheme
$l = \min (d,g)$, we get an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A} \rightarrow S$ (whose relative dimension we denote by
$\mathcal {A} \rightarrow S$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that
$g_{\mathcal {B}}$) such that
for the following.

Case (i). By assumption ![]() $\mathcal {B}$ is either the whole
$\mathcal {B}$ is either the whole ![]() $\mathcal {A}$ or the zero section of
$\mathcal {A}$ or the zero section of ![]() $\mathcal {A} \rightarrow S$. In the former case,
$\mathcal {A} \rightarrow S$. In the former case, ![]() $g_{\mathcal {B}} = g$. But then (9.3) cannot hold. In the latter case,
$g_{\mathcal {B}} = g$. But then (9.3) cannot hold. In the latter case, ![]() $g_{\mathcal {B}} = 0$,
$g_{\mathcal {B}} = 0$, ![]() $p_{\mathcal {B}} = \mathrm {id}_{\mathcal {A}}$, and
$p_{\mathcal {B}} = \mathrm {id}_{\mathcal {A}}$, and ![]() $\iota _{/\mathcal {B}} = \iota$. So
$\iota _{/\mathcal {B}} = \iota$. So ![]() $\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim \iota (X) = d$. But then (9.3) cannot hold.
$\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim \iota (X) = d$. But then (9.3) cannot hold.
Case (ii). If ![]() $\mathcal {B} = \mathcal {A}$, then
$\mathcal {B} = \mathcal {A}$, then ![]() $g = g_{\mathcal {B}}$, and hence (9.3) cannot hold. So
$g = g_{\mathcal {B}}$, and hence (9.3) cannot hold. So ![]() $\mathcal {A}/\mathcal {B} \rightarrow S$ is a non-trivial abelian scheme. Applying the modular map
$\mathcal {A}/\mathcal {B} \rightarrow S$ is a non-trivial abelian scheme. Applying the modular map ![]() $\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (and
$\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (and ![]() $\iota _S \colon S \rightarrow \mathbb {A}_g$) to (9.4), we obtain the following.
$\iota _S \colon S \rightarrow \mathbb {A}_g$) to (9.4), we obtain the following.

It is not hard to check ![]() $(\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$.
$(\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$.
By construction of ![]() $\iota '_{/\mathcal {B},S}$,
$\iota '_{/\mathcal {B},S}$, ![]() $(\iota (\mathcal {A})/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$ is an isotrivial abelian scheme. Taking a splitting of
$(\iota (\mathcal {A})/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$ is an isotrivial abelian scheme. Taking a splitting of ![]() $p'_{\mathcal {B}}$ yields an isotrivial abelian subscheme of
$p'_{\mathcal {B}}$ yields an isotrivial abelian subscheme of ![]() $\iota (\mathcal {A})|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$, which is non-trivial. For each
$\iota (\mathcal {A})|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$, which is non-trivial. For each ![]() $a$ Hodge generic in
$a$ Hodge generic in ![]() $\iota '_{/\mathcal {B},S}(\iota (S))$, we have that
$\iota '_{/\mathcal {B},S}(\iota (S))$, we have that ![]() $\iota _{/\mathcal {B},S}^{'-1}(a)$ is Hodge generic in
$\iota _{/\mathcal {B},S}^{'-1}(a)$ is Hodge generic in ![]() $\iota _S(S)$. But then our hypothesis forces
$\iota _S(S)$. But then our hypothesis forces ![]() $\dim \iota _{/\mathcal {B},S}^{'-1}(a) = 0$. Hence
$\dim \iota _{/\mathcal {B},S}^{'-1}(a) = 0$. Hence ![]() $\iota '_{/\mathcal {B},S}$ is quasi-finite, and so is
$\iota '_{/\mathcal {B},S}$ is quasi-finite, and so is ![]() $\iota '_{/\mathcal {B}}$. So
$\iota '_{/\mathcal {B}}$. So ![]() $\dim (\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = \dim p'_{\mathcal {B}}(\iota (X)) \ge \dim \iota (X) - g_{\mathcal {B}}$
$\dim (\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = \dim p'_{\mathcal {B}}(\iota (X)) \ge \dim \iota (X) - g_{\mathcal {B}}$ ![]() $= d - g_{\mathcal {B}} \ge \min (d,g) - g_{\mathcal {B}}$. This contradicts (9.3) as
$= d - g_{\mathcal {B}} \ge \min (d,g) - g_{\mathcal {B}}$. This contradicts (9.3) as ![]() $\dim (\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$.
$\dim (\iota '_{/\mathcal {B}}\circ p'_{\mathcal {B}})(\iota (X)) = \dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X)$.
Example 9.4 The extra hypotheses (i) or (ii) in Theorem 9.2 are necessary. We illustrate this with an example with ![]() $g = 4$. Consider
$g = 4$. Consider ![]() $\mathfrak {A}_4 \rightarrow \mathbb {A}_4$. Now that
$\mathfrak {A}_4 \rightarrow \mathbb {A}_4$. Now that ![]() $\mathfrak {A}_2 \times \mathfrak {A}_2 \rightarrow \mathbb {A}_2 \times \mathbb {A}_2$ is an abelian scheme of relative dimension
$\mathfrak {A}_2 \times \mathfrak {A}_2 \rightarrow \mathbb {A}_2 \times \mathbb {A}_2$ is an abelian scheme of relative dimension ![]() $4$, it induces canonically the following modular map.
$4$, it induces canonically the following modular map.

By abuse of notation we write ![]() $\mathfrak {A}_2 \times \mathfrak {A}_2$, resp.
$\mathfrak {A}_2 \times \mathfrak {A}_2$, resp. ![]() $\mathbb {A}_2 \times \mathbb {A}_2$, for the image of the morphism on the top, resp. on the bottom.
$\mathbb {A}_2 \times \mathbb {A}_2$, for the image of the morphism on the top, resp. on the bottom.
Let ![]() $S_1$ and
$S_1$ and ![]() $S_2$ be irreducible subvarieties of
$S_2$ be irreducible subvarieties of ![]() $\mathbb {A}_2$, then
$\mathbb {A}_2$, then ![]() $S := S_1 \times S_2 \subseteq \mathbb {A}_2 \times \mathbb {A}_2$. The above diagram implies that
$S := S_1 \times S_2 \subseteq \mathbb {A}_2 \times \mathbb {A}_2$. The above diagram implies that ![]() $\mathfrak {A}_4|_S \rightarrow S$ is the product of the two abelian schemes
$\mathfrak {A}_4|_S \rightarrow S$ is the product of the two abelian schemes ![]() $\mathfrak {A}_2|_{S_1} \rightarrow S_1$ and
$\mathfrak {A}_2|_{S_1} \rightarrow S_1$ and ![]() $\mathfrak {A}_2|_{S_2} \rightarrow S_2$.
$\mathfrak {A}_2|_{S_2} \rightarrow S_2$.
Let ![]() $i \in \{1,2\}$. Let
$i \in \{1,2\}$. Let ![]() $\xi _i$ be a section of
$\xi _i$ be a section of ![]() $\mathfrak {A}_2|_{S_i} \rightarrow S_i$ such that
$\mathfrak {A}_2|_{S_i} \rightarrow S_i$ such that ![]() $\mathbb {Z}\xi _i$ is Zariski dense in
$\mathbb {Z}\xi _i$ is Zariski dense in ![]() $\mathfrak {A}_2|_{S_i}$ for
$\mathfrak {A}_2|_{S_i}$ for ![]() $i \in \{1,2\}$. For the Betti map
$i \in \{1,2\}$. For the Betti map ![]() $b_{\Delta _i} \colon \mathfrak {A}_2|_{\Delta _i} \rightarrow \mathbb {T}^4$, where
$b_{\Delta _i} \colon \mathfrak {A}_2|_{\Delta _i} \rightarrow \mathbb {T}^4$, where ![]() $\Delta _i \subseteq (S_i)^{\mathrm {an}}$ is an open subset, we have
$\Delta _i \subseteq (S_i)^{\mathrm {an}}$ is an open subset, we have ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _i}|_{\xi _i})_{s_i} \le 2\min (\dim S_i, 2)$ for all
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _i}|_{\xi _i})_{s_i} \le 2\min (\dim S_i, 2)$ for all ![]() $s_i \in S_i(\mathbb {C})$.
$s_i \in S_i(\mathbb {C})$.
Now ![]() $\xi = (\xi _1,\xi _2)$ is a section of
$\xi = (\xi _1,\xi _2)$ is a section of ![]() $\mathfrak {A}_4|_S \rightarrow S$ such that
$\mathfrak {A}_4|_S \rightarrow S$ such that ![]() $\mathbb {Z}\xi$ is Zariski dense in
$\mathbb {Z}\xi$ is Zariski dense in ![]() $\mathfrak {A}_4|_S$.
$\mathfrak {A}_4|_S$.
Take ![]() $S_1 = \mathbb {A}_2$ and
$S_1 = \mathbb {A}_2$ and ![]() $S_2$ to be a curve in
$S_2$ to be a curve in ![]() $\mathbb {A}_2$ such that
$\mathbb {A}_2$ such that ![]() $\mathfrak {A}_2|_{S_2}$ has no fixed part (over any finite étale covering of
$\mathfrak {A}_2|_{S_2}$ has no fixed part (over any finite étale covering of ![]() $S_2$), then
$S_2$), then ![]() $\mathfrak {A}_4|_S \rightarrow S$ has no fixed part (over any finite étale covering of
$\mathfrak {A}_4|_S \rightarrow S$ has no fixed part (over any finite étale covering of ![]() $S$) and
$S$) and ![]() $\dim S = 4 = g$. Let
$\dim S = 4 = g$. Let ![]() $\Delta = \Delta _1 \times \Delta _2$. Then the Betti map
$\Delta = \Delta _1 \times \Delta _2$. Then the Betti map ![]() $b_{\Delta }$ equals
$b_{\Delta }$ equals ![]() $(b_{\Delta _1},b_{\Delta _2})$. So
$(b_{\Delta _1},b_{\Delta _2})$. So ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\xi })_s \le \max _{s_1 \in \Delta _1}\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _1}|_{\xi _1})_{s_1}$
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\xi })_s \le \max _{s_1 \in \Delta _1}\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _1}|_{\xi _1})_{s_1}$ ![]() $ + \max _{s_2 \in \Delta _2} \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _2}|_{\xi _2})_{s_2} \le 2 (2 + \dim S_2) = 6 < 8 = 2\min (\dim \xi (S) ,g)$ for any
$ + \max _{s_2 \in \Delta _2} \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta _2}|_{\xi _2})_{s_2} \le 2 (2 + \dim S_2) = 6 < 8 = 2\min (\dim \xi (S) ,g)$ for any ![]() $s \in \Delta$.
$s \in \Delta$.
10. Application to fibered powers
The goal of this section is to prove (a generalized form of) Theorem 1.3.
Recall the setting up. Let ![]() $S$ be an irreducible subvariety over
$S$ be an irreducible subvariety over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g_0 \ge 1$. We have the following modular map (4.1).
$g_0 \ge 1$. We have the following modular map (4.1).

Let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$ such that
$\mathcal {A}$ such that ![]() $\pi _S(X) = S$.
$\pi _S(X) = S$.
For any integer ![]() $m \ge 1$, set
$m \ge 1$, set ![]() $\mathcal {A}^{[m]} = \mathcal {A}\times _S \cdots \times _S \mathcal {A}$ (
$\mathcal {A}^{[m]} = \mathcal {A}\times _S \cdots \times _S \mathcal {A}$ (![]() $m$-copies),
$m$-copies), ![]() $X^{[m]} = X \times _S \cdots \times _S X$ (
$X^{[m]} = X \times _S \cdots \times _S X$ (![]() $m$-copies) and
$m$-copies) and ![]() $b^{[m]}_{\Delta } = (b_{\Delta }, \ldots , b_{\Delta }) \colon \mathcal {A}^{[m]}_{\Delta } \rightarrow \mathbb {T}^{2mg}$.
$b^{[m]}_{\Delta } = (b_{\Delta }, \ldots , b_{\Delta }) \colon \mathcal {A}^{[m]}_{\Delta } \rightarrow \mathbb {T}^{2mg}$.
The modular map ![]() $\iota$ induces a morphism
$\iota$ induces a morphism ![]() $\iota ^{[m]} \colon \mathcal {A}^{[m]} \rightarrow \mathfrak {A}_{mg_0}$. Set
$\iota ^{[m]} \colon \mathcal {A}^{[m]} \rightarrow \mathfrak {A}_{mg_0}$. Set ![]() $X^{[m]}_{\iota } = \iota ^{[m]}(X^{[m]})$. It is a closed subvariety of
$X^{[m]}_{\iota } = \iota ^{[m]}(X^{[m]})$. It is a closed subvariety of ![]() $\iota (X)\times _{\iota _S(S)} \cdots \times _{\iota _S(S)}\iota (X)$, which may be proper.
$\iota (X)\times _{\iota _S(S)} \cdots \times _{\iota _S(S)}\iota (X)$, which may be proper.
Let ![]() $\mathscr {D}_m^{\mathcal {A}} \colon \mathcal {A}^{[m+1]} \rightarrow \mathcal {A}^{[m]}$ be the
$\mathscr {D}_m^{\mathcal {A}} \colon \mathcal {A}^{[m+1]} \rightarrow \mathcal {A}^{[m]}$ be the ![]() $m$th Faltings–Zhang map fiberwise defined by
$m$th Faltings–Zhang map fiberwise defined by ![]() $(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$. In the particular case where
$(P_0, P_1, \ldots , P_m) \mapsto (P_1 - P_0, \ldots , P_m - P_0)$. In the particular case where ![]() $\mathcal {A} \rightarrow S$ is
$\mathcal {A} \rightarrow S$ is ![]() $\mathfrak {A}_{g_0} \rightarrow \mathbb {A}_{g_0}$, abbreviate
$\mathfrak {A}_{g_0} \rightarrow \mathbb {A}_{g_0}$, abbreviate ![]() $\mathscr {D}_m = \mathscr {D}_m^{\mathfrak {A}_{g_0}}$. Then
$\mathscr {D}_m = \mathscr {D}_m^{\mathfrak {A}_{g_0}}$. Then ![]() $\iota ^{[m]} \circ \mathscr {D}_m^{\mathcal {A}} = \mathscr {D}_m \circ \iota ^{[m+1]}$.
$\iota ^{[m]} \circ \mathscr {D}_m^{\mathcal {A}} = \mathscr {D}_m \circ \iota ^{[m+1]}$.
Theorem 10.1 Assume that ![]() $X$ satisfies the following conditions:
$X$ satisfies the following conditions:
(a) we have
 $\dim X > \dim S$;
$\dim X > \dim S$;(b) the subvariety
 $X$ is not contained in the translate of any proper abelian subscheme of
$X$ is not contained in the translate of any proper abelian subscheme of  $\mathcal {A} \rightarrow S$ by a torsion section;
$\mathcal {A} \rightarrow S$ by a torsion section;(c) we have
 $X + \mathcal {A}' \not \subseteq X$ for any non-isotrivial abelian subscheme
$X + \mathcal {A}' \not \subseteq X$ for any non-isotrivial abelian subscheme  $\mathcal {A}'$ of
$\mathcal {A}'$ of  $\mathcal {A} \rightarrow S$.
$\mathcal {A} \rightarrow S$.
Then for each ![]() $t \ge 0$, we have the following:
$t \ge 0$, we have the following:
(i)
 $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{X^{[m]}}) \ge 2(\dim X_{\iota }^{[m]} - t)$ for all
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{X^{[m]}}) \ge 2(\dim X_{\iota }^{[m]} - t)$ for all  $m \ge \dim S - t$.
$m \ge \dim S - t$.(ii)
 $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]}}) \ge 2(\dim \mathscr {D}_m(X_{\iota }^{[m+1]}) - t)$ for all
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]}}) \ge 2(\dim \mathscr {D}_m(X_{\iota }^{[m+1]}) - t)$ for all  $m \ge \dim X - t$.
$m \ge \dim X - t$.
Before proceeding to the proof, let us fix some notation. Set ![]() $d = \dim X - \dim S > 0$. For any
$d = \dim X - \dim S > 0$. For any ![]() $m \ge 1$, we have
$m \ge 1$, we have ![]() $\dim X^{[m]} - \dim S = md$. In particular,
$\dim X^{[m]} - \dim S = md$. In particular, ![]() $\dim X^{[m]}_{\iota } \le \dim X^{[m]} = md + \dim S$.
$\dim X^{[m]}_{\iota } \le \dim X^{[m]} = md + \dim S$.
For notation let ![]() $\mathcal {A}_{X^{[m]}}$ be the translate of an abelian subscheme of
$\mathcal {A}_{X^{[m]}}$ be the translate of an abelian subscheme of ![]() $\mathcal {A}^{[m]} \rightarrow S$ by a torsion section which contains
$\mathcal {A}^{[m]} \rightarrow S$ by a torsion section which contains ![]() $X^{[m]}$, minimal for this property. Hypothesis (b) then implies
$X^{[m]}$, minimal for this property. Hypothesis (b) then implies ![]() $\mathcal {A}_{X^{[1]}} = \mathcal {A}$. Hence by hypothesis (a) on
$\mathcal {A}_{X^{[1]}} = \mathcal {A}$. Hence by hypothesis (a) on ![]() $X$, we have
$X$, we have ![]() $\mathcal {A}_{X^{[m]}} = \mathcal {A}^{[m]}$ for all
$\mathcal {A}_{X^{[m]}} = \mathcal {A}^{[m]}$ for all ![]() $m \ge 1$.
$m \ge 1$.
Proof of Theorem 10.1(i) Suppose ![]() $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{X^{[m]}}) < 2(\dim X_{\iota }^{[m]} - t)$. Then by Theorem 1.1, there exists an abelian subscheme
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{X^{[m]}}) < 2(\dim X_{\iota }^{[m]} - t)$. Then by Theorem 1.1, there exists an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}^{[m]} \rightarrow S$ (whose relative dimension we denote by
$\mathcal {A}^{[m]} \rightarrow S$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that
$g_{\mathcal {B}}$) such that
for the following diagram.

The following fact will be proved in Appendix B. There exists an isogeny
such that ![]() $\rho (\mathcal {B}) = \mathcal {B}_1 \times _S \cdots \times _S \mathcal {B}_m$ for some abelian subschemes
$\rho (\mathcal {B}) = \mathcal {B}_1 \times _S \cdots \times _S \mathcal {B}_m$ for some abelian subschemes ![]() $\mathcal {B}_1,\ldots ,\mathcal {B}_m$ of
$\mathcal {B}_1,\ldots ,\mathcal {B}_m$ of ![]() $\mathcal {A}$. Moreover, we may assume that
$\mathcal {A}$. Moreover, we may assume that ![]() $\rho$ satisfies the following property:
$\rho$ satisfies the following property: ![]() $q_1 \circ \rho = \rho _1 \circ q_1$ for some isogeny
$q_1 \circ \rho = \rho _1 \circ q_1$ for some isogeny ![]() $\rho _1 \colon \mathcal {A}\rightarrow \mathcal {A}$, where
$\rho _1 \colon \mathcal {A}\rightarrow \mathcal {A}$, where ![]() $q_1 \colon \mathcal {A}^{[m]} \rightarrow \mathcal {A}$ is the projection to the first factor.
$q_1 \colon \mathcal {A}^{[m]} \rightarrow \mathcal {A}$ is the projection to the first factor.
Lemma 10.2 ![]() $\mathcal {B}_i \rightarrow S$ is non-isotrivial for each
$\mathcal {B}_i \rightarrow S$ is non-isotrivial for each ![]() $i \in \{1,\ldots , m\}$.
$i \in \{1,\ldots , m\}$.
We will see that Lemma 10.2 implies the following naive lower bound for ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]})$:
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]})$:
Let us finish the proof by assuming Lemma 10.2 and hence (10.4). We have
 \begin{align*} g_{\mathcal{B}} - (\dim X^{[m]}_{\iota} - \dim (\iota_{/\mathcal{B}} \circ p_{\mathcal{B}})(X^{[m]})) &= g_{\mathcal{B}} + \dim (\iota_{/\mathcal{B}} \circ p_{\mathcal{B}})(X^{[m]}) - \dim X^{[m]}_{\iota} \\ & \ge m(d+1) - (md+\dim S) \\ & \ge m - \dim S. \end{align*}
\begin{align*} g_{\mathcal{B}} - (\dim X^{[m]}_{\iota} - \dim (\iota_{/\mathcal{B}} \circ p_{\mathcal{B}})(X^{[m]})) &= g_{\mathcal{B}} + \dim (\iota_{/\mathcal{B}} \circ p_{\mathcal{B}})(X^{[m]}) - \dim X^{[m]}_{\iota} \\ & \ge m(d+1) - (md+\dim S) \\ & \ge m - \dim S. \end{align*} This contradicts (10.1) for ![]() $m \ge \dim S - t$. So we are done.
$m \ge \dim S - t$. So we are done.
Proof of Lemma 10.2 Suppose ![]() $\mathcal {B}_{i_0} \rightarrow S$ is isotrivial for some
$\mathcal {B}_{i_0} \rightarrow S$ is isotrivial for some ![]() $i_0$. Note that
$i_0$. Note that ![]() $(\mathcal {A}^{[m]}/\mathcal {B})|_{\iota _{/\mathcal {B},S}^{-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{-1}(a)$ is an isotrivial abelian scheme for each
$(\mathcal {A}^{[m]}/\mathcal {B})|_{\iota _{/\mathcal {B},S}^{-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{-1}(a)$ is an isotrivial abelian scheme for each ![]() $a$. Hence
$a$. Hence ![]() $\mathcal {A}/\mathcal {B}_{i_0}$, being an abelian subscheme of
$\mathcal {A}/\mathcal {B}_{i_0}$, being an abelian subscheme of ![]() $\mathcal {A}^{[m]}/\mathcal {B}$ via the decomposition (10.3), is isotrivial when restricted to
$\mathcal {A}^{[m]}/\mathcal {B}$ via the decomposition (10.3), is isotrivial when restricted to ![]() ${\iota _{/\mathcal {B},S}^{-1}(a)}$. Thus
${\iota _{/\mathcal {B},S}^{-1}(a)}$. Thus ![]() $\mathcal {A}|_{\iota _{/\mathcal {B},S}^{-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{-1}(a)$ is isotrivial. So by the discussion at the end of §2,
$\mathcal {A}|_{\iota _{/\mathcal {B},S}^{-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{-1}(a)$ is isotrivial. So by the discussion at the end of §2, ![]() $\dim \iota _S(\iota _{/\mathcal {B},S}^{-1}(a)) = 0$, where
$\dim \iota _S(\iota _{/\mathcal {B},S}^{-1}(a)) = 0$, where ![]() $\iota _S \colon S \rightarrow \mathbb {A}_{g_0}$ is the modular map for
$\iota _S \colon S \rightarrow \mathbb {A}_{g_0}$ is the modular map for ![]() $\mathcal {A} \rightarrow S$.
$\mathcal {A} \rightarrow S$.
Applying the modular map ![]() $\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_{g_0}$ (and
$\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_{g_0}$ (and ![]() $\iota _S \colon S \rightarrow \mathbb {A}_{g_0}$) to (10.2), we obtain (denote by
$\iota _S \colon S \rightarrow \mathbb {A}_{g_0}$) to (10.2), we obtain (denote by ![]() $\mathcal {A}^{[m]}_{\iota } = \iota ^{[m]}(\mathcal {A}^{[m]})$) the following diagram.
$\mathcal {A}^{[m]}_{\iota } = \iota ^{[m]}(\mathcal {A}^{[m]})$) the following diagram.

The previous paragraph implies that ![]() $\dim (\iota '_{/\mathcal {B},S})^{-1}(a') =0$ for each
$\dim (\iota '_{/\mathcal {B},S})^{-1}(a') =0$ for each ![]() $a'$. Thus
$a'$. Thus ![]() $\iota '_{/\mathcal {B},S}$ is generically finite, and so is
$\iota '_{/\mathcal {B},S}$ is generically finite, and so is ![]() $\iota '_{/\mathcal {B}}$.
$\iota '_{/\mathcal {B}}$.
It is not hard to check that ![]() $(\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X^{[m]}) = (\iota '_{/\mathcal {B}} \circ p_{\iota ^{[m]}(\mathcal {B})})(X^{[m]}_{\iota })$. So
$(\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X^{[m]}) = (\iota '_{/\mathcal {B}} \circ p_{\iota ^{[m]}(\mathcal {B})})(X^{[m]}_{\iota })$. So
where the last inequality holds because ![]() $\iota ^{[m]}(\mathcal {B}) \rightarrow \iota _S(S)$ has relative dimension
$\iota ^{[m]}(\mathcal {B}) \rightarrow \iota _S(S)$ has relative dimension ![]() $g_{\mathcal {B}}$. This contradicts (10.1) since
$g_{\mathcal {B}}$. This contradicts (10.1) since ![]() $t \ge 0$.
$t \ge 0$.
Proof of (10.4) Use the notation in (10.2). Take a point ![]() $s \in S$ such that
$s \in S$ such that ![]() $(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}) \rightarrow \pi '((\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$ is flat over
$(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}) \rightarrow \pi '((\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$ is flat over ![]() $s' := \iota _{/\mathcal {B},S}(s)$. Then
$s' := \iota _{/\mathcal {B},S}(s)$. Then ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}) = \dim \pi '((\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}) = \dim \pi '((\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$ ![]() $+ \dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]})) \ge \dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$. So it suffices to prove the lower bound for
$+ \dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]})) \ge \dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$. So it suffices to prove the lower bound for ![]() $\dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$.
$\dim ((\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$.
On the other hand ![]() $(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(\mathcal {A}^{[m]}_s \cap X^{[m]}) \subseteq (\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$ by the commutative diagram (10.2). Hence it suffices to prove the lower bound for
$(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(\mathcal {A}^{[m]}_s \cap X^{[m]}) \subseteq (\pi ')^{-1}(s') \cap (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X^{[m]}))$ by the commutative diagram (10.2). Hence it suffices to prove the lower bound for ![]() $\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(\mathcal {A}^{[m]}_s \cap X^{[m]})$. But
$\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(\mathcal {A}^{[m]}_s \cap X^{[m]})$. But ![]() $p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]})$ is contained in one fiber of
$p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]})$ is contained in one fiber of ![]() $\pi _{/\mathcal {B}}$. So
$\pi _{/\mathcal {B}}$. So ![]() $\iota _{\mathcal {B}}|_{p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]})}$ is an isomorphism. So
$\iota _{\mathcal {B}}|_{p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]})}$ is an isomorphism. So
Thus it suffices to prove the lower bound for ![]() $\dim p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]}) = \dim p_{\mathcal {B}}(X_s^m)$.
$\dim p_{\mathcal {B}}(\mathcal {A}^{[m]}_s \cap X^{[m]}) = \dim p_{\mathcal {B}}(X_s^m)$.
The isogeny ![]() $\rho$ in (10.3) gives an isogeny
$\rho$ in (10.3) gives an isogeny ![]() $\mathcal {A}_s^m \rightarrow \mathcal {A}_s^m$, which we still denote by
$\mathcal {A}_s^m \rightarrow \mathcal {A}_s^m$, which we still denote by ![]() $\rho$ by abuse of notation. Set for simplicity
$\rho$ by abuse of notation. Set for simplicity ![]() $B = \mathcal {B}_s$,
$B = \mathcal {B}_s$, ![]() $B_i = (\mathcal {B}_i)_s$ for
$B_i = (\mathcal {B}_i)_s$ for ![]() $i \in \{1,\ldots ,m\}$. Denote by
$i \in \{1,\ldots ,m\}$. Denote by ![]() $p_i \colon \mathcal {A}_s \rightarrow \mathcal {A}_s/B_i$ the quotient. Then by the last paragraph, to prove (10.4) it suffices to prove
$p_i \colon \mathcal {A}_s \rightarrow \mathcal {A}_s/B_i$ the quotient. Then by the last paragraph, to prove (10.4) it suffices to prove
 \begin{equation} \dim (p_1,\ldots,p_m)(\rho(X_s^m)) \ge m(d+1) - \sum_{i=1}^m \dim B_i. \end{equation}
\begin{equation} \dim (p_1,\ldots,p_m)(\rho(X_s^m)) \ge m(d+1) - \sum_{i=1}^m \dim B_i. \end{equation} By hypothesis (c) on ![]() $X$, for a very general
$X$, for a very general ![]() $s$ we have
$s$ we have ![]() $X_s + \mathcal {A}'_s \not \subseteq X_s$ for any non-isotrivial abelian subscheme
$X_s + \mathcal {A}'_s \not \subseteq X_s$ for any non-isotrivial abelian subscheme ![]() $\mathcal {A}'$ of
$\mathcal {A}'$ of ![]() $\mathcal {A}$. In particular,
$\mathcal {A}$. In particular, ![]() $X_s + B_i \not \subseteq X_s$ by Lemma 10.2. Thus
$X_s + B_i \not \subseteq X_s$ by Lemma 10.2. Thus
Let us prove (10.6) for such an ![]() $s$ by induction on
$s$ by induction on ![]() $m$. For
$m$. For ![]() $m = 1$, this is precisely (10.7). For general
$m = 1$, this is precisely (10.7). For general ![]() $m \ge 2$, denote by
$m \ge 2$, denote by ![]() $q_1 \colon \mathcal {A}_s^m \rightarrow \mathcal {A}_s$ the projection to the first factor. Recall that
$q_1 \colon \mathcal {A}_s^m \rightarrow \mathcal {A}_s$ the projection to the first factor. Recall that ![]() $q_1 \circ \rho = \rho _1 \circ q_1$ for some isogeny
$q_1 \circ \rho = \rho _1 \circ q_1$ for some isogeny ![]() $\rho _1 \colon \mathcal {A}_s \rightarrow \mathcal {A}_s$; see below (10.3). For each
$\rho _1 \colon \mathcal {A}_s \rightarrow \mathcal {A}_s$; see below (10.3). For each ![]() $z \in \rho _1(X_s)$, we have
$z \in \rho _1(X_s)$, we have
 \begin{align*} \rho(X_s^m) \cap q_1^{-1}(z) & = \rho \left(X_s^m \cap \rho^{-1}(q_1^{-1}(z)) \right) = \rho \left(X_s^m \cap (q_1\circ \rho)^{-1}(z) \right) \\ & = \rho \left(X_s^m \cap (\rho_1\circ q_1)^{-1}(z) \right) = \rho \left(X_s^m \cap q_1^{-1}(\rho_1^{-1}(z)) \right) \\ & = \rho \left(X_s^m \cap \{\rho_1^{-1}(z)\} \times \mathcal{A}_s^{m-1} \right) = \bigcup_{z' \in X_s \cap \rho_1^{-1}(z)} \rho(\{z'\} \times X_s^{m-1}). \end{align*}
\begin{align*} \rho(X_s^m) \cap q_1^{-1}(z) & = \rho \left(X_s^m \cap \rho^{-1}(q_1^{-1}(z)) \right) = \rho \left(X_s^m \cap (q_1\circ \rho)^{-1}(z) \right) \\ & = \rho \left(X_s^m \cap (\rho_1\circ q_1)^{-1}(z) \right) = \rho \left(X_s^m \cap q_1^{-1}(\rho_1^{-1}(z)) \right) \\ & = \rho \left(X_s^m \cap \{\rho_1^{-1}(z)\} \times \mathcal{A}_s^{m-1} \right) = \bigcup_{z' \in X_s \cap \rho_1^{-1}(z)} \rho(\{z'\} \times X_s^{m-1}). \end{align*}
Thus each irreducible component of a non-empty fiber of ![]() $q_1|_{\rho (X_s^m)}$ is a translate of
$q_1|_{\rho (X_s^m)}$ is a translate of ![]() $\rho '_1(X_s^{m-1})$ for the isogeny
$\rho '_1(X_s^{m-1})$ for the isogeny ![]() $\rho '_1 \colon \mathcal {A}_s^{m-1} \rightarrow \mathcal {A}_s^{m-1}$ obtained from
$\rho '_1 \colon \mathcal {A}_s^{m-1} \rightarrow \mathcal {A}_s^{m-1}$ obtained from ![]() $\rho |_{\{0\}\times \mathcal {A}_s^{m-1}}$.
$\rho |_{\{0\}\times \mathcal {A}_s^{m-1}}$.
We wish to apply the induction hypothesis to ![]() $\rho '_1(X_s^{m-1})$ and the quotient morphism
$\rho '_1(X_s^{m-1})$ and the quotient morphism ![]() $(p_2,\ldots ,p_m)$. However we cannot directly do this because
$(p_2,\ldots ,p_m)$. However we cannot directly do this because ![]() $\rho '_1$ may not satisfy the extra property that
$\rho '_1$ may not satisfy the extra property that ![]() $q_1 \circ \rho '_1$ and
$q_1 \circ \rho '_1$ and ![]() $q_1$ differ from an isogeny
$q_1$ differ from an isogeny ![]() $\mathcal {A}_s \rightarrow \mathcal {A}_s$.
$\mathcal {A}_s \rightarrow \mathcal {A}_s$.
To solve this problem, let ![]() $\mathcal {B}_1^{\perp }$ be the neutral component of
$\mathcal {B}_1^{\perp }$ be the neutral component of ![]() $\rho ^{-1}(\epsilon _S\times _S \mathcal {B}_2 \times _S \cdots \times _S \mathcal {B}_m) \subseteq \rho ^{-1}(\epsilon _S \times _S \mathcal {A}^{[m-1]})$, where
$\rho ^{-1}(\epsilon _S\times _S \mathcal {B}_2 \times _S \cdots \times _S \mathcal {B}_m) \subseteq \rho ^{-1}(\epsilon _S \times _S \mathcal {A}^{[m-1]})$, where ![]() $\epsilon _S$ is the zero section of
$\epsilon _S$ is the zero section of ![]() $\mathcal {A} \rightarrow S$. Apply (10.3) to
$\mathcal {A} \rightarrow S$. Apply (10.3) to ![]() $\mathcal {B}_1^\perp \subseteq \mathcal {A}^{[m-1]}$. We thus obtain an isogeny
$\mathcal {B}_1^\perp \subseteq \mathcal {A}^{[m-1]}$. We thus obtain an isogeny
such that ![]() $\rho '(\mathcal {B}_1^\perp ) = \mathcal {B}'_2 \times _S \cdots \times _S \mathcal {B}'_m$ and that
$\rho '(\mathcal {B}_1^\perp ) = \mathcal {B}'_2 \times _S \cdots \times _S \mathcal {B}'_m$ and that ![]() $q_1 \circ \rho ' = \rho _2 \circ q_1$ for some isogeny
$q_1 \circ \rho ' = \rho _2 \circ q_1$ for some isogeny ![]() $\rho _2 \colon \mathcal {A} \rightarrow \mathcal {A}$. As
$\rho _2 \colon \mathcal {A} \rightarrow \mathcal {A}$. As ![]() $\rho '_1 \colon \mathcal {A}_s^{m-1} \rightarrow \mathcal {A}_s^{m-1}$ is obtained from
$\rho '_1 \colon \mathcal {A}_s^{m-1} \rightarrow \mathcal {A}_s^{m-1}$ is obtained from ![]() $\rho |_{\{0\}\times \mathcal {A}_s^{m-1}}$, we have
$\rho |_{\{0\}\times \mathcal {A}_s^{m-1}}$, we have
where ![]() $p_i' \colon \mathcal {A}_s \rightarrow \mathcal {A}_s/(\mathcal {B}'_i)_s$ is the quotient morphism.
$p_i' \colon \mathcal {A}_s \rightarrow \mathcal {A}_s/(\mathcal {B}'_i)_s$ is the quotient morphism.
Lemma 10.2 applies to ![]() $\mathcal {B}'_i$ since
$\mathcal {B}'_i$ since ![]() $\mathcal {A}/\mathcal {B}'_i$ is still an abelian subscheme of
$\mathcal {A}/\mathcal {B}'_i$ is still an abelian subscheme of ![]() $\mathcal {A}^{[m]}/\mathcal {B}$. So
$\mathcal {A}^{[m]}/\mathcal {B}$. So ![]() $\mathcal {B}'_i \rightarrow S$ is non-isotrivial. Hence we can apply the induction hypothesis to
$\mathcal {B}'_i \rightarrow S$ is non-isotrivial. Hence we can apply the induction hypothesis to ![]() $\rho '(X_s^{m-1})$ and
$\rho '(X_s^{m-1})$ and ![]() $(p_2',\ldots ,p_m')$. So
$(p_2',\ldots ,p_m')$. So
 \[ \dim(p_2',\ldots,p_m')(\rho'(X_s^{m-1})) \ge (m-1)(d+1) - \sum_{i=2}^m \dim (\mathcal{B}'_i)_s = (m-1)(d+1) - \sum_{i=2}^m \dim B_i. \]
\[ \dim(p_2',\ldots,p_m')(\rho'(X_s^{m-1})) \ge (m-1)(d+1) - \sum_{i=2}^m \dim (\mathcal{B}'_i)_s = (m-1)(d+1) - \sum_{i=2}^m \dim B_i. \]
Denote by ![]() $\bar {q}_1 \colon \mathcal {A}_s/B_1 \times \cdots \mathcal {A}_s/B_m \rightarrow \mathcal {A}_s/B_1$ the projection to the first factor. Then we have
$\bar {q}_1 \colon \mathcal {A}_s/B_1 \times \cdots \mathcal {A}_s/B_m \rightarrow \mathcal {A}_s/B_1$ the projection to the first factor. Then we have ![]() $\bar {q}_1((p_1,\ldots ,p_m)(\rho (X_s^m))) = p_1(q_1(\rho (X_s^m))) = p_1(q_1\circ \rho (X_s^m))$
$\bar {q}_1((p_1,\ldots ,p_m)(\rho (X_s^m))) = p_1(q_1(\rho (X_s^m))) = p_1(q_1\circ \rho (X_s^m))$ ![]() $ = p_1(\rho _1\circ q_1(X_s^m)) \!=\! p_1(\rho _1(X_s))$. But
$ = p_1(\rho _1\circ q_1(X_s^m)) \!=\! p_1(\rho _1(X_s))$. But ![]() $\dim p_1(\rho _1(X_s)) \ge d - (\dim B_1 - 1)$ by a similar argument used to prove (10.7). Hence by the fiber dimension theorem we have
$\dim p_1(\rho _1(X_s)) \ge d - (\dim B_1 - 1)$ by a similar argument used to prove (10.7). Hence by the fiber dimension theorem we have
 \begin{align*} \dim (p_1,\ldots,p_m)(\rho(X_s^m)) & \ge \left(d - (\dim B_1 - 1)\right) + \biggl((m-1)(d+1) - \sum_{i=2}^m \dim B_i\biggr) \\ & = m(d+1) - \sum_{i=1}^m\dim B_i. \end{align*}
\begin{align*} \dim (p_1,\ldots,p_m)(\rho(X_s^m)) & \ge \left(d - (\dim B_1 - 1)\right) + \biggl((m-1)(d+1) - \sum_{i=2}^m \dim B_i\biggr) \\ & = m(d+1) - \sum_{i=1}^m\dim B_i. \end{align*}This finishes the proof.
Proof of Theorem 10.1(ii) The proof of part (ii) is similar. Let us sketch it.
We reduce (ii) to the case where ![]() $X$ contains the zero section of
$X$ contains the zero section of ![]() $\pi _{\mathcal {A}} \colon \mathcal {A} \rightarrow S$. Indeed, up to replacing
$\pi _{\mathcal {A}} \colon \mathcal {A} \rightarrow S$. Indeed, up to replacing ![]() $S$ by a Zariski open subset (which does not change the generic Betti rank in question) we can take a section
$S$ by a Zariski open subset (which does not change the generic Betti rank in question) we can take a section ![]() $\sigma \colon S \rightarrow X$ of
$\sigma \colon S \rightarrow X$ of ![]() $\pi _{\mathcal {A}}|_X$. Then
$\pi _{\mathcal {A}}|_X$. Then ![]() $\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]}) = \mathscr {D}_m^{\mathcal {A}}((X-\sigma (S))^{[m+1]})$ for all
$\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]}) = \mathscr {D}_m^{\mathcal {A}}((X-\sigma (S))^{[m+1]})$ for all ![]() $m \ge 1$. It suffices then to replace
$m \ge 1$. It suffices then to replace ![]() $X$ by
$X$ by ![]() $X-\sigma (S)$.
$X-\sigma (S)$.
Set ![]() $Y := \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$. We have
$Y := \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$. We have ![]() $Y \supseteq X^{[m]}$ because
$Y \supseteq X^{[m]}$ because ![]() $X^{[m]} = \mathscr {D}_m^{\mathcal {A}}(0_S \times _S X \times _S \cdots \times _S X) \subseteq \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$. Let
$X^{[m]} = \mathscr {D}_m^{\mathcal {A}}(0_S \times _S X \times _S \cdots \times _S X) \subseteq \mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})$. Let ![]() $\mathcal {A}_Y$ be the translate of an abelian subscheme of
$\mathcal {A}_Y$ be the translate of an abelian subscheme of ![]() $\mathcal {A}^{[m]} \rightarrow S$ by a torsion section which contains
$\mathcal {A}^{[m]} \rightarrow S$ by a torsion section which contains ![]() $Y$, minimal for this property. Then
$Y$, minimal for this property. Then ![]() $\mathcal {A}_Y = \mathcal {A}^{[m]}$ since
$\mathcal {A}_Y = \mathcal {A}^{[m]}$ since ![]() $\mathcal {A}_{X^{[m]}} = \mathcal {A}$.
$\mathcal {A}_{X^{[m]}} = \mathcal {A}$.
Suppose ![]() $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y) < 2(\dim \iota ^{[m]}(Y) - t)$. Applying Theorem 1.1(i) to
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y) < 2(\dim \iota ^{[m]}(Y) - t)$. Applying Theorem 1.1(i) to ![]() $Y$, we get an abelian subscheme
$Y$, we get an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}^{[m]} \rightarrow S$ (whose relative dimension we denote by
$\mathcal {A}^{[m]} \rightarrow S$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that for the map
$g_{\mathcal {B}}$) such that for the map ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ as in (10.2), we have
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ as in (10.2), we have ![]() $\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(Y) < \dim \iota ^{[m]}(Y) - t - g_{\mathcal {B}}$. This
$\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(Y) < \dim \iota ^{[m]}(Y) - t - g_{\mathcal {B}}$. This ![]() $\mathcal {B}$ is different from the one in the proof of part (i).
$\mathcal {B}$ is different from the one in the proof of part (i).
Under a possibly new decomposition (up to isogeny) ![]() $\mathcal {A}^{[m]} \simeq \mathcal {A} \times _S \cdots \times _S \mathcal {A}$ (
$\mathcal {A}^{[m]} \simeq \mathcal {A} \times _S \cdots \times _S \mathcal {A}$ (![]() $m$-copies), we may write
$m$-copies), we may write ![]() $\mathcal {B} = \mathcal {B}_1 \times _S \ldots \times _S \mathcal {B}_m$ for some abelian subschemes
$\mathcal {B} = \mathcal {B}_1 \times _S \ldots \times _S \mathcal {B}_m$ for some abelian subschemes ![]() $\mathcal {B}_1,\ldots ,\mathcal {B}_m$ of
$\mathcal {B}_1,\ldots ,\mathcal {B}_m$ of ![]() $\mathcal {A}$. One can show that
$\mathcal {A}$. One can show that ![]() $\mathcal {B}_i \rightarrow S$ is non-isotrivial for each
$\mathcal {B}_i \rightarrow S$ is non-isotrivial for each ![]() $i \in \{1,\ldots , m\}$: indeed it suffices to take a verbalized copy of the proof of Lemma 10.2 with
$i \in \{1,\ldots , m\}$: indeed it suffices to take a verbalized copy of the proof of Lemma 10.2 with ![]() $X^{[m]}$ replaced by
$X^{[m]}$ replaced by ![]() $Y$ and
$Y$ and ![]() $X^{[m]}_{\iota }$ replace by
$X^{[m]}_{\iota }$ replace by ![]() $\iota ^{[m]}(Y)$.
$\iota ^{[m]}(Y)$.
Then (10.4) holds for this new ![]() $\mathcal {B}$. Thus
$\mathcal {B}$. Thus
 \begin{align*} & g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(Y) - \dim Y \\ & \quad \ge g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(Y) - ((m+1)d + \dim S) \\ & \quad \ge g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(X^{[m]}) - (m+1)d - \dim S + mr \quad \text{ since $X^{[m]} \subseteq Y$} \\ & \quad \ge t + m - d - \dim S \quad \text{ by \eqref{eqn39} and \eqref{eqn40}} \\ & \quad = t + m - \dim X. \end{align*}
\begin{align*} & g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(Y) - \dim Y \\ & \quad \ge g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(Y) - ((m+1)d + \dim S) \\ & \quad \ge g_{\mathcal{B}} + t + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(X^{[m]}) - (m+1)d - \dim S + mr \quad \text{ since $X^{[m]} \subseteq Y$} \\ & \quad \ge t + m - d - \dim S \quad \text{ by \eqref{eqn39} and \eqref{eqn40}} \\ & \quad = t + m - \dim X. \end{align*}
This contradicts ![]() $\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(Y) < \dim \iota ^{[m]}(Y) - t - g_{\mathcal {B}}$ when
$\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(Y) < \dim \iota ^{[m]}(Y) - t - g_{\mathcal {B}}$ when ![]() $m \ge \dim X - t$.
$m \ge \dim X - t$.
So ![]() $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y) \ge 2(\dim \iota ^{[m]}(Y) - t)$ when
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y) \ge 2(\dim \iota ^{[m]}(Y) - t)$ when ![]() $m \ge \dim X - t$. So the conclusion follows because
$m \ge \dim X - t$. So the conclusion follows because ![]() $\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})}) = \mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y)$ and
$\mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_{\mathscr {D}_m^{\mathcal {A}}(X^{[m+1]})}) = \mathrm {rank}_{\mathbb {R}}(\mathrm {d}b_{\Delta }^{[m]}|_Y)$ and ![]() $\dim \mathscr {D}_m(X^{[m+1]}_{\iota }) = \dim (\iota ^{[m]} \circ \mathscr {D}_m^{\mathcal {A}})(X^{[m+1]}) = \dim \iota ^{[m]}(Y)$.
$\dim \mathscr {D}_m(X^{[m+1]}_{\iota }) = \dim (\iota ^{[m]} \circ \mathscr {D}_m^{\mathcal {A}})(X^{[m+1]}) = \dim \iota ^{[m]}(Y)$.
11. Link with relative Manin–Mumford
In this section, we discuss about the relative Manin–Mumford conjecture. It is closely related to ![]() $X^{\mathrm {deg}}(1)$.
$X^{\mathrm {deg}}(1)$.
Let ![]() $S$ be an irreducible variety over
$S$ be an irreducible variety over ![]() $\mathbb {C}$, and let
$\mathbb {C}$, and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g \ge 1$. Denote by
$g \ge 1$. Denote by ![]() $\mathcal {A}_{\mathrm {tor}}$ the set of points
$\mathcal {A}_{\mathrm {tor}}$ the set of points ![]() $x \in \mathcal {A}(\mathbb {C})$ such that
$x \in \mathcal {A}(\mathbb {C})$ such that ![]() $[N]x$ lies in the zero section of
$[N]x$ lies in the zero section of ![]() $\mathcal {A} \rightarrow S$ for some integer
$\mathcal {A} \rightarrow S$ for some integer ![]() $N$. In other words,
$N$. In other words, ![]() $x$ is a torsion point in its fiber.
$x$ is a torsion point in its fiber.
Let ![]() $X$ be a closed irreducible subvariety such that
$X$ be a closed irreducible subvariety such that ![]() $\pi _S(X) = S$. Denote by
$\pi _S(X) = S$. Denote by ![]() $\mathcal {A}_X$ the translate of an abelian subscheme of
$\mathcal {A}_X$ the translate of an abelian subscheme of ![]() $\mathcal {A} \rightarrow S$ by a torsion section which contains
$\mathcal {A} \rightarrow S$ by a torsion section which contains ![]() $X$, minimal for this property.
$X$, minimal for this property.
Relative Manin–Mumford Conjecture. If ![]() $(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then
$(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then ![]() $\operatorname {codim}_{\mathcal {A}_X}(X) \le \dim S$.
$\operatorname {codim}_{\mathcal {A}_X}(X) \le \dim S$.
Conjecture 11.1 Assume ![]() $S$,
$S$, ![]() $\pi _S$, and
$\pi _S$, and ![]() $X$ are defined over
$X$ are defined over ![]() $\bar {\mathbb {Q}}$. If
$\bar {\mathbb {Q}}$. If ![]() $(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then
$(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, then ![]() $X^{\mathrm {deg}}(1)$ is Zariski dense in
$X^{\mathrm {deg}}(1)$ is Zariski dense in ![]() $X$.
$X$.
The goal is to reduce the relative Manin–Mumford conjecture to Conjecture 11.1.
Proposition 11.2 Conjecture 11.1 implies the relative Manin–Mumford conjecture. More precisely, for ![]() $X \subseteq \mathcal {A} \rightarrow S$ such that
$X \subseteq \mathcal {A} \rightarrow S$ such that ![]() $(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, we have
$(X \cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$, we have ![]() $\operatorname {codim}_{\mathcal {A}_X}(X) \le \dim S$ if Conjecture 11.1 holds for any irreducible subvariety
$\operatorname {codim}_{\mathcal {A}_X}(X) \le \dim S$ if Conjecture 11.1 holds for any irreducible subvariety ![]() $X' \subseteq \mathfrak {A}_{g'}$ defined over
$X' \subseteq \mathfrak {A}_{g'}$ defined over ![]() $\bar {\mathbb {Q}}$ with
$\bar {\mathbb {Q}}$ with ![]() $1 \le g' \le g$,
$1 \le g' \le g$, ![]() $\dim X' \le \dim X$ and
$\dim X' \le \dim X$ and ![]() $\dim \pi '(X') \le \dim S$.Footnote 8
$\dim \pi '(X') \le \dim S$.Footnote 8
Proof. First let us note that by standard specialization argument, if relative Manin–Mumford holds for all ![]() $S$,
$S$, ![]() $\pi _S$ and
$\pi _S$ and ![]() $X$ defined over
$X$ defined over ![]() $\bar {\mathbb {Q}}$, then it holds for all
$\bar {\mathbb {Q}}$, then it holds for all ![]() $S$,
$S$, ![]() $\pi _S$ and
$\pi _S$ and ![]() $X$ defined over
$X$ defined over ![]() $\mathbb {C}$.
$\mathbb {C}$.
Let ![]() $X \subseteq \mathcal {A} \rightarrow S$ be as in the relative Manin–Mumford conjecture, which is defined over
$X \subseteq \mathcal {A} \rightarrow S$ be as in the relative Manin–Mumford conjecture, which is defined over ![]() $\bar {\mathbb {Q}}$. Note that
$\bar {\mathbb {Q}}$. Note that ![]() $\mathcal {A}_X \rightarrow S$ itself is an abelian scheme. Replacing
$\mathcal {A}_X \rightarrow S$ itself is an abelian scheme. Replacing ![]() $\mathcal {A} \rightarrow S$ by
$\mathcal {A} \rightarrow S$ by ![]() $\mathcal {A}_X \rightarrow S$, we may assume
$\mathcal {A}_X \rightarrow S$, we may assume ![]() $\mathcal {A}_X = \mathcal {A}$. It suffices to prove
$\mathcal {A}_X = \mathcal {A}$. It suffices to prove ![]() $\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
$\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
Let us prove it by induction on ![]() $(\dim S, g)$, upward on both parameters. When
$(\dim S, g)$, upward on both parameters. When ![]() $\dim S = 0$ it follows from the classical Manin–Mumford conjecture (first proved by Raynaud [Reference RaynaudRay83] and then re-proved by many others). The conclusion for the case
$\dim S = 0$ it follows from the classical Manin–Mumford conjecture (first proved by Raynaud [Reference RaynaudRay83] and then re-proved by many others). The conclusion for the case ![]() $g = 0$ is easily true.
$g = 0$ is easily true.
In general, consider the following modular map (4.1).

Let ![]() $B = \iota _S(S)$. Then
$B = \iota _S(S)$. Then ![]() $\iota (\mathcal {A}) = \pi ^{-1}(B) =: \mathfrak {A}_g|_B$. Now
$\iota (\mathcal {A}) = \pi ^{-1}(B) =: \mathfrak {A}_g|_B$. Now ![]() $(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$ implies
$(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$ implies ![]() $(\iota (X) \cap \iota (\mathcal {A})_{\mathrm {tor}})^{\mathrm {Zar}} = \iota (X)$. Applying Conjecture 11.1 to
$(\iota (X) \cap \iota (\mathcal {A})_{\mathrm {tor}})^{\mathrm {Zar}} = \iota (X)$. Applying Conjecture 11.1 to ![]() $\iota (X) \subseteq \iota (\mathcal {A})$,Footnote 9 we get that
$\iota (X) \subseteq \iota (\mathcal {A})$,Footnote 9 we get that ![]() $\iota (X)^{\mathrm {deg}}(1)$ is Zariski dense in
$\iota (X)^{\mathrm {deg}}(1)$ is Zariski dense in ![]() $\iota (X)$. Hence by Theorem 7.1 we have
$\iota (X)$. Hence by Theorem 7.1 we have ![]() $\iota (X)^{\mathrm {deg}}(1) = \iota (X)$. Applying Theorem 8.1 to
$\iota (X)^{\mathrm {deg}}(1) = \iota (X)$. Applying Theorem 8.1 to ![]() $t = 1$ and
$t = 1$ and ![]() $\iota (X)$, we get an abelian subscheme
$\iota (X)$, we get an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathfrak {A}_g|_B \rightarrow B$ (whose relative dimension we denote by
$\mathfrak {A}_g|_B \rightarrow B$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that for
$g_{\mathcal {B}}$) such that for

we have that ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite and
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite and
Hence we have (denote by ![]() $\mathfrak {A}_{g - g_{\mathcal {B}}}|_{\iota _{/\mathcal {B},G}(B)} = (\pi ')^{-1}(\iota _{/\mathcal {B}.G}(B))$)
$\mathfrak {A}_{g - g_{\mathcal {B}}}|_{\iota _{/\mathcal {B},G}(B)} = (\pi ')^{-1}(\iota _{/\mathcal {B}.G}(B))$)
 \begin{align*} & { (\operatorname{codim}_{\mathcal{A}}(X) - \dim S) - \bigl(\operatorname{codim}_{(\mathfrak{A}_{g - g_{\mathcal{B}}}|_{\iota_{/\mathcal{B},G}(B)})}(\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) - \dim \iota_{/\mathcal{B},G}(B) \bigr) } \\ &\quad= { (\dim \mathcal{A} - \dim S - \dim X) - \bigl(\dim (\mathfrak{A}_{g - g_{\mathcal{B}}}|_{\iota_{/\mathcal{B},G}(B)}) - \dim \iota_{/\mathcal{B},G}(B) - \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) \bigr) } \\ &\quad= g - \dim X - (g-g_{\mathcal{B}}) + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) \\ &\quad= - \dim X + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) + g_{\mathcal{B}} \\ &\quad\le - \dim \iota(X) + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) + g_{\mathcal{B}} \le 0, \end{align*}
\begin{align*} & { (\operatorname{codim}_{\mathcal{A}}(X) - \dim S) - \bigl(\operatorname{codim}_{(\mathfrak{A}_{g - g_{\mathcal{B}}}|_{\iota_{/\mathcal{B},G}(B)})}(\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) - \dim \iota_{/\mathcal{B},G}(B) \bigr) } \\ &\quad= { (\dim \mathcal{A} - \dim S - \dim X) - \bigl(\dim (\mathfrak{A}_{g - g_{\mathcal{B}}}|_{\iota_{/\mathcal{B},G}(B)}) - \dim \iota_{/\mathcal{B},G}(B) - \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) \bigr) } \\ &\quad= g - \dim X - (g-g_{\mathcal{B}}) + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) \\ &\quad= - \dim X + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) + g_{\mathcal{B}} \\ &\quad\le - \dim \iota(X) + \dim (\iota_{/\mathcal{B}}\circ p_{\mathcal{B}})(\iota(X)) + g_{\mathcal{B}} \le 0, \end{align*}and so
If ![]() $\dim \iota _{/\mathcal {B},G}(B) < \dim B$, then
$\dim \iota _{/\mathcal {B},G}(B) < \dim B$, then ![]() $\dim \iota _{/\mathcal {B},G}(B) < \dim S$ since
$\dim \iota _{/\mathcal {B},G}(B) < \dim S$ since ![]() $\dim B = \dim \iota _S(S) \le \dim S$. Now we can apply the induction hypothesis on
$\dim B = \dim \iota _S(S) \le \dim S$. Now we can apply the induction hypothesis on ![]() $\dim S$ to get
$\dim S$ to get
So ![]() $\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$ by (11.2).
$\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$ by (11.2).
If ![]() $\dim \iota _{/\mathcal {B},G}(B) = \dim B$, then
$\dim \iota _{/\mathcal {B},G}(B) = \dim B$, then ![]() $\iota _{/\mathcal {B},G}$ is generically finite. So
$\iota _{/\mathcal {B},G}$ is generically finite. So ![]() $\iota _{/\mathcal {B}}$ is generically finite. But
$\iota _{/\mathcal {B}}$ is generically finite. But ![]() $\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite. So
$\iota _{/\mathcal {B}} \circ p_{\mathcal {B}}$ is not generically finite. So ![]() $g_{\mathcal {B}} > 0$. Moreover,
$g_{\mathcal {B}} > 0$. Moreover,
and hence ![]() $\dim p_{\mathcal {B}}(\iota (X)) = \dim \iota (X) - g_{\mathcal {B}}$ by (11.1). So
$\dim p_{\mathcal {B}}(\iota (X)) = \dim \iota (X) - g_{\mathcal {B}}$ by (11.1). So ![]() $\iota (X) + \mathcal {B} = \iota (X)$.
$\iota (X) + \mathcal {B} = \iota (X)$.
Now the assumption ![]() $(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$ implies
$(X\cap \mathcal {A}_{\mathrm {tor}})^{\mathrm {Zar}} = X$ implies
As ![]() $(\mathfrak {A}_g|_B)/\mathcal {B} \rightarrow B$ has relative dimension
$(\mathfrak {A}_g|_B)/\mathcal {B} \rightarrow B$ has relative dimension ![]() $g - g_{\mathcal {B}} < g$, we can apply the induction hypothesis on
$g - g_{\mathcal {B}} < g$, we can apply the induction hypothesis on ![]() $g$ to get
$g$ to get ![]() $\operatorname {codim}_{(\mathfrak {A}_g|_B)/\mathcal {B}}(p_{\mathcal {B}}(\iota (X))) \le \dim B$.
$\operatorname {codim}_{(\mathfrak {A}_g|_B)/\mathcal {B}}(p_{\mathcal {B}}(\iota (X))) \le \dim B$.
As both ![]() $\iota _{/\mathcal {B}}$ and
$\iota _{/\mathcal {B}}$ and ![]() $\iota _{/\mathcal {B},G}$ are generically finite, we have
$\iota _{/\mathcal {B},G}$ are generically finite, we have ![]() $\dim (\mathfrak {A}_g|_B)/\mathcal {B} = \dim \iota _{/\mathcal {B}}((\mathfrak {A}_g|_B)/\mathcal {B}) = \dim \mathfrak {A}_{g-g_{\mathcal {B}}}|_{\iota _{\mathcal {B},G}(B)}$,
$\dim (\mathfrak {A}_g|_B)/\mathcal {B} = \dim \iota _{/\mathcal {B}}((\mathfrak {A}_g|_B)/\mathcal {B}) = \dim \mathfrak {A}_{g-g_{\mathcal {B}}}|_{\iota _{\mathcal {B},G}(B)}$, ![]() $\dim p_{\mathcal {B}}(\iota (X)) = \dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(\iota (X))$ and
$\dim p_{\mathcal {B}}(\iota (X)) = \dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(\iota (X))$ and ![]() $\dim B = \dim \iota _{/\mathcal {B},G}(B)$. So the left hand side of (11.2) holds by the previous paragraph. Thus
$\dim B = \dim \iota _{/\mathcal {B},G}(B)$. So the left hand side of (11.2) holds by the previous paragraph. Thus ![]() $\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
$\operatorname {codim}_{\mathcal {A}}(X) \le \dim S$.
Acknowledgements
The author would like to thank Umberto Zannier for relevant discussions, especially on the historical notes on the Betti map. The author would like to thank Fabrizio Berroero, Philipp Habegger, and Umberto Zannier on relavant discussions on relative Manin–Mumford. The author would like to thank Yves André, Daniel Bertrand, Bruno Klingler, Emmanuel Ullmo, Xinyi Yuan, and Shouwu Zhang for their comments and suggestions for improving the manuscript. The author would also like to thank the referees for their comments and suggestions. The author would like to thank the Institute for Advanced Studies (NJ, USA) and the Morningside Center of Mathematics (Beijing, China) for their hospitality during the preparation of this work.
Appendix A. Discussion when the base takes some simple form
Let ![]() $S$ be an irreducible subvariety over
$S$ be an irreducible subvariety over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme of relative dimension ![]() $g \ge 1$. Let
$g \ge 1$. Let ![]() $X$ be a closed irreducible subvariety of
$X$ be a closed irreducible subvariety of ![]() $\mathcal {A}$ with
$\mathcal {A}$ with ![]() $\dim \pi _S(X) = S$.
$\dim \pi _S(X) = S$.
Definition A.1 Denote by ![]() $\langle X \rangle _{\textrm {gen-sp}}$ the smallest subvariety of
$\langle X \rangle _{\textrm {gen-sp}}$ the smallest subvariety of ![]() $\mathcal {A}$ of the following form, which contains
$\mathcal {A}$ of the following form, which contains ![]() $X$: up to taking a finite covering of
$X$: up to taking a finite covering of ![]() $S$, we have
$S$, we have ![]() $\langle X \rangle _{\textrm {gen-sp}} = \sigma + \mathcal {Z} + \mathcal {B}$, where
$\langle X \rangle _{\textrm {gen-sp}} = \sigma + \mathcal {Z} + \mathcal {B}$, where ![]() $\mathcal {B}$ is an abelian subscheme of
$\mathcal {B}$ is an abelian subscheme of ![]() $\mathcal {A} \rightarrow S$,
$\mathcal {A} \rightarrow S$, ![]() $\sigma$ is a torsion section of
$\sigma$ is a torsion section of ![]() $\mathcal {A} \rightarrow S$, and
$\mathcal {A} \rightarrow S$, and ![]() $\mathcal {Z} = Z \times S$ where
$\mathcal {Z} = Z \times S$ where ![]() $C \times S$ is the largest constant abelian subscheme of
$C \times S$ is the largest constant abelian subscheme of ![]() $\mathcal {A} \rightarrow S$ and
$\mathcal {A} \rightarrow S$ and ![]() $Z \subseteq C$.
$Z \subseteq C$.
If we furthermore require ![]() $Z$ to be a point, then we obtain
$Z$ to be a point, then we obtain ![]() $\langle X \rangle _{\mathrm {sg}}$ (Definition 1.5).
$\langle X \rangle _{\mathrm {sg}}$ (Definition 1.5).
Let ![]() $\mathcal {A}_X$ be the translate of an abelian subscheme of
$\mathcal {A}_X$ be the translate of an abelian subscheme of ![]() $\mathcal {A} \rightarrow S$ by a torsion section, which contains
$\mathcal {A} \rightarrow S$ by a torsion section, which contains ![]() $X$, minimal for this property. Then
$X$, minimal for this property. Then ![]() $\mathcal {A}_X \rightarrow S$ itself is an abelian scheme, whose relative dimension we denote by
$\mathcal {A}_X \rightarrow S$ itself is an abelian scheme, whose relative dimension we denote by ![]() $g_X$. It is easy to see
$g_X$. It is easy to see ![]() $\langle X \rangle _{\mathrm {gen-sp}} \subseteq \langle X \rangle _{\mathrm {sg}} \subseteq \mathcal {A}_X$.
$\langle X \rangle _{\mathrm {gen-sp}} \subseteq \langle X \rangle _{\mathrm {sg}} \subseteq \mathcal {A}_X$.
The variety ![]() $\langle X \rangle _{\textrm {gen-sp}}$ is closely related to
$\langle X \rangle _{\textrm {gen-sp}}$ is closely related to ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$. Let us start with the following proposition, saying that
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$. Let us start with the following proposition, saying that ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$ attains its minimal value if and only if
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$ attains its minimal value if and only if ![]() $X = \langle X \rangle _{\textrm {gen-sp}}$.
$X = \langle X \rangle _{\textrm {gen-sp}}$.
Proposition A.2 ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = 2(\dim X - \dim S) \Longleftrightarrow X = \langle X \rangle _{\mathrm {gen-sp}}$.
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = 2(\dim X - \dim S) \Longleftrightarrow X = \langle X \rangle _{\mathrm {gen-sp}}$.
In particular, if ![]() $\dim S = 1$, then either
$\dim S = 1$, then either ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = 2 \dim X$ or
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) = 2 \dim X$ or ![]() $X = \langle X \rangle _{\mathrm {gen-sp}}$.
$X = \langle X \rangle _{\mathrm {gen-sp}}$.
Proof. The direction ![]() $\Leftarrow$ is not hard to check. Let us prove
$\Leftarrow$ is not hard to check. Let us prove ![]() $\Rightarrow$ now.
$\Rightarrow$ now.
Apply Theorem 1.1(i) to ![]() $l = \dim X - \dim S + 1$. Then
$l = \dim X - \dim S + 1$. Then ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) < 2(\dim X - \dim S + 1)$ if and only if there exists an abelian subscheme
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) < 2(\dim X - \dim S + 1)$ if and only if there exists an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}_X \rightarrow S$ such that
$\mathcal {A}_X \rightarrow S$ such that
for the following.

Thus ![]() $2(\dim X - \dim S) = \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2g_{\mathcal {B}}$
$2(\dim X - \dim S) = \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2g_{\mathcal {B}}$
![]() $+ 2\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \le 2(\dim X - \dim S)$.
$+ 2\dim (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \le 2(\dim X - \dim S)$.
This implies ![]() $\dim p_{\mathcal {B}}(X) = \dim X - g_{\mathcal {B}}$, and
$\dim p_{\mathcal {B}}(X) = \dim X - g_{\mathcal {B}}$, and ![]() $\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim X - \dim S - g_{\mathcal {B}} = \dim p_{\mathcal {B}}(X) - \dim S$. So
$\dim (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim X - \dim S - g_{\mathcal {B}} = \dim p_{\mathcal {B}}(X) - \dim S$. So ![]() $p_{\mathcal {B}}|_X$ has relative dimension
$p_{\mathcal {B}}|_X$ has relative dimension ![]() $g_{\mathcal {B}}$, and
$g_{\mathcal {B}}$, and ![]() $\iota _{/\mathcal {B}}|_{p_{\mathcal {B}}(X)}$ has relative dimension
$\iota _{/\mathcal {B}}|_{p_{\mathcal {B}}(X)}$ has relative dimension ![]() $\dim S$. So
$\dim S$. So ![]() $X = p_{\mathcal {B}}^{-1}(p_{\mathcal {B}}(X))$ as
$X = p_{\mathcal {B}}^{-1}(p_{\mathcal {B}}(X))$ as ![]() $p_{\mathcal {B}}$ has relative dimension
$p_{\mathcal {B}}$ has relative dimension ![]() $g_{\mathcal {B}}$, and
$g_{\mathcal {B}}$, and ![]() $p_{\mathcal {B}}(X)= \iota _{/\mathcal {B}}^{-1}(\iota _{/\mathcal {B}}(p_{\mathcal {B}}(X)))$ with
$p_{\mathcal {B}}(X)= \iota _{/\mathcal {B}}^{-1}(\iota _{/\mathcal {B}}(p_{\mathcal {B}}(X)))$ with ![]() $\iota _{/\mathcal {B}}$ having relative dimension
$\iota _{/\mathcal {B}}$ having relative dimension ![]() $\dim S$. So
$\dim S$. So ![]() $\iota _{/\mathcal {B},S}$ has relative dimension
$\iota _{/\mathcal {B},S}$ has relative dimension ![]() $\dim S$, making
$\dim S$, making ![]() $\iota _{/\mathcal {B},S}(S)$ a point.
$\iota _{/\mathcal {B},S}(S)$ a point.
Now ![]() $X = (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})^{-1}(\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X)$ and
$X = (\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})^{-1}(\iota _{/\mathcal {B}}\circ p_{\mathcal {B}})(X)$ and ![]() $\iota _{/\mathcal {B},S}(S)$ is a point. So
$\iota _{/\mathcal {B},S}(S)$ is a point. So ![]() $X = \langle X \rangle _{\mathrm {gen-sp}}$.
$X = \langle X \rangle _{\mathrm {gen-sp}}$.
To further investigate the relation between ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$ with
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X)$ with ![]() $\langle X \rangle _{\textrm {gen-sp}}$, let us first of all recall the following modular map (4.1).
$\langle X \rangle _{\textrm {gen-sp}}$, let us first of all recall the following modular map (4.1).

Proposition A.3 We have the following:
(i)
 $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2\min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$;
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2\min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$;(ii) assume
 $\dim \iota _S(S) = 1$ or the connected algebraic monodromy group of
$\dim \iota _S(S) = 1$ or the connected algebraic monodromy group of  $\iota _S(S)$ is simple. Then
$\iota _S(S)$ is simple. Then  $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \ge 2\min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$.
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \ge 2\min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$.
Before proving this proposition, let us see its direct corollary on the Betti rank.
Corollary A.4 Assume that ![]() $\iota _S(S)$ has dimension
$\iota _S(S)$ has dimension ![]() $1$ or has simple connected algebraic monodromy group. Then
$1$ or has simple connected algebraic monodromy group. Then
We point out that the hypotheses in Corollary A.4 cannot be removed; see Example 9.4.
Remark A.5 Let ![]() $\mathfrak {C}_g$ be the universal curve embedded in
$\mathfrak {C}_g$ be the universal curve embedded in ![]() $\mathfrak {A}_g$. Use notation in Theorems 1.2 and 1.2′. It is clearly true that
$\mathfrak {A}_g$. Use notation in Theorems 1.2 and 1.2′. It is clearly true that ![]() $\langle \mathfrak {C}_S^{[m]} \rangle _{\mathrm {gen-sp}} = \mathfrak {A}_{mg} \times _{\mathbb {A}_{mg}} S$ for all
$\langle \mathfrak {C}_S^{[m]} \rangle _{\mathrm {gen-sp}} = \mathfrak {A}_{mg} \times _{\mathbb {A}_{mg}} S$ for all ![]() $m \ge 1$.Footnote 10 If
$m \ge 1$.Footnote 10 If ![]() $S$ has dimension
$S$ has dimension ![]() $1$ or has simple connected algebraic monodromy group (for example when
$1$ or has simple connected algebraic monodromy group (for example when ![]() $S$ is the whole Torelli locus), then Corollary A.4 has the following immediate corollaries:
$S$ is the whole Torelli locus), then Corollary A.4 has the following immediate corollaries: ![]() $\mathfrak {C}_S^{[m]}$ has maximal generic Betti rank for all
$\mathfrak {C}_S^{[m]}$ has maximal generic Betti rank for all ![]() $m \ge 3$ and
$m \ge 3$ and ![]() $g \ge 2$,
$g \ge 2$, ![]() $\mathscr {D}_m(\mathfrak {C}_S^{[m+1]})$ has maximal generic Betti rank for all
$\mathscr {D}_m(\mathfrak {C}_S^{[m+1]})$ has maximal generic Betti rank for all ![]() $m \ge 4$ and
$m \ge 4$ and ![]() $g \ge 2$, and
$g \ge 2$, and ![]() $\mathfrak {C}_S^{[m]} - \mathfrak {C}_S^{[m]}$ has maximal generic Betti rank for all
$\mathfrak {C}_S^{[m]} - \mathfrak {C}_S^{[m]}$ has maximal generic Betti rank for all ![]() $m \ge 4$ when
$m \ge 4$ when ![]() $g \ge 5$, for all
$g \ge 5$, for all ![]() $m \ge 5$ when
$m \ge 5$ when ![]() $g = 4$ and for all
$g = 4$ and for all ![]() $m \ge 6$ for
$m \ge 6$ for ![]() $g = 3$.
$g = 3$.
Proof of Proposition A.3 (i) We have seen ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2\dim \iota (X)$ at the end of § 4. On the other hand it is not hard to check
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le 2\dim \iota (X)$ at the end of § 4. On the other hand it is not hard to check ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\langle X \rangle _{\mathrm {gen-sp}}}) = 2 (\dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$ by the definitions of
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\langle X \rangle _{\mathrm {gen-sp}}}) = 2 (\dim \langle X \rangle _{\mathrm {gen-sp}} - \dim S)$ by the definitions of ![]() $b_{\Delta }$ and
$b_{\Delta }$ and ![]() $\langle X \rangle _{\mathrm {gen-sp}}$. Hence we are done because
$\langle X \rangle _{\mathrm {gen-sp}}$. Hence we are done because ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\langle X \rangle _{\mathrm {gen-sp}}})$.
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) \le \mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_{\langle X \rangle _{\mathrm {gen-sp}}})$.
(ii) Set ![]() $l = \min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}}- \dim S)$. Assume
$l = \min (\dim \iota (X), \dim \langle X \rangle _{\mathrm {gen-sp}}- \dim S)$. Assume ![]() $\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) < 2l$. Then by Theorem 1.1(i), there exists an abelian subscheme
$\mathrm {rank}_{\mathbb {R}}({d}b_{\Delta }|_X) < 2l$. Then by Theorem 1.1(i), there exists an abelian subscheme ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {A}_X \rightarrow B$ (whose relative dimension we denote by
$\mathcal {A}_X \rightarrow B$ (whose relative dimension we denote by ![]() $g_{\mathcal {B}}$) such that
$g_{\mathcal {B}}$) such that
for the following.

Observe that ![]() $\langle X \rangle _{\mathrm {gen-sp}} \subseteq p_{\mathcal {B}}^{-1}\Big (\iota _{/\mathcal {B}}^{-1}\big ( \langle (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \rangle _{\mathrm {gen-sp}}\big )\Big )$. So
$\langle X \rangle _{\mathrm {gen-sp}} \subseteq p_{\mathcal {B}}^{-1}\Big (\iota _{/\mathcal {B}}^{-1}\big ( \langle (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \rangle _{\mathrm {gen-sp}}\big )\Big )$. So
and thus ![]() $(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \not = \langle (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \rangle _{\mathrm {gen-sp}}$ by (A.1). So
$(\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \not = \langle (\iota _{/\mathcal {B}} \circ p_{\mathcal {B}})(X) \rangle _{\mathrm {gen-sp}}$ by (A.1). So ![]() $\iota _{/\mathcal {B},S}(S)$ is not a point.
$\iota _{/\mathcal {B},S}(S)$ is not a point.
Apply the modular map ![]() $\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (and
$\iota \colon \mathcal {A} \rightarrow \mathfrak {A}_g$ (and ![]() $\iota _S \colon S \rightarrow \mathbb {A}_g$) to (A.2). Let
$\iota _S \colon S \rightarrow \mathbb {A}_g$) to (A.2). Let ![]() $B = \iota _S(S)$. Then we get the following.
$B = \iota _S(S)$. Then we get the following.

Let ![]() $G_B$ be the connected algebraic monodromy group of
$G_B$ be the connected algebraic monodromy group of ![]() $B \subseteq \mathbb {A}_g$, and let
$B \subseteq \mathbb {A}_g$, and let ![]() $G_Q$ be the Mumford–Tate group of
$G_Q$ be the Mumford–Tate group of ![]() $B \subseteq \mathbb {A}_g$. Then
$B \subseteq \mathbb {A}_g$. Then ![]() $G_B < G_Q^{\mathrm {der}}$.
$G_B < G_Q^{\mathrm {der}}$.
We have that ![]() $(\iota (\mathcal {A}_X)/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)}$ is an isotrivial abelian scheme over
$(\iota (\mathcal {A}_X)/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)}$ is an isotrivial abelian scheme over ![]() $\iota _{/\mathcal {B},S}^{'-1}(a)$. Take
$\iota _{/\mathcal {B},S}^{'-1}(a)$. Take ![]() $a$ to be Hodge generic in
$a$ to be Hodge generic in ![]() $\iota '_{/\mathcal {B},S}(B)$, then by a theorem of Deligne and André [Reference AndréAnd92, § 5, Theorem 1], the connected algebraic monodromy group
$\iota '_{/\mathcal {B},S}(B)$, then by a theorem of Deligne and André [Reference AndréAnd92, § 5, Theorem 1], the connected algebraic monodromy group ![]() $H$ of
$H$ of ![]() $\iota _{/\mathcal {B},S}^{'-1}(a)$ is a normal subgroup of
$\iota _{/\mathcal {B},S}^{'-1}(a)$ is a normal subgroup of ![]() $G_Q^{\mathrm {der}}$. Moreover,
$G_Q^{\mathrm {der}}$. Moreover, ![]() $H < G_B$ since
$H < G_B$ since ![]() $\iota _{/\mathcal {B},S}^{'-1}(a) \subseteq B$. Thus
$\iota _{/\mathcal {B},S}^{'-1}(a) \subseteq B$. Thus ![]() $H\lhd G_B$.
$H\lhd G_B$.
Recall the assumption: either ![]() $\dim B = 1$ or
$\dim B = 1$ or ![]() $H$ is simple. In the first case, either
$H$ is simple. In the first case, either ![]() $\iota '_{/\mathcal {B},S}(B)$ is a point or
$\iota '_{/\mathcal {B},S}(B)$ is a point or ![]() $\iota '_{/\mathcal {B},S}$ is quasi-finite. In the second case, either
$\iota '_{/\mathcal {B},S}$ is quasi-finite. In the second case, either ![]() $H = G_B$ or
$H = G_B$ or ![]() $H = 1$ by the previous paragraph. If
$H = 1$ by the previous paragraph. If ![]() $H = G_B$, then the fact that
$H = G_B$, then the fact that ![]() $(\iota (\mathcal {A}_X)/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$ is isotrivial implies that
$(\iota (\mathcal {A}_X)/\iota (\mathcal {B}))|_{\iota _{/\mathcal {B},S}^{'-1}(a)} \rightarrow \iota _{/\mathcal {B},S}^{'-1}(a)$ is isotrivial implies that ![]() $\iota (\mathcal {A}_X)/\iota (\mathcal {B}) \rightarrow B$ is isotrivial. Hence
$\iota (\mathcal {A}_X)/\iota (\mathcal {B}) \rightarrow B$ is isotrivial. Hence ![]() $\iota '_{/\mathcal {B},S}(B)$ is a point. If
$\iota '_{/\mathcal {B},S}(B)$ is a point. If ![]() $H = 1$, then
$H = 1$, then ![]() $\dim \iota _{/\mathcal {B},S}^{'-1}(a) = 0$, and hence
$\dim \iota _{/\mathcal {B},S}^{'-1}(a) = 0$, and hence ![]() $\iota '_{/\mathcal {B},S}$ is generically quasi-finite.
$\iota '_{/\mathcal {B},S}$ is generically quasi-finite.
As ![]() $\iota '_{/\mathcal {B},S}(B) = \iota _{/\mathcal {B},S}(S)$ is not a point, we have that
$\iota '_{/\mathcal {B},S}(B) = \iota _{/\mathcal {B},S}(S)$ is not a point, we have that ![]() $\iota '_{/\mathcal {B},S}$ is generically quasi-finite. So
$\iota '_{/\mathcal {B},S}$ is generically quasi-finite. So ![]() $\iota '_{\mathcal {B}}$ is generically quasi-finite, and so
$\iota '_{\mathcal {B}}$ is generically quasi-finite, and so ![]() $\dim (\iota _{\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim (\iota '_{/\mathcal {B}} \circ p'_{\mathcal {B}})(\iota (X)) = \dim p'_{\mathcal {B}}(\iota (X)) \ge \dim \iota (X) - g_{\mathcal {B}}$, contradicting (A.1).
$\dim (\iota _{\mathcal {B}}\circ p_{\mathcal {B}})(X) = \dim (\iota '_{/\mathcal {B}} \circ p'_{\mathcal {B}})(\iota (X)) = \dim p'_{\mathcal {B}}(\iota (X)) \ge \dim \iota (X) - g_{\mathcal {B}}$, contradicting (A.1).
Appendix B. Decomposition of abelian subschemes
The goal of this appendix is to prove (10.3).
B.1 Linear algebra
Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $V$ be a finite-dimensional
$V$ be a finite-dimensional ![]() $G$-representation, both defined over
$G$-representation, both defined over ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
Let ![]() $m \ge 1$ be an integer and let
$m \ge 1$ be an integer and let ![]() $W$ be a
$W$ be a ![]() $G$-submodule of
$G$-submodule of ![]() $V^{\oplus m}$. The goal of this section is to prove the following proposition.
$V^{\oplus m}$. The goal of this section is to prove the following proposition.
Proposition B.1 There exists a ![]() $G$-linear isomorphism
$G$-linear isomorphism
such that
for some ![]() $G$-submodules
$G$-submodules ![]() $W_1,\ldots ,W_m$ of
$W_1,\ldots ,W_m$ of ![]() $V$. Moreover,
$V$. Moreover, ![]() $\tau$ can be chosen such that
$\tau$ can be chosen such that ![]() $q_1\circ \tau = q_1$, where
$q_1\circ \tau = q_1$, where ![]() $q_1 \colon V^{\oplus m} \rightarrow V$ is the projection to the first factor.
$q_1 \colon V^{\oplus m} \rightarrow V$ is the projection to the first factor.
The key to prove this proposition is the following lemma.
Lemma B.2 Let ![]() $q \colon V^{\oplus m} \rightarrow V^{\oplus m'}$ be a linear projection. Then there exists a
$q \colon V^{\oplus m} \rightarrow V^{\oplus m'}$ be a linear projection. Then there exists a ![]() $G$-homomorphism
$G$-homomorphism ![]() $i \colon V^{\oplus m'} \rightarrow V^{\oplus m}$ such that
$i \colon V^{\oplus m'} \rightarrow V^{\oplus m}$ such that
(i)
 $q\circ i = 1_{V^{\oplus m'}}$;
$q\circ i = 1_{V^{\oplus m'}}$;(ii)
 $i(q(W)) = i(V^{\oplus m'}) \cap W$;
$i(q(W)) = i(V^{\oplus m'}) \cap W$;(iii)
 $i|_{q(W)}$ is injective.
$i|_{q(W)}$ is injective.
Proof. As ![]() $G$ is a reductive group and
$G$ is a reductive group and ![]() $\mathrm {char}\,\mathbb {Q}=0$, there exists a
$\mathrm {char}\,\mathbb {Q}=0$, there exists a ![]() $G$-submodule
$G$-submodule ![]() $W_0$ of
$W_0$ of ![]() $W$ such that
$W$ such that ![]() $W = (W\cap \operatorname {Ker} q) \oplus W_0$. In particular
$W = (W\cap \operatorname {Ker} q) \oplus W_0$. In particular ![]() $W_0 \cap \operatorname {Ker} q = W_0 \cap W \cap \operatorname {Ker} q = \{0\}$. Thus
$W_0 \cap \operatorname {Ker} q = W_0 \cap W \cap \operatorname {Ker} q = \{0\}$. Thus ![]() $W_0 + \operatorname {Ker} q = W_0 \oplus \operatorname {Ker} q$. Note that
$W_0 + \operatorname {Ker} q = W_0 \oplus \operatorname {Ker} q$. Note that ![]() $q(W) = q(W_0)$, and
$q(W) = q(W_0)$, and ![]() $q|_{W_0}$ is injective.
$q|_{W_0}$ is injective.
Now ![]() $W_0 \oplus \operatorname {Ker} q$ is a
$W_0 \oplus \operatorname {Ker} q$ is a ![]() $G$-submodule of
$G$-submodule of ![]() $V^{\oplus m}$. Again as
$V^{\oplus m}$. Again as ![]() $G$ is a reductive group and
$G$ is a reductive group and ![]() $\mathrm {char}\,\mathbb {Q}=0$, there exists a
$\mathrm {char}\,\mathbb {Q}=0$, there exists a ![]() $G$-submodule
$G$-submodule ![]() $W_0'$ of
$W_0'$ of ![]() $V^{\oplus m}$ such that
$V^{\oplus m}$ such that ![]() $V^{\oplus m} = (W_0 \oplus \operatorname {Ker} q) \oplus W_0'$. Moreover we claim that
$V^{\oplus m} = (W_0 \oplus \operatorname {Ker} q) \oplus W_0'$. Moreover we claim that ![]() $W_0' \cap W = 0$. Indeed,
$W_0' \cap W = 0$. Indeed, ![]() $W = (W\cap \operatorname {Ker} q) \oplus W_0 \subseteq \operatorname {Ker} q \oplus W_0$, and
$W = (W\cap \operatorname {Ker} q) \oplus W_0 \subseteq \operatorname {Ker} q \oplus W_0$, and ![]() $W_0' \cap (\operatorname {Ker} q \oplus W_0) = 0$. Thus
$W_0' \cap (\operatorname {Ker} q \oplus W_0) = 0$. Thus ![]() $(W_0 \oplus W_0') \cap W = W_0$.
$(W_0 \oplus W_0') \cap W = W_0$.
As ![]() $V^{\oplus m} = (W_0 \oplus \operatorname {Ker} q) \oplus W_0'$, we have that
$V^{\oplus m} = (W_0 \oplus \operatorname {Ker} q) \oplus W_0'$, we have that ![]() $q|_{W_0 \oplus W_0'} \colon W_0 \oplus W_0' \rightarrow V^{\oplus m'}$ is injective and both sides have the same dimension. So
$q|_{W_0 \oplus W_0'} \colon W_0 \oplus W_0' \rightarrow V^{\oplus m'}$ is injective and both sides have the same dimension. So ![]() $q|_{W_0 \oplus W_0'}$ is an isomorphism.
$q|_{W_0 \oplus W_0'}$ is an isomorphism.
Let ![]() $i \colon V^{\oplus m'} \rightarrow V^{\oplus m}$ be the composite of the inclusion
$i \colon V^{\oplus m'} \rightarrow V^{\oplus m}$ be the composite of the inclusion ![]() $W_0 \oplus W_0' \subseteq V^{\oplus m}$ with
$W_0 \oplus W_0' \subseteq V^{\oplus m}$ with ![]() $(q|_{W_0 \oplus W_0'})^{-1}$. Then
$(q|_{W_0 \oplus W_0'})^{-1}$. Then ![]() $i(V^{\oplus m'}) = W_0\oplus W_0'$.
$i(V^{\oplus m'}) = W_0\oplus W_0'$.
Let us show that ![]() $i$ is the desired map. Property (i) clearly holds. To see (ii) and (iii), recall that
$i$ is the desired map. Property (i) clearly holds. To see (ii) and (iii), recall that ![]() $q(W) = q(W_0)$, and hence
$q(W) = q(W_0)$, and hence ![]() $i|_{q(W)} = i|_{q(W_0)} = (q|_{W_0 \oplus W_0'})^{-1}|_{q(W_0)} \colon q(W_0) \simeq W_0$
$i|_{q(W)} = i|_{q(W_0)} = (q|_{W_0 \oplus W_0'})^{-1}|_{q(W_0)} \colon q(W_0) \simeq W_0$ ![]() $= (W_0 \oplus W_0') \cap W = i(V^{\oplus m'}) \cap W$.
$= (W_0 \oplus W_0') \cap W = i(V^{\oplus m'}) \cap W$.
Proof of Proposition B.1 We prove the proposition by induction on ![]() $m$. When
$m$. When ![]() $m = 1$, the proposition trivially holds true.
$m = 1$, the proposition trivially holds true.
Now for a general ![]() $m \ge 1$, suppose the proposition is proved for
$m \ge 1$, suppose the proposition is proved for ![]() $1,\ldots , m-1$.
$1,\ldots , m-1$.
Apply Lemma B.2 to ![]() $q_1 \colon V^{\oplus m} \rightarrow V$ the projection to the first component. We thus obtain
$q_1 \colon V^{\oplus m} \rightarrow V$ the projection to the first component. We thus obtain ![]() $i_1 \colon V \rightarrow V^{\oplus m}$ with the three properties. In particular
$i_1 \colon V \rightarrow V^{\oplus m}$ with the three properties. In particular ![]() $V^{\oplus m} = i_1(V) \oplus \operatorname {Ker} q_1$.
$V^{\oplus m} = i_1(V) \oplus \operatorname {Ker} q_1$.
Let ![]() $q'_1 \colon V^{\oplus m} \rightarrow V^{\oplus (m-1)}$ be the quotient by
$q'_1 \colon V^{\oplus m} \rightarrow V^{\oplus (m-1)}$ be the quotient by ![]() $i_1(V)$. Then
$i_1(V)$. Then ![]() $\operatorname {Ker} q'_1 \cap W = i_1(V) \cap W = i_1(q_1(W))$ by property (ii) of
$\operatorname {Ker} q'_1 \cap W = i_1(V) \cap W = i_1(q_1(W))$ by property (ii) of ![]() $i_1$. Let
$i_1$. Let ![]() $i'_1 \colon V^{\oplus (m-1)} \rightarrow V^{\oplus m}$,
$i'_1 \colon V^{\oplus (m-1)} \rightarrow V^{\oplus m}$, ![]() $v \mapsto (0,v)$. Then
$v \mapsto (0,v)$. Then ![]() $i'_1(V^{\oplus (m-1)}) = \operatorname {Ker} q_1$ and from the last paragraph we have
$i'_1(V^{\oplus (m-1)}) = \operatorname {Ker} q_1$ and from the last paragraph we have ![]() $V^{\oplus m} = i_1(V) \oplus i_1'(V^{\oplus (m-1)})$. Define
$V^{\oplus m} = i_1(V) \oplus i_1'(V^{\oplus (m-1)})$. Define
Then ![]() $\tau _1$ is a
$\tau _1$ is a ![]() $G$-isomorphism, and
$G$-isomorphism, and ![]() $\tau _1(W) \subseteq i_1\circ q_1(W) \oplus i'_1 \circ q'_1(W)$. But
$\tau _1(W) \subseteq i_1\circ q_1(W) \oplus i'_1 \circ q'_1(W)$. But ![]() $\dim i'_1 \circ q'_1(W) \!=\! \dim q'_1(W) \!=\! \dim W \!-\! \dim (\operatorname {Ker} q'_1 \cap W) = \dim W - \dim i_1(q_1(W))$. Hence
$\dim i'_1 \circ q'_1(W) \!=\! \dim q'_1(W) \!=\! \dim W \!-\! \dim (\operatorname {Ker} q'_1 \cap W) = \dim W - \dim i_1(q_1(W))$. Hence ![]() $\dim W = \dim \tau _1(W) \le \dim i_1\circ q_1(W) + \dim i'_1 \circ q'_1(W)$
$\dim W = \dim \tau _1(W) \le \dim i_1\circ q_1(W) + \dim i'_1 \circ q'_1(W)$ ![]() $= \dim i_1\circ q_1(W) + \dim W - \dim i_1\circ q_1(W) = \dim W$. Hence
$= \dim i_1\circ q_1(W) + \dim W - \dim i_1\circ q_1(W) = \dim W$. Hence ![]() $\tau _1(W) = i_1\circ q_1(W) \oplus i'_1 \circ q'_1(W)$.
$\tau _1(W) = i_1\circ q_1(W) \oplus i'_1 \circ q'_1(W)$.
Set ![]() $W_1 = i_1\circ q_1(W)$ and
$W_1 = i_1\circ q_1(W)$ and ![]() $W_1^{\perp } = i'_1 \circ q'_1(W)$.
$W_1^{\perp } = i'_1 \circ q'_1(W)$.
By the induction hypothesis applied to ![]() $W_1^{\perp } \subseteq V^{\oplus (m-1)}$, there exists a
$W_1^{\perp } \subseteq V^{\oplus (m-1)}$, there exists a ![]() $G$-linear
$G$-linear ![]() $\tau _1' \colon V^{\oplus (m-1)} \simeq V^{\oplus (m-1)}$ such that
$\tau _1' \colon V^{\oplus (m-1)} \simeq V^{\oplus (m-1)}$ such that ![]() $\tau _1'(W_1^{\perp }) = W_2 \oplus \cdots \oplus W_m$ for some
$\tau _1'(W_1^{\perp }) = W_2 \oplus \cdots \oplus W_m$ for some ![]() $G$-submodules
$G$-submodules ![]() $W_2,\ldots ,W_m$ of
$W_2,\ldots ,W_m$ of ![]() $V$.
$V$.
Let ![]() $\tau$ be the composite
$\tau$ be the composite
Then ![]() $\tau (W) = W_1 \oplus W_2 \oplus \cdots \oplus W_m$. Hence we are done for the construction of
$\tau (W) = W_1 \oplus W_2 \oplus \cdots \oplus W_m$. Hence we are done for the construction of ![]() $\tau$.
$\tau$.
Let us prove the ‘Moreover’ part. By our construction of ![]() $\tau$, we have
$\tau$, we have ![]() $q_1\circ \tau = q_1\circ (1_V, \tau _1') \circ \tau _1 =q_1\circ \tau _1 = q_1\circ (i_1 \circ q_1 + i'_1 \circ q'_1) = q_1$ as
$q_1\circ \tau = q_1\circ (1_V, \tau _1') \circ \tau _1 =q_1\circ \tau _1 = q_1\circ (i_1 \circ q_1 + i'_1 \circ q'_1) = q_1$ as ![]() $q_1 \circ i_1 = 1_V$ and
$q_1 \circ i_1 = 1_V$ and ![]() $q_1 \circ i'_1 = 0$.
$q_1 \circ i'_1 = 0$.
B.2 Proof of (10.3)
Now we are ready to prove (10.3). Let ![]() $\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme,
$\pi _S \colon \mathcal {A} \rightarrow S$ be an abelian scheme, ![]() $\mathcal {A}^{[m]}$ be the
$\mathcal {A}^{[m]}$ be the ![]() $m$-fold fibered power, and
$m$-fold fibered power, and ![]() $\mathcal {B}$ be an abelian subscheme of
$\mathcal {B}$ be an abelian subscheme of ![]() $\pi _S^{[m]} \colon \mathcal {A}^{[m]} \rightarrow S$.
$\pi _S^{[m]} \colon \mathcal {A}^{[m]} \rightarrow S$.
The variation of Hodge structures (V![]() $\mathbb {Q}$HS)
$\mathbb {Q}$HS) ![]() $(R^1 (\pi _S)_*\mathbb {Q})^\vee$ over
$(R^1 (\pi _S)_*\mathbb {Q})^\vee$ over ![]() $S$ is polarizable of type
$S$ is polarizable of type ![]() $(-1,0)+(0,-1)$. Its generic Mumford–Tate group
$(-1,0)+(0,-1)$. Its generic Mumford–Tate group ![]() $G$ is a reductive group defined over
$G$ is a reductive group defined over ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
As ![]() $\mathrm {End}_{\text {V}\mathbb {Q}-\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$ is a variation of Hodge structures of
$\mathrm {End}_{\text {V}\mathbb {Q}-\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$ is a variation of Hodge structures of ![]() $S$ of weight
$S$ of weight ![]() $0$, there exists
$0$, there exists ![]() $s \in S(\mathbb {C})$ such that each element in
$s \in S(\mathbb {C})$ such that each element in ![]() $\mathrm {End}_{\mathbb {Q}-\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee _s)$ extends to an element in
$\mathrm {End}_{\mathbb {Q}-\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee _s)$ extends to an element in ![]() $\mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$, up to replacing
$\mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$, up to replacing ![]() $S$ by a finite covering. See [Reference Peters and SteenbrinkPS08, proof of Theorem 10.20].
$S$ by a finite covering. See [Reference Peters and SteenbrinkPS08, proof of Theorem 10.20].
Set ![]() $V=(R^1 (\pi _S)_*\mathbb {Q})^\vee _s = H_1(\mathcal {A}_s,\mathbb {Q})$. Apply Proposition B.1 to
$V=(R^1 (\pi _S)_*\mathbb {Q})^\vee _s = H_1(\mathcal {A}_s,\mathbb {Q})$. Apply Proposition B.1 to ![]() $W = H_1(\mathcal {B}_s,\mathbb {Q})$. We obtain a
$W = H_1(\mathcal {B}_s,\mathbb {Q})$. We obtain a ![]() $G$-isomorphism
$G$-isomorphism ![]() $\tau \colon V^{\oplus m} \simeq V^{\oplus m}$ such that
$\tau \colon V^{\oplus m} \simeq V^{\oplus m}$ such that ![]() $\tau (W) = W_1 \oplus \cdots \oplus W_m$ for some
$\tau (W) = W_1 \oplus \cdots \oplus W_m$ for some ![]() $G$-submodules
$G$-submodules ![]() $W_1,\ldots ,W_m$ of
$W_1,\ldots ,W_m$ of ![]() $V$. Moreover,
$V$. Moreover, ![]() $q_1 \circ \tau = q_1$ with
$q_1 \circ \tau = q_1$ with ![]() $q_1 \colon V^{\oplus m} \rightarrow V$ the projection to the first factor.
$q_1 \colon V^{\oplus m} \rightarrow V$ the projection to the first factor.
For each ![]() $i \in \{1,\ldots ,m\}$,
$i \in \{1,\ldots ,m\}$, ![]() $W_i = \operatorname {Ker} \alpha _i$ for some
$W_i = \operatorname {Ker} \alpha _i$ for some ![]() $\alpha _i \in \mathrm {End}_G(V)$. But
$\alpha _i \in \mathrm {End}_G(V)$. But ![]() $\mathrm {End}_G(V) \subseteq \mathrm {End}_{\mathbb {Q}-\text {HS}}(V)$, so by the discussion above each
$\mathrm {End}_G(V) \subseteq \mathrm {End}_{\mathbb {Q}-\text {HS}}(V)$, so by the discussion above each ![]() $\alpha _i$ extends to an element in
$\alpha _i$ extends to an element in ![]() $\mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$, which by abuse of notation is still denoted by
$\mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S)_*\mathbb {Q})^\vee )$, which by abuse of notation is still denoted by ![]() $\alpha _i$. Similarly
$\alpha _i$. Similarly ![]() $\tau$ extends to some
$\tau$ extends to some ![]() $\rho \in \mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S^{[m]})_*\mathbb {Q})^\vee )$. We then have
$\rho \in \mathrm {End}_{\text {V}\mathbb {Q}\text {HS}}((R^1 (\pi _S^{[m]})_*\mathbb {Q})^\vee )$. We then have ![]() $\rho ((R^1 (\pi _S^{[m]}|_{\mathcal {B}})_*\mathbb {Q})^\vee ) = \operatorname {Ker}(\alpha _1) \times _S \cdots \times _S \operatorname {Ker}(\alpha _m)$.
$\rho ((R^1 (\pi _S^{[m]}|_{\mathcal {B}})_*\mathbb {Q})^\vee ) = \operatorname {Ker}(\alpha _1) \times _S \cdots \times _S \operatorname {Ker}(\alpha _m)$.
By [Reference DeligneDel71, Rappel 4.4.3], ![]() $\rho$ gives rise to an isogeny
$\rho$ gives rise to an isogeny ![]() $\mathcal {A}^{[m]} \rightarrow \mathcal {A}^{[m]}$ and each
$\mathcal {A}^{[m]} \rightarrow \mathcal {A}^{[m]}$ and each ![]() $\alpha _i$ gives rise to an isogeny
$\alpha _i$ gives rise to an isogeny ![]() $\mathcal {A} \rightarrow \mathcal {A}$. By abuse of notation we still use
$\mathcal {A} \rightarrow \mathcal {A}$. By abuse of notation we still use ![]() $\rho$,
$\rho$, ![]() $\alpha _i$ to denote them. Then
$\alpha _i$ to denote them. Then ![]() $\rho (\mathcal {B}) = \operatorname {Ker}(\alpha _i) \times _S \cdots \times _S \operatorname {Ker}(\alpha _m)$. It suffices to take
$\rho (\mathcal {B}) = \operatorname {Ker}(\alpha _i) \times _S \cdots \times _S \operatorname {Ker}(\alpha _m)$. It suffices to take ![]() $\mathcal {B}_i = \operatorname {Ker}(\alpha _i)$.
$\mathcal {B}_i = \operatorname {Ker}(\alpha _i)$.
The ‘Moreover’ part of (10.3) follows from the same argument and the equality ![]() $q_1 \circ \tau = q_1$ above.
$q_1 \circ \tau = q_1$ above.