Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aizenbud, Avraham
Gourevitch, Dmitry
and
Sayag, Eitan
2009.
Generalized Harish-Chandra descent, Gelfand pairs, and an Archimedean analog of Jacquet-Rallis's theorem.
Duke Mathematical Journal,
Vol. 149,
Issue. 3,
Aizenbud, Avraham
Gourevitch, Dmitry
Rallis, Stephen
and
Schiffmann, Gérard
2010.
Multiplicity one theorems.
Annals of Mathematics,
Vol. 172,
Issue. 2,
p.
1413.
Zhang, Lei
2010.
Gelfand pairs(Sp4n(F),Sp2n(E)).
Journal of Number Theory,
Vol. 130,
Issue. 11,
p.
2428.
Jiang, Dihua
Sun, Binyong
and
Zhu, Chen-Bo
2010.
Uniqueness of Ginzburg-Rallis models: The Archimedean case.
Transactions of the American Mathematical Society,
Vol. 363,
Issue. 5,
p.
2763.
Sun, Binyong
and
Zhu, Chen-Bo
2011.
A general form of Gelfand–Kazhdan criterion.
Manuscripta Mathematica,
Vol. 136,
Issue. 1-2,
p.
185.
Aizenbud, Avraham
Offen, Omer
and
Sayag, Eitan
2011.
Disjoint pairs for GLn(R) and GLn(C).
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 1-2,
p.
9.
Feigon, Brooke
Lapid, Erez
and
Offen, Omer
2012.
On representations distinguished by unitary groups.
Publications mathématiques de l'IHÉS,
Vol. 115,
Issue. 1,
p.
185.
Sun, Binyong
and
Zhu, Chen-Bo
2012.
Multiplicity one theorems: the Archimedean case.
Annals of Mathematics,
Vol. 175,
Issue. 1,
p.
23.
Gourevitch, Dmitry
Offen, Omer
Sahi, Siddhartha
and
Sayag, Eitan
2012.
Existence of Klyachko models for GL(n,R) and GL(n,C).
Journal of Functional Analysis,
Vol. 262,
Issue. 8,
p.
3585.
Venketasubramanian, C. G.
2013.
On representations of GL(n) distinguished by GL(n − 1) over a p-adic field.
Israel Journal of Mathematics,
Vol. 194,
Issue. 1,
p.
1.
Aizenbud, Avraham
2013.
A partial analog of the integrability theorem for distributions on p-adic spaces and applications.
Israel Journal of Mathematics,
Vol. 193,
Issue. 1,
p.
233.
GOUREVITCH, DMITRY
SAHI, SIDDHARTHA
and
SAYAG, EITAN
2015.
INVARIANT FUNCTIONALS ON SPEH REPRESENTATIONS.
Transformation Groups,
Vol. 20,
Issue. 4,
p.
1023.
Chai, Jingsong
2015.
Some results on archimedean Rankin–Selberg integrals.
Pacific Journal of Mathematics,
Vol. 273,
Issue. 2,
p.
277.
Lapid, Erez
and
Mao, Zhengyu
2015.
Model Transition for Representations of Metaplectic Type.
International Mathematics Research Notices,
Vol. 2015,
Issue. 19,
p.
9486.
Kemarsky, Alexander
2015.
Gamma factors of distinguished representations of GLn(ℂ).
Pacific Journal of Mathematics,
Vol. 278,
Issue. 1,
p.
137.
Kemarsky, Alexander
2015.
Distinguished representations of GL n (ℂ).
Israel Journal of Mathematics,
Vol. 207,
Issue. 1,
p.
435.
Sécherre, Vincent
and
Venketasubramanian, Coolimuttam G.
2016.
Modular Representations of ${\rm GL}{(n)}$ Distinguished by ${\rm GL}{(n-1)}$ over a $p$-Adic Field.
International Mathematics Research Notices,
p.
rnw150.
Alldridge, Alexander
2016.
Fréchet Globalisations of Harish-Chandra Supermodules.
International Mathematics Research Notices,
p.
rnw155.
Alesker, Semyon
Gourevitch, Dmitry
and
Sahi, Siddhartha
2016.
On an analytic description of the α-cosine transform on real Grassmannians.
Communications in Contemporary Mathematics,
Vol. 18,
Issue. 02,
p.
1550025.
Aizenbud, Avraham
and
Sayag, Eitan
2020.
Homological multiplicities in representation theory of p-adic groups.
Mathematische Zeitschrift,
Vol. 294,
Issue. 1-2,
p.
451.

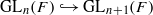 and the two-sided action of GL
and the two-sided action of GL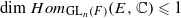 . For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.
. For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.