Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:14:12.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke action on the principal block

Part of: Linear algebraic groups and related topics (Co)homology theory Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  19 July 2022

Roman Bezrukavnikov  and
Simon Riche
Roman Bezrukavnikov
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA bezrukav@math.mit.edu
Simon Riche
Affiliation:
Université Clermont Auvergne, CNRS, LMBP, F-63000 Clermont-Ferrand, France simon.riche@uca.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we construct an action of the affine Hecke category (in its ‘Soergel bimodules’ incarnation) on the principal block of representations of a simply connected semisimple algebraic group over an algebraically closed field of characteristic bigger than the Coxeter number. This confirms a conjecture of G. Williamson and the second author, and provides a new proof of the tilting character formula in terms of antispherical 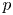$p$-Kazhdan–Lusztig polynomials.

Keywords

Hecke categoryreductive algebraic groupsaffine Weyl group

MSC classification

Primary: 20G05: Representation theory
Secondary: 17B45: Lie algebras of linear algebraic groups 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 5 , May 2022 , pp. 953 - 1019
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

R.B. was supported by NSF grant no. DMS-1601953, and his work was partly supported by grants from the Institute for Advanced Study and Carnegie Corporation of New York. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (S.R., grant agreements no. 677147 and no. 101002592).

References

Abe, N., A Hecke action on $G_1T$-modules, Preprint (2019), arXiv:1904.11350.Google Scholar
Abe, N., A homomorphism between Bott–Samelson bimodules, Preprint (2020), arXiv:2012.09414.Google Scholar
Abe, N., A bimodule description of the Hecke category, Compos. Math. 157 (2021), 2133–2159.10.1112/S0010437X21007466CrossRefGoogle Scholar
Achar, P., Makisumi, S., Riche, S. and Williamson, G., Free-monodromic mixed tilting sheaves on flag varieties, Preprint (2017), arXiv:1703.05843.Google Scholar
Achar, P., Makisumi, S., Riche, S. and Williamson, G., Koszul duality for Kac–Moody groups and characters of tilting modules, J. Amer. Math. Soc. 32 (2019), 261–310.10.1090/jams/905CrossRefGoogle Scholar
Atiyah, M. and Macdonald, I., Introduction to commutative algebra (Addison-Wesley, 1969).Google Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 1–67.10.1007/s10240-015-0077-xCrossRefGoogle Scholar
Bezrukavnikov, R. and Mirković, I., Representations of semisimple Lie algebras in prime characteristic and the noncommutative Springer resolution, with an appendix by E. Sommers, Ann. of Math. (2) 178 (2013), 835–919.10.4007/annals.2013.178.3.2CrossRefGoogle Scholar
Bezrukavnikov, R., Mirković, I. and Rumynin, D., Singular localization and intertwining functors for reductive Lie algebras in prime characteristic, Nagoya Math. J. 184 (2006), 1–55.10.1017/S0027763000009302CrossRefGoogle Scholar
Bezrukavnikov, R., Mirković, I. and Rumynin, D., Localization of modules for a semisimple Lie algebra in prime characteristic, with an appendix by R. Bezrukavnikov and S. Riche, Ann. of Math. (2) 167 (2008), 945–991.10.4007/annals.2008.167.945CrossRefGoogle Scholar
Bezrukavnikov, R. and Riche, S., Affine braid group actions on Springer resolutions, Ann. Sci. Éc. Norm. Supér. 45 (2012), 535–599.10.24033/asens.2173CrossRefGoogle Scholar
Bezrukavnikov, R., Riche, S. and Rider, L., Modular affine Hecke category and regular unipotent centralizer, I, Preprint (2020), arXiv:2005.05583.Google Scholar
Bouthier, A. and Cesnavicius, K., Torsors on loop groups and the Hitchin fibration, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2019), arXiv:1908.07480.Google Scholar
Brion, M. and Kumar, S., Frobenius splitting methods in geometry and representation theory, Progress in Mathematics, vol. 231 (Birkhäuser, Boston, 2005).10.1007/b137486CrossRefGoogle Scholar
Brown, K. A. and Goodearl, K. R., Homological aspects of Noetherian PI Hopf algebras and irreducible modules of maximal dimension, J. Algebra 198 (1997), 240–265.10.1006/jabr.1997.7109CrossRefGoogle Scholar
Brown, K. A. and Gordon, I., The ramification of centres: Lie algebras in positive characteristic and quantised enveloping algebras, Math. Z. 238 (2001), 733–779.10.1007/s002090100274CrossRefGoogle Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, 1997).Google Scholar
Ciappara, J., Hecke category actions via Smith–Treumann theory, Preprint (2021), arXiv:2103.07091.Google Scholar
Dodd, C., Equivariant coherent sheaves, Soergel bimodules, and categorification of affine Hecke algebras, Preprint (2011), arXiv:1108.4028.Google Scholar
Elias, B., Gaitsgory's central sheaves via the diagrammatic Hecke category, Preprint (2018), arXiv:11.06188.Google Scholar
Elias, B. and Losev, I., Modular representation theory in type A via Soergel bimodules, Preprint (2017), arXiv:1701.00560.Google Scholar
Elias, B. and Williamson, G., Soergel calculus, Represent. Theory 20 (2016), 295–374.10.1090/ert/481CrossRefGoogle Scholar
Elias, B. and Williamson, G., Localized calculus for the Hecke category, Preprint (2020), arXiv:2011.05432.Google Scholar
Härterich, M., Kazhdan–Lusztig-Basen, unzerlegbare Bimoduln und die Topologie der Fahnenmannigfaltigkeit einer Kac–Moody-Gruppe, PhD thesis, University of Freiburg (1999), https://freidok.uni-freiburg.de/data/18.Google Scholar
Jantzen, J. C., Representations of Lie algebras in prime characteristic, notes by Iain Gordon, in Representation theories and algebraic geometry (Montreal, PQ, 1997), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 514 (Kluwer Academic, 1998), 185–235.10.1007/978-94-015-9131-7_5CrossRefGoogle Scholar
Jantzen, J. C., Representations of algebraic groups, second edition, Mathematical Surveys and Monographs, vol. 107 (American Mathematical Society, 2003).Google Scholar
Jantzen, J. C., Nilpotent orbits in representation theory, in Lie theory, Progress in Mathematics, vol. 228 (Birkhäuser, Boston, 2004), 1–211.10.1007/978-0-8176-8192-0CrossRefGoogle Scholar
Jensen, L. T. and Williamson, G., The p-canonical basis for Hecke algebras, in Categorification and higher representation theory, Contemporary Mathematics, vol. 683 (American Mathematical Society, 2017), 333–361.10.1090/conm/683/13719CrossRefGoogle Scholar
Juteau, D., Mautner, C. and Williamson, G., Parity sheaves, J. Amer. Math. Soc. 27 (2014), 1169–1212.10.1090/S0894-0347-2014-00804-3CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras, Invent. Math. 87 (1987), 153–215.10.1007/BF01389157CrossRefGoogle Scholar
Knus, M.-A. and Ojanguren, M., Théorie de la descente et algèbres d'Azumaya, Lecture Notes in Mathematics, vol. 389 (Springer, 1974).10.1007/BFb0057799CrossRefGoogle Scholar
Lusztig, G., Some problems in the representation theory of finite Chevalley groups, in The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979), Proceedings of Symposia in Pure Mathematics, vol. 37 (American Mathematical Society, 1980), 313–317.Google Scholar
Mackaay, M. and Thiel, A.-L., Categorifications of the extended affine Hecke algebra and the affine $q$-Schur algebra $\hat {\mathbf {S}}(n, r)$ for $3 \leq r < n$, Quantum Topol. 8 (2017), 113–203.10.4171/QT/88CrossRefGoogle Scholar
Mautner, C. and Riche, S., Exotic tilting sheaves, parity sheaves on affine Grassmannians, and the Mirković–Vilonen conjecture, J. Eur. Math. Soc. 20 (2018), 2259–2332.10.4171/JEMS/812CrossRefGoogle Scholar
Mirković, I. and Rumynin, D., Centers of reduced enveloping algebras, Math. Z. 231 (1999), 123–132.10.1007/PL00004719CrossRefGoogle Scholar
Peskine, C., An algebraic introduction to complex projective geometry. I. Commutative algebra, Cambridge Studies in Advanced Mathematics, vol. 47 (Cambridge University Press, 1996).Google Scholar
Premet, A. and Skryabin, S., Representations of restricted Lie algebras and families of associative $\mathscr {L}$-algebras, J. Reine Angew. Math. 507 (1999), 189–218.10.1515/crll.1999.507.189CrossRefGoogle Scholar
Riche, S., Koszul duality and modular representations of semi-simple Lie algebras, Duke Math. J. 154 (2010), 31–134.10.1215/00127094-2010-034CrossRefGoogle Scholar
Riche, S., Kostant section, universal centralizer, and a modular derived Satake equivalence, Math. Z. 286 (2017), 223–261.10.1007/s00209-016-1761-3CrossRefGoogle Scholar
Riche, S. and Williamson, G., Tilting modules and the $p$-canonical basis, Astérisque 397 (2018).Google Scholar
Riche, S. and Williamson, G., Smith–Treumann theory and the linkage principle, Publ. Math. Inst. Hautes Études Sci., to appear. Preprint (2020), arXiv:2003.08522.Google Scholar
Rouquier, R., $2$-Kac–Moody algebras, Preprint (2008), arXiv:0812.5023.Google Scholar
A. Grothendieck and M. Raynaud, Revêtements étales et groupe fondamental (SGA 1), in Documents Mathématiques (Paris), vol. 3 (Société Mathématique de France, 2003). Updated and annotated reprint of the 1971 original.10.1007/BFb0058656CrossRefGoogle Scholar
Soergel, W., The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 429 (1992), 49–74.Google Scholar
Soergel, W., Langlands’ philosophy and Koszul duality, in Algebra—representation theory (Constanta, 2000), NATO Science Series II: Mathematics, Physics and Chemistry, vol. 28 (Kluwer Academic, 2001), 379–414.10.1007/978-94-010-0814-3_17CrossRefGoogle Scholar
Soergel, W., Kazhdan–Lusztig-Polynome und unzerlegbare Bimoduln über Polynomringen, J. Inst. Math. Jussieu 6 (2007), 501–525.10.1017/S1474748007000023CrossRefGoogle Scholar
The Stacks Project authors, The Stacks Project (2020), https://stacks.math.columbia.edu.Google Scholar
Verma, D.-N., The rôle of affine Weyl groups in the representation theory of algebraic Chevalley groups and their Lie algebras, in Lie groups and their representations (Proc. Summer School, Bolyai János Math. Soc., Budapest, 1971) (Halsted, 1975), 653–705.Google Scholar
Williamson, G., Parity sheaves and the Hecke category, in Proceedings of the International Congress of Mathematicians–Rio de Janeiro 2018. Vol. I. Plenary lectures (World Scientific, 2018), 979–1015.Google Scholar