Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:07:54.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Height pairings on orthogonal Shimura varieties

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  02 March 2017

Fabrizio Andreatta ,
Eyal Z. Goren ,
Benjamin Howard  and
Keerthi Madapusi Pera
Fabrizio Andreatta
Affiliation:
Dipartimento di Matematica ‘Federigo Enriques’, Università di Milano, via C. Saldini 50, Milano, Italia email fabrizio.andreatta@unimi.it
Eyal Z. Goren
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke St. West, Montreal, QC, Canada email eyal.goren@mcgill.ca
Benjamin Howard
Affiliation:
Department of Mathematics, Boston College, 140 Commonwealth Ave, Chestnut Hill, MA, USA email howardbe@bc.edu
Keerthi Madapusi Pera
Affiliation:
Department of Mathematics, University of Chicago, 5734 S University Ave, Chicago, IL, USA email keerthi@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

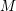Let $M$ be the Shimura variety associated to the group of spinor similitudes of a quadratic space over 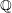$\mathbb{Q}$ of signature 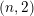$(n,2)$. We prove a conjecture of Bruinier and Yang, relating the arithmetic intersection multiplicities of special divisors and complex multiplication points on 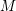$M$ to the central derivatives of certain 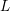$L$-functions. Each such $L$-function is the Rankin–Selberg convolution associated with a cusp form of half-integral weight 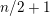$n/2+1$, and the weight 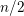$n/2$ theta series of a positive definite quadratic space of rank $n$. When 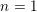$n=1$ the Shimura variety 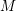$M$ is a classical quaternionic Shimura curve, and our result is a variant of the Gross–Zagier theorem on heights of Heegner points.

Keywords

Shimura varietiesarithmetic intersection theorycomplex multiplicationspecial divisor

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties 14G40: Arithmetic varieties and schemes; Arakelov theory; heights
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 3 , March 2017 , pp. 474 - 534
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F., Goren, E. Z., Howard, B. and Madapusi Pera, K., Faltings heights of abelian varieties with complex multiplication, Preprint (2015), arXiv:1508.00178.Google Scholar
Bass, H., Clifford algebras and spinor norms over a commutative ring , Amer. J. Math. 96 (1974), 156–206.Google Scholar
Borcherds, R. E., Automorphic forms with singularities on Grassmannians , Invent. Math. 132 (1998), 491–562.Google Scholar
Bruinier, J. H., Borcherds products on O (2, l) and Chern classes of Heegner divisors, Lecture Notes in Mathematics, vol. 1780 (Springer, 2002).Google Scholar
Bruinier, J. H. and Funke, J., On two geometric theta lifts , Duke Math. J. 125 (2004), 45–90.Google Scholar
Bruinier, J. H., Howard, B. and Yang, T., Heights of Kudla–Rapoport divisors and derivatives of L-functions , Invent. Math. 201 (2015), 1–95.Google Scholar
Bruinier, J. H., Kudla, S. S. and Yang, T., Special values of Green functions at big CM points , Int. Math. Res. Not. IMRN (2012), 1917–1967.Google Scholar
Bruinier, J. H. and Yang, T., Faltings heights of CM cycles and derivatives of L-functions , Invent. Math. 177 (2009), 631–681.Google Scholar
Deligne, P., Travaux de Shimura , in Séminaire Bourbaki, Vol. 1970/71, Exposés 382–399, Lecture Notes in Mathematics, vol. 244 (Springer, Berlin, Heidelberg, 1972), 123–165.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of abelian varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 22 (Springer, Berlin, 1990).Google Scholar
Fantechi, B., Göttsche, L., Illusie, L., Kleiman, S. L., Nitsure, N. and Vistoli, A., Fundamental algebraic geometry, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Gillet, H. and Soulé, C., Arithmetic intersection theory , Publ. Math. Inst. Hautes Études Sci. 72 (1990), 94–174.CrossRefGoogle Scholar
Gross, B. H., On canonical and quasi-canonical liftings , Invent. Math. 84 (1986), 321–326.CrossRefGoogle Scholar
Hida, H., p-adic automorphic forms on Shimura varieties, Springer Monographs in Mathematics (Springer, Berlin, Heidelberg, 2004).Google Scholar
Howard, B., Complex multiplication cycles and Kudla–Rapoport divisors , Ann. of Math. (2) 176 (2012), 1097–1171.CrossRefGoogle Scholar
Howard, B. and Yang, T., Intersections of Hirzebruch–Zagier divisors and CM cycles, Lecture Notes in Mathematics, vol. 2041 (Springer, Berlin, Heidelberg, 2012).Google Scholar
Hu, J., Specialization of Green forms and arithmetic intersection theory, PhD thesis, University of Illinois Chicago (1999).Google Scholar
Kim, W. and Madapusi Pera, K., 2-adic integral canonical models and the Tate conjecture in characteristic 2 , Forum Math. Sigma 4 (2016), e28.Google Scholar
Kisin, M., Integral models for Shimura varieties of abelian type , J. Amer. Math. Soc. 23 (2010), 967–1012.CrossRefGoogle Scholar
Kudla, S. S., Special cycles and derivatives of Eisenstein series , in Heegner Points and Rankin L-Series, Mathematical Sciences Research Institute Publications, vol. 49 (Cambridge University Press, Cambridge, 2004), 243–270.CrossRefGoogle Scholar
Kudla, S. S. and Rapoport, M., Arithmetic Hirzebruch–Zagier cycles , J. Reine Angew. Math. 515 (1999), 155–244.CrossRefGoogle Scholar
Kudla, S. S. and Rapoport, M., Cycles on Siegel threefolds and derivatives of Eisenstein series , Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 695–756.CrossRefGoogle Scholar
Kudla, S. S., Rapoport, M. and Yang, T., On the derivative of an Eisenstein series of weight one , Int. Math. Res. Not. IMRN 7 (1999), 347–385.Google Scholar
Kudla, S. S., Rapoport, M. and Yang, T., Derivatives of Eisenstein series and Faltings heights , Compositio Math. 140 (2004), 887–951.CrossRefGoogle Scholar
Kudla, S. S., Rapoport, M. and Yang, T., Modular forms and special cycles on Shimura curves, Annals of Mathematics Studies, vol. 161 (Princeton University Press, 2006).Google Scholar
Kudla, S. S. and Yang, T., On the pullback of an arithmetic theta function , Manuscripta Math. 140 (2013), 393–440.Google Scholar
Madapusi Pera, K., Integral canonical models for spin Shimura varieties , Compositio Math. 152 (2016), 769–824.Google Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory , Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34 (Springer, Berlin, 1994).Google Scholar
Schofer, J., Borcherds forms and generalizations of singular moduli , J. Reine Angew. Math. 629 (2009), 1–36.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Documents Mathématiques (Paris), vol. 3 (Société Mathématique de France, Paris, 2003).Google Scholar
Tsimerman, J., A proof of the André–Oort conjecture for $A_{g}$ , Preprint (2015),arXiv:1506.01466.Google Scholar
van der Geer, G., Hilbert modular surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 16 (Springer, Berlin, 1988).Google Scholar
Vistoli, A., Intersection theory on algebraic stacks and on their moduli spaces , Invent. Math. 97 (1989), 613–670.Google Scholar
Yang, T., The Chowla–Selberg formula and the Colmez conjecture , Canad. J. Math. 62 (2010), 456–472.Google Scholar