Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T04:07:59.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher preprojective algebras, Koszul algebras, and superpotentials

Part of: Representation theory of rings and algebras Algebraic geometry: Foundations Abelian categories

Published online by Cambridge University Press:  01 February 2021

Joseph Grant  and
Osamu Iyama
Joseph Grant
Affiliation:
School of Mathematics, University of East Anglia, NorwichNR4 7TJ, UKj.grant@uea.ac.uk
Osamu Iyama
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya, 464-8602Japaniyama@math.nagoya-u.ac.jp, iyama@ms.u-tokyo.ac.jp Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo153-8914, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we study higher preprojective algebras, showing that various known results for ordinary preprojective algebras generalize to the higher setting. We first show that the quiver of the higher preprojective algebra is obtained by adding arrows to the quiver of the original algebra, and these arrows can be read off from the last term of the bimodule resolution of the original algebra. In the Koszul case, we are able to obtain the new relations of the higher preprojective algebra by differentiating a superpotential and we show that when our original algebra is 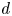$d$-hereditary, all the relations come from the superpotential. We then construct projective resolutions of all simple modules for the higher preprojective algebra of a 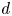$d$-hereditary algebra. This allows us to recover various known homological properties of the higher preprojective algebras and to obtain a large class of almost Koszul dual pairs of algebras. We also show that when our original algebra is Koszul there is a natural map from the quadratic dual of the higher preprojective algebra to a graded trivial extension algebra.

Keywords

preprojective algebraJacobi algebrasuperpotentialCalabi–Yau algebraperiodic resolution

MSC classification

Primary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers
Secondary: 18E30: Derived categories, triangulated categories 14A22: Noncommutative algebraic geometry 16G20: Representations of quivers and partially ordered sets
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2588 - 2627
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

J.G. was supported first by the Japan Society for the Promotion of Science and then by the Engineering and Physical Sciences Research Council [grant number EP/G007497/1]. O.I. was supported by JSPS Grant-in-Aid for Scientific Research (B) 24340004, (B) 16H03923, (C) 18K03209 and (S) 15H05738.

References

Amiot, C. and Oppermann, S., Higher preprojective algebras and stably Calabi–Yau properties, Math. Res. Lett. 21 (2014), 617–647.CrossRefGoogle Scholar
Artin, M. and Schelter, W., Graded algebras of global dimension 3, Adv. Math. 66 (1987), 171–216.CrossRefGoogle Scholar
Auslander, M., Rational singularities and almost split sequences, Trans. Amer. Math. Soc. 293 (1986), 511–531.CrossRefGoogle Scholar
Baer, D., Geigle, W. and Lenzing, H., The preprojective algebra of a tame hereditary Artin algebra, Comm. Algebra 15 (1987), 425–457.CrossRefGoogle Scholar
Bautista, R. and López-Aguayo, D., Potentials for some tensor algebras, Preprint (2015), arXiv:1506.05880.Google Scholar
Beilinson, A., Ginzburg, V. and Soergel, W., Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9 (1996), 473–527.CrossRefGoogle Scholar
Bocklandt, R., Schedler, T. and Wemyss, M., Superpotentials and higher order derivations, J. Pure Appl. Algebra 214 (2010), 1501–1522.CrossRefGoogle Scholar
Braverman, A. and Gaitsgory, D., Poincaré–Birkhoff–Witt theorem for quadratic algebras of Koszul type, J. Algebra 181 (1996), 315–328.CrossRefGoogle Scholar
Brenner, S., Butler, M. and King, A., Periodic algebras which are almost Koszul, Algebr. Represent. Theory 5 (2002), 331–367.CrossRefGoogle Scholar
Bridgeland, T. and Stern, D., Helices on del Pezzo surfaces and tilting Calabi–Yau algebras, Adv. Math. 224 (2010), 1672–1716.Google Scholar
Buchweitz, R. O. and Hille, L., Higher representation–infinite algebras from geometry, in Representation theory of quivers and finite dimensional algebras, Oberwolfach Reports, vol. 11(1) (EMS Publishing House, 2014), 466–469.CrossRefGoogle Scholar
Butler, M. and King, A., Minimal resolutions of algebras, J. Algebra 212 (1999), 323–362.CrossRefGoogle Scholar
Crawley-Boevey, W., Notes on homological properties of preprojective algebras, unpublished manuscript, November 1998.Google Scholar
Crawley-Boevey, W., Preprojective algebras, differential operators and a Conze embedding for deformations of Kleinian singularities, Comment. Math. Helv. 74 (1999), 548–574.CrossRefGoogle Scholar
Crawley-Boevey, W., On the exceptional fibres of Kleinian singularities, Amer. J. Math. 122 (2000), 1027–1037.CrossRefGoogle Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations I: mutations, Selecta Math. (N.S.) 14 (2008), 59–119.CrossRefGoogle Scholar
Dlab, V. and Ringel, C., The preprojective algebra of a modulated graph, in Representation theory, II (Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979), Lecture Notes in Mathematics, vol. 832 (Springer, Berlin, 1980), 216–231.Google Scholar
Dubois-Violette, M., Multilinear forms and graded algebras, J. Algebra 317 (2007), 198–225.Google Scholar
Dugas, A., Periodicity of $d$-cluster-tilted algebras, J. Algebra 368 (2012), 40–52.CrossRefGoogle Scholar
Evans, D. and Pugh, M., The Nakayama automorphism of the almost Calabi–Yau algebras associated to $SU(3)$ modular invariants, Comm. Math. Phys. 312 (2012), 179–222.Google Scholar
Evans, D. and Pugh, M., On the homology of almost Calabi–Yau algebras associated to $SU(3)$ modular invariants, J. Algebra 368 (2012), 92–125.CrossRefGoogle Scholar
Geigle, W. and Lenzing, H., Perpendicular categories with applications to representations and sheaves, J. Algebra 144 (1991), 273–343.CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J., Cluster algebras in algebraic Lie theory, Transform. Groups 18 (2013), 149–178.CrossRefGoogle Scholar
Gelfand, I. M. and Ponomarev, V. A., Model algebras and representations of graphs, Funktsional. Anal. i Prilozhen. 13 (1979), 1–12.Google Scholar
Grant, J., Higher zigzag algebras, Doc. Math. 24 (2019), 749–814.Google Scholar
Green, E., Snashall, N. and Solberg, Ø., The Hochschild cohomology ring of a selfinjective algebra of finite representation type, Proc. Amer. Math. Soc. 131 (2003), 3387–3393.CrossRefGoogle Scholar
Guo, J., On trivial extensions and higher preprojective algebras, J. Algebra 547 (2020), 379–397.CrossRefGoogle Scholar
Herschend, M. and Iyama, O., Selfinjective quivers with potential and $2$-representation-finite algebras, Compos. Math. 147 (2011), 1885–1920.CrossRefGoogle Scholar
Herschend, M., Iyama, O., Minamoto, H. and Oppermann, S., Representation theory of Geigle-Lenzing complete intersections, Mem. Amer. Math. Soc., to appear. Preprint (2014), arXiv:1409.0668.Google Scholar
Herschend, M., Iyama, O. and Oppermann, S., $n$-representation infinite algebras, Adv. Math. 252 (2014), 292–342.CrossRefGoogle Scholar
Hille, L., Consistent algebras and special tilting sequences, Math. Z. 220 (1995), 189–205.CrossRefGoogle Scholar
Huerfano, R. S. and Khovanov, M., A category for the adjoint representation, J. Algebra 246 (2001), 514–542.CrossRefGoogle Scholar
Ivanov, S. O. and Volkov, Y. V., Stable Calabi–Yau dimension of self-injective algebras of finite type, J. Algebra 413 (2014), 72–99.CrossRefGoogle Scholar
Iyama, O., Higher-dimensional Auslander–Reiten theory on maximal orthogonal subcategories, Adv. Math. 210 (2007), 22–50.CrossRefGoogle Scholar
Iyama, O., Cluster tilting for higher Auslander algebras, Adv. Math. 226 (2011), 1–61.CrossRefGoogle Scholar
Iyama, O. and Oppermann, S., $n$-representation-finite algebras and $n$-APR tilting, Trans. Amer. Math. Soc. 363 (2011), 6575–6614.CrossRefGoogle Scholar
Iyama, O. and Oppermann, S., Stable categories of higher preprojective algebras, Adv. Math. 244 (2013), 23–68.CrossRefGoogle Scholar
Iyama, O. and Yoshino, Y., Mutation in triangulated categories and rigid Cohen–Macaulay modules, Invent. Math. 172 (2008), 117–168.CrossRefGoogle Scholar
Kashiwara, M. and Saito, Y., Geometric construction of crystal bases, Duke Math. J. 89 (1997), 9–36.CrossRefGoogle Scholar
Keller, B., Deformed Calabi–Yau completions, J. Reine Angew. Math. 654 (2011), 125–180. With an appendix by M. Van den Bergh.Google Scholar
Labardini-Fragoso, D. and Zelevinsky, A., Strongly primitive species with potentials I: mutations, Bol. Soc. Mat. Mex. (3) 22 (2016), 47–115.CrossRefGoogle Scholar
Lusztig, G., Quivers, perverse sheaves, and quantized enveloping algebras, J. Amer. Math. Soc. 4 (1991), 365–421.CrossRefGoogle Scholar
Martínez-Villa, R., Serre duality for generalized Auslander regular algebras, in Trends in the representation theory of finite-dimensional algebras (Seattle, WA, 1997), Contemp. Math., vol. 229 (Amer. Math. Soc., Providence, RI, 1998), 237–263.CrossRefGoogle Scholar
Martínez-Villa, R., Graded, selfinjective, and Koszul algebras, J. Algebra 215 (1999), 34–72.CrossRefGoogle Scholar
Martínez-Villa, R. and Solberg, O., Artin–Schelter regular algebras and categories, J. Pure Appl. Algebra 215 (2011), 546–565.CrossRefGoogle Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings, Graduate Studies in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Minamoto, H., Ampleness of two-sided tilting complexes, Int. Math. Res. Not. IMRN 2012 (2012), 67–101.CrossRefGoogle Scholar
Minamoto, H. and Mori, I., The structure of AS-Gorenstein algebras, Adv. Math. 226 (2011), 4061–4095.CrossRefGoogle Scholar
Mori, I. and Smith, P., $m$-Koszul Artin–Schelter regular algebras, J. Algebra 446 (2016), 373–399.CrossRefGoogle Scholar
Nakajima, H., Instantons on ALE spaces, quiver varieties, and Kac-Moody algebras, Duke Math. J. 76 (1994), 365–416.CrossRefGoogle Scholar
Nastasescu, C. and Van Oystaeyen, F., Graded and filtered rings and modules, Lecture Notes in Mathematics, vol. 758 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Nastasescu, C. and Van Oystaeyen, F., Methods of graded rings, Lecture Notes in Mathematics, vol. 1836 (Springer, Berlin, 2004).CrossRefGoogle Scholar
Nguefack, B., Potentials and Jacobian algebras for tensor algebras of bimodules, Preprint (2010), arXiv:1004.2213.Google Scholar
Priddy, S., Koszul resolutions, Trans. Amer. Math. Soc. 152 (1970), 39–60.CrossRefGoogle Scholar
Reyes, M. and Rogalski, D., Graded twisted Calabi–Yau algebras are generalized Artin–Schelter regular, Preprint (2018), arXiv:1807.10249.Google Scholar
Rickard, J., Equivalences of derived categories for symmetric algebras, J. Algebra 257 (2002), 460–481.CrossRefGoogle Scholar
Ringel, C., The preprojective algebra of a quiver, in Algebras and modules, II (Geiranger, 1996), CMS Conference Proceedings, vol. 24 (American Mathematical Society, Providence, RI, 1998), 467–480.Google Scholar
Ringel, C. and Schofield, A., Wild algebras with periodic Auslander–Reiten translate, unpublished manuscript.Google Scholar
Thibault, L.-P., Preprojective algebra structure on skew-group algebras, Adv. Math. 365 (2020), 107033.CrossRefGoogle Scholar
Van den Bergh, M., Calabi–Yau algebras and superpotentials, Selecta Math. (N.S.) 21 (2015), 555–603.CrossRefGoogle Scholar
Vaso, L., $n$-Cluster tilting subcategories of representation-directed algebras, J. Pure Appl. Algebra 223 (2019), 2101–2122.CrossRefGoogle Scholar
Weibel, C., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar