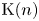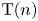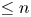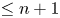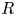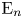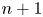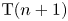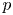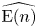1. Introduction
1.1 Overview
1.1.1 Descent and redshift
Algebraic K-theory ![]() $\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ is a rich invariant of stable
$\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ is a rich invariant of stable ![]() $\infty$-categories and thus of rings and ring spectra. Ausoni and Rognes [Reference Ausoni and RognesAR02, Reference Ausoni and RognesAR08] suggested a fascinating program concerning the interaction between algebraic K-theory and the chromatic filtration on spectra, now known as the redshift philosophy. Namely, that algebraic K-theory increases the chromatic height of ring spectra by
$\infty$-categories and thus of rings and ring spectra. Ausoni and Rognes [Reference Ausoni and RognesAR02, Reference Ausoni and RognesAR08] suggested a fascinating program concerning the interaction between algebraic K-theory and the chromatic filtration on spectra, now known as the redshift philosophy. Namely, that algebraic K-theory increases the chromatic height of ring spectra by ![]() $1$. They demonstrated this phenomenon at height
$1$. They demonstrated this phenomenon at height ![]() $1$, and conjectured that it persists to arbitrary heights. Another interesting aspect of algebraic K-theory is its descent properties. For example, it is known by [Reference Thomason and TrobaughTT90] that it satisfies Nisnevich descent for ordinary rings, while it fails to satisfy étale descent due to its failure to satisfy Galois descent. The recent breakthroughs of [Reference Clausen, Mathew, Naumann and NoelCMNN20, Reference Land, Mathew, Meier and TammeLMMT20] have shown that chromatically localized K-theory does satisfy Galois descent under certain hypotheses, which was used to prove the following part of the redshift conjecture.
$1$, and conjectured that it persists to arbitrary heights. Another interesting aspect of algebraic K-theory is its descent properties. For example, it is known by [Reference Thomason and TrobaughTT90] that it satisfies Nisnevich descent for ordinary rings, while it fails to satisfy étale descent due to its failure to satisfy Galois descent. The recent breakthroughs of [Reference Clausen, Mathew, Naumann and NoelCMNN20, Reference Land, Mathew, Meier and TammeLMMT20] have shown that chromatically localized K-theory does satisfy Galois descent under certain hypotheses, which was used to prove the following part of the redshift conjecture.
Theorem 1.1 [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem A]
Let ![]() $R \in \operatorname {CAlg}(\mathrm {Sp})$ and
$R \in \operatorname {CAlg}(\mathrm {Sp})$ and ![]() $n \geq 0$. If
$n \geq 0$. If ![]() $L_{\mathrm {T}(n)} R = 0$, then
$L_{\mathrm {T}(n)} R = 0$, then ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}(R) = 0$.
$L_{\mathrm {T}(n+1)} \mathrm {K}(R) = 0$.
In addition, Hahn and Wilson [Reference Hahn and WilsonHW22] and Yuan [Reference YuanYua21] give the first examples of non-vanishing of ![]() $\mathrm {T}(n+1)$-localized K-theory for ring spectra of chromatic height
$\mathrm {T}(n+1)$-localized K-theory for ring spectra of chromatic height ![]() $n$, at arbitrary heights
$n$, at arbitrary heights ![]() $n \geq 0$. Building on this, Burklund, Yuan, and the second author [Reference Burklund, Schlank and YuanBSY22] have recently proved the non-vanishing of
$n \geq 0$. Building on this, Burklund, Yuan, and the second author [Reference Burklund, Schlank and YuanBSY22] have recently proved the non-vanishing of ![]() $\mathrm {T}(n+1)$-localized K-theory for all commutative ring spectra of chromatic height
$\mathrm {T}(n+1)$-localized K-theory for all commutative ring spectra of chromatic height ![]() $n$.
$n$.
1.1.2 Higher semiadditivity
Hopkins and Lurie [Reference Hopkins and LurieHL13, Theorem 5.2.1] and Carmeli, Yanovski, and the second author [Reference Carmeli, Schlank and YanovskiCSY22, Theorem A] proved that the chromatically localized ![]() $\infty$-categories
$\infty$-categories ![]() $\mathrm {Sp}_{\mathrm {K}(n)}$ and
$\mathrm {Sp}_{\mathrm {K}(n)}$ and ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$ (respectively) are
$\mathrm {Sp}_{\mathrm {T}(n)}$ (respectively) are ![]() $\infty$-semiadditive. Namely, that there is a canonical natural equivalence between limits and colimits indexed by
$\infty$-semiadditive. Namely, that there is a canonical natural equivalence between limits and colimits indexed by ![]() $\pi$-finite spaces (i.e. spaces with finitely many connected components and finitely many non-zero homotopy groups all of which are finite). In this paper, we will only make use of
$\pi$-finite spaces (i.e. spaces with finitely many connected components and finitely many non-zero homotopy groups all of which are finite). In this paper, we will only make use of ![]() $p$-typical higher semiadditivity, that is, relaxing the condition to
$p$-typical higher semiadditivity, that is, relaxing the condition to ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces (i.e.
$p$-spaces (i.e. ![]() $\pi$-finite spaces whose homotopy groups are all
$\pi$-finite spaces whose homotopy groups are all ![]() $p$-groups), which we thus simply call higher semiadditivity.
$p$-groups), which we thus simply call higher semiadditivity.
Harpaz [Reference HarpazHar20] studied the connection between ![]() $\infty$-semiadditivity and
$\infty$-semiadditivity and ![]() $\infty$-commutative monoids. Recall that a (
$\infty$-commutative monoids. Recall that a (![]() $0$-)commutative monoid is, roughly speaking, the structure of summation of finite families of elements (in a coherently associative and commutative way). Similarly, a (
$0$-)commutative monoid is, roughly speaking, the structure of summation of finite families of elements (in a coherently associative and commutative way). Similarly, a (![]() $p$-typical)
$p$-typical) ![]() $\infty$-commutative monoid is, roughly speaking, the structure of ‘integration’ of families of elements indexed by a
$\infty$-commutative monoid is, roughly speaking, the structure of ‘integration’ of families of elements indexed by a ![]() $\pi$-finite
$\pi$-finite ![]() $p$-space (in a coherently associative and commutative way). More precisely, given an
$p$-space (in a coherently associative and commutative way). More precisely, given an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$, the
$\mathcal {C}$, the ![]() $\infty$-category of (
$\infty$-category of (![]() $p$-typical)
$p$-typical) ![]() $\infty$-commutative monoids in
$\infty$-commutative monoids in ![]() $\mathcal {C}$ is defined to be
$\mathcal {C}$ is defined to be ![]() $\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {C})} = \operatorname {Fun}^{\mathrm {seg}}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op},\mathcal {C})$, the full subcategory of those functors from spans of
$\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {C})} = \operatorname {Fun}^{\mathrm {seg}}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op},\mathcal {C})$, the full subcategory of those functors from spans of ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces that satisfy the
$p$-spaces that satisfy the ![]() $\infty$-Segal condition. In [Reference HarpazHar20, Corollary 5.19] and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.1] it is shown that the property of being a (
$\infty$-Segal condition. In [Reference HarpazHar20, Corollary 5.19] and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.1] it is shown that the property of being a (![]() $p$-typically)
$p$-typically) ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-category is classified by the mode
$\infty$-category is classified by the mode ![]() $\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ of
$\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ of ![]() $\infty$-commutative monoids in spaces.Footnote 1 That is, a presentable
$\infty$-commutative monoids in spaces.Footnote 1 That is, a presentable ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ is
$\mathcal {C}$ is ![]() $\infty$-semiadditive if and only if it admits a (necessarily unique) module structure over
$\infty$-semiadditive if and only if it admits a (necessarily unique) module structure over ![]() $\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ in
$\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ in ![]() $\mathrm {Pr}^\mathrm {L}$. Furthermore, any object
$\mathrm {Pr}^\mathrm {L}$. Furthermore, any object ![]() $X \in \mathcal {C}$ in an
$X \in \mathcal {C}$ in an ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ is canonically endowed with the structure of an
$\mathcal {C}$ is canonically endowed with the structure of an ![]() $\infty$-commutative monoid, that is, there is an equivalence
$\infty$-commutative monoid, that is, there is an equivalence ![]() $\mathcal {C} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_{\infty }^{(p)}{(\mathcal {C})}$.
$\mathcal {C} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_{\infty }^{(p)}{(\mathcal {C})}$.
Using this ![]() $\infty$-commutative monoid structure, [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 3.1.6] introduces the semiadditive height of an object
$\infty$-commutative monoid structure, [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 3.1.6] introduces the semiadditive height of an object ![]() $X \in \mathcal {C}$, denoted by
$X \in \mathcal {C}$, denoted by ![]() $\mathrm {ht}(X)$. The notion of semiadditive height, which is defined in arbitrary
$\mathrm {ht}(X)$. The notion of semiadditive height, which is defined in arbitrary ![]() $\infty$-semiadditive
$\infty$-semiadditive ![]() $\infty$-categories, is related to the chromatic height. For example, all objects of
$\infty$-categories, is related to the chromatic height. For example, all objects of ![]() $\mathrm {Sp}_{\mathrm {K}(n)}$ and
$\mathrm {Sp}_{\mathrm {K}(n)}$ and ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$ are of semiadditive height
$\mathrm {Sp}_{\mathrm {T}(n)}$ are of semiadditive height ![]() $n$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.4.5].
$n$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.4.5].
A particularly interesting example of an ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-category, which is studied in [Reference Carmeli, Schlank and YanovskiCSY21a], is the mode classifying the property of being a
$\infty$-category, which is studied in [Reference Carmeli, Schlank and YanovskiCSY21a], is the mode classifying the property of being a ![]() $p$-local stable
$p$-local stable ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-category,
$\infty$-category, ![]() ${{\unicode{x05E6}}} = \mathrm {CMon}_{\infty }^{(p)}{(\mathrm {Sp}_{(p)})}$, consisting of (
${{\unicode{x05E6}}} = \mathrm {CMon}_{\infty }^{(p)}{(\mathrm {Sp}_{(p)})}$, consisting of (![]() $p$-typical)
$p$-typical) ![]() $\infty$-commutative monoids in
$\infty$-commutative monoids in ![]() $p$-local spectra (see Definition 4.11). By construction, there is a canonical map of modes
$p$-local spectra (see Definition 4.11). By construction, there is a canonical map of modes ![]() $(-)^{\mathrm {gpc}}\colon \mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})} \to {{\unicode{x05E6}}}$, which we call the group-completion. In addition, there is a canonical map of modes
$(-)^{\mathrm {gpc}}\colon \mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})} \to {{\unicode{x05E6}}}$, which we call the group-completion. In addition, there is a canonical map of modes ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$, which by [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.14] is a smashing localization, and in particular has a fully faithful right adjoint.
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$, which by [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.14] is a smashing localization, and in particular has a fully faithful right adjoint.
Another important example of an ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-category is
$\infty$-category is ![]() $\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$, consisting of
$\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$, consisting of ![]() $\infty$-categories admitting colimits over all
$\infty$-categories admitting colimits over all ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces (see [Reference HarpazHar20, Theorem 5.23] and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.2.7]). As an
$p$-spaces (see [Reference HarpazHar20, Theorem 5.23] and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.2.7]). As an ![]() $\infty$-semiadditive
$\infty$-semiadditive ![]() $\infty$-category, its objects, which are themselves
$\infty$-category, its objects, which are themselves ![]() $\infty$-categories, can have a semiadditive height. In addition, there is an interplay between the semiadditive height of objects in an
$\infty$-categories, can have a semiadditive height. In addition, there is an interplay between the semiadditive height of objects in an ![]() $\infty$-semiadditive
$\infty$-semiadditive ![]() $\infty$-category and the semiadditive height of the
$\infty$-category and the semiadditive height of the ![]() $\infty$-category itself as an object of
$\infty$-category itself as an object of ![]() $\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$, which we view as the crucial step at which redshift happens.
$\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$, which we view as the crucial step at which redshift happens.
Theorem 1.2 (Semiadditive redshift [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem B])
Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $\infty$-semiadditive
$\infty$-semiadditive ![]() $\infty$-category, then
$\infty$-category, then ![]() $\mathrm {ht}(X) \leq n$ for all
$\mathrm {ht}(X) \leq n$ for all ![]() $X \in \mathcal {C}$ if and only if
$X \in \mathcal {C}$ if and only if ![]() $\mathrm {ht}(\mathcal {C}) \leq n + 1$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n + 1$ as an object of ![]() $\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$.
$\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$.
1.1.3 Higher semiadditive algebraic K-theory of categories
In this paper we study the confluence of the above ideas. As ![]() $\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$ is itself
$\mathrm {Cat}_{\pi \text {-}\mathrm {fin}}$ is itself ![]() $\infty$-semiadditive, the
$\infty$-semiadditive, the ![]() $\infty$-categories therein admit a canonical structure of
$\infty$-categories therein admit a canonical structure of ![]() $\infty$-commutative monoids, called the
$\infty$-commutative monoids, called the ![]() $\infty$-cocartesian structure, via the equivalence
$\infty$-cocartesian structure, via the equivalence ![]() $\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \xrightarrow {(-)^\sqcup } \mathrm {CMon}_{\infty }^{(p)}{(\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}})}$, where the integration of a family of objects is given by their colimit. We observe that the
$\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \xrightarrow {(-)^\sqcup } \mathrm {CMon}_{\infty }^{(p)}{(\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}})}$, where the integration of a family of objects is given by their colimit. We observe that the ![]() $S_\bullet$-construction preserves limits, thus it preserves
$S_\bullet$-construction preserves limits, thus it preserves ![]() $\infty$-commutative monoid structure. This observation along with the group-completion functor described above lead us to the main definition of the present paper. By analogy with the definition of ordinary algebraic K-theory, in Definition 6.5 we define
$\infty$-commutative monoid structure. This observation along with the group-completion functor described above lead us to the main definition of the present paper. By analogy with the definition of ordinary algebraic K-theory, in Definition 6.5 we define ![]() $\infty$-semiadditive algebraic K-theory
$\infty$-semiadditive algebraic K-theory ![]() $\mathrm {K}^{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to {{\unicode{x05E6}}}$ as the composition
$\mathrm {K}^{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to {{\unicode{x05E6}}}$ as the composition
It is immediate from this definition that ![]() $\mathrm {K}^{[\infty ]}$ is
$\mathrm {K}^{[\infty ]}$ is ![]() $\infty$-semiadditive, i.e. preserves (co)limits indexed by
$\infty$-semiadditive, i.e. preserves (co)limits indexed by ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces.
$p$-spaces.
We give a second construction of ![]() $\mathrm {K}^{[\infty ]}$ which connects it to ordinary algebraic K-theory. We show that
$\mathrm {K}^{[\infty ]}$ which connects it to ordinary algebraic K-theory. We show that ![]() $\mathrm {K}^{[\infty ]}(\mathcal {C})$ is obtained by taking the
$\mathrm {K}^{[\infty ]}(\mathcal {C})$ is obtained by taking the ![]() $\infty$-cocartesian structure on
$\infty$-cocartesian structure on ![]() $\mathcal {C}$, applying ordinary algebraic K-theory level-wise, and forcing the result to satisfy the
$\mathcal {C}$, applying ordinary algebraic K-theory level-wise, and forcing the result to satisfy the ![]() $\infty$-Segal condition. More precisely, we define the functor
$\infty$-Segal condition. More precisely, we define the functor ![]() $\mathrm {K}_{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op}, \mathrm {Sp}_{(p)})$ by the composition
$\mathrm {K}_{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op}, \mathrm {Sp}_{(p)})$ by the composition
and construct a natural transformation ![]() $\mathrm {K}_{[\infty ]} \Rightarrow \mathrm {K}^{[\infty ]}$. Then, in Corollary 6.10 we show that after reflecting to the subcategory
$\mathrm {K}_{[\infty ]} \Rightarrow \mathrm {K}^{[\infty ]}$. Then, in Corollary 6.10 we show that after reflecting to the subcategory ![]() ${{\unicode{x05E6}}} \subset \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op}, \mathrm {Sp}_{(p)})$ of functors satisfying the
${{\unicode{x05E6}}} \subset \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)})^\mathrm {op}, \mathrm {Sp}_{(p)})$ of functors satisfying the ![]() $\infty$-Segal condition, the map becomes an equivalence
$\infty$-Segal condition, the map becomes an equivalence ![]() $L^{\mathrm {seg}} \mathrm {K}_{[\infty ]}(\mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[\infty ]}(\mathcal {C}) \in {{\unicode{x05E6}}}$. Note that evaluation of the original map at
$L^{\mathrm {seg}} \mathrm {K}_{[\infty ]}(\mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[\infty ]}(\mathcal {C}) \in {{\unicode{x05E6}}}$. Note that evaluation of the original map at ![]() $* \in \mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)}$ gives a comparison map
$* \in \mathcal {S}_{\pi \text {-}\mathrm {fin}}^{(p)}$ gives a comparison map ![]() $\mathrm {K}(\mathcal {C}) \to \underline {\mathrm {K}^{[\infty ]}(\mathcal {C})} \in \mathrm {Sp}_{(p)}$.
$\mathrm {K}(\mathcal {C}) \to \underline {\mathrm {K}^{[\infty ]}(\mathcal {C})} \in \mathrm {Sp}_{(p)}$.
Using the second construction of ![]() $\mathrm {K}^{[\infty ]}$ and the lax symmetric monoidal structure on ordinary algebraic K-theory, in Theorem 6.18 we endow
$\mathrm {K}^{[\infty ]}$ and the lax symmetric monoidal structure on ordinary algebraic K-theory, in Theorem 6.18 we endow ![]() $\mathrm {K}^{[\infty ]}$ with a lax symmetric monoidal structure. To that end, we prove certain results about Day convolution and its connection to the mode symmetric monoidal structure on
$\mathrm {K}^{[\infty ]}$ with a lax symmetric monoidal structure. To that end, we prove certain results about Day convolution and its connection to the mode symmetric monoidal structure on ![]() $\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ (see Theorem 4.26).
$\mathrm {CMon}_{\infty }^{(p)}{(\mathcal {S})}$ (see Theorem 4.26).
Similar constructions can be carried in the (![]() $p$-typically)
$p$-typically) ![]() $m$-semiadditive context, for any
$m$-semiadditive context, for any ![]() $0 \leq m \leq \infty$. We define an
$0 \leq m \leq \infty$. We define an ![]() $m$-semiadditive version of algebraic K-theory
$m$-semiadditive version of algebraic K-theory ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ from the
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ from the ![]() $\infty$-category of stable
$\infty$-category of stable ![]() $\infty$-categories admitting colimits indexed by
$\infty$-categories admitting colimits indexed by ![]() $m$-finite
$m$-finite ![]() $p$-spaces to the universal
$p$-spaces to the universal ![]() $p$-local stable (
$p$-local stable (![]() $p$-typically)
$p$-typically) ![]() $m$-semiadditive presentable
$m$-semiadditive presentable ![]() $\infty$-category. The case
$\infty$-category. The case ![]() $m=\infty$ is
$m=\infty$ is ![]() $\mathrm {K}^{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to {{\unicode{x05E6}}}$ mentioned above. The case
$\mathrm {K}^{[\infty ]}\colon \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}} \to {{\unicode{x05E6}}}$ mentioned above. The case ![]() $m=0$ reproduces the
$m=0$ reproduces the ![]() $p$-localization of ordinary algebraic K-theory by Example 6.6. The case
$p$-localization of ordinary algebraic K-theory by Example 6.6. The case ![]() $m=1$ is closely related to equivariant algebraic K-theory. In equivariant algebraic K-theory, given finite groups
$m=1$ is closely related to equivariant algebraic K-theory. In equivariant algebraic K-theory, given finite groups ![]() $H < G$, there is a corresponding transfer map. Assuming
$H < G$, there is a corresponding transfer map. Assuming ![]() $H$ and
$H$ and ![]() $G$ are
$G$ are ![]() $p$-groups,
$p$-groups, ![]() $\mathrm {B} H \to \mathrm {B} G$ is a map of
$\mathrm {B} H \to \mathrm {B} G$ is a map of ![]() $1$-finite
$1$-finite ![]() $p$-spaces, which gives an integration operation on
$p$-spaces, which gives an integration operation on ![]() $\mathrm {K}_{[1]}(\mathcal {C})$ for
$\mathrm {K}_{[1]}(\mathcal {C})$ for ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{1\text {-}\mathrm {fin}}$, arising from the left Kan extension
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{1\text {-}\mathrm {fin}}$, arising from the left Kan extension ![]() $\mathcal {C}^{\mathrm {B} H} \to \mathcal {C}^{\mathrm {B} G}$, which reproduces the transfer map on equivariant algebraic K-theory. Thus,
$\mathcal {C}^{\mathrm {B} H} \to \mathcal {C}^{\mathrm {B} G}$, which reproduces the transfer map on equivariant algebraic K-theory. Thus, ![]() $\mathrm {K}^{[1]}$ is essentially obtained from equivariant algebraic K-theory by forcing the
$\mathrm {K}^{[1]}$ is essentially obtained from equivariant algebraic K-theory by forcing the ![]() $1$-Segal condition.
$1$-Segal condition.
1.1.4 Higher semiadditive algebraic K-theory of algebras
The above discussion gives the definition of the ![]() $\infty$-semiadditive algebraic K-theory of
$\infty$-semiadditive algebraic K-theory of ![]() $\infty$-categories in
$\infty$-categories in ![]() $\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$. One rich source of such
$\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$. One rich source of such ![]() $\infty$-categories is the
$\infty$-categories is the ![]() $\infty$-category
$\infty$-category ![]() $\mathrm {LMod}_R$ for an algebra
$\mathrm {LMod}_R$ for an algebra ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$. However, even though this
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$. However, even though this ![]() $\infty$-category is stable and has all colimits indexed by
$\infty$-category is stable and has all colimits indexed by ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces, it is too large. In order to avoid the Eilenberg swindle, one has to pass to a smaller
$p$-spaces, it is too large. In order to avoid the Eilenberg swindle, one has to pass to a smaller ![]() $\infty$-category, which still enjoys these properties. We show that passing to the left dualizable modules gives
$\infty$-category, which still enjoys these properties. We show that passing to the left dualizable modules gives ![]() $\mathrm {LMod}_R^\mathrm {ldbl} \in \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$, leading us to define
$\mathrm {LMod}_R^\mathrm {ldbl} \in \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$, leading us to define
Recall that ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization, so that if
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization, so that if ![]() $R \in \mathrm {Sp}_{\mathrm {T}(n)}$, then the
$R \in \mathrm {Sp}_{\mathrm {T}(n)}$, then the ![]() $\infty$-categories of modules in
$\infty$-categories of modules in ![]() ${{\unicode{x05E6}}}$ and in
${{\unicode{x05E6}}}$ and in ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$ coincide. We generalize the passage from all modules to the left dualizable modules, and make it into a lax symmetric monoidal functor, via the theory of atomic objects, as explained later in the introduction. This allows us to endow
$\mathrm {Sp}_{\mathrm {T}(n)}$ coincide. We generalize the passage from all modules to the left dualizable modules, and make it into a lax symmetric monoidal functor, via the theory of atomic objects, as explained later in the introduction. This allows us to endow ![]() $\mathrm {K}^{[\infty ]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ) \to {{\unicode{x05E6}}}$ with a lax symmetric monoidal structure.
$\mathrm {K}^{[\infty ]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ) \to {{\unicode{x05E6}}}$ with a lax symmetric monoidal structure.
1.1.5 Redshift
Recall that ![]() $\mathrm {K}^{[\infty ]}$ is an
$\mathrm {K}^{[\infty ]}$ is an ![]() $\infty$-semiadditive functor. As
$\infty$-semiadditive functor. As ![]() $\infty$-semiadditive functors can only decrease semiadditive height, we immediately get that if
$\infty$-semiadditive functors can only decrease semiadditive height, we immediately get that if ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$ has
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$ has ![]() $\mathrm {ht}(\mathcal {C}) \leq n$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$, then
$\mathrm {Cat}^{\mathrm {st}}_{\pi \text {-}\mathrm {fin}}$, then ![]() $\mathrm {ht}(\mathrm {K}^{[\infty ]}(\mathcal {C})) \leq n$ (see Proposition 7.7). Evidently, this does not exhibit the increase in height postulated by the redshift philosophy. Instead, the increase in height happens at the stage of categorification, turning from considering the height of objects to the height of their
$\mathrm {ht}(\mathrm {K}^{[\infty ]}(\mathcal {C})) \leq n$ (see Proposition 7.7). Evidently, this does not exhibit the increase in height postulated by the redshift philosophy. Instead, the increase in height happens at the stage of categorification, turning from considering the height of objects to the height of their ![]() $\infty$-category, as in Theorem 1.2. Using Theorem 1.2 and Proposition 7.7 we deduce our first main result.
$\infty$-category, as in Theorem 1.2. Using Theorem 1.2 and Proposition 7.7 we deduce our first main result.
Theorem 1 (Theorem 7.12)
Let ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ have
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ have ![]() $\mathrm {ht}(R) \leq n$ and let
$\mathrm {ht}(R) \leq n$ and let ![]() $m > n$, then
$m > n$, then
To give a lower bound on the height, we make use of the higher height analogues of cyclotomic extensions defined in [Reference Carmeli, Schlank and YanovskiCSY21b, Definition 4.7]. Recall that for ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ of
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ of ![]() $\mathrm {ht}(R)=n$, there is a (
$\mathrm {ht}(R)=n$, there is a (![]() $(\mathbb {Z}/p)^\times$-equivariant) splitting of algebras
$(\mathbb {Z}/p)^\times$-equivariant) splitting of algebras ![]() $R[\mathrm {B}^n C_p] \cong R \times R[\omega ^{(n)}_p]$, where
$R[\mathrm {B}^n C_p] \cong R \times R[\omega ^{(n)}_p]$, where ![]() $R[\omega ^{(n)}_p]$ is called the (height
$R[\omega ^{(n)}_p]$ is called the (height ![]() $n$)
$n$) ![]() $p$-cyclotomic extension of
$p$-cyclotomic extension of ![]() $R$, which generalizes ordinary cyclotomic extensions at height
$R$, which generalizes ordinary cyclotomic extensions at height ![]() $0$ (i.e. for algebras over the rationals). We say that
$0$ (i.e. for algebras over the rationals). We say that ![]() $R$ has (height
$R$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity if the cyclotomic extension splits as a product
$p$th roots of unity if the cyclotomic extension splits as a product ![]() $R[\omega ^{(n)}_p] \cong \prod _{(\mathbb {Z}/p)^\times } R$ (see Definition 7.17). For example, by [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.1], the Lubin–Tate spectrum
$R[\omega ^{(n)}_p] \cong \prod _{(\mathbb {Z}/p)^\times } R$ (see Definition 7.17). For example, by [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.1], the Lubin–Tate spectrum ![]() $\mathrm {E}_n$ has (height
$\mathrm {E}_n$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity. For such
$p$th roots of unity. For such ![]() $R$, we get an equivalence of
$R$, we get an equivalence of ![]() $R$-modules
$R$-modules ![]() $R[\mathrm {B}^n C_p] \cong R^p$, from which we immediately deduce the following strengthening of Theorem A.
$R[\mathrm {B}^n C_p] \cong R^p$, from which we immediately deduce the following strengthening of Theorem A.
Theorem 2 (Theorem 7.25)
Let ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ of
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ of ![]() $\mathrm {ht}(R) = n$ have (height
$\mathrm {ht}(R) = n$ have (height ![]() $n$)
$n$) ![]() $p$th roots of unity and let
$p$th roots of unity and let ![]() $m > n$, then
$m > n$, then
In particular, ![]() $\mathrm {ht}(\mathrm {K}^{[m]}(\mathrm {E}_n)) = n+1$.
$\mathrm {ht}(\mathrm {K}^{[m]}(\mathrm {E}_n)) = n+1$.
A natural question left open is the following.
Question 1.3 Can the assumption of having (height ![]() $n$)
$n$) ![]() $p$th roots of unity be dropped? Namely, is it true that if
$p$th roots of unity be dropped? Namely, is it true that if ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ is of height
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ is of height ![]() $n$, then
$n$, then ![]() $\mathrm {K}^{[m]}(R)$ is of height exactly
$\mathrm {K}^{[m]}(R)$ is of height exactly ![]() $n+1$?
$n+1$?
1.1.6 Relationship to chromatically localized K-theory
As we have seen in Theorems A and B, ![]() $\mathrm {K}^{[m]}$ satisfies a form of the redshift conjecture with respect to semiadditive height. A natural next direction is connecting these results to ordinary algebraic K-theory and the chromatic height. Let
$\mathrm {K}^{[m]}$ satisfies a form of the redshift conjecture with respect to semiadditive height. A natural next direction is connecting these results to ordinary algebraic K-theory and the chromatic height. Let ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$. The inclusion
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$. The inclusion ![]() $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset \mathrm {Sp}$ admits a left adjoint
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset \mathrm {Sp}$ admits a left adjoint ![]() $L_{\mathrm {T}(n+1)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since
$L_{\mathrm {T}(n+1)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since ![]() $\mathrm {K}(R) \in \mathrm {Sp}$, we can consider
$\mathrm {K}(R) \in \mathrm {Sp}$, we can consider ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Similarly, there is an inclusion
$L_{\mathrm {T}(n+1)} \mathrm {K}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Similarly, there is an inclusion ![]() $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$, which admits a left adjoint
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$, which admits a left adjoint ![]() $L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since
$L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since ![]() $\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} ^{[m]}$, we can consider
$\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} ^{[m]}$, we can consider ![]() $L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. The comparison map between ordinary algebraic K-theory and higher semiadditive algebraic K-theory yields a comparison mapFootnote 2
$L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. The comparison map between ordinary algebraic K-theory and higher semiadditive algebraic K-theory yields a comparison mapFootnote 2
This raises two independent questions.
(1) Does
 $\mathrm {K}^{[m]}(R)$ land in
$\mathrm {K}^{[m]}(R)$ land in  $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$?
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$?(2) Is the comparison map an equivalence?
A positive answer to both questions will imply that ![]() $\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$ (see Conjecture 1.4). The first question is closely related to the Quillen–Lichtenbaum conjecture for
$\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$ (see Conjecture 1.4). The first question is closely related to the Quillen–Lichtenbaum conjecture for ![]() $R$, in the guise of having a non-zero finite spectrum
$R$, in the guise of having a non-zero finite spectrum ![]() $X$ such that
$X$ such that ![]() $\mathrm {K}(R) \otimes X$ is bounded above, as we show in Proposition 8.4. The second question is equivalent to
$\mathrm {K}(R) \otimes X$ is bounded above, as we show in Proposition 8.4. The second question is equivalent to ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}_{[m]}(R)$ satisfying the
$L_{\mathrm {T}(n+1)} \mathrm {K}_{[m]}(R)$ satisfying the ![]() $m$-Segal condition. More informally, having descent properties for chromatically localized K-theory.
$m$-Segal condition. More informally, having descent properties for chromatically localized K-theory.
Using the Galois descent results for ![]() $\mathrm {T}(n+1)$-localized K-theory of [Reference Clausen, Mathew, Naumann and NoelCMNN20], this second question is answered in the affirmative for
$\mathrm {T}(n+1)$-localized K-theory of [Reference Clausen, Mathew, Naumann and NoelCMNN20], this second question is answered in the affirmative for ![]() $m = 1$ in Proposition 8.6. In our work with Carmeli and Yanovski [Reference Ben-Moshe, Carmeli, Schlank and YanovskiBCSY23] we show that the descent result for chromatically localized K-theory generalizes from finite
$m = 1$ in Proposition 8.6. In our work with Carmeli and Yanovski [Reference Ben-Moshe, Carmeli, Schlank and YanovskiBCSY23] we show that the descent result for chromatically localized K-theory generalizes from finite ![]() $p$-groups to arbitrary
$p$-groups to arbitrary ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces. This would give a positive answer to the second question for every
$p$-spaces. This would give a positive answer to the second question for every ![]() $m \geq 1$.
$m \geq 1$.
Next, we focus on the case of height ![]() $0$, answering both question in the affirmative in complete generality. Using the Quillen–Lichtenbaum property of
$0$, answering both question in the affirmative in complete generality. Using the Quillen–Lichtenbaum property of ![]() $\mathbb {S}[p^{-1}]$ together with Galois descent we obtain the following.
$\mathbb {S}[p^{-1}]$ together with Galois descent we obtain the following.
Theorem 3 (Theorem 8.10)
Let ![]() $R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ and let
$R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ and let ![]() $m \geq 1$, then
$m \geq 1$, then
In particular, ![]() $\mathrm {K}^{[m]}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$.
$\mathrm {K}^{[m]}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$.
Finally, we study the completed Johnson–Wilson spectrum ![]() $\widehat {\mathrm {E}(n)}$ at height
$\widehat {\mathrm {E}(n)}$ at height ![]() $n \geq 1$. In [Reference Hahn and WilsonHW22], Hahn and Wilson produced an
$n \geq 1$. In [Reference Hahn and WilsonHW22], Hahn and Wilson produced an ![]() $\mathbb {E}_3$-algebra structure on
$\mathbb {E}_3$-algebra structure on ![]() $\mathrm {BP}\langle n \rangle$, for which they have proven a version of the Quillen–Lichtenbaum conjecture. This structure also endows
$\mathrm {BP}\langle n \rangle$, for which they have proven a version of the Quillen–Lichtenbaum conjecture. This structure also endows ![]() $\widehat {\mathrm {E}(n)}$ with an
$\widehat {\mathrm {E}(n)}$ with an ![]() $\mathbb {E}_3$-algebra structure. Using their Quillen–Lichtenbaum result, along with a comparison of two direct computations of the higher commutative monoid structure on
$\mathbb {E}_3$-algebra structure. Using their Quillen–Lichtenbaum result, along with a comparison of two direct computations of the higher commutative monoid structure on ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$, we obtain the following strengthening of Theorem B for
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$, we obtain the following strengthening of Theorem B for ![]() $\widehat {\mathrm {E}(n)}$-algebras. We would like to thank the anonymous referee for suggesting crucial parts of the proof of this result.
$\widehat {\mathrm {E}(n)}$-algebras. We would like to thank the anonymous referee for suggesting crucial parts of the proof of this result.
Theorem 4 (Theorem 8.23)
Let ![]() $R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ where
$R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ where ![]() $\widehat {\mathrm {E}(n)}$ is endowed with the Hahn–Wilson
$\widehat {\mathrm {E}(n)}$ is endowed with the Hahn–Wilson ![]() $\mathbb {E}_3$-algebra structure, and let
$\mathbb {E}_3$-algebra structure, and let ![]() $m \geq 1$, then
$m \geq 1$, then
Using Galois descent for chromatically localized K-theory from [Reference Clausen, Mathew, Naumann and NoelCMNN20] as mentioned above, we immediately get the following result at ![]() $m = 1$.
$m = 1$.
Theorem 5 (Corollary 8.24)
Let ![]() $R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ where
$R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ where ![]() $\widehat {\mathrm {E}(n)}$ is endowed with the Hahn–Wilson
$\widehat {\mathrm {E}(n)}$ is endowed with the Hahn–Wilson ![]() $\mathbb {E}_3$-algebra structure, then
$\mathbb {E}_3$-algebra structure, then
In particular, ![]() $\mathrm {K}^{[1]}(\widehat {\mathrm {E}(n)}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\widehat {\mathrm {E}(n)})$.
$\mathrm {K}^{[1]}(\widehat {\mathrm {E}(n)}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\widehat {\mathrm {E}(n)})$.
As mentioned above, our work with Carmeli and Yanovski [Reference Ben-Moshe, Carmeli, Schlank and YanovskiBCSY23] implies that Theorem E generalizes to ![]() $m$-semiadditive K-theory for any
$m$-semiadditive K-theory for any ![]() $m \geq 1$. This generalization, along with Theorem C answering the case of height
$m \geq 1$. This generalization, along with Theorem C answering the case of height ![]() $0$, lead us to conjecture the following.
$0$, lead us to conjecture the following.
Conjecture 1.4 For any ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$ and
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$ and ![]() $m \geq 1$ we have
$m \geq 1$ we have
We would like to highlight two interesting phenomena exemplified by Theorems C and E. First, higher semiadditive algebraic K-theory lands in the highest non-zero height predicted by the redshift conjecture, without forcing it be in a pure height from the outside. Second, algebraic K-theory can be modified to have a higher commutative monoid structure in two ways: either by chromatically localizing it from the outside, or by internally remembering the higher commutative monoid structure on the input ![]() $\infty$-category. These results show that these two a priori distinct objects coincide, at least in some cases. This identification gives different approaches to study the higher commutative monoid structure, similarly to the proof of Theorem D itself.
$\infty$-category. These results show that these two a priori distinct objects coincide, at least in some cases. This identification gives different approaches to study the higher commutative monoid structure, similarly to the proof of Theorem D itself.
1.1.7 Atomic objects and a monoidal natural Yoneda
Recall that in the construction of the higher semiadditive algebraic K-theory of ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ described above, we passed to the left dualizable objects. In order to study the functoriality of this construction in
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$ described above, we passed to the left dualizable objects. In order to study the functoriality of this construction in ![]() $R$, as well as to generalize the construction to stable
$R$, as well as to generalize the construction to stable ![]() $\infty$-semiadditive presentable
$\infty$-semiadditive presentable ![]() $\infty$-categories other than
$\infty$-categories other than ![]() $\infty$-categories of modules, we define and study
$\infty$-categories of modules, we define and study ![]() $\mathcal {M}$-atomic objects for any mode
$\mathcal {M}$-atomic objects for any mode ![]() $\mathcal {M}$ (see Definition 2.3). One of our main results is that
$\mathcal {M}$ (see Definition 2.3). One of our main results is that ![]() $\mathcal {M}$-atomic objects indeed coincide with left dualizable objects in left modules, i.e.
$\mathcal {M}$-atomic objects indeed coincide with left dualizable objects in left modules, i.e. ![]() $\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$ for any
$\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$ for any ![]() $R \in \operatorname {Alg}(\mathcal {M})$ (see Proposition 2.54). Another direction of generalization is the case
$R \in \operatorname {Alg}(\mathcal {M})$ (see Proposition 2.54). Another direction of generalization is the case ![]() $\mathcal {M} = \mathrm {Sp}$, where
$\mathcal {M} = \mathrm {Sp}$, where ![]() $\mathrm {Sp}$-atomic objects coincide with compact objects. We also show that for any absolute limit of
$\mathrm {Sp}$-atomic objects coincide with compact objects. We also show that for any absolute limit of ![]() $\mathcal {M}$, the
$\mathcal {M}$, the ![]() $\mathcal {M}$-atomic objects are closed under
$\mathcal {M}$-atomic objects are closed under ![]() $I^\mathrm {op}$-shaped colimits (see Proposition 2.24). These two results are then applied in Proposition 4.15 to show that for
$I^\mathrm {op}$-shaped colimits (see Proposition 2.24). These two results are then applied in Proposition 4.15 to show that for ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} )$, we have
$R \in \operatorname {Alg}({{\unicode{x05E6}}} )$, we have ![]() $\mathrm {LMod}_R^\mathrm {ldbl} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, so that it can be used as an input to higher semiadditive algebraic K-theory.
$\mathrm {LMod}_R^\mathrm {ldbl} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, so that it can be used as an input to higher semiadditive algebraic K-theory.
Another key result is the strong connection between the functor ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}$ taking
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}$ taking ![]() $\mathcal {M}$-valued presheaves and the functor taking
$\mathcal {M}$-valued presheaves and the functor taking ![]() $\mathcal {M}$-atomic objects. Let
$\mathcal {M}$-atomic objects. Let ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ denote the subcategory of
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ denote the subcategory of ![]() $\mathrm {Pr}^\mathrm {L}$ consisting of
$\mathrm {Pr}^\mathrm {L}$ consisting of ![]() $\infty$-categories in the mode
$\infty$-categories in the mode ![]() $\mathcal {M}$ and internally left adjoint functors (that is, left adjoint functors whose right adjoint admits a further right adjoint), which inherits a symmetric monoidal structure from
$\mathcal {M}$ and internally left adjoint functors (that is, left adjoint functors whose right adjoint admits a further right adjoint), which inherits a symmetric monoidal structure from ![]() $\mathrm {Pr}^\mathrm {L}$. We then have the following.
$\mathrm {Pr}^\mathrm {L}$. We then have the following.
Theorem 6 (Theorem 2.46)
There is a symmetric monoidal adjunction
i.e. ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}$ is symmetric monoidal with a lax symmetric monoidal right adjoint
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}$ is symmetric monoidal with a lax symmetric monoidal right adjoint ![]() $(-)^{{\mathcal {M}\text {-}}\mathrm {at}}$.
$(-)^{{\mathcal {M}\text {-}}\mathrm {at}}$.
Building on the work of Glasman [Reference GlasmanGla16] and Haugseng, Hebestreit, Linskens, and Nuiten [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN20, Theorem 8.1] on the Yoneda embedding, the adjunction is constructed such that the unit is (the factorization through the ![]() $\mathcal {M}$-atomic objects of) the Yoneda map
$\mathcal {M}$-atomic objects of) the Yoneda map ![]() ${\unicode{x3088}}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, reproducing the ordinary Yoneda embedding for
${\unicode{x3088}}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, reproducing the ordinary Yoneda embedding for ![]() $\mathcal {M} = \mathcal {S}$. As an immediate consequence, we obtain a monoidal and natural version of the Yoneda map for any operad
$\mathcal {M} = \mathcal {S}$. As an immediate consequence, we obtain a monoidal and natural version of the Yoneda map for any operad ![]() $\mathcal {O}$, which may be of independent interest.
$\mathcal {O}$, which may be of independent interest.
Theorem 7 (Corollary 2.47)
The Yoneda map ![]() ${\unicode{x3088}}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is
${\unicode{x3088}}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is ![]() $\mathcal {O}$-monoidal and natural in
$\mathcal {O}$-monoidal and natural in ![]() $\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat})$.
$\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat})$.
1.2 Organization
In § 2, we develop the notion of ![]() $\mathcal {M}$-atomic objects in a presentable
$\mathcal {M}$-atomic objects in a presentable ![]() $\infty$-category in the mode
$\infty$-category in the mode ![]() $\mathcal {M}$. We study the connection between
$\mathcal {M}$. We study the connection between ![]() $\mathcal {M}$-atomic objects and
$\mathcal {M}$-atomic objects and ![]() $\mathcal {M}$-valued presheaves, and leverage this connection to endow the functor taking the
$\mathcal {M}$-valued presheaves, and leverage this connection to endow the functor taking the ![]() $\mathcal {M}$-atomic objects with a lax symmetric monoidal structure. As a byproduct, we obtain a monoidal natural version of the Yoneda map.
$\mathcal {M}$-atomic objects with a lax symmetric monoidal structure. As a byproduct, we obtain a monoidal natural version of the Yoneda map.
In § 3, we recall the universal property of the Day convolution, and study its functoriality in the source and the target.
In § 4, we recall some facts about (![]() $p$-typical) (pre-)
$p$-typical) (pre-)![]() $m$-commutative monoids, and study their multiplicative structure. We observe that the
$m$-commutative monoids, and study their multiplicative structure. We observe that the ![]() $\infty$-category of
$\infty$-category of ![]() $m$-commutative monoids can naturally be endowed with two symmetric monoidal structures, and we show that these two structures coincide.
$m$-commutative monoids can naturally be endowed with two symmetric monoidal structures, and we show that these two structures coincide.
In § 5, we recall the definition of the higher cocartesian structure, and show that it satisfies certain expected properties. In particular, we show that tensoring a family of objects is indeed given by their colimit.
In § 6, we define ![]() $m$-semiadditive algebraic K-theory using the tools developed in the previous sections, and study its properties. We construct it in two different ways, first using the
$m$-semiadditive algebraic K-theory using the tools developed in the previous sections, and study its properties. We construct it in two different ways, first using the ![]() $S_\bullet$-construction, and second by exhibiting it as the universal way to make ordinary algebraic K-theory into an
$S_\bullet$-construction, and second by exhibiting it as the universal way to make ordinary algebraic K-theory into an ![]() $m$-semiadditive functor. We leverage the second definition of
$m$-semiadditive functor. We leverage the second definition of ![]() $m$-semiadditive algebraic K-theory to endow it with a lax symmetric monoidal structure.
$m$-semiadditive algebraic K-theory to endow it with a lax symmetric monoidal structure.
In § 7, we study the interplay between ![]() $m$-semiadditive algebraic K-theory and semiadditive height. In particular, we show that it can increase the height of rings at most by one. Furthermore, we show that if the ring has (height
$m$-semiadditive algebraic K-theory and semiadditive height. In particular, we show that it can increase the height of rings at most by one. Furthermore, we show that if the ring has (height ![]() $n$)
$n$) ![]() $p$th roots of unity, then the height of its
$p$th roots of unity, then the height of its ![]() $m$-semiadditive algebraic K-theory is exactly
$m$-semiadditive algebraic K-theory is exactly ![]() $n+1$.
$n+1$.
In § 8, we study the connection between higher semiadditive algebraic K-theory and chromatically localized K-theory. We apply the Quillen–Lichtenbaum conjecture and the Galois descent result for chromatically localized K-theory, to show that the higher semiadditive algebraic K-theory of ![]() $p$-invertible algebras coincides with their
$p$-invertible algebras coincides with their ![]() $\mathrm {T}(1)$-localized algebraic K-theory. Finally, we use the Quillen–Lichtenbaum result for
$\mathrm {T}(1)$-localized algebraic K-theory. Finally, we use the Quillen–Lichtenbaum result for ![]() $\mathrm {BP}\langle n \rangle$ to show that the higher semiadditive algebraic K-theory of
$\mathrm {BP}\langle n \rangle$ to show that the higher semiadditive algebraic K-theory of ![]() $\widehat {\mathrm {E}(n)}$-algebras lands in
$\widehat {\mathrm {E}(n)}$-algebras lands in ![]() $\mathrm {T}(n+1)$-local spectra, and that specifically their
$\mathrm {T}(n+1)$-local spectra, and that specifically their ![]() $1$-semiadditive algebraic K-theory coincides with their
$1$-semiadditive algebraic K-theory coincides with their ![]() $\mathrm {T}(1)$-localized algebraic K-theory.
$\mathrm {T}(1)$-localized algebraic K-theory.
1.3 Conventions
Throughout the paper, we work in the framework of ![]() $\infty$-categories, mostly following the notation of [Reference LurieLur09, Reference LurieLur17]. For brevity, we use the word category to mean an
$\infty$-categories, mostly following the notation of [Reference LurieLur09, Reference LurieLur17]. For brevity, we use the word category to mean an ![]() $\infty$-category. We also generally follow the notation and terminology of [Reference Carmeli, Schlank and YanovskiCSY21a] related to higher semiadditivity, but we diverge by working exclusively in the
$\infty$-category. We also generally follow the notation and terminology of [Reference Carmeli, Schlank and YanovskiCSY21a] related to higher semiadditivity, but we diverge by working exclusively in the ![]() $p$-typical case.
$p$-typical case.
(1) We denote the space of morphisms between two objects
 $X, Y \in \mathcal {C}$ by
$X, Y \in \mathcal {C}$ by  ${\hom _\mathcal {C}(X, Y)}$ and omit
${\hom _\mathcal {C}(X, Y)}$ and omit  $\mathcal {C}$ when it is clear from the context. If
$\mathcal {C}$ when it is clear from the context. If  $\mathcal {C}$ is
$\mathcal {C}$ is  $\mathcal {D}$-enriched (e.g. in a mode
$\mathcal {D}$-enriched (e.g. in a mode  $\mathcal {D} = \mathcal {M}$, or closed symmetric monoidal
$\mathcal {D} = \mathcal {M}$, or closed symmetric monoidal  $\mathcal {D} = \mathcal {C}$), we denote by
$\mathcal {D} = \mathcal {C}$), we denote by  ${\hom ^\mathcal {D}_\mathcal {C}(X, Y)}$ the
${\hom ^\mathcal {D}_\mathcal {C}(X, Y)}$ the  $\mathcal {D}$-object of morphisms and omit
$\mathcal {D}$-object of morphisms and omit  $\mathcal {C}$ when it is clear from the context.
$\mathcal {C}$ when it is clear from the context.(2) We say that a space
 $A \in \mathcal {S}$ is:
$A \in \mathcal {S}$ is:
(a) a
 $p$-space, if all the homotopy groups of
$p$-space, if all the homotopy groups of  $A$ are
$A$ are  $p$-groups;
$p$-groups;(b)
 $m$-finite for
$m$-finite for  $m \ge -2$, if
$m \ge -2$, if  $m = -2$ and
$m = -2$ and  $A$ is contractible, or
$A$ is contractible, or  $m \ge -1$, the set
$m \ge -1$, the set  $\pi _{0}A$ is finite and all the fibers of the diagonal map
$\pi _{0}A$ is finite and all the fibers of the diagonal map  $\Delta \colon A\to A\times A$ are
$\Delta \colon A\to A\times A$ are  $(m-1)$-finite;Footnote 3
$(m-1)$-finite;Footnote 3(c)
 $\pi$-finite or
$\pi$-finite or  $\infty$-finite, if it is
$\infty$-finite, if it is  $m$-finite for some integer
$m$-finite for some integer  $m \ge -2$.
$m \ge -2$.
(3) For
 $-2 \leq m \leq \infty$, we denote by
$-2 \leq m \leq \infty$, we denote by  ${\mathcal {S}_m^{(p)}} \subset \mathcal {S}$ the full subcategory spanned by all
${\mathcal {S}_m^{(p)}} \subset \mathcal {S}$ the full subcategory spanned by all  $m$-finite
$m$-finite  $p$-spaces.
$p$-spaces.(4) We say that a category
 $\mathcal {C}$ is (
$\mathcal {C}$ is (  $p$-typically)
$p$-typically)  $m$-semiadditive if all
$m$-semiadditive if all  $m$-finite
$m$-finite  $p$-spaces
$p$-spaces  $A \in \mathcal {S}_m^{(p)}$ are
$A \in \mathcal {S}_m^{(p)}$ are  $\mathcal {C}$-ambidextrous.
$\mathcal {C}$-ambidextrous.(5) We denote by
 ${\mathrm {Cat}^{\mathrm {st}}} \subset \mathrm {Cat}$ the subcategory spanned by all stable categories and exact functors.
${\mathrm {Cat}^{\mathrm {st}}} \subset \mathrm {Cat}$ the subcategory spanned by all stable categories and exact functors.(6) For a collection
 $\mathcal {K}$ of indexing categories, we let
$\mathcal {K}$ of indexing categories, we let  ${\mathrm {Cat}_\mathcal {K}} \subset \mathrm {Cat}$ be the subcategory spanned by all categories admitting all colimits indexed by
${\mathrm {Cat}_\mathcal {K}} \subset \mathrm {Cat}$ be the subcategory spanned by all categories admitting all colimits indexed by  $I \in \mathcal {K}$ and functors preserving them.
$I \in \mathcal {K}$ and functors preserving them.(7) For
 $-2 \leq m \leq \infty$, we define
$-2 \leq m \leq \infty$, we define  ${\mathrm {Cat}_{m\text {-}\mathrm {fin}}} = \mathrm {Cat}_\mathcal {K}$ for
${\mathrm {Cat}_{m\text {-}\mathrm {fin}}} = \mathrm {Cat}_\mathcal {K}$ for  $\mathcal {K} = \mathcal {S}_m^{(p)}$, and we let
$\mathcal {K} = \mathcal {S}_m^{(p)}$, and we let  ${\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}} \subset \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ be the subcategory of those categories which are additionally stable and functors which are additionally exact.
${\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}} \subset \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ be the subcategory of those categories which are additionally stable and functors which are additionally exact.
2. Atomic objects
Let ![]() $\mathcal {M}$ be a mode, that is, an idempotent algebra in
$\mathcal {M}$ be a mode, that is, an idempotent algebra in ![]() $\mathrm {Pr}^\mathrm {L}$ (see [Reference Carmeli, Schlank and YanovskiCSY21a, § 5] for generalities on modes). In this section we study
$\mathrm {Pr}^\mathrm {L}$ (see [Reference Carmeli, Schlank and YanovskiCSY21a, § 5] for generalities on modes). In this section we study ![]() $\mathcal {M}$-atomic objects (see Definition 2.3), a finiteness property of objects in categories
$\mathcal {M}$-atomic objects (see Definition 2.3), a finiteness property of objects in categories ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$ in the mode
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$ in the mode ![]() $\mathcal {M}$, which generalizes both compactness (for the case
$\mathcal {M}$, which generalizes both compactness (for the case ![]() $\mathcal {M} = \mathrm {Sp}$, see Proposition 2.8) and dualizability of modules (for the case
$\mathcal {M} = \mathrm {Sp}$, see Proposition 2.8) and dualizability of modules (for the case ![]() $\mathcal {C} = \mathrm {LMod}_R(\mathcal {M})$, see Proposition 2.54). The results of this section are subsequently used in Definition 6.20 to define the higher semiadditive algebraic K-theory of algebras in
$\mathcal {C} = \mathrm {LMod}_R(\mathcal {M})$, see Proposition 2.54). The results of this section are subsequently used in Definition 6.20 to define the higher semiadditive algebraic K-theory of algebras in ![]() ${{\unicode{x05E6}}} ^{[m]}$ (see Definition 4.11), and in particular for algebras in
${{\unicode{x05E6}}} ^{[m]}$ (see Definition 4.11), and in particular for algebras in ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$, including its lax symmetric monoidal structure.
$\mathrm {Sp}_{\mathrm {T}(n)}$, including its lax symmetric monoidal structure.
In § 2.1 we give the definition of atomic objects (see Definition 2.3) and study their basic properties. We show that taking atomic objects is functorial in internally left adjoint functors (see Definition 2.12). Analogously to the condition of being compactly generated, we study the condition of being generated under colimits and the action of ![]() $\mathcal {M}$ from the
$\mathcal {M}$ from the ![]() $\mathcal {M}$-atomic objects, which we call being
$\mathcal {M}$-atomic objects, which we call being ![]() $\mathcal {M}$-molecular (see Definition 2.10), and we explain its relationship to internally left adjoint functors. Lastly, in Proposition 2.24 we show that for any absolute limit
$\mathcal {M}$-molecular (see Definition 2.10), and we explain its relationship to internally left adjoint functors. Lastly, in Proposition 2.24 we show that for any absolute limit ![]() $I$ of
$I$ of ![]() $\mathcal {M}$ (see Definition 2.18), the atomic objects are closed under
$\mathcal {M}$ (see Definition 2.18), the atomic objects are closed under ![]() $I^\mathrm {op}$-shaped colimits. This yields a functor
$I^\mathrm {op}$-shaped colimits. This yields a functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}_\mathcal {K}$ where
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}_\mathcal {K}$ where ![]() $\mathcal {K}$ is any small collection of opposites of absolute limits of
$\mathcal {K}$ is any small collection of opposites of absolute limits of ![]() $\mathcal {M}$.
$\mathcal {M}$.
In §§ 2.2 and 2.3 we study the connection between ![]() $\mathcal {M}$-atomic objects and
$\mathcal {M}$-atomic objects and ![]() $\mathcal {M}$-valued presheaves (see Definition 2.27), and the multiplicative structure of both functors. The main result of this section is Theorem 2.46, exhibiting a symmetric monoidal adjunction
$\mathcal {M}$-valued presheaves (see Definition 2.27), and the multiplicative structure of both functors. The main result of this section is Theorem 2.46, exhibiting a symmetric monoidal adjunction
Moreover, the unit of this adjunction is the Yoneda map, and as an immediate consequence, Corollary 2.47 shows that ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is ![]() $\mathcal {O}$-monoidal and natural in
$\mathcal {O}$-monoidal and natural in ![]() $\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K})$, which may be of independent interest.
$\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K})$, which may be of independent interest.
Lastly, in § 2.4 we study atomic objects in categories of left modules. In Proposition 2.54 we show that atomic objects and left dualizable left modules coincide, i.e. ![]() $\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$.
$\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$.
Remark 2.1 Many of the results of this section can be generalized to modules in ![]() $\mathrm {Pr}^\mathrm {L}$ over any presentably monoidal category
$\mathrm {Pr}^\mathrm {L}$ over any presentably monoidal category ![]() $\mathcal {V} \in \operatorname {Alg}(\mathrm {Pr}^\mathrm {L})$ and
$\mathcal {V} \in \operatorname {Alg}(\mathrm {Pr}^\mathrm {L})$ and ![]() $\mathcal {V}$-linear functors. Parts of these generalizations were carried out by the first author in [Reference Ben-MosheBen23], building on the works of [Reference Gepner and HaugsengGH15, Reference HinichHin20, Reference HinichHin23, Reference HeineHei23]. The main feature of modes is that being an
$\mathcal {V}$-linear functors. Parts of these generalizations were carried out by the first author in [Reference Ben-MosheBen23], building on the works of [Reference Gepner and HaugsengGH15, Reference HinichHin20, Reference HinichHin23, Reference HeineHei23]. The main feature of modes is that being an ![]() $\mathcal {M}$-module is a property rather than extra structure, and that any left adjoint functor is automatically
$\mathcal {M}$-module is a property rather than extra structure, and that any left adjoint functor is automatically ![]() $\mathcal {M}$-linear. As such, working over a mode simplifies the definitions and proofs, and avoids using enriched category theory. Since this suffices for our applications in the rest of the paper, we have restricted to this case.
$\mathcal {M}$-linear. As such, working over a mode simplifies the definitions and proofs, and avoids using enriched category theory. Since this suffices for our applications in the rest of the paper, we have restricted to this case.
2.1 Atomics and internally left adjoints
Lemma 2.2 Let ![]() $F\colon \mathcal {C} \rightleftarrows \mathcal {D}\colon G$ be an adjunction with
$F\colon \mathcal {C} \rightleftarrows \mathcal {D}\colon G$ be an adjunction with ![]() $\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$. Let
$\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$. Let ![]() $X \in \mathcal {C}$ and
$X \in \mathcal {C}$ and ![]() $Y \in \mathcal {D}$, then there is an equivalence
$Y \in \mathcal {D}$, then there is an equivalence ![]() $\hom ^\mathcal {M}(FX, Y) \cong \hom ^\mathcal {M}(X, GY)$ lifting the equivalence
$\hom ^\mathcal {M}(FX, Y) \cong \hom ^\mathcal {M}(X, GY)$ lifting the equivalence ![]() $\hom (FX, Y) \cong \hom (X, GY)$.
$\hom (FX, Y) \cong \hom (X, GY)$.
Proof. We prove this using the Yoneda lemma. Let ![]() $m \in \mathcal {M}$. Recall that
$m \in \mathcal {M}$. Recall that ![]() $F\colon \mathcal {C} \to \mathcal {D}$ is a map in
$F\colon \mathcal {C} \to \mathcal {D}$ is a map in ![]() $\mathrm {Mod}_\mathcal {M}$, so that it commutes with
$\mathrm {Mod}_\mathcal {M}$, so that it commutes with ![]() $m \otimes -$, so we conclude that
$m \otimes -$, so we conclude that
 \begin{align*} \hom(m, \hom^\mathcal{M}(FX, Y)) &\cong \hom(m \otimes FX, Y)\\ &\cong \hom(F(m \otimes X), Y)\\ &\cong \hom(m \otimes X, GY)\\ &\cong \hom(m, \hom^\mathcal{M}(X, GY)) . \end{align*}
\begin{align*} \hom(m, \hom^\mathcal{M}(FX, Y)) &\cong \hom(m \otimes FX, Y)\\ &\cong \hom(F(m \otimes X), Y)\\ &\cong \hom(m \otimes X, GY)\\ &\cong \hom(m, \hom^\mathcal{M}(X, GY)) . \end{align*}
The fact that it is a lift of the ![]() $\mathcal {S}$-enriched hom is the case
$\mathcal {S}$-enriched hom is the case ![]() $m = \mathbf {1}_\mathcal {M}$.
$m = \mathbf {1}_\mathcal {M}$.
Definition 2.3 Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. An object
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. An object ![]() $X \in \mathcal {C}$ is called
$X \in \mathcal {C}$ is called ![]() $\mathcal {M}$-atomic, if
$\mathcal {M}$-atomic, if ![]() $\hom ^\mathcal {M}(X, -)\colon \mathcal {C} \to \mathcal {M}$ commutes with colimits. We denote by
$\hom ^\mathcal {M}(X, -)\colon \mathcal {C} \to \mathcal {M}$ commutes with colimits. We denote by ![]() ${\mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}} \subseteq \mathcal {C}$ the full subcategory of the
${\mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}} \subseteq \mathcal {C}$ the full subcategory of the ![]() $\mathcal {M}$-atomic objects. When the mode is clear from the context, it is dropped from the notation.
$\mathcal {M}$-atomic objects. When the mode is clear from the context, it is dropped from the notation.
Remark 2.4 The definition of atomic objects will be made functorial in Definition 2.17.
Remark 2.5 If ![]() $X \in \mathcal {C}$ is atomic, then
$X \in \mathcal {C}$ is atomic, then ![]() $\hom ^\mathcal {M}(X, -)$ is a left adjoint functor, thus a morphism in
$\hom ^\mathcal {M}(X, -)$ is a left adjoint functor, thus a morphism in ![]() $\mathrm {Mod}_\mathcal {M}$, so that it also commutes with the action of
$\mathrm {Mod}_\mathcal {M}$, so that it also commutes with the action of ![]() $\mathcal {M}$. That is, for any
$\mathcal {M}$. That is, for any ![]() $m \in \mathcal {M}$ we have
$m \in \mathcal {M}$ we have ![]() $\hom ^\mathcal {M}(X, - \otimes m) \cong \hom ^\mathcal {M}(X, -) \otimes m$.
$\hom ^\mathcal {M}(X, - \otimes m) \cong \hom ^\mathcal {M}(X, -) \otimes m$.
Example 2.6 The unit ![]() $\mathbf {1}_\mathcal {M} \in \mathcal {M}$ is atomic because the functor
$\mathbf {1}_\mathcal {M} \in \mathcal {M}$ is atomic because the functor ![]() $\hom ^\mathcal {M}(\mathbf {1}_\mathcal {M}, -)\colon \mathcal {M} \to \mathcal {M}$ is the identity functor and in particular commutes with colimits.
$\hom ^\mathcal {M}(\mathbf {1}_\mathcal {M}, -)\colon \mathcal {M} \to \mathcal {M}$ is the identity functor and in particular commutes with colimits.
Proposition 2.7 The only ![]() $\mathcal {S}$-atomic object in
$\mathcal {S}$-atomic object in ![]() $\mathcal {S}$ is the point
$\mathcal {S}$ is the point ![]() $*$.
$*$.
Proof. Let ![]() $X \in \mathcal {S}^{\mathrm {at}}$ be atomic, then for any
$X \in \mathcal {S}^{\mathrm {at}}$ be atomic, then for any ![]() $Y \in \mathcal {S}$ we have
$Y \in \mathcal {S}$ we have
Thus, ![]() $X$ corepresents the identity functor
$X$ corepresents the identity functor ![]() $\mathrm {id}\colon \mathcal {S} \to \mathcal {S}$, namely
$\mathrm {id}\colon \mathcal {S} \to \mathcal {S}$, namely ![]() $X = *$.
$X = *$.
Proposition 2.8 Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathrm {Sp}$ be a presentable stable category, then the
$\mathcal {C} \in \mathrm {Mod}_\mathrm {Sp}$ be a presentable stable category, then the ![]() $\mathrm {Sp}$-atomics are the compact objects, i.e.
$\mathrm {Sp}$-atomics are the compact objects, i.e. ![]() $\mathcal {C}^{{\mathrm {Sp}\text {-}}\mathrm {at}} = \mathcal {C}^{\omega }$.
$\mathcal {C}^{{\mathrm {Sp}\text {-}}\mathrm {at}} = \mathcal {C}^{\omega }$.
Proof. Let ![]() $X \in \mathcal {C}$. First assume that
$X \in \mathcal {C}$. First assume that ![]() $X$ is atomic. Recall that
$X$ is atomic. Recall that ![]() $\Omega ^\infty \colon \mathrm {Sp} \to \mathcal {S}$ commutes with filtered colimits, so that
$\Omega ^\infty \colon \mathrm {Sp} \to \mathcal {S}$ commutes with filtered colimits, so that ![]() $\hom (X, -) \cong \Omega ^\infty \hom ^\mathrm {Sp}(X, -)$ commutes with filtered colimits, i.e. it is compact.
$\hom (X, -) \cong \Omega ^\infty \hom ^\mathrm {Sp}(X, -)$ commutes with filtered colimits, i.e. it is compact.
Now assume that ![]() $X$ is compact. Recall that for any
$X$ is compact. Recall that for any ![]() $n \in \mathbb {Z}$, the functor
$n \in \mathbb {Z}$, the functor ![]() $\Sigma ^n\colon \mathrm {Sp} \to \mathrm {Sp}$ commutes with all limits and colimits and in particular with filtered colimits, thus
$\Sigma ^n\colon \mathrm {Sp} \to \mathrm {Sp}$ commutes with all limits and colimits and in particular with filtered colimits, thus ![]() $\hom (X, \Sigma ^n -) \cong \Omega ^\infty \Sigma ^n \hom ^\mathrm {Sp}(X, -)$ also commutes with filtered colimits. In addition, the functors
$\hom (X, \Sigma ^n -) \cong \Omega ^\infty \Sigma ^n \hom ^\mathrm {Sp}(X, -)$ also commutes with filtered colimits. In addition, the functors ![]() $\Omega ^\infty \Sigma ^n\colon \mathrm {Sp} \to \mathcal {S}$ are jointly conservative, implying that
$\Omega ^\infty \Sigma ^n\colon \mathrm {Sp} \to \mathcal {S}$ are jointly conservative, implying that ![]() $\hom ^\mathrm {Sp}(X, -)$ commutes with filtered colimits. Furthermore, it commutes with finite limits, thus by stability also with all finite colimits, which together with filtered colimits generate all colimits.
$\hom ^\mathrm {Sp}(X, -)$ commutes with filtered colimits. Furthermore, it commutes with finite limits, thus by stability also with all finite colimits, which together with filtered colimits generate all colimits.
Proposition 2.9 Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, then
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, then ![]() $\mathcal {C}^{\mathrm {at}} \in \mathrm {Cat}$ is a small category.
$\mathcal {C}^{\mathrm {at}} \in \mathrm {Cat}$ is a small category.
Proof. Let ![]() $\kappa$ be a regular cardinal such that the unit
$\kappa$ be a regular cardinal such that the unit ![]() $\mathbf {1}_\mathcal {M} \in \mathcal {M}$ is
$\mathbf {1}_\mathcal {M} \in \mathcal {M}$ is ![]() $\kappa$-compact. We show that
$\kappa$-compact. We show that ![]() $\mathcal {C}^{\mathrm {at}} \subseteq \mathcal {C}^\kappa$, that is the atomics are
$\mathcal {C}^{\mathrm {at}} \subseteq \mathcal {C}^\kappa$, that is the atomics are ![]() $\kappa$-compact. Let
$\kappa$-compact. Let ![]() $X \in \mathcal {C}$ be an atomic object, so in particular
$X \in \mathcal {C}$ be an atomic object, so in particular ![]() $\hom ^\mathcal {M}(X,-)$ commutes with
$\hom ^\mathcal {M}(X,-)$ commutes with ![]() $\kappa$-filtered colimits. Since
$\kappa$-filtered colimits. Since ![]() $\mathbf {1}_\mathcal {M}$ is
$\mathbf {1}_\mathcal {M}$ is ![]() $\kappa$-compact,
$\kappa$-compact, ![]() $\hom (\mathbf {1}_\mathcal {M},-)$ commutes with
$\hom (\mathbf {1}_\mathcal {M},-)$ commutes with ![]() $\kappa$-filtered colimits, implying that the composition
$\kappa$-filtered colimits, implying that the composition ![]() $\hom (X,-) \cong \hom (\mathbf {1}_\mathcal {M}, \hom ^\mathcal {M}(X,-))$ commutes with
$\hom (X,-) \cong \hom (\mathbf {1}_\mathcal {M}, \hom ^\mathcal {M}(X,-))$ commutes with ![]() $\kappa$-filtered colimits.
$\kappa$-filtered colimits.
Definition 2.10 Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. We say that a collection of atomic objects
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. We say that a collection of atomic objects ![]() $B \subseteq \mathcal {C}^{\mathrm {at}}$ are
$B \subseteq \mathcal {C}^{\mathrm {at}}$ are ![]() $\mathcal {M}$-atomic generators, if
$\mathcal {M}$-atomic generators, if ![]() $\mathcal {C}$ is generated from
$\mathcal {C}$ is generated from ![]() $B$ under colimits and the action of
$B$ under colimits and the action of ![]() $\mathcal {M}$.Footnote 4 If such
$\mathcal {M}$.Footnote 4 If such ![]() $B$ exists, we say that
$B$ exists, we say that ![]() $\mathcal {C}$ is
$\mathcal {C}$ is ![]() $\mathcal {M}$-molecular.Footnote 5 If the mode is clear from the context, we call
$\mathcal {M}$-molecular.Footnote 5 If the mode is clear from the context, we call ![]() $\mathcal {C}$ molecular and say that
$\mathcal {C}$ molecular and say that ![]() $B$ are atomic generators.
$B$ are atomic generators.
Example 2.11 Every mode ![]() $\mathcal {M}$ is itself
$\mathcal {M}$ is itself ![]() $\mathcal {M}$-molecular, because the unit
$\mathcal {M}$-molecular, because the unit ![]() $\mathbf {1}_\mathcal {M}$ is atomic and any object
$\mathbf {1}_\mathcal {M}$ is atomic and any object ![]() $m$ can be written as
$m$ can be written as ![]() $m \otimes \mathbf {1}_\mathcal {M}$.Footnote 6
$m \otimes \mathbf {1}_\mathcal {M}$.Footnote 6
Definition 2.12 Let ![]() $\mathcal {C}, \mathcal {D} \in \mathrm {Pr}^\mathrm {L}$. We say that a functor
$\mathcal {C}, \mathcal {D} \in \mathrm {Pr}^\mathrm {L}$. We say that a functor ![]() $F\colon \mathcal {C} \to \mathcal {D}$ is internally left adjoint if it is left adjoint in
$F\colon \mathcal {C} \to \mathcal {D}$ is internally left adjoint if it is left adjoint in ![]() $\mathrm {Pr}^\mathrm {L}$, namely if it is a left adjoint functor and its right adjoint
$\mathrm {Pr}^\mathrm {L}$, namely if it is a left adjoint functor and its right adjoint ![]() $G\colon \mathcal {D} \to \mathcal {C}$ is itself a left adjoint. We denote by
$G\colon \mathcal {D} \to \mathcal {C}$ is itself a left adjoint. We denote by ![]() ${\operatorname {Fun}^\mathrm {iL}(\mathcal {C}, \mathcal {D})} \subseteq \operatorname {Fun}^\mathrm {L}(\mathcal {C}, \mathcal {D})$ the full subcategory of internally left adjoint functors. We let
${\operatorname {Fun}^\mathrm {iL}(\mathcal {C}, \mathcal {D})} \subseteq \operatorname {Fun}^\mathrm {L}(\mathcal {C}, \mathcal {D})$ the full subcategory of internally left adjoint functors. We let ![]() ${\mathrm {Mod}_\mathcal {M}^\mathrm {iL}}$ be the wide subcategory of
${\mathrm {Mod}_\mathcal {M}^\mathrm {iL}}$ be the wide subcategory of ![]() $\mathrm {Mod}_\mathcal {M}$ with the same objects, and morphisms the internally left adjoint functors.
$\mathrm {Mod}_\mathcal {M}$ with the same objects, and morphisms the internally left adjoint functors.
Proposition 2.13 Let ![]() $\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$, and let
$\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$, and let ![]() $F\colon \mathcal {C} \to \mathcal {D}$ be an internally left adjoint functor, then it sends atomic objects to atomic objects.
$F\colon \mathcal {C} \to \mathcal {D}$ be an internally left adjoint functor, then it sends atomic objects to atomic objects.
Proof. By assumption the right adjoint ![]() $G\colon \mathcal {D} \to \mathcal {C}$ is itself a left adjoint, thus preserves colimits. Let
$G\colon \mathcal {D} \to \mathcal {C}$ is itself a left adjoint, thus preserves colimits. Let ![]() $X \in \mathcal {C}^{\mathrm {at}}$ be an atomic object, then using Lemma 2.2
$X \in \mathcal {C}^{\mathrm {at}}$ be an atomic object, then using Lemma 2.2 ![]() $\hom ^\mathcal {M}(FX,-) \cong \hom ^\mathcal {M}(X, G-)$, which is the composition of
$\hom ^\mathcal {M}(FX,-) \cong \hom ^\mathcal {M}(X, G-)$, which is the composition of ![]() $G$ and
$G$ and ![]() $\hom ^\mathcal {M}(X, -)$, both of which preserve colimits, so that
$\hom ^\mathcal {M}(X, -)$, both of which preserve colimits, so that ![]() $FX$ is atomic.
$FX$ is atomic.
Proposition 2.14 Let ![]() $\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$, and let
$\mathcal {C}, \mathcal {D} \in \mathrm {Mod}_\mathcal {M}$, and let ![]() $F\colon \mathcal {C} \to \mathcal {D}$ be a left adjoint functor. If
$F\colon \mathcal {C} \to \mathcal {D}$ be a left adjoint functor. If ![]() $\mathcal {C}$ is molecular and
$\mathcal {C}$ is molecular and ![]() $F$ sends a collection of atomic generators
$F$ sends a collection of atomic generators ![]() $B \subset \mathcal {C}$ to atomic objects in
$B \subset \mathcal {C}$ to atomic objects in ![]() $\mathcal {D}$, then
$\mathcal {D}$, then ![]() $F$ is internally left adjoint.
$F$ is internally left adjoint.
Proof. We wish to show that ![]() $G$, the right adjoint of
$G$, the right adjoint of ![]() $F$, is itself a left adjoint, namely that it preserves colimits. Let
$F$, is itself a left adjoint, namely that it preserves colimits. Let ![]() $Y_i\colon I \to \mathcal {D}$ be a diagram, and we wish to show that
$Y_i\colon I \to \mathcal {D}$ be a diagram, and we wish to show that ![]() $G(\operatorname *{colim} Y_i) \cong \operatorname *{colim} G Y_i$. By the Yoneda lemma, this is equivalent to checking that for every
$G(\operatorname *{colim} Y_i) \cong \operatorname *{colim} G Y_i$. By the Yoneda lemma, this is equivalent to checking that for every ![]() $X \in \mathcal {C}$ we have
$X \in \mathcal {C}$ we have
Since ![]() $\hom (-, -) \cong \hom (\mathbf {1}_\mathcal {M}, \hom ^\mathcal {M}(-, -))$, it suffices to check that for every
$\hom (-, -) \cong \hom (\mathbf {1}_\mathcal {M}, \hom ^\mathcal {M}(-, -))$, it suffices to check that for every ![]() $X \in \mathcal {C}$ we have
$X \in \mathcal {C}$ we have
Let ![]() $A$ denote the collection of
$A$ denote the collection of ![]() $X \in \mathcal {C}$ for which this condition holds, and we shall show that
$X \in \mathcal {C}$ for which this condition holds, and we shall show that ![]() $A = \mathcal {C}$.
$A = \mathcal {C}$.
First, for every ![]() $X \in B$, we know that
$X \in B$, we know that
 \begin{align*} \hom^\mathcal{M}(X, G(\operatorname*{colim}_I Y_i)) &\cong \hom^\mathcal{M}(F X, \operatorname*{colim}_I Y_i)\\ &\cong \operatorname*{colim}_I \hom^\mathcal{M}(F X, Y_i)\\ &\cong \operatorname*{colim}_I \hom^\mathcal{M}(X, G Y_i)\\ &\cong \hom^\mathcal{M}(X, \operatorname*{colim}_I G Y_i), \end{align*}
\begin{align*} \hom^\mathcal{M}(X, G(\operatorname*{colim}_I Y_i)) &\cong \hom^\mathcal{M}(F X, \operatorname*{colim}_I Y_i)\\ &\cong \operatorname*{colim}_I \hom^\mathcal{M}(F X, Y_i)\\ &\cong \operatorname*{colim}_I \hom^\mathcal{M}(X, G Y_i)\\ &\cong \hom^\mathcal{M}(X, \operatorname*{colim}_I G Y_i), \end{align*}
where the first and third steps follow from Lemma 2.2, the second step follows from the assumption that ![]() $FX$ is atomic since
$FX$ is atomic since ![]() $X \in B$ and
$X \in B$ and ![]() $F$ sends
$F$ sends ![]() $B$ to atomic objects, and the fourth step follows from the fact
$B$ to atomic objects, and the fourth step follows from the fact ![]() $X$ is atomic. Therefore,
$X$ is atomic. Therefore, ![]() $B \subseteq A$.
$B \subseteq A$.
Second, for every ![]() $X \in A$ and
$X \in A$ and ![]() $m \in \mathcal {M}$, we know that
$m \in \mathcal {M}$, we know that ![]() $\hom ^\mathcal {M}(m \otimes X, -) \cong \hom ^\mathcal {M}(m, \hom ^\mathcal {M}(X, -))$ so that
$\hom ^\mathcal {M}(m \otimes X, -) \cong \hom ^\mathcal {M}(m, \hom ^\mathcal {M}(X, -))$ so that ![]() $m \otimes X \in A$, i.e.
$m \otimes X \in A$, i.e. ![]() $A$ is closed under the action of
$A$ is closed under the action of ![]() $\mathcal {M}$.
$\mathcal {M}$.
Third, for every diagram ![]() $X_j\colon J \to \mathcal {C}$ landing in
$X_j\colon J \to \mathcal {C}$ landing in ![]() $A$, we know that
$A$, we know that ![]() $\hom ^\mathcal {M}(\operatorname *{colim}_J X_j, -) \cong \lim _{J^\mathrm {op}} \hom ^\mathcal {M}(X_j, -)$ so that
$\hom ^\mathcal {M}(\operatorname *{colim}_J X_j, -) \cong \lim _{J^\mathrm {op}} \hom ^\mathcal {M}(X_j, -)$ so that ![]() $\operatorname *{colim}_J X_j \in A$, i.e.
$\operatorname *{colim}_J X_j \in A$, i.e. ![]() $A$ is closed under colimits.
$A$ is closed under colimits.
We have shown that ![]() $B \subseteq A$ and that
$B \subseteq A$ and that ![]() $A$ is closed under the action of
$A$ is closed under the action of ![]() $\mathcal {M}$ and colimits, and by assumption
$\mathcal {M}$ and colimits, and by assumption ![]() $B$ are atomic generators, thus
$B$ are atomic generators, thus ![]() $A = \mathcal {C}$ as needed.
$A = \mathcal {C}$ as needed.
Recall that for ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$ we have an equivalence
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$ we have an equivalence ![]() $\operatorname {Fun}^\mathrm {L}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}$ given by evaluation at
$\operatorname {Fun}^\mathrm {L}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}$ given by evaluation at ![]() $\mathbf {1}_\mathcal {M}$. Its inverse sends
$\mathbf {1}_\mathcal {M}$. Its inverse sends ![]() $X \in \mathcal {C}$ to the functor
$X \in \mathcal {C}$ to the functor ![]() $- \otimes X\colon \mathcal {M} \to \mathcal {C}$ (part of the data admitting
$- \otimes X\colon \mathcal {M} \to \mathcal {C}$ (part of the data admitting ![]() $\mathcal {C}$ as an
$\mathcal {C}$ as an ![]() $\mathcal {M}$-module). Furthermore, the right adjoint of
$\mathcal {M}$-module). Furthermore, the right adjoint of ![]() $- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is
$- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is ![]() $\hom ^\mathcal {M}(X, -)\colon \mathcal {C} \to \mathcal {M}$.
$\hom ^\mathcal {M}(X, -)\colon \mathcal {C} \to \mathcal {M}$.
Proposition 2.15 Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, then the equivalence
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, then the equivalence ![]() $\operatorname {Fun}^\mathrm {L}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}$ restricts to an equivalence
$\operatorname {Fun}^\mathrm {L}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}$ restricts to an equivalence ![]() $\operatorname {Fun}^\mathrm {iL}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}^{\mathrm {at}}$. In addition, if
$\operatorname {Fun}^\mathrm {iL}(\mathcal {M}, \mathcal {C}) \xrightarrow {\smash {{\scriptstyle \sim }}} \mathcal {C}^{\mathrm {at}}$. In addition, if ![]() $X \in \mathcal {C}$ and
$X \in \mathcal {C}$ and ![]() $m \in \mathcal {M}$ are atomic, then so is
$m \in \mathcal {M}$ are atomic, then so is ![]() ${m \otimes X \in \mathcal {C}}$.
${m \otimes X \in \mathcal {C}}$.
Proof. First, by Proposition 2.13 and the fact that the ![]() $\mathbf {1}_\mathcal {M}$ is atomic, the functor indeed lands in the full subcategory
$\mathbf {1}_\mathcal {M}$ is atomic, the functor indeed lands in the full subcategory ![]() $\mathcal {C}^{\mathrm {at}}$. In particular, it is also fully faithful as the restriction of an equivalence to two full subcategories. We need to show that it is essentially surjective, i.e. that if
$\mathcal {C}^{\mathrm {at}}$. In particular, it is also fully faithful as the restriction of an equivalence to two full subcategories. We need to show that it is essentially surjective, i.e. that if ![]() $X \in \mathcal {C}^{\mathrm {at}}$ then
$X \in \mathcal {C}^{\mathrm {at}}$ then ![]() $- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is internally left adjoint. This holds since its right adjoint is
$- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is internally left adjoint. This holds since its right adjoint is ![]() ${\hom ^\mathcal {M}(X, -)\colon\mathcal {C} \to \mathcal {M}}$, which by assumption preserves colimits.
${\hom ^\mathcal {M}(X, -)\colon\mathcal {C} \to \mathcal {M}}$, which by assumption preserves colimits.
For the last part, as ![]() $- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is internally left adjoint, Proposition 2.13 implies that it sends atomic objects to atomic objects.
$- \otimes X\colon \mathcal {M} \to \mathcal {C}$ is internally left adjoint, Proposition 2.13 implies that it sends atomic objects to atomic objects.
Remark 2.16 In Corollary 2.48 we extend the last part of the proposition to show that, in fact, ![]() $\mathcal {C}^{\mathrm {at}}$ is a module over
$\mathcal {C}^{\mathrm {at}}$ is a module over ![]() $\mathcal {M}^{\mathrm {at}}$.
$\mathcal {M}^{\mathrm {at}}$.
In light of this proposition, we construct the functor of taking atomics functorially. We also recall from Proposition 2.9 that ![]() $\mathcal {C}^{\mathrm {at}}$ is a small category.
$\mathcal {C}^{\mathrm {at}}$ is a small category.
Definition 2.17 We define the functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}$ by
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}$ by ![]() $(-)^{\mathrm {at}} = \operatorname {Fun}^\mathrm {iL}(\mathcal {M}, -)$.
$(-)^{\mathrm {at}} = \operatorname {Fun}^\mathrm {iL}(\mathcal {M}, -)$.
Definition 2.18 Let ![]() $I$ be an indexing category. We say that
$I$ be an indexing category. We say that ![]() $I$ is an absolute limit of
$I$ is an absolute limit of ![]() $\mathcal {M}$ if for any
$\mathcal {M}$ if for any ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$,
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, ![]() $I$-shaped limits in
$I$-shaped limits in ![]() $\mathcal {C}$ commute with colimits.
$\mathcal {C}$ commute with colimits.
Remark 2.19 The term absolute limit is usually used in the context of enriched categories, saying that ![]() $I$ is an absolute limit of
$I$ is an absolute limit of ![]() $\mathcal {V} \in \mathrm {Mon}(\mathrm {Cat})$ if any
$\mathcal {V} \in \mathrm {Mon}(\mathrm {Cat})$ if any ![]() $\mathcal {V}$-enriched functor commutes with
$\mathcal {V}$-enriched functor commutes with ![]() $I$-shaped limits. We will not use this condition in this paper, but for the convenience of the reader we remark on the connection between this condition and the one appearing in Definition 2.18 when
$I$-shaped limits. We will not use this condition in this paper, but for the convenience of the reader we remark on the connection between this condition and the one appearing in Definition 2.18 when ![]() $\mathcal {V}$ is a mode.
$\mathcal {V}$ is a mode.
Assume that ![]() $I$ is an absolute limit in the ordinary sense, namely that
$I$ is an absolute limit in the ordinary sense, namely that ![]() $\mathcal {V}$-enriched functors commute with
$\mathcal {V}$-enriched functors commute with ![]() $I$-shaped limits. Let
$I$-shaped limits. Let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {V}$. For any indexing category
$\mathcal {C} \in \mathrm {Mod}_\mathcal {V}$. For any indexing category ![]() $J$ consider
$J$ consider ![]() $\operatorname *{colim}_J\colon \mathcal {C}^J \to \mathcal {C}$. This functor commutes with colimits, and since
$\operatorname *{colim}_J\colon \mathcal {C}^J \to \mathcal {C}$. This functor commutes with colimits, and since ![]() $\mathcal {V}$ is a mode, it is a morphism in
$\mathcal {V}$ is a mode, it is a morphism in ![]() $\mathrm {Mod}_\mathcal {V}$, so, as referred to in Remark 2.1, it is canonically
$\mathrm {Mod}_\mathcal {V}$, so, as referred to in Remark 2.1, it is canonically ![]() $\mathcal {V}$-enriched, and therefore commutes with
$\mathcal {V}$-enriched, and therefore commutes with ![]() $I$-shaped limits. This holds for any
$I$-shaped limits. This holds for any ![]() $J$, meaning that
$J$, meaning that ![]() $I$-shaped limits in
$I$-shaped limits in ![]() $\mathcal {C}$ commute with colimits, reproducing Definition 2.18.
$\mathcal {C}$ commute with colimits, reproducing Definition 2.18.
The implication in the other direction should follow from a working theory of enriched left Kan extensions and their compatibility with the enriched Yoneda embedding, which we are unaware of a reference for.
Lemma 2.20 If ![]() $I$ is an absolute limit of
$I$ is an absolute limit of ![]() $\mathcal {M}$ and
$\mathcal {M}$ and ![]() $\mathcal {M} \to \mathcal {N}$ is map of modes, then
$\mathcal {M} \to \mathcal {N}$ is map of modes, then ![]() $I$ is an absolute limit of
$I$ is an absolute limit of ![]() $\mathcal {N}$ as well.
$\mathcal {N}$ as well.
Proof. This is immediate from the fact that ![]() $\mathrm {Mod}_\mathcal {N} \subseteq \mathrm {Mod}_\mathcal {M}$.
$\mathrm {Mod}_\mathcal {N} \subseteq \mathrm {Mod}_\mathcal {M}$.
Lemma 2.21 Let ![]() $I$ be an absolute limit of
$I$ be an absolute limit of ![]() $\mathcal {M}$, and
$\mathcal {M}$, and ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. Then
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$. Then ![]() $m \otimes -\colon \mathcal {C} \to \mathcal {C}$ commutes with
$m \otimes -\colon \mathcal {C} \to \mathcal {C}$ commutes with ![]() $I$-shaped limits, for any
$I$-shaped limits, for any ![]() $m \in \mathcal {M}$.
$m \in \mathcal {M}$.
Proof. By assumption, ![]() $\lim _I\colon \mathcal {C}^I \to \mathcal {C}$ commutes with colimits. Therefore, it is a map in
$\lim _I\colon \mathcal {C}^I \to \mathcal {C}$ commutes with colimits. Therefore, it is a map in ![]() $\mathrm {Mod}_\mathcal {M}$, so that it also commutes
$\mathrm {Mod}_\mathcal {M}$, so that it also commutes ![]() $m \otimes -\colon \mathcal {C} \to \mathcal {C}$ for any
$m \otimes -\colon \mathcal {C} \to \mathcal {C}$ for any ![]() $m \in \mathcal {M}$.
$m \in \mathcal {M}$.
Proposition 2.22 Let ![]() $I$ be an absolute limit of
$I$ be an absolute limit of ![]() $\mathcal {M}$, then for any
$\mathcal {M}$, then for any ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, the atomics
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, the atomics ![]() $\mathcal {C}^{\mathrm {at}} \subset \mathcal {C}$ are closed under
$\mathcal {C}^{\mathrm {at}} \subset \mathcal {C}$ are closed under ![]() $I^\mathrm {op}$-shaped colimits.
$I^\mathrm {op}$-shaped colimits.
Proof. Let ![]() $X_i\colon I^\mathrm {op} \to \mathcal {C}$ be a diagram landing in the atomics. Recall that
$X_i\colon I^\mathrm {op} \to \mathcal {C}$ be a diagram landing in the atomics. Recall that ![]() $\hom ^\mathcal {M}(-, -)\colon \mathcal {C}^\mathrm {op} \times \mathcal {C} \to \mathcal {M}$ commutes with limits in the first coordinate, thus
$\hom ^\mathcal {M}(-, -)\colon \mathcal {C}^\mathrm {op} \times \mathcal {C} \to \mathcal {M}$ commutes with limits in the first coordinate, thus ![]() $\hom ^\mathcal {M}(\operatorname *{colim}_{I^\mathrm {op}} X_i, -)$ is equivalent to
$\hom ^\mathcal {M}(\operatorname *{colim}_{I^\mathrm {op}} X_i, -)$ is equivalent to
The functor ![]() $\Delta$ commutes with colimits since colimits in functor categories are computed level-wise. Since each
$\Delta$ commutes with colimits since colimits in functor categories are computed level-wise. Since each ![]() $X_i$ is atomic, each
$X_i$ is atomic, each ![]() $\hom ^\mathcal {M}(X_i, -)$ commutes with colimits, and as colimits in functor categories are computed level-wise, we get that
$\hom ^\mathcal {M}(X_i, -)$ commutes with colimits, and as colimits in functor categories are computed level-wise, we get that ![]() $(\hom ^\mathcal {M}(X_i, -))_I$ commutes with colimits. By assumption,
$(\hom ^\mathcal {M}(X_i, -))_I$ commutes with colimits. By assumption, ![]() $I$ is an absolute limit of
$I$ is an absolute limit of ![]() $\mathcal {M}$, thus
$\mathcal {M}$, thus ![]() $\lim _I$ commutes with colimits. This shows that
$\lim _I$ commutes with colimits. This shows that ![]() $\hom ^\mathcal {M}(\operatorname *{colim}_{I^\mathrm {op}} X_i, -)$ commutes with colimits, i.e. that
$\hom ^\mathcal {M}(\operatorname *{colim}_{I^\mathrm {op}} X_i, -)$ commutes with colimits, i.e. that ![]() $\operatorname *{colim}_{I^\mathrm {op}} X_i$ is indeed atomic.
$\operatorname *{colim}_{I^\mathrm {op}} X_i$ is indeed atomic.
Remark 2.23 Let ![]() $F\colon \mathcal {C} \to \mathcal {D}$ be an internally left adjoint functor, and let
$F\colon \mathcal {C} \to \mathcal {D}$ be an internally left adjoint functor, and let ![]() $I$ be an absolute limit of
$I$ be an absolute limit of ![]() $\mathcal {M}$. Then
$\mathcal {M}$. Then ![]() $F$ preserves colimits, and the atomics are closed under
$F$ preserves colimits, and the atomics are closed under ![]() $I^\mathrm {op}$-shaped colimits, so that the induced functor between the atomics preserves
$I^\mathrm {op}$-shaped colimits, so that the induced functor between the atomics preserves ![]() $I^\mathrm {op}$-shaped colimits.
$I^\mathrm {op}$-shaped colimits.
The following claim immediately follows.
Proposition 2.24 Let ![]() $\mathcal {K} \subset \{ I^\mathrm {op} \mid I \text { absolute limit of } \mathcal {M} \}$ be a collection of opposites of absolute limits of
$\mathcal {K} \subset \{ I^\mathrm {op} \mid I \text { absolute limit of } \mathcal {M} \}$ be a collection of opposites of absolute limits of ![]() $\mathcal {M}$, then the functor of taking atomics
$\mathcal {M}$, then the functor of taking atomics ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}$ factors through
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Cat}$ factors through ![]() $\mathrm {Cat}_\mathcal {K}$.
$\mathrm {Cat}_\mathcal {K}$.
Proposition 2.25 Let ![]() $\mathcal {M}$ be a stable mode, then all finite categories are absolute limits. Furthermore, for any
$\mathcal {M}$ be a stable mode, then all finite categories are absolute limits. Furthermore, for any ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$,
$\mathcal {C} \in \mathrm {Mod}_\mathcal {M}$, ![]() $\mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$ is a stable subcategory of
$\mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$ is a stable subcategory of ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Recall that ![]() $\mathcal {C}$ itself is stable, so the first part follows from the commutativity of finite limits and colimits in stable categories. For the second part, first note that the zero object is obviously atomic. As finite limits are absolute, the atomics are closed under finite colimits, so it suffices to show that the atomics are also closed under desuspensions. Let
$\mathcal {C}$ itself is stable, so the first part follows from the commutativity of finite limits and colimits in stable categories. For the second part, first note that the zero object is obviously atomic. As finite limits are absolute, the atomics are closed under finite colimits, so it suffices to show that the atomics are also closed under desuspensions. Let ![]() $X \in \mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$, then indeed
$X \in \mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$, then indeed ![]() $\hom ^\mathcal {M}(\Sigma ^{-1} X, -) \cong \Sigma \hom ^\mathcal {M}(X, -)$ is colimit preserving, because
$\hom ^\mathcal {M}(\Sigma ^{-1} X, -) \cong \Sigma \hom ^\mathcal {M}(X, -)$ is colimit preserving, because ![]() $X$ is atomic and
$X$ is atomic and ![]() $\Sigma \colon \mathcal {M} \to \mathcal {M}$ is colimit preserving.
$\Sigma \colon \mathcal {M} \to \mathcal {M}$ is colimit preserving.
Proposition 2.26 Let ![]() $F\colon \mathcal {M} \to \mathcal {N}$ be a smashing localization of modes (see [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 5.1.2]), and let
$F\colon \mathcal {M} \to \mathcal {N}$ be a smashing localization of modes (see [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 5.1.2]), and let ![]() $\mathcal {C} \in \mathrm {Mod}_\mathcal {N}$. Then the
$\mathcal {C} \in \mathrm {Mod}_\mathcal {N}$. Then the ![]() $\mathcal {N}$-atomics coincide with the
$\mathcal {N}$-atomics coincide with the ![]() $\mathcal {M}$-atomics, that is
$\mathcal {M}$-atomics, that is ![]() $\mathcal {C}^{\mathcal {N}\text {-}\mathrm {at}} = \mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$.
$\mathcal {C}^{\mathcal {N}\text {-}\mathrm {at}} = \mathcal {C}^{{\mathcal {M}\text {-}}\mathrm {at}}$.
Proof. By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.2.15], the localization is smashing if and only if the right adjoint of ![]() $F\colon \mathcal {M} \to \mathcal {N}$ is itself a left adjoint (i.e. if
$F\colon \mathcal {M} \to \mathcal {N}$ is itself a left adjoint (i.e. if ![]() $F$ is internally left adjoint). This allows us to treat
$F$ is internally left adjoint). This allows us to treat ![]() $\mathcal {N}$ as a full subcategory of
$\mathcal {N}$ as a full subcategory of ![]() $\mathcal {M}$ closed under both limits and colimits. Now, [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.2.10] shows that
$\mathcal {M}$ closed under both limits and colimits. Now, [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.2.10] shows that ![]() $\mathcal {N}$ classifies the property of being in the mode
$\mathcal {N}$ classifies the property of being in the mode ![]() $\mathcal {M}$ such that all
$\mathcal {M}$ such that all ![]() $\mathcal {M}$-enriched
$\mathcal {M}$-enriched ![]() $\hom$'s land in
$\hom$'s land in ![]() $\mathcal {N}$, i.e.
$\mathcal {N}$, i.e. ![]() $\hom ^\mathcal {M}(X,-) = \hom ^\mathcal {N}(X,-)$, thus by the closure of
$\hom ^\mathcal {M}(X,-) = \hom ^\mathcal {N}(X,-)$, thus by the closure of ![]() $\mathcal {N} \subseteq \mathcal {M}$ under colimits,
$\mathcal {N} \subseteq \mathcal {M}$ under colimits, ![]() $\hom ^\mathcal {M}(X,-)\colon \mathcal {C} \to \mathcal {M}$ commutes with colimits if and only if
$\hom ^\mathcal {M}(X,-)\colon \mathcal {C} \to \mathcal {M}$ commutes with colimits if and only if ![]() $\hom ^\mathcal {N}(X,-)\colon \mathcal {C} \to \mathcal {N}$ does.
$\hom ^\mathcal {N}(X,-)\colon \mathcal {C} \to \mathcal {N}$ does.
2.2 Atomics and presheaves
Throughout this subsection, let ![]() $\mathcal {K} \subset \{ I^\mathrm {op} \mid I \text { absolute limit of } \mathcal {M} \}$ be some small collection of opposites of absolute limits of
$\mathcal {K} \subset \{ I^\mathrm {op} \mid I \text { absolute limit of } \mathcal {M} \}$ be some small collection of opposites of absolute limits of ![]() $\mathcal {M}$ (not necessarily all of them, for instance,
$\mathcal {M}$ (not necessarily all of them, for instance, ![]() $\mathcal {K}$ is allowed to be empty). We also let
$\mathcal {K}$ is allowed to be empty). We also let ![]() ${\mathcal {K}^\mathrm {op}} = \{ I \mid I^\mathrm {op} \in \mathcal {K} \}$ be the collection of all of the opposite categories.
${\mathcal {K}^\mathrm {op}} = \{ I \mid I^\mathrm {op} \in \mathcal {K} \}$ be the collection of all of the opposite categories.
Definition 2.27 For ![]() $\mathcal {C}_0 \in \mathrm {Cat}$, we define the category of
$\mathcal {C}_0 \in \mathrm {Cat}$, we define the category of ![]() $\mathcal {M}$-valued presheaves by
$\mathcal {M}$-valued presheaves by ![]() ${\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)} = \operatorname {Fun}(\mathcal {C}_0^\mathrm {op}, \mathcal {M})$. If
${\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)} = \operatorname {Fun}(\mathcal {C}_0^\mathrm {op}, \mathcal {M})$. If ![]() $\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$, we let
$\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$, we let ![]() ${\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)} = \operatorname {Fun}^{\mathcal {K}^\mathrm {op}}(\mathcal {C}_0^\mathrm {op}, \mathcal {M})$ be the full subcategory of
${\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)} = \operatorname {Fun}^{\mathcal {K}^\mathrm {op}}(\mathcal {C}_0^\mathrm {op}, \mathcal {M})$ be the full subcategory of ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ on those functors that preserve all limits indexed by
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ on those functors that preserve all limits indexed by ![]() $I \in {\mathcal {K}^\mathrm {op}}$, namely functors
$I \in {\mathcal {K}^\mathrm {op}}$, namely functors ![]() $F\colon \mathcal {C}_0^\mathrm {op} \to \mathcal {M}$ that send
$F\colon \mathcal {C}_0^\mathrm {op} \to \mathcal {M}$ that send ![]() $I^\mathrm {op}$-shaped colimits in
$I^\mathrm {op}$-shaped colimits in ![]() $\mathcal {C}_0$ to
$\mathcal {C}_0$ to ![]() $I$-shaped limits in
$I$-shaped limits in ![]() $\mathcal {M}$.
$\mathcal {M}$.
Remark 2.28 The definition will be made functorial in Definition 2.34.
For the case ![]() $\mathcal {M} = \mathcal {S}$, [Reference Gepner, Haugseng and NikolausGHN17, Lemma 10.6] shows that
$\mathcal {M} = \mathcal {S}$, [Reference Gepner, Haugseng and NikolausGHN17, Lemma 10.6] shows that ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}(\mathcal {C}_0)$ is presentable. From this we deduce the following.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}(\mathcal {C}_0)$ is presentable. From this we deduce the following.
Proposition 2.29 There is an equivalence ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \cong \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}(\mathcal {C}_0) \otimes \mathcal {M}$, and in particular it is presentable and in the mode
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \cong \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}(\mathcal {C}_0) \otimes \mathcal {M}$, and in particular it is presentable and in the mode ![]() $\mathcal {M}$.
$\mathcal {M}$.
Proof. Indeed, we have an equivalence
 \begin{align*} \operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0) \otimes \mathcal{M} &\cong \operatorname{Fun}^\mathrm{R}(\operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0)^\mathrm{op}, \mathcal{M})\\ &\cong \operatorname{Fun}^\mathrm{L}(\operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0), \mathcal{M}^\mathrm{op})^\mathrm{op}\\ &\cong \operatorname{Fun}_\mathcal{K}(\mathcal{C}_0, \mathcal{M}^\mathrm{op})^\mathrm{op}\\ &\cong \operatorname{Fun}^{\mathcal{K}^\mathrm{op}}(\mathcal{C}_0^\mathrm{op}, \mathcal{M})\\ &= \operatorname{\operatorname{\mathcal{P}}_\mathcal{K}^\mathcal{M}}(\mathcal{C}_0) , \end{align*}
\begin{align*} \operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0) \otimes \mathcal{M} &\cong \operatorname{Fun}^\mathrm{R}(\operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0)^\mathrm{op}, \mathcal{M})\\ &\cong \operatorname{Fun}^\mathrm{L}(\operatorname{\operatorname{\mathcal{P}}_\mathcal{K}}(\mathcal{C}_0), \mathcal{M}^\mathrm{op})^\mathrm{op}\\ &\cong \operatorname{Fun}_\mathcal{K}(\mathcal{C}_0, \mathcal{M}^\mathrm{op})^\mathrm{op}\\ &\cong \operatorname{Fun}^{\mathcal{K}^\mathrm{op}}(\mathcal{C}_0^\mathrm{op}, \mathcal{M})\\ &= \operatorname{\operatorname{\mathcal{P}}_\mathcal{K}^\mathcal{M}}(\mathcal{C}_0) , \end{align*}
where the first equality is [Reference LurieLur17, Proposition 4.8.1.17], the second is passing to the opposite, the third is the universal property of ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}$ given in [Reference LurieLur09, Corollary 5.3.6.10], the fourth is by passing to the opposite, and the last is by definition.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}$ given in [Reference LurieLur09, Corollary 5.3.6.10], the fourth is by passing to the opposite, and the last is by definition.
Lemma 2.30 Let ![]() $\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$, then
$\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$, then ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \subseteq \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is closed under limits and colimits, thus the inclusion has both adjoints.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \subseteq \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is closed under limits and colimits, thus the inclusion has both adjoints.
Proof. Let ![]() $F_j\colon J \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ be a diagram landing in
$F_j\colon J \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ be a diagram landing in ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$. We need to show that
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$. We need to show that ![]() $\operatorname *{colim}_J F_j$ and
$\operatorname *{colim}_J F_j$ and ![]() $\lim _J F_j$ are again in
$\lim _J F_j$ are again in ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, i.e. that they commute with all limits indexed by
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, i.e. that they commute with all limits indexed by ![]() $I \in {\mathcal {K}^\mathrm {op}}$. Let
$I \in {\mathcal {K}^\mathrm {op}}$. Let ![]() $X_i\colon I^\mathrm {op} \to \mathcal {C}_0$ be a diagram. Using the fact that colimits and limits in functor categories are computed level-wise, and that
$X_i\colon I^\mathrm {op} \to \mathcal {C}_0$ be a diagram. Using the fact that colimits and limits in functor categories are computed level-wise, and that ![]() $I$ is an absolute limit, we get
$I$ is an absolute limit, we get
Similarly ![]() $\lim _J F_j \in \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, since limits commute with limits.
$\lim _J F_j \in \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, since limits commute with limits.
Definition 2.31 Let ![]() $\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$. We denote by
$\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$. We denote by ![]() ${L_\mathcal {K}}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ the (internally) left adjoint of the inclusion
${L_\mathcal {K}}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ the (internally) left adjoint of the inclusion ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \subseteq \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \subseteq \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$.
Lemma 2.32 For ![]() $f\colon \mathcal {C}_0 \to \mathcal {D}_0$, a morphism in
$f\colon \mathcal {C}_0 \to \mathcal {D}_0$, a morphism in ![]() $\mathrm {Cat}_\mathcal {K}$, the restriction of
$\mathrm {Cat}_\mathcal {K}$, the restriction of ![]() $f^*\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {D}_0) \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ to
$f^*\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {D}_0) \to \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ to ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$ lands in
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$ lands in ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$.
Proof. Recall that ![]() $f^*$ is given by pre-composition with
$f^*$ is given by pre-composition with ![]() $f^\mathrm {op}\colon \mathcal {C}_0^\mathrm {op} \to \mathcal {D}_0^\mathrm {op}$, which preserves limits indexed by
$f^\mathrm {op}\colon \mathcal {C}_0^\mathrm {op} \to \mathcal {D}_0^\mathrm {op}$, which preserves limits indexed by ![]() $I \in {\mathcal {K}^\mathrm {op}}$, as the opposite of a morphism in
$I \in {\mathcal {K}^\mathrm {op}}$, as the opposite of a morphism in ![]() $\mathrm {Cat}_\mathcal {K}$.
$\mathrm {Cat}_\mathcal {K}$.
Lemma 2.33 For ![]() $f\colon \mathcal {C}_0 \to \mathcal {D}_0$ a morphism in
$f\colon \mathcal {C}_0 \to \mathcal {D}_0$ a morphism in ![]() $\mathrm {Cat}_\mathcal {K}$, the functor
$\mathrm {Cat}_\mathcal {K}$, the functor ![]() $f^*\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ preserves all limits and colimits and thus has a right adjoint
$f^*\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ preserves all limits and colimits and thus has a right adjoint ![]() $f_*$ and a left adjoint
$f_*$ and a left adjoint ![]() $f_!$.
$f_!$.
Proof. By Lemma 2.30, ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is closed under limits and colimits in
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is closed under limits and colimits in ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, which are thus computed level-wise, and similarly for
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, which are thus computed level-wise, and similarly for ![]() $\mathcal {D}_0$. Therefore, we get
$\mathcal {D}_0$. Therefore, we get
showing that ![]() $f^*$ commutes with colimits, and similarly for limits.
$f^*$ commutes with colimits, and similarly for limits.
Lemma 2.32 shows that the functor ![]() $\operatorname {Fun}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \widehat {\mathrm {Cat}}$, sending
$\operatorname {Fun}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \widehat {\mathrm {Cat}}$, sending ![]() $\mathcal {C}_0$ to
$\mathcal {C}_0$ to ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ and
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ and ![]() $f$ to
$f$ to ![]() $f^*$, has a subfunctor
$f^*$, has a subfunctor ![]() $\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \widehat {\mathrm {Cat}}$ sending
$\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \widehat {\mathrm {Cat}}$ sending ![]() $\mathcal {C}_0$ to
$\mathcal {C}_0$ to ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ and
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ and ![]() $f$ to
$f$ to ![]() $f^*$. By Proposition 2.29, the categories
$f^*$. By Proposition 2.29, the categories ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ are in the mode
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ are in the mode ![]() $\mathcal {M}$, and by Lemma 2.33, the morphism
$\mathcal {M}$, and by Lemma 2.33, the morphism ![]() $f^*$ is a right adjoint, so that the functor factors as
$f^*$ is a right adjoint, so that the functor factors as ![]() $\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$.
$\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$.
Definition 2.34 We define the functor ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ by passing to the left adjoints in
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ by passing to the left adjoints in ![]() $\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$, that is the functor sending
$\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$, that is the functor sending ![]() $\mathcal {C}_0$ to
$\mathcal {C}_0$ to ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ and
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ and ![]() $f\colon \mathcal {C}_0 \to \mathcal {D}_0$ to
$f\colon \mathcal {C}_0 \to \mathcal {D}_0$ to ![]() $f_!\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$.
$f_!\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$.
Proposition 2.35 The functor ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ lands in
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ lands in ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$.
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$.
Proof. Lemma 2.33 shows that ![]() $f_!\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$ is internally left adjoint.
$f_!\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {D}_0)$ is internally left adjoint.
Proposition 2.36 There is a natural transformation ![]() $L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ of functors
$L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ of functors ![]() $\mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$, making the construction of Definition 2.31 natural.
$\mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$, making the construction of Definition 2.31 natural.
Proof. Since ![]() $\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$ is a subfunctor of
$\operatorname {Fun}^{\mathcal {K}^\mathrm {op}}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$ is a subfunctor of ![]() $\operatorname {Fun}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$, there is a natural transformation from the former to the latter given by the inclusion. Applying [Reference LurieLur17, Corollary 4.7.4.18 (3)] for
$\operatorname {Fun}((-)^\mathrm {op}, \mathcal {M})\colon \mathrm {Cat}_\mathcal {K}^\mathrm {op} \to \mathrm {Pr}^\mathrm {R}$, there is a natural transformation from the former to the latter given by the inclusion. Applying [Reference LurieLur17, Corollary 4.7.4.18 (3)] for ![]() $S = \mathrm {Cat}_\mathcal {K}^\mathrm {op}$ (and considering our functors as landing in
$S = \mathrm {Cat}_\mathcal {K}^\mathrm {op}$ (and considering our functors as landing in ![]() $\widehat {\mathrm {Cat}}$) shows that by passing to the left adjoints in the target and in the natural transformation, we obtain a natural transformation
$\widehat {\mathrm {Cat}}$) shows that by passing to the left adjoints in the target and in the natural transformation, we obtain a natural transformation ![]() $L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$. Indeed,
$L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$. Indeed, ![]() $L_\mathcal {K}$ was defined in Definition 2.31 as the left adjoint of the inclusion.
$L_\mathcal {K}$ was defined in Definition 2.31 as the left adjoint of the inclusion.
Definition 2.37 We define the Yoneda map ![]() ${{\unicode{x3088}}_\mathcal {K}^\mathcal {M}}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ as the composition
${{\unicode{x3088}}_\mathcal {K}^\mathcal {M}}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ as the composition
where ![]() ${\unicode{x3088}}$ is the ordinary Yoneda embedding, and the second map is given by tensoring with the unit map
${\unicode{x3088}}$ is the ordinary Yoneda embedding, and the second map is given by tensoring with the unit map ![]() $\mathcal {S} \to \mathcal {M}$.
$\mathcal {S} \to \mathcal {M}$.
Remark 2.38 Generally, the Yoneda map ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is not fully faithful. For example, in the case where
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is not fully faithful. For example, in the case where ![]() $\mathcal {K} = \emptyset$ and
$\mathcal {K} = \emptyset$ and ![]() $\mathcal {C}_0 = *$, the map is
$\mathcal {C}_0 = *$, the map is ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon * \to \mathcal {M}$, which induces
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon * \to \mathcal {M}$, which induces ![]() $\hom (*, *) \to \hom (\mathbf {1}_\mathcal {M}, \mathbf {1}_\mathcal {M})$ that is usually not an equivalence.
$\hom (*, *) \to \hom (\mathbf {1}_\mathcal {M}, \mathbf {1}_\mathcal {M})$ that is usually not an equivalence.
Proposition 2.39 The Yoneda map can be upgraded to a natural transformation ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ from the inclusion
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ from the inclusion ![]() $\iota _{\mathcal {K}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Cat} \to \widehat {\mathrm {Cat}}$ to
$\iota _{\mathcal {K}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Cat} \to \widehat {\mathrm {Cat}}$ to ![]() $\mathrm {Cat}_\mathcal {K} \xrightarrow {\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}} \mathrm {Pr}^\mathrm {L} \to \widehat {\mathrm {Cat}}$.
$\mathrm {Cat}_\mathcal {K} \xrightarrow {\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}} \mathrm {Pr}^\mathrm {L} \to \widehat {\mathrm {Cat}}$.
Proof. The natural transformation is obtained by the following diagram.

Here ![]() ${\unicode{x3088}}\colon \iota \Rightarrow \operatorname {\mathcal {P}}$ is the ordinary Yoneda natural transformation constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN20, Theorem 8.1], the natural transformation
${\unicode{x3088}}\colon \iota \Rightarrow \operatorname {\mathcal {P}}$ is the ordinary Yoneda natural transformation constructed in [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN20, Theorem 8.1], the natural transformation ![]() $u\colon \mathrm {id} \Rightarrow - \otimes \mathcal {M}$ is the unit map of the free-forgetful adjunction
$u\colon \mathrm {id} \Rightarrow - \otimes \mathcal {M}$ is the unit map of the free-forgetful adjunction ![]() $- \otimes \mathcal {M}\colon \mathrm {Pr}^\mathrm {L} \rightleftarrows \mathrm {Mod}_\mathcal {M}\colon \underline {({-})}$ given by tensoring with
$- \otimes \mathcal {M}\colon \mathrm {Pr}^\mathrm {L} \rightleftarrows \mathrm {Mod}_\mathcal {M}\colon \underline {({-})}$ given by tensoring with ![]() $\mathcal {S} \to \mathcal {M}$, and
$\mathcal {S} \to \mathcal {M}$, and ![]() $L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ is the natural transformation of Proposition 2.36.
$L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ is the natural transformation of Proposition 2.36.
Proposition 2.40 For ![]() $X \in \mathcal {C}_0$ and
$X \in \mathcal {C}_0$ and ![]() $F \in \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ we have
$F \in \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ we have ![]() $\hom ^\mathcal {M}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X), F) \cong F(X)$.
$\hom ^\mathcal {M}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X), F) \cong F(X)$.
Proof. We first reduce to the case where ![]() $\mathcal {K} = \emptyset$. Since
$\mathcal {K} = \emptyset$. Since ![]() $L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is the left adjoint of the inclusion, using Lemma 2.2 we get
$L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is the left adjoint of the inclusion, using Lemma 2.2 we get
We finish the proof by showing that the latter is equivalent to ![]() $F(X)$, using the Yoneda lemma in the category
$F(X)$, using the Yoneda lemma in the category ![]() $\mathcal {M}$. Indeed, let
$\mathcal {M}$. Indeed, let ![]() $m \in \mathcal {M}$ be any object, then
$m \in \mathcal {M}$ be any object, then
 \begin{align*} \hom(m, \hom^\mathcal{M}({\unicode{x3088}}^\mathcal{M}(X), F)) &\cong \hom(m \otimes {\unicode{x3088}}^\mathcal{M}(X), F)\\ &\cong \hom({\unicode{x3088}}^\mathcal{M}(X), \hom^\mathcal{M}(m, F))\\ &\cong \hom({\unicode{x3088}}(X), \hom(m, F))\\ &\cong \hom(m, F)(X)\\ &\cong \hom(m, F(X)) , \end{align*}
\begin{align*} \hom(m, \hom^\mathcal{M}({\unicode{x3088}}^\mathcal{M}(X), F)) &\cong \hom(m \otimes {\unicode{x3088}}^\mathcal{M}(X), F)\\ &\cong \hom({\unicode{x3088}}^\mathcal{M}(X), \hom^\mathcal{M}(m, F))\\ &\cong \hom({\unicode{x3088}}(X), \hom(m, F))\\ &\cong \hom(m, F)(X)\\ &\cong \hom(m, F(X)) , \end{align*}
where the first and second step use the exponential adjunction, the third uses the free-forgetful adjunction ![]() $\mathcal {C} \to \mathcal {C} \otimes \mathcal {M}$, the fourth uses the ordinary Yoneda lemma for
$\mathcal {C} \to \mathcal {C} \otimes \mathcal {M}$, the fourth uses the ordinary Yoneda lemma for ![]() $\mathcal {C}_0$ and the last step uses that the action of
$\mathcal {C}_0$ and the last step uses that the action of ![]() $\mathcal {M}$ is level-wise.
$\mathcal {M}$ is level-wise.
Corollary 2.41 The Yoneda map ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ lands in the atomics.
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ lands in the atomics.
Proof. By Lemma 2.30, ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is closed under colimits and limits in
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is closed under colimits and limits in ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, which are therefore computed level-wise, so that
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, which are therefore computed level-wise, so that ![]() $\hom ^\mathcal {M}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X), F) \cong F(X)$ commutes with all colimits in the
$\hom ^\mathcal {M}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X), F) \cong F(X)$ commutes with all colimits in the ![]() $F$-coordinate.
$F$-coordinate.
We use the same notation ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)^{\mathrm {at}}$ to denote the factorization. Recall from Proposition 2.39 that the Yoneda map gives a natural transformation
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)^{\mathrm {at}}$ to denote the factorization. Recall from Proposition 2.39 that the Yoneda map gives a natural transformation ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ of functors
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ of functors ![]() $\mathrm {Cat}_\mathcal {K} \to \widehat {\mathrm {Cat}}$. Since taking the atomics lands in
$\mathrm {Cat}_\mathcal {K} \to \widehat {\mathrm {Cat}}$. Since taking the atomics lands in ![]() $\mathrm {Cat}_\mathcal {K}$ by Proposition 2.24, together with Corollary 2.41, we obtain a natural transformation
$\mathrm {Cat}_\mathcal {K}$ by Proposition 2.24, together with Corollary 2.41, we obtain a natural transformation ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathrm {id} \Rightarrow \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(-)^{\mathrm {at}}$ of functors
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathrm {id} \Rightarrow \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(-)^{\mathrm {at}}$ of functors ![]() $\mathrm {Cat}_\mathcal {K} \to \mathrm {Cat}_\mathcal {K}$.
$\mathrm {Cat}_\mathcal {K} \to \mathrm {Cat}_\mathcal {K}$.
Proposition 2.42 For any ![]() $\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$ the category
$\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$ the category ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is molecular, with atomic generators
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is molecular, with atomic generators ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ for
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ for ![]() $X \in \mathcal {C}_0$.
$X \in \mathcal {C}_0$.
Proof. We first show the result for ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, i.e. for the case
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$, i.e. for the case ![]() $\mathcal {K}=\emptyset$. Recall that
$\mathcal {K}=\emptyset$. Recall that ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \cong \operatorname {\mathcal {P}}(\mathcal {C}_0) \otimes \mathcal {M}$ is generated under colimits from the image of
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \cong \operatorname {\mathcal {P}}(\mathcal {C}_0) \otimes \mathcal {M}$ is generated under colimits from the image of ![]() $\operatorname {\mathcal {P}}(\mathcal {C}_0) \times \mathcal {M}$, i.e. from objects of the form
$\operatorname {\mathcal {P}}(\mathcal {C}_0) \times \mathcal {M}$, i.e. from objects of the form ![]() $F \otimes m$. Second,
$F \otimes m$. Second, ![]() $\operatorname {\mathcal {P}}(\mathcal {C}_0)$ is generated under colimits from objects of the form
$\operatorname {\mathcal {P}}(\mathcal {C}_0)$ is generated under colimits from objects of the form ![]() ${\unicode{x3088}}(X)$ for
${\unicode{x3088}}(X)$ for ![]() $X \in \mathcal {C}$. Therefore,
$X \in \mathcal {C}$. Therefore, ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is generated under colimits and the action of
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ is generated under colimits and the action of ![]() $\mathcal {M}$ from objects of the form
$\mathcal {M}$ from objects of the form ![]() ${\unicode{x3088}}^\mathcal {M}(X)$ for
${\unicode{x3088}}^\mathcal {M}(X)$ for ![]() $X \in \mathcal {C}$, which are indeed atomic by Corollary 2.41.
$X \in \mathcal {C}$, which are indeed atomic by Corollary 2.41.
For the general case, recall that ![]() $L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is an internally left adjoint functor so it sends atomic objects to atomic objects by Proposition 2.13, thus
$L_\mathcal {K}\colon \operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0) \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is an internally left adjoint functor so it sends atomic objects to atomic objects by Proposition 2.13, thus ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ is atomic for any
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ is atomic for any ![]() $X \in \mathcal {C}$. Since it preserves colimits and the action of
$X \in \mathcal {C}$. Since it preserves colimits and the action of ![]() $\mathcal {M}$, and
$\mathcal {M}$, and ![]() ${\unicode{x3088}}^\mathcal {M}(X)$ generate
${\unicode{x3088}}^\mathcal {M}(X)$ generate ![]() $\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ under these operations, their images
$\operatorname {\operatorname {\mathcal {P}}^\mathcal {M}}(\mathcal {C}_0)$ under these operations, their images ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ generate the essential image of
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ generate the essential image of ![]() $L_\mathcal {K}$ under these operations. In addition,
$L_\mathcal {K}$ under these operations. In addition, ![]() $L_\mathcal {K}$ is essentially surjective, so that
$L_\mathcal {K}$ is essentially surjective, so that ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ are atomic generators of
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)$ are atomic generators of ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ as needed.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ as needed.
Proposition 2.43 There is an adjunction
with unit ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathrm {id} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(-)^{\mathrm {at}}$.
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathrm {id} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(-)^{\mathrm {at}}$.
Proof. To check that the data in the theorem supports an adjunction, it suffices to check that for any ![]() $\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$ and
$\mathcal {C}_0 \in \mathrm {Cat}_\mathcal {K}$ and ![]() $\mathcal {D} \in \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$, the canonical map
$\mathcal {D} \in \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$, the canonical map
is an equivalence (in fact, it suffices to show this for the hom spaces, rather than the functor categories, but we show that the stronger statement holds). Note that
Furthermore, both the first and last categories in (1) are full subcategories of the first and last categories in (2), showing that the composition in (1) is also fully faithful.
To finish the argument, we need to show that (1) is essentially surjective. To that end, let ![]() $F\colon \mathcal {C}_0 \to \mathcal {D}^{\mathrm {at}}$ be a functor preserving
$F\colon \mathcal {C}_0 \to \mathcal {D}^{\mathrm {at}}$ be a functor preserving ![]() $I^\mathrm {op}$-shaped colimits for
$I^\mathrm {op}$-shaped colimits for ![]() $I^\mathrm {op} \in \mathcal {K}$. We can post-compose it with the inclusion
$I^\mathrm {op} \in \mathcal {K}$. We can post-compose it with the inclusion ![]() $\mathcal {D}^{\mathrm {at}} \to \mathcal {D}$, and using (2) we get a left adjoint functor
$\mathcal {D}^{\mathrm {at}} \to \mathcal {D}$, and using (2) we get a left adjoint functor ![]() $\tilde {F}\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \mathcal {D}$, and we need to show that it is in fact internally left adjoint. By construction, for any
$\tilde {F}\colon \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0) \to \mathcal {D}$, and we need to show that it is in fact internally left adjoint. By construction, for any ![]() $X \in \mathcal {C}_0$ we have that
$X \in \mathcal {C}_0$ we have that ![]() $\tilde {F}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)) \cong F(X) \in \mathcal {D}^{\mathrm {at}}$ is atomic. Proposition 2.42 shows that these are atomic generators for
$\tilde {F}({\unicode{x3088}}_\mathcal {K}^\mathcal {M}(X)) \cong F(X) \in \mathcal {D}^{\mathrm {at}}$ is atomic. Proposition 2.42 shows that these are atomic generators for ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, so Proposition 2.14 shows that
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$, so Proposition 2.14 shows that ![]() $\tilde {F}$ is indeed internally left adjoint.
$\tilde {F}$ is indeed internally left adjoint.
2.3 Tensor product of atomics
Proposition 2.44 The symmetric monoidal structure on ![]() $\mathrm {Mod}_\mathcal {M}$ restricts to a symmetric monoidal structure on the subcategory
$\mathrm {Mod}_\mathcal {M}$ restricts to a symmetric monoidal structure on the subcategory ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$.
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$.
Proof. Since ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ is a wide subcategory of
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ is a wide subcategory of ![]() $\mathrm {Mod}_\mathcal {M}$, all we need to show is that if
$\mathrm {Mod}_\mathcal {M}$, all we need to show is that if ![]() $L_i\colon \mathcal {C}_i \to \mathcal {D}_i$,
$L_i\colon \mathcal {C}_i \to \mathcal {D}_i$, ![]() $i=1,2$, are in
$i=1,2$, are in ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$, then so is
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$, then so is ![]() $L_1 \otimes L_2\colon \mathcal {C}_1 \otimes \mathcal {C}_2 \to \mathcal {D}_1 \otimes \mathcal {D}_2$. Let
$L_1 \otimes L_2\colon \mathcal {C}_1 \otimes \mathcal {C}_2 \to \mathcal {D}_1 \otimes \mathcal {D}_2$. Let ![]() $R_i$ be the right adjoints of
$R_i$ be the right adjoints of ![]() $L_i$, which by assumption are themselves left adjoints. Because they are left adjoints, we can tensor them to obtain another left adjoint functor
$L_i$, which by assumption are themselves left adjoints. Because they are left adjoints, we can tensor them to obtain another left adjoint functor ![]() $R_1 \otimes R_2\colon \mathcal {D}_1 \otimes \mathcal {D}_2 \to \mathcal {C}_1 \otimes \mathcal {C}_2$. It is then straightforward to check that tensoring the unit and counit of
$R_1 \otimes R_2\colon \mathcal {D}_1 \otimes \mathcal {D}_2 \to \mathcal {C}_1 \otimes \mathcal {C}_2$. It is then straightforward to check that tensoring the unit and counit of ![]() $L_i \dashv R_i$ exhibit an adjunction
$L_i \dashv R_i$ exhibit an adjunction ![]() $L_1 \otimes L_2 \dashv R_1 \otimes R_2$, showing that
$L_1 \otimes L_2 \dashv R_1 \otimes R_2$, showing that ![]() $L_1 \otimes L_2$ is an internally left adjoint functor.
$L_1 \otimes L_2$ is an internally left adjoint functor.
We recall that the category ![]() $\mathrm {Cat}_\mathcal {K}$ has a symmetric monoidal structure, developed in [Reference LurieLur17, § 4.8.1].
$\mathrm {Cat}_\mathcal {K}$ has a symmetric monoidal structure, developed in [Reference LurieLur17, § 4.8.1].
Corollary 2.45 The functor ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ of Proposition 2.35 is symmetric monoidal.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ of Proposition 2.35 is symmetric monoidal.
Proof. Since the symmetric monoidal structure on ![]() $\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ is inherited from
$\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}$ is inherited from ![]() $\mathrm {Mod}_\mathcal {M}$, it suffices to show that
$\mathrm {Mod}_\mathcal {M}$, it suffices to show that ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ is symmetric monoidal. Indeed, [Reference LurieLur17, Remark 4.8.1.8] shows that
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Mod}_\mathcal {M}$ is symmetric monoidal. Indeed, [Reference LurieLur17, Remark 4.8.1.8] shows that ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Pr}^\mathrm {L}$ is symmetric monoidal,
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}\colon \mathrm {Cat}_\mathcal {K} \to \mathrm {Pr}^\mathrm {L}$ is symmetric monoidal, ![]() $- \otimes \mathcal {M}\colon \mathrm {Pr}^\mathrm {L} \to \mathrm {Mod}_\mathcal {M}$ is symmetric monoidal, and by Proposition 2.29,
$- \otimes \mathcal {M}\colon \mathrm {Pr}^\mathrm {L} \to \mathrm {Mod}_\mathcal {M}$ is symmetric monoidal, and by Proposition 2.29, ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}} \otimes \mathcal {M} \cong \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}} \otimes \mathcal {M} \cong \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$.
Applying [Reference LurieLur17, Corollary 7.3.2.7], we immediately obtain the following.
Theorem 2.46 The adjunction ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \rightleftarrows \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}\colon (-)^{\mathrm {at}}$ of Proposition 2.43 is symmetric monoidal, i.e.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}\colon \mathrm {Cat}_\mathcal {K} \rightleftarrows \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}}\colon (-)^{\mathrm {at}}$ of Proposition 2.43 is symmetric monoidal, i.e. ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ is symmetric monoidal with a lax symmetric monoidal right adjoint
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}$ is symmetric monoidal with a lax symmetric monoidal right adjoint ![]() $(-)^{\mathrm {at}}$.
$(-)^{\mathrm {at}}$.
Note that for any operad ![]() $\mathcal {O}$ we get an induced adjunction
$\mathcal {O}$ we get an induced adjunction
whose unit is an enhancement of the Yoneda map (landing in the atomics) to ![]() $\mathcal {O}$-algebras. Furthermore, for any
$\mathcal {O}$-algebras. Furthermore, for any ![]() $\mathcal {C} \in \operatorname {Alg}_\mathcal {O}(\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}})$ we see that
$\mathcal {C} \in \operatorname {Alg}_\mathcal {O}(\mathrm {Mod}_\mathcal {M}^{\mathrm {iL}})$ we see that ![]() $\mathcal {C}^{\mathrm {at}} \subset \mathcal {C}$ is, in fact, an
$\mathcal {C}^{\mathrm {at}} \subset \mathcal {C}$ is, in fact, an ![]() $\mathcal {O}$-monoidal subcategory. We therefore get the following corollary, which generalizes [Reference GlasmanGla16, § 3] and [Reference LurieLur17, Corollary 4.8.1.12] from the case of
$\mathcal {O}$-monoidal subcategory. We therefore get the following corollary, which generalizes [Reference GlasmanGla16, § 3] and [Reference LurieLur17, Corollary 4.8.1.12] from the case of ![]() $\mathcal {M} = \mathcal {S}, \mathcal {K} = \emptyset$ and
$\mathcal {M} = \mathcal {S}, \mathcal {K} = \emptyset$ and ![]() $\mathcal {O} = \mathbb {E}_\infty$ and makes them natural.
$\mathcal {O} = \mathbb {E}_\infty$ and makes them natural.
Corollary 2.47 The Yoneda natural transformation lifts to a natural transformation ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(-)$ of functors
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \iota _{\mathcal {K}} \Rightarrow \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(-)$ of functors ![]() $\operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K}) \to \operatorname {Alg}_\mathcal {O}(\widehat {\mathrm {Cat}})$. That is, the Yoneda map
$\operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K}) \to \operatorname {Alg}_\mathcal {O}(\widehat {\mathrm {Cat}})$. That is, the Yoneda map ![]() ${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is
${\unicode{x3088}}_\mathcal {K}^\mathcal {M}\colon \mathcal {C}_0 \to \operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)$ is ![]() $\mathcal {O}$-monoidal and natural in
$\mathcal {O}$-monoidal and natural in ![]() $\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K})$, and factors through the atomics
$\mathcal {C}_0 \in \operatorname {Alg}_\mathcal {O}(\mathrm {Cat}_\mathcal {K})$, and factors through the atomics ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)^{\mathrm {at}}$.
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}(\mathcal {C}_0)^{\mathrm {at}}$.
Recall that in Proposition 2.15 we showed that if ![]() $X \in \mathcal {C}^{\mathrm {at}}$ and
$X \in \mathcal {C}^{\mathrm {at}}$ and ![]() $m \in \mathcal {M}^{\mathrm {at}}$, then
$m \in \mathcal {M}^{\mathrm {at}}$, then ![]() $m \otimes X \in \mathcal {C}^{\mathrm {at}}$. Using Theorem 2.46, we strengthen this into a module structure, using the fact that any lax symmetric monoidal functor lands in modules over the image of the unit.
$m \otimes X \in \mathcal {C}^{\mathrm {at}}$. Using Theorem 2.46, we strengthen this into a module structure, using the fact that any lax symmetric monoidal functor lands in modules over the image of the unit.
Corollary 2.48 The functor of atomic objects factors as a lax symmetric monoidal functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Mod}_{\mathcal {M}^{\mathrm {at}}}(\mathrm {Cat}_\mathcal {K})$.
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_\mathcal {M}^{\mathrm {iL}} \to \mathrm {Mod}_{\mathcal {M}^{\mathrm {at}}}(\mathrm {Cat}_\mathcal {K})$.
We also mention the following easy corollary of Proposition 2.44.
Lemma 2.49 Let ![]() $L\colon \mathcal {M}_1 \to \mathcal {M}_2$ be a smashing localization of modes and let
$L\colon \mathcal {M}_1 \to \mathcal {M}_2$ be a smashing localization of modes and let ![]() $\mathcal {N}$ be another mode Then,
$\mathcal {N}$ be another mode Then, ![]() $L \otimes \mathrm {id}_\mathcal {N}\colon \mathcal {M}_1 \otimes \mathcal {N} \to \mathcal {M}_2 \otimes \mathcal {N}$ is also a smashing localization of modes.
$L \otimes \mathrm {id}_\mathcal {N}\colon \mathcal {M}_1 \otimes \mathcal {N} \to \mathcal {M}_2 \otimes \mathcal {N}$ is also a smashing localization of modes.
Proof. First, by [Reference Carmeli, Schlank and YanovskiCSY21a, Lemma 5.2.1], the functor ![]() $L \otimes \mathrm {id}_\mathcal {N}$ is a localization as well. By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.2.15], a localization of modes is smashing if and only if it is an internally left adjoint functor in
$L \otimes \mathrm {id}_\mathcal {N}$ is a localization as well. By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.2.15], a localization of modes is smashing if and only if it is an internally left adjoint functor in ![]() $\mathrm {Pr}^\mathrm {L}$. Thus,
$\mathrm {Pr}^\mathrm {L}$. Thus, ![]() $L$ is internally left adjoint, and by Proposition 2.44 we conclude that
$L$ is internally left adjoint, and by Proposition 2.44 we conclude that ![]() $L \otimes \mathrm {id}_\mathcal {N}$ is also internally left adjoint, so that it is also a smashing localization.
$L \otimes \mathrm {id}_\mathcal {N}$ is also internally left adjoint, so that it is also a smashing localization.
2.4 Atomic modules
In the remainder of the section we show that the atomic objects in ![]() $\mathrm {LMod}_R$ for
$\mathrm {LMod}_R$ for ![]() $R \in \operatorname {Alg}(\mathcal {M})$ are the left dualizable left modules (in the sense of [Reference LurieLur17, Definition 4.6.2.3]), summarized in Corollary 2.56. We begin by collecting certain basic facts about the category of left modules from [Reference LurieLur17, § 4.8.5].
$R \in \operatorname {Alg}(\mathcal {M})$ are the left dualizable left modules (in the sense of [Reference LurieLur17, Definition 4.6.2.3]), summarized in Corollary 2.56. We begin by collecting certain basic facts about the category of left modules from [Reference LurieLur17, § 4.8.5].
Theorem 2.50 There is a symmetric monoidal functor ![]() $\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}^\mathrm {iL}$, sending
$\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}^\mathrm {iL}$, sending ![]() $R$ to
$R$ to ![]() $\mathrm {LMod}_R$ and
$\mathrm {LMod}_R$ and ![]() $f\colon R \to S$ to
$f\colon R \to S$ to ![]() $f_!\colon \mathrm {LMod}_R \to \mathrm {LMod}_S$.
$f_!\colon \mathrm {LMod}_R \to \mathrm {LMod}_S$.
Proof. Let ![]() $\mathcal {K}$ denote the collection of all (small) categories, then by [Reference LurieLur17, Remark 4.8.5.17] there is a symmetric monoidal functor
$\mathcal {K}$ denote the collection of all (small) categories, then by [Reference LurieLur17, Remark 4.8.5.17] there is a symmetric monoidal functor ![]() $\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}(\widehat {\mathrm {Cat}}_\mathcal {K})$. As in [Reference LurieLur17, Notation 4.8.5.10],
$\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}(\widehat {\mathrm {Cat}}_\mathcal {K})$. As in [Reference LurieLur17, Notation 4.8.5.10], ![]() $\mathrm {LMod}_R$ is presentable and
$\mathrm {LMod}_R$ is presentable and ![]() $f_!$ is left adjoint to
$f_!$ is left adjoint to ![]() $f^*$. Furthermore, [Reference LurieLur17, Corollary 4.2.3.7 (2)] shows that the right adjoint
$f^*$. Furthermore, [Reference LurieLur17, Corollary 4.2.3.7 (2)] shows that the right adjoint ![]() $f^*$ of
$f^*$ of ![]() $f_!$ is itself a left adjoint, so that the functor lands in
$f_!$ is itself a left adjoint, so that the functor lands in ![]() $\mathrm {Mod}_\mathcal {M}^\mathrm {iL}$. As the symmetric monoidal structure on
$\mathrm {Mod}_\mathcal {M}^\mathrm {iL}$. As the symmetric monoidal structure on ![]() $\mathrm {Mod}_\mathcal {M}^\mathrm {iL}$ is restricted from
$\mathrm {Mod}_\mathcal {M}^\mathrm {iL}$ is restricted from ![]() $\mathrm {Mod}_\mathcal {M}(\widehat {\mathrm {Cat}}_\mathcal {K})$, the factorization
$\mathrm {Mod}_\mathcal {M}(\widehat {\mathrm {Cat}}_\mathcal {K})$, the factorization ![]() $\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}^\mathrm {iL}$ is indeed symmetric monoidal.
$\mathrm {LMod}_{(-)}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Mod}_\mathcal {M}^\mathrm {iL}$ is indeed symmetric monoidal.
We now recall the following result about left dualizability and adjunctions.
Proposition 2.51 Let ![]() $X \in \mathrm {LMod}_R, Y \in \mathrm {RMod}_R$. Then
$X \in \mathrm {LMod}_R, Y \in \mathrm {RMod}_R$. Then ![]() $Y$ is left dual to
$Y$ is left dual to ![]() $X$ if and only if there is an adjunction
$X$ if and only if there is an adjunction
Proof. We explain how this follows from [Reference LurieLur17, Proposition 4.6.2.18], with ![]() $\mathcal {C} = \mathcal {M}$,
$\mathcal {C} = \mathcal {M}$, ![]() $A = R^{\mathrm {rev}}$ and the roles of
$A = R^{\mathrm {rev}}$ and the roles of ![]() $X$ and
$X$ and ![]() $Y$ reversed (see also [Reference LurieLur17, Remark 4.6.3.16]).
$Y$ reversed (see also [Reference LurieLur17, Remark 4.6.3.16]).
For the first direction, assume that there is an adjunction and let ![]() $\eta \colon \mathrm {id}_\mathcal {M} \Rightarrow Y \otimes _R X \otimes _{\mathbf {1}_\mathcal {M}} -$ be the unit. By the adjunction, we know that for each
$\eta \colon \mathrm {id}_\mathcal {M} \Rightarrow Y \otimes _R X \otimes _{\mathbf {1}_\mathcal {M}} -$ be the unit. By the adjunction, we know that for each ![]() $P \in \mathcal {M}$ and
$P \in \mathcal {M}$ and ![]() $Q \in \mathrm {LMod}_R$ the composition
$Q \in \mathrm {LMod}_R$ the composition
is an equivalence. Since both functors in the adjunction preserve colimits, and the categories are in the mode ![]() $\mathcal {M}$, the adjunction is
$\mathcal {M}$, the adjunction is ![]() $\mathcal {M}$-linear. Therefore, the two maps
$\mathcal {M}$-linear. Therefore, the two maps
coincide. This shows that ![]() $c = \eta _{\mathbf {1}_\mathcal {M}}$ satisfies condition
$c = \eta _{\mathbf {1}_\mathcal {M}}$ satisfies condition ![]() $(*)$ of the cited proposition.
$(*)$ of the cited proposition.
Similarly, for the other direction, if ![]() $Y$ is left dual to
$Y$ is left dual to ![]() $X$ then the coevaluation map
$X$ then the coevaluation map ![]() $c\colon \mathbf {1}_\mathcal {M} \to Y \otimes _R X$ gives an (
$c\colon \mathbf {1}_\mathcal {M} \to Y \otimes _R X$ gives an (![]() $\mathcal {M}$-linear) natural transformation
$\mathcal {M}$-linear) natural transformation ![]() $c \otimes _{\mathbf {1}_\mathcal {M}} -\colon \mathrm {id}_\mathcal {M} \Rightarrow Y \otimes _R X \otimes _{\mathbf {1}_\mathcal {M}} -$, which is a unit of an adjunction by condition
$c \otimes _{\mathbf {1}_\mathcal {M}} -\colon \mathrm {id}_\mathcal {M} \Rightarrow Y \otimes _R X \otimes _{\mathbf {1}_\mathcal {M}} -$, which is a unit of an adjunction by condition ![]() $(*)$ of the cited proposition.
$(*)$ of the cited proposition.
Lemma 2.52 Let ![]() $R \in \operatorname {Alg}(\mathcal {M})$, then
$R \in \operatorname {Alg}(\mathcal {M})$, then ![]() $R \in \mathrm {LMod}_R$ is atomic;
$R \in \mathrm {LMod}_R$ is atomic; ![]() $R \otimes m$ is also atomic for any
$R \otimes m$ is also atomic for any ![]() $m \in \mathcal {M}^{\mathrm {at}}$.
$m \in \mathcal {M}^{\mathrm {at}}$.
Proof. Consider [Reference LurieLur17, Corollary 4.2.3.7 (2)] where both ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {M}$ in the reference's notation are our
$\mathcal {M}$ in the reference's notation are our ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $A = \mathbf {1}_\mathcal {C}$ and
$A = \mathbf {1}_\mathcal {C}$ and ![]() $B = R$. Then, the functor
$B = R$. Then, the functor ![]() $\mathrm {LMod}_B \to \mathrm {LMod}_A$ is
$\mathrm {LMod}_B \to \mathrm {LMod}_A$ is ![]() $\hom ^\mathcal {M}(R, -)\colon \mathrm {LMod}_R \to \mathcal {M}$, which therefore commutes with all colimits, showing that
$\hom ^\mathcal {M}(R, -)\colon \mathrm {LMod}_R \to \mathcal {M}$, which therefore commutes with all colimits, showing that ![]() $R$ is atomic. The second part follows from Proposition 2.15.
$R$ is atomic. The second part follows from Proposition 2.15.
Proposition 2.53 Let ![]() $R \in \operatorname {Alg}(\mathcal {M})$. Then
$R \in \operatorname {Alg}(\mathcal {M})$. Then ![]() $\mathrm {LMod}_R$ is molecular with
$\mathrm {LMod}_R$ is molecular with ![]() $R$ as an atomic generator.
$R$ as an atomic generator.
Proof. The previous lemma shows that ![]() $R$ is indeed atomic, and we need to show that it generates
$R$ is indeed atomic, and we need to show that it generates ![]() $\mathrm {LMod}_R$ under colimits and the action of
$\mathrm {LMod}_R$ under colimits and the action of ![]() $\mathcal {M}$. Specifically, we will show that
$\mathcal {M}$. Specifically, we will show that ![]() $\mathrm {LMod}_R$ is generated under colimits from
$\mathrm {LMod}_R$ is generated under colimits from ![]() $R \otimes m$ for
$R \otimes m$ for ![]() $m \in \mathcal {M}$. By [Reference YanovskiYan22, Corollary 2.5], this is equivalent to showing that
$m \in \mathcal {M}$. By [Reference YanovskiYan22, Corollary 2.5], this is equivalent to showing that ![]() $\hom (R \otimes m, -)\colon \mathrm {LMod}_R \to \mathcal {S}$ are jointly conservative. Note that
$\hom (R \otimes m, -)\colon \mathrm {LMod}_R \to \mathcal {S}$ are jointly conservative. Note that ![]() $R \otimes -\colon \mathcal {M} \to \mathrm {LMod}_R$ is the left adjoint of
$R \otimes -\colon \mathcal {M} \to \mathrm {LMod}_R$ is the left adjoint of ![]() $\underline {({-})}\colon \mathrm {LMod}_R \to \mathcal {M}$, so that
$\underline {({-})}\colon \mathrm {LMod}_R \to \mathcal {M}$, so that ![]() $\hom (R \otimes m, -) \cong \hom (m, \underline {({-})})$. These functors are indeed jointly conservative since
$\hom (R \otimes m, -) \cong \hom (m, \underline {({-})})$. These functors are indeed jointly conservative since ![]() $\underline {({-})}\colon \mathrm {LMod}_R \to \mathcal {M}$ is conservative, and
$\underline {({-})}\colon \mathrm {LMod}_R \to \mathcal {M}$ is conservative, and ![]() $\hom (m, -)\colon \mathcal {M} \to \mathcal {S}$ over all
$\hom (m, -)\colon \mathcal {M} \to \mathcal {S}$ over all ![]() $m \in \mathcal {M}$ are jointly conservative.
$m \in \mathcal {M}$ are jointly conservative.
Let ![]() $X \in \mathrm {LMod}_R$, and consider the functor
$X \in \mathrm {LMod}_R$, and consider the functor ![]() $\hom ^\mathcal {M}(X, -)\colon \mathrm {LMod}_R \to \mathcal {M}$. Note that
$\hom ^\mathcal {M}(X, -)\colon \mathrm {LMod}_R \to \mathcal {M}$. Note that ![]() $\hom ^\mathcal {M}(X, R)$ is equipped with a canonical right
$\hom ^\mathcal {M}(X, R)$ is equipped with a canonical right ![]() $R$-module structure which we denote by
$R$-module structure which we denote by ![]() $X^\vee \in \mathrm {RMod}_R$. In addition, there is a canonical map
$X^\vee \in \mathrm {RMod}_R$. In addition, there is a canonical map ![]() $X^\vee \otimes _R - \to \hom ^\mathcal {M}(X, -)$.
$X^\vee \otimes _R - \to \hom ^\mathcal {M}(X, -)$.
Proposition 2.54 We have ![]() $\mathrm {LMod}_R^\mathrm {ldbl} = \mathrm {LMod}_R^{\mathrm {at}}$, that is, the left dualizable objects are atomic.
$\mathrm {LMod}_R^\mathrm {ldbl} = \mathrm {LMod}_R^{\mathrm {at}}$, that is, the left dualizable objects are atomic.
Proof. Recall that for ![]() $X \in \mathrm {LMod}_R$, the functor
$X \in \mathrm {LMod}_R$, the functor ![]() $X \otimes _{\mathbf {1}_\mathcal {M}} -\colon \mathcal {M} \to \mathrm {LMod}_R$ is left adjoint to
$X \otimes _{\mathbf {1}_\mathcal {M}} -\colon \mathcal {M} \to \mathrm {LMod}_R$ is left adjoint to ![]() $\hom ^\mathcal {M}(X, -)$.
$\hom ^\mathcal {M}(X, -)$.
If ![]() $X$ is left dualizable, then
$X$ is left dualizable, then ![]() $X \otimes _{\mathbf {1}_\mathcal {M}} -$ is left adjoint to
$X \otimes _{\mathbf {1}_\mathcal {M}} -$ is left adjoint to ![]() $Y \otimes _R -$ for some
$Y \otimes _R -$ for some ![]() $Y \in \mathrm {RMod}_R$ by Proposition 2.51. By the uniqueness of adjoints we get that
$Y \in \mathrm {RMod}_R$ by Proposition 2.51. By the uniqueness of adjoints we get that ![]() $\hom ^\mathcal {M}(X, -) \cong Y \otimes _R -$. Since
$\hom ^\mathcal {M}(X, -) \cong Y \otimes _R -$. Since ![]() $Y \otimes _R -$ commutes with colimits, we get that
$Y \otimes _R -$ commutes with colimits, we get that ![]() $X$ is atomic.
$X$ is atomic.
Now assume that ![]() $X$ is atomic. The two functors
$X$ is atomic. The two functors ![]() $\hom ^\mathcal {M}(X, -)$ and
$\hom ^\mathcal {M}(X, -)$ and ![]() $X^\vee \otimes _R -$ are colimit preserving, i.e. morphisms in
$X^\vee \otimes _R -$ are colimit preserving, i.e. morphisms in ![]() $\mathrm {Mod}_\mathcal {M}$, thus also commute with tensor from
$\mathrm {Mod}_\mathcal {M}$, thus also commute with tensor from ![]() $\mathcal {M}$. Proposition 2.53 shows that
$\mathcal {M}$. Proposition 2.53 shows that ![]() $\mathrm {LMod}_R$ is generated from
$\mathrm {LMod}_R$ is generated from ![]() $R$ by these operations, and by the construction of
$R$ by these operations, and by the construction of ![]() $X^\vee$, they agree on
$X^\vee$, they agree on ![]() $R$, so the canonical map between the two is an equivalence. This shows that
$R$, so the canonical map between the two is an equivalence. This shows that ![]() $X \otimes _{\mathbf {1}_\mathcal {M}} -$ is left adjoint to
$X \otimes _{\mathbf {1}_\mathcal {M}} -$ is left adjoint to ![]() $\hom ^\mathcal {M}(X, -) \cong X^\vee \otimes _R -$, concluding by Proposition 2.51.
$\hom ^\mathcal {M}(X, -) \cong X^\vee \otimes _R -$, concluding by Proposition 2.51.
Remark 2.55 If ![]() $R \in \operatorname {CAlg}(\mathcal {M})$, then left and right
$R \in \operatorname {CAlg}(\mathcal {M})$, then left and right ![]() $R$-modules coincide, and the category of modules
$R$-modules coincide, and the category of modules ![]() $\mathrm {Mod}_R$ is equipped with a symmetric monoidal structure for which dualizable modules coincide with left dualizable modules, thus also with atomic objects, that is
$\mathrm {Mod}_R$ is equipped with a symmetric monoidal structure for which dualizable modules coincide with left dualizable modules, thus also with atomic objects, that is ![]() $\mathrm {Mod}_R^\mathrm {dbl} = \mathrm {Mod}_R^{\mathrm {at}}$.
$\mathrm {Mod}_R^\mathrm {dbl} = \mathrm {Mod}_R^{\mathrm {at}}$.
Combining Theorem 2.46, Theorem 2.50, and Proposition 2.54 we obtain the following main result.
Corollary 2.56 There is a lax symmetric monoidal functor ![]() $\mathrm {LMod}_{(-)}^{\mathrm {at}}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Cat}_\mathcal {K}$, and
$\mathrm {LMod}_{(-)}^{\mathrm {at}}\colon \operatorname {Alg}(\mathcal {M}) \to \mathrm {Cat}_\mathcal {K}$, and ![]() $\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$.
$\mathrm {LMod}_R^{\mathrm {at}} = \mathrm {LMod}_R^\mathrm {ldbl}$.
As a byproduct, we also obtain the following result.
Lemma 2.57 Let ![]() $F\colon \mathcal {M} \to \mathcal {N}$ be a map of modes, then it sends
$F\colon \mathcal {M} \to \mathcal {N}$ be a map of modes, then it sends ![]() $\mathcal {M}$-atomic objects to
$\mathcal {M}$-atomic objects to ![]() $\mathcal {N}$-atomic objects.
$\mathcal {N}$-atomic objects.
Proof. By Proposition 2.54, the ![]() $\mathcal {M}$-atomic objects in
$\mathcal {M}$-atomic objects in ![]() $\mathcal {M}$ are the dualizable objects. Since
$\mathcal {M}$ are the dualizable objects. Since ![]() $F$ is symmetric monoidal it sends dualizable objects to dualizable objects. Thus, the
$F$ is symmetric monoidal it sends dualizable objects to dualizable objects. Thus, the ![]() $\mathcal {M}$-atomic objects are sent to dualizable objects in
$\mathcal {M}$-atomic objects are sent to dualizable objects in ![]() $\mathcal {N}$. Again by Proposition 2.54, the dualizable objects in
$\mathcal {N}$. Again by Proposition 2.54, the dualizable objects in ![]() $\mathcal {N}$ are
$\mathcal {N}$ are ![]() $\mathcal {N}$-atomic.
$\mathcal {N}$-atomic.
3. Day convolution
The Day convolution on functor categories was developed in [Reference GlasmanGla16, Reference LurieLur17]. In this section we prove results about the Day convolution, specifically its functoriality in the source and target. The results of this section are used in Theorem 4.26 to show that the mode symmetric monoidal structure on higher commutative monoids coincides with the localization of the Day convolution. This is subsequently used in Theorem 6.18 to endow higher semiadditive algebraic K-theory with a lax symmetric monoidal structure.
We begin by recalling the universal property of the Day convolution.
Theorem 3.1 [Reference LurieLur17, Remark 2.2.6.8]
Let ![]() $I, \mathcal {C}$ be symmetric monoidal categories, and assume that
$I, \mathcal {C}$ be symmetric monoidal categories, and assume that ![]() $\mathcal {C}$ has all colimits and that its tensor product preserves colimits in each coordinate separately. Then, there is a symmetric monoidal structure on
$\mathcal {C}$ has all colimits and that its tensor product preserves colimits in each coordinate separately. Then, there is a symmetric monoidal structure on ![]() $\operatorname {Fun}(I, \mathcal {C})$, called the Day convolution denoted by
$\operatorname {Fun}(I, \mathcal {C})$, called the Day convolution denoted by ![]() ${\circledast }$, satisfying the following universal property: There is an equivalence of functors
${\circledast }$, satisfying the following universal property: There is an equivalence of functors ![]() $\mathrm {CMon}(\mathrm {Cat}) \to \mathrm {Cat}$
$\mathrm {CMon}(\mathrm {Cat}) \to \mathrm {Cat}$
which lifts the equivalence of functors ![]() $\mathrm {Cat} \to \mathrm {Cat}$
$\mathrm {Cat} \to \mathrm {Cat}$
Example 3.2 Let ![]() $I$ be a symmetric monoidal category. Then
$I$ be a symmetric monoidal category. Then ![]() $I^\mathrm {op}$ is also endowed with a symmetric monoidal structure, and
$I^\mathrm {op}$ is also endowed with a symmetric monoidal structure, and ![]() $\mathcal {S}$ can be endowed with the cartesian structure, yielding the Day convolution on
$\mathcal {S}$ can be endowed with the cartesian structure, yielding the Day convolution on ![]() $\operatorname {\mathcal {P}}(I) = \operatorname {Fun}(I^\mathrm {op}, \mathcal {S})$. By [Reference LurieLur17, Remark 4.8.1.13], this agrees with the symmetric monoidal structure on
$\operatorname {\mathcal {P}}(I) = \operatorname {Fun}(I^\mathrm {op}, \mathcal {S})$. By [Reference LurieLur17, Remark 4.8.1.13], this agrees with the symmetric monoidal structure on ![]() $\operatorname {\mathcal {P}}(I)$ of [Reference LurieLur17, Remark 4.8.1.8] used in the proof of Corollary 2.45.
$\operatorname {\mathcal {P}}(I)$ of [Reference LurieLur17, Remark 4.8.1.8] used in the proof of Corollary 2.45.
Proposition 3.3 Let ![]() $I, \mathcal {C}$, and
$I, \mathcal {C}$, and ![]() $\mathcal {D}$ be symmetric monoidal categories, and assume that
$\mathcal {D}$ be symmetric monoidal categories, and assume that ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {D}$ have all colimits and that their tensor product preserve colimits in each coordinate. Let
$\mathcal {D}$ have all colimits and that their tensor product preserve colimits in each coordinate. Let ![]() $F\colon \mathcal {C} \to \mathcal {D}$ be a functor and let
$F\colon \mathcal {C} \to \mathcal {D}$ be a functor and let ![]() $\tilde {F}\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {D})$ be the functor induced by post-composition. If
$\tilde {F}\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {D})$ be the functor induced by post-composition. If ![]() $F$ is lax symmetric monoidal, then so is
$F$ is lax symmetric monoidal, then so is ![]() $\tilde {F}$. If
$\tilde {F}$. If ![]() $F$ is colimit preserving, then so is
$F$ is colimit preserving, then so is ![]() $\tilde {F}$. If
$\tilde {F}$. If ![]() $F$ is both colimit preserving and symmetric monoidal, then so is
$F$ is both colimit preserving and symmetric monoidal, then so is ![]() $\tilde {F}$.
$\tilde {F}$.
Proof. We begin with the first part. The identity functor of ![]() $\operatorname {Fun}(I, \mathcal {C})$ is (lax) symmetric monoidal, therefore by the universal property of the Day convolution, the corresponding functor
$\operatorname {Fun}(I, \mathcal {C})$ is (lax) symmetric monoidal, therefore by the universal property of the Day convolution, the corresponding functor ![]() $\operatorname {Fun}(I, \mathcal {C}) \times I \to \mathcal {C}$ is also lax symmetric monoidal. Post-composition of this functor with the lax symmetric monoidal functor
$\operatorname {Fun}(I, \mathcal {C}) \times I \to \mathcal {C}$ is also lax symmetric monoidal. Post-composition of this functor with the lax symmetric monoidal functor ![]() $F$ gives a lax symmetric monoidal functor
$F$ gives a lax symmetric monoidal functor ![]() $\operatorname {Fun}(I, \mathcal {C}) \times I \to \mathcal {D}$. Using the universal property again, we get that
$\operatorname {Fun}(I, \mathcal {C}) \times I \to \mathcal {D}$. Using the universal property again, we get that ![]() $\tilde {F}\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {D})$ is also lax symmetric monoidal.
$\tilde {F}\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {D})$ is also lax symmetric monoidal.
For the second part, if ![]() $F$ is colimit preserving, then since colimits in functor categories are computed level-wise,
$F$ is colimit preserving, then since colimits in functor categories are computed level-wise, ![]() $\tilde {F}$ is colimit preserving.
$\tilde {F}$ is colimit preserving.
Lastly, we assume that ![]() $F$ is both colimit preserving and symmetric monoidal. We already know from the second part that
$F$ is both colimit preserving and symmetric monoidal. We already know from the second part that ![]() $\tilde {F}$ is colimit preserving. We show that the lax symmetric monoidal structure from the first part is, in fact, symmetric monoidal. Recall that by [Reference LurieLur17, Example 2.2.6.17], the Day convolution of
$\tilde {F}$ is colimit preserving. We show that the lax symmetric monoidal structure from the first part is, in fact, symmetric monoidal. Recall that by [Reference LurieLur17, Example 2.2.6.17], the Day convolution of ![]() $X, Y\in \operatorname {Fun}(I, \mathcal {C})$ is given on objects by
$X, Y\in \operatorname {Fun}(I, \mathcal {C})$ is given on objects by
The lax symmetric monoidal structure of ![]() $\tilde {F}$ is then given by the canonical map:
$\tilde {F}$ is then given by the canonical map:
 \begin{align*} (\tilde{F}X \circledast \tilde{F}Y)(i) &\cong \operatorname*{colim}_{i_1 \otimes i_2 \to i} FX(i_1) \otimes FY(i_2)\\ &\xrightarrow{\text(1)} \operatorname*{colim}_{i_1 \otimes i_2 \to i} F(X(i_1) \otimes Y(i_2))\\ &\xrightarrow{\text(2)} F\bigl(\operatorname*{colim}_{i_1 \otimes i_2 \to i} X(i_1) \otimes Y(i_2)\bigr)\\ &\cong (\tilde{F}(X \circledast Y))(i), \end{align*}
\begin{align*} (\tilde{F}X \circledast \tilde{F}Y)(i) &\cong \operatorname*{colim}_{i_1 \otimes i_2 \to i} FX(i_1) \otimes FY(i_2)\\ &\xrightarrow{\text(1)} \operatorname*{colim}_{i_1 \otimes i_2 \to i} F(X(i_1) \otimes Y(i_2))\\ &\xrightarrow{\text(2)} F\bigl(\operatorname*{colim}_{i_1 \otimes i_2 \to i} X(i_1) \otimes Y(i_2)\bigr)\\ &\cong (\tilde{F}(X \circledast Y))(i), \end{align*}
where map (1) uses the fact ![]() $F$ is lax symmetric monoidal, and (2) is the assembly map. Since
$F$ is lax symmetric monoidal, and (2) is the assembly map. Since ![]() $F$ is symmetric monoidal (1) is an equivalence, and since
$F$ is symmetric monoidal (1) is an equivalence, and since ![]() $F$ is colimit preserving (2) is an equivalence, showing that
$F$ is colimit preserving (2) is an equivalence, showing that ![]() $\tilde {F}$ is, in fact, symmetric monoidal.
$\tilde {F}$ is, in fact, symmetric monoidal.
Our next goal is to study the behavior of the Day convolution under the change of the source ![]() $I$, namely given a symmetric monoidal functor
$I$, namely given a symmetric monoidal functor ![]() $p\colon I \to J$, what can we say about
$p\colon I \to J$, what can we say about ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ and
$p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ and ![]() $p^*\colon \operatorname {Fun}(J, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {C})$.
$p^*\colon \operatorname {Fun}(J, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {C})$.
We wish to thank Lior Yanovski for suggesting the following argument to prove Proposition 3.6.
Lemma 3.4 Let ![]() $\mathcal {C} = \mathcal {S}$ equipped with the cartesian structure, then
$\mathcal {C} = \mathcal {S}$ equipped with the cartesian structure, then ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(J, \mathcal {S})$ is symmetric monoidal.
$p_!\colon \operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(J, \mathcal {S})$ is symmetric monoidal.
Proof. This is [Reference LurieLur17, Remark 4.8.1.8] applied to ![]() $p^\mathrm {op}\colon I^\mathrm {op} \to J^\mathrm {op}$.
$p^\mathrm {op}\colon I^\mathrm {op} \to J^\mathrm {op}$.
Lemma 3.5 Let ![]() $K$ be a symmetric monoidal category, and let
$K$ be a symmetric monoidal category, and let ![]() $\mathcal {C} = \operatorname {Fun}(K, \mathcal {S})$ equipped with the Day convolution, then
$\mathcal {C} = \operatorname {Fun}(K, \mathcal {S})$ equipped with the Day convolution, then ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ is symmetric monoidal.
$p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ is symmetric monoidal.
Proof. By applying the universal property of the Day convolution twice, we know that there is an equivalence of functors:
Using the same reasoning with the roles of ![]() $I$ and
$I$ and ![]() $K$ reversed, and the equivalence
$K$ reversed, and the equivalence ![]() $I \times K \cong K \times I$, the universal property of the Day convolution implies that there is a symmetric monoidal equivalence:
$I \times K \cong K \times I$, the universal property of the Day convolution implies that there is a symmetric monoidal equivalence:
Similarly, we have an equivalence with ![]() $J$ in place of
$J$ in place of ![]() $I$.
$I$.
Lemma 3.4 constructs a symmetric monoidal functor ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(J, \mathcal {S})$. Since this functor is also colimit preserving, by Proposition 3.3, post-composition with it gives a symmetric monoidal functor
$p_!\colon \operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(J, \mathcal {S})$. Since this functor is also colimit preserving, by Proposition 3.3, post-composition with it gives a symmetric monoidal functor
which under the equivalences above gives the desired map ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$.
$p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$.
Proposition 3.6 Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ is symmetric monoidal.
$p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$ is symmetric monoidal.
Proof. By [Reference Nikolaus and SagaveNS17, Proposition 2.2], there is a symmetric monoidal reflective localization ![]() $\tilde {\mathcal {C}} \to \mathcal {C}$, for some
$\tilde {\mathcal {C}} \to \mathcal {C}$, for some ![]() $\tilde {\mathcal {C}} = \operatorname {Fun}(K, \mathcal {S})$. Then
$\tilde {\mathcal {C}} = \operatorname {Fun}(K, \mathcal {S})$. Then ![]() $\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(I, \mathcal {C})$ given by post-composition is also a reflective localization, and by Proposition 3.3 it is also symmetric monoidal, and the same holds with
$\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(I, \mathcal {C})$ given by post-composition is also a reflective localization, and by Proposition 3.3 it is also symmetric monoidal, and the same holds with ![]() $J$ in place of
$J$ in place of ![]() $I$.
$I$.
By Lemma 3.5, we have a symmetric monoidal functor ![]() $p_!\colon \operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \tilde {\mathcal {C}})$. Composing this with the symmetric monoidal localization
$p_!\colon \operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \tilde {\mathcal {C}})$. Composing this with the symmetric monoidal localization ![]() $\operatorname {Fun}(J, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \mathcal {C})$, we get a symmetric monoidal functor
$\operatorname {Fun}(J, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \mathcal {C})$, we get a symmetric monoidal functor ![]() $\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \mathcal {C})$. This functor factors through the symmetric monoidal localization
$\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(J, \mathcal {C})$. This functor factors through the symmetric monoidal localization ![]() $\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(I, \mathcal {C})$, yielding the symmetric monoidal structure on
$\operatorname {Fun}(I, \tilde {\mathcal {C}}) \to \operatorname {Fun}(I, \mathcal {C})$, yielding the symmetric monoidal structure on ![]() $p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$.
$p_!\colon \operatorname {Fun}(I, \mathcal {C}) \to \operatorname {Fun}(J, \mathcal {C})$.
Applying this to the special case where ![]() $p$ is the unit map
$p$ is the unit map ![]() $* \to I$ we obtain the following.
$* \to I$ we obtain the following.
Corollary 3.7 There is a map ![]() $F\colon \mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ in
$F\colon \mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ in ![]() $\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$.
$\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$.
Furthermore, applying [Reference LurieLur17, Corollary 7.3.2.7] to the adjunction ![]() $p^* \dashv p_!$ we obtain the following.
$p^* \dashv p_!$ we obtain the following.
Corollary 3.8 Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then ![]() $p^*\colon \operatorname {Fun}(J, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {C})$ is lax symmetric monoidal.
$p^*\colon \operatorname {Fun}(J, \mathcal {C}) \to \operatorname {Fun}(I, \mathcal {C})$ is lax symmetric monoidal.
Remark 3.9 One can directly use the universal property of the Day convolution to show that ![]() $p^*$ is lax symmetric monoidal, even only assuming that
$p^*$ is lax symmetric monoidal, even only assuming that ![]() $p$ is lax symmetric monoidal. In fact, one can use the main result of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] to construct an oplax symmetric monoidal structure on
$p$ is lax symmetric monoidal. In fact, one can use the main result of [Reference Haugseng, Hebestreit, Linskens and NuitenHHLN23] to construct an oplax symmetric monoidal structure on ![]() $p_!$ in this way while only assuming that
$p_!$ in this way while only assuming that ![]() $p$ is lax symmetric monoidal, and prove that it is symmetric monoidal in case
$p$ is lax symmetric monoidal, and prove that it is symmetric monoidal in case ![]() $p$ is. However, we have not shown that the lax symmetric monoidal structure on
$p$ is. However, we have not shown that the lax symmetric monoidal structure on ![]() $p^*$ obtained in the above corollary coincides with that obtained directly from the universal property of the Day convolution.
$p^*$ obtained in the above corollary coincides with that obtained directly from the universal property of the Day convolution.
Proposition 3.10 Let ![]() $I \in \operatorname {CAlg}(\mathrm {Cat}) \cong \mathrm {CMon}(\mathrm {Cat})$ and
$I \in \operatorname {CAlg}(\mathrm {Cat}) \cong \mathrm {CMon}(\mathrm {Cat})$ and ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$. Then the equivalence
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$. Then the equivalence ![]() $\operatorname {Fun}(I, \mathcal {S}) \otimes \mathcal {C} \xrightarrow {\smash {{\scriptstyle \sim }}} \operatorname {Fun}(I, \mathcal {C})$ is symmetric monoidal.
$\operatorname {Fun}(I, \mathcal {S}) \otimes \mathcal {C} \xrightarrow {\smash {{\scriptstyle \sim }}} \operatorname {Fun}(I, \mathcal {C})$ is symmetric monoidal.
Proof. Since the tensor product is the coproduct in ![]() $\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, to upgrade the equivalence into a symmetric monoidal functor, it suffices to upgrade the functors
$\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, to upgrade the equivalence into a symmetric monoidal functor, it suffices to upgrade the functors ![]() $\operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(I, \mathcal {C})$ and
$\operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(I, \mathcal {C})$ and ![]() $\mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ to symmetric monoidal functors. Indeed, by Proposition 3.3 post-composition with the unit map
$\mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ to symmetric monoidal functors. Indeed, by Proposition 3.3 post-composition with the unit map ![]() $\mathcal {S} \to \mathcal {C}$ yields a symmetric monoidal functor
$\mathcal {S} \to \mathcal {C}$ yields a symmetric monoidal functor ![]() $\operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(I, \mathcal {C})$, and Corollary 3.7 shows that
$\operatorname {Fun}(I, \mathcal {S}) \to \operatorname {Fun}(I, \mathcal {C})$, and Corollary 3.7 shows that ![]() $\mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ is symmetric monoidal.
$\mathcal {C} \to \operatorname {Fun}(I, \mathcal {C})$ is symmetric monoidal.
4. Higher commutative monoids
In this section we recall the notion of (![]() $p$-typical)
$p$-typical) ![]() $m$-commutative monoids as developed in [Reference HarpazHar20] and [Reference Carmeli, Schlank and YanovskiCSY21a] (see Definition 4.2), and their relationship to higher semiadditivity (see Theorem 4.9), which feature prominently in the definition of higher semiadditive algebraic K-theory in Definition 6.5. A key result of this section is Theorem 4.26, which shows that for
$m$-commutative monoids as developed in [Reference HarpazHar20] and [Reference Carmeli, Schlank and YanovskiCSY21a] (see Definition 4.2), and their relationship to higher semiadditivity (see Theorem 4.9), which feature prominently in the definition of higher semiadditive algebraic K-theory in Definition 6.5. A key result of this section is Theorem 4.26, which shows that for ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, the symmetric monoidal structures on
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, the symmetric monoidal structures on ![]() $\mathrm {CMon}_m^{(p)}(\mathcal {C})$ coming from the mode structure on
$\mathrm {CMon}_m^{(p)}(\mathcal {C})$ coming from the mode structure on ![]() $\mathrm {CMon}_m^{(p)}(\mathcal {S})$ and from the Day convolution coincide. This result is used in Theorem 6.18 to endow higher semiadditive algebraic K-theory with a lax symmetric monoidal structure.
$\mathrm {CMon}_m^{(p)}(\mathcal {S})$ and from the Day convolution coincide. This result is used in Theorem 6.18 to endow higher semiadditive algebraic K-theory with a lax symmetric monoidal structure.
4.1 Definition and properties
Definition 4.1 Let ![]() $\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ be a presentable category. We define the category of (
$\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ be a presentable category. We define the category of ( ![]() $p$-typical) pre-
$p$-typical) pre- ![]() $m$-commutative monoids in
$m$-commutative monoids in ![]() $\mathcal {C}$ by
$\mathcal {C}$ by ![]() ${\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}} = \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C})$. We define the underlying object functor
${\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}} = \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C})$. We define the underlying object functor ![]() ${\underline {({-})}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}\to \mathcal {C}$ by pre-composition with
${\underline {({-})}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}\to \mathcal {C}$ by pre-composition with ![]() $* \to \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$, i.e.
$* \to \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$, i.e. ![]() $\underline {X} = X(*)$.
$\underline {X} = X(*)$.
Definition 4.2 We say that a pre-![]() $m$-commutative monoid
$m$-commutative monoid ![]() $X \in \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ is a (
$X \in \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ is a ( ![]() $p$-typical)
$p$-typical) ![]() $m$-commutative monoid if it satisfies the
$m$-commutative monoid if it satisfies the ![]() $m$-Segal condition, i.e. the assembly map
$m$-Segal condition, i.e. the assembly map ![]() $X(A) \to \lim _{A}\underline {X}$ is an equivalence for any
$X(A) \to \lim _{A}\underline {X}$ is an equivalence for any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$. Their category is the full subcategory
$A$. Their category is the full subcategory ![]() ${\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}} = \operatorname {Fun}^{\mathrm {seg}}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C}) \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
${\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}} = \operatorname {Fun}^{\mathrm {seg}}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C}) \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
Remark 4.3 The ![]() $m$-Segal condition for
$m$-Segal condition for ![]() $X$ is equivalent to
$X$ is equivalent to ![]() $X$ preserving limits indexed by
$X$ preserving limits indexed by ![]() $A \in \mathcal {S}_m^{(p)}$.
$A \in \mathcal {S}_m^{(p)}$.
Proposition 4.4 The restriction of the underlying functor ![]() $\underline {({-})}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}\to \mathcal {C}$ is conservative.
$\underline {({-})}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}\to \mathcal {C}$ is conservative.
Proof. Follows immediately from the ![]() $m$-Segal condition.
$m$-Segal condition.
Lemma 4.5 Let ![]() $\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ be a
$\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ be a ![]() $\kappa$-presentable category. Then,
$\kappa$-presentable category. Then, ![]() $\mu$-filtered colimits commute with
$\mu$-filtered colimits commute with ![]() $\mu$-small limits in
$\mu$-small limits in ![]() $\mathcal {C}$, for any
$\mathcal {C}$, for any ![]() $\mu \geq \kappa$.
$\mu \geq \kappa$.
Proof. First, the case ![]() $\mathcal {C} = \mathcal {S}$ is [Reference LurieLur09, Proposition 5.3.3.3]. Second, the case
$\mathcal {C} = \mathcal {S}$ is [Reference LurieLur09, Proposition 5.3.3.3]. Second, the case ![]() $\mathcal {C} = \operatorname {\mathcal {P}}(\mathcal {C}_0)$ follows from the previous case, since limits and colimits are computed level-wise in functor categories. Lastly, for the general case we have that
$\mathcal {C} = \operatorname {\mathcal {P}}(\mathcal {C}_0)$ follows from the previous case, since limits and colimits are computed level-wise in functor categories. Lastly, for the general case we have that ![]() $\mathcal {C} \cong \mathrm {Ind}_\kappa (\mathcal {C}^\kappa )$. By [Reference LurieLur09, Proposition 5.3.5.3],
$\mathcal {C} \cong \mathrm {Ind}_\kappa (\mathcal {C}^\kappa )$. By [Reference LurieLur09, Proposition 5.3.5.3], ![]() $\mathcal {C} \subseteq \operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ is closed under
$\mathcal {C} \subseteq \operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ is closed under ![]() $\kappa$-filtered colimits. In addition, [Reference LurieLur09, Corollary 5.3.5.4 (3)] shows that it is also closed under limits, since limits commute with limits. To conclude,
$\kappa$-filtered colimits. In addition, [Reference LurieLur09, Corollary 5.3.5.4 (3)] shows that it is also closed under limits, since limits commute with limits. To conclude, ![]() $\mathcal {C}$ is closed under
$\mathcal {C}$ is closed under ![]() $\mu$-filtered colimits and
$\mu$-filtered colimits and ![]() $\mu$-small limits in
$\mu$-small limits in ![]() $\operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ for any
$\operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ for any ![]() $\mu \geq \kappa$, and by the second case the result holds for
$\mu \geq \kappa$, and by the second case the result holds for ![]() $\operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ for any
$\operatorname {\mathcal {P}}(\mathcal {C}^\kappa )$ for any ![]() $\mu$.
$\mu$.
Proposition 4.6 The inclusion ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ preserves all limits and
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ preserves all limits and ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is presentable.
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is presentable.
Proof. We essentially repeat the proof in [Reference HarpazHar20, Lemma 5.17]. Recall that ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is the full subcategory of
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is the full subcategory of ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ on those functors that preserve limits index by
$\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ on those functors that preserve limits index by ![]() $A \in \mathcal {S}_m^{(p)}$. As limits commute with limits, and limits are computed level-wise in
$A \in \mathcal {S}_m^{(p)}$. As limits commute with limits, and limits are computed level-wise in ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$, we get that
$\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$, we get that ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is closed under limits. Let
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is closed under limits. Let ![]() $\kappa$ be any cardinal such that
$\kappa$ be any cardinal such that ![]() $\mathcal {C}$ is
$\mathcal {C}$ is ![]() $\kappa$-presentable and all
$\kappa$-presentable and all ![]() $A \in \mathcal {S}_m^{(p)}$ are
$A \in \mathcal {S}_m^{(p)}$ are ![]() $\kappa$-small, then by Lemma 4.5, limits indexed by
$\kappa$-small, then by Lemma 4.5, limits indexed by ![]() $A \in \mathcal {S}_m^{(p)}$ commute with
$A \in \mathcal {S}_m^{(p)}$ commute with ![]() $\kappa$-filtered colimits in
$\kappa$-filtered colimits in ![]() $\mathcal {C}$. Again, as colimits are computed level-wise in
$\mathcal {C}$. Again, as colimits are computed level-wise in ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$, we get that
$\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$, we get that ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is closed under
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is closed under ![]() $\kappa$-filtered colimits. It follows that
$\kappa$-filtered colimits. It follows that ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is presentable by the reflection principle of [Reference Ragimov and SchlankRS21]. Alternatively, the presentability follows from [Reference Chu and HaugsengCH21, Lemma 2.11(iv)].
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is presentable by the reflection principle of [Reference Ragimov and SchlankRS21]. Alternatively, the presentability follows from [Reference Chu and HaugsengCH21, Lemma 2.11(iv)].
Definition 4.7 Let ![]() $\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$. We denote by
$\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$. We denote by ![]() ${L^{\mathrm {seg}}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ the left adjoint of the inclusion
${L^{\mathrm {seg}}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ the left adjoint of the inclusion ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
Given a functor ![]() $F\colon \mathcal {C} \to \mathcal {D}$ we get an induced functor
$F\colon \mathcal {C} \to \mathcal {D}$ we get an induced functor ![]() $F\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {D}})}$ by post-composing level-wise with
$F\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {D}})}$ by post-composing level-wise with ![]() $F$.
$F$.
Proposition 4.8 If ![]() $F\colon \mathcal {C} \to \mathcal {D}$ commutes with limits indexed by any
$F\colon \mathcal {C} \to \mathcal {D}$ commutes with limits indexed by any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$, then the restriction of
$A$, then the restriction of ![]() $F\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {D}})}$ to
$F\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {D}})}$ to ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ lands in
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ lands in ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$, yielding a functor
$\mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$, yielding a functor ![]() $F\colon \mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$.
$F\colon \mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$.
Proof. Follows immediately from the characterization given in Remark 4.3 and the fact that ![]() $F$ commutes with these limits.
$F$ commutes with these limits.
4.2 Higher commutative monoids and semiadditivity
The underlying object functor ![]() $\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to \mathcal {S}$ has a left adjoint
$\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to \mathcal {S}$ has a left adjoint ![]() $F^{\mathrm {seg}} \colon \mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$. The fact that this endows
$F^{\mathrm {seg}} \colon \mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$. The fact that this endows ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ with the structure of a mode was first proved in [Reference HarpazHar20, Corollary 5.19] (for
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ with the structure of a mode was first proved in [Reference HarpazHar20, Corollary 5.19] (for ![]() $m < \infty$), and subsequently developed in [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.1].
$m < \infty$), and subsequently developed in [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.1].
Theorem 4.9 [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.1]
The category ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode, that is, it is an idempotent presentable symmetric monoidal category. As such, it classifies the property of being (
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode, that is, it is an idempotent presentable symmetric monoidal category. As such, it classifies the property of being (![]() $p$-typically)
$p$-typically) ![]() $m$-semiadditive. Furthermore, for any
$m$-semiadditive. Furthermore, for any ![]() $\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ there is an equivalence
$\mathcal {C} \in \mathrm {Pr}^\mathrm {L}$ there is an equivalence ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathcal {C}$, and tensoring the unit map
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathcal {C}$, and tensoring the unit map ![]() $\mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ with
$\mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ with ![]() $\mathcal {C}$ yields a left adjoint functor
$\mathcal {C}$ yields a left adjoint functor ![]() $F^{\mathrm {seg}}\colon \mathcal {C} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$.
$F^{\mathrm {seg}}\colon \mathcal {C} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$.
Remark 4.10 The cited papers prove the result in the non-![]() $p$-typical case, i.e. for all
$p$-typical case, i.e. for all ![]() $m$-finite spaces, but the same proofs work for the
$m$-finite spaces, but the same proofs work for the ![]() $p$-typical case.
$p$-typical case.
Following [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 5.3.3], we make the following definition.
Definition 4.11 We define ![]() ${{{\unicode{x05E6}}} ^{[m]}} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{(p)}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathrm {Sp}_{(p)}$. This is the mode which classifies the property of being a
${{{\unicode{x05E6}}} ^{[m]}} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{(p)}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathrm {Sp}_{(p)}$. This is the mode which classifies the property of being a ![]() $p$-local stable and (
$p$-local stable and ( ![]() $p$-typically)
$p$-typically) ![]() $m$-semiadditive presentable category. There is a canonical map of modes, which we call the group completion
$m$-semiadditive presentable category. There is a canonical map of modes, which we call the group completion ![]() ${(-)^{\mathrm {gpc}}}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to {{\unicode{x05E6}}} ^{[m]}$.
${(-)^{\mathrm {gpc}}}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to {{\unicode{x05E6}}} ^{[m]}$.
Example 4.12 The case ![]() $m = 0$ reproduces
$m = 0$ reproduces ![]() ${{\unicode{x05E6}}} ^{[0]} \cong \mathrm {Sp}_{(p)}$ and the group completion is the map
${{\unicode{x05E6}}} ^{[0]} \cong \mathrm {Sp}_{(p)}$ and the group completion is the map
We recall the following.
Proposition 4.13 The inclusions ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}$,
$\mathrm {Cat}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}$, ![]() $\mathrm {Cat}^{\mathrm {st}} \to \mathrm {Cat}$ and
$\mathrm {Cat}^{\mathrm {st}} \to \mathrm {Cat}$ and ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ create all limits.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ create all limits.
Proof. The first part is [Reference LurieLur09, Corollary 5.3.6.10] for ![]() $\mathcal {K} = \emptyset$ and
$\mathcal {K} = \emptyset$ and ![]() $\mathcal {K}' = \mathcal {S}_m^{(p)}$. The second part is [Reference LurieLur17, Theorem 1.1.4.4]. The third part follows from the combination of the first two.
$\mathcal {K}' = \mathcal {S}_m^{(p)}$. The second part is [Reference LurieLur17, Theorem 1.1.4.4]. The third part follows from the combination of the first two.
Combining Propositions 4.8 and 4.13, we get the following.
Corollary 4.14 The inclusions ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ and
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ and ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}$ induce inclusions
$\mathrm {Cat}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}$ induce inclusions ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ and
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ and ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
Proposition 4.15 Let ![]() $\mathcal {M} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$, then for any
$\mathcal {M} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$, then for any ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathcal {M}}$, the category
$\mathcal {C} \in \mathrm {Mod}_{\mathcal {M}}$, the category ![]() $\mathcal {C}^{\mathrm {at}}$ is stable and
$\mathcal {C}^{\mathrm {at}}$ is stable and ![]() $m$-semiadditive. Furthermore, the functor taking the atomics gives a lax symmetric monoidal functor
$m$-semiadditive. Furthermore, the functor taking the atomics gives a lax symmetric monoidal functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. The same holds for the mode
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. The same holds for the mode ![]() ${{\unicode{x05E6}}} ^{[m]} \cong \mathcal {M} \otimes \mathrm {Sp}_{(p)}$, and the corresponding functor
${{\unicode{x05E6}}} ^{[m]} \cong \mathcal {M} \otimes \mathrm {Sp}_{(p)}$, and the corresponding functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the restriction of the previous functor.
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the restriction of the previous functor.
Proof. We first show that for any ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathcal {M}}$,
$\mathcal {C} \in \mathrm {Mod}_{\mathcal {M}}$, ![]() $\mathcal {C}^{\mathrm {at}}$ is stable and
$\mathcal {C}^{\mathrm {at}}$ is stable and ![]() $m$-semiadditive. Recall from [Reference Hopkins and LurieHL13, Proposition 4.3.9] that for any
$m$-semiadditive. Recall from [Reference Hopkins and LurieHL13, Proposition 4.3.9] that for any ![]() $\mathcal {C}$ in the mode
$\mathcal {C}$ in the mode ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ and
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ and ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$,
$A$, ![]() $A$-shaped limits in
$A$-shaped limits in ![]() $\mathcal {C}$ commute with all colimits, showing that all
$\mathcal {C}$ commute with all colimits, showing that all ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$ are absolute limits in
$A$ are absolute limits in ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, and by Lemma 2.20 also in
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, and by Lemma 2.20 also in ![]() $\mathcal {M}$. Since
$\mathcal {M}$. Since ![]() $\mathcal {C}^{\mathrm {at}}$ is a full subcategory of the
$\mathcal {C}^{\mathrm {at}}$ is a full subcategory of the ![]() $m$-semiadditive category
$m$-semiadditive category ![]() $\mathcal {C}$, and is closed under all colimits indexed by any
$\mathcal {C}$, and is closed under all colimits indexed by any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$, it is, in fact,
$A$, it is, in fact, ![]() $m$-semiadditive by [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.1.4(4)]. The stability statement follows from Proposition 2.25.
$m$-semiadditive by [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.1.4(4)]. The stability statement follows from Proposition 2.25.
In particular, this shows that ![]() $\mathcal {K}$, the collection of all finite categories and
$\mathcal {K}$, the collection of all finite categories and ![]() $m$-finite
$m$-finite ![]() $p$-spaces, is a collection of absolute limits of
$p$-spaces, is a collection of absolute limits of ![]() $\mathcal {M}$. Theorem 2.46 then shows that there is a lax symmetric monoidal functor
$\mathcal {M}$. Theorem 2.46 then shows that there is a lax symmetric monoidal functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}_\mathcal {K}$. Recall that there is a fully faithful functor
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}_\mathcal {K}$. Recall that there is a fully faithful functor ![]() $(-)^\otimes \colon \mathrm {CMon}(\mathrm {Cat})^\mathrm {lax} \to \mathrm {Op}$ from the category of symmetric monoidal categories and lax symmetric monoidal functors to operads. Note that
$(-)^\otimes \colon \mathrm {CMon}(\mathrm {Cat})^\mathrm {lax} \to \mathrm {Op}$ from the category of symmetric monoidal categories and lax symmetric monoidal functors to operads. Note that ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \subset \mathrm {Cat}_\mathcal {K}$ is the full subcategory on those categories which are in addition stable, but it is not a sub-symmetric monoidal category, since the unit of
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \subset \mathrm {Cat}_\mathcal {K}$ is the full subcategory on those categories which are in addition stable, but it is not a sub-symmetric monoidal category, since the unit of ![]() $\mathrm {Cat}_\mathcal {K}$ is not stable. However, it is true that the tensor product of a family of categories in either category is the same, in particular
$\mathrm {Cat}_\mathcal {K}$ is not stable. However, it is true that the tensor product of a family of categories in either category is the same, in particular ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$ is a sub-operad of
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$ is a sub-operad of ![]() $\mathrm {Cat}_\mathcal {K}^\otimes$. Therefore, we get that the map of operads
$\mathrm {Cat}_\mathcal {K}^\otimes$. Therefore, we get that the map of operads ![]() $(-)^{\mathrm {at}}\colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL},\otimes } \to \mathrm {Cat}_\mathcal {K}^\otimes$ factors through the operad
$(-)^{\mathrm {at}}\colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL},\otimes } \to \mathrm {Cat}_\mathcal {K}^\otimes$ factors through the operad ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$, which corresponds to the desired lax symmetric monoidal functor
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$, which corresponds to the desired lax symmetric monoidal functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
Note that ![]() ${{\unicode{x05E6}}} ^{[m]} \cong \mathcal {M} \otimes \mathrm {Sp}_{(p)}$ is a smashing localization of
${{\unicode{x05E6}}} ^{[m]} \cong \mathcal {M} \otimes \mathrm {Sp}_{(p)}$ is a smashing localization of ![]() $\mathcal {M}$. The argument above works for
$\mathcal {M}$. The argument above works for ![]() ${{\unicode{x05E6}}} ^{[m]}$ in place of
${{\unicode{x05E6}}} ^{[m]}$ in place of ![]() $\mathcal {M}$. Furthermore, by Proposition 2.26, the atomic objects with respect to either one are the same, showing that
$\mathcal {M}$. Furthermore, by Proposition 2.26, the atomic objects with respect to either one are the same, showing that ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is indeed the restriction of
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is indeed the restriction of ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. We also note that the lax symmetric monoidal structure on the latter restricts to the lax symmetric monoidal structure on the former. To see that, observe that the symmetric monoidal left adjoint of the latter
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. We also note that the lax symmetric monoidal structure on the latter restricts to the lax symmetric monoidal structure on the former. To see that, observe that the symmetric monoidal left adjoint of the latter ![]() $\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}^{{{\unicode{x05E6}}} ^{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}}$ factors as the composition of the symmetric monoidal functors
$\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}}^{{{\unicode{x05E6}}} ^{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}}$ factors as the composition of the symmetric monoidal functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \xrightarrow {\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}} \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \xrightarrow {- \otimes {{\unicode{x05E6}}} ^{[m]}} \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}}$, so the lax symmetric monoidal right adjoint factors accordingly.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \xrightarrow {\operatorname {\operatorname {\mathcal {P}}_\mathcal {K}^\mathcal {M}}} \mathrm {Mod}_{\mathcal {M}}^{\mathrm {iL}} \xrightarrow {- \otimes {{\unicode{x05E6}}} ^{[m]}} \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}}$, so the lax symmetric monoidal right adjoint factors accordingly.
4.3 Tensor product of higher commutative monoids
Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. In this subsection, we endow
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. In this subsection, we endow ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with two symmetric monoidal structures, and show that they coincide. The first, which we call the mode symmetric monoidal structure (see Definition 4.16), comes from the fact that
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with two symmetric monoidal structures, and show that they coincide. The first, which we call the mode symmetric monoidal structure (see Definition 4.16), comes from the fact that ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode. The second, which we call the localized Day convolution (see Definition 4.25), is obtained by localizing the Day convolution on
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode. The second, which we call the localized Day convolution (see Definition 4.25), is obtained by localizing the Day convolution on ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$. Finally, in Theorem 4.26 we show that the two structures coincide.
$\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$. Finally, in Theorem 4.26 we show that the two structures coincide.
Recall that by Theorem 4.9, ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode and, in particular, it is equipped with a symmetric monoidal structure.
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode and, in particular, it is equipped with a symmetric monoidal structure.
Definition 4.16 Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. The equivalence
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. The equivalence ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathcal {C}$ of Theorem 4.9 endows
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \cong \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \otimes \mathcal {C}$ of Theorem 4.9 endows ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with a presentably symmetric monoidal structure which we call the mode symmetric monoidal structure and denote by
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with a presentably symmetric monoidal structure which we call the mode symmetric monoidal structure and denote by ![]() ${\otimes }$. Furthermore, by construction,
${\otimes }$. Furthermore, by construction, ![]() $F^{\mathrm {seg}}\colon \mathcal {C} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is endowed with a symmetric monoidal structure.
$F^{\mathrm {seg}}\colon \mathcal {C} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is endowed with a symmetric monoidal structure.
In a different direction, consider the category ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})$. Since
$\operatorname {Span}(\mathcal {S}_m^{(p)})$. Since ![]() $\mathcal {S}_m^{(p)}$ is closed under products, it has a cartesian monoidal structure. By [Reference HaugsengHau17, Theorem 1.2(iv)], its span category
$\mathcal {S}_m^{(p)}$ is closed under products, it has a cartesian monoidal structure. By [Reference HaugsengHau17, Theorem 1.2(iv)], its span category ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})$ is endowed with a symmetric monoidal structure given on objects by their cartesian product in
$\operatorname {Span}(\mathcal {S}_m^{(p)})$ is endowed with a symmetric monoidal structure given on objects by their cartesian product in ![]() $\mathcal {S}_m^{(p)}$. Therefore, the opposite category
$\mathcal {S}_m^{(p)}$. Therefore, the opposite category ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$ is also endowed with a symmetric monoidal structure.
$\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$ is also endowed with a symmetric monoidal structure.
Remark 4.17 The symmetric monoidal structure on ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})$ that we use is not the cartesian or cocartesian structure. In fact, the cartesian and cocartesian structures coincide (since products and coproducts coincide in
$\operatorname {Span}(\mathcal {S}_m^{(p)})$ that we use is not the cartesian or cocartesian structure. In fact, the cartesian and cocartesian structures coincide (since products and coproducts coincide in ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})$, being a semiadditive category), and are given on objects by the disjoint union of spaces, whereas the symmetric monoidal structure we use is given on objects by the product of spaces.
$\operatorname {Span}(\mathcal {S}_m^{(p)})$, being a semiadditive category), and are given on objects by the disjoint union of spaces, whereas the symmetric monoidal structure we use is given on objects by the product of spaces.
Definition 4.18 Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. We endow
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ be a presentably symmetric monoidal category. We endow ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} = \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C})$ with the Day convolution of Theorem 3.1, which we denote by
$\mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} = \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathcal {C})$ with the Day convolution of Theorem 3.1, which we denote by ![]() ${\circledast }$. By Corollary 3.7, we have a symmetric monoidal functor
${\circledast }$. By Corollary 3.7, we have a symmetric monoidal functor ![]() $F\colon \mathcal {C} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
$F\colon \mathcal {C} \to \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$.
Our next goal, achieved in Proposition 4.24, is to show that the Day convolution is compatible with the reflective localization ![]() $L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$, endowing it with a localized symmetric monoidal structure. Recall from [Reference LurieLur17, Example 2.2.1.7] that for a symmetric monoidal category
$L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$, endowing it with a localized symmetric monoidal structure. Recall from [Reference LurieLur17, Example 2.2.1.7] that for a symmetric monoidal category ![]() $\mathcal {D}$, we say that a reflective localization
$\mathcal {D}$, we say that a reflective localization ![]() $L\colon \mathcal {D} \to \mathcal {D}_0$ is compatible with the symmetric monoidal structure, if and only if for any
$L\colon \mathcal {D} \to \mathcal {D}_0$ is compatible with the symmetric monoidal structure, if and only if for any ![]() $L$-equivalence
$L$-equivalence ![]() $X \to Y \in \mathcal {D}$ and
$X \to Y \in \mathcal {D}$ and ![]() $Z \in \mathcal {D}$, the morphism
$Z \in \mathcal {D}$, the morphism ![]() $X \otimes Z \to Y \otimes Z \in \mathcal {D}$ is an
$X \otimes Z \to Y \otimes Z \in \mathcal {D}$ is an ![]() $L$-equivalence.
$L$-equivalence.
Remark 4.19 By the Yoneda lemma, a map ![]() $X \to Y$ is an
$X \to Y$ is an ![]() $L$-equivalence if and only if for any
$L$-equivalence if and only if for any ![]() $T \in \mathcal {D}_0$ the induced map
$T \in \mathcal {D}_0$ the induced map ![]() $\hom (Y, T) \to \hom (X, T)$ is an equivalence.
$\hom (Y, T) \to \hom (X, T)$ is an equivalence.
Lemma 4.20 Let ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $L$ be as above, and assume further that the symmetric monoidal structure on
$L$ be as above, and assume further that the symmetric monoidal structure on ![]() $\mathcal {D}$ is closed. Then, the reflective localization is compatible with the symmetric monoidal structure if and only if for any
$\mathcal {D}$ is closed. Then, the reflective localization is compatible with the symmetric monoidal structure if and only if for any ![]() $L$-equivalence
$L$-equivalence ![]() $X \to Y \in \mathcal {D}$ and
$X \to Y \in \mathcal {D}$ and ![]() $T \in \mathcal {D}_0$ the induced map on internal homs
$T \in \mathcal {D}_0$ the induced map on internal homs ![]() $\hom ^\mathcal {D}(Y, T) \to \hom ^\mathcal {D}(X, T)$ is an equivalence.
$\hom ^\mathcal {D}(Y, T) \to \hom ^\mathcal {D}(X, T)$ is an equivalence.
Proof. Fix a map ![]() $X \to Y \in \mathcal {D}$. By the Yoneda lemma,
$X \to Y \in \mathcal {D}$. By the Yoneda lemma, ![]() $\hom ^\mathcal {D}(Y, T) \to \hom ^\mathcal {D}(X, T)$ is an equivalence for any
$\hom ^\mathcal {D}(Y, T) \to \hom ^\mathcal {D}(X, T)$ is an equivalence for any ![]() $T \in \mathcal {D}_0$, if and only if the map
$T \in \mathcal {D}_0$, if and only if the map ![]() $\hom (Z, \hom ^\mathcal {D}(Y, T)) \to \hom (Z, \hom ^\mathcal {D}(X, T))$ is an equivalence for any
$\hom (Z, \hom ^\mathcal {D}(Y, T)) \to \hom (Z, \hom ^\mathcal {D}(X, T))$ is an equivalence for any ![]() $Z \in \mathcal {D}, T \in \mathcal {D}_0$. By adjunction, the latter holds if and only if
$Z \in \mathcal {D}, T \in \mathcal {D}_0$. By adjunction, the latter holds if and only if ![]() $\hom (Y \otimes Z, T) \to \hom (X \otimes Z, T)$ is an equivalence for any
$\hom (Y \otimes Z, T) \to \hom (X \otimes Z, T)$ is an equivalence for any ![]() $Z \in \mathcal {D}, T \in \mathcal {D}_0$. By the Yoneda lemma, this holds if and only if
$Z \in \mathcal {D}, T \in \mathcal {D}_0$. By the Yoneda lemma, this holds if and only if ![]() $X \otimes Z \to Y \otimes Z$ is an
$X \otimes Z \to Y \otimes Z$ is an ![]() $L$-equivalence for any
$L$-equivalence for any ![]() $Z \in \mathcal {D}$.
$Z \in \mathcal {D}$.
Lemma 4.21 Let ![]() $\mathcal {D}, \mathcal {D}_0, \mathcal {E} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ and let
$\mathcal {D}, \mathcal {D}_0, \mathcal {E} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ and let ![]() $L\colon \mathcal {D} \to \mathcal {D}_0$ be a reflective localization which is compatible with symmetric monoidal structure. Then
$L\colon \mathcal {D} \to \mathcal {D}_0$ be a reflective localization which is compatible with symmetric monoidal structure. Then ![]() $L \otimes \mathrm {id}\colon \mathcal {D} \otimes \mathcal {E} \to \mathcal {D}_0 \otimes \mathcal {E}$ is also a reflective localization compatible with the symmetric monoidal structure on
$L \otimes \mathrm {id}\colon \mathcal {D} \otimes \mathcal {E} \to \mathcal {D}_0 \otimes \mathcal {E}$ is also a reflective localization compatible with the symmetric monoidal structure on ![]() $\mathcal {D} \otimes \mathcal {E}$.
$\mathcal {D} \otimes \mathcal {E}$.
Proof. We let ![]() $L' = L \otimes \mathrm {id}$. First note that
$L' = L \otimes \mathrm {id}$. First note that ![]() $L'$ is indeed a reflective localization by [Reference Carmeli, Schlank and YanovskiCSY21a, Lemma 5.2.1]. Using [Reference LurieLur17, Proposition 2.2.1.9] we endow
$L'$ is indeed a reflective localization by [Reference Carmeli, Schlank and YanovskiCSY21a, Lemma 5.2.1]. Using [Reference LurieLur17, Proposition 2.2.1.9] we endow ![]() $\mathcal {D}_0$ with the localized symmetric monoidal structure, making
$\mathcal {D}_0$ with the localized symmetric monoidal structure, making ![]() $L$ into a symmetric monoidal functor. Since
$L$ into a symmetric monoidal functor. Since ![]() $\otimes$ is the coproduct of
$\otimes$ is the coproduct of ![]() $\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, this makes the categories and the map
$\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, this makes the categories and the map ![]() $L'\colon \mathcal {D} \otimes \mathcal {E} \to \mathcal {D}_0 \otimes \mathcal {E}$ symmetric monoidal. Now let
$L'\colon \mathcal {D} \otimes \mathcal {E} \to \mathcal {D}_0 \otimes \mathcal {E}$ symmetric monoidal. Now let ![]() $X \to Y \in \mathcal {D} \otimes \mathcal {E}$ be an
$X \to Y \in \mathcal {D} \otimes \mathcal {E}$ be an ![]() $L'$-equivalence. For any
$L'$-equivalence. For any ![]() $Z \in \mathcal {D} \otimes \mathcal {E}$, we have
$Z \in \mathcal {D} \otimes \mathcal {E}$, we have
which is an equivalence.
Note that by the Yoneda lemma, for any ![]() $A \in \mathcal {S}_m^{(p)}$, the object
$A \in \mathcal {S}_m^{(p)}$, the object ![]() ${\unicode{x3088}}(A) \in \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ corepresents the evaluation at
${\unicode{x3088}}(A) \in \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ corepresents the evaluation at ![]() $A$ functor
$A$ functor ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathcal {S}$ given by
$\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathcal {S}$ given by ![]() $X \mapsto X(A)$. We also note that these functors over all
$X \mapsto X(A)$. We also note that these functors over all ![]() $A \in \mathcal {S}_m^{(p)}$ are jointly conservative.
$A \in \mathcal {S}_m^{(p)}$ are jointly conservative.
Lemma 4.22 Let ![]() $X \in \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$, and
$X \in \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$, and ![]() $A \in \mathcal {S}_m^{(p)}$, then
$A \in \mathcal {S}_m^{(p)}$, then
In particular, if ![]() $X \in \mathrm {CMon}{({\mathcal {S}})}$, then so is
$X \in \mathrm {CMon}{({\mathcal {S}})}$, then so is ![]() $\hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), X)$.
$\hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), X)$.
Proof. By [Reference LurieLur17, Corollary 4.8.1.12], the Yoneda embedding ![]() ${\unicode{x3088}}\colon \operatorname {Span}(\mathcal {S}_m^{(p)}) \to \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is symmetric monoidal, so that
${\unicode{x3088}}\colon \operatorname {Span}(\mathcal {S}_m^{(p)}) \to \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is symmetric monoidal, so that ![]() ${\unicode{x3088}}(A) \otimes {\unicode{x3088}}(-) \cong {\unicode{x3088}}(A \times -)$. Therefore, we get
${\unicode{x3088}}(A) \otimes {\unicode{x3088}}(-) \cong {\unicode{x3088}}(A \times -)$. Therefore, we get
 \begin{align*} \hom^{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(A), X)(-) &\cong \hom({\unicode{x3088}}(-), \hom^{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(A), X))\\ &\cong \hom({\unicode{x3088}}(A) \otimes {\unicode{x3088}}(-), X)\\ &\cong \hom({\unicode{x3088}}(A \times -), X)\\ &\cong X(A \times -) . \end{align*}
\begin{align*} \hom^{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(A), X)(-) &\cong \hom({\unicode{x3088}}(-), \hom^{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(A), X))\\ &\cong \hom({\unicode{x3088}}(A) \otimes {\unicode{x3088}}(-), X)\\ &\cong \hom({\unicode{x3088}}(A \times -), X)\\ &\cong X(A \times -) . \end{align*}
For the second part, note that ![]() $X(A \times -)$ is the pre-composition of
$X(A \times -)$ is the pre-composition of ![]() $X$ with
$X$ with ![]() $A \times -\colon \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$ which preserves limits indexed by
$A \times -\colon \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op}$ which preserves limits indexed by ![]() $B \in \mathcal {S}_m^{(p)}$. By Remark 4.3, the
$B \in \mathcal {S}_m^{(p)}$. By Remark 4.3, the ![]() $m$-Segal condition is equivalent to preservation of limits indexed by
$m$-Segal condition is equivalent to preservation of limits indexed by ![]() $B \in \mathcal {S}_m^{(p)}$, so the result follows.
$B \in \mathcal {S}_m^{(p)}$, so the result follows.
Lemma 4.23 The reflective localization ![]() $L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is compatible with the Day convolution.
$L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is compatible with the Day convolution.
Proof. By Lemma 4.20, it suffices to show that for any ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$-equivalence
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$-equivalence ![]() $X \to Y$ and
$X \to Y$ and ![]() $T \in \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ the induced map
$T \in \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ the induced map ![]() $\hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(Y, T) \to \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(X, T)$ is an equivalence. Since the evaluations at
$\hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(Y, T) \to \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(X, T)$ is an equivalence. Since the evaluations at ![]() $A \in \mathcal {S}_m^{(p)}$ are jointly conservative, it suffices to show that for any
$A \in \mathcal {S}_m^{(p)}$ are jointly conservative, it suffices to show that for any ![]() $A \in \mathcal {S}_m^{(p)}$ the map
$A \in \mathcal {S}_m^{(p)}$ the map ![]() $\hom ({\unicode{x3088}}(A), \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(Y, T)) \to \hom ({\unicode{x3088}}(A), \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(X, T))$ is an equivalence. By adjunction, this is equivalent to showing that
$\hom ({\unicode{x3088}}(A), \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(Y, T)) \to \hom ({\unicode{x3088}}(A), \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}(X, T))$ is an equivalence. By adjunction, this is equivalent to showing that ![]() $\hom (Y, \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), T)) \to \hom (X, \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), T))$ is an equivalence. By assumption
$\hom (Y, \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), T)) \to \hom (X, \hom ^{\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}}({\unicode{x3088}}(A), T))$ is an equivalence. By assumption ![]() $X \to Y$ is an
$X \to Y$ is an ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$-equivalence and
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$-equivalence and ![]() $T \in \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, so the result follow from the second part of Lemma 4.22.
$T \in \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, so the result follow from the second part of Lemma 4.22.
Proposition 4.24 The reflective localization ![]() $L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is compatible with the Day convolution.
$L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ is compatible with the Day convolution.
Proof. Consider the following commutative diagram in ![]() $\mathrm {Pr}^\mathrm {L}$.
$\mathrm {Pr}^\mathrm {L}$.

The bottom map is an equivalence by Theorem 4.9. The top map is a symmetric monoidal equivalence by Proposition 3.10. By Lemma 4.23, ![]() $L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is compatible with the Day convolution, so by Lemma 4.21 the left map is also compatible with the symmetric monoidal structure. Therefore, the right map is also compatible with the Day convolution.
$L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is compatible with the Day convolution, so by Lemma 4.21 the left map is also compatible with the symmetric monoidal structure. Therefore, the right map is also compatible with the Day convolution.
Definition 4.25 Using [Reference LurieLur17, Proposition 2.2.1.9], we endow ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ with the induced symmetric monoidal structure, which we call the localized Day convolution and denote by
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ with the induced symmetric monoidal structure, which we call the localized Day convolution and denote by ![]() ${\hat {\circledast }}$. This makes the functor
${\hat {\circledast }}$. This makes the functor ![]() $L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ symmetric monoidal (with respect to the localized Day convolution), thus by [Reference LurieLur17, Corollary 7.3.2.7] the right adjoint
$L^{\mathrm {seg}}\colon \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ symmetric monoidal (with respect to the localized Day convolution), thus by [Reference LurieLur17, Corollary 7.3.2.7] the right adjoint ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ is lax symmetric monoidal.
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathcal {C}})}$ is lax symmetric monoidal.
The main result of this subsection is the following.
Theorem 4.26 Let ![]() $\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then the mode symmetric monoidal structure and the localized Day convolution on
$\mathcal {C} \in \operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$, then the mode symmetric monoidal structure and the localized Day convolution on ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ coincide, making the following diagram in
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ coincide, making the following diagram in ![]() $\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ commute.
$\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ commute.

We begin by proving the result for ![]() $\mathcal {C} = \mathcal {S}$.
$\mathcal {C} = \mathcal {S}$.
Lemma 4.27 The localized Day convolution and the mode symmetric monoidal structure on ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide, and
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide, and ![]() $L^{\mathrm {seg}} F \cong F^{\mathrm {seg}}$.
$L^{\mathrm {seg}} F \cong F^{\mathrm {seg}}$.
Proof. The right adjoint of ![]() $F^{\mathrm {seg}}$ is the underlying object functor
$F^{\mathrm {seg}}$ is the underlying object functor ![]() $\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to \mathcal {S}$, which by adjunction is represented by
$\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathcal {S}})} \to \mathcal {S}$, which by adjunction is represented by ![]() $F^{\mathrm {seg}}(*) \cong \mathbf {1}^{\otimes }$. By [Reference LurieLur17, Corollary 4.8.1.12], the Yoneda embedding
$F^{\mathrm {seg}}(*) \cong \mathbf {1}^{\otimes }$. By [Reference LurieLur17, Corollary 4.8.1.12], the Yoneda embedding ![]() ${\unicode{x3088}}\colon \operatorname {Span}(\mathcal {S}_m^{(p)}) \to \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is symmetric monoidal, and in particular the unit of
${\unicode{x3088}}\colon \operatorname {Span}(\mathcal {S}_m^{(p)}) \to \mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is symmetric monoidal, and in particular the unit of ![]() $\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is
$\mathrm {PCMon}_m^{(p)} {({\mathcal {S}})}$ is ![]() $\mathbf {1}^{\circledast } \cong {\unicode{x3088}}(*)$. Using the Yoneda lemma we get
$\mathbf {1}^{\circledast } \cong {\unicode{x3088}}(*)$. Using the Yoneda lemma we get
 \begin{align*} \hom_{\mathrm{CMon}_m^{(p)}{({\mathcal{S}})}}(\mathbf{1}^{\hat{\circledast}},X) &\cong \hom_{\mathrm{CMon}_m^{(p)}{({\mathcal{S}})}}(L^{\mathrm{seg}} \mathbf{1}^{\circledast},X)\\ &\cong \hom_{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}(\mathbf{1}^{\circledast},X)\\ &\cong \hom_{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(*),X)\\ &\cong \underline{X} . \end{align*}
\begin{align*} \hom_{\mathrm{CMon}_m^{(p)}{({\mathcal{S}})}}(\mathbf{1}^{\hat{\circledast}},X) &\cong \hom_{\mathrm{CMon}_m^{(p)}{({\mathcal{S}})}}(L^{\mathrm{seg}} \mathbf{1}^{\circledast},X)\\ &\cong \hom_{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}(\mathbf{1}^{\circledast},X)\\ &\cong \hom_{\mathrm{PCMon}_m^{(p)} {({\mathcal{S}})}}({\unicode{x3088}}(*),X)\\ &\cong \underline{X} . \end{align*}
Therefore, ![]() $\mathbf {1}^{\hat {\circledast }}$ also represents
$\mathbf {1}^{\hat {\circledast }}$ also represents ![]() $\underline {(-)}$, so that
$\underline {(-)}$, so that ![]() $\mathbf {1}^{\hat {\circledast }} \cong \mathbf {1}^{\otimes }$. Since
$\mathbf {1}^{\hat {\circledast }} \cong \mathbf {1}^{\otimes }$. Since ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode, it has a unique presentably symmetric monoidal structure with the given unit as in [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.1.6], so that localized Day convolution and the mode symmetric monoidal structure on
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ is a mode, it has a unique presentably symmetric monoidal structure with the given unit as in [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.1.6], so that localized Day convolution and the mode symmetric monoidal structure on ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide. Since there is a unique map of modes
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide. Since there is a unique map of modes ![]() $\mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, the functors
$\mathcal {S} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$, the functors ![]() $L^{\mathrm {seg}} F$ and
$L^{\mathrm {seg}} F$ and ![]() $F^{\mathrm {seg}}$ coincide.
$F^{\mathrm {seg}}$ coincide.
Proof of Theorem 4.26 Consider the following diagram in ![]() $\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ where we endow
$\operatorname {CAlg}(\mathrm {Pr}^\mathrm {L})$ where we endow ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with the localized Day convolution structure (and the rest of the categories are endowed with a single symmetric monoidal structure, as we have shown that the two structures on
$\mathrm {CMon}_m^{(p)}{({\mathcal {C}})}$ with the localized Day convolution structure (and the rest of the categories are endowed with a single symmetric monoidal structure, as we have shown that the two structures on ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide).
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}$ coincide).

The bottom map is an equivalence by Theorem 4.9, and we wish to upgrade it to a symmetric monoidal equivalence.
The top map is a symmetric monoidal equivalence by Proposition 3.10. As in the proof of Proposition 4.24, both the left and the right maps are symmetric monoidal. This shows that the bottom map is the localization of the top map, and thus inherits the structure of a symmetric monoidal equivalence.
5. Higher cocartesian structure
Endowing a category ![]() $\mathcal {C} \in \mathrm {Cat}$ with a symmetric monoidal structure is the same as providing a lift
$\mathcal {C} \in \mathrm {Cat}$ with a symmetric monoidal structure is the same as providing a lift ![]() $\mathcal {C}^\otimes \in \mathrm {CMon}{({\mathrm {Cat}})}$. If
$\mathcal {C}^\otimes \in \mathrm {CMon}{({\mathrm {Cat}})}$. If ![]() $\mathcal {C}$ has finite coproducts, it has a cocartesian structure
$\mathcal {C}$ has finite coproducts, it has a cocartesian structure ![]() $\mathcal {C}^\sqcup$ given by the coproduct. An Eckmann–Hilton-style argument characterizes it as the unique symmetric monoidal structure that commutes with coproducts (in all coordinates together), namely satisfying
$\mathcal {C}^\sqcup$ given by the coproduct. An Eckmann–Hilton-style argument characterizes it as the unique symmetric monoidal structure that commutes with coproducts (in all coordinates together), namely satisfying
Building on [Reference HarpazHar20, Theorem 5.23], in this section we define the (![]() $p$-typical)
$p$-typical) ![]() $m$-cocartesian structure as an
$m$-cocartesian structure as an ![]() $m$-commutative monoid structure, and in Theorem 5.3 we show that it enjoys the expected properties, which in particular gives a construction of the ordinary cocartesian structure. The results of this section feature in the definition of higher semiadditive algebraic K-theory in Definition 6.5, by preserving the
$m$-commutative monoid structure, and in Theorem 5.3 we show that it enjoys the expected properties, which in particular gives a construction of the ordinary cocartesian structure. The results of this section feature in the definition of higher semiadditive algebraic K-theory in Definition 6.5, by preserving the ![]() $m$-commutative monoid structure afforded by the
$m$-commutative monoid structure afforded by the ![]() $m$-cocartesian structure.
$m$-cocartesian structure.
Definition 5.1 The category of categories with a ![]() $\textit{(}p$-typical)
$\textit{(}p$-typical) ![]() $m$-symmetric monoidal structure is
$m$-symmetric monoidal structure is ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$. That is, an
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$. That is, an ![]() $m$-symmetric monoidal structure on
$m$-symmetric monoidal structure on ![]() $\mathcal {C} \in \mathrm {Cat}$ is a lift
$\mathcal {C} \in \mathrm {Cat}$ is a lift ![]() $\mathcal {C}^\otimes \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
$\mathcal {C}^\otimes \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
In [Reference HarpazHar20, Theorem 5.23] and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.2.7] it is shown that the category ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$ of categories admitting colimits indexed by
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$ of categories admitting colimits indexed by ![]() $m$-finite
$m$-finite ![]() $p$-spaces is itself an (
$p$-spaces is itself an (![]() $p$-typically)
$p$-typically) ![]() $m$-semiadditive category for any
$m$-semiadditive category for any ![]() $-2 \leq m \leq \infty$ (the proofs in the cited papers are not in the
$-2 \leq m \leq \infty$ (the proofs in the cited papers are not in the ![]() $p$-typical case, but the same proofs work in the
$p$-typical case, but the same proofs work in the ![]() $p$-typical case). In other words, the underlying functor
$p$-typical case). In other words, the underlying functor
is an equivalence. We denote its inverse by ![]() ${(-)^{{\sqcup _m}}}\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. We recall from Corollary 4.14 that there is an inclusion
${(-)^{{\sqcup _m}}}\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. We recall from Corollary 4.14 that there is an inclusion ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
Definition 5.2 For every ![]() $\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, we call
$\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, we call ![]() ${\mathcal {C}^{{\sqcup _m}}} \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$ the
${\mathcal {C}^{{\sqcup _m}}} \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$ the ![]() $m$-cocartesian structure on
$m$-cocartesian structure on ![]() $\mathcal {C}$. When
$\mathcal {C}$. When ![]() $m$ is clear from the context, we shall write
$m$ is clear from the context, we shall write ![]() $\mathcal {C}^\sqcup$ for
$\mathcal {C}^\sqcup$ for ![]() $\mathcal {C}^{{\sqcup _m}}$.
$\mathcal {C}^{{\sqcup _m}}$.
Our next goal is to justify this name. In particular, we will show that for every ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$, the map
$A$, the map ![]() $\mathcal {C}^A \to \mathcal {C}$ induced by evaluating
$\mathcal {C}^A \to \mathcal {C}$ induced by evaluating ![]() $\mathcal {C}^\sqcup$ at
$\mathcal {C}^\sqcup$ at ![]() $A \to *$ is given by taking the colimit over
$A \to *$ is given by taking the colimit over ![]() $A$. More precisely, for any
$A$. More precisely, for any ![]() $\mathcal {C} \in \mathrm {Cat}$, let
$\mathcal {C} \in \mathrm {Cat}$, let ![]() $\mathcal {C}^* \in \operatorname {Fun}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ be the functor
$\mathcal {C}^* \in \operatorname {Fun}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ be the functor ![]() $\operatorname {Fun}(-, \mathcal {C})$, given by sending
$\operatorname {Fun}(-, \mathcal {C})$, given by sending ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$ to
$A$ to ![]() $\mathcal {C}^A$ and
$\mathcal {C}^A$ and ![]() $q\colon A \to B$ to
$q\colon A \to B$ to ![]() $q^*\colon \mathcal {C}^B \to \mathcal {C}^A$. If we assume that
$q^*\colon \mathcal {C}^B \to \mathcal {C}^A$. If we assume that ![]() $\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, then
$\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, then ![]() $q^*\colon \mathcal {C}^B \to \mathcal {C}^A$ has a left adjoint
$q^*\colon \mathcal {C}^B \to \mathcal {C}^A$ has a left adjoint ![]() $q_!\colon \mathcal {C}^A \to \mathcal {C}^B$. By passing to the left adjoints, we obtain a functor
$q_!\colon \mathcal {C}^A \to \mathcal {C}^B$. By passing to the left adjoints, we obtain a functor ![]() $\mathcal {C}_! \in \operatorname {Fun}(\mathcal {S}_m^{(p)},\mathrm {Cat})$. The main result of this section is then as follows.
$\mathcal {C}_! \in \operatorname {Fun}(\mathcal {S}_m^{(p)},\mathrm {Cat})$. The main result of this section is then as follows.
Theorem 5.3 The restriction of ![]() $\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$ along the right-way maps
$\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$ along the right-way maps ![]() $\mathcal {S}_m^{(p)} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is
$\mathcal {S}_m^{(p)} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is ![]() $\mathcal {C}^*$, and similarly along the wrong-way maps
$\mathcal {C}^*$, and similarly along the wrong-way maps ![]() $(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is
$(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is ![]() $\mathcal {C}_!$.
$\mathcal {C}_!$.
To prove this, we first note that not only each ![]() $q^*$ has a left adjoint
$q^*$ has a left adjoint ![]() $q_!$, but they also satisfy the Beck–Chevalley condition. This means that
$q_!$, but they also satisfy the Beck–Chevalley condition. This means that ![]() $\mathcal {C}^*$ is in fact in
$\mathcal {C}^*$ is in fact in ![]() $\operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ (where
$\operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ (where ![]() $\operatorname {Fun}^{\mathrm {BC}}$ are functors such that each morphism is mapped to a right adjoint, such that the Beck–Chevalley condition is satisfied). We will use Barwick's unfurling construction [Reference BarwickBar17, Definition 11.3]. Barwick works in a more general context, allowing to prescribe only certain right- and wrong-way morphisms, but we shall not use this generality. After straightening, the unfurling construction for
$\operatorname {Fun}^{\mathrm {BC}}$ are functors such that each morphism is mapped to a right adjoint, such that the Beck–Chevalley condition is satisfied). We will use Barwick's unfurling construction [Reference BarwickBar17, Definition 11.3]. Barwick works in a more general context, allowing to prescribe only certain right- and wrong-way morphisms, but we shall not use this generality. After straightening, the unfurling construction for ![]() $(\mathcal {S}_m^{(p)})^\mathrm {op}$ takes a functor
$(\mathcal {S}_m^{(p)})^\mathrm {op}$ takes a functor ![]() $F \in \operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, and produces a new functor
$F \in \operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, and produces a new functor ![]() $\Upsilon (F) \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, and enjoys the following properties.
$\Upsilon (F) \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, and enjoys the following properties.
Theorem 5.4 [Reference BarwickBar17, Proposition 11.6 and Theorem 12.2]
For any ![]() $F \in \operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, the restriction of
$F \in \operatorname {Fun}^{\mathrm {BC}}((\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$, the restriction of ![]() $\Upsilon (F)$ along the right-way maps
$\Upsilon (F)$ along the right-way maps ![]() $\mathcal {S}_m^{(p)} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is
$\mathcal {S}_m^{(p)} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is ![]() $F$, and similarly along the wrong-way
$F$, and similarly along the wrong-way ![]() $(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is the functor sending the morphisms to the left adjoints.
$(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is the functor sending the morphisms to the left adjoints.
Using this result, we our now in position to prove Theorem 5.3.
Proof of Theorem 5.3 By Barwick's theorem, ![]() $\Upsilon (\mathcal {C}^*)$ has the properties we ought to prove for
$\Upsilon (\mathcal {C}^*)$ has the properties we ought to prove for ![]() $\mathcal {C}^\sqcup$, so it suffices to show that
$\mathcal {C}^\sqcup$, so it suffices to show that ![]() $\mathcal {C}^\sqcup \cong \Upsilon (\mathcal {C}^*)$. Furthermore, recall that the underlying functor
$\mathcal {C}^\sqcup \cong \Upsilon (\mathcal {C}^*)$. Furthermore, recall that the underlying functor ![]() $\underline {({-})}\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ is an equivalence, so each
$\underline {({-})}\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ is an equivalence, so each ![]() $\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ has a unique lift to
$\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ has a unique lift to ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. Therefore, it suffices to show that
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. Therefore, it suffices to show that ![]() $\Upsilon (\mathcal {C}^*) \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ is in
$\Upsilon (\mathcal {C}^*) \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat})$ is in ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$, i.e. that it satisfies the
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$, i.e. that it satisfies the ![]() $m$-Segal condition and that it takes values in
$m$-Segal condition and that it takes values in ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
First, by construction, ![]() $\mathcal {C}^*$ satisfies the
$\mathcal {C}^*$ satisfies the ![]() $m$-Segal condition. Since the restriction of
$m$-Segal condition. Since the restriction of ![]() $\Upsilon (\mathcal {C}^*)$ along
$\Upsilon (\mathcal {C}^*)$ along ![]() $(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is
$(\mathcal {S}_m^{(p)})^\mathrm {op} \to \operatorname {Span}(\mathcal {S}_m^{(p)})$ is ![]() $\mathcal {C}^*$, it follows that it satisfies the
$\mathcal {C}^*$, it follows that it satisfies the ![]() $m$-Segal condition as well, thus
$m$-Segal condition as well, thus ![]() $\Upsilon (\mathcal {C}^*) \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
$\Upsilon (\mathcal {C}^*) \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}})}$.
Second, we need to show that ![]() $\Upsilon (\mathcal {C}^*)$ lands in
$\Upsilon (\mathcal {C}^*)$ lands in ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$. By assumption
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$. By assumption ![]() $\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, thus the same holds for
$\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$, thus the same holds for ![]() $\mathcal {C}^A$ for all
$\mathcal {C}^A$ for all ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$. For morphisms, we need to show they are sent to functors that commute with colimits indexed by any
$A$. For morphisms, we need to show they are sent to functors that commute with colimits indexed by any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$. Any morphism in
$A$. Any morphism in ![]() $\operatorname {Span}(\mathcal {S}_m^{(p)})$ is the composition of a right-way and a wrong-way map, so we can check these separately. So let
$\operatorname {Span}(\mathcal {S}_m^{(p)})$ is the composition of a right-way and a wrong-way map, so we can check these separately. So let ![]() $q\colon A \to B$ be a morphism of
$q\colon A \to B$ be a morphism of ![]() $m$-finite
$m$-finite ![]() $p$-spaces. Since
$p$-spaces. Since ![]() $q_!$ is a left adjoint, it commutes with colimits indexed by any
$q_!$ is a left adjoint, it commutes with colimits indexed by any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$, so it is a morphism in
$A$, so it is a morphism in ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$. Since colimits in functor categories are computed level-wise, the functor
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$. Since colimits in functor categories are computed level-wise, the functor ![]() $q^*$ commutes with them, so it is also a morphism in
$q^*$ commutes with them, so it is also a morphism in ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
Remark 5.5 In light of Barwick's construction, one could define the ![]() $m$-cocartesian structure simply by
$m$-cocartesian structure simply by ![]() $\mathcal {C}^\sqcup = \Upsilon (\mathcal {C}^*)$. The reason why we define it via the equivalence
$\mathcal {C}^\sqcup = \Upsilon (\mathcal {C}^*)$. The reason why we define it via the equivalence ![]() $(-)^{\sqcup }\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ is twofold. First, this construction characterizes
$(-)^{\sqcup }\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ is twofold. First, this construction characterizes ![]() $\mathcal {C}^\sqcup$ in a universal way. Second, Barwick's unfurling construction, although much more general than our definition, is not shown to be functorial in
$\mathcal {C}^\sqcup$ in a universal way. Second, Barwick's unfurling construction, although much more general than our definition, is not shown to be functorial in ![]() $F$, which will be used crucially for
$F$, which will be used crucially for ![]() $\mathcal {C}^\sqcup$ in our definition of semiadditive algebraic K-theory.
$\mathcal {C}^\sqcup$ in our definition of semiadditive algebraic K-theory.
Theorem 5.6 The restriction of ![]() $(-)^{\sqcup }\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ to
$(-)^{\sqcup }\colon \mathrm {Cat}_{m\text {-}\mathrm {fin}} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$ to ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ lands in
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ lands in ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$, and induces an equivalence
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$, and induces an equivalence ![]() $(-)^{\sqcup }\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}\xrightarrow {\smash {{\scriptstyle \sim }}}\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
$(-)^{\sqcup }\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}\xrightarrow {\smash {{\scriptstyle \sim }}}\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
Proof. Let ![]() $\mathcal {C}\in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. We know that
$\mathcal {C}\in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. We know that ![]() $\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. By Proposition 4.13, for any
$\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. By Proposition 4.13, for any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$,
$A$, ![]() $\mathcal {C}^A$ is computed the same in
$\mathcal {C}^A$ is computed the same in ![]() $\mathrm {Cat}$,
$\mathrm {Cat}$, ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$, and
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$, and ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and in particular it is stable. Furthermore, for any
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and in particular it is stable. Furthermore, for any ![]() $q\colon A \to B$, both
$q\colon A \to B$, both ![]() $q_!$ and
$q_!$ and ![]() $q^*$ are exact. Thus,
$q^*$ are exact. Thus, ![]() $\mathcal {C}^\sqcup \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})$. Again by Proposition 4.13, it satisfies the
$\mathcal {C}^\sqcup \in \operatorname {Fun}(\operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op},\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})$. Again by Proposition 4.13, it satisfies the ![]() $m$-Segal condition so that
$m$-Segal condition so that ![]() $\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
$\mathcal {C}^\sqcup \in \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
For a functor ![]() $F\colon \mathcal {C} \to \mathcal {D}$ in
$F\colon \mathcal {C} \to \mathcal {D}$ in ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, we have an induced functor
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, we have an induced functor ![]() $\mathcal {C}^\sqcup \to \mathcal {D}^{\sqcup }$ in
$\mathcal {C}^\sqcup \to \mathcal {D}^{\sqcup }$ in ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. At every point it is given by
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. At every point it is given by ![]() $F\circ -\colon \mathcal {C}^A \to \mathcal {D}^{A}$, which is exact, thus a map in
$F\circ -\colon \mathcal {C}^A \to \mathcal {D}^{A}$, which is exact, thus a map in ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. This finishes the first part, showing that
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. This finishes the first part, showing that ![]() $(-)^{\sqcup }$ lands in
$(-)^{\sqcup }$ lands in ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
By Corollary 4.14, the inclusion ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ induces an inclusion
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ induces an inclusion ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}\to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. The maps
$\mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}\to \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})}$. The maps ![]() $\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \rightleftarrows \mathrm {Cat}_{m\text {-}\mathrm {fin}} \colon (-)^{\sqcup }$, which are inverses to each other, restrict to maps between the subcategories, which are therefore inverses to each other as well.
$\underline {(-)}\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}_{m\text {-}\mathrm {fin}}})} \rightleftarrows \mathrm {Cat}_{m\text {-}\mathrm {fin}} \colon (-)^{\sqcup }$, which are inverses to each other, restrict to maps between the subcategories, which are therefore inverses to each other as well.
6. Semiadditive algebraic K-theory
In this section we define an ![]() $m$-semiadditive version of algebraic K-theory. We begin by recalling the construction of ordinary algebraic K-theory, and present it in a way which is amenable to generalizations. We then generalize the definition to construct
$m$-semiadditive version of algebraic K-theory. We begin by recalling the construction of ordinary algebraic K-theory, and present it in a way which is amenable to generalizations. We then generalize the definition to construct ![]() $m$-semiadditive algebraic K-theory in Definition 6.5, and connect it to ordinary algebraic K-theory in Corollary 6.10. We leverage this connection in Theorem 6.18 to endow the functor of
$m$-semiadditive algebraic K-theory in Definition 6.5, and connect it to ordinary algebraic K-theory in Corollary 6.10. We leverage this connection in Theorem 6.18 to endow the functor of ![]() $m$-semiadditive algebraic K-theory with a lax symmetric monoidal structure. This is later used to prove Theorems 8.10 and 8.23, two of the main results of this paper.
$m$-semiadditive algebraic K-theory with a lax symmetric monoidal structure. This is later used to prove Theorems 8.10 and 8.23, two of the main results of this paper.
6.1 Ordinary algebraic K-theory
We recall the definition of the ![]() $S_\bullet$-construction for stable categories and exact functors. One defines the functor
$S_\bullet$-construction for stable categories and exact functors. One defines the functor ![]() $S_{\bullet }\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ by letting
$S_{\bullet }\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ by letting ![]() $S_n \mathcal {C}$ be the subspace of those functors
$S_n \mathcal {C}$ be the subspace of those functors ![]() $X\colon [n]^{[1]} \to \mathcal {C}$ that satisfy:
$X\colon [n]^{[1]} \to \mathcal {C}$ that satisfy:
(1)
 $X_{ii}=0$;
$X_{ii}=0$;(2) for all
 $i\leq j\leq k$ the following is a bicartesian square
that is,
$i\leq j\leq k$ the following is a bicartesian square
that is,
 $X_{ij}\to X_{ik}\to X_{jk}$ is a (co)fiber sequence.
$X_{ij}\to X_{ik}\to X_{jk}$ is a (co)fiber sequence.
The algebraic K-theory space functor ![]() ${\underline {\mathrm {K}}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ is then defined as the composition
${\underline {\mathrm {K}}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ is then defined as the composition ![]() $\underline {\mathrm {K}}(\mathcal {C}) = \Omega |S_\bullet \mathcal {C}|$. One then proceeds to lift to (connective) spectra, e.g. by means of iterated
$\underline {\mathrm {K}}(\mathcal {C}) = \Omega |S_\bullet \mathcal {C}|$. One then proceeds to lift to (connective) spectra, e.g. by means of iterated ![]() $S_\bullet$-construction. We will give an equivalent construction of the spectrum structure, which will be easier to generalize. To that end, we show the following.
$S_\bullet$-construction. We will give an equivalent construction of the spectrum structure, which will be easier to generalize. To that end, we show the following.
Lemma 6.1 The functor ![]() $S_\bullet \colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ commutes with limits.
$S_\bullet \colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ commutes with limits.
Proof. For each ![]() $n$, the functor
$n$, the functor ![]() $S_n\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ is equivalent to
$S_n\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ is equivalent to ![]() $\hom ([n-1],-)$, and in particular it commutes with limits. Since limits in the functor category
$\hom ([n-1],-)$, and in particular it commutes with limits. Since limits in the functor category ![]() $\mathcal {S}^{\Delta ^\mathrm {op}}$ are computed level-wise, this implies that
$\mathcal {S}^{\Delta ^\mathrm {op}}$ are computed level-wise, this implies that ![]() $S_\bullet$ commutes with limits as well.
$S_\bullet$ commutes with limits as well.
This together with Proposition 4.8 implies that we get an induced functor ![]() $S_{\bullet }\colon \mathrm {CMon}{({\mathrm {Cat}^{\mathrm {st}}})}\to \mathrm {CMon}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$. Employing Theorem 5.6, we give the following definition.
$S_{\bullet }\colon \mathrm {CMon}{({\mathrm {Cat}^{\mathrm {st}}})}\to \mathrm {CMon}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$. Employing Theorem 5.6, we give the following definition.
Definition 6.2 We define algebraic K-theory ![]() ${\mathrm {K}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ by
${\mathrm {K}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ by ![]() $\mathrm {K}(\mathcal {C})=\Omega |(S_\bullet (\mathcal {C}^\sqcup ))^{\mathrm {gpc}}|$, that is, as the following composition
$\mathrm {K}(\mathcal {C})=\Omega |(S_\bullet (\mathcal {C}^\sqcup ))^{\mathrm {gpc}}|$, that is, as the following composition
Lemma 6.3 The composition of ![]() $\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ with
$\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}$ with ![]() $\Omega ^\infty \colon \mathrm {Sp} \to \mathcal {S}$ is
$\Omega ^\infty \colon \mathrm {Sp} \to \mathcal {S}$ is ![]() $\underline {\mathrm {K}}$.
$\underline {\mathrm {K}}$.
Proof. First note that ![]() $(-)^{\mathrm {gpc}}\colon \mathrm {CMon}{({\mathcal {S}})} \to \mathrm {Sp}$ is a left adjoint, and therefore commutes with the colimit
$(-)^{\mathrm {gpc}}\colon \mathrm {CMon}{({\mathcal {S}})} \to \mathrm {Sp}$ is a left adjoint, and therefore commutes with the colimit ![]() $|-|$, and that
$|-|$, and that ![]() $\Omega ((-)^{\mathrm {gpc}}) \cong \Omega$ as functors
$\Omega ((-)^{\mathrm {gpc}}) \cong \Omega$ as functors ![]() $\mathrm {CMon}{({\mathcal {S}})} \to \mathrm {Sp}$. This shows that our definition of algebraic K-theory is equivalent to the composition
$\mathrm {CMon}{({\mathcal {S}})} \to \mathrm {Sp}$. This shows that our definition of algebraic K-theory is equivalent to the composition
Consider the following diagram.

Square (1) commutes because ![]() $(-)^\sqcup$ and
$(-)^\sqcup$ and ![]() $\underline {({-})}$ are inverses by Theorem 5.6. Square (2) commutes by the definition of the extension of
$\underline {({-})}$ are inverses by Theorem 5.6. Square (2) commutes by the definition of the extension of ![]() $S_\bullet$ to
$S_\bullet$ to ![]() $\mathrm {CMon}{()}$. Square (3) commutes since the underlying commutes with geometric realizations. Square (4) commutes because
$\mathrm {CMon}{()}$. Square (3) commutes since the underlying commutes with geometric realizations. Square (4) commutes because ![]() $\Omega$ is a limit and the underlying is a right adjoint functor. Finally, the top-right composition is
$\Omega$ is a limit and the underlying is a right adjoint functor. Finally, the top-right composition is ![]() $\Omega ^\infty \mathrm {K}$, whereas the left-bottom composition is
$\Omega ^\infty \mathrm {K}$, whereas the left-bottom composition is ![]() $\underline {\mathrm {K}}$.
$\underline {\mathrm {K}}$.
We now claim that the above definition of the spectrum structure coincides with the standard one. Note that, by construction, ![]() $\mathrm {K}$ in fact lands in connective spectra.
$\mathrm {K}$ in fact lands in connective spectra.
Proposition 6.4 There is a unique lift of ![]() $\underline {\mathrm {K}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ to
$\underline {\mathrm {K}}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathcal {S}$ to ![]() $\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}_{\geq 0}$.
$\mathrm {K}\colon \mathrm {Cat}^{\mathrm {st}} \to \mathrm {Sp}_{\geq 0}$.
Proof. The universal property of commutative monoids given in [Reference HarpazHar20, Corollary 5.15] implies that if ![]() $\mathcal {D}$ has finite products and
$\mathcal {D}$ has finite products and ![]() $\mathcal {C}$ is semiadditive, then
$\mathcal {C}$ is semiadditive, then ![]() $\operatorname {Fun}^\times (\mathcal {C}, \mathcal {D}) \cong \operatorname {Fun}^\times (\mathcal {C}, \mathrm {CMon}{({\mathcal {D}})})$. Since
$\operatorname {Fun}^\times (\mathcal {C}, \mathcal {D}) \cong \operatorname {Fun}^\times (\mathcal {C}, \mathrm {CMon}{({\mathcal {D}})})$. Since ![]() $\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {D}})} \subseteq \mathrm {CMon}{({\mathcal {D}})}$ is a full subcategory closed under products,
$\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {D}})} \subseteq \mathrm {CMon}{({\mathcal {D}})}$ is a full subcategory closed under products,
is a full subcategory. Therefore, the forgetful
is fully faithful, meaning that product preserving functors ![]() $\mathcal {C} \to \mathcal {D}$ have unique or no lifts to
$\mathcal {C} \to \mathcal {D}$ have unique or no lifts to ![]() $\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {D}})}$. In particular, for
$\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {D}})}$. In particular, for ![]() $\mathcal {D} = \mathcal {S}$, using the equivalence
$\mathcal {D} = \mathcal {S}$, using the equivalence ![]() $\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {S}})} \cong \mathrm {Sp}_{\geq 0}$, we get that the forgetful
$\mathrm {CMon}^{\mathrm {gl}}{({\mathcal {S}})} \cong \mathrm {Sp}_{\geq 0}$, we get that the forgetful
is fully faithful.
Applying this to the case ![]() $\mathcal {C} = \mathrm {Cat}^{\mathrm {st}}$, the result follows since
$\mathcal {C} = \mathrm {Cat}^{\mathrm {st}}$, the result follows since ![]() $\underline {\mathrm {K}}$ has a lift, which is therefore unique.
$\underline {\mathrm {K}}$ has a lift, which is therefore unique.
6.2 Definition of semiadditive algebraic K-theory
We restrict the ![]() $S_\bullet$-construction to
$S_\bullet$-construction to ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and use the same notation, i.e.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and use the same notation, i.e. ![]() $S_\bullet \colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$. Proposition 4.13 shows that
$S_\bullet \colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$. Proposition 4.13 shows that ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ preserve limits, thus by Lemma 6.1, the restriction
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ preserve limits, thus by Lemma 6.1, the restriction ![]() $S_\bullet \colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ preserves limits as well, so using Proposition 4.8 again we get an induced functor
$S_\bullet \colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathcal {S}^{\Delta ^\mathrm {op}}$ preserves limits as well, so using Proposition 4.8 again we get an induced functor ![]() $S_{\bullet }\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$. Employing Theorem 5.6, we give the following definition.
$S_{\bullet }\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \to \mathrm {CMon}_m^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$. Employing Theorem 5.6, we give the following definition.
Definition 6.5 We define ![]() $m$-semiadditive algebraic K-theory
$m$-semiadditive algebraic K-theory ![]() ${\mathrm {K}^{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ by
${\mathrm {K}^{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ by ![]() $\mathrm {K}^{[m]}(\mathcal {C})=\Omega |(S_\bullet (\mathcal {C}^\sqcup ))^{\mathrm {gpc}}|$, that is, as the following composition
$\mathrm {K}^{[m]}(\mathcal {C})=\Omega |(S_\bullet (\mathcal {C}^\sqcup ))^{\mathrm {gpc}}|$, that is, as the following composition
Example 6.6 Proposition 6.4 shows that the case ![]() $m = 0$ recovers the
$m = 0$ recovers the ![]() $p$-localization of the ordinary K-theory of stable categories.
$p$-localization of the ordinary K-theory of stable categories.
Proposition 6.7 The functor ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is an
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is an ![]() $m$-semiadditive functor, i.e. commutes with all limits indexed by an
$m$-semiadditive functor, i.e. commutes with all limits indexed by an ![]() $m$-finite
$m$-finite ![]() $p$-space. In particular,
$p$-space. In particular, ![]() $\mathrm {K}^{[m]}(\mathcal {C}^A) \cong \mathrm {K}^{[m]}(\mathcal {C})^A$ for any
$\mathrm {K}^{[m]}(\mathcal {C}^A) \cong \mathrm {K}^{[m]}(\mathcal {C})^A$ for any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$.
$A$.
Proof. The functor ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is defined as the composition of functors between
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is defined as the composition of functors between ![]() $m$-semiadditive categories ([Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.1.4(1) and (2)] imply the
$m$-semiadditive categories ([Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.1.4(1) and (2)] imply the ![]() $m$-semiadditivity of
$m$-semiadditivity of ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$ and
$\mathrm {CMon}_m^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}$ and ![]() $({{\unicode{x05E6}}} ^{[m]})^{\Delta ^\mathrm {op}}$). All of the functors either preserve all limits (in the case of
$({{\unicode{x05E6}}} ^{[m]})^{\Delta ^\mathrm {op}}$). All of the functors either preserve all limits (in the case of ![]() $(-)^\sqcup, S_\bullet$ and
$(-)^\sqcup, S_\bullet$ and ![]() $\Omega$) or preserve all colimits (in the case of
$\Omega$) or preserve all colimits (in the case of ![]() $(-)^{\mathrm {gpc}}$ and
$(-)^{\mathrm {gpc}}$ and ![]() $|-|$). In particular, they are all
$|-|$). In particular, they are all ![]() $m$-semiadditive functors, thus the composition is an
$m$-semiadditive functors, thus the composition is an ![]() $m$-semiadditive functor as well.
$m$-semiadditive functor as well.
6.3 Relationship to ordinary algebraic K-theory
Proposition 6.7 shows that ![]() $\mathrm {K}^{[m]}$ is an
$\mathrm {K}^{[m]}$ is an ![]() $m$-semiadditive functor and, in particular, satisfies
$m$-semiadditive functor and, in particular, satisfies ![]() $\mathrm {K}^{[m]}(\mathcal {C}^A) \cong \mathrm {K}^{[m]}(\mathcal {C})^A$ for any
$\mathrm {K}^{[m]}(\mathcal {C}^A) \cong \mathrm {K}^{[m]}(\mathcal {C})^A$ for any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$. One may wonder if
$A$. One may wonder if ![]() $\mathrm {K}^{[m]}$ can be obtained by forcing ordinary algebraic K-theory to satisfy this condition. In this subsection we show a more general result of this sort. To be more specific, let
$\mathrm {K}^{[m]}$ can be obtained by forcing ordinary algebraic K-theory to satisfy this condition. In this subsection we show a more general result of this sort. To be more specific, let ![]() $m_0 \leq m$, then Definition 6.8 introduces a functor
$m_0 \leq m$, then Definition 6.8 introduces a functor ![]() $\mathrm {K}^{[m_0]}_{[m]}$, which associates to
$\mathrm {K}^{[m_0]}_{[m]}$, which associates to ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ the pre-
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ the pre-![]() $m$-commutative monoid given on objects by
$m$-commutative monoid given on objects by ![]() $A \mapsto \mathrm {K}^{[m_0]}(\mathcal {C}^A)$. The main result of this subsection is Theorem 6.9, which shows that forcing the
$A \mapsto \mathrm {K}^{[m_0]}(\mathcal {C}^A)$. The main result of this subsection is Theorem 6.9, which shows that forcing the ![]() $m$-Segal condition on
$m$-Segal condition on ![]() $\mathrm {K}^{[m_0]}_{[m]}$ is indeed
$\mathrm {K}^{[m_0]}_{[m]}$ is indeed ![]() $\mathrm {K}^{[m]}$. In particular, the case
$\mathrm {K}^{[m]}$. In particular, the case ![]() $m_0 = 0$ yields an alternative definition of
$m_0 = 0$ yields an alternative definition of ![]() $m$-semiadditive algebraic K-theory, by forcing
$m$-semiadditive algebraic K-theory, by forcing ![]() $A \mapsto \mathrm {K}(\mathcal {C}^A)$ to satisfy the
$A \mapsto \mathrm {K}(\mathcal {C}^A)$ to satisfy the ![]() $m$-Segal condition.
$m$-Segal condition.
Consider the inclusion ![]() $i\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \subseteq \mathrm {PCMon}_m^{(p)} {(\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Cat}^{\mathrm {st}}_{m_0\text {-}\mathrm {fin}})}$. Using this we are lead to the main definition.
$i\colon \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})} \subseteq \mathrm {PCMon}_m^{(p)} {(\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Cat}^{\mathrm {st}}_{m_0\text {-}\mathrm {fin}})}$. Using this we are lead to the main definition.
Definition 6.8 We define the functor ![]() ${\mathrm {K}^{[m_0]}_{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$ by the following composition:
${\mathrm {K}^{[m_0]}_{[m]}}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$ by the following composition:
We recall that for any ![]() $\mathcal {D}$ we have an equivalence
$\mathcal {D}$ we have an equivalence ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {D}})} \cong \mathrm {CMon}_m^{(p)}{({{\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {D}})}}})}$ (which is given by sending
$\mathrm {CMon}_m^{(p)}{({\mathcal {D}})} \cong \mathrm {CMon}_m^{(p)}{({{\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {D}})}}})}$ (which is given by sending ![]() $X \in \mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$ to the iterated commutative monoid given on objects by
$X \in \mathrm {CMon}_m^{(p)}{({\mathcal {D}})}$ to the iterated commutative monoid given on objects by ![]() $A \mapsto (B \mapsto X(A \times B))$). In particular, we can consider it as a full subcategory
$A \mapsto (B \mapsto X(A \times B))$). In particular, we can consider it as a full subcategory ![]() $\mathrm {CMon}_m^{(p)}{({\mathcal {D}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {D}})}})}$, and this inclusion has a left adjoint
$\mathrm {CMon}_m^{(p)}{({\mathcal {D}})} \subseteq \mathrm {PCMon}_m^{(p)} {({\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {D}})}})}$, and this inclusion has a left adjoint ![]() $L^{\mathrm {seg}}$.
$L^{\mathrm {seg}}$.
Applying the above for ![]() $\mathcal {D} = \mathrm {Sp}_{(p)}$ shows that we have an inclusion of a full subcategory
$\mathcal {D} = \mathrm {Sp}_{(p)}$ shows that we have an inclusion of a full subcategory ![]() ${{\unicode{x05E6}}} ^{[m]} \subseteq \mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$ with a left adjoint
${{\unicode{x05E6}}} ^{[m]} \subseteq \mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$ with a left adjoint ![]() $L^{\mathrm {seg}}$. This allows us consider
$L^{\mathrm {seg}}$. This allows us consider ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ as a functor to
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ as a functor to ![]() $\mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$.
$\mathrm {PCMon}_m^{(p)} {({{\unicode{x05E6}}} ^{[m_0]})}$.
Theorem 6.9 There is a natural equivalence ![]() $L^{\mathrm {seg}} \mathrm {K}^{[m_0]}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of functors
$L^{\mathrm {seg}} \mathrm {K}^{[m_0]}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$.
Proof. We show that the square

commutes by admitting it as a (horizontal) composition of commutative squares, following the definition of the two functors.
Both functors start with ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \xrightarrow {(-)^\sqcup } \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \xrightarrow {(-)^\sqcup } \mathrm {CMon}_m^{(p)}{({\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}})}$.
Consider the following square.

The lift of ![]() $S_\bullet$ to (pre-)
$S_\bullet$ to (pre-)![]() $m$-commutative monoids is given by post-composition. From this description, the upper composition in fact lands in
$m$-commutative monoids is given by post-composition. From this description, the upper composition in fact lands in ![]() $\mathrm {CMon}_m^{(p)}{({{\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}}})}$, so
$\mathrm {CMon}_m^{(p)}{({{\mathrm {CMon}_{m_0}^{(p)}{({\mathcal {S}})}^{\Delta ^\mathrm {op}}}})}$, so ![]() $L^{\mathrm {seg}}$ acts on the image as the identity, making the square commute.
$L^{\mathrm {seg}}$ acts on the image as the identity, making the square commute.
The following square commutes because all maps are left adjoints and the square of right adjoints commutes because they are all forgetfuls.

The following square commutes because ![]() $L^{\mathrm {seg}}$ is a left adjoint, thus commutes with colimits.
$L^{\mathrm {seg}}$ is a left adjoint, thus commutes with colimits.

Lastly, ![]() $L^{\mathrm {seg}}$ is an exact functor between stable categories, thus it commutes with finite limits, so the following square commutes.
$L^{\mathrm {seg}}$ is an exact functor between stable categories, thus it commutes with finite limits, so the following square commutes.

In particular, restricting to the case ![]() $m_0 = 0$, we get that the functor
$m_0 = 0$, we get that the functor ![]() $\mathrm {K}_{[m]}$ given by
$\mathrm {K}_{[m]}$ given by ![]() $A \mapsto \mathrm {K}(\mathcal {C}^A)$ satisfies the following:
$A \mapsto \mathrm {K}(\mathcal {C}^A)$ satisfies the following:
Corollary 6.10 There is a natural equivalence ![]() $L^{\mathrm {seg}} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of functors
$L^{\mathrm {seg}} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$. In particular, if
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$. In particular, if ![]() $\mathrm {K}_{[m]}(\mathcal {C})\colon \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op} \to \mathrm {Sp}_{(p)}$ satisfies the
$\mathrm {K}_{[m]}(\mathcal {C})\colon \operatorname {Span}(\mathcal {S}_m^{(p)})^\mathrm {op} \to \mathrm {Sp}_{(p)}$ satisfies the ![]() $m$-Segal condition, then
$m$-Segal condition, then ![]() $\mathrm {K}^{[m]}(\mathcal {C}) \cong \mathrm {K}_{[m]}(\mathcal {C})$.
$\mathrm {K}^{[m]}(\mathcal {C}) \cong \mathrm {K}_{[m]}(\mathcal {C})$.
Corollary 6.11 There is a natural transformation ![]() $\mathrm {K} \to \underline {\mathrm {K}^{[m]}}$ of functors
$\mathrm {K} \to \underline {\mathrm {K}^{[m]}}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Sp}_{(p)}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Sp}_{(p)}$.
Proof. By adjunction, the equivalence ![]() $L^{\mathrm {seg}} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of Corollary 6.10 corresponds to a natural transformation
$L^{\mathrm {seg}} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$ of Corollary 6.10 corresponds to a natural transformation ![]() $\mathrm {K}_{[m]} \to \mathrm {K}^{[m]}$ of functors
$\mathrm {K}_{[m]} \to \mathrm {K}^{[m]}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{(p)})}$, where the target lands in
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{(p)})}$, where the target lands in ![]() ${{\unicode{x05E6}}} ^{[m]}$. Evaluating the pre-
${{\unicode{x05E6}}} ^{[m]}$. Evaluating the pre-![]() $m$-commutative monoids at the point gives the desired natural transformation.
$m$-commutative monoids at the point gives the desired natural transformation.
Recall that ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$ is
$\mathrm {Sp}_{\mathrm {T}(n)}$ is ![]() $\infty$-semiadditive. In particular,
$\infty$-semiadditive. In particular, ![]() $\mathrm {Sp}_{\mathrm {T}(n)} \cong \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})}$. In addition, there is a canonical map of modes
$\mathrm {Sp}_{\mathrm {T}(n)} \cong \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})}$. In addition, there is a canonical map of modes ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$. Recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.14] that
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$. Recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.14] that ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization, here we prove a slight generalization.
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} }\colon {{\unicode{x05E6}}} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization, here we prove a slight generalization.
Lemma 6.12 For any ![]() $m \geq 1$ and
$m \geq 1$ and ![]() $n \geq 0$, the functor
$n \geq 0$, the functor ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization of modes.
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization of modes.
Proof. Recall that ![]() $L_n^f\colon \mathrm {Sp} \to L_n^f\mathrm {Sp}$ is a smashing localization. Tensoring with the stable mode
$L_n^f\colon \mathrm {Sp} \to L_n^f\mathrm {Sp}$ is a smashing localization. Tensoring with the stable mode ![]() ${{\unicode{x05E6}}} ^{[m]}$, by Lemma 2.49 we get that
${{\unicode{x05E6}}} ^{[m]}$, by Lemma 2.49 we get that ![]() ${{\unicode{x05E6}}} ^{[m]} \to {{\unicode{x05E6}}} ^{[m]} \otimes L_n^f\mathrm {Sp}$ is a smashing localization of modes. Now, by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem G] we know that
${{\unicode{x05E6}}} ^{[m]} \to {{\unicode{x05E6}}} ^{[m]} \otimes L_n^f\mathrm {Sp}$ is a smashing localization of modes. Now, by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem G] we know that ![]() ${{\unicode{x05E6}}} ^{[m]} \otimes L_n^f\mathrm {Sp} \cong \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n)}$, and the projection to a factor is a smashing localization of modes as well. Therefore, the composition
${{\unicode{x05E6}}} ^{[m]} \otimes L_n^f\mathrm {Sp} \cong \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n)}$, and the projection to a factor is a smashing localization of modes as well. Therefore, the composition ![]() $L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is also smashing localization of modes.
$L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n)}$ is also smashing localization of modes.
Proposition 6.13 The following square commutes.

Proof. First recall that by definition ![]() ${{\unicode{x05E6}}} ^{[m]} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{(p)}})}$, and as explained above,
${{\unicode{x05E6}}} ^{[m]} = \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{(p)}})}$, and as explained above, ![]() $\mathrm {Sp}_{\mathrm {T}(n)} \cong \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})}$. All of the morphisms in the square in the statement are left adjoints. Using the two identifications and passing to the right adjoints we obtain the following square.
$\mathrm {Sp}_{\mathrm {T}(n)} \cong \mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})}$. All of the morphisms in the square in the statement are left adjoints. Using the two identifications and passing to the right adjoints we obtain the following square.

This square commutes as all morphisms are inclusions, thus the original square of left adjoints commutes as well.
Corollary 6.14 There is an equivalence ![]() $L^{\mathrm {seg}} L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$. In particular, if
$L^{\mathrm {seg}} L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$. In particular, if ![]() $L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ satisfies the
$L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ satisfies the ![]() $m$-Segal condition, then
$m$-Segal condition, then ![]() $L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$.
$L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$.
Proof. The first part follows immediately from Corollary 6.10 and Proposition 6.13. For the second part, if ![]() $L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ satisfies the
$L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ satisfies the ![]() $m$-Segal condition, then by the first part there is an equivalence
$m$-Segal condition, then by the first part there is an equivalence ![]() $L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$. The equivalence
$L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$. The equivalence ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})} \cong \mathrm {Sp}_{\mathrm {T}(n)}$, given by taking the underlying object, identifies
$\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})} \cong \mathrm {Sp}_{\mathrm {T}(n)}$, given by taking the underlying object, identifies ![]() $L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ with
$L_{\mathrm {T}(n)} \mathrm {K}_{[m]}(\mathcal {C})$ with ![]() $L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C})$, showing that indeed
$L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C})$, showing that indeed ![]() $L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$.
$L_{\mathrm {T}(n)} \mathrm {K}(\mathcal {C}) \cong L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(\mathcal {C})$.
Corollary 6.15 There is a natural transformation ![]() $L_{\mathrm {T}(n)} \mathrm {K} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of functors
$L_{\mathrm {T}(n)} \mathrm {K} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Sp}_{\mathrm {T}(n)}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Sp}_{\mathrm {T}(n)}$.
Proof. Similarly to Corollary 6.11, by adjunction, the equivalence ![]() $L^{\mathrm {seg}} L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of Corollary 6.14 corresponds to a natural transformation
$L^{\mathrm {seg}} L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of Corollary 6.14 corresponds to a natural transformation ![]() $L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of functors
$L_{\mathrm {T}(n)} \mathrm {K}_{[m]} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ of functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{\mathrm {T}(n)})}$, where the target lands in
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{\mathrm {T}(n)})}$, where the target lands in ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})} \cong \mathrm {Sp}_{\mathrm {T}(n)}$. Evaluating the pre-
$\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}_{\mathrm {T}(n)}})} \cong \mathrm {Sp}_{\mathrm {T}(n)}$. Evaluating the pre-![]() $m$-commutative monoids at the point gives the desired natural transformation.
$m$-commutative monoids at the point gives the desired natural transformation.
6.4 Multiplicative structure
Using Corollary 6.10 we leverage the lax symmetric monoidal structure on algebraic K-theory developed in [Reference Blumberg, Gepner and TabuadaBGT14, Corollary 1.6] and [Reference BarwickBar15, Proposition 3.8] to construct a lax symmetric monoidal structure on ![]() $m$-semiadditive algebraic K-theory.
$m$-semiadditive algebraic K-theory.
Recall that for any collection of indexing categories ![]() $\mathcal {K}$,
$\mathcal {K}$, ![]() $\mathrm {Cat}_\mathcal {K}$ has a symmetric monoidal structure constructed in [Reference LurieLur17, § 4.8.1]. If
$\mathrm {Cat}_\mathcal {K}$ has a symmetric monoidal structure constructed in [Reference LurieLur17, § 4.8.1]. If ![]() $\mathcal {K}$ contains all finite categories, then
$\mathcal {K}$ contains all finite categories, then ![]() $\mathrm {Cat}^{\mathrm {st}}_\mathcal {K}$ is the full subcategory on those categories that are in addition stable, which is also endowed with a symmetric monoidal structure (but is not a sub-symmetric monoidal category of
$\mathrm {Cat}^{\mathrm {st}}_\mathcal {K}$ is the full subcategory on those categories that are in addition stable, which is also endowed with a symmetric monoidal structure (but is not a sub-symmetric monoidal category of ![]() $\mathrm {Cat}_\mathcal {K}$, whose unit is not stable).
$\mathrm {Cat}_\mathcal {K}$, whose unit is not stable).
Lemma 6.16 The inclusion ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ is lax symmetric monoidal.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ is lax symmetric monoidal.
Proof. We argue similarly to the proof of Proposition 4.15. Recall again that there is a fully faithful functor ![]() $(-)^\otimes \colon \mathrm {CMon}(\mathrm {Cat})^\mathrm {lax} \to \mathrm {Op}$ from the category of symmetric monoidal categories and lax symmetric monoidal functors to operads. For any collection of indexing categories
$(-)^\otimes \colon \mathrm {CMon}(\mathrm {Cat})^\mathrm {lax} \to \mathrm {Op}$ from the category of symmetric monoidal categories and lax symmetric monoidal functors to operads. For any collection of indexing categories ![]() $\mathcal {K}$ the operad
$\mathcal {K}$ the operad ![]() $\mathrm {Cat}_\mathcal {K}^{\mathrm {st},\otimes }$ is a sub-operad of
$\mathrm {Cat}_\mathcal {K}^{\mathrm {st},\otimes }$ is a sub-operad of ![]() $\mathrm {Cat}_\mathcal {K}^\otimes$.
$\mathrm {Cat}_\mathcal {K}^\otimes$.
The category ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the case where
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the case where ![]() $\mathcal {K}$ is the collection of all finite categories and
$\mathcal {K}$ is the collection of all finite categories and ![]() $m$-finite
$m$-finite ![]() $p$-spaces, and
$p$-spaces, and ![]() $\mathrm {Cat}^{\mathrm {st}}$ is the case where
$\mathrm {Cat}^{\mathrm {st}}$ is the case where ![]() $\mathcal {K}'$ the collection of all finite categories. The same proof of [Reference LurieLur17, Corollary 4.8.1.4] shows that the inclusion
$\mathcal {K}'$ the collection of all finite categories. The same proof of [Reference LurieLur17, Corollary 4.8.1.4] shows that the inclusion ![]() $\mathrm {Cat}_\mathcal {K} \to \mathrm {Cat}_{\mathcal {K}'}$ is lax symmetric monoidal. We thus get a map of operads
$\mathrm {Cat}_\mathcal {K} \to \mathrm {Cat}_{\mathcal {K}'}$ is lax symmetric monoidal. We thus get a map of operads ![]() $\mathrm {Cat}_\mathcal {K}^\otimes \to \mathrm {Cat}_{\mathcal {K}'}^\otimes$. The restriction of this map to
$\mathrm {Cat}_\mathcal {K}^\otimes \to \mathrm {Cat}_{\mathcal {K}'}^\otimes$. The restriction of this map to ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$ lands in
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes }$ lands in ![]() $\mathrm {Cat}^{\mathrm {st},\otimes }$, so we get a map of operads
$\mathrm {Cat}^{\mathrm {st},\otimes }$, so we get a map of operads ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes } \to \mathrm {Cat}^{\mathrm {st},\otimes }$, that is, a lax symmetric monoidal functor
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}^{\mathrm {st},\otimes } \to \mathrm {Cat}^{\mathrm {st},\otimes }$, that is, a lax symmetric monoidal functor ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$.
Proposition 6.17 The functor ![]() $\mathrm {K}_{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{(p)})}$ is lax symmetric monoidal.
$\mathrm {K}_{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {PCMon}_m^{(p)} {(\mathrm {Sp}_{(p)})}$ is lax symmetric monoidal.
Proof. Recall that ![]() $\mathrm {K}_{[m]}$ is given by the composition
$\mathrm {K}_{[m]}$ is given by the composition
 \begin{align*} \mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}} &\xrightarrow{(-)^\sqcup} \mathrm{CMon}_m^{(p)}{({\mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}}})}\\ &\subseteq \mathrm{PCMon}_m^{(p)} {(\mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}})}\\ &\to \mathrm{PCMon}_m^{(p)} {(\mathrm{Cat}^{\mathrm{st}})}\\ &\xrightarrow{\mathrm{K}\circ-} \mathrm{PCMon}_m^{(p)} {(\mathrm{Sp}_{(p)})}. \end{align*}
\begin{align*} \mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}} &\xrightarrow{(-)^\sqcup} \mathrm{CMon}_m^{(p)}{({\mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}}})}\\ &\subseteq \mathrm{PCMon}_m^{(p)} {(\mathrm{Cat}^{\mathrm{st}}_{m\text{-}\mathrm{fin}})}\\ &\to \mathrm{PCMon}_m^{(p)} {(\mathrm{Cat}^{\mathrm{st}})}\\ &\xrightarrow{\mathrm{K}\circ-} \mathrm{PCMon}_m^{(p)} {(\mathrm{Sp}_{(p)})}. \end{align*}
The first functor is symmetric monoidal by Theorem 4.26, which also shows that the second map is lax symmetric monoidal as the right adjoint of the symmetric monoidal functor ![]() $L^{\mathrm {seg}}$. The third and fourth maps are post-composition with the lax symmetric monoidal functors
$L^{\mathrm {seg}}$. The third and fourth maps are post-composition with the lax symmetric monoidal functors ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ and
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to \mathrm {Cat}^{\mathrm {st}}$ and ![]() $\mathrm {K}$, which are therefore also lax symmetric monoidal by Proposition 3.3.
$\mathrm {K}$, which are therefore also lax symmetric monoidal by Proposition 3.3.
Theorem 6.18 The functor ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is lax symmetric monoidal.
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is lax symmetric monoidal.
Proof. Recall from Corollary 6.10 that ![]() $\mathrm {K}^{[m]} \cong L^{\mathrm {seg}} \mathrm {K}_{[m]}$. Proposition 6.17 shows that
$\mathrm {K}^{[m]} \cong L^{\mathrm {seg}} \mathrm {K}_{[m]}$. Proposition 6.17 shows that ![]() $\mathrm {K}_{[m]}$ is lax symmetric monoidal, and
$\mathrm {K}_{[m]}$ is lax symmetric monoidal, and ![]() $L^{\mathrm {seg}}$ is symmetric monoidal by Theorem 4.26.
$L^{\mathrm {seg}}$ is symmetric monoidal by Theorem 4.26.
By construction, the lax symmetric monoidal structure on ![]() $\mathrm {K}^{[m]}$ is compatible with that of
$\mathrm {K}^{[m]}$ is compatible with that of ![]() $\mathrm {K}_{[m]}$, so we immediately obtain the following.
$\mathrm {K}_{[m]}$, so we immediately obtain the following.
Corollary 6.19 The natural transformations ![]() $\mathrm {K} \to \underline {\mathrm {K}^{[m]}}$ and
$\mathrm {K} \to \underline {\mathrm {K}^{[m]}}$ and ![]() $L_{\mathrm {T}(n)} \mathrm {K} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ from Corollary 6.11 and Corollary 6.15 (respectively) are symmetric monoidal.
$L_{\mathrm {T}(n)} \mathrm {K} \to L_{\mathrm {T}(n)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}$ from Corollary 6.11 and Corollary 6.15 (respectively) are symmetric monoidal.
Recall from Theorem 2.50 that there is a lax symmetric monoidal functor ![]() $\mathrm {LMod}_{(-)}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^\mathrm {iL}$. In addition, Proposition 4.15 gives a lax symmetric monoidal functor
$\mathrm {LMod}_{(-)}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^\mathrm {iL}$. In addition, Proposition 4.15 gives a lax symmetric monoidal functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. Composing all of the above we arrive at the following definition.
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. Composing all of the above we arrive at the following definition.
Definition 6.20 We define the lax symmetric monoidal functor ![]() $\mathrm {K}^{[m]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to {{\unicode{x05E6}}} ^{[m]}$ by
$\mathrm {K}^{[m]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to {{\unicode{x05E6}}} ^{[m]}$ by ![]() ${\mathrm {K}^{[m]}}(R) = \mathrm {K}^{[m]}(\mathrm {LMod}_R^{\mathrm {at}})$, i.e. the composition
${\mathrm {K}^{[m]}}(R) = \mathrm {K}^{[m]}(\mathrm {LMod}_R^{\mathrm {at}})$, i.e. the composition
Remark 6.21 Recall from Proposition 2.54 that the atomics coincide with the left dualizable modules, therefore ![]() $\mathrm {K}^{[m]}(R) = \mathrm {K}^{[m]}(\mathrm {LMod}_R^{\mathrm {ldbl}})$.
$\mathrm {K}^{[m]}(R) = \mathrm {K}^{[m]}(\mathrm {LMod}_R^{\mathrm {ldbl}})$.
Remark 6.22 Note that if ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$ and
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$ and ![]() $m \geq n$, then since
$m \geq n$, then since ![]() $\mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization of
$\mathrm {Sp}_{\mathrm {T}(n)}$ is a smashing localization of ![]() ${{\unicode{x05E6}}} ^{[m]}$ by Lemma 6.12, we know that
${{\unicode{x05E6}}} ^{[m]}$ by Lemma 6.12, we know that ![]() $\mathrm {LMod}_R({{\unicode{x05E6}}} ^{[m]}) \cong \mathrm {LMod}_R(\mathrm {Sp}_{\mathrm {T}(n)})$, and the atomics are the left dualizable objects. Therefore, we get that
$\mathrm {LMod}_R({{\unicode{x05E6}}} ^{[m]}) \cong \mathrm {LMod}_R(\mathrm {Sp}_{\mathrm {T}(n)})$, and the atomics are the left dualizable objects. Therefore, we get that ![]() $\mathrm {K}^{[m]}(R) \cong \mathrm {K}^{[m]}(\mathrm {LMod}_R(\mathrm {Sp}_{\mathrm {T}(n)})^\mathrm {ldbl})$.
$\mathrm {K}^{[m]}(R) \cong \mathrm {K}^{[m]}(\mathrm {LMod}_R(\mathrm {Sp}_{\mathrm {T}(n)})^\mathrm {ldbl})$.
Remark 6.23 As ![]() $\mathrm {K}^{[m]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to {{\unicode{x05E6}}} ^{[m]}$ is lax symmetric monoidal, we conclude that it sends
$\mathrm {K}^{[m]}\colon \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}) \to {{\unicode{x05E6}}} ^{[m]}$ is lax symmetric monoidal, we conclude that it sends ![]() $\mathcal {O} \otimes \mathbb {E}_1$-algebras in
$\mathcal {O} \otimes \mathbb {E}_1$-algebras in ![]() ${{\unicode{x05E6}}} ^{[m]}$ to
${{\unicode{x05E6}}} ^{[m]}$ to ![]() $\mathcal {O}$-algebras in
$\mathcal {O}$-algebras in ![]() ${{\unicode{x05E6}}} ^{[m]}$ for any operad
${{\unicode{x05E6}}} ^{[m]}$ for any operad ![]() $\mathcal {O}$. In particular, for the case
$\mathcal {O}$. In particular, for the case ![]() $\mathcal {O} = \mathbb {E}_n$, we get that
$\mathcal {O} = \mathbb {E}_n$, we get that ![]() $\mathrm {K}^{[m]}$ sends
$\mathrm {K}^{[m]}$ sends ![]() $\mathbb {E}_{n+1}$-algebras to
$\mathbb {E}_{n+1}$-algebras to ![]() $\mathbb {E}_n$-algebras, and for
$\mathbb {E}_n$-algebras, and for ![]() $\mathcal {O} = \mathbb {E}_\infty$ we get
$\mathcal {O} = \mathbb {E}_\infty$ we get ![]() $\mathrm {K}^{[m]}\colon \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]}) \to \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]})$. As in Remark 2.55, in this case
$\mathrm {K}^{[m]}\colon \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]}) \to \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]})$. As in Remark 2.55, in this case ![]() $\mathrm {K}^{[m]}(R) = \mathrm {K}^{[m]}(\mathrm {Mod}_R^\mathrm {dbl})$.
$\mathrm {K}^{[m]}(R) = \mathrm {K}^{[m]}(\mathrm {Mod}_R^\mathrm {dbl})$.
7. Redshift
Recall that the redshift philosophy predicts that algebraic K-theory increases height by ![]() $1$. In this section we prove some results concerning the interplay between semiadditive height and higher semiadditive algebraic K-theory.
$1$. In this section we prove some results concerning the interplay between semiadditive height and higher semiadditive algebraic K-theory.
An immediate application of the redshift result of [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem B], gives an upper bound, showing that if ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]})$ has semiadditive height
$R \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]})$ has semiadditive height ![]() $\leq n$ for some finite
$\leq n$ for some finite ![]() $n < m$, then
$n < m$, then ![]() $\mathrm {K}^{[m]}(R)$ has semiadditive height
$\mathrm {K}^{[m]}(R)$ has semiadditive height ![]() $\leq n+1$ (see Theorem 7.12). Furthermore, in Theorem 7.25 we show that if
$\leq n+1$ (see Theorem 7.12). Furthermore, in Theorem 7.25 we show that if ![]() $R$ has semiadditive height exactly
$R$ has semiadditive height exactly ![]() $n$, and has (height
$n$, and has (height ![]() $n$)
$n$) ![]() $p$th roots of unity (see Definition 7.17), then
$p$th roots of unity (see Definition 7.17), then ![]() $\mathrm {K}^{[m]}(R)$ has semiadditive height exactly
$\mathrm {K}^{[m]}(R)$ has semiadditive height exactly ![]() $n+1$, i.e. lands in
$n+1$, i.e. lands in ![]() ${{\unicode{x05E6}}} _{n+1}$. In particular, the Lubin–Tate spectrum
${{\unicode{x05E6}}} _{n+1}$. In particular, the Lubin–Tate spectrum ![]() $\mathrm {E}_n$ has this property, so we conclude that
$\mathrm {E}_n$ has this property, so we conclude that ![]() $\mathrm {K}^{[m]}(\mathrm {E}_n) \in {{\unicode{x05E6}}} _{n+1}$ (see Corollary 7.26).
$\mathrm {K}^{[m]}(\mathrm {E}_n) \in {{\unicode{x05E6}}} _{n+1}$ (see Corollary 7.26).
7.1 Semiadditive height
We begin by recalling the notion of (semiadditive) height from [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 3.1.6] and making a few observations which will be used to study the interaction between height and semiadditive algebraic K-theory. We recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 3.1.3] that for every ![]() $m$-semiadditive category
$m$-semiadditive category ![]() $\mathcal {D}$, and finite
$\mathcal {D}$, and finite ![]() $n \leq m$, there is a natural transformation of the identity
$n \leq m$, there is a natural transformation of the identity ![]() $p_{(n)}\colon \mathrm {id}_\mathcal {D} \Rightarrow \mathrm {id}_\mathcal {D}$, also denoted by
$p_{(n)}\colon \mathrm {id}_\mathcal {D} \Rightarrow \mathrm {id}_\mathcal {D}$, also denoted by ![]() $|\mathrm {B}^n C_p|$, which is given on an object
$|\mathrm {B}^n C_p|$, which is given on an object ![]() $Y \in \mathcal {D}$ by
$Y \in \mathcal {D}$ by
using the fact that the norm map is an equivalence. Alternatively, as ![]() $\mathcal {D}$ is
$\mathcal {D}$ is ![]() $m$-semiadditive, its objects have a canonical
$m$-semiadditive, its objects have a canonical ![]() $m$-commutative monoid structure in
$m$-commutative monoid structure in ![]() $\mathcal {D}$, so that the map is given by
$\mathcal {D}$, so that the map is given by ![]() $q_! q^*$ where
$q_! q^*$ where ![]() $q\colon \mathrm {B}^n C_p \to *$ is the unique map.
$q\colon \mathrm {B}^n C_p \to *$ is the unique map.
Definition 7.1 [Reference Carmeli, Schlank and YanovskiCSY21a, Definition 3.1.6]
Let ![]() $Y \in \mathcal {D}$, then its semiadditive height is defined as follows:
$Y \in \mathcal {D}$, then its semiadditive height is defined as follows:
(1)
 $\mathrm {ht}(Y) \leq n$ if
$\mathrm {ht}(Y) \leq n$ if  $p_{(n)}\colon Y \to Y$ is invertible;
$p_{(n)}\colon Y \to Y$ is invertible;(2)
 $\mathrm {ht}(Y) > n$ if
$\mathrm {ht}(Y) > n$ if  $Y$ is
$Y$ is  $p_{(n)}$-complete (i.e. for every
$p_{(n)}$-complete (i.e. for every  $Z \in \mathcal {D}$ with
$Z \in \mathcal {D}$ with  $p_{(n)}\colon Z \to Z$ invertible,
$p_{(n)}\colon Z \to Z$ invertible,  $\hom (Z, Y) = *$);
$\hom (Z, Y) = *$);(3)
 $\mathrm {ht}(Y) = n$ if
$\mathrm {ht}(Y) = n$ if  $\mathrm {ht}(Y) \leq n$ and
$\mathrm {ht}(Y) \leq n$ and  $\mathrm {ht}(Y) > n-1$.
$\mathrm {ht}(Y) > n-1$.
We denote by ![]() $\mathcal {D}_{\leq n}$ the full subcategory of objects
$\mathcal {D}_{\leq n}$ the full subcategory of objects ![]() $Y \in \mathcal {D}$ with
$Y \in \mathcal {D}$ with ![]() $\mathrm {ht}(Y) \leq n$, and similarly
$\mathrm {ht}(Y) \leq n$, and similarly ![]() $\mathcal {D}_{>n}$ for objects of height
$\mathcal {D}_{>n}$ for objects of height ![]() $> n$ and
$> n$ and ![]() $\mathcal {D}_n$ for object of height exactly
$\mathcal {D}_n$ for object of height exactly ![]() $n$.
$n$.
Proposition 7.2 [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem A]
Let ![]() $\mathcal {D}$ be an
$\mathcal {D}$ be an ![]() $m$-semiadditive category which admits all limits and colimits indexed by
$m$-semiadditive category which admits all limits and colimits indexed by ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces, and let
$p$-spaces, and let ![]() $n \leq m$ be a finite number, then
$n \leq m$ be a finite number, then ![]() $\mathcal {D}_{\leq n}$ is
$\mathcal {D}_{\leq n}$ is ![]() $\infty$-semiadditive.
$\infty$-semiadditive.
Proposition 7.3 [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 3.1.13]
Let ![]() $F\colon \mathcal {D} \to \mathcal {E}$ be an
$F\colon \mathcal {D} \to \mathcal {E}$ be an ![]() $m$-semiadditive functor, between
$m$-semiadditive functor, between ![]() $m$-semiadditive categories, and let
$m$-semiadditive categories, and let ![]() $n \leq m$ be a finite number. Then
$n \leq m$ be a finite number. Then ![]() $F$ sends
$F$ sends ![]() $p_{(n)}$ of
$p_{(n)}$ of ![]() $\mathcal {D}$ to
$\mathcal {D}$ to ![]() $p_{(n)}$ of
$p_{(n)}$ of ![]() $\mathcal {E}$. In particular, if
$\mathcal {E}$. In particular, if ![]() $\mathrm {ht}(Y) \leq n$, then
$\mathrm {ht}(Y) \leq n$, then ![]() $\mathrm {ht}(FY) \leq n$, that is, it induces a functor
$\mathrm {ht}(FY) \leq n$, that is, it induces a functor ![]() $F\colon \mathcal {D}_{\leq n} \to \mathcal {E}_{\leq n}$.
$F\colon \mathcal {D}_{\leq n} \to \mathcal {E}_{\leq n}$.
Corollary 7.4 Let ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {E}$ be
$\mathcal {E}$ be ![]() $m$-semiadditive categories,
$m$-semiadditive categories, ![]() $F\colon \mathcal {D} \rightleftarrows \mathcal {E} \colon G$ an adjunction, and
$F\colon \mathcal {D} \rightleftarrows \mathcal {E} \colon G$ an adjunction, and ![]() $n \leq m$ a finite number. Then the adjunction restricts to an adjunction
$n \leq m$ a finite number. Then the adjunction restricts to an adjunction ![]() $F\colon \mathcal {D}_{\leq n} \rightleftarrows \mathcal {E}_{\leq n} \colon G$. Furthermore, if
$F\colon \mathcal {D}_{\leq n} \rightleftarrows \mathcal {E}_{\leq n} \colon G$. Furthermore, if ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {E}$ admit all limits and colimits indexed by
$\mathcal {E}$ admit all limits and colimits indexed by ![]() $\pi$-finite
$\pi$-finite ![]() $p$-spaces, then the restricted functors are
$p$-spaces, then the restricted functors are ![]() $\infty$-semiadditive.
$\infty$-semiadditive.
Proof. Since ![]() $G$ and
$G$ and ![]() $F$ preserves limits and colimits respectively, they are
$F$ preserves limits and colimits respectively, they are ![]() $m$-semiadditive. By Proposition 7.3, their restrictions to objects of height
$m$-semiadditive. By Proposition 7.3, their restrictions to objects of height ![]() $\leq n$ land in objects of height
$\leq n$ land in objects of height ![]() $\leq n$. Since by Proposition 7.2
$\leq n$. Since by Proposition 7.2 ![]() $\mathcal {D}_{\leq n}$ and
$\mathcal {D}_{\leq n}$ and ![]() $\mathcal {E}_{\leq n}$ are
$\mathcal {E}_{\leq n}$ are ![]() $\infty$-semiadditive, and the restricted functors preserve limits or colimits, they are in fact
$\infty$-semiadditive, and the restricted functors preserve limits or colimits, they are in fact ![]() $\infty$-semiadditive.
$\infty$-semiadditive.
Proposition 7.5 Let ![]() $n \leq m$ be a finite number, then the mode
$n \leq m$ be a finite number, then the mode ![]() ${{\unicode{x05E6}}} ^{[m]}_{\leq n} \cong {{\unicode{x05E6}}} _{\leq n}$ is independent of
${{\unicode{x05E6}}} ^{[m]}_{\leq n} \cong {{\unicode{x05E6}}} _{\leq n}$ is independent of ![]() $m$, and is the mode classifying the property of being stable
$m$, and is the mode classifying the property of being stable ![]() $p$-local
$p$-local ![]() $\infty$-semiadditive and having all objects of height
$\infty$-semiadditive and having all objects of height ![]() $\leq n$. Furthermore, it decomposes as a product
$\leq n$. Furthermore, it decomposes as a product
where ![]() ${{\unicode{x05E6}}} _k$ is the mode classifying the property of being stable
${{\unicode{x05E6}}} _k$ is the mode classifying the property of being stable ![]() $p$-local
$p$-local ![]() $\infty$-semiadditive and having all objects of height exactly
$\infty$-semiadditive and having all objects of height exactly ![]() $n$.
$n$.
Proof. If ![]() $n < m$, then this follows immediately from [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7 and Theorem 5.3.6]. If
$n < m$, then this follows immediately from [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7 and Theorem 5.3.6]. If ![]() $n = m$, then the same results show that
$n = m$, then the same results show that
By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 4.2.1], ![]() ${{\unicode{x05E6}}} ^{[m]}_{>n-1}$ is a recollement of
${{\unicode{x05E6}}} ^{[m]}_{>n-1}$ is a recollement of ![]() ${{\unicode{x05E6}}} _n$ and
${{\unicode{x05E6}}} _n$ and ![]() ${{\unicode{x05E6}}} ^{[m]}_{> n}$, but
${{\unicode{x05E6}}} ^{[m]}_{> n}$, but ![]() $({{\unicode{x05E6}}} ^{[m]}_{> n})_{\leq n} = 0$, so the result follows upon taking objects of height
$({{\unicode{x05E6}}} ^{[m]}_{> n})_{\leq n} = 0$, so the result follows upon taking objects of height ![]() $\leq n$.
$\leq n$.
Consider the case ![]() $\mathcal {D} = \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. In this case, the objects are themselves categories
$\mathcal {D} = \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. In this case, the objects are themselves categories ![]() $\mathcal {C} \in \mathcal {D}$ on which
$\mathcal {C} \in \mathcal {D}$ on which ![]() $p_{(n)}$ acts, and can have heights
$p_{(n)}$ acts, and can have heights ![]() $\mathrm {ht}(\mathcal {C})$ as objects of
$\mathrm {ht}(\mathcal {C})$ as objects of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
Proposition 7.6 Let ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. For any
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$. For any ![]() $m$-finite
$m$-finite ![]() $p$-space
$p$-space ![]() $A$, the map
$A$, the map ![]() $|A|\colon \mathcal {C} \to \mathcal {C}$ is given by
$|A|\colon \mathcal {C} \to \mathcal {C}$ is given by ![]() $|A|(X) \cong \operatorname *{colim}_A X$. In particular,
$|A|(X) \cong \operatorname *{colim}_A X$. In particular, ![]() $p_{(n)}(X) \cong \operatorname *{colim}_{\mathrm {B}^n C_p} X$.
$p_{(n)}(X) \cong \operatorname *{colim}_{\mathrm {B}^n C_p} X$.
Proof. Recall that if we consider the objects of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ as equipped with the canonical
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ as equipped with the canonical ![]() $\mathrm {CMon}_m^{(p)}{({})}$ structure, then
$\mathrm {CMon}_m^{(p)}{({})}$ structure, then ![]() $p_{(n)} \cong q_! q^*$ where
$p_{(n)} \cong q_! q^*$ where ![]() $q\colon A \to *$ is the unique map. Theorems 5.3 and 5.6 then show that
$q\colon A \to *$ is the unique map. Theorems 5.3 and 5.6 then show that ![]() $q^*\colon \mathcal {C} \to \mathcal {C}^A$ is taking the constant diagram and that
$q^*\colon \mathcal {C} \to \mathcal {C}^A$ is taking the constant diagram and that ![]() $q_!\colon \mathcal {C}^A \to \mathcal {C}$ is computing the colimit.
$q_!\colon \mathcal {C}^A \to \mathcal {C}$ is computing the colimit.
7.2 Upper bound
Proposition 7.7 Let ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ and assume that
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ and assume that ![]() $\mathrm {ht}(\mathcal {C}) \leq n$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite ![]() $n \leq m$, then
$n \leq m$, then ![]() $\mathrm {ht}(\mathrm {K}^{[m]}(\mathcal {C})) \leq n$. That is,
$\mathrm {ht}(\mathrm {K}^{[m]}(\mathcal {C})) \leq n$. That is, ![]() $\mathrm {K}^{[m]}$ restricts to a functor
$\mathrm {K}^{[m]}$ restricts to a functor ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$.
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$.
Proof. We have that ![]() $\mathrm {K}^{[m]}$ is
$\mathrm {K}^{[m]}$ is ![]() $m$-semiadditive by Proposition 6.7, so the result follows from Proposition 7.3.
$m$-semiadditive by Proposition 6.7, so the result follows from Proposition 7.3.
By Proposition 7.2, ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ and
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ and ![]() ${{\unicode{x05E6}}} _{\leq n}$ are
${{\unicode{x05E6}}} _{\leq n}$ are ![]() $\infty$-semiadditive.
$\infty$-semiadditive.
Proposition 7.8 We have that ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is ![]() $\infty$-semiadditive. Furthermore, let
$\infty$-semiadditive. Furthermore, let ![]() $n \leq m_0 \leq m$ with
$n \leq m_0 \leq m$ with ![]() $n$ a finite number, then
$n$ a finite number, then ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ and the restriction of
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ and the restriction of ![]() $\mathrm {K}^{[m_0]}$ to the (not full) subcategory
$\mathrm {K}^{[m_0]}$ to the (not full) subcategory ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ coincide.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ coincide.
Proof. By construction, ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is a composition of left and right adjoints between
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}} \to {{\unicode{x05E6}}} ^{[m]}$ is a composition of left and right adjoints between ![]() $m$-semiadditive categories (as used in the proof of Proposition 6.7), all of which admit all limits and colimits (as all categories are presentable). By Corollary 7.4,
$m$-semiadditive categories (as used in the proof of Proposition 6.7), all of which admit all limits and colimits (as all categories are presentable). By Corollary 7.4, ![]() $\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is the composition the adjoints restricted to objects of height
$\mathrm {K}^{[m]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is the composition the adjoints restricted to objects of height ![]() $\leq n$, which are
$\leq n$, which are ![]() $\infty$-semiadditive functors.
$\infty$-semiadditive functors.
For the second part, note that ![]() $\mathrm {K}^{[m_0]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is also
$\mathrm {K}^{[m_0]}\colon \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n} \to {{\unicode{x05E6}}} _{\leq n}$ is also ![]() $\infty$-semiadditive and, in particular,
$\infty$-semiadditive and, in particular, ![]() $m$-semiadditive. Recall from Theorem 6.9 that there is an equivalence
$m$-semiadditive. Recall from Theorem 6.9 that there is an equivalence ![]() $L^{\mathrm {seg}} \mathrm {K}^{[m_0]}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$, so when
$L^{\mathrm {seg}} \mathrm {K}^{[m_0]}_{[m]} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {K}^{[m]}$, so when ![]() $\mathrm {K}^{[m_0]}_{[m]}$ is restricted to
$\mathrm {K}^{[m_0]}_{[m]}$ is restricted to ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ it already satisfies the
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin},\leq n}$ it already satisfies the ![]() $m$-Segal condition and is, thus, equivalent to
$m$-Segal condition and is, thus, equivalent to ![]() $\mathrm {K}^{[m]}$.
$\mathrm {K}^{[m]}$.
We recall the following redshift result, which we view as the step along the construction at which redshift happens.
Theorem 7.9 (Semiadditive redshift [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem B])
Let ![]() $\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ be an
$\mathcal {C} \in \mathrm {Cat}_{m\text {-}\mathrm {fin}}$ be an ![]() $m$-semiadditive category and let
$m$-semiadditive category and let ![]() $n < m$ be a finite number. Then,
$n < m$ be a finite number. Then, ![]() $\mathrm {ht}(X) \leq n$ for all
$\mathrm {ht}(X) \leq n$ for all ![]() $X \in \mathcal {C}$ if and only if
$X \in \mathcal {C}$ if and only if ![]() $\mathrm {ht}(\mathcal {C}) \leq n + 1$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n + 1$ as an object of ![]() $\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}_{m\text {-}\mathrm {fin}}$.
Corollary 7.10 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}} \subset \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}$ for some finite number
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}} \subset \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}$ for some finite number ![]() $n < m$, then
$n < m$, then ![]() $\mathcal {C}^{\mathrm {at}} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is an
$\mathcal {C}^{\mathrm {at}} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is an ![]() $m$-semiadditive category and has
$m$-semiadditive category and has ![]() $\mathrm {ht}(\mathcal {C}^{\mathrm {at}}) \leq n+1$ as an object of
$\mathrm {ht}(\mathcal {C}^{\mathrm {at}}) \leq n+1$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
Proof. It is in ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ and
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ and ![]() $m$-semiadditive by Proposition 4.15. By Proposition 7.5,
$m$-semiadditive by Proposition 4.15. By Proposition 7.5, ![]() ${{\unicode{x05E6}}} _{\leq n}$ classifies the property of having all objects of height
${{\unicode{x05E6}}} _{\leq n}$ classifies the property of having all objects of height ![]() $\leq n$, so together with Theorem 7.9, this implies that
$\leq n$, so together with Theorem 7.9, this implies that ![]() $\mathrm {ht}(\mathcal {C}^{\mathrm {at}}) \leq n+1$ as an object of
$\mathrm {ht}(\mathcal {C}^{\mathrm {at}}) \leq n+1$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$.
Remark 7.11 The mode ![]() ${{\unicode{x05E6}}} _{\leq n}$ is a smashing localization of
${{\unicode{x05E6}}} _{\leq n}$ is a smashing localization of ![]() ${{\unicode{x05E6}}} ^{[m]}$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7]. By Proposition 2.26 we get that atomics in
${{\unicode{x05E6}}} ^{[m]}$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7]. By Proposition 2.26 we get that atomics in ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$ with respect to either mode coincide. In addition, for
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$ with respect to either mode coincide. In addition, for ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _{\leq n})$ left modules over
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _{\leq n})$ left modules over ![]() $R$ in either mode agree.
$R$ in either mode agree.
Theorem 7.12 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}} \subset \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}$ for some finite number
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}} \subset \mathrm {Mod}_{{{\unicode{x05E6}}} ^{[m]}}$ for some finite number ![]() $n < m$, then
$n < m$, then ![]() $\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{\leq n+1}$. In particular, if
$\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{\leq n+1}$. In particular, if ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _{\leq n})$, then
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _{\leq n})$, then ![]() $\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} _{\leq n+1}$.
$\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} _{\leq n+1}$.
Proposition 7.7 shows that ![]() $p_{n}\colon \mathrm {K}^{[m]}(\mathcal {C}) \to \mathrm {K}^{[m]}(\mathcal {C})$ is invertible, but in fact we can prove the following stronger result if we assume that
$p_{n}\colon \mathrm {K}^{[m]}(\mathcal {C}) \to \mathrm {K}^{[m]}(\mathcal {C})$ is invertible, but in fact we can prove the following stronger result if we assume that ![]() $\mathcal {C}$ is
$\mathcal {C}$ is ![]() $m$-semiadditive. Note that as we know now that
$m$-semiadditive. Note that as we know now that ![]() $\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{\leq n}$, it is an object of an
$\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{\leq n}$, it is an object of an ![]() $\infty$-semiadditive category, so that
$\infty$-semiadditive category, so that ![]() $p_{(k)}$ is defined for all
$p_{(k)}$ is defined for all ![]() $k$.
$k$.
Proposition 7.13 Let ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ be an
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ be an ![]() $m$-semiadditive category with
$m$-semiadditive category with ![]() $\mathrm {ht}(\mathcal {C}) \leq n+1$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n+1$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite ![]() $n < m$. Then
$n < m$. Then ![]() $p_{(k)}\colon \mathrm {K}^{[m]}(\mathcal {C}) \to \mathrm {K}^{[m]}(\mathcal {C})$ is the identity for every
$p_{(k)}\colon \mathrm {K}^{[m]}(\mathcal {C}) \to \mathrm {K}^{[m]}(\mathcal {C})$ is the identity for every ![]() $k \geq n+1$. In particular, for
$k \geq n+1$. In particular, for ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$, the map
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$, the map ![]() $p_{(k)}\colon \mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \to \mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}})$ is the identity for every
$p_{(k)}\colon \mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \to \mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}})$ is the identity for every ![]() $k \geq n+1$.
$k \geq n+1$.
Proof. Recall from Theorem 7.9 that for every ![]() $X \in \mathcal {C}$ we have
$X \in \mathcal {C}$ we have ![]() $\mathrm {ht}(X) \leq n$, i.e.
$\mathrm {ht}(X) \leq n$, i.e. ![]() $|\mathrm {B}^n C_p|\colon X \to X$ is invertible. Applying [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7(1)] to the case
$|\mathrm {B}^n C_p|\colon X \to X$ is invertible. Applying [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7(1)] to the case ![]() $A = \mathrm {B}^{n+1} C_p$ shows that
$A = \mathrm {B}^{n+1} C_p$ shows that ![]() $\operatorname *{colim}_{\mathrm {B}^{n+1} C_p} X \xrightarrow {\nabla } X$ is an equivalence. By Proposition 7.6,
$\operatorname *{colim}_{\mathrm {B}^{n+1} C_p} X \xrightarrow {\nabla } X$ is an equivalence. By Proposition 7.6, ![]() $p_{(n+1)}\colon \mathcal {C} \to \mathcal {C}$ is given by
$p_{(n+1)}\colon \mathcal {C} \to \mathcal {C}$ is given by ![]() $p_{(n+1)}(X) \cong \operatorname *{colim}_{\mathrm {B}^{n+1} C_p} X$, which by the above is
$p_{(n+1)}(X) \cong \operatorname *{colim}_{\mathrm {B}^{n+1} C_p} X$, which by the above is ![]() $X$ itself, i.e.
$X$ itself, i.e. ![]() $p_{(n+1)}$ is the identity. By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7], if
$p_{(n+1)}$ is the identity. By [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7], if ![]() $p_{(k)}$ is invertible, then
$p_{(k)}$ is invertible, then ![]() $p_{(k+1)}$ is also invertible and is its inverse, finishing by induction. For the second part apply Corollary 7.10.
$p_{(k+1)}$ is also invertible and is its inverse, finishing by induction. For the second part apply Corollary 7.10.
7.3 Lower bound
Proposition 7.14 Let ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ be an
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ be an ![]() $m$-semiadditive category with
$m$-semiadditive category with ![]() $\mathrm {ht}(\mathcal {C}) \leq n+1$ as an object of
$\mathrm {ht}(\mathcal {C}) \leq n+1$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ for some finite ![]() $n < m$. Then
$n < m$. Then ![]() $\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$. In particular, for
$\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$. In particular, for ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$ we have that
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _{\leq n}}$ we have that ![]() $\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$.
$\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$.
Proof. Recall from Proposition 7.7 that ![]() $\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{\leq n+1}$, and that
$\mathrm {K}^{[m]}(\mathcal {C}) \in {{\unicode{x05E6}}} _{\leq n+1}$, and that ![]() ${{\unicode{x05E6}}} _{\leq n+1}$ is
${{\unicode{x05E6}}} _{\leq n+1}$ is ![]() $\infty$-semiadditive. We thus need to show that
$\infty$-semiadditive. We thus need to show that ![]() $L_0 \mathrm {K}^{[m]}(\mathcal {C}) = 0$ where
$L_0 \mathrm {K}^{[m]}(\mathcal {C}) = 0$ where ![]() $L_0\colon {{\unicode{x05E6}}} _{\leq n+1} \to {{\unicode{x05E6}}} _0$ is the projection. By Proposition 7.3, the map
$L_0\colon {{\unicode{x05E6}}} _{\leq n+1} \to {{\unicode{x05E6}}} _0$ is the projection. By Proposition 7.3, the map ![]() $L_0$ preserves
$L_0$ preserves ![]() $p_{(k)}$, so by Proposition 7.13 we know that
$p_{(k)}$, so by Proposition 7.13 we know that ![]() $p_{(k)}$ acts as the identity on
$p_{(k)}$ acts as the identity on ![]() $L_0 \mathrm {K}^{[m]}(\mathcal {C})$ for every
$L_0 \mathrm {K}^{[m]}(\mathcal {C})$ for every ![]() $k \geq n+1$. Since
$k \geq n+1$. Since ![]() $L_0 \mathrm {K}^{[m]}(\mathcal {C})$ is of height
$L_0 \mathrm {K}^{[m]}(\mathcal {C})$ is of height ![]() $\leq 0$, it is
$\leq 0$, it is ![]() $p_{(0)} = p$-invertible, and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7] then shows inductively that
$p_{(0)} = p$-invertible, and [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.4.7] then shows inductively that ![]() $p_{(2k)} \cong p$ for any
$p_{(2k)} \cong p$ for any ![]() $k \geq 0$. Choose some
$k \geq 0$. Choose some ![]() $k$ such that
$k$ such that ![]() $2k \geq n+1$, then we get that
$2k \geq n+1$, then we get that ![]() $p \cong p_{(2k)} \cong 1$, so that
$p \cong p_{(2k)} \cong 1$, so that ![]() $p - 1$ is the zero morphism on
$p - 1$ is the zero morphism on ![]() $L_0 \mathrm {K}^{[m]}(\mathcal {C})$. However, since
$L_0 \mathrm {K}^{[m]}(\mathcal {C})$. However, since ![]() ${{\unicode{x05E6}}} _0$ is
${{\unicode{x05E6}}} _0$ is ![]() $p$-local, this morphism is invertible, thus
$p$-local, this morphism is invertible, thus ![]() $L_0 \mathrm {K}^{[m]}(\mathcal {C}) = 0$. For the second part apply Corollary 7.10.
$L_0 \mathrm {K}^{[m]}(\mathcal {C}) = 0$. For the second part apply Corollary 7.10.
Let ![]() $\mathbf {1}$ be the unit of
$\mathbf {1}$ be the unit of ![]() ${{\unicode{x05E6}}} _n$, and consider
${{\unicode{x05E6}}} _n$, and consider ![]() $\mathbf {1}[\mathrm {B}^n C_p] = \operatorname *{colim}_{\mathrm {B}^n C_p} \mathbf {1} \in \operatorname {CAlg}({{\unicode{x05E6}}} _n)$ (which carries an action of
$\mathbf {1}[\mathrm {B}^n C_p] = \operatorname *{colim}_{\mathrm {B}^n C_p} \mathbf {1} \in \operatorname {CAlg}({{\unicode{x05E6}}} _n)$ (which carries an action of ![]() $(\mathbb {Z}/p)^\times \cong \operatorname {Aut}(C_p)$). We then have the following result.
$(\mathbb {Z}/p)^\times \cong \operatorname {Aut}(C_p)$). We then have the following result.
Proposition 7.15 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$, then
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$, then ![]() $p_{(n)}\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$ is given by
$p_{(n)}\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$ is given by ![]() $\mathbf {1}[\mathrm {B}^n C_p] \otimes -$.
$\mathbf {1}[\mathrm {B}^n C_p] \otimes -$.
Proof. Recall that the action of ![]() ${{\unicode{x05E6}}} _n$ on
${{\unicode{x05E6}}} _n$ on ![]() $\mathcal {C}$ commutes with colimits. Then, by Proposition 7.6,
$\mathcal {C}$ commutes with colimits. Then, by Proposition 7.6,
Motivated by this result, we further study the action of ![]() $\mathbf {1}[\mathrm {B}^n C_p]$. To that end, we recall the following.
$\mathbf {1}[\mathrm {B}^n C_p]$. To that end, we recall the following.
Definition 7.16 [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 4.5 and Definition 4.7]
The ring ![]() $\mathbf {1}[\mathrm {B}^n C_p]$ splits (
$\mathbf {1}[\mathrm {B}^n C_p]$ splits (![]() $(\mathbb {Z}/p)^\times$-equivariantly) as a product in
$(\mathbb {Z}/p)^\times$-equivariantly) as a product in ![]() $\operatorname {CAlg}({{\unicode{x05E6}}} _n)$
$\operatorname {CAlg}({{\unicode{x05E6}}} _n)$
where ![]() $\mathbf {1}[\omega ^{(n)}_p] \in \operatorname {CAlg}({{\unicode{x05E6}}} _n)$ is called the (height
$\mathbf {1}[\omega ^{(n)}_p] \in \operatorname {CAlg}({{\unicode{x05E6}}} _n)$ is called the (height ![]() $n$)
$n$) ![]() $p$th cyclotomic extension of
$p$th cyclotomic extension of ![]() $\mathbf {1}$. For any
$\mathbf {1}$. For any ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$, we define the
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$, we define the ![]() $R$-algebra
$R$-algebra ![]() $R[\omega ^{(n)}_p] = \mathbf {1}[\omega ^{(n)}_p] \otimes R$.
$R[\omega ^{(n)}_p] = \mathbf {1}[\omega ^{(n)}_p] \otimes R$.
Definition 7.17 We say that a category ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ has (height
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity if
$p$th roots of unity if ![]() $\mathbf {1}[\omega ^{(n)}_p] \otimes -$ is equivalent to
$\mathbf {1}[\omega ^{(n)}_p] \otimes -$ is equivalent to ![]() $\prod _{(\mathbb {Z}/p)^\times } -$ as functors
$\prod _{(\mathbb {Z}/p)^\times } -$ as functors ![]() $\mathcal {C} \to \mathcal {C}$. Similarly, we say that
$\mathcal {C} \to \mathcal {C}$. Similarly, we say that ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ has (height
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity if
$p$th roots of unity if ![]() $R[\omega ^{(n)}_p]$ is equivalent to
$R[\omega ^{(n)}_p]$ is equivalent to ![]() $\prod _{(\mathbb {Z}/p)^\times } R$ as an
$\prod _{(\mathbb {Z}/p)^\times } R$ as an ![]() $R$-algebra.
$R$-algebra.
Remark 7.18 It makes sense to require the equivalence to be ![]() $(\mathbb {Z}/p)^\times$-equivariant, but we will not use this assumption.
$(\mathbb {Z}/p)^\times$-equivariant, but we will not use this assumption.
Remark 7.19 For ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$, it is always true that the (height
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$, it is always true that the (height ![]() $n$)
$n$) ![]() $p$th cyclotomic extension
$p$th cyclotomic extension ![]() $R[\omega ^{(n)}_p]$ has (height
$R[\omega ^{(n)}_p]$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity. Indeed, [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.2] shows that
$p$th roots of unity. Indeed, [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.2] shows that ![]() $R[\omega ^{(n)}_p]$ is a Galois extension of
$R[\omega ^{(n)}_p]$ is a Galois extension of ![]() $R$, which immediately implies the condition of having (height
$R$, which immediately implies the condition of having (height ![]() $n$)
$n$) ![]() $p$th roots of unity. However, it is not true in general for
$p$th roots of unity. However, it is not true in general for ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$, by a counterexample constructed by Allen Yuan.
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$, by a counterexample constructed by Allen Yuan.
Example 7.20 [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.1]
The Lubin–Tate spectrum ![]() $\mathrm {E}_n \in \operatorname {CAlg}(\mathrm {Sp}_{\mathrm {K}(n)})$ has (height
$\mathrm {E}_n \in \operatorname {CAlg}(\mathrm {Sp}_{\mathrm {K}(n)})$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity.
$p$th roots of unity.
Example 7.21 At the prime ![]() $p = 2$, any
$p = 2$, any ![]() $\mathcal {C} = \mathrm {LMod}_R$ for
$\mathcal {C} = \mathrm {LMod}_R$ for ![]() $R \in \mathrm {Sp}_{\mathrm {T}(n)}$, and, more generally,
$R \in \mathrm {Sp}_{\mathrm {T}(n)}$, and, more generally, ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}_{\mathrm {T}(n)}}$, has (height
$\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}_{\mathrm {T}(n)}}$, has (height ![]() $n$)
$n$) ![]() $p$th roots of unity. This is true because [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.2] shows that
$p$th roots of unity. This is true because [Reference Carmeli, Schlank and YanovskiCSY21b, Proposition 5.2] shows that ![]() $\mathbb {S}_{\mathrm {T}(n)}[\omega ^{(n)}_p]$ is a
$\mathbb {S}_{\mathrm {T}(n)}[\omega ^{(n)}_p]$ is a ![]() $(\mathbb {Z}/p)^\times$-Galois extension of
$(\mathbb {Z}/p)^\times$-Galois extension of ![]() $\mathbb {S}_{\mathrm {T}(n)}$. Since
$\mathbb {S}_{\mathrm {T}(n)}$. Since ![]() $p = 2$, it is a Galois extension of order
$p = 2$, it is a Galois extension of order ![]() $p-1=1$, i.e.
$p-1=1$, i.e. ![]() $\mathbb {S}_{\mathrm {T}(n)}[\omega ^{(n)}_p] \cong \mathbb {S}_{\mathrm {T}(n)}$, so the condition is automatic.
$\mathbb {S}_{\mathrm {T}(n)}[\omega ^{(n)}_p] \cong \mathbb {S}_{\mathrm {T}(n)}$, so the condition is automatic.
Lemma 7.22 Let ![]() $\mathcal {C}$ be a monoidal category,
$\mathcal {C}$ be a monoidal category, ![]() $R \in \operatorname {Alg}(\mathcal {C})$ and
$R \in \operatorname {Alg}(\mathcal {C})$ and ![]() $n$ a natural number. Consider
$n$ a natural number. Consider ![]() $R^n$ as an algebra under
$R^n$ as an algebra under ![]() $R$ via the diagonal map
$R$ via the diagonal map ![]() $\Delta \colon R \to R^n$. Then the composition of the extension of scalars and the restriction of scalars
$\Delta \colon R \to R^n$. Then the composition of the extension of scalars and the restriction of scalars ![]() $\mathrm {LMod}_R \xrightarrow {\Delta _!} \mathrm {LMod}_{R^n} \xrightarrow {\Delta ^*} \mathrm {LMod}_R$ is equivalent to the functor
$\mathrm {LMod}_R \xrightarrow {\Delta _!} \mathrm {LMod}_{R^n} \xrightarrow {\Delta ^*} \mathrm {LMod}_R$ is equivalent to the functor ![]() $(-)^n\colon \mathrm {LMod}_R \to \mathrm {LMod}_R$.
$(-)^n\colon \mathrm {LMod}_R \to \mathrm {LMod}_R$.
Proof. Consider the ![]() $i$th projection
$i$th projection ![]() $\pi _i\colon R^n \to R$. The extension of scalars along it gives a functor
$\pi _i\colon R^n \to R$. The extension of scalars along it gives a functor ![]() $\mathrm {LMod}_{R^n} \to \mathrm {LMod}_R$. The
$\mathrm {LMod}_{R^n} \to \mathrm {LMod}_R$. The ![]() $n$ functors together give an equivalence
$n$ functors together give an equivalence ![]() $\mathrm {LMod}_{R^n} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_R^n$. Since
$\mathrm {LMod}_{R^n} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_R^n$. Since ![]() $R \xrightarrow {\Delta } R^n \xrightarrow {\pi _i} R$ is the identity, so are
$R \xrightarrow {\Delta } R^n \xrightarrow {\pi _i} R$ is the identity, so are ![]() $(\pi _i \Delta )_!$ and
$(\pi _i \Delta )_!$ and ![]() $(\pi _i \Delta )^*$. Therefore,
$(\pi _i \Delta )^*$. Therefore, ![]() $\mathrm {LMod}_R \xrightarrow {\Delta _!} \mathrm {LMod}_{R^n} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_R^n$ is the diagonal, and
$\mathrm {LMod}_R \xrightarrow {\Delta _!} \mathrm {LMod}_{R^n} \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_R^n$ is the diagonal, and ![]() $\mathrm {LMod}_R^n \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_{R^n} \to \mathrm {LMod}_R$ is the multiplication of modules, so we conclude that their composition is indeed
$\mathrm {LMod}_R^n \xrightarrow {\smash {{\scriptstyle \sim }}} \mathrm {LMod}_{R^n} \to \mathrm {LMod}_R$ is the multiplication of modules, so we conclude that their composition is indeed ![]() $(-)^n\colon \mathrm {LMod}_R \to \mathrm {LMod}_R$.
$(-)^n\colon \mathrm {LMod}_R \to \mathrm {LMod}_R$.
Proposition 7.23 Let ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ have (height
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ have (height ![]() $n$)
$n$) ![]() $p$th roots of unity, then
$p$th roots of unity, then ![]() $\mathrm {LMod}_R \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ has (height
$\mathrm {LMod}_R \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity.
$p$th roots of unity.
Proof. First note that the map ![]() $\mathbf {1}[\omega ^{(n)}_p] \otimes -\colon {{\unicode{x05E6}}} _n \to {{\unicode{x05E6}}} _n$ is equivalent to the composition of the extension of scalars and restriction of scalars along
$\mathbf {1}[\omega ^{(n)}_p] \otimes -\colon {{\unicode{x05E6}}} _n \to {{\unicode{x05E6}}} _n$ is equivalent to the composition of the extension of scalars and restriction of scalars along ![]() $\mathbf {1} \to \mathbf {1}[\omega ^{(n)}_p]$. Since by definition
$\mathbf {1} \to \mathbf {1}[\omega ^{(n)}_p]$. Since by definition ![]() $R[\omega ^{(n)}_p] = \mathbf {1}[\omega ^{(n)}_p] \otimes R$, we get an
$R[\omega ^{(n)}_p] = \mathbf {1}[\omega ^{(n)}_p] \otimes R$, we get an ![]() $R$-algebra map
$R$-algebra map ![]() $R \to R[\omega ^{(n)}_p]$. Then, the composition of the extension of scalars and restriction of scalars along this map gives a functor
$R \to R[\omega ^{(n)}_p]$. Then, the composition of the extension of scalars and restriction of scalars along this map gives a functor ![]() $\mathrm {LMod}_R \to \mathrm {LMod}_R$, which is equivalent to the action of
$\mathrm {LMod}_R \to \mathrm {LMod}_R$, which is equivalent to the action of ![]() $\mathbf {1}[\omega ^{(n)}_p]$ on
$\mathbf {1}[\omega ^{(n)}_p]$ on ![]() $\mathrm {LMod}_R$. By assumption,
$\mathrm {LMod}_R$. By assumption, ![]() $R[\omega ^{(n)}_p] \cong \prod _{(\mathbb {Z}/p)^\times } R$ as an
$R[\omega ^{(n)}_p] \cong \prod _{(\mathbb {Z}/p)^\times } R$ as an ![]() $R$-algebra, so the previous lemma implies that
$R$-algebra, so the previous lemma implies that ![]() $\mathbf {1}[\omega ^{(n)}_p] \otimes -$ is equivalent to
$\mathbf {1}[\omega ^{(n)}_p] \otimes -$ is equivalent to ![]() $\prod _{(\mathbb {Z}/p)^\times } -$.
$\prod _{(\mathbb {Z}/p)^\times } -$.
Proposition 7.24 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ have (height
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ have (height ![]() $n$)
$n$) ![]() $p$th roots of unity, then
$p$th roots of unity, then ![]() $p_{(n)}\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$ is equivalent to
$p_{(n)}\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$ is equivalent to ![]() $p\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$.
$p\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$.
Proof. Recall that the action of ![]() ${{\unicode{x05E6}}} _n$ on
${{\unicode{x05E6}}} _n$ on ![]() $\mathcal {C}$ commutes with colimits, so that
$\mathcal {C}$ commutes with colimits, so that ![]() $\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C} \to \mathcal {C}$ commutes with colimits. In addition,
$\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C} \to \mathcal {C}$ commutes with colimits. In addition, ![]() ${{\unicode{x05E6}}} _n$ is semiadditive, so finite products and coproducts coincide, so that
${{\unicode{x05E6}}} _n$ is semiadditive, so finite products and coproducts coincide, so that ![]() $\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C} \to \mathcal {C}$ also commutes with finite products, and the same holds for the restriction to the atomics
$\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C} \to \mathcal {C}$ also commutes with finite products, and the same holds for the restriction to the atomics ![]() $\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$. By Proposition 7.15,
$\mathbf {1}[\mathrm {B}^n C_p] \otimes -\colon \mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$. By Proposition 7.15, ![]() $p_{(n)} \cong \mathbf {1}[\mathrm {B}^n C_p] \otimes -$ on
$p_{(n)} \cong \mathbf {1}[\mathrm {B}^n C_p] \otimes -$ on ![]() $\mathcal {C}^{\mathrm {at}}$. Now, using Definition 7.16 and the assumption that
$\mathcal {C}^{\mathrm {at}}$. Now, using Definition 7.16 and the assumption that ![]() $\mathcal {C}$ has
$\mathcal {C}$ has ![]() $p$th roots of unity, we get an equivalence of functors
$p$th roots of unity, we get an equivalence of functors ![]() $\mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$
$\mathcal {C}^{\mathrm {at}} \to \mathcal {C}^{\mathrm {at}}$
Theorem 7.25 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ have (height
$\mathcal {C} \in \mathrm {Mod}_{{{\unicode{x05E6}}} _n}$ have (height ![]() $n$)
$n$) ![]() $p$th roots, and
$p$th roots, and ![]() $n < m$ a finite number, then
$n < m$ a finite number, then ![]() $\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{n+1}$. In particular, if
$\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{n+1}$. In particular, if ![]() $R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ has (height
$R \in \operatorname {Alg}({{\unicode{x05E6}}} _n)$ has (height ![]() $n$)
$n$) ![]() $p$th roots of unity, then
$p$th roots of unity, then ![]() $\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} _{n+1}$.
$\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} _{n+1}$.
Proof. Proposition 7.14 shows that ![]() $\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$. In particular, it is of height
$\mathrm {K}^{[m]}(\mathcal {C}^{\mathrm {at}}) \in {{\unicode{x05E6}}} _{1 \leq \bullet \leq n+1}$. In particular, it is of height ![]() $> 0$, i.e.
$> 0$, i.e. ![]() $p_{(0)} = p$-complete. By Proposition 7.24,
$p_{(0)} = p$-complete. By Proposition 7.24, ![]() $p_{(n)} \cong p$, so that it is also
$p_{(n)} \cong p$, so that it is also ![]() $p_{(n)}$-complete, that is, of height
$p_{(n)}$-complete, that is, of height ![]() $> n$. The last part follows from Proposition 7.23.
$> n$. The last part follows from Proposition 7.23.
Corollary 7.26 Let ![]() $n < m$ be a finite number, then
$n < m$ be a finite number, then ![]() $\mathrm {K}^{[m]}(\mathrm {E}_n) \in \operatorname {CAlg}({{\unicode{x05E6}}} _{n+1})$.
$\mathrm {K}^{[m]}(\mathrm {E}_n) \in \operatorname {CAlg}({{\unicode{x05E6}}} _{n+1})$.
8. Relationship to chromatically localized K-theory
In § 7, we have shown that higher semiadditive algebraic K-theory interacts well with semiadditive height. For example, ![]() $\mathrm {ht}(\mathrm {K}^{[m]}(\mathrm {E}_n)) = n+1$ when
$\mathrm {ht}(\mathrm {K}^{[m]}(\mathrm {E}_n)) = n+1$ when ![]() $m > n$ by Corollary 7.26. Note that the assumption
$m > n$ by Corollary 7.26. Note that the assumption ![]() $m > n$ is necessary to even define semiadditive height
$m > n$ is necessary to even define semiadditive height ![]() $n+1$. In this section we study the connection between higher semiadditive algebraic K-theory and chromatic localizations of ordinary algebraic K-theory by other means, while also dropping the assumption
$n+1$. In this section we study the connection between higher semiadditive algebraic K-theory and chromatic localizations of ordinary algebraic K-theory by other means, while also dropping the assumption ![]() $m> n$.
$m> n$.
Let ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$. The inclusion
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$. The inclusion ![]() $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset \mathrm {Sp}$ admits a left adjoint
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset \mathrm {Sp}$ admits a left adjoint ![]() $L_{\mathrm {T}(n+1)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since
$L_{\mathrm {T}(n+1)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Since ![]() $\mathrm {K}(R) \in \mathrm {Sp}$, we can consider
$\mathrm {K}(R) \in \mathrm {Sp}$, we can consider ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Similarly, by Lemma 6.12, there is an inclusion
$L_{\mathrm {T}(n+1)} \mathrm {K}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Similarly, by Lemma 6.12, there is an inclusion ![]() $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$ for any
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$ for any ![]() $m \geq 1$, which admits a left adjoint
$m \geq 1$, which admits a left adjoint ![]() $L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Note that, in some senses,
$L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}\colon {{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$. Note that, in some senses, ![]() $L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}$ is better behaved than
$L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}}$ is better behaved than ![]() $L_{\mathrm {T}(n+1)}$, as it is a smashing localization. Since
$L_{\mathrm {T}(n+1)}$, as it is a smashing localization. Since ![]() $\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} ^{[m]}$, we can consider
$\mathrm {K}^{[m]}(R) \in {{\unicode{x05E6}}} ^{[m]}$, we can consider ![]() $L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. By Corollary 6.15, there is a natural comparison map
$L_{\mathrm {T}(n+1)}^{{{\unicode{x05E6}}} ^{[m]}} \mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. By Corollary 6.15, there is a natural comparison map
This raises two independent questions.
(1) Does
 $\mathrm {K}^{[m]}(R)$ land in
$\mathrm {K}^{[m]}(R)$ land in  $\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$?
$\mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[m]}$?(2) Is the comparison map an equivalence?
A positive answer to both questions will imply that ![]() $\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$, see Conjecture 1.4. In Proposition 8.4 we show that the first question is closely related to the Quillen–Lichtenbaum conjecture for
$\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$, see Conjecture 1.4. In Proposition 8.4 we show that the first question is closely related to the Quillen–Lichtenbaum conjecture for ![]() $R$, in the guise of having a non-zero finite spectrum
$R$, in the guise of having a non-zero finite spectrum ![]() $X$ such that
$X$ such that ![]() $\mathrm {K}(R) \otimes X$ is bounded above. By Corollary 6.14, the second question is equivalent to
$\mathrm {K}(R) \otimes X$ is bounded above. By Corollary 6.14, the second question is equivalent to ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}_{[m]}(R)$ satisfying the
$L_{\mathrm {T}(n+1)} \mathrm {K}_{[m]}(R)$ satisfying the ![]() $m$-Segal condition. More informally, having descent properties for
$m$-Segal condition. More informally, having descent properties for ![]() $\mathrm {T}(n+1)$-localized K-theory.
$\mathrm {T}(n+1)$-localized K-theory.
Using the Galois descent results for ![]() $\mathrm {T}(n+1)$-localized K-theory of [Reference Clausen, Mathew, Naumann and NoelCMNN20], the second question is answered in the affirmative for
$\mathrm {T}(n+1)$-localized K-theory of [Reference Clausen, Mathew, Naumann and NoelCMNN20], the second question is answered in the affirmative for ![]() $m = 1$ in Proposition 8.6.
$m = 1$ in Proposition 8.6.
We then study the case where ![]() $R$ has height
$R$ has height ![]() $0$. The main result is Theorem 8.10, showing that for any
$0$. The main result is Theorem 8.10, showing that for any ![]() $p$-invertible algebra
$p$-invertible algebra ![]() $R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ and
$R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ and ![]() $m \geq 1$, there is an equivalence
$m \geq 1$, there is an equivalence
This is first proved for ![]() $R = \mathbb {S}[p^{-1}]$ by employing the Quillen–Lichtenbaum property of
$R = \mathbb {S}[p^{-1}]$ by employing the Quillen–Lichtenbaum property of ![]() $\mathbb {S}[p^{-1}]$ together with Proposition 8.6 mentioned above. The general case then follows via the lax symmetric monoidal structure on
$\mathbb {S}[p^{-1}]$ together with Proposition 8.6 mentioned above. The general case then follows via the lax symmetric monoidal structure on ![]() $\mathrm {K}^{[m]}$.
$\mathrm {K}^{[m]}$.
Finally, we study the completed Johnson–Wilson spectrum ![]() $\widehat {\mathrm {E}(n)}$ at height
$\widehat {\mathrm {E}(n)}$ at height ![]() $n \geq 1$, endowed with the Hahn–Wilson [Reference Hahn and WilsonHW22]
$n \geq 1$, endowed with the Hahn–Wilson [Reference Hahn and WilsonHW22] ![]() $\mathbb {E}_3$-algebra structure (see Theorem 8.12) and, more generally, any
$\mathbb {E}_3$-algebra structure (see Theorem 8.12) and, more generally, any ![]() $R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$. In Theorem 8.23 we show that
$R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$. In Theorem 8.23 we show that
for any ![]() $m \geq 1$, strengthening Theorem 7.25 for
$m \geq 1$, strengthening Theorem 7.25 for ![]() $\widehat {\mathrm {E}(n)}$-algebras. In the case
$\widehat {\mathrm {E}(n)}$-algebras. In the case ![]() $m = 1$, Proposition 8.6 implies that
$m = 1$, Proposition 8.6 implies that
To prove Theorem 8.23, we first use the Quillen–Lichtenbaum result for ![]() $\mathrm {BP}\langle n \rangle$ of [Reference Hahn and WilsonHW22] and the lax symmetric monoidal structure on
$\mathrm {BP}\langle n \rangle$ of [Reference Hahn and WilsonHW22] and the lax symmetric monoidal structure on ![]() $\mathrm {K}^{[m]}$ to show that
$\mathrm {K}^{[m]}$ to show that ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$. We would like to thank the anonymous referee for suggesting this argument. Then, we compute the cardinality of the classifying space of the
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$. We would like to thank the anonymous referee for suggesting this argument. Then, we compute the cardinality of the classifying space of the ![]() $k$-fold wreath product of
$k$-fold wreath product of ![]() $C_p$ at each chromatic height in two different ways. We observe that they are compatible only in chromatic height
$C_p$ at each chromatic height in two different ways. We observe that they are compatible only in chromatic height ![]() $n+1$, concluding that
$n+1$, concluding that ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Using the lax symmetric monoidal structure on
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. Using the lax symmetric monoidal structure on ![]() $\mathrm {K}^{[m]}$, this is generalized to any
$\mathrm {K}^{[m]}$, this is generalized to any ![]() $\widehat {\mathrm {E}(n)}$-algebra.
$\widehat {\mathrm {E}(n)}$-algebra.
Throughout this section ![]() $F(n)$ denotes a type-
$F(n)$ denotes a type-![]() $n$ finite spectrum (for example, the generalized Moore spectrum
$n$ finite spectrum (for example, the generalized Moore spectrum ![]() $\mathbb {S}/(p^{i_0}, v_1^{i_1}, \dotsc, v_{n-1}^{i_{n-1}})$). Without loss of generality, we may assume that
$\mathbb {S}/(p^{i_0}, v_1^{i_1}, \dotsc, v_{n-1}^{i_{n-1}})$). Without loss of generality, we may assume that ![]() $F(n)$ is an algebra, i.e.
$F(n)$ is an algebra, i.e. ![]() $F(n) \in \operatorname {Alg}(\mathrm {Sp})$, by replacing it by
$F(n) \in \operatorname {Alg}(\mathrm {Sp})$, by replacing it by ![]() $F(n) \otimes DF(n) \cong \operatorname {End}(F(n))$.
$F(n) \otimes DF(n) \cong \operatorname {End}(F(n))$.
8.1 General results
We begin this subsection by recalling and slightly generalizing some results from [Reference Carmeli, Schlank and YanovskiCSY22] and [Reference Carmeli, Schlank and YanovskiCSY21a] that will be used in the rest of the section.
Lemma 8.1 Let ![]() $\mathcal {C}$ be a symmetric monoidal stable
$\mathcal {C}$ be a symmetric monoidal stable ![]() $p$-local
$p$-local ![]() $1$-semiadditive category, and let
$1$-semiadditive category, and let ![]() $R \in \operatorname {CAlg}(\mathcal {C})$. If
$R \in \operatorname {CAlg}(\mathcal {C})$. If ![]() $1 \in \pi _0 R = \hom _{h\mathcal {C}}(\mathbf {1}_\mathcal {C}, R)$ is a torsion element, then
$1 \in \pi _0 R = \hom _{h\mathcal {C}}(\mathbf {1}_\mathcal {C}, R)$ is a torsion element, then ![]() $R = 0$.
$R = 0$.
Proof. This is essentially [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 4.3.5], we repeat the argument for the convenience of the reader. By [Reference Carmeli, Schlank and YanovskiCSY22, Theorem 4.3.2], the ring ![]() $\pi _0 R$ admits an additive
$\pi _0 R$ admits an additive ![]() $p$-derivation. By assumption,
$p$-derivation. By assumption, ![]() $\pi _0 R$ is
$\pi _0 R$ is ![]() $p$-local. Since
$p$-local. Since ![]() $1 \in \pi _0 R$ is torsion, [Reference Carmeli, Schlank and YanovskiCSY22, Proposition 4.1.10] shows that it is also nilpotent, which means that
$1 \in \pi _0 R$ is torsion, [Reference Carmeli, Schlank and YanovskiCSY22, Proposition 4.1.10] shows that it is also nilpotent, which means that ![]() $1 = 0 \in \pi _0 R$. Therefore,
$1 = 0 \in \pi _0 R$. Therefore, ![]() $R = 0$.
$R = 0$.
Fix ![]() $m \geq 1$. Recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7] that
$m \geq 1$. Recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem 4.2.7] that ![]() ${{\unicode{x05E6}}} ^{[m]} \cong {{\unicode{x05E6}}} _0 \times {{\unicode{x05E6}}} ^{[m]}_{>0}$. Also, by [Reference Carmeli, Schlank and YanovskiCSY21a, Example 5.3.7],
${{\unicode{x05E6}}} ^{[m]} \cong {{\unicode{x05E6}}} _0 \times {{\unicode{x05E6}}} ^{[m]}_{>0}$. Also, by [Reference Carmeli, Schlank and YanovskiCSY21a, Example 5.3.7], ![]() ${{\unicode{x05E6}}} _0 \cong \mathrm {Sp}_{\mathrm {T}(0)} \cong \mathrm {Sp}_\mathbb {Q}$. The collection of objects
${{\unicode{x05E6}}} _0 \cong \mathrm {Sp}_{\mathrm {T}(0)} \cong \mathrm {Sp}_\mathbb {Q}$. The collection of objects ![]() $X \in {{\unicode{x05E6}}} ^{[m]}_{>0}$ such that
$X \in {{\unicode{x05E6}}} ^{[m]}_{>0}$ such that ![]() $X \otimes F(n+2) = 0$ form a full subcategory, which is equivalent to
$X \otimes F(n+2) = 0$ form a full subcategory, which is equivalent to ![]() ${{\unicode{x05E6}}} ^{[m]}_{>0} \otimes L_{n+1}^f\mathrm {Sp} \cong \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.7] and [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem G]. We thus have the following result.
${{\unicode{x05E6}}} ^{[m]}_{>0} \otimes L_{n+1}^f\mathrm {Sp} \cong \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$ by [Reference Carmeli, Schlank and YanovskiCSY21a, Corollary 5.5.7] and [Reference Carmeli, Schlank and YanovskiCSY21a, Theorem G]. We thus have the following result.
Lemma 8.2 Let ![]() $X \in {{\unicode{x05E6}}} ^{[m]}_{>0}$, then
$X \in {{\unicode{x05E6}}} ^{[m]}_{>0}$, then ![]() $X \in \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$ if and only if
$X \in \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$ if and only if ![]() $X \otimes F(n+2) = 0$.
$X \otimes F(n+2) = 0$.
Recall from [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.9] that, similarly to the ![]() $\mathrm {K}(n)$- and
$\mathrm {K}(n)$- and ![]() $\mathrm {T}(n)$-localizations, the map of modes
$\mathrm {T}(n)$-localizations, the map of modes ![]() $\mathrm {Sp} \to {{\unicode{x05E6}}} _n$ vanishes on all bounded above spectra when
$\mathrm {Sp} \to {{\unicode{x05E6}}} _n$ vanishes on all bounded above spectra when ![]() $n \geq 1$. Here we prove a slight generalization of this result.
$n \geq 1$. Here we prove a slight generalization of this result.
Lemma 8.3 Let ![]() $m \geq 1$, then the map of modes
$m \geq 1$, then the map of modes ![]() $G_{>0}\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}_{>0}$ vanishes on all bounded above spectra.
$G_{>0}\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}_{>0}$ vanishes on all bounded above spectra.
Proof. We follow closely the argument of [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 5.3.9], diverging only the case of ![]() $\mathbb {F}_p$. The class of spectra on which
$\mathbb {F}_p$. The class of spectra on which ![]() $G_{>0}$ vanishes is closed under colimits and desuspensions in
$G_{>0}$ vanishes is closed under colimits and desuspensions in ![]() $\mathrm {Sp}$. Hence, by a standard devissage argument, it suffices to show that
$\mathrm {Sp}$. Hence, by a standard devissage argument, it suffices to show that ![]() $G_{>0}$ vanishes on
$G_{>0}$ vanishes on ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $\mathbb {F}_\ell$ for all primes
$\mathbb {F}_\ell$ for all primes ![]() $\ell$. First,
$\ell$. First, ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $\mathbb {F}_\ell$ for
$\mathbb {F}_\ell$ for ![]() $\ell \neq p$ are
$\ell \neq p$ are ![]() $p$-divisible. Since
$p$-divisible. Since ![]() $G_{>0}$ is
$G_{>0}$ is ![]() $0$-semiadditive,
$0$-semiadditive, ![]() $G_{>0}(\mathbb {Q})$ and
$G_{>0}(\mathbb {Q})$ and ![]() $G_{>0}(\mathbb {F}_\ell )$ are
$G_{>0}(\mathbb {F}_\ell )$ are ![]() $p$-divisible as well, but all objects of
$p$-divisible as well, but all objects of ![]() ${{\unicode{x05E6}}} ^{[m]}_{>0}$ are
${{\unicode{x05E6}}} ^{[m]}_{>0}$ are ![]() $p$-complete, and so
$p$-complete, and so ![]() $G_{>0}(\mathbb {Q}) = G_{>0}(\mathbb {F}_\ell ) = 0$.
$G_{>0}(\mathbb {Q}) = G_{>0}(\mathbb {F}_\ell ) = 0$.
It remains to show that ![]() $G_{>0}(\mathbb {F}_p) = 0$. Since
$G_{>0}(\mathbb {F}_p) = 0$. Since ![]() $\mathbb {F}_p \in \operatorname {CAlg}(\mathrm {Sp})$ is an
$\mathbb {F}_p \in \operatorname {CAlg}(\mathrm {Sp})$ is an ![]() $\mathbb {E}_\infty$-algebra, and
$\mathbb {E}_\infty$-algebra, and ![]() $G_{>0}$ is a map of modes,
$G_{>0}$ is a map of modes, ![]() $G_{>0}(\mathbb {F}_p) \in \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]}_{>0})$ is an
$G_{>0}(\mathbb {F}_p) \in \operatorname {CAlg}({{\unicode{x05E6}}} ^{[m]}_{>0})$ is an ![]() $\mathbb {E}_\infty$-algebra as well. Similarly, since
$\mathbb {E}_\infty$-algebra as well. Similarly, since ![]() $p = 0$ in
$p = 0$ in ![]() $\mathbb {F}_p$, the same holds in
$\mathbb {F}_p$, the same holds in ![]() $\pi _0 G_{>0}(\mathbb {F}_p)$. Thus, by Lemma 8.1 with
$\pi _0 G_{>0}(\mathbb {F}_p)$. Thus, by Lemma 8.1 with ![]() $\mathcal {C} = {{\unicode{x05E6}}} ^{[m]}_{>0}$ and
$\mathcal {C} = {{\unicode{x05E6}}} ^{[m]}_{>0}$ and ![]() $R = G_{>0}(\mathbb {F}_p)$, we know that
$R = G_{>0}(\mathbb {F}_p)$, we know that ![]() $G_{>0}(\mathbb {F}_p) = 0$ which concludes the proof.
$G_{>0}(\mathbb {F}_p) = 0$ which concludes the proof.
We now move on to proving the two main results of this subsection.
Proposition 8.4 Let ![]() $\mathcal {C} \in \operatorname {Alg}(\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})$ be an
$\mathcal {C} \in \operatorname {Alg}(\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}})$ be an ![]() $m$-semiadditive category for some
$m$-semiadditive category for some ![]() ${m \geq 1}$. Assume that there exists a category
${m \geq 1}$. Assume that there exists a category ![]() $\mathcal {C}_0 \in \operatorname {Alg}(\mathrm {Cat}^{\mathrm {st}})$, a left
$\mathcal {C}_0 \in \operatorname {Alg}(\mathrm {Cat}^{\mathrm {st}})$, a left ![]() $\mathcal {C}_0$-module structure
$\mathcal {C}_0$-module structure ![]() $\mathcal {C} \in \mathrm {LMod}_{\mathcal {C}_0}(\mathrm {Cat}^{\mathrm {st}})$, and that
$\mathcal {C} \in \mathrm {LMod}_{\mathcal {C}_0}(\mathrm {Cat}^{\mathrm {st}})$, and that ![]() $\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)$ is bounded above. Then
$\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)$ is bounded above. Then ![]() $\mathrm {K}^{[m]}(\mathcal {C}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$.
$\mathrm {K}^{[m]}(\mathcal {C}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \mathrm {Sp}_{\mathrm {T}(1)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$.
Remark 8.5 Note that ![]() $\mathcal {C}_0$ need not be
$\mathcal {C}_0$ need not be ![]() $m$-semiadditive or even have
$m$-semiadditive or even have ![]() $m$-finite colimits. Moreover, we require no compatibility between the algebra structure on
$m$-finite colimits. Moreover, we require no compatibility between the algebra structure on ![]() $\mathcal {C}$ and its
$\mathcal {C}$ and its ![]() $\mathcal {C}_0$-module structure.
$\mathcal {C}_0$-module structure.
Proof. Recall the decomposition ![]() ${{\unicode{x05E6}}} ^{[m]} \cong \mathrm {Sp}_{\mathrm {T}(0)} \times {{\unicode{x05E6}}} ^{[m]}_{>0}$. By Lemma 8.2, it remains to show that the factor in
${{\unicode{x05E6}}} ^{[m]} \cong \mathrm {Sp}_{\mathrm {T}(0)} \times {{\unicode{x05E6}}} ^{[m]}_{>0}$. By Lemma 8.2, it remains to show that the factor in ![]() ${{\unicode{x05E6}}} ^{[m]}_{>0}$ satisfies
${{\unicode{x05E6}}} ^{[m]}_{>0}$ satisfies ![]() $\mathrm {K}^{[m]}(\mathcal {C})_{>0} \otimes F(n+2) = 0$. Let
$\mathrm {K}^{[m]}(\mathcal {C})_{>0} \otimes F(n+2) = 0$. Let ![]() $G\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}$ denote the map of modes, the adjoint of the underlying functor
$G\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}$ denote the map of modes, the adjoint of the underlying functor ![]() $\underline {({-})}$. We also denote by
$\underline {({-})}$. We also denote by ![]() $G_{>0}\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}_{>0}$ the composition with the projection to
$G_{>0}\colon \mathrm {Sp} \to {{\unicode{x05E6}}} ^{[m]}_{>0}$ the composition with the projection to ![]() ${{\unicode{x05E6}}} ^{[m]}_{>0}$.
${{\unicode{x05E6}}} ^{[m]}_{>0}$.
By assumption, ![]() $\mathrm {K}(\mathcal {C}_0) \otimes F(n+2) \in \mathrm {Sp}$ is bounded above, so that
$\mathrm {K}(\mathcal {C}_0) \otimes F(n+2) \in \mathrm {Sp}$ is bounded above, so that ![]() $G_{>0}(\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)) = 0 \in {{\unicode{x05E6}}} ^{[m]}_{>0}$ by Lemma 8.3. The composition
$G_{>0}(\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)) = 0 \in {{\unicode{x05E6}}} ^{[m]}_{>0}$ by Lemma 8.3. The composition ![]() $G_{>0}(\mathrm {K}(-) \otimes F(n+2))$ is lax monoidal, since
$G_{>0}(\mathrm {K}(-) \otimes F(n+2))$ is lax monoidal, since ![]() $\mathrm {K}$ is lax (symmetric) monoidal by Theorem 6.18,
$\mathrm {K}$ is lax (symmetric) monoidal by Theorem 6.18, ![]() $F(n+2) \in \operatorname {Alg}(\mathrm {Sp})$ is taken to be an algebra, and
$F(n+2) \in \operatorname {Alg}(\mathrm {Sp})$ is taken to be an algebra, and ![]() $G_{>0}$ is a map of modes. By assumption
$G_{>0}$ is a map of modes. By assumption ![]() $\mathcal {C}$ is a left module over
$\mathcal {C}$ is a left module over ![]() $\mathcal {C}_0$, thus we get that
$\mathcal {C}_0$, thus we get that ![]() $G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2))$ is a left module over
$G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2))$ is a left module over ![]() $G_{>0}(\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)) = 0$ and, thus,
$G_{>0}(\mathrm {K}(\mathcal {C}_0) \otimes F(n+2)) = 0$ and, thus, ![]() $G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2)) = 0$ as well.
$G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2)) = 0$ as well.
Recall from Corollary 6.19 that since ![]() $\mathcal {C}$ is an algebra, we get an algebra map
$\mathcal {C}$ is an algebra, we get an algebra map ![]() $\mathrm {K}(\mathcal {C}) \to \underline {\mathrm {K}^{[m]}(\mathcal {C})} \in \operatorname {Alg}(\mathrm {Sp})$. By the adjunction
$\mathrm {K}(\mathcal {C}) \to \underline {\mathrm {K}^{[m]}(\mathcal {C})} \in \operatorname {Alg}(\mathrm {Sp})$. By the adjunction ![]() $G \dashv \underline {({-})}$ and composing with the projection to
$G \dashv \underline {({-})}$ and composing with the projection to ![]() ${{\unicode{x05E6}}} ^{[m]}_{>0}$, we get an algebra map
${{\unicode{x05E6}}} ^{[m]}_{>0}$, we get an algebra map ![]() $G_{>0}(\mathrm {K}(\mathcal {C})) \to \mathrm {K}^{[m]}(\mathcal {C})_{>0} \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}_{>0})$. Since the functor
$G_{>0}(\mathrm {K}(\mathcal {C})) \to \mathrm {K}^{[m]}(\mathcal {C})_{>0} \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}_{>0})$. Since the functor ![]() $G_{>0}$ is a functor between stable modes, it commutes with the action of
$G_{>0}$ is a functor between stable modes, it commutes with the action of ![]() $\mathrm {Sp}$. Therefore, tensoring the map with the algebra
$\mathrm {Sp}$. Therefore, tensoring the map with the algebra ![]() $F(n+2)$ yields
$F(n+2)$ yields ![]() $G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2)) \to \mathrm {K}^{[m]}(\mathcal {C})_{>0} \otimes F(n+2) \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}_{>0})$. We have shown that the source is
$G_{>0}(\mathrm {K}(\mathcal {C}) \otimes F(n+2)) \to \mathrm {K}^{[m]}(\mathcal {C})_{>0} \otimes F(n+2) \in \operatorname {Alg}({{\unicode{x05E6}}} ^{[m]}_{>0})$. We have shown that the source is ![]() $0$, and since this is an algebra map, so is the target, which concludes the proof.
$0$, and since this is an algebra map, so is the target, which concludes the proof.
In the next proposition we would like to use [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem C], which applies to ![]() $L_n^f\mathbb {S}$-linear stable categories. We recall that an
$L_n^f\mathbb {S}$-linear stable categories. We recall that an ![]() $L_n^f\mathbb {S}$-linear stable category is, by definition, a module over
$L_n^f\mathbb {S}$-linear stable category is, by definition, a module over ![]() $\mathrm {Perf}(L_n^f\mathbb {S}) = \mathrm {Mod}_{L_n^f\mathbb {S}}^\mathrm {dbl}$ in
$\mathrm {Perf}(L_n^f\mathbb {S}) = \mathrm {Mod}_{L_n^f\mathbb {S}}^\mathrm {dbl}$ in ![]() $\mathrm {Cat}^{\mathrm {st}}$. Note that since
$\mathrm {Cat}^{\mathrm {st}}$. Note that since ![]() $L_n^f\mathrm {Sp}$ is a smashing localization of
$L_n^f\mathrm {Sp}$ is a smashing localization of ![]() $\mathrm {Sp}$ we have that
$\mathrm {Sp}$ we have that ![]() $\mathrm {Mod}_{L_n^f\mathbb {S}} = L_n^f\mathrm {Sp}$. In particular, for
$\mathrm {Mod}_{L_n^f\mathbb {S}} = L_n^f\mathrm {Sp}$. In particular, for ![]() $R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$, we have that
$R \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(n)})$, we have that ![]() $\mathrm {LMod}_R^{\mathrm {at}}$ is
$\mathrm {LMod}_R^{\mathrm {at}}$ is ![]() $L_n^f\mathbb {S}$-linear, since
$L_n^f\mathbb {S}$-linear, since ![]() $\mathrm {LMod}_R \in \mathrm {Mod}_{\mathrm {Sp}_{\mathrm {T}(n)}} \subset \mathrm {Mod}_{L_n^f\mathrm {Sp}}$ and left dualizable modules coincide with atomics by Proposition 2.54. Thus,
$\mathrm {LMod}_R \in \mathrm {Mod}_{\mathrm {Sp}_{\mathrm {T}(n)}} \subset \mathrm {Mod}_{L_n^f\mathrm {Sp}}$ and left dualizable modules coincide with atomics by Proposition 2.54. Thus, ![]() $\mathrm {LMod}_R^{\mathrm {at}}$ is an example for
$\mathrm {LMod}_R^{\mathrm {at}}$ is an example for ![]() $\mathcal {C}$ in the following proposition.
$\mathcal {C}$ in the following proposition.
Proposition 8.6 Let ![]() $\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{1\text {-}\mathrm {fin}}$ be
$\mathcal {C} \in \mathrm {Cat}^{\mathrm {st}}_{1\text {-}\mathrm {fin}}$ be ![]() $L_n^f\mathbb {S}$-linear for some
$L_n^f\mathbb {S}$-linear for some ![]() $n > 0$ (i.e. it admits a
$n > 0$ (i.e. it admits a ![]() $\mathrm {Perf}(L_n^f\mathbb {S})$-module structure in
$\mathrm {Perf}(L_n^f\mathbb {S})$-module structure in ![]() $\mathrm {Cat}^{\mathrm {st}}$), then
$\mathrm {Cat}^{\mathrm {st}}$), then
In particular, if ![]() $\mathrm {K}^{[1]}(\mathcal {C}) \in \mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[1]}$, then
$\mathrm {K}^{[1]}(\mathcal {C}) \in \mathrm {Sp}_{\mathrm {T}(n+1)} \subset {{\unicode{x05E6}}} ^{[1]}$, then ![]() $\mathrm {K}^{[1]}(\mathcal {C}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\mathcal {C})$.
$\mathrm {K}^{[1]}(\mathcal {C}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\mathcal {C})$.
Proof. By Corollary 6.14 it suffices to show that ![]() $L_{\mathrm {T}(n+1)} \mathrm {K}_{[1]}(\mathcal {C})$ satisfies the
$L_{\mathrm {T}(n+1)} \mathrm {K}_{[1]}(\mathcal {C})$ satisfies the ![]() $1$-Segal condition, that is, for any
$1$-Segal condition, that is, for any ![]() $1$-finite
$1$-finite ![]() $p$-space
$p$-space ![]() $A$, the canonical map
$A$, the canonical map
is an equivalence. As both sides take coproducts in ![]() $A$ to direct sums, we may assume that
$A$ to direct sums, we may assume that ![]() $A$ is connected, i.e.
$A$ is connected, i.e. ![]() $A = \mathrm {B} G$ for a finite
$A = \mathrm {B} G$ for a finite ![]() $p$-group
$p$-group ![]() $G$. This is exactly [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem C].
$G$. This is exactly [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem C].
8.2 Height  $0$
$0$
We recall a form of the Quillen–Lichtenbaum conjecture for ![]() $\mathbb {S}[p^{-1}]$.
$\mathbb {S}[p^{-1}]$.
Proposition 8.7 We have that ![]() $F(2) \otimes \mathrm {K}(\mathbb {S}[p^{-1}])$ is bounded above.
$F(2) \otimes \mathrm {K}(\mathbb {S}[p^{-1}])$ is bounded above.
Proof. By [Reference Clausen and MathewCM21, Theorems 1.1 and 1.2],
is an isomorphism on high enough ![]() $p$-local homotopy groups. Tensoring with a finite spectrum preserves the property of a map being an isomorphism on high enough homotopy groups, and
$p$-local homotopy groups. Tensoring with a finite spectrum preserves the property of a map being an isomorphism on high enough homotopy groups, and ![]() $p = 0$ in
$p = 0$ in ![]() $F(2)$, so it suffices to show that the right-hand side vanishes after tensoring with
$F(2)$, so it suffices to show that the right-hand side vanishes after tensoring with ![]() $F(2)$. The tensor product of spectra commutes with finite limits, so it suffices to show that each term on the right-hand side vanishes after tensoring with
$F(2)$. The tensor product of spectra commutes with finite limits, so it suffices to show that each term on the right-hand side vanishes after tensoring with ![]() $F(2)$.
$F(2)$.
By definition, any ![]() $L_1^f$-local spectrum vanishes after tensoring with
$L_1^f$-local spectrum vanishes after tensoring with ![]() $F(2)$, which shows that both
$F(2)$, which shows that both ![]() $L_1^f \mathrm {K}(\mathbb {S}[p^{-1}])$ and
$L_1^f \mathrm {K}(\mathbb {S}[p^{-1}])$ and ![]() $L_1^f \mathrm {TC}(\mathbb {S}[p^{-1}])$ vanish after tensoring with
$L_1^f \mathrm {TC}(\mathbb {S}[p^{-1}])$ vanish after tensoring with ![]() $F(2)$.
$F(2)$.
Now, [Reference Nikolaus and ScholzeNS18, Definition II.1.8] exhibits the functor ![]() $\mathrm {TC}\colon \operatorname {Alg}(\mathrm {Sp}) \to \mathrm {Sp}$ as the composition
$\mathrm {TC}\colon \operatorname {Alg}(\mathrm {Sp}) \to \mathrm {Sp}$ as the composition
Since ![]() $\mathrm {THH}(\mathbb {S}[p^{-1}]) \cong \mathbb {S}[p^{-1}]$, and the second functor is exact, we get that
$\mathrm {THH}(\mathbb {S}[p^{-1}]) \cong \mathbb {S}[p^{-1}]$, and the second functor is exact, we get that ![]() $\mathrm {TC}(\mathbb {S}[p^{-1}])$ is
$\mathrm {TC}(\mathbb {S}[p^{-1}])$ is ![]() $p$-invertible. Therefore,
$p$-invertible. Therefore, ![]() $\mathrm {TC}(\mathbb {S}[p^{-1}])/p = 0$, and in particular it vanishes after tensoring with
$\mathrm {TC}(\mathbb {S}[p^{-1}])/p = 0$, and in particular it vanishes after tensoring with ![]() $F(2)$.
$F(2)$.
Proposition 8.8 The category ![]() $\mathrm {Mod}_{\mathbb {S}[p^{-1}]}(\mathrm {Sp}) \cong \mathrm {Sp}[p^{-1}]$ is a mode, classifying the property of being a stable
$\mathrm {Mod}_{\mathbb {S}[p^{-1}]}(\mathrm {Sp}) \cong \mathrm {Sp}[p^{-1}]$ is a mode, classifying the property of being a stable ![]() $p$-invertible presentable category. It is (
$p$-invertible presentable category. It is (![]() $p$-typically)
$p$-typically) ![]() $\infty$-semiadditive, and a smashing localization of both
$\infty$-semiadditive, and a smashing localization of both ![]() $\mathrm {Sp}$ and of
$\mathrm {Sp}$ and of ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$. In addition, for any
$\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$. In addition, for any ![]() $m \geq 0$, there is a lax symmetric functor
$m \geq 0$, there is a lax symmetric functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$, and ![]() $\mathcal {C}^{\mathrm {at}} = \mathcal {C}^\omega$.
$\mathcal {C}^{\mathrm {at}} = \mathcal {C}^\omega$.
Proof. The fact that ![]() $\mathrm {Sp}[p^{-1}]$ is a mode, classifying the property of being stable
$\mathrm {Sp}[p^{-1}]$ is a mode, classifying the property of being stable ![]() $p$-invertible presentable category, follows from [Reference Carmeli, Schlank and YanovskiCSY21a, Propositions 5.2.17 and 5.2.10]. The fact that it is
$p$-invertible presentable category, follows from [Reference Carmeli, Schlank and YanovskiCSY21a, Propositions 5.2.17 and 5.2.10]. The fact that it is ![]() $p$-typically
$p$-typically ![]() $\infty$-semiadditive follows from [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.3.4], which is essentially the same fact that
$\infty$-semiadditive follows from [Reference Carmeli, Schlank and YanovskiCSY21a, Proposition 2.3.4], which is essentially the same fact that ![]() $\mathrm {Sp}_\mathbb {Q}$ is
$\mathrm {Sp}_\mathbb {Q}$ is ![]() $\infty$-semiadditive. It is a smashing localization of both
$\infty$-semiadditive. It is a smashing localization of both ![]() $\mathrm {Sp}$ and of
$\mathrm {Sp}$ and of ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$ because it can be obtained from both by inverting
$\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$ because it can be obtained from both by inverting ![]() $p$.
$p$.
The fact that it is a smashing localization together with Proposition 2.26 show that for ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ the
$\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ the ![]() $\mathrm {Sp}[p^{-1}]$-atomics, the
$\mathrm {Sp}[p^{-1}]$-atomics, the ![]() $\mathrm {Sp}$-atomics and the
$\mathrm {Sp}$-atomics and the ![]() $\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$-atomics all coincide. In addition, Proposition 2.8 shows that
$\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}$-atomics all coincide. In addition, Proposition 2.8 shows that ![]() $\mathrm {Sp}$-atomics are the same as compact objects. Finally, the functor
$\mathrm {Sp}$-atomics are the same as compact objects. Finally, the functor ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the restriction of
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is the restriction of ![]() $(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ from Proposition 4.15.
$(-)^{\mathrm {at}} \colon \mathrm {Mod}_{\mathrm {CMon}_m^{(p)}{({\mathrm {Sp}})}}^{\mathrm {iL}} \to \mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ from Proposition 4.15.
Corollary 8.9 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ and
$\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ and ![]() $m \geq 1$, then
$m \geq 1$, then ![]() $\mathrm {K}^{[m]}(\mathcal {C}^\omega ) \in \mathrm {Sp}_{\mathrm {T}(1)}$.
$\mathrm {K}^{[m]}(\mathcal {C}^\omega ) \in \mathrm {Sp}_{\mathrm {T}(1)}$.
Proof. First consider the universal case ![]() $\mathcal {C} = \mathrm {Sp}[p^{-1}]$. Proposition 8.7 shows that
$\mathcal {C} = \mathrm {Sp}[p^{-1}]$. Proposition 8.7 shows that ![]() $\mathrm {K}(\mathbb {S}[p^{-1}])$ is bounded above after tensoring with
$\mathrm {K}(\mathbb {S}[p^{-1}])$ is bounded above after tensoring with ![]() $F(2)$, so by Proposition 8.4
$F(2)$, so by Proposition 8.4 ![]() $\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \mathrm {Sp}_{\mathrm {T}(1)}$. Similarly to the proof of Corollary 7.10,
$\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \mathrm {Sp}_{\mathrm {T}(1)}$. Similarly to the proof of Corollary 7.10, ![]() $\mathrm {Sp}[p^{-1}]^\omega$ is
$\mathrm {Sp}[p^{-1}]^\omega$ is ![]() $\infty$-semiadditive by Proposition 4.15, and all of its objects have semiadditive height
$\infty$-semiadditive by Proposition 4.15, and all of its objects have semiadditive height ![]() $0$, thus by Proposition 7.14 we get that
$0$, thus by Proposition 7.14 we get that ![]() $\mathrm {ht}(\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}])) > 0$, so that indeed
$\mathrm {ht}(\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}])) > 0$, so that indeed ![]() $\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(1)}$.
$\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(1)}$.
We now prove the general case. Recall that by Proposition 8.8 and Theorem 6.18 ![]() $\mathrm {K}^{[m]}((-)^{\mathrm {at}})$ is a composition of lax symmetric monoidal functors, and by Proposition 8.8, atomic objects coincide with compact objects. Since every
$\mathrm {K}^{[m]}((-)^{\mathrm {at}})$ is a composition of lax symmetric monoidal functors, and by Proposition 8.8, atomic objects coincide with compact objects. Since every ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ is by definition a module over
$\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ is by definition a module over ![]() $\mathrm {Sp}[p^{-1}]$, we get that
$\mathrm {Sp}[p^{-1}]$, we get that ![]() $\mathrm {K}^{[m]}(\mathcal {C}^\omega )$ is a module over
$\mathrm {K}^{[m]}(\mathcal {C}^\omega )$ is a module over ![]() $\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}])$ in
$\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}])$ in ![]() ${{\unicode{x05E6}}} ^{[m]}$. As we have shown that
${{\unicode{x05E6}}} ^{[m]}$. As we have shown that ![]() $\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(1)}$, and
$\mathrm {K}^{[m]}(\mathbb {S}[p^{-1}]) \in \mathrm {Sp}_{\mathrm {T}(1)}$, and ![]() $\mathrm {Sp}_{\mathrm {T}(1)}$ is a smashing localization of
$\mathrm {Sp}_{\mathrm {T}(1)}$ is a smashing localization of ![]() ${{\unicode{x05E6}}} ^{[m]}$ by Lemma 6.12, we conclude that
${{\unicode{x05E6}}} ^{[m]}$ by Lemma 6.12, we conclude that ![]() $\mathrm {K}^{[m]}(\mathcal {C}^\omega ) \in \mathrm {Sp}_{\mathrm {T}(1)}$ as well.
$\mathrm {K}^{[m]}(\mathcal {C}^\omega ) \in \mathrm {Sp}_{\mathrm {T}(1)}$ as well.
Theorem 8.10 Let ![]() $\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ and
$\mathcal {C} \in \mathrm {Mod}_{\mathrm {Sp}[p^{-1}]}$ and ![]() $m \geq 1$, then
$m \geq 1$, then
In particular, for any ![]() $R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ we have
$R \in \operatorname {Alg}(\mathrm {Sp}[p^{-1}])$ we have ![]() $\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(1)}\mathrm {K}(R)$.
$\mathrm {K}^{[m]}(R) \cong L_{\mathrm {T}(1)}\mathrm {K}(R)$.
Proof. By Proposition 7.8, ![]() $\mathrm {K}^{[m]}(\mathcal {C}^\omega )$ is independent of
$\mathrm {K}^{[m]}(\mathcal {C}^\omega )$ is independent of ![]() $m \geq 1$, so we may assume that
$m \geq 1$, so we may assume that ![]() ${m = 1}$. Therefore, the result follows immediately from the combination of Corollary 8.9 and Proposition 8.6.
${m = 1}$. Therefore, the result follows immediately from the combination of Corollary 8.9 and Proposition 8.6.
Example 8.11 For any ![]() $1 \leq m \leq \infty$, there is an equivalence
$1 \leq m \leq \infty$, there is an equivalence ![]() $\mathrm {K}^{[m]}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$.
$\mathrm {K}^{[m]}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$.
Proof. The combination of [Reference SuslinSus84, Corollary 4.7] and [Reference SuslinSus83, Main Theorem] shows that there is an equivalence ![]() $\mathrm {K}(\overline {\mathbb {Q}})_p \cong \mathrm {K}(\mathbb {C})_p \cong \mathrm {ku}_p$. As
$\mathrm {K}(\overline {\mathbb {Q}})_p \cong \mathrm {K}(\mathbb {C})_p \cong \mathrm {ku}_p$. As ![]() $\mathrm {K}\mathrm {U}_p$ is
$\mathrm {K}\mathrm {U}_p$ is ![]() $\mathrm {T}(1)$-local, and
$\mathrm {T}(1)$-local, and ![]() $\mathrm {T}(1)$-localization is insensitive to connective covers,
$\mathrm {T}(1)$-localization is insensitive to connective covers, ![]() $L_{\mathrm {T}(1)} \mathrm {ku}_p \cong \mathrm {K}\mathrm {U}_p$, which shows that
$L_{\mathrm {T}(1)} \mathrm {ku}_p \cong \mathrm {K}\mathrm {U}_p$, which shows that ![]() $L_{\mathrm {T}(1)} \mathrm {K}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$, and the result follows by Theorem 8.10.
$L_{\mathrm {T}(1)} \mathrm {K}(\overline {\mathbb {Q}}) \cong \mathrm {K}\mathrm {U}_p$, and the result follows by Theorem 8.10.
8.3 Height  $n \geq 1$
$n \geq 1$
Fix some finite height ![]() $1 \leq n < \infty$. We let
$1 \leq n < \infty$. We let ![]() $\widehat {\mathrm {E}(n)} \in \mathrm {Sp}_{\mathrm {T}(n)}$ denote the completed Johnson–Wilson spectrum at height
$\widehat {\mathrm {E}(n)} \in \mathrm {Sp}_{\mathrm {T}(n)}$ denote the completed Johnson–Wilson spectrum at height ![]() $n$, namely
$n$, namely ![]() $\widehat {\mathrm {E}(n)} \cong L_{\mathrm {T}(n)} \mathrm {E}(n) \cong L_{\mathrm {T}(n)} \mathrm {BP}\langle n \rangle$ (note that
$\widehat {\mathrm {E}(n)} \cong L_{\mathrm {T}(n)} \mathrm {E}(n) \cong L_{\mathrm {T}(n)} \mathrm {BP}\langle n \rangle$ (note that ![]() $\mathrm {K}(n)$- and
$\mathrm {K}(n)$- and ![]() $\mathrm {T}(n)$-localization coincide for
$\mathrm {T}(n)$-localization coincide for ![]() $\mathrm {MU}$-modules by [Reference HoveyHov95, Corollary 1.10]). The main input to this subsection is the following result.
$\mathrm {MU}$-modules by [Reference HoveyHov95, Corollary 1.10]). The main input to this subsection is the following result.
Theorem 8.12 [Reference Hahn and WilsonHW22, Corollary of Theorem B]
There exists an ![]() $\mathbb {E}_3$-
$\mathbb {E}_3$-![]() $\mathrm {BP}$-algebra structure on
$\mathrm {BP}$-algebra structure on ![]() $\mathrm {BP}\langle n \rangle$ such that
$\mathrm {BP}\langle n \rangle$ such that
induces an isomorphism on ![]() $\pi _*$ for
$\pi _*$ for ![]() $* \gg 0$.
$* \gg 0$.
Henceforth, we shall consider ![]() $\mathrm {BP}\langle n \rangle$ as an
$\mathrm {BP}\langle n \rangle$ as an ![]() $\mathbb {E}_3$-algebra with the structure from Theorem 8.12, which also endows the localization
$\mathbb {E}_3$-algebra with the structure from Theorem 8.12, which also endows the localization ![]() $\widehat {\mathrm {E}(n)}$ with a compatible
$\widehat {\mathrm {E}(n)}$ with a compatible ![]() $\mathbb {E}_3$-algebra structure. An immediate corollary of this result is the following.
$\mathbb {E}_3$-algebra structure. An immediate corollary of this result is the following.
Corollary 8.13 The spectrum ![]() $\mathrm {K}(\mathrm {BP}\langle n \rangle ) \otimes F(n+2)$ is bounded above, where
$\mathrm {K}(\mathrm {BP}\langle n \rangle ) \otimes F(n+2)$ is bounded above, where ![]() $F(n+2)$ is a type-
$F(n+2)$ is a type-![]() $(n+2)$ finite spectrum.
$(n+2)$ finite spectrum.
Lemma 8.14 Let ![]() $m \geq 1$, then
$m \geq 1$, then ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$.
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$.
Proof. We shall employ Proposition 8.4. Consider the symmetric monoidal functor ![]() $L_{\mathrm {T}(n)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n)}$. We get an induced
$L_{\mathrm {T}(n)}\colon \mathrm {Sp} \to \mathrm {Sp}_{\mathrm {T}(n)}$. We get an induced ![]() $\mathbb {E}_2$-monoidal functor on modules
$\mathbb {E}_2$-monoidal functor on modules
which, in turn, induces an ![]() $\mathbb {E}_2$-monoidal functor on left dualizable objects
$\mathbb {E}_2$-monoidal functor on left dualizable objects
The latter map exhibits the target as a module over the source. By Corollary 8.13, we know that ![]() $\mathrm {K}(\mathrm {LMod}_{\mathrm {BP}\langle n \rangle }(\mathrm {Sp})^\mathrm {ldbl}) \otimes F(n+2) = \mathrm {K}(\mathrm {BP}\langle n \rangle ) \otimes F(n+2)$ is bounded above. By Proposition 2.54 we know that
$\mathrm {K}(\mathrm {LMod}_{\mathrm {BP}\langle n \rangle }(\mathrm {Sp})^\mathrm {ldbl}) \otimes F(n+2) = \mathrm {K}(\mathrm {BP}\langle n \rangle ) \otimes F(n+2)$ is bounded above. By Proposition 2.54 we know that
The result now follows immediately from Proposition 8.4.
Our next goal, achieved in Lemma 8.22, is to show that in fact ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. For that, we need to show that each
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$. For that, we need to show that each ![]() $\mathrm {T}(k)$-local part vanishes for
$\mathrm {T}(k)$-local part vanishes for ![]() $0 \leq k \leq n$, and in fact it will suffice to show this after tensoring with the Lubin–Tate spectrum
$0 \leq k \leq n$, and in fact it will suffice to show this after tensoring with the Lubin–Tate spectrum ![]() $\mathrm {E}_k$. To do so, we shall compute the action of
$\mathrm {E}_k$. To do so, we shall compute the action of ![]() $|\mathrm {B}(\wr _k C_p)|$, where
$|\mathrm {B}(\wr _k C_p)|$, where ![]() $\wr _k C_p$ is the
$\wr _k C_p$ is the ![]() $k$-fold wreath product of
$k$-fold wreath product of ![]() $C_p$ with itself, in two different ways. First, in general in
$C_p$ with itself, in two different ways. First, in general in ![]() $\mathrm {E}_k$-modules (see Proposition 8.17), and second by studying the dimension of the
$\mathrm {E}_k$-modules (see Proposition 8.17), and second by studying the dimension of the ![]() $\widehat {\mathrm {E}(n)}$-module
$\widehat {\mathrm {E}(n)}$-module ![]() $\widehat {\mathrm {E}(n)}{}^{\mathrm {B}(\wr _k C_p)}$ and deducing the result for the higher semiadditive algebraic K-theory (see Proposition 8.21).
$\widehat {\mathrm {E}(n)}{}^{\mathrm {B}(\wr _k C_p)}$ and deducing the result for the higher semiadditive algebraic K-theory (see Proposition 8.21).
Definition 8.15 Let ![]() $k \geq 0$. We denote by
$k \geq 0$. We denote by ![]() ${\widehat {\mathrm {Mod}}_{\mathrm {E}_k}} = \mathrm {Mod}_{\mathrm {E}_k}(\mathrm {Sp}_{\mathrm {K}(k)})$ the category of
${\widehat {\mathrm {Mod}}_{\mathrm {E}_k}} = \mathrm {Mod}_{\mathrm {E}_k}(\mathrm {Sp}_{\mathrm {K}(k)})$ the category of ![]() $\mathrm {K}(k)$-local
$\mathrm {K}(k)$-local ![]() $\mathrm {E}_k$-modules.
$\mathrm {E}_k$-modules.
We recall from [Reference Carmeli, Schlank and YanovskiCSY22, Theorem 5.3.1] that ![]() $\widehat {\mathrm {Mod}}_{\mathrm {E}_k}$ is
$\widehat {\mathrm {Mod}}_{\mathrm {E}_k}$ is ![]() $\infty$-semiadditive.
$\infty$-semiadditive.
Definition 8.16 For a ![]() $\pi$-finite space
$\pi$-finite space ![]() $A$, we denote
$A$, we denote
Also note that by [Reference Carmeli, Schlank and YanovskiCSY22, Proposition 2.2.6, see also § 5.4], the cardinality ![]() $|A|_k$ in fact lands in
$|A|_k$ in fact lands in ![]() $\mathbb {Z}_p \subseteq \pi _0(\mathrm {E}_k)$.
$\mathbb {Z}_p \subseteq \pi _0(\mathrm {E}_k)$.
Proposition 8.17 Let ![]() $k \geq 1$ and let
$k \geq 1$ and let ![]() $G$ be a finite group. If
$G$ be a finite group. If ![]() $v_p(|\mathrm {B} G|_k) > 0$, then
$v_p(|\mathrm {B} G|_k) > 0$, then ![]() $v_p(|\mathrm {B} G \wr C_p|_k) = v_p(|\mathrm {B} G|_k) - 1$. Moreover,
$v_p(|\mathrm {B} G \wr C_p|_k) = v_p(|\mathrm {B} G|_k) - 1$. Moreover, ![]() $|\mathrm {B}(\wr _k C_p)|_k$ is invertible.
$|\mathrm {B}(\wr _k C_p)|_k$ is invertible.
Proof. This is similar to the proof of [Reference Carmeli, Schlank and YanovskiCSY22, Proposition 4.3.7]. Recall the additive ![]() $p$-derivation
$p$-derivation ![]() $\delta \colon \pi _0(\mathrm {E}_k) \to \pi _0(\mathrm {E}_k)$ from [Reference Carmeli, Schlank and YanovskiCSY22, Definition 4.3.1], which by [Reference Carmeli, Schlank and YanovskiCSY22, Theorem 4.2.12] satisfies
$\delta \colon \pi _0(\mathrm {E}_k) \to \pi _0(\mathrm {E}_k)$ from [Reference Carmeli, Schlank and YanovskiCSY22, Definition 4.3.1], which by [Reference Carmeli, Schlank and YanovskiCSY22, Theorem 4.2.12] satisfies
By [Reference Carmeli, Schlank and YanovskiCSY21a, Lemma 5.4.6], for ![]() $x \in \mathbb {Z}_p \subset \pi _0(\mathrm {E}_k)$, if
$x \in \mathbb {Z}_p \subset \pi _0(\mathrm {E}_k)$, if ![]() $v_p(x)>0$, then
$v_p(x)>0$, then ![]() $v_p(\delta (x)) = v_p(x)-1$. Note that
$v_p(\delta (x)) = v_p(x)-1$. Note that ![]() $v_p(|\mathrm {B} C_p|_k |\mathrm {B} G|_k) = v_p(|\mathrm {B} C_p|_k) + v_p(|\mathrm {B} G|_k) \geq v_p(|\mathrm {B} G|_k)$. Combining the two, we get
$v_p(|\mathrm {B} C_p|_k |\mathrm {B} G|_k) = v_p(|\mathrm {B} C_p|_k) + v_p(|\mathrm {B} G|_k) \geq v_p(|\mathrm {B} G|_k)$. Combining the two, we get
For the second part, by [Reference Carmeli, Schlank and YanovskiCSY22, Lemma 5.3.3], we have ![]() $|\mathrm {B} C_p|_k = p^{k-1}$. Thus, applying the first part
$|\mathrm {B} C_p|_k = p^{k-1}$. Thus, applying the first part ![]() $(k-1)$-times, we get
$(k-1)$-times, we get ![]() $v_p(|\mathrm {B}(\wr _k C_p)|_k) = v_p(|\mathrm {B} C_p|_k)-(k-1) = 0$.
$v_p(|\mathrm {B}(\wr _k C_p)|_k) = v_p(|\mathrm {B} C_p|_k)-(k-1) = 0$.
For a finite ![]() $p$-group
$p$-group ![]() $G$, we consider
$G$, we consider ![]() $\hom (\mathbb {Z}_p^n, G)$, the set of
$\hom (\mathbb {Z}_p^n, G)$, the set of ![]() $n$-tuples commuting elements in
$n$-tuples commuting elements in ![]() $G$. This set is endowed with an action of
$G$. This set is endowed with an action of ![]() $\mathrm {GL}_n(\mathbb {Z}_p)$ by pre-composition. We shall, in particular, be interested in the integer
$\mathrm {GL}_n(\mathbb {Z}_p)$ by pre-composition. We shall, in particular, be interested in the integer
where the ![]() $G$-action in the second term is by conjugation point-wise, and the second equality is Burnside's lemma [Reference Hopkins, Kuhn and RavenelHKR00, Lemma 4.13].
$G$-action in the second term is by conjugation point-wise, and the second equality is Burnside's lemma [Reference Hopkins, Kuhn and RavenelHKR00, Lemma 4.13].
Proposition 8.18 Let ![]() $G$ be a finite
$G$ be a finite ![]() $p$-group, then
$p$-group, then
Proof. We shall prove
Since ![]() $|G \wr C_p| = p|G|^p$, the result immediately follows (when changing
$|G \wr C_p| = p|G|^p$, the result immediately follows (when changing ![]() $n$ to
$n$ to ![]() $n+1$).
$n+1$).
In this proof, we will write elements of ![]() $C_p$ additively, namely, identify it with
$C_p$ additively, namely, identify it with ![]() $\mathbb {Z}/p$. Elements of
$\mathbb {Z}/p$. Elements of ![]() $G \wr C_p$ will be denoted by pairs
$G \wr C_p$ will be denoted by pairs ![]() $(a, f)$ where
$(a, f)$ where ![]() $a \in C_p$ and
$a \in C_p$ and ![]() $f\colon C_p \to G$. Elements of
$f\colon C_p \to G$. Elements of ![]() $\hom (\mathbb {Z}_p^n, C_p)$ will be denoted by
$\hom (\mathbb {Z}_p^n, C_p)$ will be denoted by ![]() $\alpha = (a_1, \dotsc, a_n)$. Similarly, elements of
$\alpha = (a_1, \dotsc, a_n)$. Similarly, elements of ![]() $\hom (\mathbb {Z}_p^n, G \wr C_p)$ will be denoted by
$\hom (\mathbb {Z}_p^n, G \wr C_p)$ will be denoted by ![]() $\beta = ((a_1, f_1), \dotsc, (a_n, f_n))$.
$\beta = ((a_1, f_1), \dotsc, (a_n, f_n))$.
Consider the projection ![]() $G \wr C_p \to C_p$, which by post-composition induces
$G \wr C_p \to C_p$, which by post-composition induces ![]() $\pi \colon \hom (\mathbb {Z}_p^n, G \wr C_p) \to \hom (\mathbb {Z}_p^n, C_p)$. By construction of the action,
$\pi \colon \hom (\mathbb {Z}_p^n, G \wr C_p) \to \hom (\mathbb {Z}_p^n, C_p)$. By construction of the action, ![]() $\pi$ is
$\pi$ is ![]() $\mathrm {GL}_n(\mathbb {Z}_p)$-equivariant. We let
$\mathrm {GL}_n(\mathbb {Z}_p)$-equivariant. We let ![]() $\hom ^\alpha (\mathbb {Z}_p^n, G \wr C_p) = \pi ^{-1}(\alpha )$ denote the fiber. Observe that the
$\hom ^\alpha (\mathbb {Z}_p^n, G \wr C_p) = \pi ^{-1}(\alpha )$ denote the fiber. Observe that the ![]() $\mathrm {GL}_n(\mathbb {Z}_p)$-action on
$\mathrm {GL}_n(\mathbb {Z}_p)$-action on ![]() $\hom (\mathbb {Z}_p^n, C_p) \cong C_p^n$ has two orbits: one which is the singleton
$\hom (\mathbb {Z}_p^n, C_p) \cong C_p^n$ has two orbits: one which is the singleton ![]() $\alpha = 0$, and the second of size
$\alpha = 0$, and the second of size ![]() $p^n-1$ containing all
$p^n-1$ containing all ![]() $\alpha \neq 0$. We let
$\alpha \neq 0$. We let ![]() $\alpha _1 = (1, 0, \dotsc, 0)$, an element of the second orbit. Since
$\alpha _1 = (1, 0, \dotsc, 0)$, an element of the second orbit. Since ![]() $\pi$ is equivariant, all of the fibers in the same orbit have the same size, so that
$\pi$ is equivariant, all of the fibers in the same orbit have the same size, so that
We shall now compute the sizes of the two fibers.
For the first fiber, observe that ![]() $\hom ^0(\mathbb {Z}_p^n, G \wr C_p) \subset \hom (\mathbb {Z}_p^n, G \wr C_p)$ is the subset of those tuples landing in
$\hom ^0(\mathbb {Z}_p^n, G \wr C_p) \subset \hom (\mathbb {Z}_p^n, G \wr C_p)$ is the subset of those tuples landing in ![]() $G^p < G \wr C_p$. Therefore,
$G^p < G \wr C_p$. Therefore,
For the second fiber, we being with the following observations. A pair of elements ![]() $(0, f), (0, f') \in G \wr C_p$ commute if and only if
$(0, f), (0, f') \in G \wr C_p$ commute if and only if ![]() $f, f' \in G^p$ commute, i.e. if and only if
$f, f' \in G^p$ commute, i.e. if and only if ![]() $f(a), f'(a) \in G$ commute for all
$f(a), f'(a) \in G$ commute for all ![]() $a \in C_p$. A pair of elements
$a \in C_p$. A pair of elements ![]() $(1, f), (0, f') \in G \wr C_p$ commute if and only if
$(1, f), (0, f') \in G \wr C_p$ commute if and only if ![]() $f(a) f'(1+a) = f'(a) f(a)$ for all
$f(a) f'(1+a) = f'(a) f(a)$ for all ![]() $a \in C_p$. Applying this inductively, we see that
$a \in C_p$. Applying this inductively, we see that ![]() $f'$ is uniquely determined by
$f'$ is uniquely determined by ![]() $f$ and
$f$ and ![]() $f'(0)$ and subject to the condition that
$f'(0)$ and subject to the condition that ![]() $f'(0), \prod f(a) \in G$ commute. Using these observations, we can say when an
$f'(0), \prod f(a) \in G$ commute. Using these observations, we can say when an ![]() $n$-tuple of elements in
$n$-tuple of elements in ![]() $G \wr C_p$, denoted
$G \wr C_p$, denoted ![]() $\beta = ((1, f_1), (0, f_2), \dotsc, (0, f_n))$, pairwise commute, i.e.
$\beta = ((1, f_1), (0, f_2), \dotsc, (0, f_n))$, pairwise commute, i.e. ![]() $\beta \in \hom ^{\alpha _1}(\mathbb {Z}_p^n, G \wr C_p)$. The commutativity of
$\beta \in \hom ^{\alpha _1}(\mathbb {Z}_p^n, G \wr C_p)$. The commutativity of ![]() $(1, f_1)$ and
$(1, f_1)$ and ![]() $(0, f_i)$ (for
$(0, f_i)$ (for ![]() $i \geq 2$) says that
$i \geq 2$) says that ![]() $f_i$ is determined by
$f_i$ is determined by ![]() $f_1$ and
$f_1$ and ![]() $f_i(0)$ and forces the condition that
$f_i(0)$ and forces the condition that ![]() $f_i(0), \prod f_1(a)$ commute. The commutativity of
$f_i(0), \prod f_1(a)$ commute. The commutativity of ![]() $(0, f_i)$ and
$(0, f_i)$ and ![]() $(0, f_j)$ (for
$(0, f_j)$ (for ![]() $i,j \geq 2$) forces the condition that
$i,j \geq 2$) forces the condition that ![]() $f_i(0)$ and
$f_i(0)$ and ![]() $f_j(0)$ commute. We thus see that
$f_j(0)$ commute. We thus see that ![]() $\beta$ is uniquely specified by
$\beta$ is uniquely specified by ![]() $f_1$ and
$f_1$ and ![]() $f_2(0), \dotsc, f_n(0)$, subject to the condition that
$f_2(0), \dotsc, f_n(0)$, subject to the condition that ![]() $(\prod f_1(a), f_2(0), \dotsc, f_n(0))$ pairwise commute. In other words, we have a bijection
$(\prod f_1(a), f_2(0), \dotsc, f_n(0))$ pairwise commute. In other words, we have a bijection
 \begin{gather*} \hom^{\alpha_1}(\mathbb{Z}_p^n, G \wr C_p) \xrightarrow{\smash {{\scriptstyle \sim }}} G^{p-1} \times \hom(\mathbb{Z}_p^n, G),\\ \beta \mapsto ((f_1(0), \dotsc, f_1(p-2)), \biggl(\prod f_1(a), f_2(0), \dotsc, f_n(0))\biggr). \end{gather*}
\begin{gather*} \hom^{\alpha_1}(\mathbb{Z}_p^n, G \wr C_p) \xrightarrow{\smash {{\scriptstyle \sim }}} G^{p-1} \times \hom(\mathbb{Z}_p^n, G),\\ \beta \mapsto ((f_1(0), \dotsc, f_1(p-2)), \biggl(\prod f_1(a), f_2(0), \dotsc, f_n(0))\biggr). \end{gather*}
To conclude, we have shown
 \begin{align*} |\hom(\mathbb{Z}_p^n, G \wr C_p)| &= |\hom^0(\mathbb{Z}_p^n, G \wr C_p)| + (p^n-1)|\hom^{\alpha_1}(\mathbb{Z}_p^n, G \wr C_p)|\\ &= |\hom(\mathbb{Z}_p^n, G)|^p + (p^n-1)|G|^{p-1}|\hom(\mathbb{Z}_p^n, G)|, \end{align*}
\begin{align*} |\hom(\mathbb{Z}_p^n, G \wr C_p)| &= |\hom^0(\mathbb{Z}_p^n, G \wr C_p)| + (p^n-1)|\hom^{\alpha_1}(\mathbb{Z}_p^n, G \wr C_p)|\\ &= |\hom(\mathbb{Z}_p^n, G)|^p + (p^n-1)|G|^{p-1}|\hom(\mathbb{Z}_p^n, G)|, \end{align*}
as required.
Proposition 8.19 For ![]() $1 \leq k \leq n$ we have
$1 \leq k \leq n$ we have ![]() $v_p(\mathrm {L}^n(\wr _k C_p)) = n - (k-1)$. In particular
$v_p(\mathrm {L}^n(\wr _k C_p)) = n - (k-1)$. In particular ![]() $\mathrm {L}^n(\wr _k C_p) \in \mathbb {Z}_p$ is not invertible.
$\mathrm {L}^n(\wr _k C_p) \in \mathbb {Z}_p$ is not invertible.
Proof. First, for ![]() $k = 1$ we have
$k = 1$ we have
so that ![]() $v_p(\mathrm {L}^n(C_p)) = n$. Now assume inductively that
$v_p(\mathrm {L}^n(C_p)) = n$. Now assume inductively that ![]() $v_p(\mathrm {L}^n(\wr _k C_p)) = n - (k-1)$. Since
$v_p(\mathrm {L}^n(\wr _k C_p)) = n - (k-1)$. Since
we get that
Thus, by Proposition 8.18, we get the required result
We now recall the following result.
Proposition 8.20 Let ![]() $X$ be a space with
$X$ be a space with ![]() $\dim _{\mathbb {F}_p}(\mathrm {K}(n)_0(X)) = d < \infty$ and
$\dim _{\mathbb {F}_p}(\mathrm {K}(n)_0(X)) = d < \infty$ and ![]() $\mathrm {K}(n)_1(X) = 0$. Then,
$\mathrm {K}(n)_1(X) = 0$. Then, ![]() $\widehat {\mathrm {E}(n)}[X] \in \mathrm {LMod}_{\widehat {\mathrm {E}(n)}}$ is a free
$\widehat {\mathrm {E}(n)}[X] \in \mathrm {LMod}_{\widehat {\mathrm {E}(n)}}$ is a free ![]() $\widehat {\mathrm {E}(n)}$-module of dimension
$\widehat {\mathrm {E}(n)}$-module of dimension ![]() $d$ and, in particular, dualizable.
$d$ and, in particular, dualizable.
Proof. This is the content of [Reference Hovey and StricklandHS99, Proposition 8.4] (see also [Reference Hopkins and LurieHL13, Proposition 3.4.3] and [Reference Carmeli, Schlank and YanovskiCSY22, Lemma 5.1.7]).
Proposition 8.21 Let ![]() $1 \leq k \leq n$ and let
$1 \leq k \leq n$ and let ![]() $m \geq 1$. The action of
$m \geq 1$. The action of ![]() $|\mathrm {B}(\wr _k C_p)|$ on
$|\mathrm {B}(\wr _k C_p)|$ on ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in {{\unicode{x05E6}}} ^{[m]}$ is by multiplication by a non-invertible
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in {{\unicode{x05E6}}} ^{[m]}$ is by multiplication by a non-invertible ![]() $p$-adic number.
$p$-adic number.
Proof. By [Reference Hopkins, Kuhn and RavenelHKR00, Theorem E], the group ![]() $\wr _k C_p$ is good in the sense of [Reference Hopkins, Kuhn and RavenelHKR00, Definition 7.1] and, in particular,
$\wr _k C_p$ is good in the sense of [Reference Hopkins, Kuhn and RavenelHKR00, Definition 7.1] and, in particular, ![]() $\mathrm {K}(n)_1(\mathrm {B}(\wr _k C_p)) = 0$. Thus, by [Reference Hopkins, Kuhn and RavenelHKR00, Theorem B and Lemma 4.13], we know that
$\mathrm {K}(n)_1(\mathrm {B}(\wr _k C_p)) = 0$. Thus, by [Reference Hopkins, Kuhn and RavenelHKR00, Theorem B and Lemma 4.13], we know that ![]() $\dim _{\mathbb {F}_p}(\mathrm {K}(n)_0(\wr _k C_p)) = \mathrm {L}^n(\wr _k C_p)$. By Proposition 8.20, we conclude that
$\dim _{\mathbb {F}_p}(\mathrm {K}(n)_0(\wr _k C_p)) = \mathrm {L}^n(\wr _k C_p)$. By Proposition 8.20, we conclude that ![]() $\widehat {\mathrm {E}(n)}[\mathrm {B}(\wr _k C_p)]$ is a free
$\widehat {\mathrm {E}(n)}[\mathrm {B}(\wr _k C_p)]$ is a free ![]() $\widehat {\mathrm {E}(n)}$-module of dimension
$\widehat {\mathrm {E}(n)}$-module of dimension ![]() $\mathrm {L}^n(\wr _k C_p)$. Recall from Proposition 7.6 that the action of
$\mathrm {L}^n(\wr _k C_p)$. Recall from Proposition 7.6 that the action of ![]() $|\mathrm {B}(\wr _k C_p)|$ on
$|\mathrm {B}(\wr _k C_p)|$ on ![]() $\mathrm {LMod}_{\widehat {\mathrm {E}(n)}}^{\mathrm {at}}$ as an object of
$\mathrm {LMod}_{\widehat {\mathrm {E}(n)}}^{\mathrm {at}}$ as an object of ![]() $\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is by
$\mathrm {Cat}^{\mathrm {st}}_{m\text {-}\mathrm {fin}}$ is by ![]() $\widehat {\mathrm {E}(n)}[\mathrm {B}(\wr _k C_p)] \otimes (-)$, namely by multiplication by
$\widehat {\mathrm {E}(n)}[\mathrm {B}(\wr _k C_p)] \otimes (-)$, namely by multiplication by ![]() $\mathrm {L}^n(\wr _k C_p)$. Since
$\mathrm {L}^n(\wr _k C_p)$. Since ![]() $\mathrm {K}^{[m]}$ is a
$\mathrm {K}^{[m]}$ is a ![]() $1$-semiadditive functor by Proposition 6.7, the same holds for the action of
$1$-semiadditive functor by Proposition 6.7, the same holds for the action of ![]() $|\mathrm {B}(\wr _k C_p)|$ on
$|\mathrm {B}(\wr _k C_p)|$ on ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ by [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 3.2.7]. By Proposition 8.19, this number is indeed a non-invertible
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ by [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 3.2.7]. By Proposition 8.19, this number is indeed a non-invertible ![]() $p$-adic number.
$p$-adic number.
Lemma 8.22 Let ![]() $m \geq 1$, then
$m \geq 1$, then ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$.
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$.
Proof. By Lemma 8.14, we know that ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$. It remains to show that the
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)}) \in \mathrm {Sp}_{\mathrm {T}(0)} \times \cdots \times \mathrm {Sp}_{\mathrm {T}(n+1)}$. It remains to show that the ![]() $\mathrm {T}(k)$-local part, which for brevity we denote by
$\mathrm {T}(k)$-local part, which for brevity we denote by ![]() $A_k \in \mathrm {Sp}_{\mathrm {T}(k)}$, vanishes for every
$A_k \in \mathrm {Sp}_{\mathrm {T}(k)}$, vanishes for every ![]() $0 \leq k \leq n$.
$0 \leq k \leq n$.
We first deal with the case ![]() $1 \leq k \leq n$. Recall from [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 5.1.17] that the functor
$1 \leq k \leq n$. Recall from [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 5.1.17] that the functor
is nil-conservative in the sense of [Reference Carmeli, Schlank and YanovskiCSY22, Definition 4.4], that is, for any ![]() $A \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(k)})$, if
$A \in \operatorname {Alg}(\mathrm {Sp}_{\mathrm {T}(k)})$, if ![]() $\mathrm {E}_k[A] = 0$, then
$\mathrm {E}_k[A] = 0$, then ![]() $A = 0$. Therefore, it suffices to check that
$A = 0$. Therefore, it suffices to check that ![]() $\mathrm {E}_k[A_k] = 0$. We have shown in Proposition 8.21 that
$\mathrm {E}_k[A_k] = 0$. We have shown in Proposition 8.21 that ![]() $|\mathrm {B}(\wr _k C_p)|$ acts on
$|\mathrm {B}(\wr _k C_p)|$ acts on ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ by multiplication by a non-invertible
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ by multiplication by a non-invertible ![]() $p$-adic number. Since
$p$-adic number. Since ![]() $\mathrm {E}_k[(-)_k]$ is a
$\mathrm {E}_k[(-)_k]$ is a ![]() $1$-semiadditive functor by Proposition 6.7, the same holds for
$1$-semiadditive functor by Proposition 6.7, the same holds for ![]() $\mathrm {E}_k[A_k]$ by [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 3.2.7]. We thus have shown that
$\mathrm {E}_k[A_k]$ by [Reference Carmeli, Schlank and YanovskiCSY22, Corollary 3.2.7]. We thus have shown that ![]() $|\mathrm {B}(\wr _k C_p)|$ acts on
$|\mathrm {B}(\wr _k C_p)|$ acts on ![]() $\mathrm {E}_k[A_k]$ as a
$\mathrm {E}_k[A_k]$ as a ![]() $p$-adic number of positive valuation. Since by Proposition 8.17
$p$-adic number of positive valuation. Since by Proposition 8.17 ![]() $|\mathrm {B}(\wr _k C_p)|_k$ is invertible, and
$|\mathrm {B}(\wr _k C_p)|_k$ is invertible, and ![]() $\widehat {\mathrm {Mod}}_{\mathrm {E}_k}$ is
$\widehat {\mathrm {Mod}}_{\mathrm {E}_k}$ is ![]() $p$-complete, we conclude that
$p$-complete, we conclude that ![]() $\mathrm {E}_k[A_k] = 0$.
$\mathrm {E}_k[A_k] = 0$.
We now prove the remaining case ![]() $k = 0$. As above, Proposition 8.21 shows that
$k = 0$. As above, Proposition 8.21 shows that ![]() $|\mathrm {B} C_p|$ acts on
$|\mathrm {B} C_p|$ acts on ![]() $A_0$ by
$A_0$ by ![]() $\mathrm {L}^n(C_p) = p$. On the other hand,
$\mathrm {L}^n(C_p) = p$. On the other hand, ![]() $|\mathrm {B} C_p|_0 = p^{-1}$ by [Reference Carmeli, Schlank and YanovskiCSY22, Lemma 5.3.3]. Namely
$|\mathrm {B} C_p|_0 = p^{-1}$ by [Reference Carmeli, Schlank and YanovskiCSY22, Lemma 5.3.3]. Namely ![]() $p = p^{-1}$ on the rational spectrum
$p = p^{-1}$ on the rational spectrum ![]() $A_0$, thus
$A_0$, thus ![]() $A_0 = 0$.
$A_0 = 0$.
Theorem 8.23 Let ![]() $R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ and
$R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$ and ![]() $m \geq 1$, then
$m \geq 1$, then ![]() $\mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$.
$\mathrm {K}^{[m]}(R) \in \mathrm {Sp}_{\mathrm {T}(n+1)}$.
Proof. The category ![]() $\mathrm {LMod}_R$ is a right module over
$\mathrm {LMod}_R$ is a right module over ![]() $\mathrm {LMod}_{\widehat {\mathrm {E}(n)}}$. Recall from Theorem 2.46 that taking the atomics is a lax symmetric monoidal functor, and from Theorem 6.18 that
$\mathrm {LMod}_{\widehat {\mathrm {E}(n)}}$. Recall from Theorem 2.46 that taking the atomics is a lax symmetric monoidal functor, and from Theorem 6.18 that ![]() $\mathrm {K}^{[m]}$ is lax symmetric monoidal. Thus, we get that
$\mathrm {K}^{[m]}$ is lax symmetric monoidal. Thus, we get that ![]() $\mathrm {K}^{[m]}(R)$ is a right module over
$\mathrm {K}^{[m]}(R)$ is a right module over ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$. In addition, by Lemma 6.12,
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$. In addition, by Lemma 6.12, ![]() ${{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$ is a smashing localization, and since
${{\unicode{x05E6}}} ^{[m]} \to \mathrm {Sp}_{\mathrm {T}(n+1)}$ is a smashing localization, and since ![]() $\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ lands in the smashing localization by Lemma 8.22, so does
$\mathrm {K}^{[m]}(\widehat {\mathrm {E}(n)})$ lands in the smashing localization by Lemma 8.22, so does ![]() $\mathrm {K}^{[m]}(R)$.
$\mathrm {K}^{[m]}(R)$.
Corollary 8.24 Let ![]() $R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$, then
$R \in \operatorname {Alg}(\mathrm {LMod}_{\widehat {\mathrm {E}(n)}})$, then ![]() $\mathrm {K}^{[1]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$. In particular,
$\mathrm {K}^{[1]}(R) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(R)$. In particular, ![]() $\mathrm {K}^{[1]}(\widehat {\mathrm {E}(n)}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\widehat {\mathrm {E}(n)})$.
$\mathrm {K}^{[1]}(\widehat {\mathrm {E}(n)}) \cong L_{\mathrm {T}(n+1)} \mathrm {K}(\widehat {\mathrm {E}(n)})$.
In our work with Carmeli and Yanovski [Reference Ben-Moshe, Carmeli, Schlank and YanovskiBCSY23] we show that Corollary 8.24 holds for ![]() $m$-semiadditive K-theory for any
$m$-semiadditive K-theory for any ![]() $m \geq 1$.
$m \geq 1$.
Acknowledgements
We are grateful to the anonymous referees for valuable suggestions and corrections, particularly for suggesting the strategy for Theorem D. We would like to thank the entire Seminarak group, especially S. Barkan, S. Carmeli, S. Ragimov, and L. Yanovski, for useful discussions on different aspects of this project, and for their valuable comments on the paper's first draft. In particular, we would like to thank L. Yanovski for sharing many ideas regarding atomic objects appearing in § 2, and for suggesting the proof of Proposition 3.6. We would also like to thank B. Cnossen and M. Ramzi for helpful comments on the paper's first version.
Conflicts of Interest
None.