Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T09:44:25.817Z Has data issue: false hasContentIssue false
  • English
  • Français

The Kodaira dimension of complex hyperbolic manifolds with cusps

Part of: Lie groups Complex manifolds Cycles and subschemes

Published online by Cambridge University Press:  28 November 2017

Benjamin Bakker  and
Jacob Tsimerman
Benjamin Bakker
Affiliation:
Department of Mathematics, University of Georgia, Boyd Graduate Studies Research Center, Athens, GA 30602, USA email bakker@math.uga.edu
Jacob Tsimerman
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, 40 St. George Street, Room 6290, Toronto, Ontario, Canada M5S 2E4 email jacobt@math.toronto.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a bound relating the volume of a curve near a cusp in a complex ball quotient 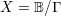$X=\mathbb{B}/\unicode[STIX]{x1D6E4}$ to its multiplicity at the cusp. There are a number of consequences: we show that for an $n$-dimensional toroidal compactification 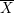$\overline{X}$ with boundary 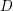$D$, 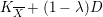$K_{\overline{X}}+(1-\unicode[STIX]{x1D706})D$ is ample for 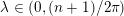$\unicode[STIX]{x1D706}\in (0,(n+1)/2\unicode[STIX]{x1D70B})$, and in particular that 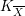$K_{\overline{X}}$ is ample for 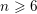$n\geqslant 6$. By an independent algebraic argument, we prove that every ball quotient of dimension 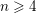$n\geqslant 4$ is of general type, and conclude that the phenomenon famously exhibited by Hirzebruch in dimension 2 does not occur in higher dimensions. Finally, we investigate the applications to the problem of bounding the number of cusps and to the Green–Griffiths conjecture.

Keywords

hyperbolic manifoldball quotientKodaira dimensiontoroidal compactification

MSC classification

Primary: 32Q45: Hyperbolic and Kobayashi hyperbolic manifolds
Secondary: 14C20: Divisors, linear systems, invertible sheaves 22E40: Discrete subgroups of Lie groups
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 3 , March 2018 , pp. 549 - 564
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allcock, D., Carlson, J. A. and Toledo, D., The moduli space of cubic threefolds as a ball quotient , Mem. Amer. Math. Soc. 209 (2011).Google Scholar
Ash, A., Mumford, D., Rapoport, M. and Tai, Y., Smooth compactification of locally symmetric varieties, Lie Groups: History, Frontiers and Applications, vol. IV (Mathematical Science Press, Brookline, MA, 1975).Google Scholar
Baily, W. L. Jr. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains , Ann. of Math. (2) 84 (1966), 442–528.Google Scholar
Bakker, B. and Tsimerman, J., The geometric torsion conjecture for abelian varieties with real multiplication, J. Differential Geom., to appear.Google Scholar
Bauer, T., Campana, F., Eckl, T., Kebekus, S., Peternell, T., Rams, S., Szemberg, T. and Wotzlaw, L., A reduction map for nef line bundles , in Complex geometry (Göttingen 2000) (Springer, Berlin, 2002), 27–36.Google Scholar
Debarre, O., Higher-dimensional algebraic geometry (Springer, New York, 2001).CrossRefGoogle Scholar
Deligne, P. and Mostow, G., Commensurabilities among lattices in PU(1, n), Annals of Mathematics Studies, vol. 132 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Demailly, J.-P., Analytic methods in algebraic geometry, Surveys of Modern Mathematics, vol. 1 (International Press, Boston, 2012).Google Scholar
Di Cerbo, G. and Di Cerbo, L. F., A sharp cusp count for complex hyperbolic surfaces and related results , Arch. Math. 103 (2014), 75–84.Google Scholar
Di Cerbo, G. and Di Cerbo, L. F., Effective results for complex hyperbolic manifolds , J. Lond. Math. Soc. (2) 91 (2015), 89–104.CrossRefGoogle Scholar
Di Cerbo, G. and Di Cerbo, L. F., On the canonical divisor of smooth toroidal compactifications of complex hyperbolic manifolds, Math. Res. Lett., to appear.Google Scholar
Di Cerbo, L. and Stover, M., Classification and arithmeticity of toroidal compactifications with 3c2 = c1 2 = 3 , Geom. Topol., to appear.Google Scholar
Dolgachev, I. V. and Kondō, S., Moduli of K3 surfaces and complex ball quotients , in Arithmetic and geometry around hypergeometric functions, Progress in Mathematics, vol. 260 (Birkhäuser, Basel, 2007), 43–100.Google Scholar
Green, M. and Griffiths, P., Two applications of algebraic geometry to entire holomorphic mappings , in The Chern symposium 1979 (Proc. internat. sympos., Berkeley, CA, 1979) (Springer, New York, 1980), 41–74.Google Scholar
Hirzebruch, F., Chern numbers of algebraic surfaces: an example , Math. Ann. 266 (1984), 351–356.Google Scholar
Hummel, C., Rank one lattices whose parabolic isometries have no rotational part , Proc. Amer. Math. Soc. 126 (1998), 2453–2458.Google Scholar
Hwang, J., On the volumes of complex hyperbolic manifolds with cusps , Int. J. Math. 15 (2004), 567–572.Google Scholar
Hwang, J. and To, W., Volumes of complex analytic subvarieties of Hermitian symmetric spaces , Amer. J. Math. 124 (2002), 1221–1246.CrossRefGoogle Scholar
Kawamata, Y., Abundance theorem for minimal threefolds , Invent. Math. 108 (1992), 229–246.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 48 (Springer, Berlin, 2004).Google Scholar
Margulis, G. A., Arithmeticity of the irreducible lattices in the semi-simple groups of rank greater than 1 , Invent. Math. 76 (1984), 93–120.Google Scholar
Mok, N., Projective algebraicity of minimal compactifications of complex-hyperbolic space forms of finite volume , in Perspectives in analysis, geometry, and topology, Progress in Mathematics, vol. 296 (Birkhäuser/Springer, New York, 2012), 331–354.Google Scholar
Mostow, G. D., On a remarkable class of polyhedra in complex hyperbolic space , Pacific J. Math. 86 (1980), 171–276.CrossRefGoogle Scholar
Mumford, D., Hirzebruch’s proportionality theorem in the noncompact case , Invent. Math. 42 (1977), 239–272.Google Scholar
Nadel, A. M., The nonexistence of certain level structures on abelian varieties over complex function fields , Ann. of Math. (2) 129 (1989), 161–178.Google Scholar
Parker, J. R., On the volumes of cusped, complex hyperbolic manifolds and orbifolds , Duke Math. J. 94 (1998), 433–464.Google Scholar
Shepherd-Barron, N. I., Perfect forms and the moduli space of abelian varieties , Invent. Math. 163 (2006), 25–45.Google Scholar
Siu, Y. T. and Yau, S. T., Compactification of negatively curved complete Kähler manifolds of finite volume , in Seminar on differential geometry, Annals of Mathematics Studies, vol. 102, (Princeton, NJ, 1982), 363–380.Google Scholar