Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:40:00.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Laurent phenomenon and simple modules of quiver Hecke algebras

Part of: Lie algebras and Lie superalgebras Arithmetic rings and other special rings Groups and algebras in quantum theory

Published online by Cambridge University Press:  04 October 2019

Masaki Kashiwara  and
Myungho Kim
Masaki Kashiwara
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan email masaki@kurims.kyoto-u.ac.jp Korea Institute for Advanced Study, Seoul 02455, Korea email masaki@kurims.kyoto-u.ac.jp
Myungho Kim
Affiliation:
Department of Mathematics, Kyung Hee University, Seoul 02447, Korea email mkim@khu.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study consequences of the results of Kang et al. [Monoidal categorification of cluster algebras, J. Amer. Math. Soc. 31 (2018), 349–426] on a monoidal categorification of the unipotent quantum coordinate ring 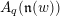$A_{q}(\mathfrak{n}(w))$ together with the Laurent phenomenon of cluster algebras. We show that if a simple module 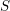$S$ in the category 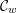${\mathcal{C}}_{w}$ strongly commutes with all the cluster variables in a cluster 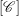$[\mathscr{C}]$, then 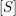$[S]$ is a cluster monomial in 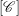$[\mathscr{C}]$. If 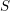$S$ strongly commutes with cluster variables except for exactly one cluster variable 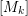$[M_{k}]$, then 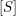$[S]$ is either a cluster monomial in 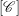$[\mathscr{C}]$ or a cluster monomial in 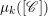$\unicode[STIX]{x1D707}_{k}([\mathscr{C}])$. We give a new proof of the fact that the upper global basis is a common triangular basis (in the sense of Qin [Triangular bases in quantum cluster algebras and monoidal categorification conjectures, Duke Math. 166 (2017), 2337–2442]) of the localization 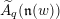$\widetilde{A}_{q}(\mathfrak{n}(w))$ of 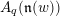$A_{q}(\mathfrak{n}(w))$ at the frozen variables. A characterization on the commutativity of a simple module 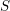$S$ with cluster variables in a cluster 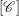$[\mathscr{C}]$ is given in terms of the denominator vector of 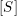$[S]$ with respect to the cluster 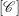$[\mathscr{C}]$.

Keywords

cluster algebraLaurent phenomenonmonoidal categorificationquiver Hecke algebraunipotent quantum coordinate ring

MSC classification

Primary: 13F60: Cluster algebras 81R50: Quantum groups and related algebraic methods 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 12 , December 2019 , pp. 2263 - 2295
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by Grant-in-Aid for Scientific Research (B) 22340005, Japan Society for the Promotion of Science. This work was supported by the National Research Foundation of Korea (NF) grant funded by the Korea government (MSIP) (No. NRF-2017R1C1B2007824).

References

Berenstein, A. and Zelevinsky, A., Quantum cluster algebras , Adv. Math. 195 (2005), 405–455.Google Scholar
Cao, P. and Li, F., The enough $g$ -pairs property and denominator vectors of cluster algebras. Preprint (2018), arXiv:1803.05281v2.Google Scholar
Casbi, E., Dominance order and monoidal categorification of cluster algebras. Preprint (2018), arXiv:1810.00970.Google Scholar
Fock, V. V. and Goncharov, A. B., Cluster ensembles, quantization and the dilogarithm , Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 865–930.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras I. Foundations , J. Amer. Math. Soc. 15 (2002), 497–529.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras IV. Coefficients , Compos. Math. 143 (2007), 112–164.Google Scholar
Geiß, C., Leclerc, B. and Schröer, J., Kac–Moody groups and cluster algebras , Adv. Math. 228 (2011), 329–433.Google Scholar
Geiß, C., Leclerc, B. and Schröer, J., Factorial cluster algebras , Doc. Math. 18 (2013), 249–274.Google Scholar
Geiß, C., Leclerc, B. and Schröer, J., Cluster structures on quantum coordinate rings , Selecta Math. (N.S.) 19 (2013), 337–397.Google Scholar
Hernandez, D. and Leclerc, B., Cluster algebras and quantum affine algebras , Duke Math. J. 154 (2010), 265–341.Google Scholar
Kang, S.-J., Kashiwara, M. and Kim, M., Symmetric quiver Hecke algebras and R-matrices of quantum affine algebras , Invent. Math. 211 (2018), 591–685.Google Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-J., Simplicity of heads and socles of tensor products , Compos. Math. 151 (2015), 377–396.Google Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-J., Monoidal categorification of cluster algebras , J. Amer. Math. Soc. 31 (2018), 349–426.Google Scholar
Kashiwara, M., Kim, M., Oh, S.-J. and Park, E., Monoidal categories associated with strata of flag manifolds , Adv. Math. 328 (2018), 959–1009.Google Scholar
Kashiwara, M., Kim, M., Oh, S.-J. and Park, E., Localizations for quiver Hecke algebras. Preprint (2019), arXiv:1901.09319v1.Google Scholar
Khovanov, M. and Lauda, A., A diagrammatic approach to categorification of quantum groups I , Represent. Theory 13 (2009), 309–347.Google Scholar
Kimura, Y., Quantum unipotent subgroup and dual canonical basis , Kyoto J. Math. 52 (2012), 277–331.Google Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras , Ann. of Math. (2) 182 (2015), 73–125.Google Scholar
Qin, F., Triangular bases in quantum cluster algebras and monoidal categorification conjectures , Duke Math. 166 (2017), 2337–2442.Google Scholar
Rouquier, R., 2-Kac–Moody algebras. Preprint (2008), arXiv:0812.5023v1.Google Scholar
Rouquier, R., Quiver Hecke algebras and 2-Lie algebras , Algebra Colloq. 19 (2012), 359–410.Google Scholar
Tingley, P. and Webster, B., Mirković–Vilonen polytopes and Khovanov–Lauda–Rouquier algebras , Compos. Math. 152 (2016), 1648–1696.Google Scholar
Varagnolo, M. and Vasserot, E., Canonical bases and KLR algebras , J. reine angew. Math. 659 (2011), 67–100.Google Scholar