Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T08:53:44.941Z Has data issue: false hasContentIssue false
  • English
  • Français

The level of distribution of the Thue–Morse sequence

Part of: Multiplicative number theory Sequences and sets Probabilistic theory: distribution modulo $1$; metric theory of algorithms Elementary number theory

Published online by Cambridge University Press:  25 January 2021

Lukas Spiegelhofer
Lukas Spiegelhofer*
Affiliation:
Institute of Discrete Mathematics and Geometry, Vienna University of Technology, Wiedner Hauptstrasse 8–10, 1040Vienna, Austrialukas.spiegelhofer@unileoben.ac.at Department of Mathematics and Information Technology, Montanuniversität Leoben, Franz-Josef-Straße 18, 8700Leoben, Austria
Get access Rights & Permissions [Opens in a new window]

Abstract

The level of distribution of a complex-valued sequence 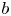$b$ measures the quality of distribution of 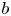$b$ along sparse arithmetic progressions 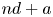$nd+a$. We prove that the Thue–Morse sequence has level of distribution 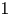$1$, which is essentially best possible. More precisely, this sequence gives one of the first nontrivial examples of a sequence satisfying a Bombieri–Vinogradov-type theorem for each exponent 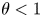$\theta <1$. This result improves on the level of distribution 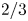$2/3$ obtained by Müllner and the author. As an application of our method, we show that the subsequence of the Thue–Morse sequence indexed by 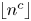$\lfloor n^c\rfloor$, where 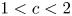$1 < c < 2$, is simply normal. This result improves on the range 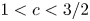$1 < c < 3/2$ obtained by Müllner and the author and closes the gap that appeared when Mauduit and Rivat proved (in particular) that the Thue–Morse sequence along the squares is simply normal.

Keywords

Thue–Morse sequencelevel of distributionBombieri–Vinogradov theoremElliott–Halberstam conjecturearithmetic progressionPiatetski-Shapiro sequencenormal sequenceGel'fond problem

MSC classification

Primary: 11N69: Distribution of integers in special residue classes 11B25: Arithmetic progressions 11B85: Automata sequences
Secondary: 11A63: Radix representation; digital problems 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc. 11B83: Special sequences and polynomials
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2560 - 2587
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author acknowledges support by the Austrian Science Fund (FWF), Project F5502-N26, which is a part of the Special Research Program ‘Quasi Monte Carlo Methods: Theory and Applications’. The author also wishes to acknowledge support by the project MuDeRa, which is a joint project between the FWF (I-1751-N26) and the ANR (Agence Nationale de la Recherche, France, ANR-14-CE34-0009).

References

Allouche, J.-P. and Shallit, J., The ubiquitous Prouhet–Thue–Morse sequence, in Sequences and their applications (Singapore, 1998), Springer Series in Discrete Mathematics and Theoretical Computer Science (Springer, London, 1999), 1–16.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic sequences: theory, applications, generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli, Acta Math. 156 (1986), 203–251.CrossRefGoogle Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli. II, Math. Ann. 277 (1987), 361–393.CrossRefGoogle Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli. III, J. Amer. Math. Soc. 2 (1989), 215–224.CrossRefGoogle Scholar
Dartyge, C. and Tenenbaum, G., Congruences de sommes de chiffres de valeurs polynomiales, Bull. Lond. Math. Soc. 38 (2006), 61–69.Google Scholar
Deshouillers, J.-M., Drmota, M. and Morgenbesser, J. F., Subsequences of automatic sequences indexed by $\lfloor n^c\rfloor$ and correlations, J. Number Theory 132 (2012), 1837–1866.CrossRefGoogle Scholar
Drmota, M., Mauduit, C. and Rivat, J., Normality along squares, J. Eur. Math. Soc. 21 (2019), 507–548.CrossRefGoogle Scholar
Drmota, M. and Rivat, J., The sum-of-digits function of squares, J. Lond. Math. Soc. (2) 72 (2005), 273–292.CrossRefGoogle Scholar
Elliott, P. D. T. A. and Halberstam, H., A conjecture in prime number theory, in Symposia Mathematica, Vol. IV (INDAM, Rome, 1968/69) (Academic Press, London, 1970), 59–72.Google Scholar
Fouvry, E., Répartition des suites dans les progressions arithmétiques, Acta Arith. 41 (1982), 359–382.CrossRefGoogle Scholar
Fouvry, E., Autour du théorème de Bombieri–Vinogradov, Acta Math. 152 (1984), 219–244.CrossRefGoogle Scholar
Fouvry, E. and Iwaniec, H., On a theorem of Bombieri–Vinogradov type, Mathematika 27 (1980), 135–152.CrossRefGoogle Scholar
Fouvry, E. and Mauduit, C., Méthodes de crible et fonctions sommes des chiffres, Acta Arith. 77 (1996), 339–351.CrossRefGoogle Scholar
Fouvry, E. and Mauduit, C., Sommes des chiffres et nombres presque premiers, Math. Ann. 305 (1996), 571–599.CrossRefGoogle Scholar
Friedlander, J. B. and Iwaniec, H., Incomplete Kloosterman sums and a divisor problem, Ann. of Math. (2) 121 (1985), 319–350. With an appendix by Bryan J. Birch and Enrico Bombieri.CrossRefGoogle Scholar
Friedlander, J. and Iwaniec, H., Opera de cribro (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Gel'fond, A. O., Sur les nombres qui ont des propriétés additives et multiplicatives données, Acta Arith. 13 (1967–1968), 259–265.CrossRefGoogle Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., Primes in tuples. I, Ann. of Math. (2) 170 (2009), 819–862.CrossRefGoogle Scholar
Gowers, W. T., A new proof of Szemerédi's theorem for arithmetic progressions of length four, Geom. Funct. Anal. 8 (1998), 529–551.CrossRefGoogle Scholar
Gowers, W. T., A new proof of Szemerédi's theorem, Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Green, B. and Tao, T., The primes contain arbitrarily long arithmetic progressions, Ann. of Math. (2) 167 (2008), 481–547.CrossRefGoogle Scholar
Green, B. and Tao, T., An arithmetic regularity lemma, an associated counting lemma, and applications, in An irregular mind, Bolyai Society Mathematical Studies, vol. 21 (János Bolyai Mathematical Society, Budapest, 2010), 261–334.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, third edition (Clarendon Press, Oxford, 1954).Google Scholar
Kontorovich, A., Levels of distribution and the affine sieve, Ann. Fac. Sci. Toulouse Math. (6) 23 (2014), 933–966.CrossRefGoogle Scholar
Konieczny, J., Gowers norms for the Thue–Morse and Rudin–Shapiro sequences, Ann. Inst. Fourier (Grenoble) 69 (2019), 1897–1913.CrossRefGoogle Scholar
Martin, B., Mauduit, C. and Rivat, J., Théoréme des nombres premiers pour les fonctions digitales, Acta Arith. 165 (2014), 11–45.CrossRefGoogle Scholar
Mauduit, C., Multiplicative properties of the Thue–Morse sequence, Period. Math. Hungar. 43 (2001), 137–153.CrossRefGoogle Scholar
Mauduit, C. and Rivat, J., Répartition des fonctions $q$-multiplicatives dans la suite $([n^c])_{n\in {\boldsymbol N}}, c > 1$, Acta Arith. 71 (1995), 171–179.CrossRefGoogle Scholar
Mauduit, C. and Rivat, J., Propriétés $q$-multiplicatives de la suite $\lfloor n^c\rfloor$, $c>1$, Acta Arith. 118 (2005), 187–203.CrossRefGoogle Scholar
Mauduit, C. and Rivat, J., La somme des chiffres des carrés, Acta Math. 203 (2009), 107–148.CrossRefGoogle Scholar
Mauduit, C. and Rivat, J., Sur un problème de Gelfond: la somme des chiffres des nombres premiers, Ann. of Math. (2) 171 (2010), 1591–1646.CrossRefGoogle Scholar
Maynard, J., Small gaps between primes, Ann. of Math. (2) 181 (2015), 383–413.CrossRefGoogle Scholar
Morgenbesser, J. F., The sum of digits of $\lfloor n^c\rfloor$, Acta Arith. 148 (2011), 367–393.CrossRefGoogle Scholar
Morgenbesser, J. F., Shallit, J. and Stoll, T., Thue–Morse at multiples of an integer, J. Number Theory 131 (2011), 1498–1512.CrossRefGoogle Scholar
Moshe, Y., On the subword complexity of Thue–Morse polynomial extractions, Theoret. Comput. Sci. 389 (2007), 318–329.CrossRefGoogle Scholar
Müllner, C. and Spiegelhofer, L., Normality of the Thue–Morse sequence along Piatetski-Shapiro sequences, II, Israel J. Math. 220 (2017), 691–738.CrossRefGoogle Scholar
Piatetski-Shapiro, I. I., On the distribution of prime numbers in sequences of the form $[f(n)]$, Mat. Sb. 33 (1953), 559–566.Google Scholar
Rivat, J. and Sargos, P., Nombres premiers de la forme $\lfloor n^c\rfloor$, Canad. J. Math. 53 (2001), 414–433.CrossRefGoogle Scholar
Spiegelhofer, L., Piatetski-Shapiro sequences via Beatty sequences, Acta Arith. 166 (2014), 201–229.CrossRefGoogle Scholar
Spiegelhofer, L., Normality of the Thue–Morse sequence along Piatetski-Shapiro sequences, Q. J. Math. 66 (2015), 1127–1138.CrossRefGoogle Scholar
Tao, T., Higher order Fourier analysis, Graduate Studies in Mathematics, vol. 142 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Zhang, Y., Bounded gaps between primes, Ann. of Math. (2) 179 (2014), 1121–1174.CrossRefGoogle Scholar