Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T15:03:55.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Level-raising and symmetric power functoriality, I

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 March 2014

Laurent Clozel  and
Jack A. Thorne
Laurent Clozel
Affiliation:
Université Paris-Sud, 91405 Orsay Cedex, France email Laurent.Clozel@math.u-psud.fr
Jack A. Thorne
Affiliation:
Harvard University, Cambridge, MA 02138, USA email thorne@math.harvard.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

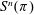As the simplest case of Langlands functoriality, one expects the existence of the symmetric power $S^n(\pi )$, where $\pi $ is an automorphic representation of 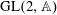${\rm GL}(2,{\mathbb{A}})$ and 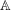${\mathbb{A}}$ denotes the adeles of a number field 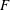$F$. This should be an automorphic representation of 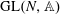${\rm GL}(N,{\mathbb{A}})$ (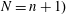$N=n+1)$. This is known for 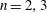$n=2,3$ and 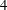$4$. In this paper we show how to deduce the general case from a recent result of J.T. on deformation theory for ‘Schur representations’, combined with expected results on level-raising, as well as another case (a particular tensor product) of Langlands functoriality. Our methods assume 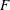$F$ totally real, and the initial representation $\pi $ of classical type.

Keywords

modular and automorphic functionsLanglands L-functionsGalois representations

MSC classification

Secondary: 11F03: Modular and automorphic functions 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 5 , May 2014 , pp. 729 - 748
Copyright
© The Author(s) 2014 

References

Arthur, J., A stable trace formula. III. Proof of the main theorems, Ann. of Math. (2) 158 (2003), 769–873.Google Scholar
Arthur, J. and Clozel, L., Simple algebras, base change, and the advanced theory of the trace formula, Annals of Mathematics Studies, vol. 120 (Princeton University Press, Princeton, NJ, 1989).Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., The Sato–Tate conjecture for Hilbert modular forms, J. Amer. Math. Soc. 24 (2011), 411–469.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609.Google Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.Google Scholar
Caraiani, A., Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161 (2012), 2311–2413.Google Scholar
Chenevier, G. and Harris, M., Construction of automorphic Galois representations II, Cambridge J. Math. 1 (2013), 53–73.Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181; with Appendix A summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.CrossRefGoogle Scholar
Clozel, L., Motifs et formes automorphes: applications du principe de fonctorialité, in Automorphic forms, Shimura varieties, and L-functions, Vol. I (Ann Arbor, MI, 1988), Perspectives in Mathematics, vol. 10 (Academic Press, Boston, 1990), 77–159.Google Scholar
Clozel, L., Identités de caractères en la place archimédienne, in On the stabilization of the trace formula, Stab. Trace Formula Shimura Var. Arith. Appl., vol. 1 (International Press, Somerville, MA, 2011), 351–367.Google Scholar
Clozel, L. and Thorne, J. A., Level raising and symmetric power functoriality, II, Preprint.Google Scholar
Dimitrov, M., Galois representations modulo p and cohomology of Hilbert modular varieties, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 505–551.Google Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350 (2011), 107–144.Google Scholar
Geraghty, D., Modularity lifting theorems for ordinary Galois representations, Preprint.Google Scholar
Gelbart, S. and Jacquet, H., A relation between automorphic representations of GL(2) and GL(3), Ann. Sci. Éc. Norm. Supér. (4) 11 (1978), 471–542.CrossRefGoogle Scholar
Gee, T. and Kisin, M., The Breuil–Mézard conjecture for potentially Barsotti–Tate representations, Preprint.Google Scholar
Guerberoff, L., Modularity lifting theorems for Galois representations of unitary type, Compositio Math. 147 (2011), 1022–1058.Google Scholar
Guralnick, R., Adequacy of representations of finite groups of Lie type, Preprint. Appendix to a paper by L. Dieulefait.Google Scholar
Henniart, G., Une caractérisation de la correspondance de Langlands locale pour GL(n), Bull. Soc. Math. France 130 (2002), 587–602.CrossRefGoogle Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001); With an appendix by Vladimir G. Berkovich.Google Scholar
Kim, H. H., Functoriality for the exterior square of GL4and the symmetric fourth of GL2, J. Amer. Math. Soc. 16 (2003), 139–183; (electronic), with appendix 1 by Dinakar Ramakrishnan and appendix 2 by Kim and Peter Sarnak.Google Scholar
Kim, H. H. and Shahidi, F., Functorial products for GL2×GL3and the symmetric cube for GL2, Ann. of Math. (2) 155 (2002), 837–893; with an appendix by Colin J. Bushnell and Guy Henniart.Google Scholar
Khare, C. and Wintenberger, J.-P., Serre’s modularity conjecture. I, Invent. Math. 178 (2009), 485–504.Google Scholar
Labesse, J.-P., Changement de base CM et séries discrètes, in On the stabilization of the trace formula, Stab. Trace Formula Shimura Var. Arith. Appl., vol. 1 (International Press, Somerville, MA, 2011), 429–470.Google Scholar
Langlands, R. P. and Shelstad, D., On the definition of transfer factors, Math. Ann. 278 (1987), 219–271.Google Scholar
Mínguez, A., Unramified representations of unitary groups, in On the stabilization of the trace formula, Stab. Trace Formula Shimura Var. Arith. Appl., vol. 1 (International Press, Somerville, MA, 2011), 389–410.Google Scholar
Mok, C. P., Endoscopic classification of representations of quasi-split unitary groups, Mem. Amer. Math. Soc., to appear.Google Scholar
Ramakrishnan, D., Modularity of the Rankin–Selberg L-series, and multiplicity one for SL(2), Ann. of Math. (2) 152 (2000), 45–111.Google Scholar
Ribet, K. A., Congruence relations between modular forms, in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984), 503–514.Google Scholar
Tate, J., Number theoretic background, in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 3–26.Google Scholar
Thorne, J. A., Automorphy lifting for residually reducible l-adic Galois representations, Preprint.Google Scholar
Thorne, J. A., Raising the level for $\mathrm{GL}_n$, Preprint.Google Scholar
Thorne, J. A., On the automorphy of l-adic Galois representations with small residual image, J. Inst. Math. Jussieu 11 (2012), 855–920; with an appendix by Robert Guralnick, Florian Herzig, Richard Taylor and Jack Thorne.Google Scholar
Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n), Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 165–210.Google Scholar